A normative blood velocity model in the exchange microvessels for discriminating health from disease: Healthy controls versus COVID-19 cases
Abstract
A usual practice in medicine is to search for “biomarkers” which are measurable quantities of a normal or abnormal biological process. Biomarkers can be biochemical or physical quantities of the body and although commonly used statistically in clinical settings, it is not usual for them to be connected to basic physiological models or equations. In this work, a normative blood velocity model framework for the exchange microvessels was introduced, combining the velocity-diffusion (V-J) equation and statistics, in order to define the normative range (NR) and normative area (NA) diagrams for discriminating normal (normemic) from abnormal (hyperemic or underemic) states, taking into account the microvessel diameter D. This is different from the usual statistical processing since there is a basis on the well-known physiological principle of the flow diffusion equation. The discriminative power of the average axial velocity model was successfully tested using a group of healthy individuals (Control Group) and a group of post COVID-19 patients (COVID-19 Group).
1Introduction
A usual practice in medicine is to search for “biomarkers” that are measurable characteristics of a normal or abnormal biological process or disease or pharmacological response. Biomarkers can be biochemical molecules found in body fluids (e.g. glucose, hemoglobin, low- density lipoprotein), or physical quantities of the body (e.g. blood pressure, temperature, vessel diameter, blood velocity). Nowroozpoor et al. [1] proposed the systemic nature of microvascular dysfunction by finding 16 biomarker molecules common in the microvascular disease of three vital organs: the brain, the heart, and the kidney. Sometimes, both biochemical molecules and physical variables are incorporated into an algorithm [2] for more effective sensitivity and accuracy in disease screening.
In a recent meta-analysis paper [3] a normative average axial blood velocity of 0.52 mm/s was proposed for healthy humans with an intention of examining the potential use of conjunctival microvascular hemodynamic parameters as biomarkers. In addition, disease-dependent change of axial velocity was demonstrated [3] but, with a lack of precision.
The diffusion rate J of small-size ions and molecules across the wall of the exchange microvessels depends on the blood flow Q, as it is described by the flow-diffusion (Q-J) equation [4]. Exchange microvessels are the smallest vessels of an organism, where material transport between the circulating blood and tissue takes place, comprising capillaries and postcapillary venules [5]. Recently, the Q-J equation was transformed to the velocity-diffusion (V-J) equation [6] with the axial blood velocity V as an independent variable which can be easily measured directly and noninvasively in humans by optical imaging techniques.
Although biomarkers are commonly used statistically in clinical settings, it is not usual to be connected to basic physiological models or equations. In this work, the V-J equation was used to define, a model framework for normal and abnormal average axial velocities in the exchange vessels of humans. In the context of this model, the normative range and area diagrams were introduced and the normative (normemic), hyperemic, and underemic ranges and areas were defined, taking into account the microvessel diameter D. The discriminative power of the model was then tested successfully, using the data from a group of healthy individuals (Control Group) and a group of post COVID-19 patients (COVID-19 Group).
2Methods
2.1The equilibrium state (ES) diagram for a single microvessel
The velocity-diffusion (V-J) equation [6] can be used to define a model-framework for normal and abnormal average axial velocities in the exchange microvessels of humans:
(1)
Where J is the mass diffusion rate of the solute (moles/s) through the walls of the exchange microvessel, V is the axial blood velocity inside the microvessel, κ is the velocity constant and SL is the slope parameter [6]. The slope SL depends on the difference between the solute concentration inside the vessel and the tissue interstitial fluid CI and CT, respectively, and on the microvessel and the erythrocyte diameter D and DC, respectively. The velocity constant κ depends on the permeability coefficient P of the solute substance through the vessel wall (cm/s), the microvessel length L, and on the microvessel and the erythrocyte diameter D and DC, respectively. For each solute-substance in the blood, the mass diffusion rate J depends on the axial blood velocity V in a nonlinear way as it is shown in Fig. 1. The solute can be any low molecular weight substance (nutrients or metabolic wastes).
Fig. 1
The equilibrium state (ES) diagram. The ES for a single microvessel is presented with a diagram derived from the “velocity-diffusion (V-J) equation” [6]. The independent variable V is the axial blood velocity inside the microvessel and J is the diffusion mass rate for each small molecular weight solute in the blood. Kappa (κ) is the velocity constant and PLV is the plateau value of J. At the equilibrium state the local metabolic demand is constant and so is the mass diffusion rate J for each substance. According to the V-J equation, it can be considered that the equilibrium mass diffusion rate (EJ) corresponds to an equilibrium axial blood velocity (EV). The equilibrium velocity (EV) at normal resting conditions, was taken here as equal to the velocity constant (κ). Axial velocities lower than the equilibrium velocity EV are inside the “underemic range” (UR) of velocities. Axial velocities higher than the equilibrium velocity EV are inside the “hyperemic range” (HR) ofvelocities.
![The equilibrium state (ES) diagram. The ES for a single microvessel is presented with a diagram derived from the “velocity-diffusion (V-J) equation” [6]. The independent variable V is the axial blood velocity inside the microvessel and J is the diffusion mass rate for each small molecular weight solute in the blood. Kappa (κ) is the velocity constant and PLV is the plateau value of J. At the equilibrium state the local metabolic demand is constant and so is the mass diffusion rate J for each substance. According to the V-J equation, it can be considered that the equilibrium mass diffusion rate (EJ) corresponds to an equilibrium axial blood velocity (EV). The equilibrium velocity (EV) at normal resting conditions, was taken here as equal to the velocity constant (κ). Axial velocities lower than the equilibrium velocity EV are inside the “underemic range” (UR) of velocities. Axial velocities higher than the equilibrium velocity EV are inside the “hyperemic range” (HR) ofvelocities.](https://content.iospress.com:443/media/ch/2023/84-2/ch-84-2-ch231780/ch-84-ch231780-g001.jpg)
For a specific microvessel in a specific tissue, diameter D, length L, average erythrocyte diameter DC, and average permeability coefficient P can be considered constant and thus κ can be considered constant. Assuming equilibrium at rest, CI and CT are also constant for each solute-substance in the blood of the microvessel, and thus the slope SL and the plateau value PLV are also constant [6]. At the equilibrium state the local metabolic demand is constant and so is the mass diffusion rate J for each substance. So, one can consider that an equilibrium mass diffusion rate (EJ) corresponds to an equilibrium axial blood velocity (EV), according to the V-J equation (Fig. 1).
In case the axial velocity drops below the EV, for any reason, we have a tissue situation around the microvessel, of nutrient under-supply and waste under-dispense. This situation can be defined as “underemia” and the corresponding low axial velocities define an “underemic range” UR (Fig. 1). In case the axial velocity is higher than the EV, we have a tissue situation around the microvessel, of nutrient over-supply and waste over-dispense. This situation can be defined as “hyperemia” and the corresponding high axial velocities define a “hyperemic range” HR (Fig. 1).
2.2The normative average axial velocity range (NR) diagram for many microvessels with the same diameter from many subjects
In microvascular hemodynamic studies, it is usual practice to measure velocities at different microvessels. Hemodynamically the most important parameter is the diameter so, microvessels with approximately the same diameter were considered. Even with the same diameter, the equilibrium velocities (EVs) are not going to be exactly the same for all microvessels, due to variations in the concentration differences, permeability coefficients, and microvessel lengths.
The assumption here is that the equilibrium velocities, for all the different microvessels with the same diameter and of the same tissue, examined at a specific microscopic area, will not be much different (Fig. 2). Under this assumption a normative range (NR) for average axial velocity could be defined, instead of a single equilibrium value, as it is shown at the normative average axial velocity range (NR) diagram of Fig. 3. The “normative range” refers to all equilibrium velocities of the microvessels with the same diameter, determined statistically from measurements at many healthy individuals.
Fig. 2
The velocity-diffusion (V-J) curves for 3 different microvessels with the same diameters. EV1, EV2 and EV3 are equilibrium axial blood velocities of microvessel 1, 2, and 3, respectively. EJ1, EJ2 and EJ3 are equilibrium mass diffusion rates of microvessel 1, 2, and 3, respectively.
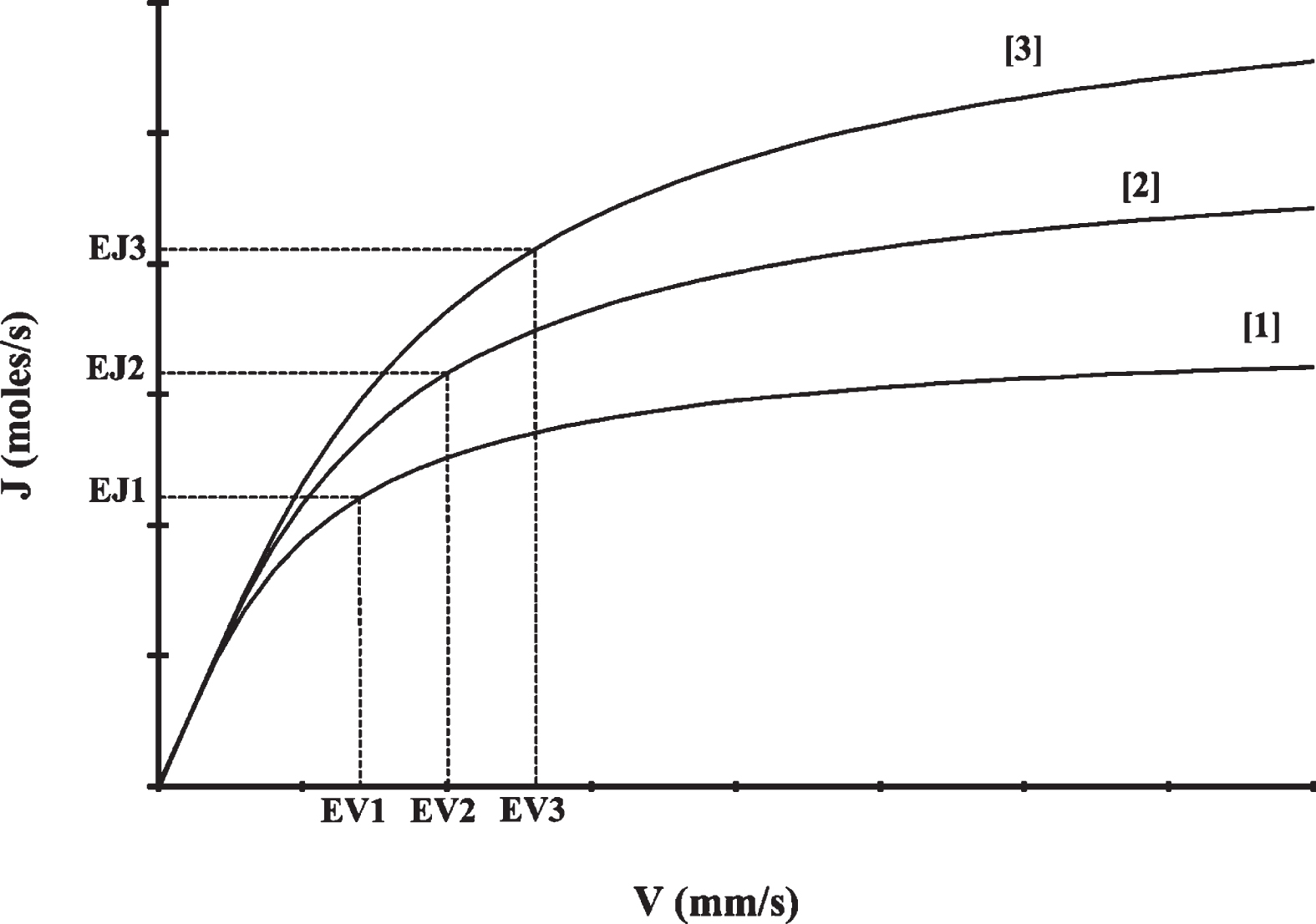
Fig. 3
The normative range (NR) diagram. After measuring axial velocities at many microvessels with the same diameter, an average axial velocity (AV) can be estimated statistically which corresponds to an average mass diffusion rate (AJ). After measuring axial velocities at many persons, a normative range (NR) can be determined statistically comprising average axial velocity values of normal, equilibrium resting conditions. UR stands for “Underemic Range” and is the range of average axial velocities corresponding to underemic conditions. HR stands for “Hyperemic Range” and is the range of average axial velocities corresponding to hyperemic conditions.
When the average axial velocity of many microvessels with the same diameter is lower than the NR, there is a local tissue situation of under-supply that can be defined as “underemia”, and when the average axial velocity is higher than the NR, there is a local tissue situation of over-supply that can be defined as “hyperemia”. Average axial velocities lower than the NR are inside the “underemic average range” (UR) and average axial velocities higher than the NR are inside the “hyperemic average range” (HR) of velocities (Fig. 3).
The persistent situation of average velocities in the UR or the HR could be considered to be a biomarker of an out of equilibrium, abnormal, or disease local tissue state. For example, very low average velocities in the UR could lead to severe hypoxia and/or thrombosis and local tissue death.
2.3The normative average axial velocity area (NA) diagram for many diameters from many subjects
In the most general case, at a given human tissue, there are axial velocity measurements from many different microvessel diameters. In this case, the effect of diameter has to be taken into account and many normative average axial velocity ranges (NRs) corresponding to many different diameters should be estimated.
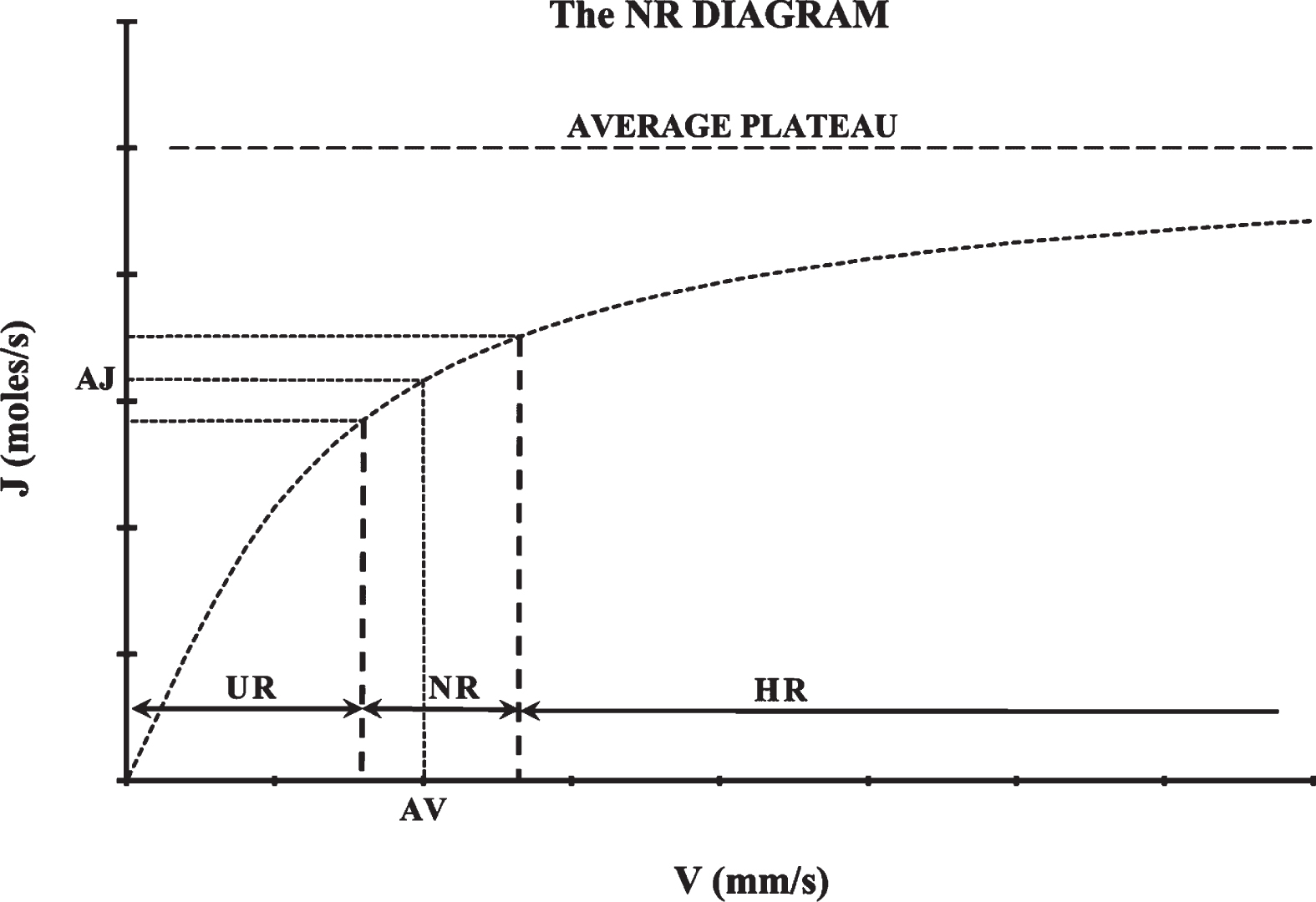
However, this could also be done by estimating the confidence interval of the regression line between axial velocity (V) and diameter (D). In this way, a 2-D normative area can be defined with a normative average axial velocity area (NA) diagram (Fig. 4). In this diagram there are 3 areas: the “normative” (or “normemic”) area (NA), the “hyperemic” area (HA), and the “underemic” area (UA). The persistent situation of average velocities in the underemic or hyperemic areas could be considered as biomarker of an out-of-the-equilibrium, abnormal or diseased local tissue state.
Fig. 4
The normative area (NA) diagram. The NR, UR, and HR described in the previous figure (Fig. 3), are shown here, for the case of D = 21μm. Instead of calculating the NR for each diameter separately, the confidence interval of the V-D trendline can be used to define a “normative average axial velocity area” or “normative area” (NA) in short. The normative (or normemic) area (NA) is shown here between the two dashed lines. Velocities below the normative area are inside the “underemic area” (UA) of the diagram and velocities above the normative area are inside the “hyperemic area” (HA) of the diagram.
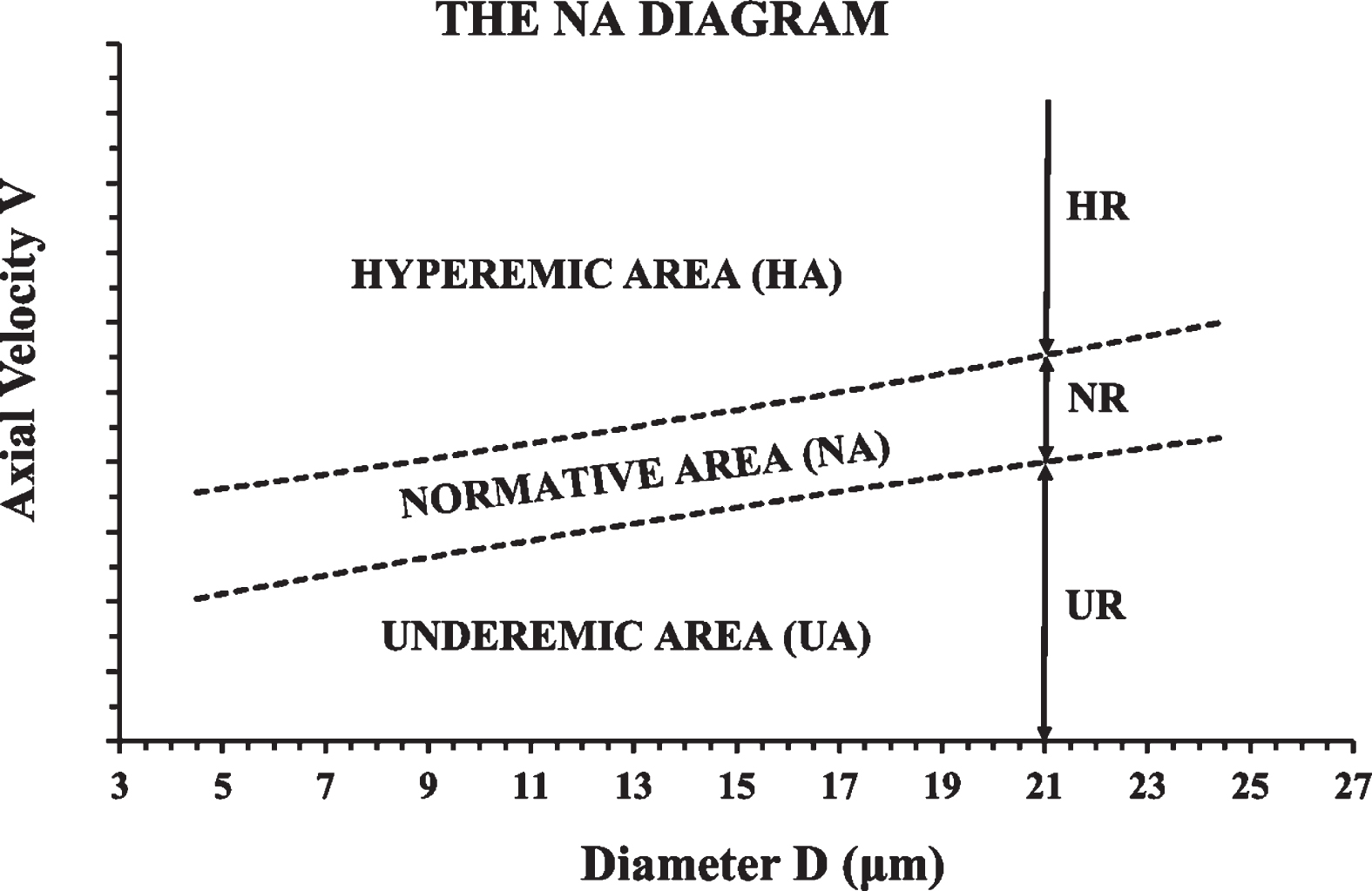
2.4Subjects and test of concept
For testing the concept of the normative model diagrams, in-vivo measurements at human conjunctival diameters between 4 and 24μm (capillaries and postcapillary venules), from the temporal side of the right eyes, from a previous work [7], were considered. In short, data from a “Control Group” (17 healthy volunteers) were used to define the normemic area in the NA diagram and data from a “COVID-19 Group” (17 COVID-19 survivors shortly after hospital exit) were used to check if the COVID-19 average trendline was inside or outside the NA.
The age for all 34 persons of both groups ranged between 39 and 68 years. Demographic clinical data, including age, body mass index (BMI), body surface area (BSA, Du Bois formula), cardiac beats per minute (BPM), and mean arterial pressure (MP), for both groups were not statistically different. Subjects with diastolic blood pressure greater than 95 mmHg were excluded from the study (both groups) as hypertensive. All normal volunteers of the Control Group had no systemic or ocular disease, no alcohol or smoking habit, were not under any medication, and had never tested positive for SARS-CoV-2. All measurements were performed in a temperature- controlled environment (21 to 23°C) after waiting for a predetermined time interval foradaptation.
2.5Experimental set up and measurement procedure
The experimental setup consisted of a slit lamp (Nikon FS-3V) connected with a high-speed CCD camera (12 bit, PCO Computer Optics GmbH, Germany) and a PC (Pentium 4, 3 GHz). The system produced digital images of 320×240 pixels at a frame rate of 96 frames per second (fps) with an enhanced maximum magnification of 242× and a digital resolution of 1.257±0.004μm/pixel. The internal diameter (D) was estimated from the coordinates of the intersection points between a vertical line to the vessel axis and the outer limits of the erythrocyte column. Axial erythrocyte velocity (V) was measured using the axial distance traveled by a RBC or a plasma gap, over a fixed time interval Δt. Velocities lower than 0.1 mm/s were discarded [7, 8].
2.6Statistical analysis
The Microsoft Office EXCEL 2016 (professional edition) and the SOFA (version 1.4, Paton-Simpson & Associates Ltd) software were used for statistics. Pearson coefficient (R) was used for measuring the strength of the correlation between D and V. The level of significance was set at p < 0.05. The 95% confidence interval of the linear regression line [9] between D and V was used for determining the normemic area in the NA diagram.
3Results
195 axial velocity measurements of the Control Group are shown in Fig. 5 in relation to microvessel diameter. The correlation was statistically significant (p < 0.001), positive, and of moderate strength (0.4 < R≤0.6). The 95% confidence interval of the linear regression line is presented with 2 black dashed lines and sets the normemic area in the NA diagram.
Fig. 5
Axial velocity measurements of the Control Group in relation to microvessel diameter. The correlation was statistically significant (p < 0.001) and the 95% confidence interval of the linear regression line is presented with 2 black dashed lines. The 95% confidence interval sets the normative area in the normative area (NA) diagram. An average axial velocity of many measurements at the same diameter, outside the NA, can be considered to be a biomarker of an abnormal state.

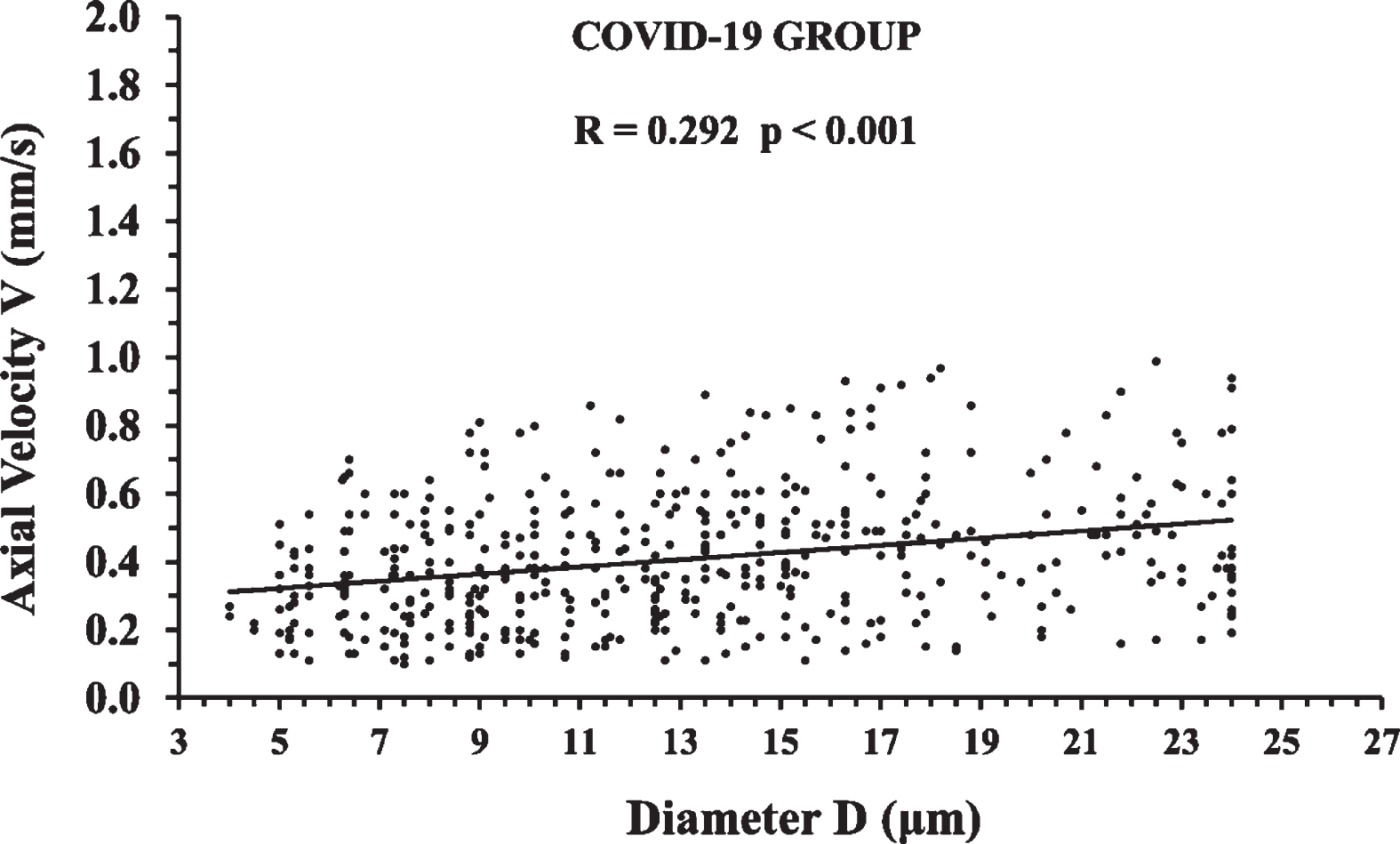
488 axial velocity measurements of the COVID-19 Group are shown in Fig. 6 in relation to microvessel diameter. The positive correlation was weak (0.2 < R≤0.4) but statistically significant (p < 0.001).
Fig. 6
Axial velocity measurements of the COVID-19 Group in relation to microvessel diameter. The correlation was statistically significant (p < 0.001) and the linear regression line is shown with a solid black line.
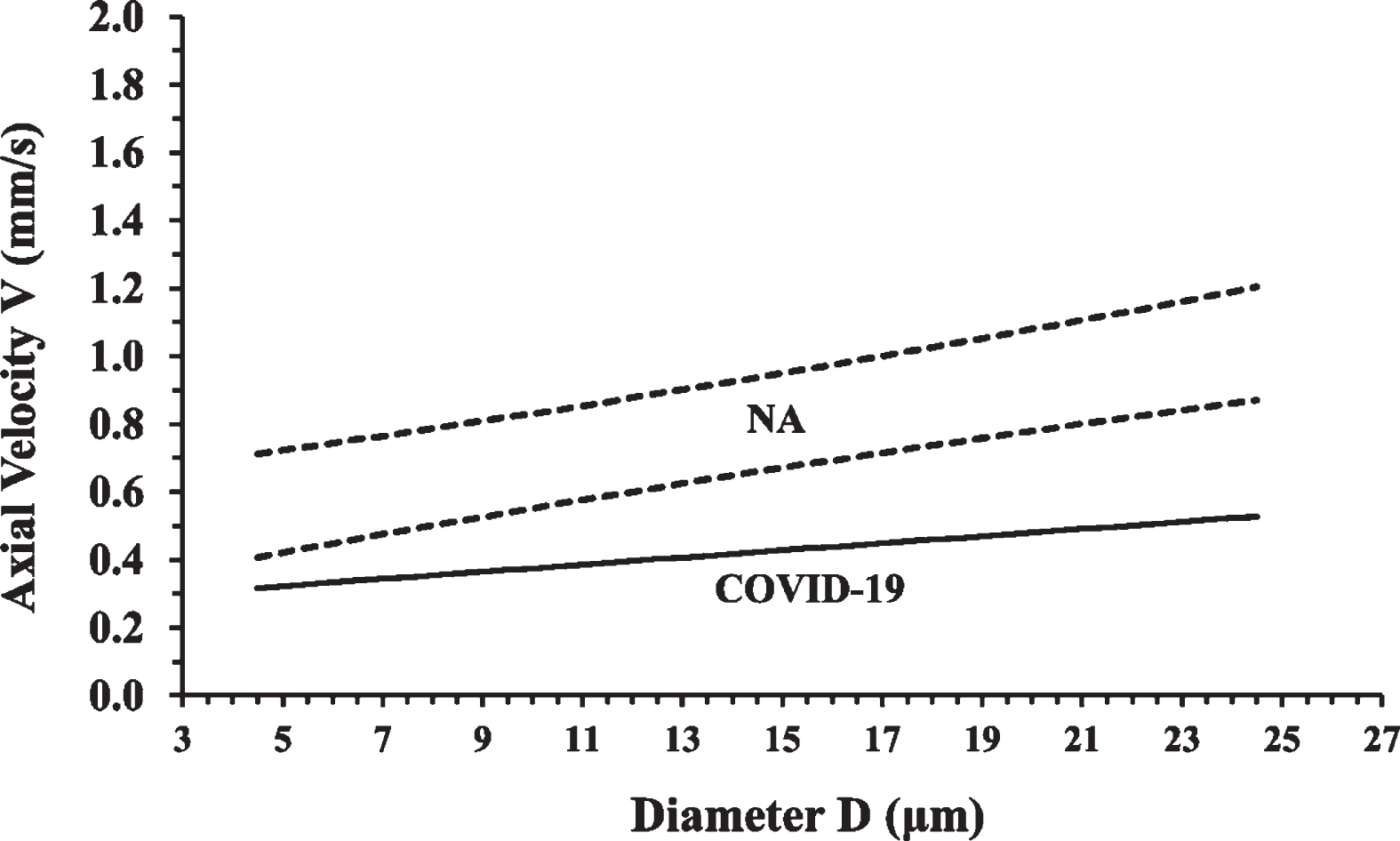
The COVID-19 Group linear trendline is clearly outside the Control Group normemic area as it is shown in Fig. 7. According to the proposed NA diagram model, the COVID-19 Group average velocities are located inside the underemic area and this can be considered to be a biomarker of a COVID-19 disease state.
Fig. 7
The normative area (NA) diagram is shown together with the COVID-19 Group linear trendline. Each point of the COVID-19 trendline represents the average axial velocity at the corresponding diameter. It is clear that the COVID-19 trendline is under the normemic area (NA) and inside the underemic area (UA) of the NA diagram.
4Discussion
In this work, a normative blood velocity model framework for the exchange microvessels was introduced, combining the velocity-diffusion (V-J) equation and statistics, in order to define the normative range (NR) and the normative area (NA) diagrams for discriminating normal from abnormal states. This is different from the usual statistical processing since there is a basis on the well-known physiological principle of the flow diffusion equation. On surplus, the NA diagram takes into account the statistically significant correlation of axial blood velocity to microvessel diameter. In a successful proof of concept for the potential use of average axial velocity as a disease biomarker, a group of post COVID-19 patients (COVID-19 Group) was discriminated from a group of healthy individuals (Control Group).
In a recent meta-analysis paper [3] on human conjunctival velocity metrics, a normative average axial velocity (V) of 0.52±0.03 mm/s (CI: 0.47–0.58) was proposed. However, there was no discrimination between the arteriolar and the venular side and the dependence of velocity on diameter was not taken into account.
In this context, the present work aims at improving the available methodological tools, having the following advantages.
First, V measurements were focused on the exchange microvessels (capillaries and postcapillary venules), eliminating the noise effect from measurements on the arteriolar side due to the blood velocity pulsation [10–13].
Second, the effect of diameter on V was taken into account by the NA diagram since the linear positive correlation between V and D was found to be statistically significant (p < 0.001). This result is in accordance with many previous reports [14–18]. The value of 0.52 mm/s proposed by the meta-analysis of Patel et al. [3] is inside the normative area of Fig. 7, but only for diameters up to 9μm.
Third, V measurements were taken from venular diameters lower than 35–45μm. At higher diameters, it is doubtful if axial velocity measurements can be performed accurately [8].
Fourth, a lower axial velocity limit was set at 0.1 mm/s [8].
Fifth, the effect of age on velocity was taken into account and the normative area of the NA diagram was determined in healthy humans (Control Group) of a particular age group, i.e. between 39 and 68 years of age.
Sixth, the NA diagram is specific for a given species, tissue, age group, and imaging setup. In contrast to other optical techniques [19], optical imaging is specific to a particular tissue. In humans, known windows to observe the exchange microvessels non-invasively in specific tissues, are the eye conjunctiva and retina, the tongue (with contact), and the finger nailfold (with contact). Consequently, a specific NA diagram would be required for each tissue.
Seventh, a number of measurements at a small diametric range would show if the average axial velocity lies inside the NA. For example, the average velocity value of 0.39 mm/s [7] for conjunctival diameters between 9 and 14μm of post COVID-19 patients is clearly outside the NA of Fig. 7. So, the average velocity at a small diametric range, at a given tissue of a subject, could be a biomarker.
It would be interesting to see if the normative velocity model framework could be applied to other abnormal cases, for detecting either underemia or hyperemia:
A] Regarding the human conjunctival tissue [20], velocity alterations have been reported from induced hyperperfusion [21], hypertension [22], sickle cell disease with and without pulmonary hypertension [14, 23], contact lens wear [15], sickle cell nephropathy [24], stroke [25], diabetic microvasculopathy [18], normal pregnancy [26], cyanotic congenital heart disease [27], myocardial infarction [28], and COVID-19 [7]. In an initial approach, it seems that most abnormal cardiovascular states are related to lower average axial velocities in the conjunctival exchange microvessels. This could be attributed to the slower nutrient supply and waste removal implied by the velocity-diffusion equation. This argument is supported by the work of Karanam et al. [29] where a negative correlation between cardiovascular risk (Framingham risk score) and conjunctival axial velocity was found: lower axial velocities corresponded to higher cardiovascular risk. In addition, it seems that the increased metabolic requirements of normal pregnancy are related to higher axial velocities in the conjunctival capillaries of pregnant women [26] even though the conjunctival tissue is not directly related to the fetus. The reported capillary average axial velocity of 0.95 mm/s in the third trimester of pregnancy [26] is clearly in the hyperemic area (HA) of the Fig. 5 diagram even though the control group of this work is not age and sex-matched to the pregnant women of Moka et al. [26].
B] Regarding the human retinal tissue, blood flow velocity measurements with high resolution digital video fluorescein angiography were reported in the capillaries of diabetic patients [30] and healthy subjects [31]. Arend et al. [30] suggested that perifoveal capillary velocity was found much higher than conjunctival capillary velocity because of the higher metabolic rate of the retinal tissue, which is in agreement with the velocity-diffusion (V-J) equation. Furthermore, the retinal capillary blood velocity in diabetic patients was found significantly reduced in comparison to normal subjects [30], which is in accordance with a later report from the conjunctiva [18] and the V-J equation. Another technology for retinal hemodynamics is adaptive optics. From the original reports on leukocyte [32] and erythrocyte [33] velocity measurements, without contrast dye, there was important progress in the last 20 years. In the meantime, there was tremendous growth in optical coherence tomography angiography [34]. With all the above technologies, there is hope for absolute axial velocity quantification in the human retina, one of the most interesting and valuable human tissues. However, there are some difficulties associated with the eye fundus [34].
C] Regarding the human sublingual tissue, velocity alterations have been reported from sickle cell disease [35], general anesthesia [36], COVID-19 [37, 38], sepsis [39, 40], cirrhosis [41], and cardiac displacement during off-pump coronary artery bypass (OPCAB) surgery [42]. In the sublingual tissue, some researchers measured velocities of the order of 0.1 mm/s [38, 39] and other researchers measured velocities of the order of 1.2 mm/s [37, 41]. There is a more than tenfold difference among these reports which is a matter of further investigation in light of the present study. Wang et al. [43] found sublingual blood flow increase in septic shock patients after receiving hydrocortisone combined with vitamin C and vitamin B1. Wagner et al. [44] reported a significant increase in sublingual microvascular flow in children undergoing major abdominal and thoracic surgery before the end of anesthesia.
D] Regarding the human nailfold tissue, velocity alterations have been reported from normal tension glaucoma [45], local cooling [46], diabetes mellitus [47–49], hypothyroidism [50], pregnancy-induced hypertension [51], systemic sclerosis [52, 53], acrocyanosis [54], primary Raynaud’s phenomenon [53, 54], and peripheral arterial occlusive disease [55].
In conclusion, a normative blood velocity model for the exchange microvessels was introduced, using a combination of the velocity-diffusion (V-J) equation and statistics, for discriminating normal from abnormal tissue perfusion states. Using this model, a group of post COVID-19 patients (COVID-19 Group) was clearly discriminated from a group of healthy individuals (Control Group), giving evidence for the potential use of average axial velocity as a disease biomarker.
Conflict of interest
The authors have declared no conflicts of interest.
Funding
No specific funding was received from any funding bodies in the public, commercial or not for-profit sectors to carry out the work described in this manuscript.
References
[1] | Nowroozpoor A , Gutterman D , Safdar B . Is microvascular dysfunction a systemic disorder with common biomarkers found in the heart, brain, and kidneys? - A scoping review, Microvasc Res.23. (2021) ;134: :104123. doi: 10.1016/j.mvr.2020.104123. |
[2] | Awuah A , Moore JS , Nesbit MA , Ruddock MW , Brennan PF , Mailey JA , McNeil AJ , Jing M , Finlay DD , Trucco E , Kurth MJ , Watt J , Lamont JV , Fitzgerald P , Spence MS , McLaughlin JAD , Moore TCB . A novel algorithm for cardiovascular screening using conjunctival microcirculatory parameters and blood biomarkers, Sci Re12. (2022) 12: (1) 6545. doi: 10.1038/s41598-022-10491-7. |
[3] | Patel NR , Duong S , Mirbod P , Xu J , Gaynes BI . A meta-analysis of variability in conjunctival microvascular hemorheology metrics, Microvasc Res.40. (2022) ;142: :104340. doi: 10.1016/j.mvr.2022.104340. |
[4] | Renkin EM.B.W . Zweifach award lecture: Regulation of the microcirculation, Microvasc Res. (1985) ;30: (3):251–63. doi: 10.1016/0026-2862(85)90057-3. |
[5] | Koutsiaris AG , Tachmitzi SV , Batis N , Kotoula MG , Karabatsas CH , Tsironi E , Chatzoulis DZ . Volume flow and wall shear stress quantification in the human conjunctival capillaries and post-capillary venules in vivo , Biorheology. (2017) ;44: (5-6):375–86 PMID: 18401076. |
[6] | Koutsiaris AG The velocity-diffusion equation in the exchange microvessels. Clin Hemorheol Microcirc. 2023; In Press. doi: 10.3233/CH-231713. |
[7] | Koutsiaris AG , Riri K , Boutlas S , Panagiotou TN , Kotoula M , Daniil Z , Tsironi EE . COVID-19 hemodynamic and thrombotic effect on the eye microcirculation after hospitalization: A quantitative case-control study, Clin Hemorheol Microcirc. (2022) ;82: (4):379–90. doi: 10.3233/CH-221554. |
[8] | Koutsiaris AG . Meta-analysis of conjunctival microvascular hemorheology metrics, Microvasc Res. (2022) ;142: :104369. doi: 10.1016/j.mvr.2022.104369. |
[9] | Altman DG , Machin D , Bryant TN , Gardner MJ Statistics with confidence. 2nd Edition, BMJ Books; (2000) . |
[10] | Nagaoka T , Yoshida A . Noninvasive evaluation of wall shear stress on retinal microcirculation in humans, Invest Ophthalmol Vis Sci.-9. (2006) ;47: (3):1113–9. doi: 10.1167/iovs.05-0218. |
[11] | Koutsiaris AG , Tachmitzi SV , Papavasileiou P , Batis N , Kotoula MG , Giannoukas AD , Tsironi E . Blood velocity pulse quantification in the human conjunctival pre-capillary arterioles, Microvasc Res. (2010) ;80: (2):202–8. doi: 10.1016/j.mvr.2010.05.001. |
[12] | Koutsiaris AG . The resistive index as a function of vessel diameter in the human carotid arterial tree, Microvasc Res. (2013) ;89: :169–71. doi: 10.1016/j.mvr.2013.06.005. |
[13] | Koutsiaris AG . Pulsatility Index quantification in the human precapillary arterioles of the eye, Microvasc Res.36-8. (2016) ;106: :36–8. doi: 10.1016/j.mvr.2016.03.008. |
[14] | Wanek J , Gaynes B , Lim JI , Molokie R , Shahidi M . Human bulbar conjunctival hemodynamics in hemoglobin SS and SC disease, Am J Hematol. (2013) ;88: (8):661–4. doi: 10.1002/ajh.23475. |
[15] | Jiang H , Zhong J , DeBuc DC , Tao A , Xu Z , Lam BL , Liu C , Wang J . Functional slit lamp biomicroscopy for imaging bulbar conjunctival microvasculature in contact lens wearers, Microvasc. Res. (2014) ;92: :62–71. doi: 10.1016/j.mvr.2014.01.005. |
[16] | Koutsiaris AG . Correlation of axial blood velocity to venular and arteriolar diameter in the human eye in vivo, Clin. Hemorheol. Microcirc. (2015) ; 429–438. doi: 10.3233/CH-141888. |
[17] | Wang L , Yuan J , Jiang H , Yan W , Cintrón-Colón HR , Perez VL , DeBuc DC , Feuer WJ , Wang J . Vessel sampling and blood flow velocity distribution with vessel diameter for characterizing the human bulbar conjunctival microvasculature, Eye Contact Lens.. (2016) ;42: (2):135–40. doi: 10.1097/ICL.0000000000000146. |
[18] | Khansari MM , Wanek J , Tan M , Joslin CE , Kresovich JK , Camardo N , Blair NP , Shahidi M . Assessment of Conjunctival Microvascular Hemodynamics in Stages of Diabetic Microvasculopathy, Sci Re6. (2017) ;7: :45916. doi: 10.1038/srep45916. |
[19] | Koutsiaris AG . Deep tissue near infrared second derivative spectrophotometry for the assessment of claudication in peripheral arterial disease, Clin Hemorheol Microcirc. (2017) ;65: (3):275–84. doi: 10.3233/CH-16181. |
[20] | Sun Z , Li Y , Liu R , Ma B , Zhou Y , Duan H , Bian L , Li W , Qi H Progress of bulbar conjunctival microcirculation alterations in the diagnosis of ocular diseases. Dis Markers. 2022;4046809. doi: 10.1155/2022/4046809. |
[21] | Jung F , Körber N , Kiesewetter H , Prünte C , Wolf S , Reim M . Measuring the microcirculation in the human conjunctiva bulbi under normal and hyperperfusion conditions, Graefes Arch Clin Exp Ophthalmol. (1983) ;220: (6):294–7. doi: 10.1007/BF00231359. |
[22] | Körber N , Jung F , Kiesewetter H , Wolf S , Prünte C , Reim M . Microcirculation in the conjunctival capillaries of healthy and hypertensive patients, Klin Wochenschr. (1986) ;64: (19):953–5. |
[23] | Kord Valeshabad A , Wanek J , Molokie RE , Machado RF , Gordeuk VR , Shahidi M . Conjunctival and pulmonary hemodynamic properties in sickle cell disease subjects with and without pulmonary hypertension, Clin Case Re-41. (2015) ;3: (12):1038–41. doi: 10.1002/ccr3.439. |
[24] | Kord Valeshabad A , Wanek J , Saraf SL , Gaynes BI , Gordeuk VR , Molokie RE , Shahidi M . Changes in conjunctival hemodynamics predict albuminuria in sickle cell nephropathy, Am J Nephrol. (2015) ;41: (6):487–93. doi: 10.1159/000438678. |
[25] | Kord Valeshabad A , Wanek J , Mukarram F , Zelkha R , Testai FD , Shahidi M . Feasibility of assessment of conjunctival microvascular hemodynamics in unilateral ischemic stroke, Microvasc Res. (2015) ;100: :4–8. doi: 10.1016/j.mvr.2015.04.007. |
[26] | Moka S , Koutsiaris AG , Garas A , Messinis I , Tachmitzi SV , Giannoukas A , Tsironi EE . Blood flow velocity comparison in the eye capillaries and postcapillary venules between normal pregnant and non-pregnant women, Microvasc Res. (2020) ;127: :103926. doi: 10.1016/j.mvr.2019.103926. |
[27] | Brennan PF , Jing M , McNeil AJ , Awuah A , Mailey J , Kelly B , Finlay DD , Blighe K , McLaughlin JAD , Nesbit MA , Trucco E , Lockhart CJ , Moore TCB , Spence MS . Assessment of the conjunctival microcirculation in adult patients with cyanotic congenital heart disease compared to healthy controls, Microvasc Res. (2021) ;136: :104167. doi: 10.1016/j.mvr.2021.104167. |
[28] | Brennan PF , McNeil AJ , Jing M , Awuah A , Moore JS , Mailey J , Finlay DD , Blighe K , McLaughlin JAD , Nesbit MA , Trucco E , Moore TCB , Spence MS . Assessment of the conjunctival microcirculation for patients presenting with acute myocardial infarction compared to healthy controls, Sci Re. (2021) ;11: (1):7660. doi: 10.1038/s41598-021-87315-7. |
[29] | Karanam VC , Tamariz L , Batawi H , Wang J , Galor A . Functional slit lamp biomicroscopy metrics correlate with cardiovascular risk, Ocul Surf.64-69. (2019) ;17: (1):64–69. doi: 10.1016/j.jtos.2018.09.002. |
[30] | Arend O , Wolf S , Jung F , Bertram B , Pöstgens H , Toonen H , Reim M . Retinal microcirculation in patients with diabetes mellitus: Dynamic and morphological analysis of perifoveal capillary network, Br J Ophthalmol. (1991) ;75: (9):514–8. doi: 10.1136/bjo.75.9.514. |
[31] | Wolf S , Arend O , Reim M . Measurement of retinal hemodynamics with scanning laser ophthalmoscopy: Reference values and variation, Surv Ophthalmol. (1994) ;38: (Suppl):S95–100. doi: 10.1016/0039-6257(94)90052-3. |
[32] | Martin JA , Roorda A . Direct and noninvasive assessment of parafoveal capillary leukocyte velocity, Ophthalmology.-24. (2005) ;112: (12):2219–24. doi: 10.1016/j.ophtha.2005.06.033. |
[33] | Zhong Z , Petrig BL , Qi X , Burns SA . In vivo measurement of erythrocyte velocity and retinal blood flow using adaptive optics scanning laser ophthalmoscopy, Opt Express.6-56. (2008) ;16: (17):6–56. doi: 10.1364/oe.16.012746. |
[34] | Koutsiaris AG , Batis V , Liakopoulou G , Tachmitzi SV , Detorakis ET , Tsironi EE Optical Coherence Tomography Angiography (OCTA) of the eye: A review on basic principles, advantages, disadvantages and device specifications. Clin Hemorheol Microcirc. 2022; In Print. doi: 10.3233/CH-221634. |
[35] | Sant S , Gouraud E , Boisson C , Nader E , Goparaju M , Cannas G , Gauthier A , Joly P , Renoux C , Merazga S , Hautier C , Connes P , Fenech M . Sublingual microcirculation specificity of sickle cell patients: Morphology of the microvascular bed, blood rheology, and local hemodynamics, Int J Mol Sci. (2023) ;24: (4):3621.. doi: 10.3390/ijms24043621. |
[36] | Flick M , Schreiber TH , Montomoli J , Krause L , de Boer HD , Kouz K , Scheeren TWL , Ince C , Hilty MP , Saugel B . Microcirculatory tissue perfusion during general anaesthesia and noncardiac surgery: An observational study using incident dark field imaging with automated video analysis, Eur J Anaesthesiol. (2022) ;39: (7):582–90. doi: 10.1097/EJA.0000000000001699. |
[37] | Kanoore Edul VS , Caminos Eguillor JF , Ferrara G , Estenssoro E , Siles DSP , Cesio CE , Dubin A . Microcirculation alterations in severe COVID-19 pneumonia, J Crit Care. (2021) ;61: :73–5. doi: 10.1016/j.jcrc.2020.10.002. |
[38] | Rovas A , Osiaevi I , Buscher K , Sackarnd J , Tepasse PR , Fobker M , Kühn J , Braune S , Göbel U , Thölking G , Gröschel A , Pavenstädt H , Vink H , Kümpers P . Microvascular dysfunction in COVID- The MYSTIC study, Angiogenesis. (2021) ;24: (1):145–57. doi: 10.1007/s10456-020-09753-7. |
[39] | Rovas A , Sackarnd J , Rossaint J , Kampmeier S , Pavenstädt H , Vink H , Kümpers P . Identification of novel sublingual parameters to analyze and diagnose microvascular dysfunction in sepsis: The NOSTRADAMUS study, Crit Care.112. (2021) ;25: (1):112. doi: 10.1186/s13054-021-03520-w. |
[40] | Dubin A , Kanoore Edul VS , Caminos Eguillor JF , Ferrara G . Monitoring microcirculation: Utility and barriers - a point-of-view review, Vasc Health Risk Manag. (2020) ;16: :577–89. doi: 10.2147/VHRM.S242635. |
[41] | Gonzalez Ballerga E , Pozo MO , Rubatto Birri PN , Kanoore Edul VS , Sorda JA , Daruich J , Dubin A . Sublingual microcirculatory alterations in cirrhotic patients, Microcirculation. (2018) ;25: (4):e12448.. doi: 10.1111/micc.12448. |
[42] | Atasever B , Boer C , Speekenbrink R , Seyffert J , Goedhart P , de Mol B , Ince C . Cardiac displacement during off-pump coronary artery bypass grafting surgery: Effect on sublingual microcirculation and cerebral oxygenation, Interact Cardiovasc Thorac Surg. (2011) ;13: (6):573–7. doi: 10.1510/icvts.2011.272047. |
[43] | Wang J , Song Q , Yang S , Wang H , Meng S , Huang L , Li Q , Xu J , Xie J , Huang Y Effects of hydrocortisone combined with vitamin C and vitamin B1 versus hydrocortisone alone on microcirculation in septic shock patients: A pilot study. Clin Hemorheol Microcirc. 2023; In Print. doi: 10.3233/CH-221444. |
[44] | Wagner M , Anzinger E , Hey F , Reiter K , Wermelt JZ , Pastor-Villaescusa B , Genzel-Boroviczény O , Nussbaum C Monitoring of the microcirculation in children undergoing major abdominal and thoracic surgery: A pilot study. Clin Hemorheol Microcirc. 2022; In Print. doi: 10.3233/CH-221617. |
[45] | Gasser P , Flammer J . Blood-cell velocity in the nailfold capillaries of patients with normal-tension and high-tension glaucoma, Am J Ophthalmol. (1991) ;111: (5) 1991: 585–8. doi: 10.1016/s0002-9394(14)73703-1. |
[46] | Gasser P . Video-nailfold-microscopy and local cold test: Morphological and hemodynamic correlates in 124 healthy subjects, Vasa. (1991) ;20: (3):244–51. |
[47] | Kiesewetter H , Jung F , Körber N , Wolf S , Kiehl R , Frank M , Reim M , Sitzmann FC , Weinges KF . Microcirculation and hemorheology of children with type I diabetes, Klin Wochenschr. (1986) ;64: (19):962–8. |
[48] | Jörneskog G , Brismar K , Fagrell B . Skin capillary circulation severely impaired in toes of patients with IDDM, with and without late diabetic complications, Diabetologia. (1995) ;38: (4):474–802. doi: 10.1007/BF00410286. |
[49] | Chang CH , Tsai RK , Wu WC , Kuo SL , Yu HS . Use of dynamic capillaroscopy for studying cutaneous microcirculation in patients with diabetes mellitus, Microvasc Res. (1997) ;53: (2):121–7. doi: 10.1006/mvre.1996.2003. |
[50] | Pazos-Moura CC , Moura EG , Breitenbach MM , Bouskela E . Nailfold capillaroscopy in hypothyroidism and hyperthyroidism: Blood flow velocity during rest and postocclusive reactive hyperemia, Angiology. (1998) ;49: (6):471–6. doi: 10.1177/000331979804900608. |
[51] | Ohlmann P , Jung F , Mrowietz C , Alt T , Alt S , Schmidt W . Peripheral microcirculation during pregnancy and in women with pregnancy induced hypertension, Clin Hemorheol Microcirc. (2001) ;24: (3):183–91. |
[52] | Mugii N , Hasegawa M , Hamaguchi Y , Tanaka C , Kaji K , Komura K , Ueda-Hayakawa I , Horie S , Ikuta M , Tachino K , Ogawa F , Sato S , Fujimoto M , Takehara K . Reduced red blood cell velocity in nail-fold capillaries as a sensitive and specific indicator of microcirculation injury in systemic sclerosis, Rheumatology (Oxford). (2009) ;48: (6):696–703. doi: 10.1093/rheumatology/kep066. |
[53] | Berks M , Dinsdale G , Murray A , Moore T , Manning J , Taylor C , Herrick AL . Automated structure and flow measurement - a promising tool in nailfold capillaroscopy, Microvasc Res. (2018) ;118: :173–7. doi: 10.1016/j.mvr.2018.03.016. |
[54] | Bollinger A , Mahler F , Meier B . Velocity patterns in nailfold capillaries of normal subjects and patients with Raynaud’s disease and acrocyanosis, Bibl Anat. (16 Pt 2). (1977) ; 142–5. |
[55] | Mrowietz C , Sievers H , Pindur G , Hiebl B , Jung F . Cutaneous microcirculation in patients with peripheral arterial occlusive disease: Comparison of capillary blood circulation in the nail fold of finger and toe, Clin Hemorheol Microcirc. (2020) ;76: (2):279–85. doi: 10.3233/CH-209220. |




