Where Do CABs Exist? Verification of a specific region containing concave Actin Bundles (CABs) in a 3-Dimensional confocal image

1Introduction

Jones et al. [1] investigated the in vitro interaction of both mature endothelial cells (ECs) and of less differentiated EC colony-forming cells to poly-ɛ-capro-lactone (PCL) fibers with diameters in 5-20μm range (scaffold micro-fibers (SMFs)). This range of diameters of fibers is within cell-size range.

In their experiment, the researchers found that ECs wrap the SMFs completely, forming a cylindrical morphology. They further investigated the distribution of F-actin microfilaments in scaffold-wrapping ECs, to determine their circumferential extension. Figure 1 (a)-(b) shows cells incubated for a longer time with SMFs. They reported the full circumferential continuity of F-actin structures by unwrapping the image in Fig. 1 (c), which is shown as a ring-like pattern occasionally crossing the nuclei.

Fig. 1

Visualization of circular gripping of SMFs by F-actin in the human umbilical vein ECs (HUVECs) (Reproduced from [1]). (a)-(c) visualized F-actin in the HUVECS. (a) An original confocal image in 2D projection. A SMF portion containing F-actin bands of interest is marked by a yellow rectangle; (b) An enlarged image of the yellow rectangle in (a); (c) Left shows a vertically oriented image projection of (b). For comparison, we unwrapped the cylinder distribution of F-action to visualize full-circle continuity of F-actin around the SMF (right). Fig (d)-(f) are examples of F-actin rings in the interaction between a cell and a scaffold(s). (d) Full-wrapping of a fiber at the cell’s extremities (yellow line) by F-action bundles. The white scale is around 10μm; (e) F-actin in a SMF-attached cell. It contains AGs (arrowhead), an actin ruffle-like structure (arrow), and a blob with abundant actin (dashed arrow); (f) A cell is laid over three intertwining SMFs. The concentration of AGs is greater at all extremities than at the interior of the cell(arrowhead).

The median portion of cells often displayed only partial F-actin arcs, which are named “concave actin bundles” (CABs). In serial optical sections, CABs were found to co-exist with fully-wrapped F-actin bands, that were preferentially located towards cell margins (Fig. 1 (c)-(d)). CABs were either shorter than a half-circle and oriented obliquely to the axis of SMFs (Fig. 1 (d)), or longer than a semicircle and showing a more transversal positioning (Fig. 1 (e)), a grading that suggests their progression towards full circles. Where CABs represent full circles, they are named “actin grips” (AGs). Thus, AGs are special cases of CABs.

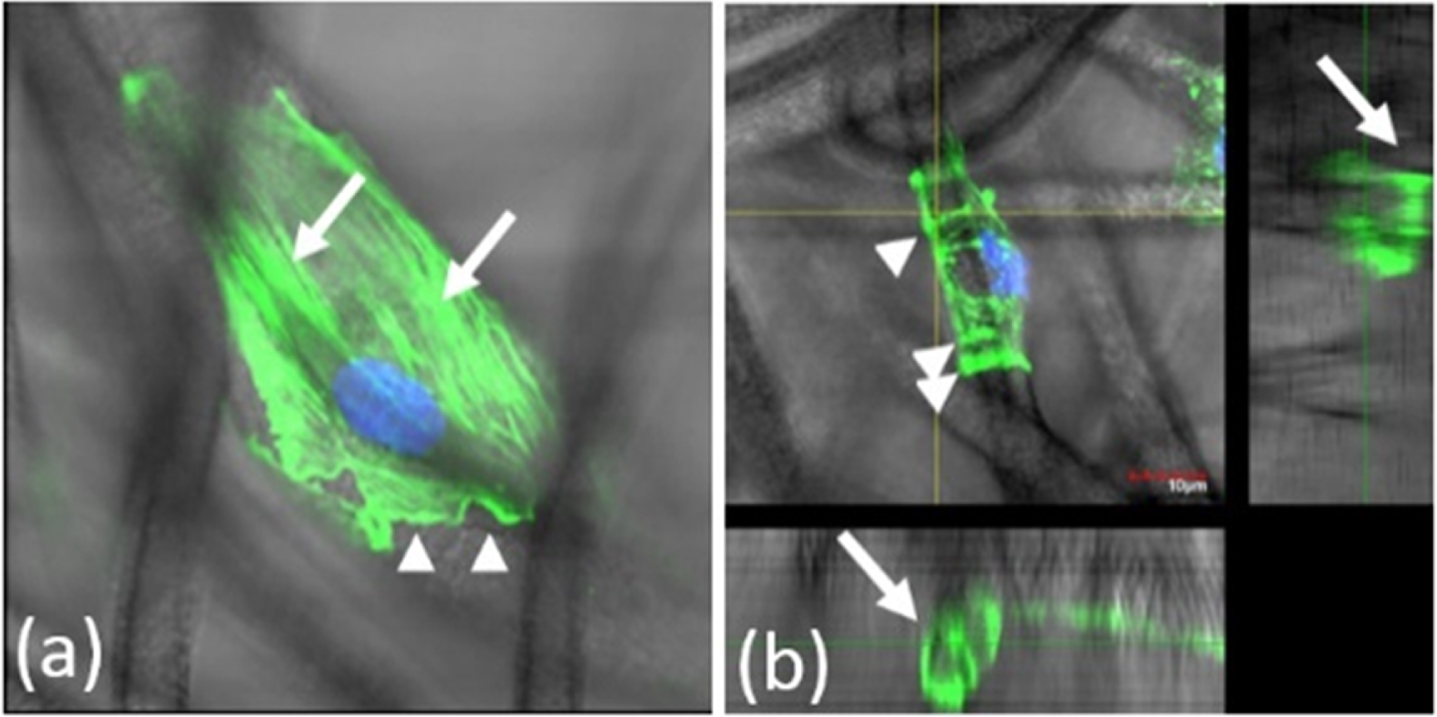
This wrapping is performed by adopting a cylindrical morphology, accompanied by the progressive reorganization of F-actin filaments in a ring-like pattern. This is a newly found type of organization of F-actin filaments mediating cell-matrix interactions. Thus, in the cells that intimately engaged individual SMFs, F-actin was distributed not only as classical stress fibers longitudinally aligned with the scaffold, but also as transversal rings, in a proportion that increased with the time in culture. Figure 2 shows these two types of organization of F-actin filaments. CABs (or AGs) are conspicuous F-actin bundles oriented transversally to scaffold’s fibers as shown in Fig. 2 (b) which is different from Fig. 2 (a).

Fig. 2

F-actin organization in cell-scaffold interaction. (a) An image of longitudinally aligned stress fibers (arrows). The arrowheads indicate F-actin containing ruffles. (b). A cross-sectional image of a supporting fiber. Concave actin bundles (CABs) (arrow) grip the fiber in a circular fashion. Green indicates F-actin. Blue indicates the nuclei.

Unlike stress fibers, CABs (or AGs) showed no co-localization with focal adhesions, or intermediate filaments. The grip formation depends on scaffold fiber diameter, with an optimum diameter around 10μm. Confocal and live-cell images showed that more grips were formed in cells which remained in culture longer, and that these cells were also less motile.

CABs helps understand how ECs solve their topological problem, when (literally) facing an unusual environment, and could also illuminate their behaviour in corresponding situations in vivo.

CABs are more dynamic structures than stress fibers. CABs also do not co-localize with the actin filaments oriented alongside the scaffold. Based on these observations, it was determined that CABs may contribute to the maintenance of an elongated endothelial morphology on the fibrillar support even in the absence of a FA-mediated adhesion, and that their dissolution may lead to cell shape modifications. These facts imply that CABs may supply (or replace) cells’ need for direct adherence, required for survival [2]. Further, CABs suggest a constrictive capacity, a function reserved only for cytokinesis furrows in ECs, and to the peri-vascular contractile cells (e.g. pericytes) [1].

Thus, CABs have multiple possible applications in tissue engineering, such as the stabilization of EC interaction with the scaffolds used as cell carriers, immuno-isolation of fibrillar scaffolds to mitigate their foreign body reaction, control of post-implantation immune responses, or controlling the differentiation of ECs via substrate-driven gene expression [1].

CABs are believed to exist for cell’s direct adherence to fibers, which provides to the attached cell essential mechanical properties. Thus, it seems that CABs exist around cells. However, we want to verity this fact, so that we may scrutinize an existential question: Where do CABs exist?

By closely probing 322 regions (which might contain a CAB) extracted by our previous algorithms described in [3] from 11 confocal image volumes (containing fiber scaffold, actin, and cells), we made a hypothesis of CABs’ existence: CABs exist largely in the area of high compactness of fibers, high compactness of actin, and high density of cells. In a confocal image volume, fibers were stained in red, actin in green, and cell in blue. We defined a fiber as a set of templates in our previous algorithms [3].

We calculated the density of fibers in the number of templates in a candidate CAB region. We calculated the density of actin as the number of green pixels in a CAB candidate region. Regarding cells, we segmented cells using the algorithm described in [4] and counted the number of pixels in the segmented cells. In the above hypothesis of CAB’s existence, if the number of templates, the number of green pixels, and the number of pixels in detected cells were above the experimental thresholds in a CAB candidate region in a confocal image volume, we defined the cases as ‘high’

If an area that has many numbers of fibers and those fibers cross each other intricately, the area has a high value of compactness of fibers. Similarly, if an area is widely and closely distributed with actin, the area has high value of compactness of actin. In addition, if an area contains many numbers of cells or large-sized cells or both, the area has Sa high value of intensity of cells.

For the purpose of proving the above hypothesis, we define a compactness measure. Using this compactness measure, we can estimate the compactness of a fiber network, and the compactness of the actin distribution in an area. The compactness measure is built on a two-point correlation function (TPCF) [5]. TPCF is the probability of both endpoints of a line segment landing in the same constituents (i.e. fibers, actin, cells, and back ground black space) of a 2D or 3D image space when a line segment of random length and orientation is placed in that image space (for details, see the Sections 4.1.1–4.1.3). Because our confocal microscopy image is in a 3-dimensional (3D) space, the line segment will be thrown into the 3D space.

Next, we calculate a probability according to the compactness of a fiber network, and the probability according to the compactness of actin distributions. We also calculate the probability distribution according to cell density. These probabilities are applied to the Bayes theorem, so that we can prove the hypothesis by comparing posterior probability to priori probability.

2Results (or proof)

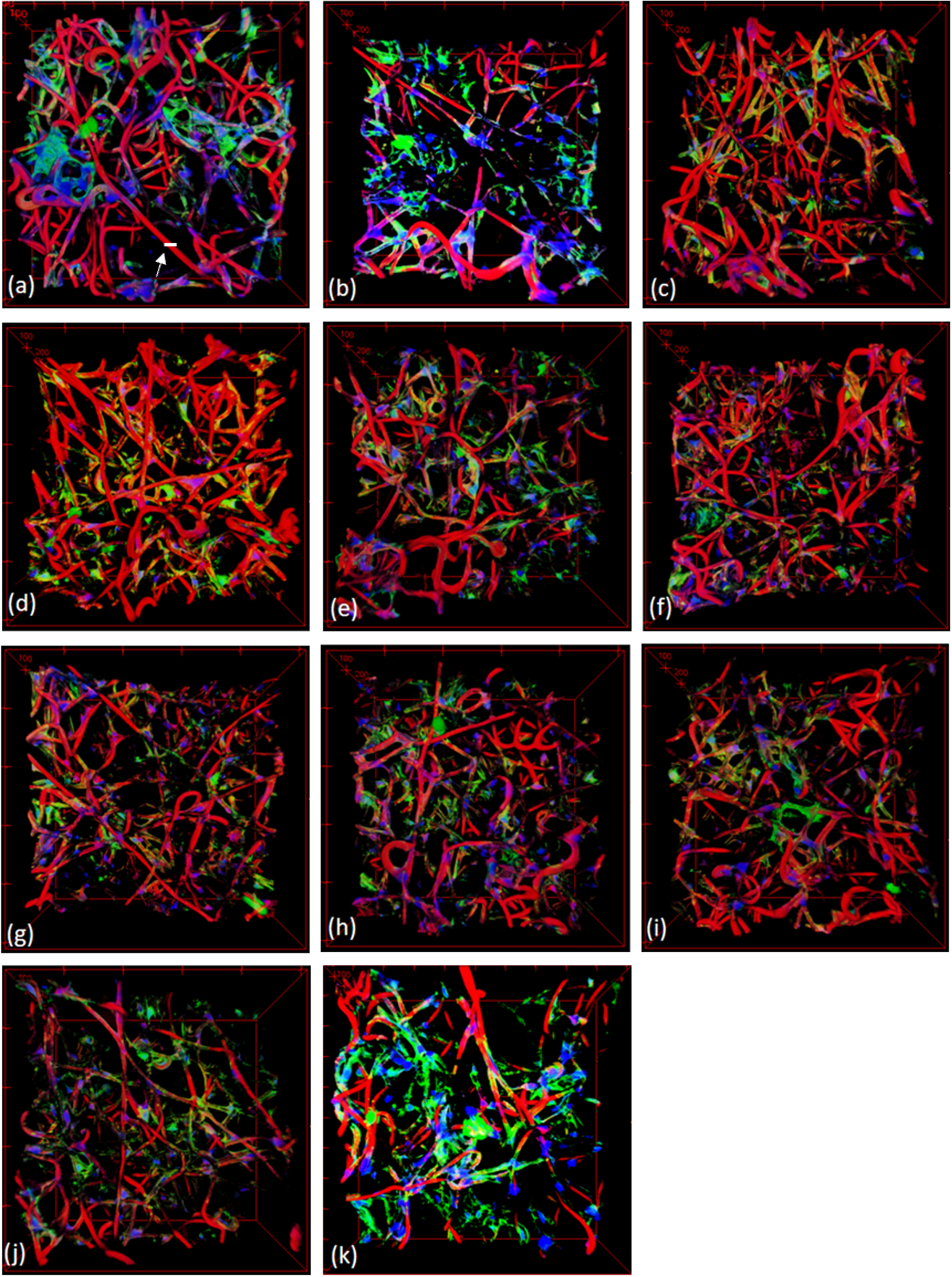
For the experiment, we have used 11 image volumes. We used a confocal microscope to obtain their original image volumes. Each voxel size of the 3D images was 1μm in the x-axis resolution, 1μm in the y-axis resolution, and 1.45μm in the z-axis resolution. The original image volumes were resampled so that the size of each voxel has the same resolution, but the number of the slices of an 3D image volume were adjusted so that it maintains the original image characteristics. The number of image slices in a 3D image volume was adjusted by multiplying the division of the z-resolution by the x-resolution to the original number of image slices for the purpose of image computation. Then, they were filtered with a Gaussian el to be resilient to noises. The volume visualized in Fig. 3(a) is of size 512×512×200, and that in Fig. 3(b) is of 512×512×322. For other cases shown in Fig. 3 (c)-(k), they were in a range between 200 and 350 in z-direction.

Fig. 3

3D confocal microscope images used for the experiment; the white scale bar designated by a white arrow in (a) is around 10μm.

After locating the upper left corner of a ω × ω × ω local widow Φ at the center of each template over all fibers in all 11 images, we calculated TPCF S2i(r) (describe in Equation 6 in the Method section) of a fiber network in the red phase, TPCF S2i(r) of an actin distribution in the green phase, and the density of cells in the blue phase in that local window Φ. The density of cells was calculated by counting the number of voxels belonging to detected cells using the algorithm in [4] in the local window Φ.

Based on the calculated S2i(r) distribution according to the distance r, we next calculated the compactness of a fiber network, and the compactness of an actin distribution in the local widow Φ according to the Equation 7 in the Method section. We also have the information about whether a template contains a CAB or not with the method described in [15]. Thus, we have the following information for a local window Φ located at each template: the compactness of a fiber network, the compactness of an actin distribution, the density of cells, and whether the template is a CAB. We collected the information over all templates of all extracted fibers from the 11 image volumes in Fig. 3 using the ‘Algorithm for Calculating Probability Distribution of Compactness and Density’ described in Section 4.4.

Figure 4 (a) shows the probability distribution of a fiber network compactness. Similarly, Fig. 4(b) is the probability distribution of actin compactness. Figure 4 (c) shows the probability distribution of cell density. In these probability distributions, the distribution over all templates (without considering if a template contains a CAB or not) in all 11 images is that in red. The distribution over templates containing CABs is in blue.

Fig. 4

Probability distributions. (a) The probability distribution of fiber network compactness; (b) the probability distribution of an actin distribution compactness; (c) the probability distribution of cell density. In these probability distributions, the distribution over all templates (without considering if a template contains a CAB or nor) is in red. The distribution over templates containing CABs is in blue.

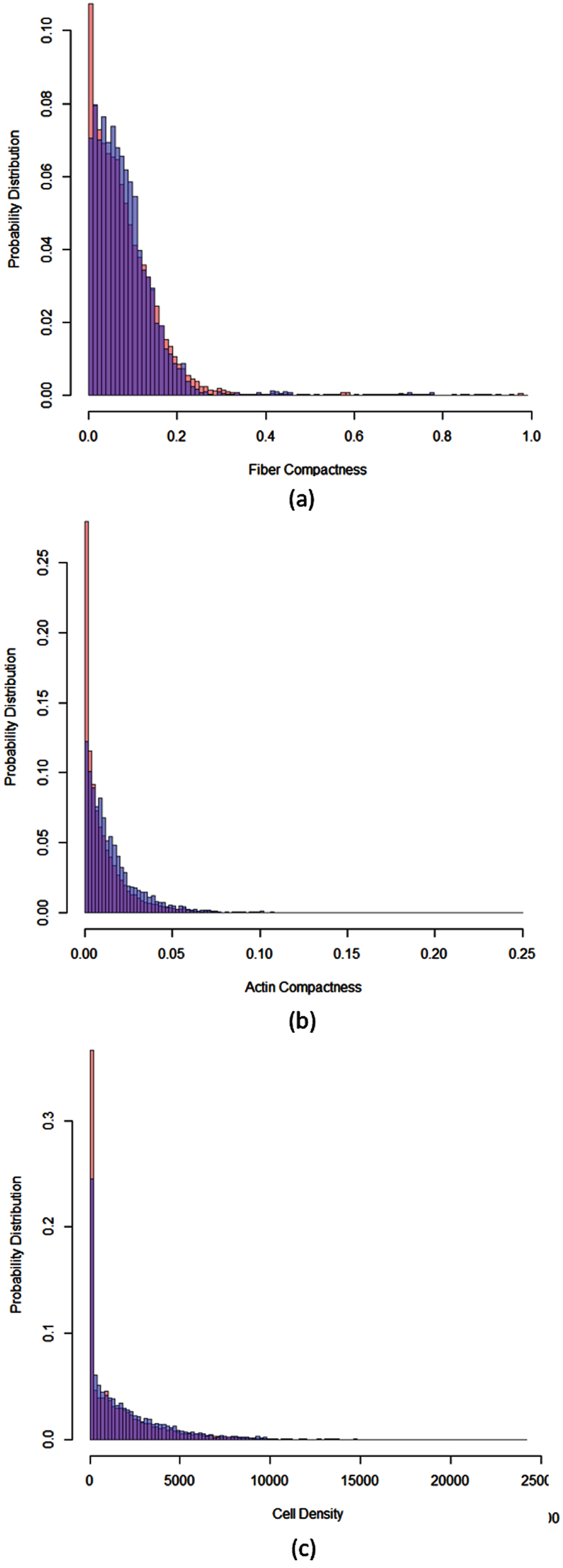
In Fig. 4 (a), the distribution in red represents P(f) and the distribution in blue represents P(f|CAB) . The distribution in red represents P(a) and the distribution in blue is P(a|CAB) in Fig. 4 (b). Similarly, the distribution in red represents P(c) and the distribution in blue is P(c|CAB) in Fig. 4 (c).

In Fig. 4, the blue distribution covers the red distribution. This indicates that P(f|CAB)>P(f) , P(a|CAB)>P(a) , and P(c|CAB)>P(c) respectively.

Therefore, we conclude that P(CAB|f,a,c)>P(CAP) . This conclusion verifies the hypothesis of CAB’s existence in (H.1) mentioned in the Method section.

3Conclusion

In this research, we hypothesized that CABs would exist largely in the area with a high compactness of fibers, high compactness of actin, and high density of cells. For this purpose, we developed a compactness measure based on a two-point correlation function (TPCF). Next, we calculated the probability distribution of the compactness of a fiber network, the probability distribution of the compactness of an actin distribution, and the probability distribution of the density of cells in a local window. We then incorporated the famous Bayes theorem to those probability distributions. Finally, we verified the CAB’s existence with these processes.

We also proposed a local parameter that refers to the compactness of a local fiber network. Although the parameter is extensible over a whole fiber network in an image and its value is comparable to the value calculated from any other fiber network (i.e, which fiber network is more compact than the other), the parameter has a drawback to represent other statistical and topological meanings (e.g, centrality, clustering, of nodes in the graph representation of a fiber network). Thus, we plan to develop such a statistical and topological network parameter and then assess the statistical significance of the difference in comparison. We plan to develop a network parameter that contains more statistical and topological information and examine if this parameter brings meaningful improvements compared to the parameter used in this research through a statistical testing.

In the present study, we verified which type of regions contains CABs. We are still trying to explore why CABs exist in specific areas. Biologically, it seems that CABs are developed to attach cells to a fibrillar scaffold firmly. This biological observation needs to be verified mathematically as well.

4Method

4.1Two-point correlation function in 3-dimensional space

4.1.1Phase image

An image is composed of a certain number of discrete constituents. For example, 3-dimensional confocal microscopy image in Fig. 3 consists of 4 discrete constituents (i.e, fibers, actin, cells, and background black space). Each constituent defines a unique phase. Thus, the image in Fig. 3 has 4 phases. In this vein, we defined a phase image as a collection of discrete constituents. In other words, a phase image is partitioned into a certain number of disjointed phases. If a phase image I is composed of n phases from P_l to P_n, then ⋃i=1nPi=I and ⋂i=1nPi=∅ .

For each phase P_i, we define an indicator function for x=(x,y,z)∈ℝ3 in I.

(1)

I(i)(x)={1,x∈Pi0else,

4.1.2N-point Correlation Function (NPCF)

Suppose we have n points in a phase image I : x₁, x₂, …, x_n. NPCF is defined as the probability that n points at positions x₁, x₂, …, x_n land in the same phase P_i. It is the expectation of the product I⁽ⁱ⁾ (x₁) I⁽ⁱ⁾ (x₂) ⋯ I⁽ⁱ⁾ (x_n). Therefore, NPCF Sn(i) is expressed as follows: size9.511

(2)

Sn(i)(x1,x2,…,xn)≡E{I(i)(x1)I(i)(x2)⋯I(i)(xn)}=P{I(i)(x1)I(i)(x2)=1,⋯,I(i)(xn)=1}

4.1.2Two-point Correlation Function (TPCF)

As a specific case of the NPCF, the TPCF is defined as the probability that two points x₁, x₂ are in the phase i. Therefore, TPCF S2(i) is expressed as follows:

(3)

S2(i)(x1,x2)≡E{I(i)(x1)I(i)(x2)}=P{I(i)(x1)=1,I(i)(x2)=1},

If S2(i) is invariant under translation of a phase image, the phase image is statistically homogeneous. In this case, S2(i) is subject to x₁₂ = x₁ - x₂ rather than absolute locations: x₁, x₂. If S2(i) is invariant under rigid-body rotation of the spatial coordinates of a phase image, the phase image is therefore homogeneous but isotropic. In this case, S2(i) is subject only to the distance r =∣ x₁₂ ∣.

Thus, in the case where a phase image is statistically homogenous and isotropic, TPCF Sx(i)(x1,x2) can be represented with S2(i) .

S2(i) is used to calculate the probability that, if we throw a needle of length r in a phase image, both ends of the needle will land in the same phase.

4.1.33D TPCF calculation

Kishore et al. [17] implemented a 2D version of TPCF for the segmentation with a 2D image. We extended it to a 3D version. A few modifications are required to implement 3D TPCF.

Given an L × M × N 3-dimensional phase image I, two-point correlation function S2(i) for a phase i are calculated from the indicator autocorrelation:

(4)

R(i)(Δx,Δy,Δz)=∑l∑m∑nI(i)(l,m,n)I(i)(l+Δx,m+Δy,n+Δz)

where Δx, Δy and Δz are integers. The equation (4) is the correlation between the phase image I and the shifted image by Δx, Δy and Δz from the image I.

Let’s define r=Δx2+Δy2+Δz2 .

R⁽ⁱ⁾ is normalized by an L × M × N matrix of ones in order to get probabilities Rˆ(i) :

(5)

Rˆ(i)=R(i),I(1L×M×N*1L×M×N)

where./ is an element-wise division, and * is convolution.

In order to get a homogeneous and isotropic TPCF, we need to sample circumferentially at a distance r from Rˆ(i)(0,0) . This process gives us S2(i)(r) from S2(i)(r) . The expression of S2(i)(r) is defined as:

(6)

S2(i)(r)=ΔφπΔθ2π∑k1=02πΔθ-1∑k2=π2π2+πΔφ-1Rˆ(i)(rcos(k1Δθ)sin(k2Δφ),rsin(k1Δθ)sin(k2Δφ),rcos(k2Δφ))

where Δθ and Δφ are the angular intervals.

4.1.4Example of TPCF distribution

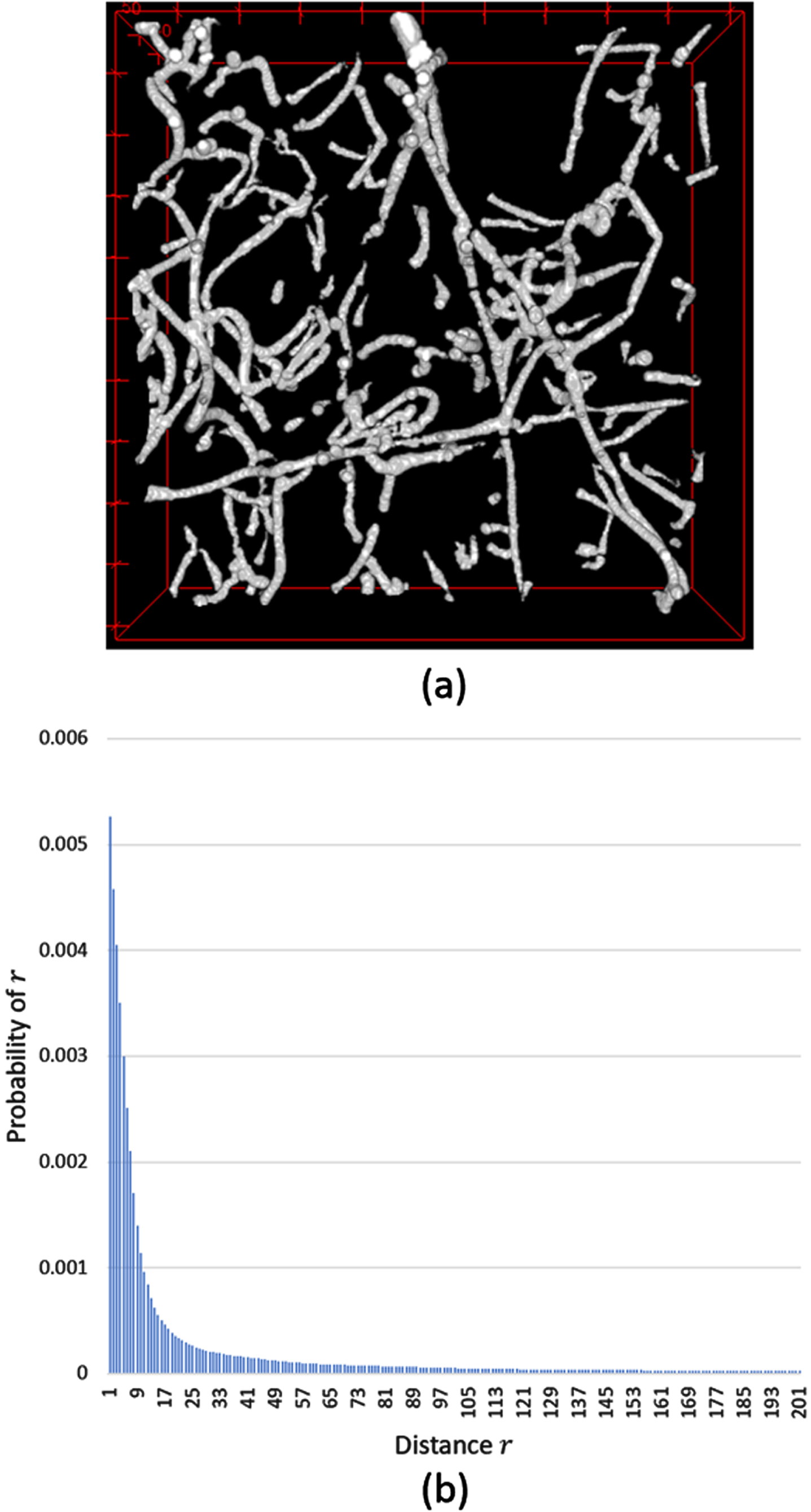
An example of the TPCF distribution according to the distance r is shown in Fig. 5 (b) for white area (a fiber network) in Fig. 5 (a). This distribution is calculated under the condition that, if we throw a needle of length r in the image Fig. 5 (a), both ends of the needle should be in that image space (that is, the needle cannot land outside the image). The distribution is the general shape of any fiber network (that is, it follows that the similar shape of poisson distribution has the shape parameter λ = 1).

Fig. 5

An example of the distribution of a two-point correlation function (TPCF) (a) The 3-dimensional image contains two phases (white phase: a fiber network, black phase: background). (b) The probability distribution of TPCF calculated from the image in (a).