Measurement of process capability indices for lower and upper tolerance with fuzzy parameters

1Introduction

Process capability indices are numerical instruments that measure how effectively a process can adhere to technical tolerances, client needs, and specifications. Lower and upper specification limits, LSL and USL, as well as a target value T that falls within these limits, make up a tolerance interval for a product feature X. If the target value and the midpoint of the specification limits coincide, a process is said to have a symmetric tolerance. But there are enough instances for the goal value to not be the midpoint of the tolerance limits. The tolerance range in these circumstances is referred to as asymmetric. The new class of indices for the process with asymmetric tolerance for crisp SLs was introduced by [1].

[2] analyzed PCIs based on different process features and then present a new class of capability indices to handle processes with asymmetric tolerances. Process yield, process centering, and process characteristics linked to loss functions are compared between the proposed new indices and the current PCIs. The findings show that the new indices outperform the pre-existing capability indices and offer more accuracy in the current applications using PCIs to gauge process potential and performance. Asymmetric tolerance PCIs have been created and effectively used to solve these issues. PCIs are very useful statistics, however, due to the clear definitions of the specification limits (SLs), mean, and variance, they have several restrictions that prohibit a thorough and flexible study. The fuzzy set theory is applied in this situation to enhance the flexibility and information of PCIs with asymmetric tolerances. It was concluded that when compared to the crisp scenario, fuzzy estimations of PCIs with asymmetric tolerances provide more information and flexibility to assess the process performance. Fuzzy formulations of the most often used PCIs with asymmetric tolerances and a real-life case study from an automobile manufacturer were presented and compared to crisp estimations of PCIs with asymmetric tolerances. It was concluded that fuzzy estimations of PCIs with asymmetric tolerances provided more information and flexibility for evaluating process performance [3]. A literature review on fuzzy process capability indices (FPCIs) for PCA was presented [4]. This study aims to give a thorough evaluation of publications that deal with FPCIs. These studies have been examined based on some of their characteristics, including the year, document type, journal name, and nation. In this work, classifications for FPCI, application area, fuzzy parameters, and type of fuzzy sets have also been presented. There have also been some statistical analyses performed. They wanted to showcase the most recent developments in FPCI research and offer a road map for researchers in this area. The primary goal is to highlight potential future areas for fuzzy PCA research. [5] proposed a fuzzy form of loss-based process capability indices L_e and L_e ^″ to overcome uncertainty. These include L˜e and its generation L˜″e . They measured both indices using fuzzy data. The comparative study of both fuzzy indices L˜e and L˜″e showed better performance of L˜″e in terms of sensitivity. Fuzzy process capability indices were developed based on non-normal distribution where SLs and target values were used as a fuzzy number, see, [6]. The degree of process conditions of the proposed fuzzy process capability indices were verified using a degree of belonging. A simulation study was also used to look at the viability and efficacy of the suggested approach. [7] proposed two fuzzy indices based on fuzzy specification boundaries and target value. In the situation where the specification limits and the target value are fuzzy but the data is crisp, the authors suggest two new fuzzy indices to address the issue with them. The authors also provide an application example to illustrate the utility and performance of the suggested indices. Fuzzy process capability indices based on fuzzy normal distribution were proposed and applied [8]. Piston diameter measurements are made using the FPCIs, FCIs, and FNCIs ratios. The findings demonstrate that, when compared to the crisp example, fuzzy estimations of PCIs, CIs, and NCIs have significantly more value to evaluate the process.

[9] suggested the intuitionistic fuzzy set-based fuzzy model of the normal distribution. The neutrosophic process capability indices (NPCIs) were proposed by [10]. It was concluded that these indices performed better than conventional PCIs in a fuzzy environment. [11] introduced a decision-making process based on fuzzy inference to enhance process capability analysis and illustrated with real life data. The indices for one-sided single tolerance were introduced by [12], and the usefulness of these indices was demonstrated using a real-life example. More details can be seen in [13–15].

Analyzing the PCA literature reveals that classical PCA is examined far too extensively. However, there are very few studies that use fuzzy set extensions. Therefore, the purpose of this work is to fill the vacuum in the literature. In order to do this, classic PCIs [12] have been examined and reorganized in this study using triangular fuzzy number (TFNs). A fuzzy formulation of these indices is proposed in the paper. Additionally, newly developed fuzzy indices are presented numerically and graphically in the paper.

2Methodology

Four traditional PCIs with asymmetric tolerance are used in this investigation. These indices undergo a fuzzy transformation. Fuzzy indices are used to construct four theorems. The suggested indices are applied to a sample of 200 piston diameters that were produced in a factory situated in Turkey’s Konya Industrial Area. The R package “Fuzzy numbers” is used to calculate and visualize the result of theorems. TFNs are used as membership functions. The R code can be found in Appendix A.

3Estimation of Cpmku and Cpmkl with fuzzy parameters

In this section, conventional process capability indices are transformed into a fuzzy form using the fuzzy parameters. Fuzzy indices are presented in the form of theorems. All four Parameters (SLs, Target value, Mean, Variance) are used as a triangular fuzzy number. Lower and upper fuzzy specification limits are presented as triangular fuzzy number (TFN), LSL˜=TFN(l1,l2 , l3) , USL˜=TFN(u1,u2 , u3) respectively. Similarly, a fuzzy form of the target value (t₁, t₂ ,  t₃), mean ( μ˜ ) and variance ( σ2˜ ).

Theorem 3.1: Fuzzy Estimate of Cpmku

It is presented that crisp CPI Cpmku with asymmetric tolerance can be converted into fuzzy form to make its specification SLs more sensitive and elastic i.e. C˜pmku(α)=C˜pmku(α)L,C˜pmku(α)R .

Proof. Formulation of the one-sided tolerance is an upper limit U.

Where T˜ is the fuzzy target value, USL˜ is the fuzzy upper specification limit, fuzzy mean μ˜ , fuzzy variance σ˜2 , k constant, and A˜u*=max(μ˜-T˜,(T˜-μ˜ )/k)

α - cut of fuzzy estimate C˜pmku

Theorem 3.2. Fuzzy Estimation of Cpmkl

It is shown that crisp CPI Cpmkl with asymmetric tolerance can be transformed into a fuzzy form to make its specification SLs more sensitive and flexible.

Proof. Formulation of the one-sided tolerance is a lower limit L.

Theorem 3.3. Fuzzy Estimate of C^u_p (u ,  v)

In this theorem, it is proved that that crisp C^u_p (u ,  v) with asymmetric tolerance can be changed into fuzzy form to make its specification SLs more sensitive and flexible.

Proof. The general formulation of the one-sided tolerance is an upper limit U.

Theorem 3.4. Fuzzy Estimate of C^l_p (u ,  v)

It is verified that that crisp CPI C^l_p (u ,  v) with asymmetric tolerance can be reformed into a vague form to make its specification SLs more sensitive and elastic.

Proof. We get the general formulation if the one-sided tolerance is a lower limit L.

4Results and discussion

Figure 1 shows the process capability index Cpmku demonstrated in theorem 3.1 in the form of a triangular fuzzy number. The results indicate membership for intermediate values between 1.44 to 1.57 at different levels of α. The maximum membership is achieved at 1.51. Figure 2 shows the process capability index C˜lp(u , v) as a triangular fuzzy number, which is verified in theorem 3.4 (1.0614, 1.1050, 1.3712). Other indices Cpmkl and C^u_p (u ,  v), as proved in theorems 3.2 and 3..3, can be graphically shown as a triangle fuzzy number (1.5723, 1.63503, 1.7106) and (1.2410, 1.5102, 1.6428) correspondingly. It improves the indexes’ flexibility and sensitivity. In traditional process capability indices, this feature is not available. When traditional process capability indices are used in a fuzzy context, the results can be misleading.

Fig. 1

Triangular fuzzy number of C^upmk (Theorem 3.1).

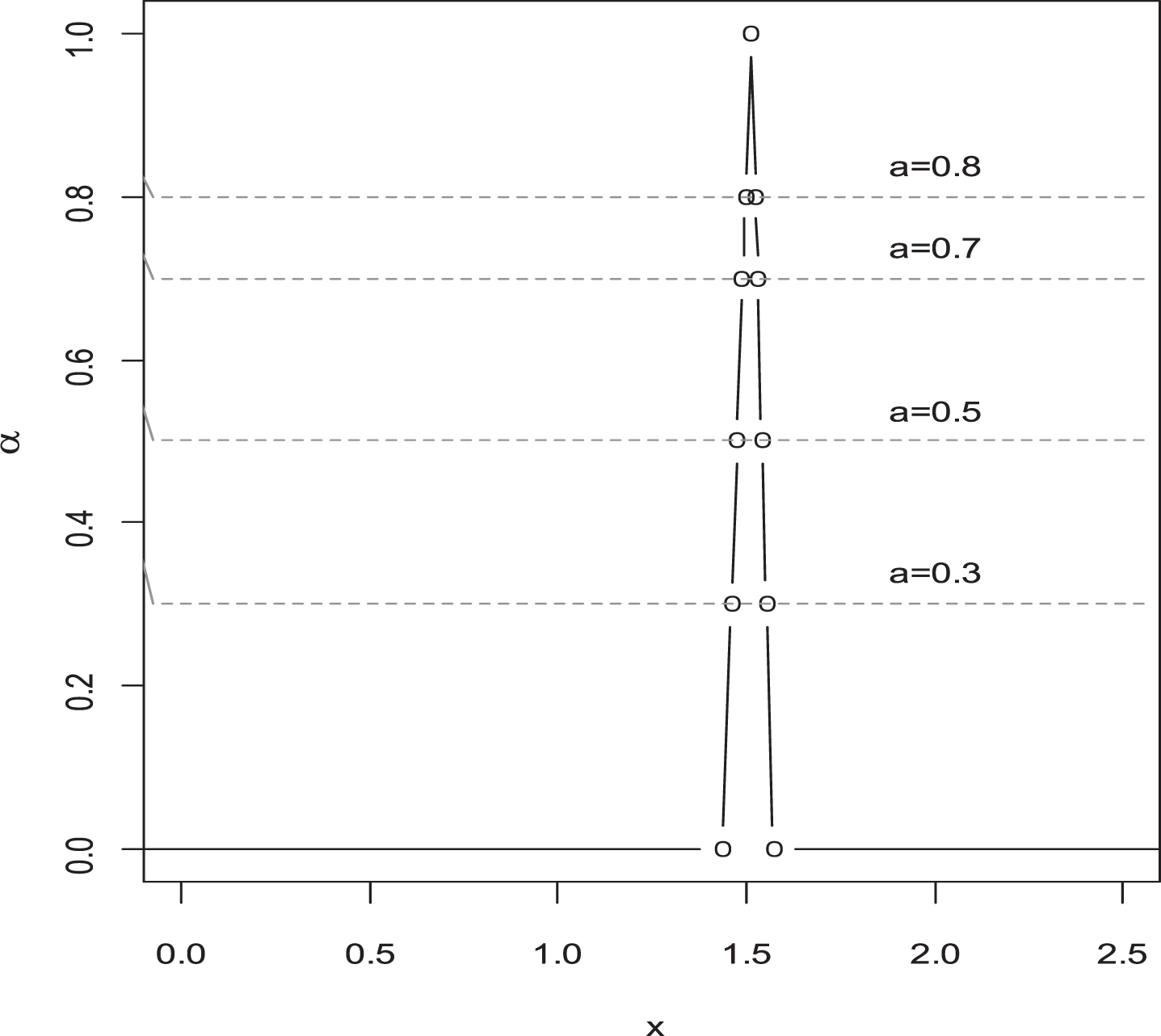
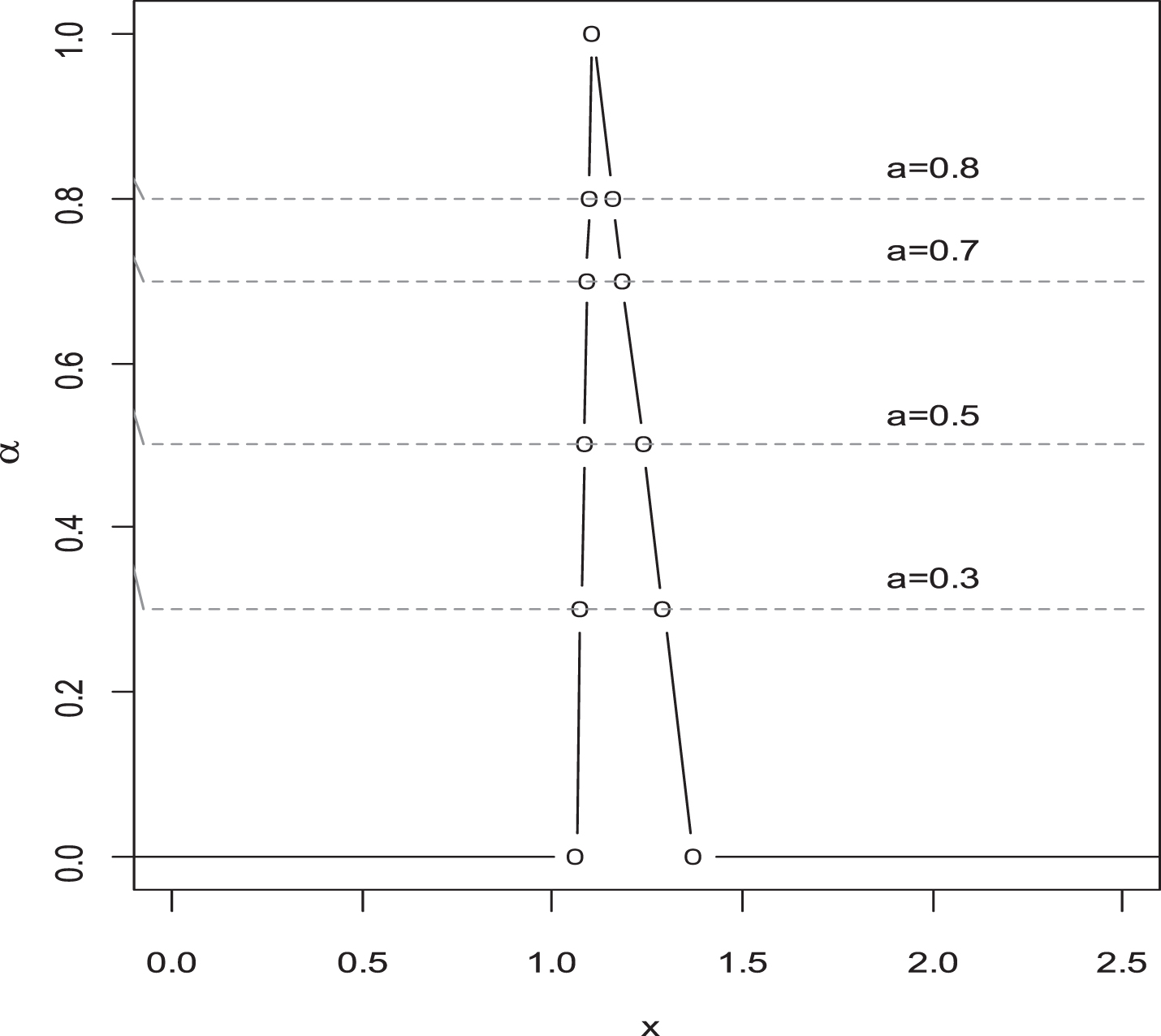
Fig. 2

Triangular fuzzy number of C˜lp(u,v) (Theorem 3.4).

5Comparative study

Grau, (2009) suggested PCIs with asymmetric tolerance when the parameters are crisp. However, these conventional PCIs are not suitable when parameters and data are fuzzy. When the data are fuzzy, the evaluation of fuzzy PCIs is more appropriate than traditional PCIs. The benefit of the suggested FPCIs is discussed in this section using fuzzy SLs. The recommended FPCIs are compared to two current PCIs proposed by [12] under classical statistics. To compare the effectiveness of the suggested FPCIs, the fuzzy values of all parameters were used. Figures 1 and 2 graphically display the FPCI values. Results in (theorems) show that, in contrast to [12] PCIs, the proposed FPCIs give fuzzy values of SLs. Furthermore, the proposed FPCIs will aid in enhancing the sensitivity and flexibility of tolerance limits. Likewise, comparison study shows, FPCIs with asymmetric tolerance can produce intermediate values. Additionally, the suggested FPCIs are more suitable and realistic to apply in a fuzzy environment.

6Conclusion

PCIs with fuzzy asymmetric tolerance are found to be more sensitive and flexible in a fuzzy environment than traditional PCIs with asymmetric tolerance. The fuzzy form of PCIs with asymmetric tolerance is numerically and graphically demonstrated in this paper. It shows how fuzzy set theory can make indices’ SLs more flexible and sensitive to variation. In comparison to existing PCIs with asymmetric tolerance, the applications of the suggested FPCIs reveal that the proposed FPCIs work better in monitoring the process. SLs with intermediate values can be investigated. Theorems based on triangular fuzzy numbers are proposed. The asymmetric fuzzy PCIs tolerances include the membership value along with the crisp values of 1.00 and display all PCIs that can exist. These outcomes are clearly more beneficial than using only one result by providing a wide variety of perspectives on process engineers adhering to process mean and variance. In the future, trapezoidal numbers can also be used to fuzzify the same indices. Additionally, other crisp indices can also benefit from using this fuzzification technique to increase their flexibility, sensitivity, and reduce information loss.

Data availability statement

The data is given in the paper.

Appendix A

R Code

R CODES

#R CODES THEORAM 1

#Fuzzynumbers pacage p = 13

rm(list = ls())

alpha< - c(0.3, 0.5, 0.7,0.8)

P3< -as.PiecewiseLinearFuzzyNumber(

TrapezoidalFuzzyNumber(1.2025,1.41003,1.41003,1.7016),

knot.n=4, knot.alpha=alpha)

P3

## Piecewise linear fuzzy number with 3 knot(s),

## support = [1,7],

## core = [2.5,4].

plot(P3, type=’b’, from = -1, to = 9, xlim = c(0,2.5))

abline(h = alpha, col=’gray’, lty = 2)

#abline(v = P3[’knot.left’], col=’gray’, lty = 3, lw = 3)

#abline(v = P3[’knot.right’], col=’gray’, lty = 3,lw=3)

text(2.0, alpha, sprintf(’a=% g’, alpha), pos = 3)

####################################################

#R CODES THEORAM 4

#Fuzzynumbers pacage p = 13

rm(list = ls())

alpha< - c(0.3, 0.5, 0.7,0.8)

P3< -as.PiecewiseLinearFuzzyNumber(

TrapezoidalFuzzyNumber(1.3071, 1.3503,1.3503,1.4106),

knot.n=4, knot.alpha=alpha)

P3

## Piecewise linear fuzzy number with 3 knot(s),

## support = [1,7],

## core = [2.5,4].

plot(P3, type=’b’, from = -1, to = 9, xlim = c(0,3))

abline(h = alpha, col=’gray’, lty = 2)

#abline(v = P3[’knot.left’], col=’gray’, lty = 3, lw = 3)

#abline(v = P3[’knot.right’], col=’gray’, lty = 3,lw=3)

text(2.0, alpha, sprintf(’a=% g’, alpha), pos = 3)