Using perceptual classes to dream policies in open-ended learning robotics

1.1Decision-making processes in LOLA

As indicated above, to achieve optimal action selection in a robot there is a need for both reactive and deliberative processes. A correct equilibrium between them under different circumstances is the key to successful robotic behaviors in real operation [12].

Deliberative capabilities permit deciding on action through a prospection/evaluation cycle following different possible action paths. They are necessary if a robot has no experience in a domain or is faced with novel circumstances. Deliberation permits selecting an action without actually having learnt a policy. It is thus a way for the robot to explore and gain experience for the generation of new knowledge. Thus, the robot must determine the best action towards the achievement of its objectives from its starting state. Consequently, appropriate world models (WM), also called state-transition models in RL, should be available to perform prospection; whereas utility models (UM) are needed to be able to evaluate states. However, in LOLA settings WMs and UMs are not known beforehand, so the cognitive architecture must also support their online learning.

In the case of the autonomous acquisition of WMs, several approaches have been recently proposed in the field of Intrinsically Motivated Open-ended Learning (IMOL) [13, 14]. These approaches make use of intrinsic motivations (IM) to induce agents to reduce the discrepancy between their knowledge and their perceptions [15]. Some of the most influential work, such as those carried out in [16, 17] on machine learning or in [18, 19] on robots, have led to algorithms that allow autonomous agents to learn models of the domain in which they operate, so that they can "predict" and anticipate the environmental effects of their actions.

Regarding UMs, different ways of acquiring and refining them have been proposed in the literature [20]. One of the most popular approaches in the field of RL is through the concept of value [21, 22] and the definition of value functions (VF). These functions generate an accurate expected value for each point in the state space, i.e., they provide the utility of each point towards the achievement of a goal. Thus, they provide an indication of how far away the goal is, allowing for a quantitative comparison of different possible trajectories towards it.

These concepts have also been applied under LOLA conditions, where different procedures have been developed to learn VFs online. An example in this line is that by [23, 24] who have presented an approach based on the use of eligibility trace strategies to construct VFs when working in continuous domains that are not known in advance.

Reactive or intuitive capabilities, on the other hand, are useful, for instance, when the robot is already competent and requires acting speedily due to real-time operational constraints imposed by dynamic environments. In this case, the robot should select an appropriate policy that outputs the optimal action to be applied as a function of the goal it seeks and its current state. The policies the robot chooses must have been previously designed in by a designer or they should have been previously learned by the robot itself. Several approaches have been proposed for learning policies in traditional robotics and in the field of RL. These go from Q-learning [25], policy gradient [26], and actor-critic methods [27] to model-free policy search [28] and many others. However, they are mainly aimed at pre-obtaining the policy given a pre-established reward function over the whole state space, with some remarkable exceptions like [29].

Figure 1.

Diagram of the decision-making processes involved in LOLA.

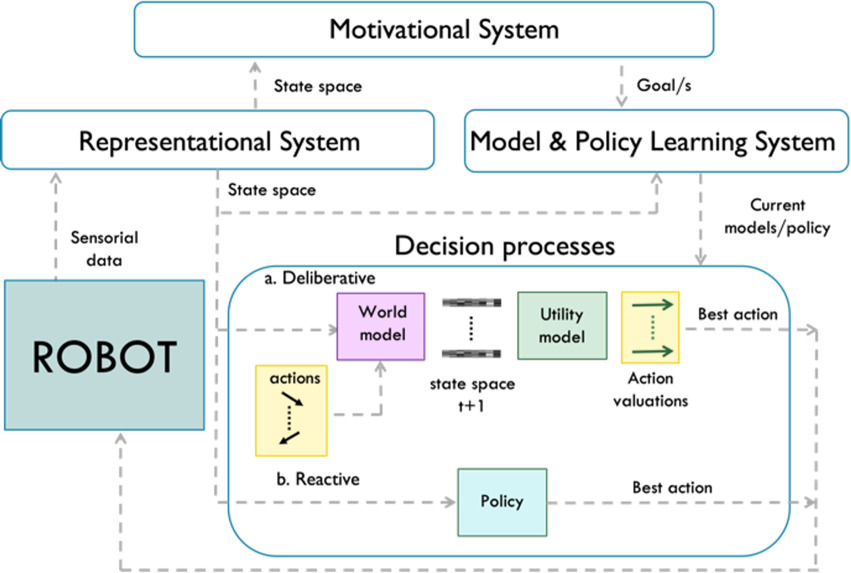
Figure 1 contains a diagram of the decision-making processes in LOLA, with the main cognitive blocks involved. Label “a. Deliberative” shows the typical execution path where, given a current state, for each action of the candidate set, the WM predictions are used as input in the UM to evaluate them, so the best one can be selected. On the other hand, “b. Reactive” shows a single policy that directly provides the best action. It is the correct balance between one branch and the other what is really challenging in this scope.

Cognitive architectures that support LOLA must support both deliberative and reactive decision processes. For this very reason, and as shown in the “Model & Policy Learning System” block of Fig. 1, they must allow WM, UM and policy learning. This learning must take place while the robot interacts with the world (not beforehand) and without any preset reward function over the entire state space. In fact, in LOLA environments, the reward that can be obtained in a domain that is new to the robot has to be discovered as the robot interacts with it. Moreover, depending on the robot’s activity in that domain, it usually does not cover the entire domain, so knowledge about the reward function is relative and imperfect.

WM or UM learning, as commented before, are relatively straightforward to transform into online processes. This is because the data they require for learning is directly accessible through interaction with the environment. They just need states, actions performed and rewards in different instants of time, no matter what the robot is doing or trying to achieve. As some authors posit [30], they may even be random.

Policies, on the other hand, involve a mapping between the states the robot may find itself in and the action to be carried out to be able to achieve a specific goal. Consequently, given this goal dependency, they are a bit more difficult to learn on-line The main problem is that to learn policies it is necessary to be able to predict or test the effects of the robot’s actions as related to the goal to be achieved. Moreover, this prediction must be possible starting from any point in the state space that is relevant. Thus, to perform this optimization the robot must either try out all the possible actions over all its real-world states (with the cost and danger this may entail) or it needs to internally perform a deliberative process using an appropriate WM and some type of UM that allows evaluating which is the most adequate action to move towards the goal.

Given the problems posed by the first approach, some authors in the RL literature have already hinted towards the second strategy for policy learning in robots that are operating online. They usually refer to it as dreaming, hallucination, or imagination, in the sense that the policy learning processes rely on internal reasoning and deliberation, as a sort of “introspection”. In [30] the authors present an experiment where they learn a policy by means of a so-called dreaming process in order to control a real robot. This dreaming process makes use of a learned WM that is used to determine trajectories to the goal. Therefore, they learn a policy by interacting with the WM instead of the real world. Similarly, in [31] the authors present an agent that learns behaviors to solve some visual control tasks. These behaviors are learned by backpropagating gradients of learned state values through imagined trajectories in the state space given by a WM, which is also learned.

However, in these RL approaches, the learning processes are possible because the goals are known in advance so perfectly defined UMs in the form of VFs can be pre-learned This means that the data required for learning the VF is well-defined, and it covers the complete domain Therefore when learning a policy using this approach, any state is a possible valid input state.

In the situations contemplated by LOLA robots, this is not usually the case. The goals the robot must achieve throughout its lifetime are not known beforehand. In fact, they have to be discovered through interaction with the world. This implies that their corresponding UMs must be created on the fly as a function of what the robot needs to achieve each moment in time. No explicit reward function is available and reward arises from the satisfaction of internal robot motivations (as will be detailed in Section 2). To make it even more challenging, the cognitive architecture must learn such UMs concurrently with the discovery of new goals and in different domains that could change over the lifetime of the robot Consequently, data for model learning could be obtained in an interspersed fashion, with different learning periods corresponding to different goals. Hence, to cope with all the uncertainties existing in LOLA settings, a new approach for policy learning must be developed.

1.2Specific scope and contributions

Figure 2.

Schematic representation of the processes involved in online policy learning for a robot in traditional RL settings and in LOLA settings. The goal represented in the figure are operational, so they are related with the task to be solved in specific domains.

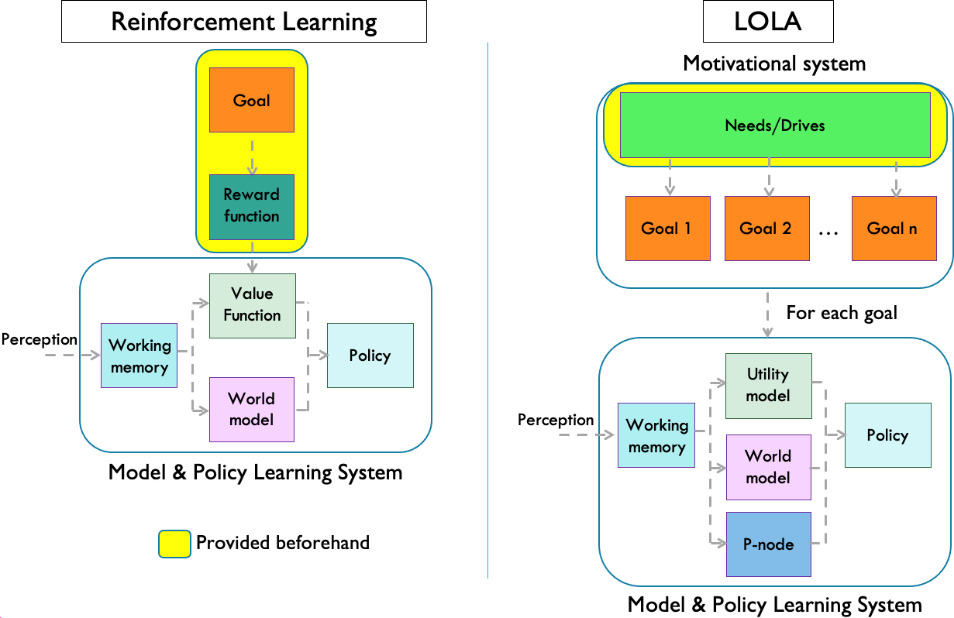
Endowing a cognitive architecture with complete decision-making capabilities (deliberative and reactive), implies solving the challenging problem of policy learning in LOLA settings. To this end, there are three main issues to be addressed.

Firstly, motivations must be defined in a domain-independent representation This allows for the autonomous determination of domain-dependent goals since we deal with unpredictable domain changes.

Secondly a method to determine expected utility under the challenging and uncertain circumstances of LOLA must be developed, so that a continuous version of UMs can be inferred. This is required because, in the most challenging case, reward or utility can only be obtained when in the state space point or area corresponding to the goal.

Finally, it is necessary to provide an efficient way to internally generate data on which perceptual states are relevant for policy learning. This is because policies do not have to be valid in the whole state space, but only in areas where WMs and UMs are well defined (since policies are learned from them by “dreaming”).

The first two issues have been previously addressed in the scope of the e-MDB cognitive architecture [32]. First, a domain-independent strategy for goal creation, based on needs and drives, has been developed and tested in real experiments with robots [33]. Second, a method for online value function learning based on predicted utility and Separable Utility Regions has been also studied in detail [23].

Dealing with the third issue established above makes up the main scientific contribution of the current work. Thus, here we propose the introduction of a metacognitive structure within the cognitive architecture that represents Perceptual Classes, which will be represented within the architecture by components called P-nodes These components, which are contextually linked to goals, as well as to WMs and UMs, are acquired and delimited during the on-line operation of the robot as it learns these models. Once learnt, they permit inferring the relevant perceptual domain from which the robot is able to achieve the goal. Thus, they can be used to generate “dreamt” or “imagined” starting state space points that allow generating “imagined” trajectories for deliberative policy learning in a very efficient way.

With these three methods implemented in a cognitive architecture, policy dreaming in LOLA settings is possible, as will be shown here by means of the execution of an experiment with a real robot. In it, a procedure for online policy learning based on neuroevolution, which uses the P-nodes as a core element for efficient data generation in internal deliberation processes (dreaming) will be tested.

The rest of the paper is structured as follows. In Section 2, a formal statement of the policy dreaming problem in LOLA setting is presented, based on a comparison with the same problem in traditional RL. Section 3 contains a brief description of the motivational system that allows for goal creation and UM learning. In Section 4, Perceptual Classes are described in detail, and the specific policy dreaming strategy based on neuroevolution is explained. Section 5 presents the experiments run to show the validity of the proposed approach. Finally, Section 6 describes the conclusions, and open issues that need to be addressed in future work.

3.1Needs and drives

Needs correspond to internal states that the robot wants to reach or preserve. Thus, a need nj is a goal point or area within the motivational state space M of the robot. M is a specific state space that is designed by the robot’s designer and its dimensions are given by domain independent variables mi usually referring to internal parameters of the robot.

Each need nj∈M has a drive Dj∈ℝ assigned to it that reflects how far the system is from satisfying nj. The value of the drive Dj is established through a function fj that provides a distance (not necessarily Euclidean) between the current motivational state of the system xt∈M and the point nj∈M where the need is satisfied:

These drive functions fj are defined by the system designer and permit assigning a purpose to the robot by balancing and prioritizing the different needs within its motivational system.

It is important to note here that the motivational space M is different from the robot operational state space S, whose structure depends on the specific representation the robot is using for a particular domain.

The fundamental idea of this motivational approach is that the robot will always strive to satisfy its needs and thus, to reduce the values of its associated drives.

3.2Goals and expected utility

Since robots operate in real domains, to reduce the values of their drives, they must find perceptual situations Si∈S that, within the particular domain they are currently operating in, result in the satisfaction of the needs in M. These perceptual situations are called goals.

Thus, a goal can be defined as a point or area Gr∈S that when achieved leads to the reduction of the value of at least one drive Dj associated to a need nj∈M. Goals provide utility. Thus, for a given domain k, the utility Uk of a point Si∈S will be a measure of the change in the value of the corresponding drive Dj when that point is reached. Therefore, by creating a utility model 𝑈𝑀k, it would be possible to know how close the robot is to satisfying a drive (or to reaching a goal), when at that point Si∈S.

The problem when working in real domains, and therefore with real operational state spaces, is that there are not too many areas that provide utility. In fact, utility often appears sparsely and in a discrete form. Consequently, finding utility can be a very complex problem. To solve this problem and to improve the chances of finding goals (areas that provide utility), an option is to model the state space utility in terms of expected utility. Thus, the expected utility, U^irk with respect to a goal Gr∈S of a point Si∈S can be defined as the probability of reaching Gr starting from that point modulated by the utility provided by the goal. Thus, an expected utility model, 𝑈𝑀^rk, could be constructed for each goal, Gr, by determining U^irk with regards to that goal for each point Si∈S. A remarkable feature of these models is that the expected utility value increases monotonously as we approach Gr. Therefore, by constructing this type of models, the robot has a mechanism to choose actions that lead to the goal in a deliberative manner. For compactness reasons, in the rest of the article we will refer to the expected utility models simply as utility models, UM.

3.3Types of needs and drives

The only control the designer has over the behavior of the robot is by defining its needs and creating the appropriate drives. Therefore, when needs and drives are created to define the behavior of a robot, it must be endowed with the necessary tools to explore the domains, find goals, and learn how to achieve them, i.e., model expected utility. These objectives lead to a classification of needs and drives into two different groups: operational and cognitive needs and drives.

Operational needs and drives (𝑛j𝑜𝑝,Dj𝑜𝑝) are associated with the purpose that must be instilled in the robot. They reflect what the designer wants the robot to do, but in a domain-independent manner. Thus, for each domain the robot faces, it must identify and learn to achieve goals to fulfill these operational needs.

Cognitive needs and drives (nj𝑐𝑔,Dj𝑐𝑔), on the other hand, enable the robot to efficiently explore and acquire relevant knowledge. These drives reflect how the designer wants the system to regulate its learning process. Therefore, their satisfaction may be related to how much is explored (e.g. novelty [38]), to obtaining WMs (e.g. curiosity [39]), to generating goals by seeking to find ways to produce effects over the environment (e.g. effectance [40]), or to acquiring competence over those goals (e.g. competence [41]).

The details of how to design these drives have been discussed in [33, 42]. What is important here is the idea that through the correct selection and design of drives a robot can acquire the ability to find goals in the domains it faces and provide motivation for modelling the domains as well as learning how to achieve those goals consistently.

4.1Perceptual classes and P-nodes

We define a perceptual class, S^j, as an area of the perceptual/statespace whose points share some operational characteristics and are thus taken as a single entity. This leads to a discretization of the perceptual/state space into areas whose points lead to the same results under specific contexts. When considering action determination, this means that the response of the robot in terms of action is the same for every point in the perceptual class when operating in the same domain and striving to reach the same goal. Thus, a perceptual class can be considered an abstraction of perceptions leading to a discrete, higher-level representation associated, in this case, to a particular response of the robot.

To represent perceptual classes within a cognitive architecture, a knowledge component called perceptual node or P-node was proposed in [43]. A P-node, denoted as Pj, is a component that is activated when a perceptual state Si belongs to a given perceptual class S^j(Pj=1↔Si∈S^j). Thus, a P-node is a metacognitive component in the form of a filter over the perceptual state space. It permits determining the presence of state space points that belong to S^j.

Under ideal conditions, a P-node Pj will be perfectly active when a perception Si belongs to its corresponding perceptual class S^j. However, in more uncertain settings, such as the real world, a probabilistic representation of P-node activation may be considered. In this representation the activation level depends on how confident the system is about Si∈S^j. This confidence function in the perceptual space, denoted as Γj⁢(Si), can be created using the information the robot has about the points it has experienced. Thus, the membership to a perceptual class S^j of a state represented by P-node Pj is given by:

where pj denotes the activation of the P-node under ideal conditions. To compute this confidence function, we make use in this article of a point-based clustering representation [43], although neural network based representations would also work, as the authors have described in [44].

In a point-based interpolation approach, the state space area represented by a P-node is given by the set of points actually perceived by the robot and some distance-based rules. This way it is possible to delimit the areas for which the system hypothesizes the P-node is active. In this line, state space points can be classified into two categories: points for which the P-node should be active (activation = 1), which will be called simply points, and points for which the P-node should be inhibited (activation = 0), which will be called anti-points. Both types of points are stored in a memory structure related to the P-node. All other points within the class, which were not actually experienced by the robot, will be assigned confidence values in the interval [0:1] depending on their distance to points and anti-points. The specific algorithm used here for learning the perceptual class that corresponds to a P-node is described in [43]. Algorithm 4.1 describes the procedure to decide on the activation of a P-node representing a perceptual class S^j and given a new perceptual situation Si. This procedure leads to the delimitation of an area in the state space that activates the P-node. Through continuous interaction with the environment, new P-nodes will be created, and existing P-nodes will be populated with new points and anti-points, so that perceptual classes will be progressively delimited.

Therefore, P-nodes are very important for determining the perceptual context when working in high-dimensional continuous domains, such as those that a real robot may encounter. So, by associating these nodes to the goals to be achieved, a high-dimensional delimitation of the perceptual state space can be established. This will make it possible to know more accurately under which perceptual conditions these goals are achievable and also to delimit those perceptual situations that need to be considered when learning a policy.

P-node activation algorithmPj={p1,…,pn,a1,…,an} P-node given by points and anti-points Pj⁢(x) denotes the activation of Pj for perception xSi is a new perception [1] Calculate k as the closest point/anti-point to Si out of those representing Pj(k∈{p1,…,pn}) Pj⁢(Si)=1/(∥k-Si∥+1)k∈{a1,…,an}Calculate the centroid of {p1,…,pn} as C(∥C-Si∥<∥C-k∥) Calculate k′ as the closest point to Si out of those   representing PjPj⁢(Si)=1/(∥k′-Si∥+1)Pj⁢(Si)=-1.0(Pj⁢(Si)<ε) Pj⁢(Si)=0.0

4.2Policy dreaming strategy

As mentioned in Section 1, given that in open-ended learning problems the domains and tasks to be addressed by the robot are not known at design time, pre-learning policies directly is not possible. However, this learning can be achieved using the deliberative models (UMs and WMs) and the perceptual classes that the robot has acquired on-line, as detailed in Section 2. Once they have been adequately learnt, these models contain the information needed to be able to decide on the optimal action to apply at each moment in time in order to reach a goal in a particular domain. They permit the implementation of prospection processes (using WMs), and the later evaluation of resulting states (using UMs). However, to take into account the areas where these models are valid, that is, the areas of the perceptual state space from which it is possible to achieve these goals, their associated perceptual classes (P-nodes) need to be known.

As previously indicated, the main objective of a robot with a motivational system, such as the one presented in Section 3, is the satisfaction of its needs. That is, the maximization of drive satisfaction. As indicated above, this can be achieved by maximizing expected utility u^ in the particular domain the robot is operating each instant of time. In other words, we are seeking a policy that results in actions leading to the maximum expected utility for a given domain or sets of domains.

In our approach, the different components (models and policies) have been implemented by means of Artificial Neural Networks (ANN). This is so because in our cognitive architecture, the e-MDB [32], knowledge is represented using neural networks. Therefore, we will address policy learning as the process of producing an ANN that implements the policy. In addition, we must consider that it is not possible to estimate beforehand how complex the task to be solved will be, which makes it difficult to decide on the appropriate ANN size. Thus, model and policy learning will be achieved by means of a neuroevolutionary algorithm. In particular, we use the NEAT [45] algorithm, that allows learning the network architecture in terms of number layers and of neurons per layer, as well as which layers connect to which, and the weights of the individual connections. Thus, it is not necessary to establish beforehand the architecture of the network.

As explained in Section 2, online policy learning starts once a reliable WM and UM have been learned in a given domain. At this point, the process begins, like any other evolutionary algorithm, by generating a population of candidate policies (Π) in the form of random ANNs. These policies are evolved taking the world and utility models as “simulators and evaluators of the current reality”. Additionally, the P-node information is used to generate the initial states from which deliberation starts, since it indicates for which perceptual states the UM is applicable. Algorithm 4.2 describes the procedure used to evaluate an individual policy πi from the policy population Π, starting from a set of perceptions/states that are extracted from P-node P*∈Pn to make them representative.

*EndForPolicy evaluation processpk: current perceptual point P∗: set of representative perceptions from the P-node Pnπi: individual policy Π: population of candidate policies π*: optimal policy from πiWM: world modelUM: utility model u^k: expected utility provided by UM for pku¯i: average expected utility for πiai⁢k: action provided by πi for pk[1] πi∈Πpk∈P*ai⁢k←πi⁢(pk)pk+1←𝑊𝑀⁢(ai⁢k,pk)u^k+1←𝑈𝑀⁢(pk+1)u¯i←𝑔𝑒𝑡𝐴𝑣𝑒𝑟𝑎𝑔𝑒⁢(u^k+1)π*←argmax⁢(u¯i)

Figure 3.

Scenario (left) and reachable areas (right). The dashed lines display the reachable area for each arm.

This process is repeated for a relevant number of representative points of P*, pk∈P* averaging the expected utility, which is used as the evolutionary fitness for policy πi. The same set of perceptions and world and utility models are employed for the evaluation of the whole policy population. This way, the best policy (the one with highest average expected utility) at the end of evolution, is the one that the robot will use to achieve that specific goal in that domain and under those specific perceptual conditions. Therefore, for each domain in which the robot operates, and whatever goals it discovers, it will have a method that will allow it to acquire the necessary policies to achieve them.

To sum up, it must be pointed out that unlike in the cases presented in [31, 34] related to more traditional RL settings, where it was assumed that models were valid throughout the whole state space, P-nodes are key elements in policy learning under LOLA settings. In the case of LOLA, goals have to be discovered and models are acquired as the robot interacts with the world. There is no guarantee, or even need, that they are valid in the whole state space. Consequently, to be able to run dream like policy learning processes that do not go into unmodeled areas of state space, and thus produce absurd predictions or evaluations, the area of validity of the models must be tracked and used when dreaming. This is precisely what is done through the use of P-nodes, hence their importance.

5.1Experimental setup

An experimental setup has been considered in which a real robot must learn to organize a set of objects located on a table. Figure 3 shows this setup, which includes a Baxter robot, a white table, a circular box, a base with a stick for stacking objects, a push button, and some movable elements: a solid red cylinder and a yellow cylinder with an axial hole. The final purpose of the robot is to pick up the red cylinder and place it in the box and insert the hollow cylinder in its base. The robot must determine that this is what it needs to do and learn to do it irrespective of the starting object positions on the table. Additionally, the box in which to deposit the solid cylinder may start out of the reach of the robot. In this case, to bring it closer, the robot will have to press the push-button first. The right image in Fig. 3 shows the areas that can be reached by the robot arms.

To achieve this response, the motivational system of the robot is the only element that has been designed beforehand. We have endowed it with four different needs and their corresponding drives (one operational and three cognitive ones). For each drive we have created an associated drive function.

The operational drive that has been defined is related to object collection. This drive, D𝑡𝑎𝑠𝑘𝑜𝑝, is associated with a need n𝑡𝑎𝑠𝑘𝑜𝑝 that is linked to a sensor that detects whether the objects are in their corresponding storage locations. Thus, each cylinder placed at its destination will produce partial satisfaction of the drive. Similarly, the drive will be fully satiated (the need achieved) when the table is completely organized (both cylinders are in their corresponding storage places). As it is an open-ended learning problem, the robot does not initially know how to satisfy its need. That is, it does not know that correctly storing the objects is what it needs to do. Consequently, it must first figure this out.

As explained in Section 3, to foster exploration, goal discovery and skill learning, the robot is endowed with a set of cognitive needs and drives based on novelty, effectance and competence. As this is not the main goal of the paper, we will not go into details of its implementation, nonetheless, a detailed explanation of it can be found in [33]. These drives (operational and cognitive) will be the ones in charge of allowing the robot to learn to grasp the cylinders and place them in their corresponding storage locations. They will guide the learning of the different deliberative models and P-nodes.

Concerning the perceptual system, P∈ℝ, in this experiment we use an RGB-D camera located on the ceiling of the room and binary sensors associated to the presence of objects in the grippers of the robot and to button pressing. The camera information is redescribed in the form of distances between the objects and the robot’s end effectors, and relative angles between the objects and the robot base. Specifically, the perceptual vector has 18 dimensions: 2 binary variables corresponding to the gripper sensors, 1 binary variable related to the button state, 10 continuous variables related to distances from each robot arm to each of the 5 objects shown in Fig. 3 (dobject-arm∈ [0: 1]), and finally 5 angles corresponding to the orientation of these objects with respect to the robot’s body (a𝑜𝑏𝑗𝑒𝑐𝑡∈ [-1: 1]):

Regarding action space, A∈ℝ, the Baxter robot presents a two-arm configuration, each offers 7 degrees of freedom. To carry out the experiment, and for the sake of clarity, we have defined a set of actions that control the motion of both arms, i.e., the change in the direction of movement of the arm end effector in sexagesimal degrees (α∈ [0: 360]) and its displacement in cm (v∈ [0: 5]). These actions are continuous in the ranges indicated. Therefore:

where α𝑙𝑒𝑓𝑡 and v𝑙𝑒𝑓𝑡 are the direction of movement and the displacement for the left gripper, and α𝑟𝑖𝑔ℎ𝑡 and v𝑟𝑖𝑔ℎ𝑡are the direction of movement and the displacement for the right one. The movement of the arms is carried out at a constant height. In addition, the actions related to the opening and closing of the grippers are predefined: if the robot reaches one of the cylinders with one of its grippers, it will automatically pick it up. Also, in the case of reaching the box or the stick when cylinder is in its grasp, it will drop it. Additionally, if both arms cross when one of them has the cylinder in its gripper and the other is empty, the robot will automatically transfer the object to the empty gripper. This action is helpful since the robot is not able to reach the whole table with only one arm.

Finally, the models and policies are implemented using Artificial Neural Networks (ANNs). The MultiNEAT implementation of the NEAT algorithm, extracted from [46], was used to evolve the ANNs corresponding to the policies. The evolutionary process was configured as shown in Table 1. The parameters not included in the table were kept at their default values. These networks have 18 inputs (the perception of the robot at each time instant), and different outputs depending on whether the policies control the movement of one of the arms (2 outputs) or both of them (4 outputs).

5.2Experiment dynamics

Initially, the robot has no idea where the goals are or how to reach them. That is, it does not know the UMs or under which perceptual conditions to use them. Consequently, to achieve its purpose, it must discover its goals and learn the UMs that allow it to reach them on demand. It must also associate them with their corresponding contexts so that goals can be reached regardless of the initial conditions of the scenario. So, for this to happen, it will also have to learn the different P-nodes. We are assuming that the WM representing the domain in which the robot is operating has already been learned in previous stages where the robot interacted freely with the world. This learning is carried out online from the values that are stored in a short-term episodic memory as the robot interacts with the world. An example of this procedure can be found in [35].

The robot will initially explore the environment in the search for novel states or states that provide effectance, which will lead to the discovery and creation of different goals. The creation of goals will also involve the creation of UMs and P-nodes associated to their achievement. Therefore, the robot will alternate between learning the UMs, modelling the activation areas of the P-nodes and exploring its environment in the search for new goals. Thus, initially the operation of the robot will be guided by cognitive drives and deliberative decision processes. However, as soon as the models used for deliberation have been adequately learnt, i.e., the robot consistently reaches the goal from whatever state it is in within the area delimited by the P-node, the dreaming-like learning of the policies can start. From the moment the policy has been learnt, the robot can resort to it as a fast reactive decision process to achieve its goal.

The results of this learning process are shown in Fig. 4. The figure displays the evolution of the time that the robot required to reach its purpose and the moments when the different UMs and P-nodes were considered learned. As a result of this learning process, the robot has discovered six different goals, and has learned their UMs and associated P-nodes. In addition, following the dreaming-like method explained in Section 4, the policies corresponding to the six UMs have also been learned. Tables 2–4 contain a summary of the content of these knowledge nodes as described by an external observer. As can be seen, the P-nodes correspond to the different perceptual situations that the robot may encounter, while the UMs and policies represent the actions to be performed to go from these perceptual situations to the associated goals. To provide an idea of the statistical distribution of the behavior of the learning process, Fig. 5 shows the results, in terms of purpose achievement, resulting from 10 different runs of the experiment. The experiments shown in Figs 4 and 5 are divided into trials, each of which ends when the robot achieves its purpose. Similarly, a trial is divided into time steps, where each time step represents the execution of an action. Remember that each action A⁢(t) moves the robot’s arms a maximum of 5 centimeters in a particular direction, so that to reach a goal it is necessary to concatenate several actuations.

Figure 4.

Number of iterations required to achieve the purpose in a representative run of the experiment. Since the UMs and P-nodes related to the same goal are learned in parallel, the end of the learning process is the same for both.

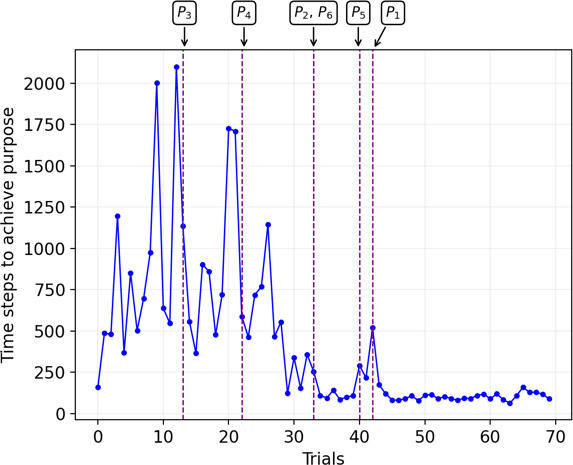
Figure 5.

Performance analysis for 10 runs of the experiment (median and 25 and 75 percentiles).

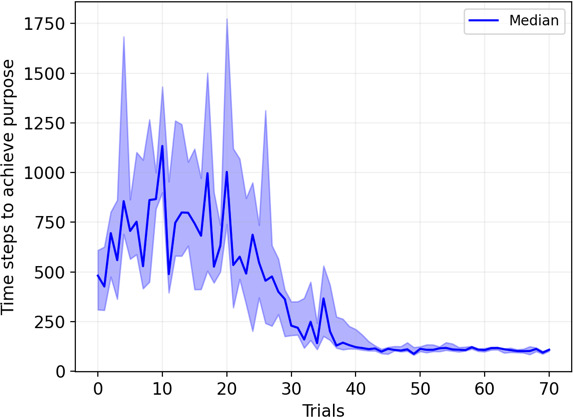
At a first glance, it can be seen from the figures that there is a gradual reduction in the number of time steps required to achieve the robot’s purpose as the robot acquires more knowledge. Moreover, this reduction is associated with the learning of the different UMs and P-nodes. Something that was expected, since as the robot learns to reach the different goals, the time to achieve its purpose also decreases. Furthermore, once it learns how to achieve the last goal, the number of steps needed to achieve the purpose converges. A video illustrating the robot operation once all the UMs and P-nodes have been learned can be found in the following link: https://github.com/GII/ICAE2023.

Figure 6.

Evolution of the activation areas of P-node P1 for trials 10, 30 and 45.

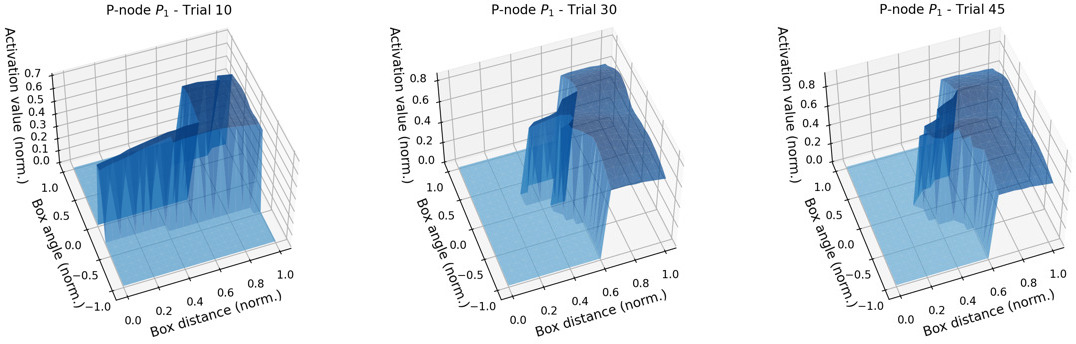
5.3P-node learning

The different P-nodes, as representations of perceptual classes, are constructed starting from the initial perception (state space point) that led the robot to reach each one of the goals for the first time. From that moment on, the P-node presents an activation value of 1.0 for that representative point and lower values (depending on the representation function used) in the hypothesis area surrounding it. This initial delimitation of the P-node is only a hypothesis and, consequently, some of the area it encompasses may actually not be part of the perceptual class.

As interactions with the environment take place involving a P-node, more information will become available, i.e., more points (P-node activating perceptions from which it was possible to reach the related goal by using the related UM) and anti-points (P-node activating perceptions, but from which, in this case, it was not possible to reach the related goal). This will lead to a progressive improvement of the delimitation of hypothesis areas corresponding to the perceptual classes. Consequently, the robot will become more efficient when trying to achieve its goals.

To illustrate this process, Fig. 6 shows the evolution in time of the hypothesis area of P-node P1. Given that in this experiment the perceptual space is eighteen-dimensional, to facilitate the visualization of the data the figures show the P-node activation map associated to the most relevant two dimensions. That is, the two sensors that play the most important role in the calculation of the activation have been chosen. In this case, as it is a P-node associated with pressing the button, and it is only useful to press it when the box is out of the robot’s reach, the most significant sensors are those corresponding to where the box is (distance and angle between the robot and the box). Bear in mind that this is just for visualization purposes, as the robot has learnt the eighteen-dimensional P-node activation map on its own and determined when it was relevant for the P-node to be activated. With this representation we want to provide an idea of how the perceptual classes work and of their importance when determining in which regions of the state space to use the different UMs.

Figure 6 shows the areas of the state space in which the P-node will be activated and in which it will be inhibited. The darker zones (higher activation values) are those that correspond to perceptions that are included within the perceptual class. From the time evolution sequence of images in the figure, it can be appreciated that when the robot has not interacted much with the environment, the perceptual class boundaries are quite poor. In fact, in this particular case, the hypothesis made by the robot on the perceptual class clearly shows that in trial 10 the robot has not experience related to when the box is on the right side of the table. However, as more points and anti-points are experienced, a much more detailed delimitation of the P-node area is obtained, leading to more accurate decisions based on it.

Figure 7 shows a similar representation to that on Fig. 6 for some P-nodes at the end of the execution of the experiment. The top graph displays the joint activation areas of P-nodes P2 and P4, which are the ones related to grasping the different objects. Thus, in the figure it can be seen how when the objects (cylinders) are close, i.e., within the robot’s reach area, the P-nodes are activated indicating that the robot can reach them. It is worth noting that this representation is complementary to that of the perceptual class shown in Fig. 6, which indicates when the object, in that case the box, is out of reach.

Another interesting plot is the one corresponding to P-node P3(Fig. 7 bottom), associated with the UM corresponding to moving an object from one gripper to the other when stacking objects. The most significant sensors are those that allow the robot to determine whether the object and the stacking stick are on the same side or not. In this case they are the angle from the robot base to the object (cylinder with an axial hole) and the angle from the robot base to the stick used to stack objects. To put the hollow cylinder there, the robot first needs to have this object in the gripper that is on the same side as the stick. This is what the perceptual class shows, when the hollow cylinder is not on the same side as the stick the robot must move it from its current gripper to the other one.

Figure 7.

Final activation areas for P-nodes P2 and P4, and P3.

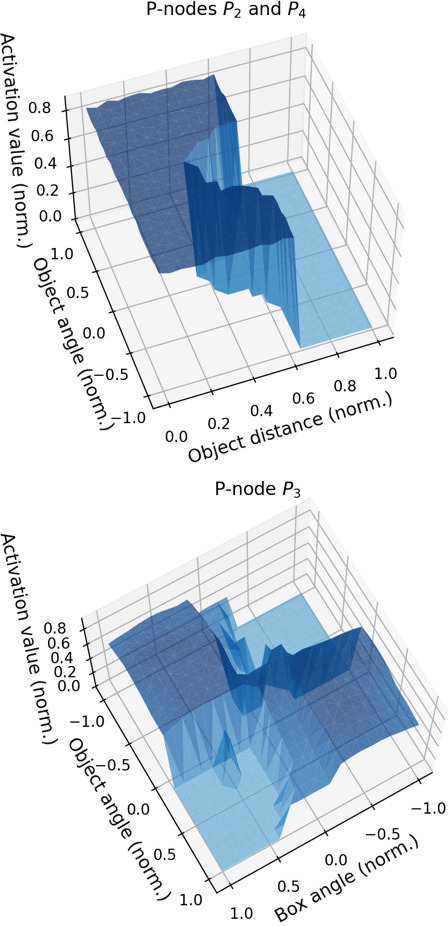
The main conclusion to be drawn from these figures is that P-nodes are a good tool for partitioning the perceptual space in terms of the context (domain and task) to be addressed. Furthermore, they are key to delimit the perceptual conditions necessary to try to achieve certain goals, as they create well-established boundaries that delimit where the P-node should be activated and, thus, where the UM that is being used to evaluate possible actions is valid. This is a fundamental issue, as we will comment in the next section, when trying to learn policies from deliberative processes that involve these learnt UMs. In addition, it must be noted that, as appreciated in Fig. 4, the correct delimitation of these classes is linked to an increase in the performance of the system when achieving its purpose as the system makes fewer erroneous evaluations of actions.

5.4Policy learning and results

As the learning process was the same for each policy, for the sake of brevity we will explain it for the ones corresponding to depositing the hollow cylinder on the base to stack objects, 𝑈𝑀5, and to moving the cylinder from one arm to the other, 𝑈𝑀3. For clarity, they will be referred to in what follows as “Put object in” and “Change hands”. These policies were chosen because they present different complexity levels. In the case of the first one, π5 or “Put object in”, given that objects were always presented on the right side of the robot, it “only” has to control the movement of the right arm. In other words π5=f⁢(α𝑙𝑒𝑓𝑡,v𝑙𝑒𝑓𝑡). In the case of the second one, π3 or “Change hands”, it must control the movement of both the right and left arm, π3=f⁢(α𝑙𝑒𝑓𝑡,v𝑙𝑒𝑓𝑡,α𝑟𝑖𝑔ℎ𝑡,v𝑟𝑖𝑔ℎ𝑡).

As mentioned in previous sections, to evaluate each of the candidate policies generated in the evolutionary process, the previously learned UMs were used. They will provide a higher utility value (higher fitness) to those actions that satisfy the description shown in Table 4 for models 𝑈𝑀3 and 𝑈𝑀5. Thus, in the case of “Put object in” candidate policies, those that provide actions that allow the robot’s right arm to move closer to the stick for stacking objects will be valued higher. While in the case of “Change hands” policies, the best valued ones will be those that provide actions that allow the robot arms to get closer to each other.

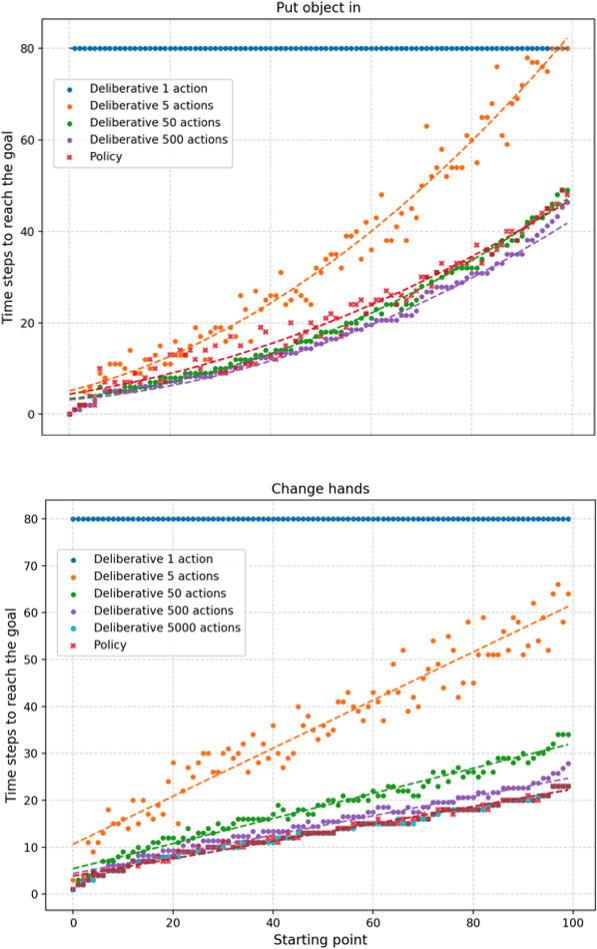
Figure 8.

Time steps needed to achieve the goals using the learned policies and deliberative models considering different numbers of actions. A maximum of 80 time-steps were allowed to reach the goal.

Additionally, to be able to evaluate candidate policies, it is essential to know the areas of the state space in which the UMs that are used for this are valid. This is where the perceptual classes play a key role since they provide the necessary information to “contextualize” the learning. It is worth remembering that in LOLA conditions this information is not available beforehand, and that P-nodes are learned autonomously. Thus, during the dream-like learning process, these perceptual classes are used in order to generate points (dreamt perceptions) belonging to the area of the perceptual state space in which the policies are going to be used, that is, where the UMs of the deliberative processes employed during dreaming are valid. These perceptions, pk, will be the inputs of the candidate policies and will allow obtaining the actions that will then be evaluated with the help of the world and UMs in a deliberative process. To illustrate this stage of the autonomous learning process, Fig. 7 bottom shows a representation of the state space covered by the P-node associated to goal G3.

To evaluate the efficiency of the policies obtained after the evolutionary process, we have compared the actions they provide with those that would be provided by the deliberative process using the learnt UMs. Figure 8 shows a representation of the number of time steps (action selections) needed to reach the goals using the learned policies. To this end, 100 random starting points from within the P-nodes associated to these UMs/policies are shown. These starting points are arranged according to their increasing distance to the goal, so that the further to the right the starting point is, the farther the robot will be from reaching the goal and the more actions it will have to take in order to achieve it.

In turn, to draw conclusions regarding the efficiency of the actions obtained using the policy, the number of time steps necessary to reach the goal is compared to those that would be necessary if the deliberative system considered 1, 5, 50, 500 and 5000 candidate actions during its deliberations. It should be remembered that these actions are generated at each time instant, that they take random values in the continuous range of possible actions and that they control the direction of movement and the displacement of the robot grippers. Therefore, the larger the repertoire of possible actions, the greater the probability of finding the optimal action for each situation. However, this will also imply a longer computational time since more actions will need to be evaluated (each one of them will imply prospection and evaluation). In the case of the policy, it directly provides the action it considers optimal, without the need for evaluation.

Figure 8 top shows the results corresponding to policy ‘Put object in’. It should be remembered that each action involves moving the robot arm a maximum of 5 centimeters in a particular direction, so that to reach an object several actions are necessary. Thus, in the figure it can be seen how the actions provided by the policy are very close to being optimal, since, on average, it needs only two more actions than the best deliberative case to reach the goal. This difference arises because the robot needs high precision in the final step towards the goal. That is, if the last actions imply too large a displacement, the robot will overshoot the position of the base to drop the object. Thus, to prevent this from happening, the policy chooses to use shorter displacements as the robot approaches the goal, which results in a slight loss of efficiency.

On the other hand, observing the results obtained for the ‘Change hands’ policy (Fig. 8 bottom), it is possible to verify that these are optimal. The actions proposed by the policy are as good as those of the deliberative system that contemplates 5000 candidate actions. It is interesting to comment that the deliberative systems need more time steps to reach this goal than the goal associated with policy “Put object in”. This is because these actions control the two arms of the robot, so that each candidate action (randomly generated) has four components, (α𝑙𝑒𝑓𝑡,v𝑙𝑒𝑓𝑡,α𝑟𝑖𝑔ℎ𝑡,v𝑟𝑖𝑔ℎ𝑡), enlarging the candidate action search space. Thus, the more complex the actions that are applied to control the robot, the more difficult it will be to find the optimal action through deliberation, and the more valuable it will become to have a policy that can do it.

To end the comparison, it is worth mentioning that the use of policies is much less computationally expensive. The reason is clear: each candidate action in a deliberative process involves the evaluation of two ANNs, one corresponding to the WM and one corresponding to the UM. Thus, 2⁢n evaluations will be needed, being n the number of candidate actions. Whereas in the case of policies, only one ANN needs to be evaluated. To demonstrate this, we have used an intel i7-7700HQ @ 2.80 GHz CPU and computed the average time for obtaining 100 different actions with each of the systems shown in Fig. 8. The order of magnitude of the computational time for the policy was 10-5 seconds, the same as for the deliberative process with 1 candidate action. In the case of 5 candidate actions, the time was 10-4 seconds, while for 50 candidate actions it was 10-3 seconds. In the same way, the average time for 500 actions was 10-2 seconds and for 5000 actions was 10-1 seconds.

To conclude, it was possible to see that the autonomous learning of policies through dreaming processes in LOLA conditions is feasible. This is possible by using the knowledge contained in the world and UMs and, above all, the information contained in the perceptual classes that provide an indication of where these models are valid and thus allow the generation of relevant starting state space points in order to generate dreamt trajectories that permit evaluating actions. It is thus possible to contextualize learning, without the need to know in advance the goals and the domains of operation.