Deblurring Medical Images Using a New Grünwald-Letnikov Fractional Mask
Abstract
In this paper, we propose a novel image deblurring approach that utilizes a new mask based on the Grünwald-Letnikov fractional derivative. We employ the first five terms of the Grünwald-Letnikov fractional derivative to construct three masks corresponding to the horizontal, vertical, and diagonal directions. Using these matrices, we generate eight additional matrices of size
1Introduction
In the realm of image processing and computer vision, the pursuit of enhancing image quality has been an ongoing endeavour. From the restoration of blurred images to the reduction of noise interference, researchers continually strive to develop sophisticated techniques that can preserve and enhance visual information effectively. One such approach gaining attention is the utilization of fractional derivation in constructing masks for image denoising and deblurring.
Traditionally, linear filtering techniques, such as Gaussian or bilateral filters, have been extensively employed for image denoising and deblurring (Buades et al., 2005). However, these techniques assume that the degradation process and noise follow Gaussian distributions, which might not always reflect real-world scenarios. To address this limitation, researchers have turned their attention towards more advanced methods, such as fractional derivation, to construct masks that facilitate the denoising and deblurring processes.
The concept of fractional calculus, an extension of traditional calculus, has gained traction in various scientific disciplines due to its ability to capture complex, non-local behaviours and characteristics (Podlubny, 1998). By leveraging fractional derivatives and integrals, researchers have been able to tackle challenging problems that evade conventional approaches. In the context of image denoising and deblurring, fractional derivation provides a valuable tool for modelling and capturing intricate image structures and features at different scales.
An image edge analysis method based on Riemann-Liouville fractional derivative was introduced in Amoako-Yirenkyi et al. (2016) that utilizes a fractional derivative mask. Chowdhury et al. (2020) employed fractional-order total variation to address non-blind and blind deconvolution challenges in the presence of Poisson noise. A new image encryption system that combines fractional-order edge detection with generalized chaotic maps has been presented in the referenced paper (Ismail et al., 2020). Ibrahim (2020) introduce a novel image denoising model that utilizes conformable fractional calculus to address multiplicative noise. An adaptive approach to image restoration using fractional-order total variation and the split Bregman iteration has been presented in Li et al. (2018). Wadhwa and Bhardwaj’s research focuses on enhancing MRI images of brain tumours using the Grünwald-Letnikov fractional differential mask (Wadhwa and Bhardwaj, 2020). Liu et al. proposed a blind deblurring method that utilizes fractional-order calculus and a local minimal pixel prior (Liu et al., 2022). Yang et al. (2016) provided a comprehensive review of the application of fractional calculus in image processing. A novel fractional-order mask for image edge detection, utilizing the Caputo-Fabrizio fractional-order derivative without a singular kernel, was introduced in Lavín-Delgado et al. (2020). We refer to (Aboutabit, 2021; Arora et al., 2022; Chandra and Bajpai, 2018; Gholami Bahador et al., 2022; Golami Bahador et al., 2023; Hacini et al., 2020; Irandoust–pakchin et al., 2021; Li and Wang, 2023; Nema et al., 2020) and references in them for more works done in the image processing with fractional derivatives. There are several other methods for image deblurring. For instance, Pooja et al. (2023) present a novel image deblurring algorithm that utilizes region-specific priors and methodologies for enhanced image correction. Zhou et al. (2023) used events to deblur low-light images. The authors introduce a robust unified two-stage framework and a motion-aware neural network designed to reconstruct sharp images by utilizing high-fidelity motion information derived from event data. The authors in Ren et al. (2023) employed multiscale structure-guided diffusion techniques for the purpose of image deblurring. Dong et al. (2023) implemented a Multi-Scale Residual Low-Pass Filter Network to address image deblurring challenges. Li et al. (2023) introduced a novel framework that leverages deep learning techniques to address ongoing challenges in the field, including the limitations of existing methods in handling real-world blur and the problems of over- and under-estimating blur.
In general, constructing masks and applying them for image processing is one of the easiest methods requiring relatively few computations compared to other approaches. However, it is important to note that constructing deblurring masks using Riemann-Liouville and Caputo fractional derivatives can be quite complex, whereas using Grünwald-Letnikov fractional derivatives is more straightforward.
In this paper, we developed an adaptive mask based on Grünwald-Letnikov fractional derivatives and carefully selected the order of the fractional derivatives using the Wakeby distribution. This approach leads to improved results, particularly when compared to other mask construction methods utilizing Grünwald-Letnikov fractional derivatives.
This article is organized as follows: In the next section, we describe the definition of the Grünwald-Letnikov (GL) fractional derivative. In Section 3, we delve into the construction of a mask using the GL fractional derivative and present our proposed method. In Section 4, we present our experimental results and provide a detailed discussion of them.
2Fundamental Definition of GL Fractional Derivative
The definition of fractional derivatives can vary depending on the context. Three commonly used definitions are the GL definition, the Riemann-Liouville (R-L) definition, and the Caputo definition. Among these, the GL definition is often considered the most appropriate for image processing applications (Frackiewicz and Palus, 2024; Mortazavi et al., 2023; Zuffi et al., 2024). The Caputo fractional derivative is typically employed in fields such as control theory (Moon, 2023; Frederico, 2008; Kamocki and Majewski, 2015; Sweilam et al., 2021; Bergounioux and Bourdin, 2020), viscoelastic materials (Freed and Diethelm, 2007; Li and Ma, 2023; Mahiuddin et al., 2020; Bhangale et al., 2023), and biological systems (Yusuf et al., 2021; Qureshi, 2020; Rahman et al., 2022; Uçar and Özdemir, 2021). In contrast, the Riemann-Liouville fractional derivative is predominantly utilized in the realms of physics and engineering (Ahmad et al., 2021; Gu et al., 2019; Khan et al., 2024; Liu et al., 2011). Caputo Fractional Derivative usually used in the field of control theory (Moon, 2023; Frederico, 2008; Kamocki and Majewski, 2015; Sweilam et al., 2021; Bergounioux and Bourdin, 2020), Viscoelastic Materials (Freed and Diethelm, 2007; Li and Ma, 2023; Mahiuddin et al., 2020; Bhangale et al., 2023), Biological Systems (Yusuf et al., 2021; Qureshi, 2020; Rahman et al., 2022; Uçar and Özdemir, 2021).
For a function
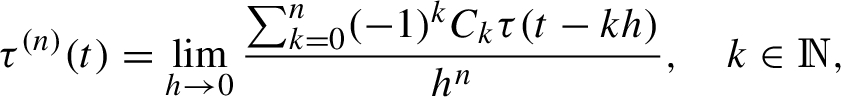
where
The concept has the potential for extension to the widely used GL fractional derivative of order v, enabling the calculation of a non-integer number of derivatives. This is expressed as Atici et al. (2021):
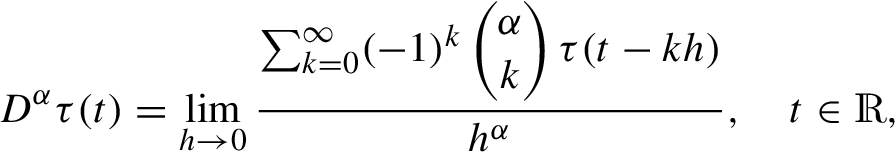
where
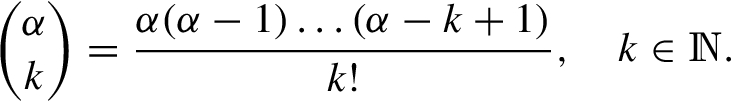
For the function 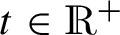 , the truncated GL fractional derivative of order α is:
, the truncated GL fractional derivative of order α is:
3Novel Approach
In this section, we outline our approach for constructing a fractional differential mask using the Grünwald-Letnikov fractional derivative, and we also present a method to choose a suitable value for the order of the fractional derivative at different points in the images.
3.1Development of Fractional Differential Masks
Suppose
Let’s consider
In a 2D digital image, the backward differences of fractional differentiation for x- and y-directions can be found as:
(1)
(2)
To create a mask of size
The pixel value in an image is influenced by its neighbouring pixels, with the influence decreasing as the distance from the pixel increases. The template in the x direction is centred at the fifth row and third column in Table 1 (the first mask). There are 5 pixels located at a distance of one pixel from the centre, and the weight
Table 1
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | ||||
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 |
In a similar manner, we apply the aforementioned approach to the second mask in the y direction as presented in Table 1. For the last mask in Table 1, there are
Table 2
Modified mask of size
| 1 | ||||
| 1 |
| 1 |
Once the masks in the eight directions
Table 3
Resultant mask of size
| 8 | ||||||||
3.2Choosing the Appropriate Fractional Order
The fractional order of derivatives in different parts of an image should be chosen in such a way that enhances the edges, preserves smooth areas and highlights the textural features. To achieve these objectives, the desired image is initially segmented into three distinct regions: edges, smooth areas, and textures. Subsequently, specific fractional derivative orders are selected for each region in order to tailor their effects accordingly. For edge enhancement, a higher value of the fractional derivative parameter (represented as α) close to 1 is chosen. This helps in enhancing the edges and capturing fine details in the image gradient. In the case of textured areas, a smaller value of the fractional derivative parameter α is considered. This allows for a more nuanced differentiation and highlight of textural features present in the image. Finally, for smooth areas, a value of α close to zero is utilized. This choice ensures that the smooth regions are preserved without introducing unnecessary high-frequency components. By carefully selecting suitable fractional derivative orders for different image regions, it becomes possible to effectively construct masks that optimize edge enhancement, maintain smooth areas, and highlight textural features, contributing to the overall quality and interpretability of the processed image.
Using statistical analysis, we can examine the data from the image matrix and identify that it conforms to the Wakeby distribution. The Wakeby distribution is characterized by its quantile function:
To utilize this distribution, we can employ the fifth and ninety-fifth percentiles in the following manner: let X be the values of the pixels in our image, arranged in a vector and sorted from least to greatest. Let n be the size of vector X and let q represent the percentile quantile. To find the qth quantile, we use the formula:
Table 4
| 1 | ||
Table 5
| 1 | ||||
Table 6
| 1 | ||||||
The categorization of pixels into edge, texture, or smooth classes relies on the computation of a gradient image. For this purpose, the image I is convolved with an averaging mask, such as the masks in Tables 4, 5 and 6 to obtain the gradient matrix G. Then, based on specific threshold values, pixels are divided into these three categories. Here we put
(3)
Smooth pixels receive a low fractional order to ensure preservation of smooth regions. The fractional order κ is applied to process the texture region in order to preserve weaker textures and enhance strong texture pixels. The value of κ is determined by the gradient value, with larger values assigned to pixels with high gradients in the range
(4)
(5)
Fig. 1
The values of PSNR, SD, Entropy, ENL, BRISQE, AG, PIQE and CV for
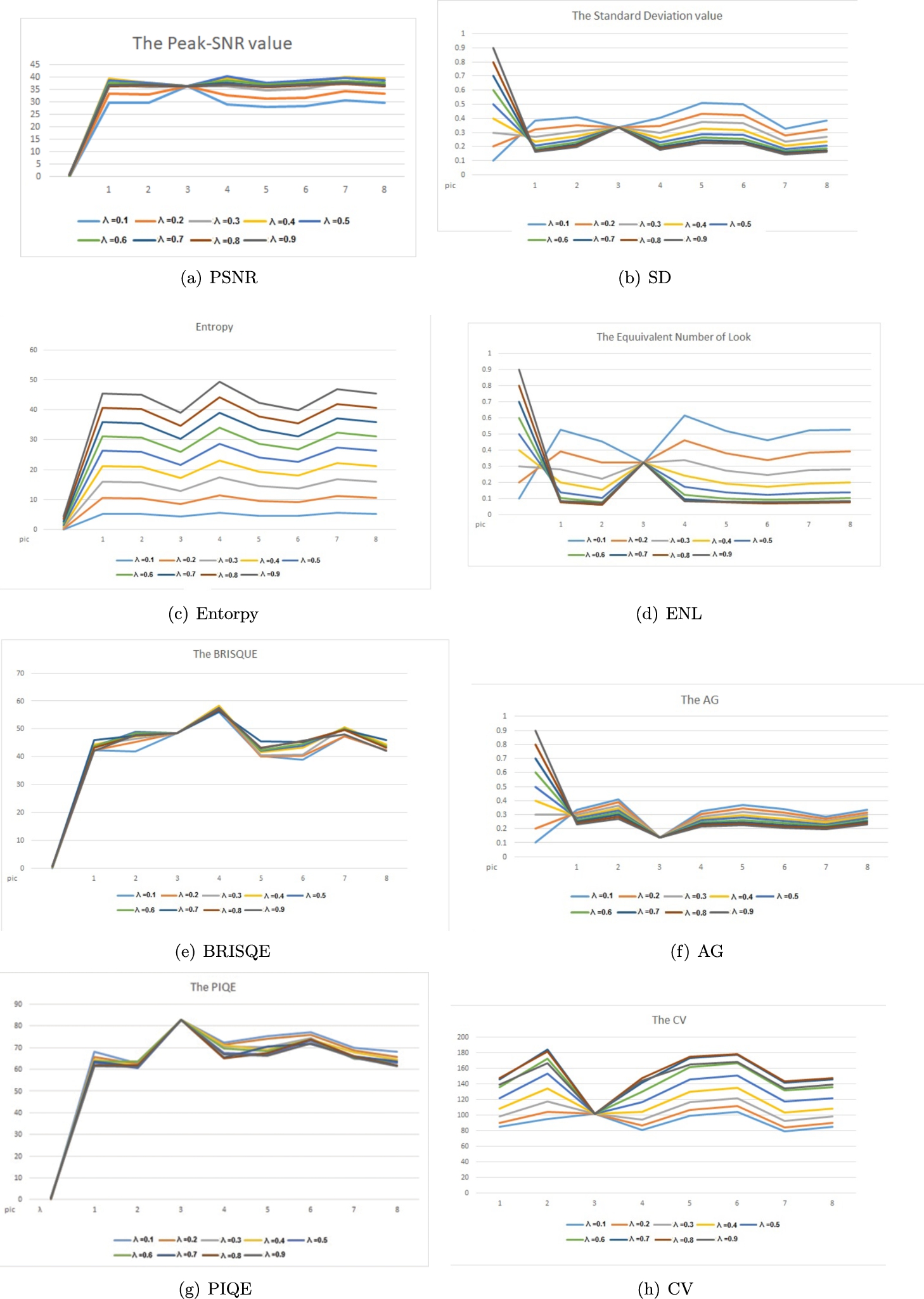
By applying an appropriate fractional order differential mask, every pixel in the image undergoes convolution, resulting in an improved image that enhances edges and highlights texture while maintaining the integrity of smooth areas.
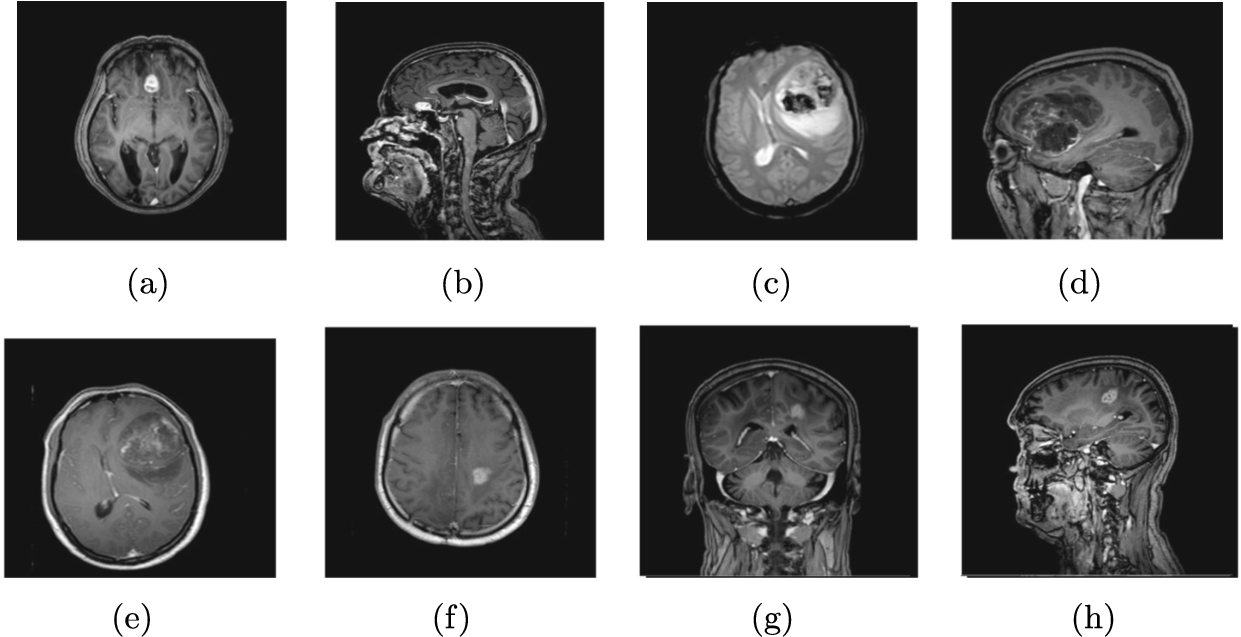
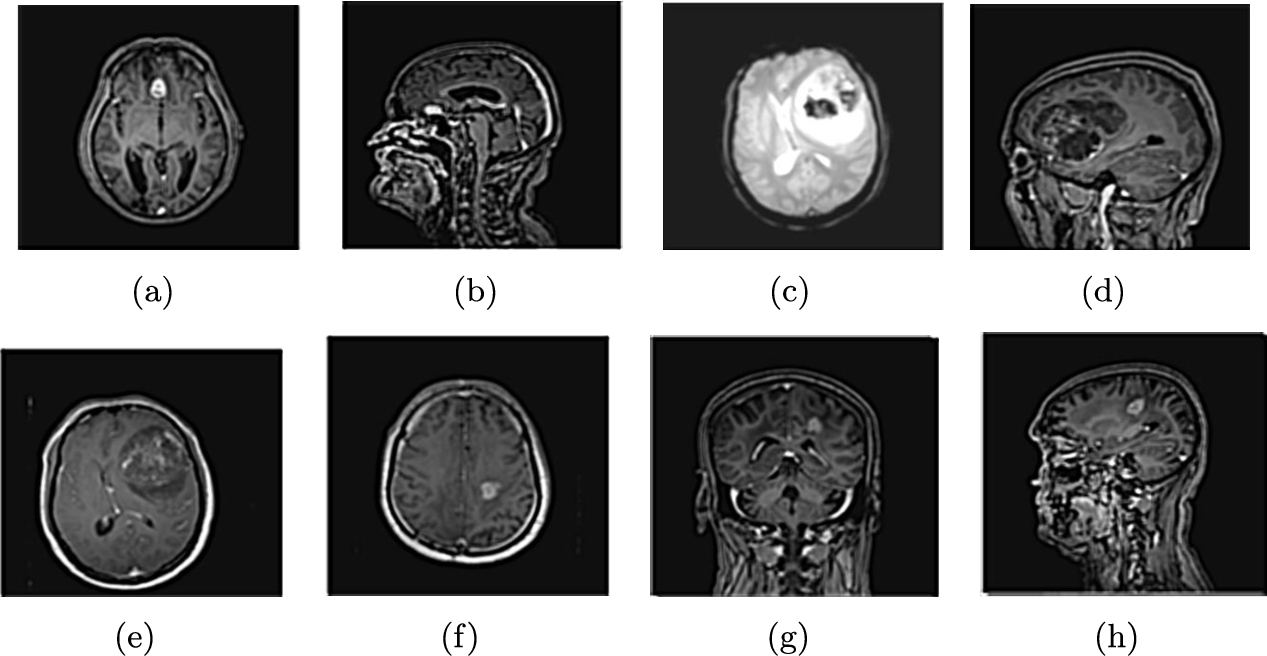
Fig. 2
Original brain images.
The following algorithm illustrates the necessary steps for image deblurring.
Fig. 3
Blurred brain images.
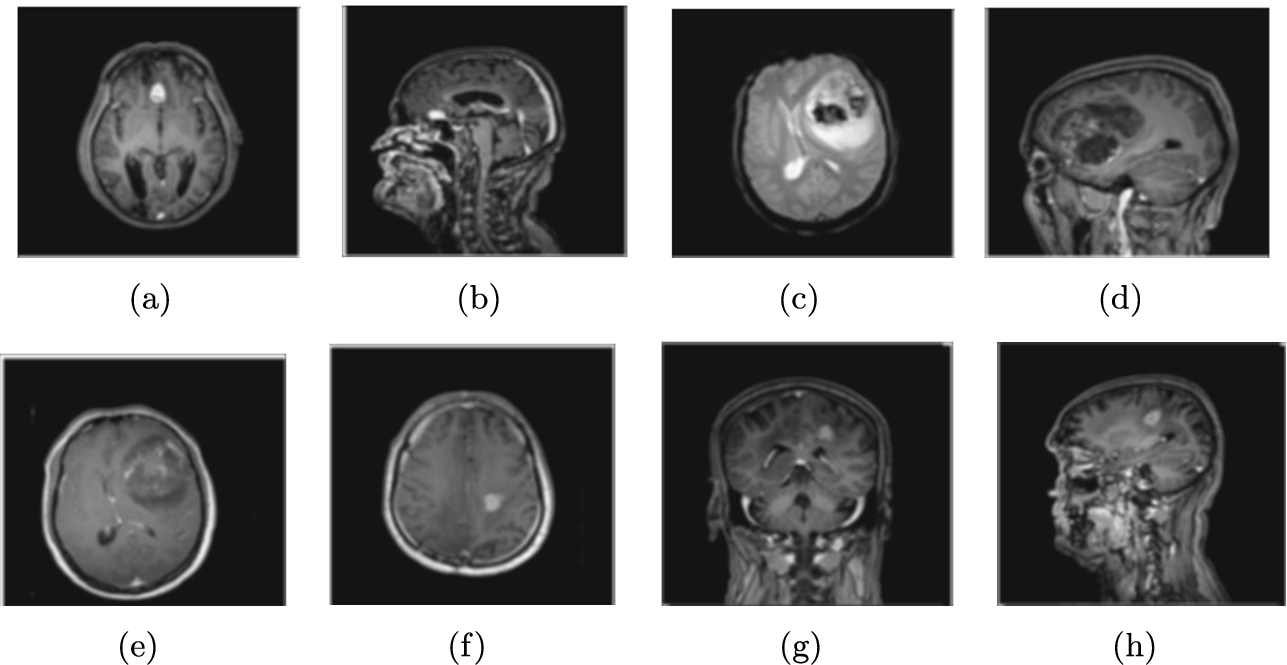
Fig. 4
Deblurred brain images.
4Empirical Findings and Discussions
The efficiency of the proposed algorithm was evaluated using eight brain images, as shown in Fig. 2. These images were blurred, as depicted in Fig. 3, and subsequently deblurred using the presented method, illustrated in Fig. 4. To demonstrate the efficiency of the presented method, we use different criteria and compare our results to other methods. We also provide brief definitions of these criteria below.
4.1PSNR
Peak Signal-to-Noise Ratio (PSNR) is a metric to measure the quality of a reconstructed or processed image compared to the original image. It is calculated by comparing the peak signal strength to the noise level in the image, providing a quantitative measure of the fidelity of the reconstructed image. The higher values of PSNR indicate a higher level of similarity between the original and modified images. The formula for calculating PSNR is:
Table 7 shows the PSNR values of deblurred test images and compares the results to other methods in the literature.
Table 7
Comparing PSNR rate for test images.
| Proposed method | MGL (Hemalatha and Anouncia, 2018) | |||||
| Image | Blurred image | Deblurred image | Adaptive (Wadhwa and Bhardwaj, 2020) | ADFA (Li and Xie, 2015) | ||
| a | 22.5824 | 31.0507 | 17.7232 | 28.5643 | 15.3211 | |
| b | 19.5427 | 30.8592 | 16.916 | 24.5577 | 12.6556 | |
| c | 22.5329 | 36.3296 | 20.6807 | 33.2279 | 17.1651 | |
| d | 22.6419 | 35.9398 | 19.7146 | 28.2865 | 13.9391 | |
| e | 21.5470 | 33.9197 | 19.5176 | 29.3097 | 16.7414 | |
| f | 21.6181 | 35.3671 | 19.847 | 30.7506 | 17.3028 | |
| g | 20.8060 | 32.5681 | 18.4106 | 27.6775 | 13.783 | |
| h | 20.1791 | 31.9848 | 16.9364 | 24.5164 | 12.6009 | |
4.2AMBE
The Average Mean Brightness Error (AMBE) is a metric used to quantify the average difference in brightness between a reference image and a processed image. It is calculated by taking the mean of the absolute differences in brightness values for corresponding pixels in the two images. AMBE provides a measure of the overall brightness distortion introduced during image processing or restoration. The best result is a zero AMBE value.
Table 8 presents the AMBE values for the deblurred test images and contrasts these results with those from other methods found in the literature. Meanwhile, Table 9 offers an in-depth comparison of the PSNR and AMBE metrics, detailing their average values and standard deviations. The findings indicate that the average scores for both PSNR and AMBE notably surpass those of existing state-of-the-art methods in nearly all cases. This highlights the effectiveness of the proposed approach in enhancing the quality of medical images.
Table 8
Comparing AMBE rate for test images.
| Proposed method | MGL (Hemalatha and Anouncia, 2018) | ||||
| Image | Deblurred image | Adaptive (Wadhwa and Bhardwaj, 2020) | ADFA (Li and Xie, 2015) | ||
| a | 0.0184 | 0.3521 | 5.0795 | 0.6157 | 8.0261 |
| b | 0.0380 | 0.5516 | 6.9137 | 1.7944 | 15.881 |
| c | 0.1048 | 0.1595 | 2.6175 | 0.4138 | 4.0873 |
| d | 0.0268 | 0.205 | 3.8883 | 0.7204 | 11.3506 |
| e | 0.0357 | 0.2615 | 2.9863 | 0.5015 | 4.3518 |
| f | 0.0338 | 0.1754 | 2.6159 | 0.3969 | 4.155 |
| g | 0.0342 | 0.4024 | 5.5945 | 1.031 | 12.9937 |
| h | 0.0366 | 0.3983 | 6.5385 | 1.6116 | 14.7137 |
Table 9
Assessment of average values and standard deviations of performance metrics for advanced methods.
| Proposed | ||
| Fuzzy (Wadhwa and Bhardwaj, 2024) | ||
| Morphology (Wadhwa and Bhardwaj, 2021) | ||
| Chaira (Ensafi and Tizhoosh, 2005) | ||
| CLAHE (Li and Xie, 2015) | ||
| HE (Li and Xie, 2015) | ||
| GC (Li and Xie, 2015) | ||
| ADFA (Li and Xie, 2015) | ||
| MGL (Hemalatha and Anouncia, 2018) |
4.3Entropy
Entropy refers to a measure of the amount of information or uncertainty present in an image. It quantifies the randomness or disorder in the distribution of pixel values within the image. Images with higher entropy contain more diverse and unpredictable pixel values, while images with lower entropy have more uniform pixel distributions. Entropy is commonly used in image analysis to assess the complexity or texture of an image, as well as to evaluate the quality of compression and encoding algorithms. The entropy of an image can be calculated as:
Table 10 displays the Entropy values for deblurred test images and contrasts the findings with those from other methods documented in the literature.
Table 10
Comparing Entropy rate for test images.
| Proposed method | MGL (Hemalatha and Anouncia, 2018) | |||||
| Image | Blurred | Deblurred image | Adaptive (Wadhwa and Bhardwaj, 2020) | ADFA (Li and Xie, 2015) | ||
| a | 3.9288 | 4.3115 | 3.2035 | 2.8469 | 3.0903 | 2.4986 |
| b | 4.7521 | 5.0517 | 3.8652 | 3.295 | 3.5492 | 2.4328 |
| c | 4.1223 | 4.3227 | 3.3237 | 3.1764 | 3.2533 | 3.0656 |
| d | 5.1789 | 5.5790 | 4.5531 | 4.299 | 4.4412 | 3.7025 |
| e | 4.4722 | 4.7190 | 3.6527 | 3.2962 | 3.5781 | 3.2188 |
| f | 4.0355 | 4.3960 | 3.2814 | 2.9551 | 3.2641 | 2.9198 |
| g | 4.7184 | 5.1486 | 4.1601 | 3.8553 | 4.005 | 3.2697 |
| h | 4.7142 | 5.0675 | 4.0502 | 3.5105 | 3.7824 | 2.6725 |
4.4Standard Deviation (SD)
The standard deviation (SD) is the square root of the noise variance and is commonly used to analyse the contrast-level of an image. It finds applications in various fields of image processing, such as image denoising and image fusion. A higher SD value typically corresponds to better perceptual image quality.
Table 11 displays the SD values for deblurred test images.
Table 11
SD rate for test images.
| a | 0.1763 | 0.2561 |
| b | 0.1616 | 0.2480 |
| c | 0.2249 | 0.3378 |
| d | 0.1643 | 0.2327 |
| e | 0.2045 | 0.2909 |
| f | 0.2024 | 0.2817 |
| g | 0.1358 | 0.1847 |
| h | 0.1608 | 0.2077 |
4.5Equivalent Number of Look (ENL)
This metric is used to evaluate the level of smoothing in an image, especially in its homogeneous areas. It is computed by taking the ratio of the mean squared value to the variance. This measure is commonly applied in the context of reducing speckle noise in images.
Table 12 displays the ENL values for deblurred test images.
Table 12
ENL rate for test images.
| a | 0.2094 | 0.1179 |
| b | 0.2463 | 0.1052 |
| c | 0.2264 | 0.3234 |
| d | 0.3129 | 0.1717 |
| e | 0.2711 | 0.1372 |
| f | 0.2396 | 0.1234 |
| g | 0.2703 | 0.1342 |
| h | 0.2665 | 0.1398 |
4.6Blind/Referenceless Image Spatial Quality Evaluator (BRISQUE)
BRISQUE utilizes a probabilistic analysis of local normalized luminance signals to evaluate the naturalness of an image. A lower BRISQUE value indicates better perceptual image quality.
Table 13 displays the BRISQUE values for deblurred test images.
Table 13
BRISQUE rate for test images.
| a | 45.2041 | 42.0564 |
| b | 43.3720 | 48.9763 |
| c | 47.766 | 48.5174 |
| d | 48.0237 | 57.7018 |
| e | 48.1939 | 42.1618 |
| f | 47.5052 | 43.9963 |
| g | 43.0546 | 50.1664 |
| h | 43.8537 | 43.7832 |
4.7Perceptual Image Quality Evaluator (PIQE)
PIQE criteria in image processing refers to a set of objective measures used to assess the quality of an image based on human perception. These criteria take into account various factors such as contrast, sharpness, colour accuracy, and noise levels to determine the overall visual quality of an image. PIQE criteria are used to evaluate and compare the performance of different image processing algorithms and to ensure that the processed images meet certain quality standards.
Table 14 displays the PIQE values for deblurred test images.
Table 14
PIQE rate for test images.
| a | 84.9719 | 72.9859 |
| b | 76.0481 | 60.5201 |
| c | 88.0273 | 82.8545 |
| d | 84.5569 | 67.5805 |
| e | 88.9995 | 67.0446 |
| f | 84.3896 | 73.2536 |
| g | 76.9363 | 65.1521 |
| h | 77.1744 | 63.1113 |
4.8Coefficient of Variation (CV)
This metric assesses the preservation of texture in non-uniform image areas, often used in the context of reducing speckle noise. It is computed as the ratio of the standard deviation to the mean value, expressed as a percentage.
Table 15 displays the CV values for deblurred test images.
Table 15
CV rate for tests images.
| a | 91.7516 | 147.3695 |
| b | 81.0006 | 153.5259 |
| c | 99.6732 | 102.2095 |
| d | 72.4598 | 116.4223 |
| e | 86.8636 | 145.5926 |
| f | 91.9231 | 151.0815 |
| g | 70.8944 | 117.2971 |
| h | 77.6679 | 121.8731 |
4.9Average Gradient (AG)
The Average Gradient (AG) is used to evaluate image sharpness, especially in image fusion applications. It assesses changes in texture and contrast features resulting from the fusion process. A higher AG value suggests enhanced perceptual image quality.
Table 16 displays the AG values for deblurred test images.
Table 16
AG rate for test images.
| a | 0.0897 | 0.2294 |
| b | 0.1247 | 0.3292 |
| c | 0.0791 | 0.1360 |
| d | 0.1024 | 0.2584 |
| e | 0.1188 | 0.2788 |
| f | 0.1099 | 0.2554 |
| g | 0.0881 | 0.2330 |
| h | 0.1019 | 0.2734 |
5Conclusion
In conclusion, our proposed method for image deblurring, based on Grünwald-Letnikov fractional derivation and image segmentation using the Wakeby distribution, has shown promising results. By selecting optimal fractional derivative values for different image categories, we have effectively improved image quality and reduced blurring. The evaluation of our method using criteria such as PSNR, AMBE, Entropy, SD, ENL, BRISQUE etc. has demonstrated its efficiency in image restoration. This approach has the potential to contribute to advancements in image processing and restoration techniques.
References
1 | Aboutabit, N. ((2021) ). A new construction of an image edge detection mask based on Caputo–Fabrizio fractional derivative. The Visual Computer, 37: (6), 1545–1557. |
2 | Amoako-Yirenkyi, P., Appati, J.K., Dontwi, I.K. ((2016) ). A new construction of a fractional derivative mask for image edge analysis based on Riemann-Liouville fractional derivative. Advances in Difference Equations, 2016: , 1–23. |
3 | Ahmad, A., Ali, M., Malik, S.A. ((2021) ). Inverse problems for diffusion equation with fractional Dzherbashian-Nersesian operator. Fractional Calculus and Applied Analysis, 24: (6), 1899–1918. |
4 | Arora, S., Mathur, T., Agarwal, S., Tiwari, K., Gupta, P. ((2022) ). Applications of fractional calculus in computer vision: a survey. Neurocomputing, 489: , 407–428. |
5 | Atici, F.M., Chang, S., Jonnalagadda, J. ((2021) ). Grunwald-Letnikov fractional operators: from past to present. Fractional Differential Equations, 11: (1), 147–159. |
6 | Bergounioux, B., Bourdin, L. ((2020) ). Pontryagin maximum principle for general caputo fractional optimal control problems with bolza cost and terminal constraints. ESAIM: Control, Optimisation and Calculus of Variations, 26: , 35. |
7 | Bhangale, N., Kachhia, K.B., Gómez-Aguilar, J.F. ((2023) ). Fractional viscoelastic models with Caputo generalized fractional derivative. Mathematical Methods in the Applied Sciences, 46: (7), 7835–7846. |
8 | Buades, A., Coll, B., Morel, J. ((2005) ). A non-local algorithm for image denoising. In: 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), pp. 60–65. |
9 | Chandra, S., Bajpai, M. ((2018) ). Effective algorithm for benign brain tumor detection using fractional calculus. In: TENCON 2018 – 2018 IEEE Region 10 Conference. IEEE, pp. 2408–2413. |
10 | Chowdhury, M.R., Qin, J., Lou, Y. ((2020) ). Non-blind and blind deconvolution under poisson noise using fractional-order total variation. Journal of Mathematical Imaging and Vision, 62: , 1238–1255. |
11 | Dong, J., Pan, J., Yang, Z., Tang, J. ((2023) ). Multi-scale residual low-pass filter network for image deblurring. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pp. 12345–12354. |
12 | Ensafi, P., Tizhoosh, H.R. ((2005) ). Type-2 fuzzy image enhancement. In: International Conference on Image Analysis and Recognition. Springer, pp. 159–166. |
13 | Frackiewicz, M., Palus, H. ((2024) ). Application of fractional derivatives in image quality assessment indices. Applied Numerical Mathematics, 204: , 101–110. |
14 | Frederico, G.S.F. ((2008) ). Fractional optimal control in the sense of Caputo and the fractional Noether’s Theorem. International Mathematical Forum, 3: (10), 479–493. |
15 | Freed, A.D., Diethelm, K. ((2007) ). Caputo derivatives in viscoelasticity: a non-linear finite-deformation theory. Fractional Calculus & Applied Analysis, 10: (3), 219–248. |
16 | Gholami Bahador, F., Mokhtary, P., Lakestani, M. ((2022) ). A fractional coupled system for simultaneous image denoising and deblurring. Computers and Mathematics with Applications, 128: , 285–299. |
17 | Golami Bahador, F., Mokhtary, P., Lakestani, M. ((2023) ). Mixed Poisson-Gaussian noise reduction using a time-space fractional differential equations. Information Sciences, 647: , 119417. |
18 | Gu, Y., Wang, H., Yu, Y. ((2019) ). Stability and synchronization for Riemann-Liouville fractional-order time-delayed inertial neural networks. Neurocomputing, 340: , 270–280. |
19 | Hacini, M., Hachouf, F., Charef, A. ((2020) ). A bi-directional fractional-order derivative mask for image processing applications. IET Image Processing, 14: (11), 2512–2524. |
20 | Hemalatha, S., Anouncia, S.M. ((2018) ). G-1 fractional differential operator modified using auto-correlation function: texture enhancement in images. Ain Shams Engineering Journal, 9: (4), 1689–1704. |
21 | Ibrahim, R.W. ((2020) ). A new image denoising model utilizing the conformable fractional calculus for multiplicative noise. SN Applied Sciences, 2: , 32. |
22 | Irandoust–pakchin, S., Babapour, S., Lakestani, M. ((2021) ). Image deblurring using adaptive fractional–order shock filter. Mathematical Methods in the Applied Sciences, 44: (6), 4907–4922. |
23 | Ismail, S.M., Said, L.A., Radwan, A.G., Madian, A.H., Abu-ElYazeed, M.F. ((2020) ). A novel image encryption system merging fractional-order edge detection and generalized chaotic maps. Signal Processing, 167: , 107280. |
24 | Kamocki, R., Majewski, M. ((2015) ). Fractional linear control systems with Caputo derivative and their optimization. Optimal Control Applications and Methods, 36: (6), 953–967. |
25 | Khan, L., Khan, L., Agha, S., Hafeez, K., Iqbal, J. ((2024) ). Passivity-based Rieman Liouville fractional order sliding mode control of three phase inverter in a grid-connected photovoltaic system. PLOS ONE, 19: (2), e0296797. |
26 | Lavín-Delgado, J.E., Solís-Pérez, J.E., Gómez-Aguilar, J.F., Escobar-Jiménez, R.F. ((2020) ). A new fractional-order mask for image edge detection based on Caputo-Fabrizio fractional-order derivative without singular kernel. Circuits, Systems, and Signal Processing, 39: , 1419–1448. |
27 | Li, B., Xie, W. ((2015) ). Adaptive fractional differential approach and its application to medical image enhancement. Computers & Electrical Engineering, 45: , 324–335. |
28 | Li, D., Tian, X., Jin, Q., Hirasawa, K. ((2018) ). Adaptive fractional-order total variation image restoration with split Bregman iteration. ISA Transactions, 82: , 210–222. |
29 | Li, J., Ma, J. ((2023) ). A unified Maxwell model with time-varying viscosity via ψ-Caputo fractional derivative coined. Chaos, Solitons & Fractals, 177: , 114230. |
30 | Li, K., Wang, X. ((2023) ). Image denoising model based on improved fractional calculus mathematical equation. Applied Mathematics and Nonlinear Sciences, 8: (1), 655–660. |
31 | Li, Z., Gao, Z., Yi, H., Fu, Y., Chen, B. ((2023) ). Image deblurring with image blurring. IEEE Transactions on Image Processing, 32: , 5595–5609. |
32 | Liu, F., Yang, Q., Turner, I., ((2011) ). Two new implicit numerical methods for the fractional cable equation. Journal of Computational and Nonlinear Dynamics, 6: (1), 011009. |
33 | Liu, J., Jieqing, T., Ge, X., Hu, D., He, L. ((2022) ). Blind deblurring with fractional-order calculus and local minimal pixel prior. Journal of Visual Communication and Image Representation, 89: , 103645. |
34 | Mahiuddin, Md., Godhani, D., Feng, L., Liu, F., Langrish, T., Karim, A. ((2020) ). Application of Caputo fractional rheological model to determine the viscoelastic and mechanical properties of fruit and vegetables. Postharvest Biology and Technology, 163: , 111147. |
35 | Moon, J. ((2023) ). On the optimality condition for optimal control of Caputo fractional differential equations with state constraints. IFAC-PapersOnLine, 56: (1), 216–221. |
36 | Mortazavi, M., Gachpazan, M., Amintoosi, M., Salahshour, S. ((2023) ). Fractional derivative approach to sparse super-resolution. The Visual Computer, 39: , 3011–3028. |
37 | Nema, N., Shukla, P., Soni, V. ((2020) ). An adaptive fractional calculus image denoising algorithm in digital reflection dispensation. Research Journal of Engineering and Technology, 11: (1), 15–23. |
38 | Podlubny, I. ((1998) ). Fractional Differential Equations. Elsevier. |
39 | Pooja, S., Mallikarjunaswamy, S., Sharmila, N. ((2023) ). Image region driven prior selection for image deblurring. Multimedia Tools and Applications, 82: , 24181–24202. |
40 | Qureshi, S. ((2020) ). Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system. Chaos, Solitons & Fractals, 134: , 109744. |
41 | Rahman M.U., Althobaiti, A., Riaz, M.B., Al-Duais, F.S. ((2022) ). A theoretical and numerical study on fractional order biological models with Caputo fabrizio derivative. Fractal and Fractional, 6: , 446. |
42 | Ren, M., Delbracio, M., Talebi, H., Gerig, G., Milanfar, P. ((2023) ). Multiscale structure guided diffusion for image deblurring. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pp. 10721–10733. |
43 | Saadia, A., Rashdi, A. ((2016) ). Echocardiography image enhancement using adaptive fractional order derivatives. In: 2016 IEEE International Conference on Signal and Image Processing (ICSIP), pp. 166–169. |
44 | Sweilam, N.H., Nagy, A.M., Al-Ajami, T.M. ((2021) ). Numerical solutions of fractional optimal control with Caputo–Katugampola derivative. Advances in Difference Equations, 2021: , 425. |
45 | Uçar, E., Özdemir, N. ((2021) ). A fractional model of cancer-immune system with Caputo and Caputo–Fabrizio derivatives. The European Physical Journal – Plus, 136: , 43. |
46 | Wadhwa, A., Bhardwaj, A. ((2020) ). Enhancement of MRI images of brain tumor using Grünwald Letnikov fractional differential mask. Multimedia Tools and Applications, 79: (35–36), 25379–25402. |
47 | Wadhwa, A., Bhardwaj, A. ((2021) ). Contrast enhancement of MRI images using morphological transforms and PSO. Multimedia Tools and Applications, 80: (14), 21595–21613. |
48 | Wadhwa, A., Bhardwaj, A. ((2024) ). Enhancement of MRI images using modified type-2 fuzzy set. Multimedia Tools and Applications, 83: , 75445–75460. https://doi.org/10.1007/s11042-024-18569-2. |
49 | Yang, Q., Chen, D., Zhao, T., Chen, Y.Q ((2016) ). Fractional calculus in image processing: a review. Fractional Calculus and Applied Analysis, 19: , 1222–1249. |
50 | Yusuf, A., Acay, B., Inc, M. ((2021) ). Analysis of fractional-order nonlinear dynamic systems under Caputo differential operator. Mathematical Methods in the Applied Sciences, 44: (13), 10861–10880. |
51 | Zhou, C., Teng, M., Han, J., Liang, J., Xu, C., Cao, G., Shi, B. ((2023) ). Deblurring low-light images with events. International Journal of Computer Vision, 131: , 1284–1298. |
52 | Zuffi, G.A., Lobato, F.S., Cavallini, A.A., Stefen, V. ((2024) ). Numerical solution and sensitivity analysis of time–space fractional near-field acoustic levitation model using Caputo and Grünwald–Letnikov derivatives. Soft Computing, 28: (13–14), 8457–8470. https://doi.org/10.1007/s00500-024-09757-1. |



