Developing a risk assessment method for infectious diseases focusing on COVID-19 based on the Delphi method and fuzzy analytical hierarchy process
Abstract
BACKGROUND:
Given the coronavirus 2019 (COVID-19) risk, it is essential to develop a comprehensive risk assessment method to manage the risk of the infectious diseases.
OBJECTIVE:
This study aimed to develop a risk assessment method for infectious diseases focusing on COVID-19.
METHOD:
This study was based on the fuzzy Delphi method (FDM) and fuzzy analytical hierarchical process (FAHP) in three steps: (a) designing the preliminary risk assessment algorithm by reviewing the literature, (b) corroborating the designed structure based on the majority opinions of the expert panel and assigning scores to different factors according to the Delphi method, and (c) determining the weight of components and their factors based on the FAHP.
RESULTS:
The COVID-19 risk index (CVRI) was found to be affected by four components and 19 factors. The four components consisted of the probability of getting sick (5 factors), disease severity (4 factors), health beliefs level (3 factors), and exposure rate (6 factors). The identified components and their relevant factors had different weights and effects on the CVIR. The weights of probability, severity, health beliefs level, and exposure rate components were 0.27, 0.20, 0.14, and 0.38, respectively. The CVRI was found to range from 0.54 to 0.82, defined in three levels.
CONCLUSION:
Given the significant effects of identified components, factors, and parameters on the incidence of COVID-19 on the one hand and using the FDM and FAHP on the other, the proposed method can be considered as an appropriate method for managing the risk of COVID-19 and other infectious diseases.
1Introduction
The coronavirus 2019 (COVID-19) outbreak has been regarded as the biggest challenge that public health, the international economy, and national/international policies have been facing in the new century [1, 2]. The COVID-19 pandemic has seriously threatened the health of employees as the most important sector of societies. The disease is highly infectious because, as of February 14, 2021, it has infected 109,252,808 people and killed 2,408,104 patients around the world. Thus, considering such a critical condition, any measures possible should be taken to manage the risk of the disease [3].
Although various methods have been proposed and developed for assessing and managing health-threatening risks in different work environments, the majority of such methods are based on mechanical, physical, chemical, and ergonomic dangers known as the most frequent sources of danger in work environments. The assessment of biological risks, particularly infectious diseases such as COVID-19, is a far cry from the risk assessment of other types of danger, which has gone mostly unnoticed by industries and organizations thus far. One of the most popular methods introduced for risk assessment is the quantitative assessment and determination of personal and environmental exposure rates and the comparison of such rates with the permissible limits [4, 5]. The risk assessment of exposure to different types of biological dangers and the risk assessment of diseases resulting from exposure to such biological dangers are based on a variety of risk factors including the potential danger of biological factors, the sensitivity of people in exposure, the disease-causing capability of biological factors, the durability condition of biological factors in the exposure environment, the availability of preventive health services, and the readiness of medical and healthcare systems to deal with biological factors [6, 7].
The evaluation of modern management systems shows that the identification and assessment of dangers and their risks are necessary steps for these systems to proceed robustly, and the assessment and control of such risks can be considered as the main aim of these systems seeking to develop and improve their organizations. Moreover, these risk assessment and management processes can eventually result in the improvement of organizations’ success rate and efficiency. Thus, given the main consequence of the COVID-19 pandemic that is endangering people’s lives, any possible measures aiming to reduce COVID-19 risk can remarkably increase the efficiency of organizations and factories, hence decreasing the negative socioeconomic and humanistic impacts of the disease [8–11].
Now that the mortality rate of COVID-19 has risen substantially across the world, it is of high importance to increase public awareness regarding the potential risks of the disease [12, 13]. Countries have tried to deal with the disease in different ways, ranging from social distancing and forcing people to wear masks to complete lockdowns. All these measures have been taken to halt the spread of COVID-19 and reduce the vulnerability of medical and healthcare systems. Nonetheless, past experiences of fighting against previous pandemics suggest that for preventive and treatment methods to be effective, the public needs to be cognizant of the risks of diseases [14].
Although reaching positive clinical results in dealing with the COVID-19 pandemic and treating COVID-19 patients successfully are vital, it is also crucially important to assess and manage COVID-19 risk in different work environments. Therefore, bearing the unique characteristics of COVID-19 in mind, impacting all work sectors and employees, the development of a comprehensive and practical assessment algorithm for assessing and managing COVID-19 risk in work environments gains immediate significance [6, 15]. Hence, this study aimed to develop a semi-quantitative method to assess COVID-19 risk.
2Materials and methods
This study was conducted based on the fuzzy Delphi method and FAHP.
3The study steps
The process of carrying out the study consisted of three steps (Fig. 1). In the first step, the authors designed the initial algorithm of COVID-19 risk assessment based on reviewed literature and the importance and role of different components and factors. In this algorithm, the risk score was measured by multiplying the four main components of exposure rate, probability of getting sick, disease severity, and health beliefs level according to the following equation:
(1)
Fig. 1
The hierarchy of components and factors affecting COVID-19 risk.
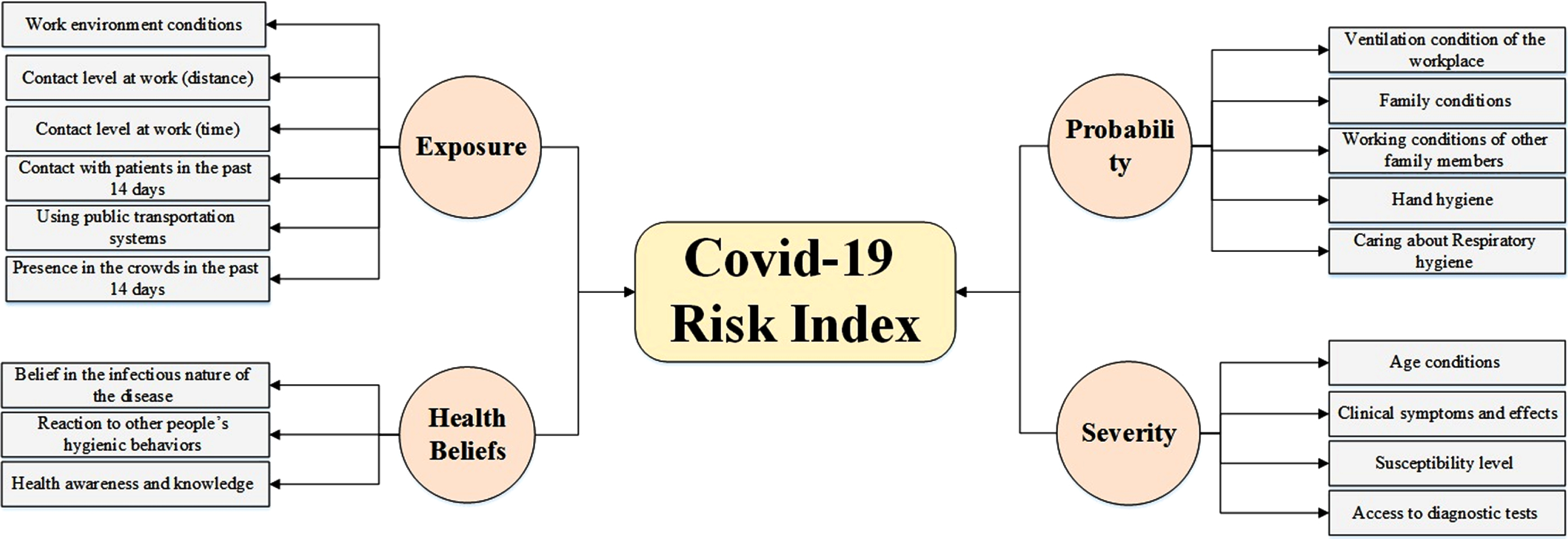
In this step, because each of the four main components was influenced by different factors, and each factor could have a different condition with a different effect on risk rates, factors and their conditions were initially extracted after reviewing previous literature. First, different previous studies on COVID-19, its risks, and its characteristics were reviewed. Then, the presented information in the ninth version of the COVID-19 diagnosis and treatment flowchart by the Iran Ministry of Health and Medical Education (January 2021) was scrutinized together with the latest guidelines issued by the World Health Organization, International Labor Organization, and the U.S. Center for Disease Control and Prevention (12–15). After extracting factors and their different conditions, the initial structure of the risk assessment worksheet, including components, factors, and conditions, was developed according to the opinions and brainstorming of the expert panel.
In the second step, the developed worksheet and its structure had to be corroborated by the majority opinion of the expert panel. Moreover, since each of the identified factors could have different conditions, it was necessary to assign a quantitative score to each factor’s condition based on the expert panel’s opinions. This step was carried out according to the fuzzy Delphi method and the majority opinion of the expert panel in three rounds. In the first round, the developed worksheet was sent to the experts, and they were asked to add any conditions that they thought were missing from the worksheet. After collecting their opinions, minor suggested modifications were applied, and the structure of the assessment worksheet was corroborated. In the second round of the Delphi method, the experts were asked to judge the effect of each factor’s condition on the main component in the form of linguistic expressions (very strong, strong, moderate, weak, and very weak). After collecting their opinions, the expressions were given quantitative weights according to triangular fuzzy numbers, and experts’ opinions were finalized. Eventually, in the third Delphi round, to measure the final scores for components and their factors, the expert panel was able to modify their opinions based on the results of the first round. After collecting the required data in the third Delphi round, the Delphi rounds were finished. In the end, the triangular fuzzy numbers were turned into crisp numbers so that each factor’s condition received a specific score. Of note, the expert panel for conducting the fuzzy Delphi method consisted of 25 experts with different specialties including risk assessment, epidemiology, health education, pulmonology, and infectious diseases.
In the third step, it was decided that the weight of the four main components and their relevant factors be measured based on the opinions of the expert panel and FAHP because it was hypothesized that the four components could not exert similar effects on COVID-19 risk. Accordingly, the hierarchy of components and their factors affecting COVID-19 risk were developed as observed in Fig. 1, and their weights were measured based on the FAHP and expert panel opinions. The expert panel for conducting FAHP consisted of 22 experts with different specialties including risk assessment, epidemiology, health education, pulmonology, and infectious diseases.
4Fuzzy logic
Using crisp scoring methods for linguistic expressions can be problematic in two aspects. First, crisp methods may result in ambiguous people’s judgments, and changes are not appropriately reflected in linguistic expressions. Second, people’s mental judgments and their prioritizations heavily affect the results [16]. Fuzzy logic is a useful tool for measuring ambiguous concepts related to people’s mental judgments [17]. It is a form of multi-valued logic in which the accuracy values of variables can be any real number ranging from zero to one [18]. This method is a robust instrument to fight against ambiguities and mistrusts in people’s mental judgments and evaluations [16].
There are different types of fuzzy numbers with triangular fuzzy numbers being the most practical ones. A triangular fuzzy number is shown as A = (l, m, u) in which l, m, and u represent a fuzzy set. The upper bound (u) is a maximum value that the fuzzy number A can take. The lower bound is the minimum value that the fuzzy number A can take. The ‘m’ value is the most probable value of a fuzzy number [16]. The membership function of a triangular fuzzy number is:
5The fuzzy Delphi method
The fuzzy Delphi technique is a qualitative method aiming to reach consensus over a group of people’s decisions. In other words, it is used to extract the majority opinions of a group of experts to reach a final judgment regarding a specific topic [19]. The fuzzy version of the Delphi method is a method in which fuzzy numbers are employed to reach final judgments based on experts’ opinions. The main advantage of this method is its simplicity to reach consensus and final decisions close to reality [20]. Therefore, the fuzzy Delphi method was used in this study. The selection of expert panel in the Delphi method is goal-oriented and according to the knowledge, experience, and expertise of experts in particular fields of study [21]. Generally, an expert panel consisting of 10 to 18 experts will be enough to reach valid results [19, 20].
6Analytical Hierarchy Process (AHP)
The Analytic Hierarchy Process (AHP) is one of the most popular, multicriteria methods of decision-making, mostly used when there are several qualitative or quantitative criteria in a research design [22]. The main aim of this process is to determine factors based on which rival options are compared to each other [23]. The next step is to measure and determine the relative weights (values) of criteria and sub-criteria by pairwise comparisons and based on expert judgments. The experts compare the selected criteria and decide on the score of each criterion in comparison to another one. In other words, the row variables are compared together pairwise and given weights. The comparison and weighing are recorded in a K×K matrix. The pairwise comparison is done based on weighing the row variable against the column variable with the weighing scores ranging from 1 to 9 in a form of linguistic expressions (Table 1). It should be mentioned that the pairwise comparison matrix is an inverse matrix, meaning that if the value of the row variable ‘a’ compared to the column variable ‘b’ equals two, the index values of the row variable ‘b’ compared to the column variable ‘a’ equal 0.5 [24].
Table 1
Linguistic expressions and their equivalent fuzzy weights
| Linguistic expressions | Numerical weights | Fuzzy weights (triangular) |
| Absolutely more important | 9 | (8, 9, 9) |
| In-between | 9 | (7, 8, 9) |
| Definitely more important | 7 | (6, 7, 8) |
| In-between | 6 | (5, 6, 7) |
| Relatively more important | 5 | (4, 5, 6) |
| In-between | 4 | (3, 4, 5) |
| A little more important | 3 | (2, 3, 4) |
| In-between | 2 | (1, 2, 3) |
| As important | 1 | (1, 1, 1) |
Different studies have combined the fuzzy method with AHP to form hybrid methods under the umbrella term FAHP to rank and weigh criteria and sub-criteria. The current study used the FAHP method introduced by Chang because it is easier to conduct with precise results. As every type of error and incompatibility in comparisons can seriously influence the final results, it is essential to corroborate the validity of the expert panel’s responses and data. If the incompatibility rate is below 0.1, the comparisons are said to be compatible, corroborating the responses of the expert panel [25]. Hence, the incompatibility rates of all pairwise comparison matrixes were measured, and incompatible responses were removed from the study.
After collecting the required information from the expert panel and corroborating the validity of the data, pairwise comparison matrixes were formed based on the opinions of the expert panel. Various methods have been introduced for measuring the mean matrix and the relative weights of criteria and sub-criteria such as the row sum, column sum, arithmetic mean, and geometric mean. In this study, the geometric mean was used. To measure the weights of options in this method, first, the mean of standard matrix rows is calculated and then normalized. Next, the relative weights of criteria and sub-criteria are measured, and the most effective factors and sub-factors are identified [25]. In an AHP, the final weights of options are calculated by multiplying the significance of criteria by the weights of options. To do so, the hierarchical combination principle is used, yielding a priority vector taking into account all the responses and opinions of the expert panel in a hierarchical fashion [26].
7Ethics approval
The study program was approved by the National Committee for Ethics in Medical Research (IR.MUQ.REC.1399.228). All procedures for studies involving human participants were performed in accordance with the ethical standards of the institutional and/or national research committee.
8Results
8.1Delphi results
In the Delphi phase of the study, 25 experts including six risk assessment specialists, four epidemiologists, six health education specialists, four infectious disease specialists, and five pulmonologists formed the expert panel. The mean and work experience of the panel were 41.52±6.38 and 8.72±3.24 years, respectively. They all had a doctorate or higher degree.
The final results of the Delphi method showed that the final risk rate was influenced by four components and 18 factors. The four components consisted of the probability of getting sick (five factors), disease severity (four factors), health beliefs level (three factors), and exposure rate (six factors). The results demonstrated that factors of the probability component comprised ventilation condition of the workplace, family conditions, working conditions of other family members (family members living with the person in the same house), hand hygiene, and caring about respiratory hygiene. The disease severity component included age conditions, clinical symptoms and effects, susceptibility level, and access to diagnostic tests. The health beliefs level component consisted of belief in the infectious nature of the disease, reaction to other people’s hygienic behaviors, and health awareness and knowledge. Finally, the exposure level component was comprised of work environment conditions, contact level at work (distance), contact level at work (time), contact with patients in the past 14 days, using transportation systems in the past 14 days, and presence in the crowds in the past 14 days. It should be noted that the weights of different conditions of each of the 18 factors were measured and determined according to the opinions of the expert panel using the fuzzy Delphi method (Appendix).
8.2FAHP results
After conducting the fuzzy Delphi method and determining the structure of the COVID-19 risk assessment framework and weighing different conditions of components, the FAHP was used to determine the weights of components and their factors. In this step, the AHP questionnaires were distributed among the expert panel. The questionnaires were then collected, and the validity of every questionnaire and pairwise comparison matrixes were corroborated by analyzing the incompatibility rates, hence removing invalid questionnaires. The mean fuzzy matrix and final normalized weights of the four components as well as their factors are presented in Tables 2–6.
Table 2
The mean fuzzy matrix and final normalized weights of COVID-19 risk
| Exposure | Probability | Severity | Health beliefs | Normalized weights | |||||||||
| Exposure | 1.00 | 1.00 | 1.00 | 0.86 | 1.20 | 1.63 | 1.25 | 1.88 | 2.44 | 1.33 | 1.83 | 2.26 | 0.38 |
| Probability | 0.61 | 0.83 | 1.17 | 1.00 | 1.00 | 1.00 | 0.77 | 1.13 | 1.63 | 0.98 | 1.43 | 1.92 | 0.27 |
| Severity | 0.41 | 0.53 | 0.80 | 0.61 | 0.89 | 1.29 | 1.00 | 1.00 | 1.00 | 0.82 | 1.21 | 1.65 | 0.20 |
| Health beliefs | 0.44 | 0.55 | 0.75 | 0.52 | 0.70 | 1.02 | 0.61 | 0.83 | 1.22 | 1.00 | 1.00 | 1.00 | 0.14 |
Table 3
The mean fuzzy matrix and final normalized weights of exposure level parameters
| Contact with patients | Contact level at work (distance) | Contact level at work (time) | Using public transportation systems | Presence in the crowds in the past 14 days | Work environment conditions | Normalized weights | |||||||||||||
| Contact with patients | 1.00 | 1.00 | 1.00 | 1.10 | 1.40 | 1.63 | 1.21 | 1.74 | 2.18 | 1.29 | 1.87 | 2.37 | 1.55 | 2.53 | 3.47 | 1.75 | 2.82 | 3.86 | 0.30 |
| Contact level at work (distance) | 0.61 | 0.71 | 0.91 | 1.00 | 1.00 | 1.00 | 0.93 | 1.34 | 1.83 | 1.25 | 1.77 | 2.20 | 1.46 | 2.13 | 2.73 | 1.54 | 2.22 | 2.82 | 0.22 |
| Contact level at work (time) | 0.46 | 0.58 | 0.83 | 0.55 | 0.75 | 1.08 | 1.00 | 1.00 | 1.00 | 1.10 | 1.45 | 1.71 | 1.21 | 1.79 | 2.29 | 1.37 | 2.19 | 2.94 | 0.18 |
| Using public transportation systems | 0.42 | 0.53 | 0.77 | 0.45 | 0.57 | 0.80 | 0.58 | 0.69 | 0.91 | 1.00 | 1.00 | 1.00 | 0.84 | 1.20 | 1.65 | 1.13 | 1.62 | 2.02 | 0.12 |
| Presence in the crowds in the past 14 days | 0.29 | 0.39 | 0.64 | 0.37 | 0.47 | 0.69 | 0.44 | 0.56 | 0.83 | 0.62 | 0.85 | 1.21 | 1.00 | 1.00 | 1.00 | 1.25 | 1.94 | 2.56 | 0.13 |
| Work environment conditions | 0.26 | 0.35 | 0.57 | 0.35 | 0.45 | 0.65 | 0.34 | 0.46 | 0.73 | 0.50 | 0.62 | 0.88 | 0.39 | 0.51 | 0.80 | 1.00 | 1.00 | 1.00 | 0.05 |
Table 4
The mean fuzzy matrix and final normalized weights of probability parameters
| Family conditions | Working conditions of other family members | Caring about respiratory hygiene | Hand hygiene | Ventilation condition of the workplace | Normalized weights | |||||||||||
| Family conditions | 1.00 | 1.00 | 1.00 | 0.80 | 1.22 | 1.83 | 1.13 | 1.71 | 2.32 | 1.29 | 2.00 | 2.61 | 1.48 | 2.31 | 3.07 | 0.33 |
| Working conditions of other family members | 0.55 | 0.82 | 1.25 | 1.00 | 1.00 | 1.00 | 0.86 | 1.13 | 1.42 | 1.10 | 1.54 | 1.89 | 1.17 | 1.82 | 2.37 | 0.25 |
| Caring about respiratory hygiene | 0.43 | 0.58 | 0.89 | 0.70 | 0.88 | 1.16 | 1.00 | 1.00 | 1.00 | 0.90 | 1.29 | 1.65 | 1.07 | 1.51 | 1.87 | 0.20 |
| Hand hygiene | 0.38 | 0.50 | 0.77 | 0.53 | 0.65 | 0.91 | 0.61 | 0.78 | 1.11 | 1.00 | 1.00 | 1.00 | 0.82 | 1.17 | 1.57 | 0.13 |
| Ventilation condition of work place | 0.33 | 0.43 | 0.68 | 0.42 | 0.55 | 0.85 | 0.54 | 0.66 | 0.94 | 0.64 | 0.85 | 1.22 | 1.00 | 1.00 | 1.00 | 0.09 |
Table 5
The mean fuzzy matrix and final normalized weights of disease severity parameters
| Susceptibility level | Clinical symptoms and effects | Access to diagnostic tests | Age conditions | Normalized weights | |||||||||
| Susceptibility level | 1.00 | 1.00 | 1.00 | 1.13 | 1.48 | 1.74 | 1.37 | 1.87 | 2.29 | 1.55 | 2.28 | 2.95 | 0.47 |
| Clinical symptoms and effects | 0.58 | 0.68 | 0.88 | 1.00 | 1.00 | 1.00 | 1.10 | 1.54 | 1.89 | 1.29 | 1.92 | 2.47 | 0.34 |
| Access to diagnostic tests | 0.44 | 0.54 | 0.73 | 0.53 | 0.65 | 0.91 | 1.00 | 1.00 | 1.00 | 0.82 | 1.21 | 1.65 | 0.14 |
| Age conditions | 0.34 | 0.44 | 0.64 | 0.41 | 0.52 | 0.78 | 0.61 | 0.83 | 1.22 | 1.00 | 1.00 | 1.00 | 0.06 |
Table 6
The mean fuzzy matrix and final normalized weights of health belief level parameters
| Reaction to other people’s hygienic behaviors | Belief in the infectious nature of the disease | Health awareness and knowledge | Normalized weights | |||||||
| Reaction to other people’s hygienic behaviors | 1.00 | 1.00 | 1.00 | 1.07 | 1.42 | 1.69 | 1.10 | 1.59 | 1.99 | 0.48 |
| Belief in the infectious nature of the disease | 0.59 | 0.70 | 0.94 | 1.00 | 1.00 | 1.00 | 0.79 | 1.14 | 1.61 | 0.29 |
| Health awareness and knowledge | 0.50 | 0.63 | 0.91 | 0.61 | 0.87 | 1.28 | 1.00 | 1.00 | 1.00 | 0.23 |
The incompatibility rate of this matrix (Table 2) was CRg = 0.008 and CRm = 0.004. The COVID-19 risk was calculated based on the determined weights according to Equation 2:
(2)
CVRI: COVID-19 risk index
E: exposure
P: probability
S: severity, B: health beliefs
The incompatibility rate of this matrix was CRg = 0.016 and CRm = 0.007 (Table 3). Based on the observed results, the exposure level was measured according to Equation 3:
(3)
ei: The score of exposure parameters
EWi: Weight of exposure sub-factors
NE: Number of exposure sub-factors
The incompatibility rate of this matrix was CRg = 0.002 and CRm = 0.0008 (Table 4). Based on the observed results, the probability factor was measured according to Equation 4:
(4)
pi: The score of probability parameters
PWi: Weight of probability sub-factors
NP: Number of probability sub-factors
The incompatibility rate of this matrix was CRg = 0.004 and CRm = 0.002 (Table 5). Based on the observed results, the probability factor was measured according to Equation 5:
(5)
Si: The score of severity parameters
SWi: Weight of severity sub-factors
NS: Number of severity sub-factors
The incompatibility rate of this matrix was CRg = 0.0002 and CRm = 0.00004 (Table 6). Based on the observed results, the probability factor was measured according to Equation 6:
(6)
Bi: The score of health beliefs parameters
BWi: Weight of health beliefs sub-factors
NB: Number of health beliefs sub-factors
The result of all the above-mentioned matrixes was a risk index ranging from 0.54 to 0.82. To rank the risk in this study, three levels were introduced. The three levels were introduced in the following manner (Fig. 2):
Fig. 2
Continuous variables changing into ordinal variables.

Accordingly, the decision-making levels of COVID-19 risk are depicted in Table 7 based on this method.
Table 7
Risk ranking
| Level | Definition | CVIR |
| 1 | Acceptable | ≥0.63 |
| 2 | Tolerable | 0.63–0.73 |
| 3 | Non-acceptable | 0.73≥ |
9Discussion
The infectious COVID-19 outbreak has precipitated a worldwide health crisis in the current century killing more than 2.5 million people across the world. Since the onset of the COVID-19 pandemic, countries, and governments have to impose different types of limitations to reduce the incidence of the disease. Such limitations have caused global recessions with economic consequences not fully unfolded yet. Generally, the incidence of COVID-19 has brought about various hygienic, economic, social, cultural, and even political effects on the countries around the globe [27].
Assessing the risk of infectious diseases with a biological nature is a key step for taking protective and preventive health measures to control and manage pandemics [14, 28]. The risk assessment process of biological dangers and infectious diseases, such as COVID-19, is different from the risk assessment process of other harmful factors in work environments conducted thus far [4, 5]. Therefore, this study aimed to develop an assessment method for the risk of infectious diseases focusing on COVID-19 based on the fuzzy Delphi method and fuzzy analytical hierarchy process (FAHP). Accordingly, the study followed two aims: (1) develop a method for assessing the risk of biological dangers in work environments with a high COVID-19 risk, and (2) use a precise, scientific, and practical approach such as FAHP to identify and determine risk levels in work environments.
The results of the study revealed that the final risk level is under the influence of four components (probability, disease severity, health belief level, and exposure rate) and 18 relevant factors. The normalized weights of the four components were found to be 0.27, 0.20, 0.14, and 0.38, respectively. These findings demonstrate that the most important component for COVID-19 risk is the exposure rate. The highest normalized weight indexes in the exposure rate component belonged to the following factors: contact with COVID-19 patients (0.30), contact level at work (distance) (0.22), and contact level at work (time) (0.18). The lowest normalized weight index belonged to the work environment conditions. Previous studies have demonstrated that the factor of contact with COVID-19 patients is the most important risk factor for COVID-19. The exposure level component is the main reason behind posing a real risk to the healthcare personnel [29, 30]. It has been shown that individuals’ contact level with colleagues and clients at the workplace is another significant risk factor for COVID-19 as the highest incidence rate has been recorded in those occupations in which there is a high contact level in terms of distance and time with other people [31].
The highest weight indexes in the effective factors of the probability component belonged to family conditions (0.33), working conditions of other family members (0.25), and caring about respiratory hygiene (0.20). The lowest weight, however, belonged to the ventilation condition of the workplace (0.9). Previous research has reported that among the most effective factors in preventing the spread of the disease and reducing the number of deaths are the living condition of the people in the household, the degree to which individuals care about health issues, and the contact level of individuals with other people around them at the workplace. Respiratory hygiene has been also mentioned by the WHO together with social distancing, hand washing, and mask-wearing as the most effective strategies to prevent the spread of COVID-19 [32].
The factors with the highest weight indexes observed in the disease severity component were susceptibility to COVID-19 (0.47) and clinical symptoms and effects (0.34). The lowest weights belonged to access to diagnostic tests (0.14) and age conditions (0.06). Various studies have revealed that COVID-19 presents graver threats to people using Cortone and people with cardiovascular diseases, pulmonary complications, and congenital immunodeficiency disorders. Likewise, cancer patients, patients undergoing chemotherapy, people with chronic kidney diseases, people suffering from diabetes, and the elderly (particularly more than 50 years of age) have been reported to be more susceptible to COVID-19 with more severe symptoms [33, 34].
As for the health beliefs component, the highest weight indexes were observed in reaction to other people’s hygienic behaviors (0.48) and belief in the infectious nature of the disease (0.29). The lowest weight index belonged to the health awareness and knowledge factor (0.23). People’s responsibility towards and awareness of appropriate personal and public health in a pandemic period is a key parameter affecting health beliefs and culture in societies. Past studies have proved that societies with appropriate health awareness and knowledge can react more efficiently to pandemics and hence control them more successfully [35].
All components and their relevant factors are among the most effective variables affecting the incidence of infectious diseases such as COVID-19 across the world. Thus, focusing on the above-mentioned parameters and trying to develop a practical risk assessment algorithm, the current study sought to optimally assess COVID-19 risk and hence emphasize appropriate, practical measures needed to be taken in work environments to prevent the spread of the disease. This study is the first of its kind trying to present a scientific, accurate, and practical method for assessing COVID-19 risk in work environments. Accordingly, the findings of this study can result in a fresh and innovative approach to assessing the risk of infectious diseases in work environments. The limitation of the study was the impossibility of implementing appropriate interventionist measures in the research design and evaluating the efficiency of the introduced risk assessment method due to time boundaries. Consequently, it is suggested that future studies include a large sample size in their research design and evaluate the effectiveness of this fuzzy risk assessment method in managing COVID-19 risk. Furthermore, designing and development of a risk assessment method for infectious diseases based on more parameters and variables can be considered in future studies. These parameters can be specific to the type of infectious disease or application of risk assessment method.
10Conclusion
The results of this study demonstrated that the final COVID-19 risk is affected by four components and 18 relevant factors including probability (five factors), disease severity (four factors), health beliefs level (three factors), and exposure rate (six factors). Given the significant effects of identified components, factors, and parameters on the incidence of COVID-19 in work environments and the benefits of using the Delphi method and FAHP, the proposed risk assessment method in this study can be considered an effective method for the optimal management of COVID-19 risk.
Ethical approval
The study program was approved by the National Committee for Ethics in Medical Research (IR.MUQ.REC.1399.228). All procedures for studies involving human participants were performed in accordance with the ethical standards of the institutional and/or national research committee.
Informed consent
Not applicable.
Conflicts of interest
There is no potential conflict of interest to disclose.
Acknowledgments
The authors would like to express their sincere gratitude to the expert pannel in this study.
Funding
The authors received specific funding for this work according to the research project no. IR.MUQ.REC.1399.228 approved by the Vice-Chancellor for Research and Technology of Qom University of Medical Sciences and Health Services.
Supplementary materials
The appendix is available from https://dx.doi.org/10.3233/WOR-220084.
References
[1] | Arefi MF , Poursadeqiyan M . A review of studies on the COVID-19 epidemic crisis disease with a preventive approach, Work (2020) ;66: (4):717–29. |
[2] | Zandian H , Alipouri-sakha M , Nasiri E , Zahirian Moghadam T . Nursing work intention, stress, and professionalism in response to the COVID-19 outbreak in Iran: A cross-sectional study. Work. 2021(Preprint):1-11. |
[3] | Boldog P , Tekeli T , Vizi Z , Dénes A , Bartha FA , Röst G . Risk assessment of novel coronavirus COVID-19outbreaks outside China, Journal of clinical medicine (2020) ;9: (2):571. |
[4] | Ozdemir Y , Gul M , Celik E . Assessment of occupational hazards and associated risks in fuzzy environment: A case study of a university chemical laboratory, Human and Ecological Risk Assessment: An International Journal (2017) ;23: (4):895–924. |
[5] | Eisler R . Handbook of chemical risk assessment: Health hazards to humans, plants, and animals, three volume set. 2000. |
[6] | Burdorf A , Porru F , Rugulies R . The COVID-19 (Coronavirus) pandemic: Consequences for occupational health, Scandinavian Journal of Work, Environment & Health (2020) ;46: (3):229–30. |
[7] | Carvalhais C , Querido M , Pereira CC , Santos J . Biological risk assessment: A challenge for occupational health and safety practitioners during the COVID-19 (SARS-CoV-2) Pandemic. Work. 2021(Preprint):1-11. |
[8] | Fana M , Pérez ST , Fernández-Macías E . Employment impact of Covid-19 crisis: From short term effectsto long terms prospects, Journal of Industrial and Business Economics (2020) ;47: (3):391–410. |
[9] | Obrenovic B , Du J , Godinic D , Tsoy D , Khan MAS , Jakhongirov I . Sustaining enterprise operations and productivity during the COVID-19 pandemic:“Enterprise Effectiveness and Sustainability Model”, Sustainability (2020) ;12: (15):5981. |
[10] | Pak A , Adegboye OA , Adekunle AI , Rahman KM , McBryde ES , Eisen DP . Economic consequences of the COVID-19 outbreak: The need for epidemic preparedness. Frontiers in Public Health. 2020;8. |
[11] | Pniak B , Leszczak J , Adamczyk M , Rusek W , Matłosz P , Guzik A . Occupational burnout among activephysiotherapists working in clinical hospitals during the COVID-19 pandemic in south-eastern Poland, Work (2021) ;68: (2):285–95. |
[12] | Sharma K , Anand A , Kumar R . The role of Yoga in working from home during the COVID-19 global lockdown, Work (2020) ;66: (4):731–7. |
[13] | Moradi V , Babaee T , Esfandiari E , Lim SB , Kordi R . Telework and telerehabilitation programs for workers with a stroke during the COVID-19 pandemic: A commentary, Work (2021) ;68: (1):77–80. |
[14] | Dryhurst S , Schneider CR , Kerr J , Freeman AL , Recchia G , Van Der Bles AM , et al. Risk perceptions of COVID-19 around the world, Journal of Risk Research (2020) ;23: (7-8):994–1006. |
[15] | Koh D . Occupational risks for COVID-19 infection, Occupational medicine (Oxford, England) (2020) ;70: (1):3. |
[16] | Mohammadfam I , Aliabadi MM , Soltanian AR , Tabibzadeh M , Mahdinia M . Investigating interactions among vital variables affecting situation awareness based on Fuzzy DEMATEL method, International Journal of Industrial Ergonomics (2019) ;74: :102842. |
[17] | Zhou Q , Huang W , Zhang Y . Identifying critical success factors in emergency management using a fuzzy DEMATEL method, Safety Science (2011) ;49: (2):243–52. |
[18] | Novák V , Perfilieva I , Mockor J , Mathematical principles of fuzzy logic: Springer Science & Business Media; 2012. |
[19] | Cafiso S , Di Graziano A , Pappalardo G . Using the Delphi method to evaluate opinions of public transport managers on bus safety, Safety Science (2013) ;57: :254–63. |
[20] | Dapari R , Ismail H , Ismail R , Ismail NH . Application of fuzzy Delphi in the selection of COPD risk factors among steel industry workers, Tanaffos (2017) ;16: (1):46. |
[21] | Boulkedid R , Abdoul H , Loustau M , Sibony O , Alberti C . Using and reporting the Delphi method for selecting healthcare quality indicators: A systematic review, PloS One (2011) ;6: (6):e20476. |
[22] | Zheng G , Zhu N , Tian Z , Chen Y , Sun B . Application of a trapezoidal fuzzy AHP method for work safety evaluation and early warning rating of hot and humid environments, Safety science (2012) ;50: (2):228–39. |
[23] | Askaripoor T , Kazemi E , Aghaei H , Marzban M . Evaluating and comparison of fuzzy logic and analytical hierarchyprocess in ranking and quantitative safety risk analysis (case study: A combined cycle power plant), SafetyPromotion and Injury Prevention (Tehran). (2015) ;3: (3):169–74. |
[24] | Sambasivan M , Fei NY . Evaluation of critical success factors of implementation of ISO 1 using analytic hierarchy process (AHP): A case study from Malaysia, Journal of Cleaner Production (2008) ;16: (13):1424–33. |
[25] | Chang D-Y . Applications of the extent analysis method on fuzzy AHP, European Journal of Operational Research (1996) ;95: (3):649–55. |
[26] | Ho W , Ma X . The state-of-the-art integrations and applications of the analytic hierarchy process, European Journal of Operational Research (2018) ;267: (2):399–414. |
[27] | Vera-Valdés JE . The political risk factors of COVID-19. International Review of Applied Economics. 2021:1-19. |
[28] | Rudisill C . How do we handle new health risks? Risk perception, optimism, and behaviors regarding the H1N1 virus, Journal of Risk Research (2013) ;16: (8):959–80. |
[29] | Wu Y-C , Chen C-S , Chan Y-J . The outbreak of COVID- An overview, Journal of the Chinese Medical Association (2020) ;83: (3):217. |
[30] | Heinzerling A , Stuckey PMJ , Scheuer T , Xu K , Perkins KM , Resseger H , et al.Transmission of COVID-19 to health care personnel during exposures to a hospitalized patient—Solano County, California, 2020. |
[31] | Abrams EM , Greenhawt M . Risk communication during COVID-19, The Journal of Allergy and Clinical Immunology: In Practice (2020) ;8: (6):1791–4. |
[32] | Doung-ngern P , Suphanchaimat R , Panjangampatthana A , Janekrongtham C , Ruampoom D , Daochaeng N , et al. Associations between wearing masks, washing hands, and social distancing practices, and risk ofCOVID-19 infection in public: A cohort-based case-control study in Thailand. 2020. |
[33] | Dai M , Liu D , Liu M , Zhou F , Li G , Chen Z , et al. Patients with cancer appear more vulnerable to SARS-CoV- A multicenter study during the COVID-19 outbreak, Cancer Discovery (2020) ;10: (6):783–91. |
[34] | Canning D , Karra M , Dayalu R , Guo M , Bloom DE . The association between age, COVID-19 symptoms, and social distancing behavior in the United States. MedRxiv. 2020. |
[35] | Reddy BV , Gupta A . Importance of effective communication during COVID-19 infodemic, Journal of Family Medicine and Primary Care (2020) ;9: (8):3793. |




