A submatrix spatial coherence approach to minimum variance beamforming combined with sign coherence factor for coherent plane wave compounding
Abstract
BACKGROUND:
The coherent plane wave compounding (CPWC) is a promising technique to enhance the imaging quality while maintaining the high frame rate in the plane wave ultrasound imaging. Recently, the spatial-coherence-based method has been specially designed to process echo matrix required by the minimum variance (MV) method.
OBJECTIVE:
In this paper, a novel beamforming method that integrates the submatrix-spatial-coherence-based MV with the sign coherence factor (SCF) is proposed to further improve the imaging quality.
METHOD:
The submatrix smoothing technique is modified to smooth and de-correlate signals of the receiving array dimension. Then, the SCF is used to modify the input vector of the beamformer, which can reduce side lobe noises with almost no increase in the amount of calculation. Simulation, phantom, in vivo, and sound velocity error experiments have been performed to verify the superiority of the proposed beamformer.
RESULTS:
The imaging results show that the proposed approach performs better in the imaging resolution and contrast compared to the traditional CPWC method.
CONCLUSION:
The robustness of the proposed method is enhanced, and the over-suppression phenomenon can be alleviated, which is a phenomenon that occurs in the original spatial-coherence and SCF methods.
1.Introduction
The plane wave imaging (PWI) is an effective mode to realize ultrafast ultrasound imaging for the visualization of rapid tissue motions [1, 2]. However, it causes the significant reduction in the imaging quality due to emitting unfocused plane waves. Lu and Cheng proposed the plane wave compounding (PWC) method to provide enhancement of the imaging quality without affecting the frame rate in the plane wave modality [3, 4, 5]. Montaldo et al. modified the PWC in 2009 and named it as the coherent plane wave compounding (CPWC). Here the echo signals from different firing angles were compounded to improve the image quality [6, 7].
The adaptive beamforming algorithm dynamically calculates the weight vector of received echo signals. Compared to the conventional delay and sum (DAS) algorithm, it can effectively enhance the ultrasound imaging quality [8]. In 1969, Capon proposed the minimum variance (MV) algorithm, which was one of representative adaptive beamforming algorithms. The core of the method is calculating the undistorted weighting vector by minimizing the output energy of the beamformer dynamically [9, 10]. The method improves the imaging resolution and suppresses the interference noise significantly.
The coherence factor (CF) is another typical adaptive beamformer. It calculates the ratio of the coherent energy to the total energy of echo signals and works as a multiplier to constrain the output of the beamformer. The phase coherence factor (PCF) is also a coherence-based method. It uses the signal phase dispersion to design the factor, which is different from the CF. The sign coherence factor (SCF) is a special case of the PCF [11]. It is simple to calculate and easy to implement. All coherence-based methods can reduce sidelobes and improve the imaging contrast. However, these methods will reduce the brightness of the speckle region owing to the over-suppression of desired signals. In addition, MV-based, CF-based and MV-CF combined methods have been extensively applied to the CPWC imaging mode [12, 13, 14].
Recently, several methods based on the MV and CF have been modified for the 2-D echo dataset of the CPWC. The joint MVDR (JTR) method proposed by our group computes two MV weighting vectors: the transmitting aperture weighting vector and receiving aperture weighting vector [15, 16]. By combining two vectors, the beamformer can obtain a significant improvement in the imaging resolution. Data compounded among transmit (DCT) MV and data compounded among receive (DCR) MV beamformers were both proposed by Nguyen et al., who used different combinations of signals to estimate the covariance matrix. It is covenient to implement since the MV weight only needs to be calculated once [17]. These two beamformers are based on the van Cittert-Zernike theorem and can improve the imaging resolution and contrast [18, 19]. However, the diagonal loding factors used by these two beamformers are much larger than the conventional range, which is the limitation of two beamformers. In addition, the over-suppression phenomenon will occur in the DCT-MV method with a small loading factor, which may affect the contrast ratio (CR) and contrast-to-noise ratio (CNR) values.
In this paper, a submatrix-spatial-coherence combined with SCF method is proposed to implement the MV beamforming, which can enhance the imaging quality of the CPWC. We use submatrix smoothing technique to divide the data matrix into overlapped submatrices over the receive dimension and full data is preserved along the transmit dimension. Afterwards, the submatrix spatial coherence is estimated to approximate the sub-covariance matrix. After averaging all results of submatrices, the final covariance matrix can be obtained. The input data vector of the beamformer is obtained by compounding data over multiple transmits of the average submatrix, which is also corrected by the SCF. There are three advantages of the method. First, the proposed beamformer achieves the better performance both on the resolution and contrast compaired with the CPWC. Second, the speckle region is preserved well. Third, the robustness is significantly improved.
The contents of other chapters are arranged as follows. The theories of existing approaches are illustrated in Section 2. The novel beamformer is described in detail in Section 3. In Section 4, the set up and results of the simulation, phantom, in vivo and sound velocity error experiments are described. In Sections 5 and 6, the discussion and conclusion are given respectively.
2.Background
2.1Coherent plane wave compounding
For the CPWC imaging mode, we record the echo signals into a two-dimensional matrix for beamforming [6]. Here we assume that the number of transducer elements is
(1)
where
(2)
where
2.2Minimum variance beamformer
The mathematical expression of MV is as follows:
(3)
where
The MV method calculates the undistorted weighting vector by a constraint process that minimizes the output power of the beamformer. It can be expressed as:
(4)
where
The solution of the above equation can be computed through the Lagrange multiplier approach:
(5)
(6)
The estimation of
(7)
where
Diagonal loading technique is also applied to the covariance matrix to obtain a comparably stable matrix. We use
The output of the MV beamformer is as follows:
(8)
2.3Sign coherence factor beamformer
To implement SCF, the normalized phase space
(9)
(10)
where
2.4Data compounded among transmit MV beamformer
This method estimates the covariance matrix by using different combinations of echo signals for each transmission angle [17]. For the 2-D data matrix
(11)
Then the covariance matrix of
(12)
For every transmit event,
(13)
where
Figure 1.
Schematics of two beamformers: (a) DCT-MV, (b) SM-DCT MV.
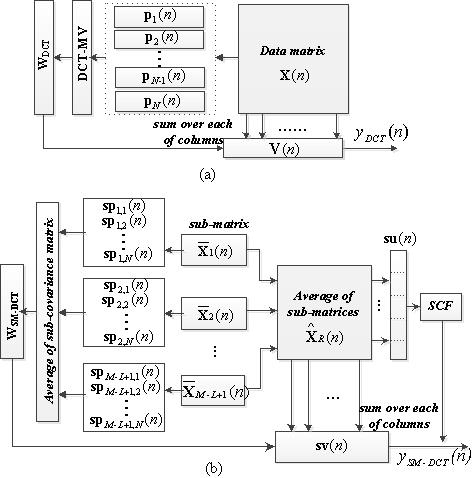
3.Methods
The proposed method is the sub-matrix data compounded among transmit MV beamformer combined with the SCF. It is named as SM-DCT MV for short. We build a new data matrix by dividing the original 2-D data matrix into overlapping submatrices. Different to the submatrix technique used by Qi et al. [16], we just smooth the data on the receive dimension and full data are kept on the other transmit dimension. It is described as follows:
(14)
(15)
We take the average of these overlapping submatrices
(16)
The input vector of the proposed SM-DCT beamformer can be obtained by a data vector compounded over different transmits afterwards. Considering that multiple steering angle signals have a certain coherence to the imaging result of the same imaging target, and the coherence to the noise and clutter is poor. Therefore, the SCF factor is used as a correction to obtain a more accurate input signal vector. First, a vector is obtained by compounding the columns of
(17)
where
Then, the new set of snapshot
(18)
Afterwards,
(19)
By averaging all results, the covariance matrix similar to the second-order statistics of
(20)
where
It is worth mentioning that we can obtain the
4.Experiments and results
4.1Experiment setup
The performance of different beamformers was evaluated using the CPWC through simulation, phantom, in vivo and sound velocity error experiments. The simulation data was acquired using Field II, the phantom and in vivo data was obtained using Verasonics ultrasound platform. The processing of different algorithms are implemented on the MATLAB platform.
For all simulations, a 128-element transducer with 0.3 mm pitch, centered at 5 MHz, was used to acquire simulation data. Both transmitting and receiving processes used full array elements. The sampling rate was 40 MHz. We simulated four point targets placed at
4.2Parameters and evaluation metrics
Parameters selected in the experimental evaluation are explained here. For the proposed SM-DCT beamformer, the submatrix length
Evaluation metrics are used for the quantitative measurement. The full width of mainlobe (FWHM) is used to evaluate the imaging resolution, and it is usually estimated by the mainlobe width at
(21)
(22)
(23)
where
4.3Simulated study
Point target simulation results of different beamforming algorithms are presented in Fig. 2.
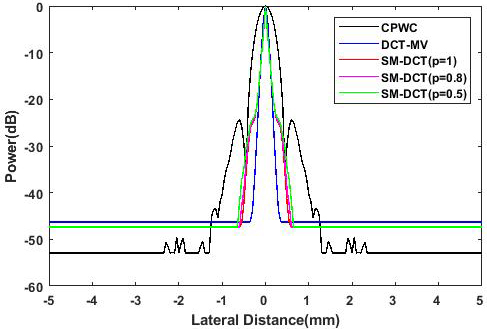
Figure 2a shows the imaging result of traditional CPWC method. It can be seen that the main lobe is wide and side lobes are obvious. In Fig. 2b, the DCT-MV method achieves a narrow mainlobe and no visible sidelobes. Figure 2c–e are results of the SM-DCT MV with
In order to evaluate the imaging resolution quantitatively, the transverse beam amplitude response diagram at
Table 1
FWHM at
| Beamformer | FWHM (mm) |
|---|---|
| CPWC | 0.49/0.80 |
| DCT-MV | 0.17/0.34 |
| SM-DCT ( | 0.13/0.38 |
| SM-DCT ( | 0.13/0.38 |
| SM-DCT ( | 0.13/0.38 |
Figure 2.
Simulated point targets imaging results: (a) CPWC, (b) DCT-MV, (c) SM-DCT MV (

Figure 3.
The transverse beam amplitude response diagram at the depth of
Cyst simulation results of different beamformers are given in Fig. 4. Figure 4a shows the imaging result of the CPWC. The noise level inside the cyst is high, which is caused by the high sidelobe amplitude of the traditional method. The result of the DCT-MV shows that the internal imaging achieves the better noise suppression, and the edge of the cyst is clear. However, the brightness of the speckle region is weakened, which results in the unsatisfactory contrast. As seen from Fig. 4c–e, results of the SM-DCT MV with
Table 2
CR, CNR and s-SNR for simulated cysts
| Beamformer | CR (dB) | CNR | s-SNR |
|---|---|---|---|
| CPWC | 33.91 | 1.69 | 1.51 |
| DCT-MV | 30.41 | 0.76 | 1.15 |
| SM-DCT ( | 36.63 | 1.30 | 1.32 |
| SM-DCT ( | 37.30 | 1.39 | 1.34 |
| SM-DCT ( | 37.00 | 1.48 | 1.39 |
The values of CR, CNR and s-SNR are displayed in Table 2 for quantitative assessment. It can be seen that the contrast of the SM-DCT with
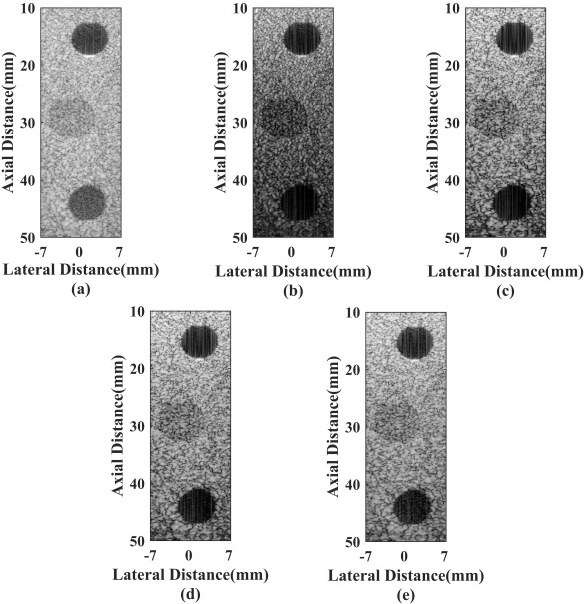
4.4Experimental phantom study
Figure 5 gives imaging results of the point targets phantom. It can be noted that although the DCT-MV method has a better point imaging effect, its speckle background is over-suppressed, leading to the loss of the image information. While the proposed SM-DCT method avoids this phenomenon successfully, the brightness of the speckle region keeps well.
Table 3
FWHM at
| Beamformer | FWHM (mm) |
|---|---|
| CPWC | 0.42/0.66 |
| DCT-MV | 0.15/0.38 |
| SM-DCT ( | 0.17/0.51 |
| SM-DCT ( | 0.17/0.54 |
| SM-DCT ( | 0.17/0.59 |
Figure 4.
Simulated cysts imaging results: (a) CPWC, (b) DCT-MV, (c) SM-DCT (
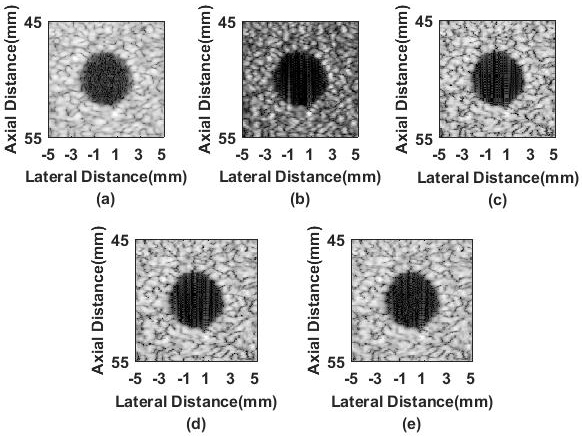
Figure 5.
Experimental point targets phantom imaging results: (a) CPWC, (b) DCT-MV, (c) SM-DCT (
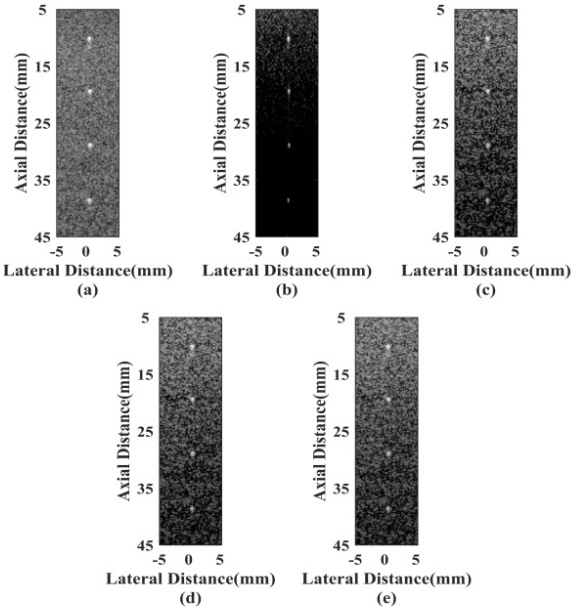
Figure 6.
Transverse beam amplitude response diagrams at the depth of
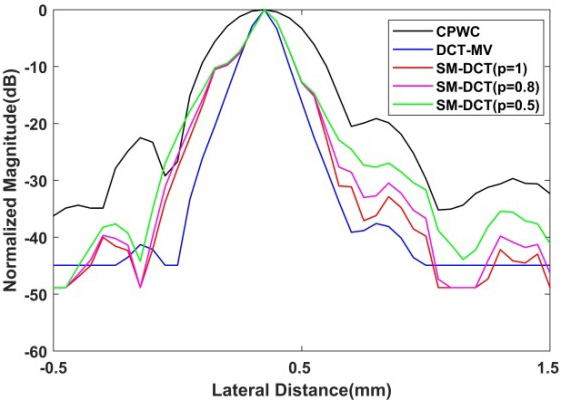
The transverse beam amplitude response diagrams at
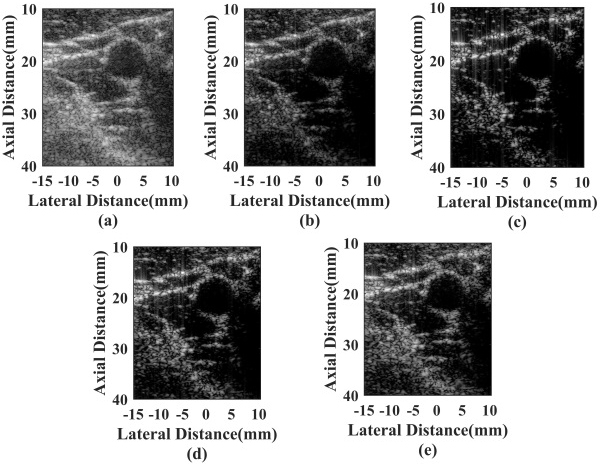
Results of the cysts phantom are presented in Fig. 7. Figure 7a shows that the noise level inside the cysts is obvious with the CPWC. Figure 7b is the result of the DCT-MV beamformer. The internal imaging of cysts is good, while the speckle area is weakened. From Fig. 7c–e, the proposed SM-DCT beamformer performs better in the internal imaging than the CPWC and the speckle background preserved better than the DCT-MV.
Table 4
CR, CNR, ands-SNR for experimental cysts
| Beamformer | CR (dB) | CNR | s-SNR |
|---|---|---|---|
| CPWC | 28.35/16.02 | 1.91/1.61 | 1.99/1.93 |
| DCT-MV | 28.63/13.01 | 1.17/0.89 | 1.21/1.16 |
| SM-DCT ( | 33.51/19.59 | 1.43/0.89 | 1.46/1.00 |
| SM-DCT ( | 33.72/20.46 | 1.53/1.08 | 1.57/1.19 |
| SM-DCT ( | 33.25/19.84 | 1.63/1.25 | 1.67/1.39 |
Figure 7.
Experimental cysts phantom imaging results: (a) CPWC, (b) DCT-MV, (c) SM-DCT (
CR, CNR, and s-SNR values are given in Table 4 for quantitative assessment. For the cyst at
4.5In vivo study
Figure 8 shows results of different beamformers using carotid artery data from an adult male. The result is similar to the cyst phantom experiment because of the similarity between the circular artery and the anechoic cyst. From Fig. 8a, it can be seen that noises are obvious inside the vessel with the CPWC. Other beamformers achieve the better performance on reducing the noise level. The proposed SM-DCT beamformer distinguishes the arteries and boundaries well, and the surrounding information preserved more completely.
Table 5
CR, CNR, and s-SNR for in vivo carotid artery
| Beamformer | CR (dB) | CNR | s-SNR |
|---|---|---|---|
| CPWC | 21.87 | 1.14 | 1.25 |
| DCT-MV | 19.12 | 0.67 | 0.77 |
| SM-DCT ( | 27.45 | 0.55 | 0.58 |
| SM-DCT ( | 27.97 | 0.71 | 0.74 |
| SM-DCT ( | 25.90 | 0.86 | 0.90 |
Figure 8.
In vivo human carotid artery imaging results: (a) CPWC, (b) DCT-MV, (c) SM-DCT (
The internal and external signals of the carotid artery are used to calculate the CR, CNR, and s-SNR values. Results are presented in Table 5 for the statistical assessment. Similar to the cyst phantom experiment, the CR of the SM-DCT (
Figure 9.
Simulated point imaging results of different sound velocity errors: (a) CPWC, (b) DCT-MV (
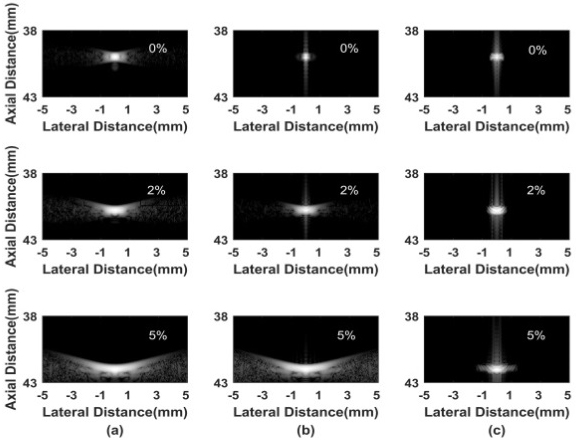
4.6Robustness to sound velocity error
Point imaging results for different sound velocity errors with different beamformers are given in Fig. 9. In Fig. 9a and b, the mainlobe width of the CPWC and DCT-MV widened and the sidelobes increased obviously with the increase of the sound velocity error. Figure 9c shows that the sidelobe level of the proposed method is lower compared with the former two methods. Point imaging results of the SM-DCT are less affected by the sound velocity and the robustness is better.
5.Discussion
From results, the SM-DCT method proposed in this paper shows its advantages in the plane wave compounding mode in terms of the enhancement of the imaging quality and the improvement of algorithm robustness. These performance advantages mainly result from two aspects. First, a submatrix spatial smoothing technique is added to the spatial coherence method to fully de-correlate received signals. By this way, a more accurate covariance matrix can be obtained, and the non-singularity of the covariance matrix can be guaranteed. In addition, the diagonal loading factor chosen in the SM-DCT MV can be a typical value. Both of the spatial smoothing and low loading factor lead to the improvement of the robustness of the algorithm. Second, the SCF is used to correct the input vector of the beamformer, which improves the imaging contrast while maintaining the mainlobe width at
As for several parameters used in all experiments, the selection of the length of submatrix
In addition to the above advantages, the proposed method also has certain limitations. From Figs 3 and 6, the mainlobe width at
6.Conclusion
A novel beamformer based on the spatial coherence method integrating the submatrix smoothing technique and sign coherence factor is proposed. Simulated and experimental results show that the SM-DCT MV obtained higher CR, CNR and s-SNR values compared with the DCT-MV method under a small diagonal loading factor condition. The
Acknowledgments
This work is supported by the National Natural Science Foundation of China (61771143 and 81627804).
Conflict of interest
None to report.
References
[1] | Wells, and PNT. Ultrasound imaging. Physics in Medicine & Biology. (2006) ; 51: (13): 83–98. doi: 10.1074/jbc.273.41.26317. |
[2] | Tanter M, Fink M. Ultrafast imaging in biomedical ultrasound. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2014) ; 61: (1): 102–119. doi: 10.1109/TUFFC.2014.2882. |
[3] | Berson M, Roncin A, Pourcelot L. Compound scanning with an electrically steered beam. Ultrasonic Imaging. (1981) ; 3: (3): 303–308. doi: 10.1016/0161-7346(81)90162-0. |
[4] | Lu JY. Experimental study of high frame rate imaging with limited diffraction beams. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (1998) ; 45: (1): 84–97. doi: 10.1109/58.646914. |
[5] | Cheng JQ, Lu JY. Extended high-frame rate imaging method with limited-diffraction beams. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (2016) ; 53: (5): 880–899. doi: 10.1109/TUFFC.2006.1632680. |
[6] | Montaldo G, Tanter M, Bercoff J, Benech N, Fink M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2009) ; 56: (3): 489–506. doi: 10.1109/TUFFC.2009.1067. |
[7] | Austeng A, Nilsen CIC, Jensen AC, Nasholm SP, Holm S. Coherent plane-wave compounding and minimum variance beamforming. Proceedings of the IEEE Ultrasonics Symposium. (2011) ; 2448–2451. doi: 10.1109/ULTSYM.2011.0608. |
[8] | Synnevag JF, Austeng A, Holm S. Adaptive beamforming applied to medical ultrasound imaging. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2007) ; 54: (8): 1606–1613. doi: 10.1109/TUFFC.2007.431. |
[9] | Capon J. High-resolution frequency-wavenumber spectrum analysis. Proceedings of the IEEE. (1969) ; 57: (8): 1408–1418. doi: 10.1109/PROC.1969.7278. |
[10] | Vignon F, Burcher MR. Capon beamforming in medical ultrasound imaging with focused beams. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. (2008) ; 55: (3): 619–628. doi: 10.1109/TUFFC.2008.686. |
[11] | Xu ML, Yang X, Ding MY, Yuchi M. Spatio-temporally smoothed coherence factor for ultrasound imaging. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2014) ; 61: (1): 182–190. doi: 10.1109/TUFFC.2014.2889. |
[12] | Wang SL, Li PC. MVDR-based coherence weighting for high-frame-rate adaptive imaging. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2009) ; 56: (10): 2097–2110. doi: 10.1109/TUFFC.2009.1293. |
[13] | Asl BM, Mahloojifar A. Minimum variance beamforming combined with adaptive coherence weighting applied to medical ultrasound imaging. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2009) ; 56: (9): 1923–1931. doi: 10.1109/TUFFC.2009.1268. |
[14] | Zhao JX, Wang YY, Yu JH, Guo W, Li TJ, Zheng YP. Subarray coherence based postfilter for eigenspace based minimum variance beamformer in ultrasound plane-wave imaging. Ultrasonics. (2016) ; 65: : 23–33. doi: 10.1016/j.ultras.2015.10.026. |
[15] | Zhao JX, Wang YY, Zeng X, Yu JH, Yiu BYS, Yu ACH. Plane wave compounding based on a joint transmitting-receiving adaptive beamformer. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2015) ; 62: (8): 1440–1452. doi: 10.1109/TUFFC.2014.006934. |
[16] | Qi YX, Wang YY, Guo W. Joint subarray coherence and minimum variance beamformer for multi-transmission ultrasound imaging modalities. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control. (2018) ; 65: (9): 1600–1617. doi: 10.1109/TUFFC.2018.2851073. |
[17] | Nguyen NQ, Prager RW. A spatial coherence approach to minimum variance beamforming for plane-wave compounding. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. (2018) ; 65: (4): 522–534. doi: 10.1109/TUFFC.2018.2793580. |
[18] | Mallart R, Fink M. The Van Cittert-Zernike theorem in pulse echo measurements. Journal of the Acoustical Society of America. (1991) ; 90: (5): 2718–2727. doi: 10.1121/1.401867. |
[19] | Mallart R, Fink M. Adaptive focusing in scattering media through sound-speed inhomogeneities: The Van Cittert-Zernike approach and focusing criterion. Journal of the Acoustical Society of America. (1994) ; 96: (6): 3721–3732. doi: 10.1121/1.410562. |
[20] | Zheng CC, Peng H, Zhao W. Ultrasound imaging based on coherent plane wave compounding weighted by sign coherence factor. Acta Electronica Sinica. (2018) ; 46: (1): 31–38. |




