ChainMail based neural dynamics modeling of soft tissue deformation for surgical simulation
Abstract
BACKGROUND:
Realistic and real-time modeling and simulation of soft tissue deformation is a fundamental research issue in the field of surgical simulation.
OBJECTIVE:
In this paper, a novel cellular neural network approach is presented for modeling and simulation of soft tissue deformation by combining neural dynamics of cellular neural network with ChainMail mechanism.
METHOD:
The proposed method formulates the problem of elastic deformation into cellular neural network activities to avoid the complex computation of elasticity. The local position adjustments of ChainMail are incorporated into the cellular neural network as the local connectivity of cells, through which the dynamic behaviors of soft tissue deformation are transformed into the neural dynamics of cellular neural network.
RESULTS:
Experiments demonstrate that the proposed neural network approach is capable of modeling the soft tissues’ nonlinear deformation and typical mechanical behaviors.
CONCLUSIONS:
The proposed method not only improves ChainMail’s linear deformation with the nonlinear characteristics of neural dynamics but also enables the cellular neural network to follow the principle of continuum mechanics to simulate soft tissue deformation.
1.Introduction
Modeling and simulation of soft tissue deformation is a fundamental research issue in the development of a surgical simulator. Surgical simulation requires realistic modeling of soft tissue deformation under tool-tissue interactions and real-time visual and haptic feedbacks [1], but it is challenging to satisfy these two conflicting requirements. Currently, the existing methods for soft tissue deformation can be grouped into two main categories. One is devoted to the computational performance such as mass-spring model (MSM) [2] for real-time soft tissue deformation, whereas the other is devoted to the physical realism such as finite element method (FEM) [3] for accurate soft tissue deformation. The former is easy in implementation and computationally efficient, but it cannot accurately reproduce the material properties of soft tissues. The latter allows accurate prediction of soft tissue deformation, but it is highly expensive in computation. There have been various techniques studied for the improvement of the runtime computation of FEM. Matrix condensation [4] improves the runtime computation by reducing the full computation of a volumetric object to the surface nodes only; however, with this simplification the deformation accuracy is significantly compromised. Pre-computation reduces the computational load by calculating the solutions [5] or spatial derivatives [6] prior to the simulation; however, the pre-computation does not permit changes on model topology during the simulation. Total Lagrangian explicit dynamics finite element algorithm [6] reduces the computation through eliminating the iterative process of solving the matrix equation; however, due to the use of explicit time integration, the simulation time step is restricted to a small value for the solution to maintain stable. The boundary element method (BEM) [7] reduces the computation by formulating the weak form of virtual work into a surface integral form, where only a discretization of object’s boundary is required. However, it cannot handle the anisotropic and heterogeneous characteristics of soft tissues due to the homogeneous material assumption. Meshless method [8], despite of being able to avoid the connectivity constraints from using mesh, requires more efforts in computer programming, and it cannot directly model the object’s surface. Although the GPU (Graphics Processing Unit) can be employed to facilitate the runtime computation from the GPU parallel computing [9], this technique is hardware-dependent and it does not fundamentally address the computational problem.
As an alternative to the aforementioned methods, ChainMail is a modeling method for real-time modeling and simulation of soft tissue deformation. It was first proposed by Gibson in 1997, named the 3D ChainMail [10]. In this method, each chain element (mass point) enforces a geometric region setting the free-moving distances of each of its neighbouring chain elements. The ChainMail has advantages in computation and is stable in numerical iteration. Although various studies have been reported for improvement of the ChainMail method [11, 12], it is still limited to linear deformation of soft tissues.
Neural network has also received attention for simulation of soft tissue deformation, given its fast computational advantage, which would be able to achieve the real-time computational performance required by surgical simulation. Zhong et al. reported a cellular neural network model [13] and a Hopfield neural network model [14] for modeling of soft tissue deformation; however, these neural networks are constructed based on the physical heat conduction process, rather than continuum mechanics for deformation.
In this paper, a new ChainMail based neural dynamics approach for modeling of soft tissue deformation is presented. It combines the ChainMail mechanism with nonlinear neural dynamics for the soft tissues’ nonlinear deformation and typical mechanical behaviors. It endows the principle of continuum mechanics to the neural network for soft tissue simulation by formulating the local connectivity of cells in the cellular neural network as the local position adjustments of ChainMail. It also improves ChainMail linear deformation with nonlinear neural dynamics. Experiments, simulations and comparisons have been performed to comprehensively evaluate the performance of the proposed method.
2.Model design
The proposed method employs the cellular neural network (CNN), which is a local-interconnected array-computing structure [15]. The neuron in the CNN is called cell, which is a nonlinear dynamic processing unit consisting of capacitors, resistors and current sources of linear and nonlinear types. Cells are locally connected and interact only with their nearest neighbors [16]; cells that are not directly connected affect each other indirectly via the global propagation effect of CNN [17].
Figure 1.
A CNN on an irregular grid: the spatial positions of
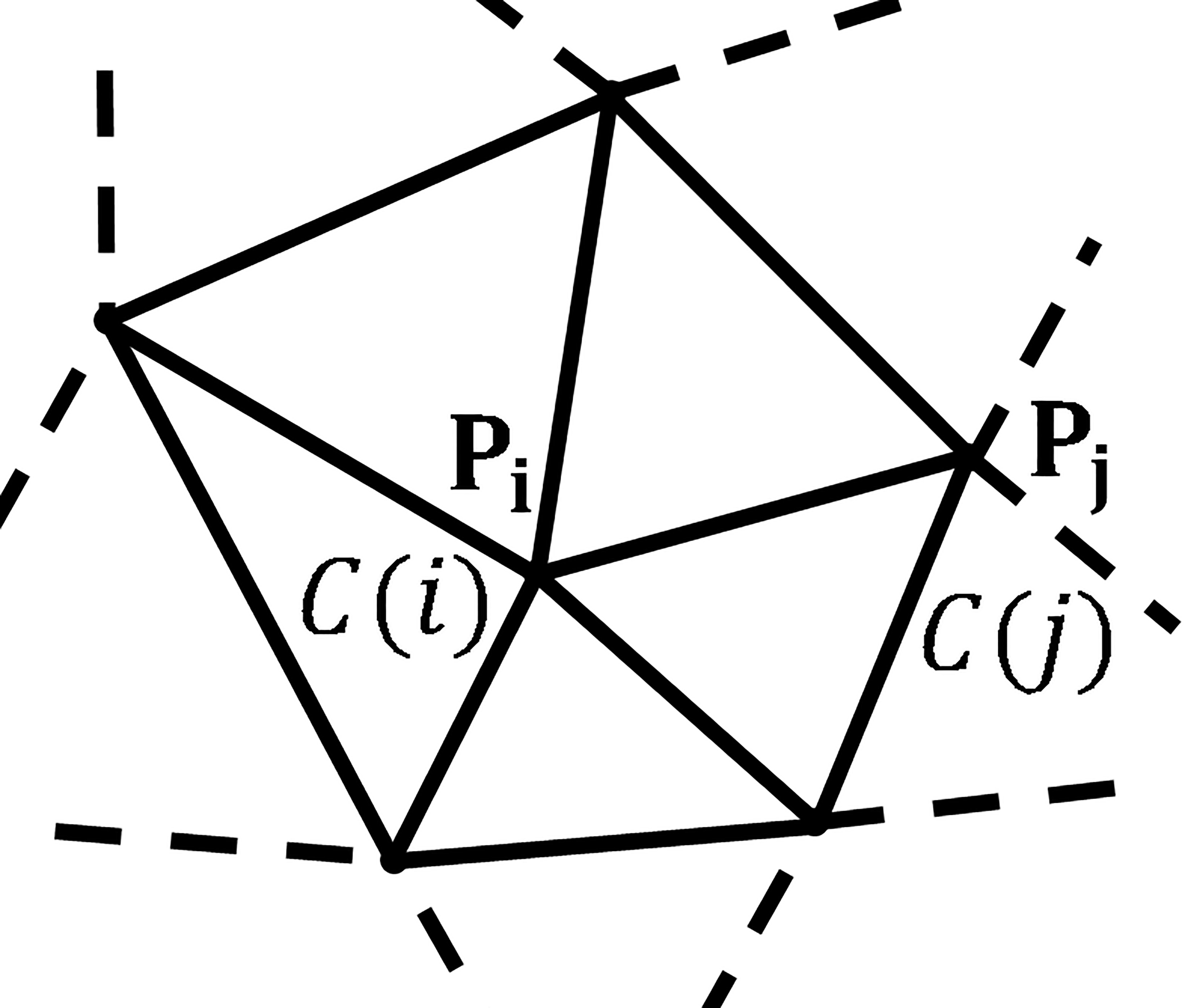
The CNN can be applied to any type of geometric grid of any dimension. Consider a geometric grid shown in Fig. 1, points
To describe the interaction range between cells, the neighborhood
(1)
where
The dynamic behaviors of cell
(2)
(3)
where
Without cell input
(4)
3.Model construction
3.1ChainMail formulation of local connectivity of cells
The CNN and ChainMail share common characteristics. Under the given initial conditions and external inputs, the dynamic behaviors of the proposed CNN are described by the local connectivity of cells. Similarly, the behaviors of ChainMail are also described by the local position adjustments under the same conditions. Further, similar to the CNN output, which is bounded by the constant
Traditional ChainMail method [10, 11] defines the compression and extension lengths with respect to (w.r.t) the coordinate axes
Define the initial length of the chain link connecting chain elements
(5)
Hence, the current length
(6)
Figure 2.
Position adjustments
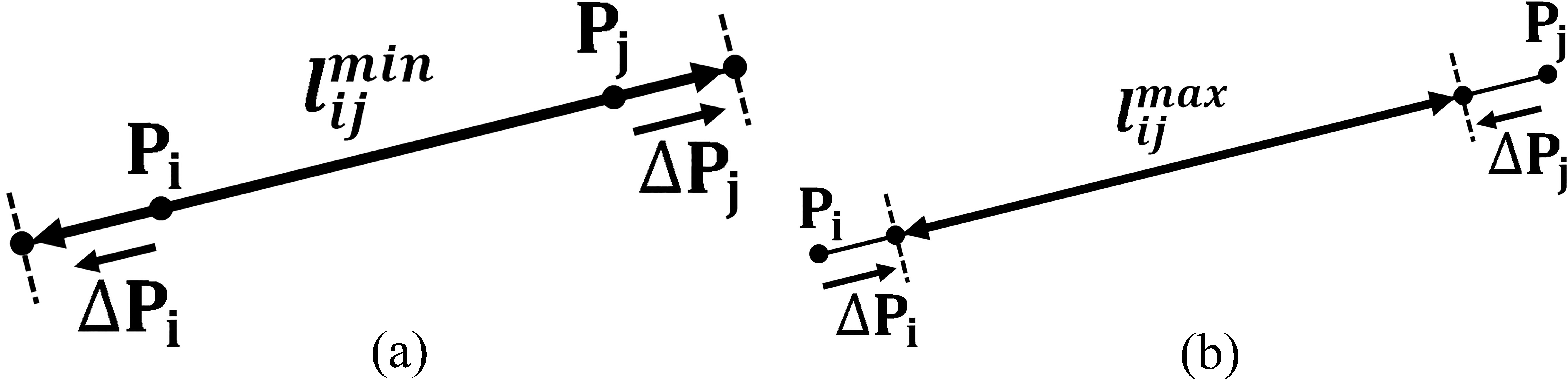
Define the position adjustments for chain elements
(7)
For the sake of conciseness, consider a simple case where a chain element is connected with four neighbors as illustrated in Fig. 3.
Figure 3.
A grid with four local connections: chain element
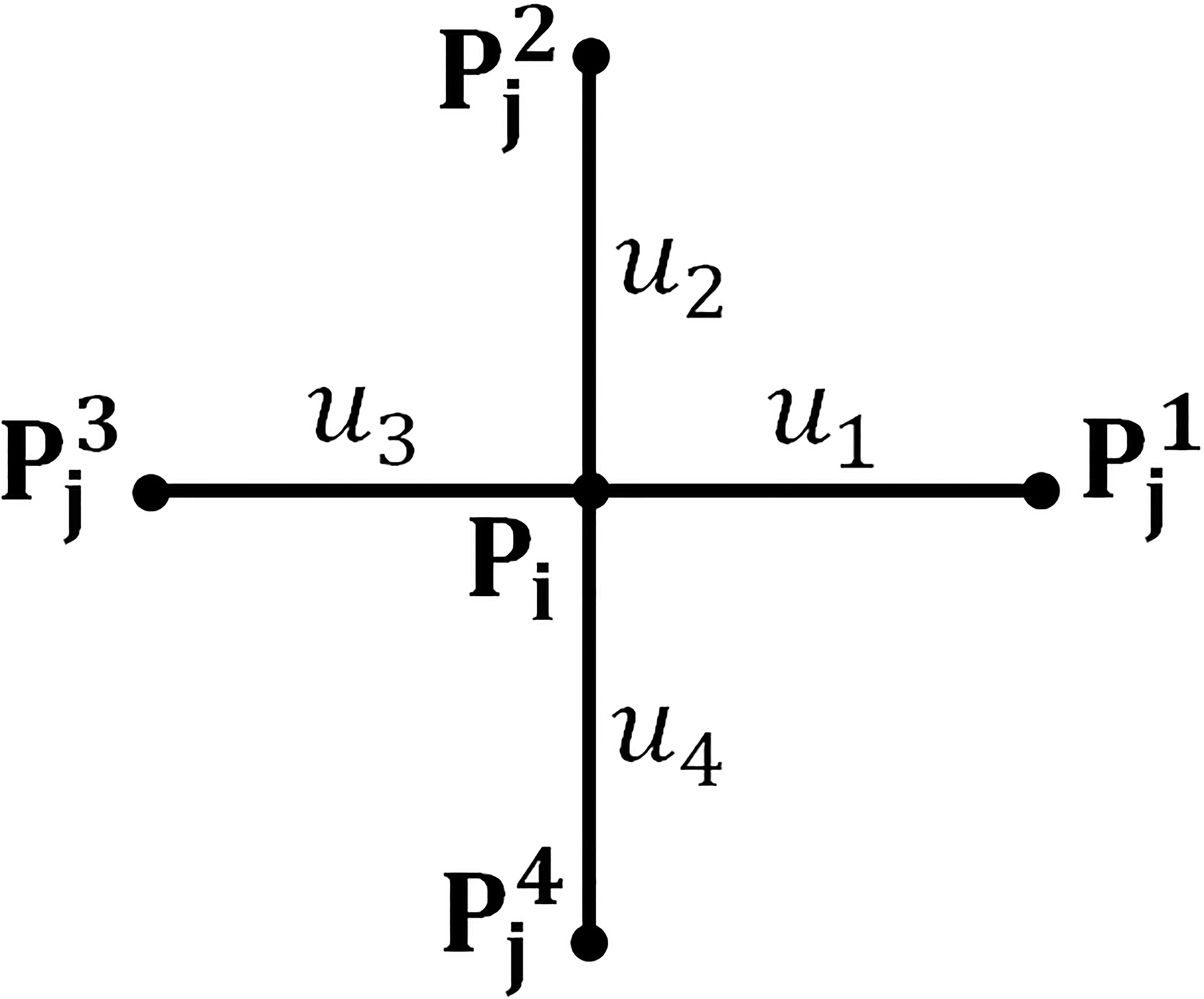
The net adjustment for chain element
(8)
where
(9)
where
(10)
By associating the cell state
(11)
In case that chain element
(12)
where
(13)
where
(14)
Similar to Eq. (11), the feedback template
(15)
3.2CNN current source, initial and boundary conditions
When a soft tissue is deformed, there is a displacement experienced at the region of contact. Hence, the current source
Figure 4.
Deformations of a plane by (a) the proposed CNN and (b) traditional ChainMail method: the deformation produced by the proposed CNN shows nonlinear behaviors whereas it shows only linear behaviors with the traditional ChainMail.
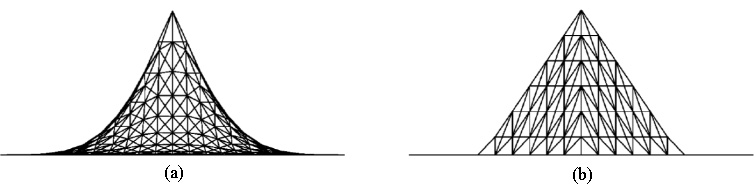
Figure 5.
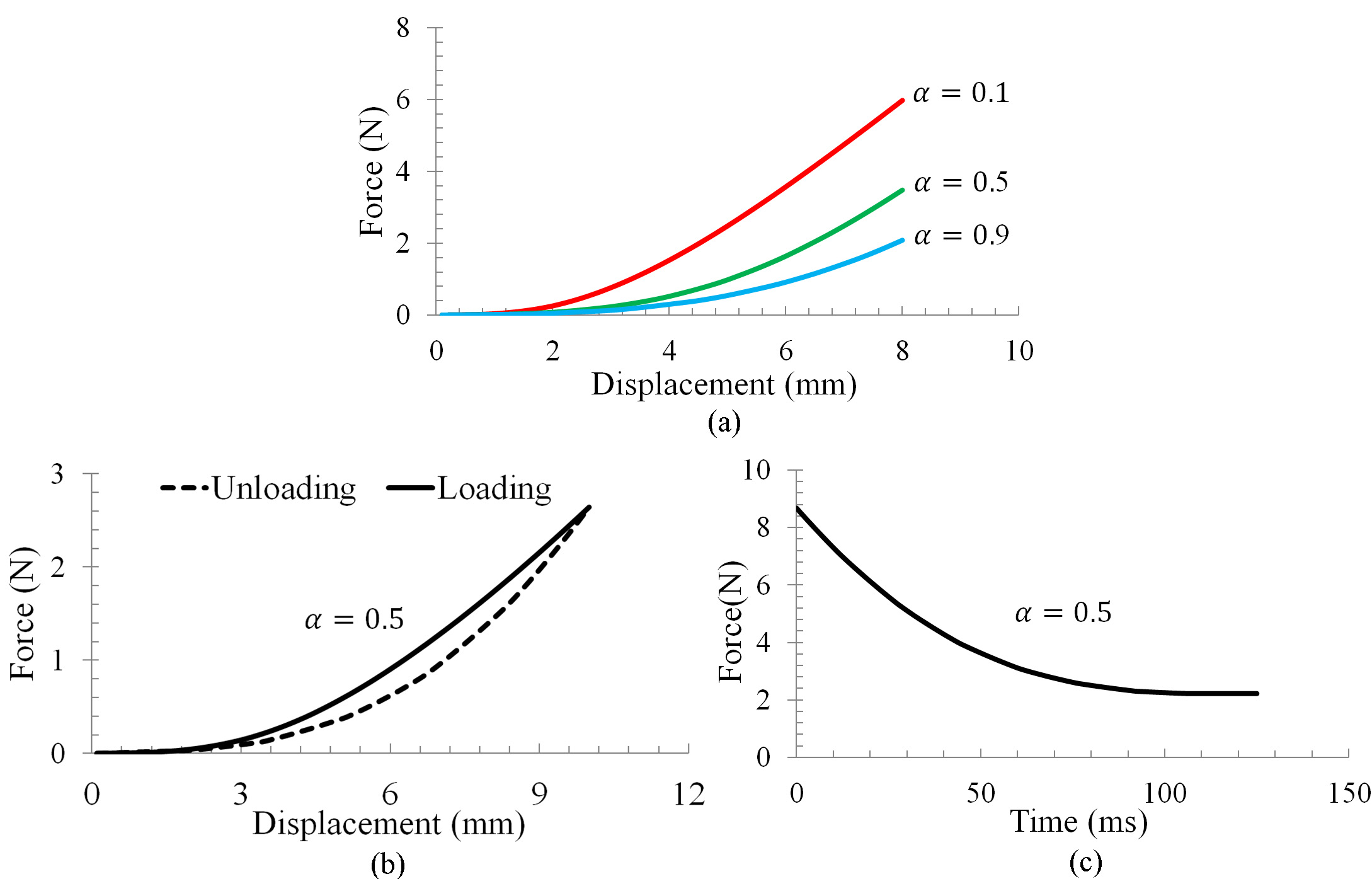
(a) Nonlinear force-displacement, (b) hysteresis and (c) stress relaxation observed from the proposed method.
4.Performance evaluation
The proposed CNN has been implemented into a prototype surgical simulation system for soft tissue deformation. Trials have been conducted with the proposed method to evaluate its performance in terms of soft tissues’ nonlinear deformation and typical mechanical behaviors. Figure 4 compares the deformations of a rectangular plane (21
Figure 6.
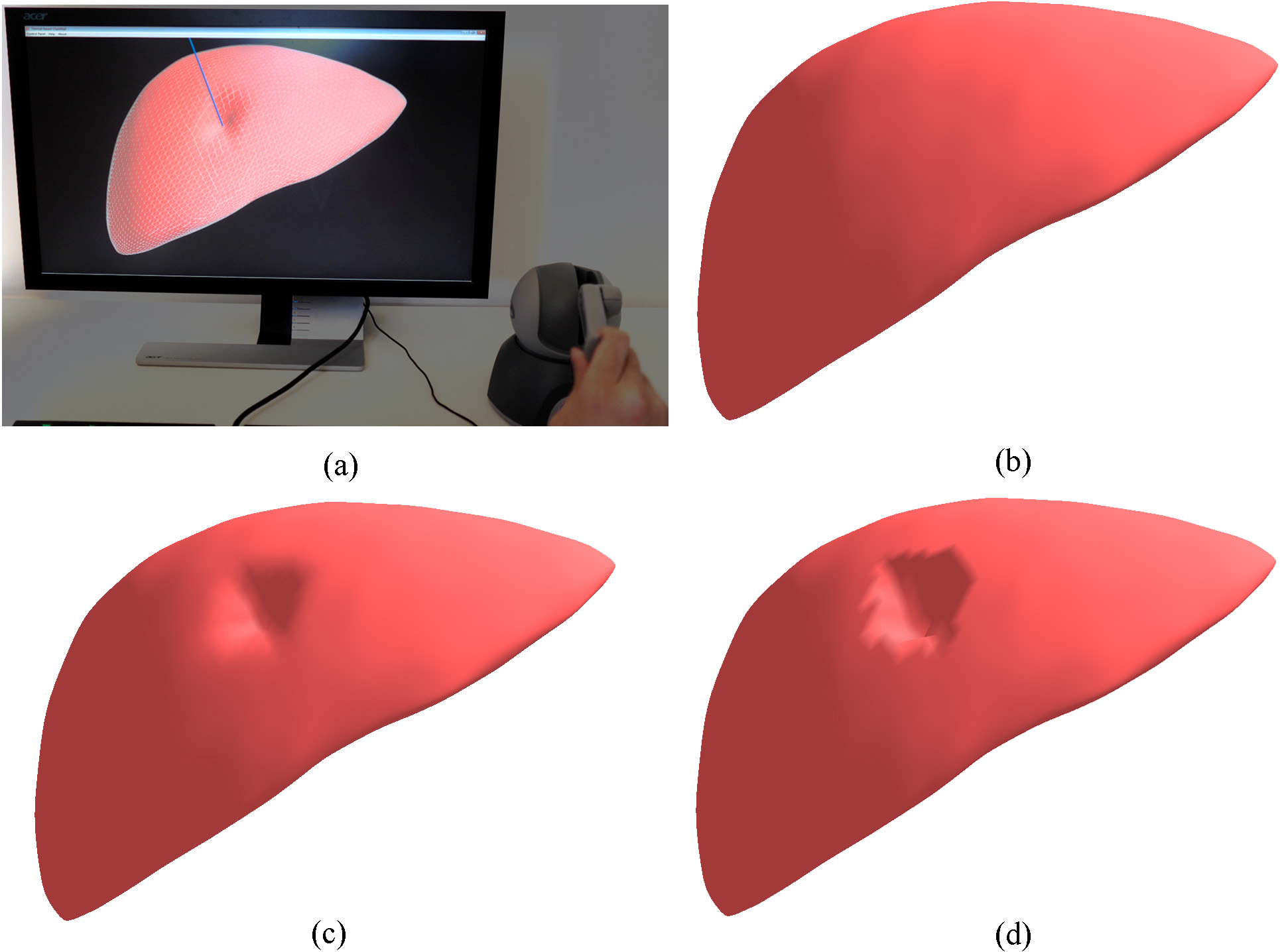
Interactive deformation of the human liver model: (a) the interactive simulation system; (b) the initial state of the volumetric liver model; (c) the deformation by the proposed CNN; (d) the deformation by the traditional ChainMail.
Trials have also been conducted to verify the proposed CNN against the soft tissues’ typical mechanical behaviors, such as the nonlinear force-displacement relationship, hysteresis and stress relaxation [19]. Nonlinear force-displacement relationship was examined using a compression test with a displacement occurred at the contact point. Figure 5a demonstrates the nonlinear force-displacement relationship. Hysteresis was examined using the same compression test for loading, while the unloading was achieved by resorting the chain links between chain elements to their initial lengths. It can be seen from Fig. 5b that the variations of force w.r.t displacement followed two distinct paths during loading and unloading, this behavior is similar to the hysteresis effect measured from living biological tissues [19]. Stress relaxation was also examined by maintaining a constant displacement at the contact point. As shown in Fig. 5c, the internal force decreased asymptotically towards a minimum value. This behavior is in agreement with the stress relaxation observed from real soft tissues [19].
The proposed CNN has been integrated into a prototype surgical simulation for interactive deformation of virtual human organs with haptic feedback. Figure 6 illustrates the prototype surgical simulation system with a comparison of deformations modeled by the proposed CNN and traditional ChainMail. The volumetric human liver model contains 5762 mass points and 20255 tetrahedrons and it is deformed via a virtual haptic probe. It can be seen that the proposed CNN generates a better deformation shape than the ChainMail method.
5.Conclusion and future work
In this paper, a new ChainMail based neural dynamics approach is presented for modeling and simulation of soft tissue deformation for surgical simulation. It models the nonlinear deformation of soft tissues via the nonlinear neural dynamics of CNN through the formulation of local connectivity of cells as the local position adjustments of ChainMail. Results demonstrate that the proposed method can produce soft tissues’ nonlinear deformation as well as the typical mechanical behaviors. Future research will be devoted to two aspects for enhancement of the proposed method. One is the scalability. Algorithms will be developed to map multiple chain elements to one single neural cell to expand the proposed method to accommodate the increase of chain elements. The other is material parameter determination. Optimization algorithms will be developed to determine optimal material parameters for the nonlinear properties of soft tissues to further improve the modeling realism.
Conflict of interest
None to report.
References
[1] | Miller K. Computational Biomechanics for Patient-Specific Applications. Annals of Biomedical Engineering. (2016) ; 44: (1): 1-2. doi 10.1007/s10439-015-1519-9. |
[2] | Duan Y, Huang W, Chang H, Chen W, Zhou J, Teo SK, et al. Volume Preserved Mass-Spring Model with Novel Constraints for Soft Tissue Deformation. IEEE Journal of Biomedical and Health Informatics. (2016) ; 20: (1): 268-80. doi 10.1109/JBHI.2014.2370059. |
[3] | Freutel M, Schmidt H, Durselen L, Ignatius A, Galbusera F. Finite element modeling of soft tissues: Material models, tissue interaction and challenges. Clinical Biomechanics. (2014) ; 29: (4): 363-72. doi 10.1016/j.clinbiomech.2014.01.006. |
[4] | Wu W, Heng PA. An improved scheme of an interactive finite element model for 3D soft-tissue cutting and deformation. The Visual Computer. (2005) ; 21: (8-10): 707-16. doi 10.1007/s00371-005-0310-6. |
[5] | Cotin S, Delingette H, Ayache N. Real-Time Elastic Deformations of Soft Tissues for Surgery Simulation. IEEE Transactions on Visualization and Computer Graphics. (1999) ; 5: (1): 62-73. doi 10.1109/2945.764872. |
[6] | Miller K, Joldes G, Lance D, Wittek A. Total Lagrangian explicit dynamics finite element algorithm for computing soft tissue deformation. Communications in Numerical Methods in Engineering. (2007) ; 23: (2): 121-34. doi 10.1002/cnm.887. |
[7] | Zhu B, Gu L. A hybrid deformable model for real-time surgical simulation. Computerized Medical Imaging and Graphics. (2012) ; 36: (5): 356-65. doi 10.1016/j.compmedimag.2012.03.001. |
[8] | Zhang GY, Wittek A, Joldes GR, Jin X, Miller K. A three-dimensional nonlinear meshfree algorithm for simulating mechanical responses of soft tissue. Engineering Analysis with Boundary Elements. (2014) ; 42: : 60-6. doi 10.1016/j.enganabound.2013.08.014. |
[9] | Johnsen SF, Taylor ZA, Clarkson MJ, Hipwell J, Modat M, Eiben B, et al. NiftySim: A GPU-based nonlinear finite element package for simulation of soft tissue biomechanics. International Journal of Computer Assisted Radiology and Surgery. (2015) ; 10: (7): 1077-95. doi 10.1007/s11548-014-1118-5. |
[10] | Frisken-Gibson SF. 3D ChainMail: a Fast Algorithm for Deforming Volumetric Objects. Proceedings of the Symposium on Interactive 3D; graphics. (1997) : 149-54. doi 10.1145/253284.253324. |
[11] | Li Y, Brodlie K. Soft Object Modelling with Generalised ChainMail - Extending the Boundaries of Web-based Graphics. Comput Graph Forum. (2003) ; 22: (4): 717-27. doi 10.1111/j.1467-8659.2003.00719.x. |
[12] | Rodriguez A, Leon A, Arroyo G, Mantas JM. SP-ChainMail: a GPU-based sparse parallel ChainMail algorithm for deforming medical volumes. J Supercomput. (2015) ; 71: (9): 3482-99. doi 10.1007/s11227-015-1445-5. |
[13] | Zhong Y, Shirinzadeh B, Alici G, Smith J. A Cellular Neural Network Methodology for Deformable Object Simulation. IEEE Transactions on Information Technology in Biomedicine. (2006) ; 10: (4): 749-62. doi 10.1109/TITB.2006.875679. |
[14] | Zhong Y, Shirinzadeh B, Smith J. Soft tissue deformation with neural dynamics for surgery simulation. International Journal of Robotics and Automation. (2007) ; 22: (1): 1-9. doi 10.2316/Journal.206.2007.1.206-1000. |
[15] | Chua LO, Yang L. Cellular Neural Networks: Theory. IEEE T Circuits Syst. (1988) ; 35: (10): 1257-72. doi 10.1109/31.7600. |
[16] | Thiran P, Setti G, Hasler M. An Approach to Information Propagation in 1-D Cellular Neural Networks - Part I: Local Diffusion. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. (1998) ; 45: (8): 777-89. doi 10.1109/81.704819. |
[17] | Setti G, Thiran P, Serpico C. An Approach to Information Propagation in 1-D Cellular Neural Networks - Part II: Global Propagation. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. (1998) ; 45: (8): 790-811. doi 10.1109/81.704820. |
[18] | Chua LO, Hasler M, Moschytz GS, Neirynck J. Autonomous Cellular Neural Networks: A Unified Paradigm for Pattern Formation and Active Wave Propagation. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. (1995) ; 42: (10): 559-77. doi 10.1109/81.473564. |
[19] | Fung Y-C. Biomechanics: Mechanical Properties of Living Tissues. ed n, editor: Springer-Verlag; (1993) . |




