A computational perspective on neural-symbolic integration

2.1.From neurons to symbols

Perhaps surprisingly, the correspondence between the neural and logical calculus has been well-established throughout history. Dating all the way back to the introduction of the first computational neuron by McCulloch and Pitts in their 1943’s paper “A logical calculus of the ideas immanent in nervous activity” [38], we can see that it was actually thought to emulate logic gates over binary propositions. The idea was based on the, now commonly exemplified, fact that logical connectives of conjunction and disjunction can be easily encoded by binary threshold units with weights (Fig. 1) – i.e., the perceptron, a learning algorithm for which was introduced shortly after.

While stacking these on top of each other was a clear path towards representation of more complex, nested logical functions, it took until the 1980’s to reintroduce the chain rule for differentiation of nested functions as the “backpropagation” method to calculate gradients in such “neural networks” which, in turn, could be efficiently trained with gradient descent. For that, however, researchers had to replace the original binary threshold units with differentiable activation functions, such as the logistic sigmoid, which started digging a gap between the neural networks and their crisp logical interpretations.

2.2.From deep learning to logic

These historical parallels might seem outlandish in the context of modern DL. However, interestingly, even the modern idea of DL was not originally described as bound to the neural networks, but rather universally to methods modeling hierarchical composition of useful concepts that are reused in different inference paths of target variables from the input samples [4]. And while this concept has most commonly been instantiated through “hidden layers” in DL, such hierarchical abstractions are common in logical reasoning, too. In fact, logic is the very science of deduction of useful concepts from simpler premises in a hierarchical (nested) fashion. While constructing a proof in logic, auxiliary lemmas are often created to reduce the complexity of the theory in scope, in a fashion very similar to DL. Thus, instead of hidden neural layers, these hierarchical abstractions may also be thought of as “complicated propositional formulae re-using many sub-formulae”.11

And from the NSI perspective, this is not just some metaphor, but actual systems reflecting this paradigm started to emerge throughout the ’90s, such as the popular Knowledge-Based Artificial Neural Network (KBANN) [50] (Fig. 1). However, as imagined by Bengio, such a direct neural-symbolic correspondence was insurmountably limited to the aforementioned propositional setting, popularly referred to as “propositional fixation” of neural networks [37].

Fig. 1.

An example correspondence between a neural network (left) and a propositional logic program (middle), based on conjunctive and disjunctive activations emulated by the respectively weighted neurons (right), in the spirit of KBANN [50].

2.3.Problems with relational logic

While the aforementioned computational correspondence between the propositional logic programs and neural networks was very direct, transferring the same principle to the relational22 setting has remained a major challenge [3]. The issue is that in the propositional setting, only the (binary) values of the existing input propositions are changing, while the structure of the logical program stays fixed. This is easy to think of as a boolean circuit (neural network) sitting on top of a propositional interpretation (feature vector).

However, the relational input interpretations can no longer be thought of as individual values over a fixed (bounded) number of propositions (interpretation vector), but an unbound set of related atoms that are true in a given world (a Herbrand model [18]). Consequently, also the structure of the logical inference unfolded upon this representation can no longer be represented by a fixed boolean circuit. Naturally, when proving a query in relational (first-order) logic, we do not know the number of objects that will form input into the proof, we do not know the number of auxiliary lemmas that will be created in the process, and we do not know the length of the proof nor the overall size of the computation. Hence, there is just no way of mapping that relational reasoning into a static neural computation with a fixed number of inputs, neurons in each layer, and overall depth, effectively corresponding to a finite state machine, principally incapable of capturing the unboundedness, characteristic to the relational logic.

2.4.Modern NSI systems

In the field of NSI, the issue with relational expressiveness, not present in the propositional setting, has alternatively been viewed as the problem of variable binding [23]. Indeed, it is actually the relational logic variables that effectively represent the unbound sets of objects, enabling to make general statements about different individuals, and facilitating the unbound variability in symbolic AI computing structures. This is in contrast to the bounded processing of fixed-size vector (tensor)33 representations characteristic to modern DL compute.

In recent years, a large number of new NSI systems building directly on top of popular deep learning frameworks emerged [26]. Many of these systems are designed to operate with some level of first-order expressiveness, seemingly resolving the old issue of propositional fixation [37] with the efficient, modern-day, static tensor-based deep learning [12]. However, following the aforementioned computational perspective, this is in principle impossible to do. Consequently, in one way or another, these efficient, modern neural-symbolic systems are necessarily dropping parts of the symbolic (relational-level) capabilities, often somewhat inconspicuously.44 This is because building upon the modern, GPU-accelerated, DL foundation always requires some mapping into the fixed-size tensor computation of the existing frameworks [1,40], inherently insufficient to capture the unbound structures of relational inference.

3.1.Propositionalization

This representation dichotomy leads to a natural urge to turn these structures into the familiar form of the vectors, and continue with our standard ML pipelines [25], following the common cognitive bias of “If all you have is a hammer, everything looks like a nail”. In relational ML, this approach is generally referred to as “propositionalization” [32] which, similarly to the “tensorization” [10,19] in modern NSI systems (Section 2.4), is an effective strategy that often works well in practice. However, it is conceptually limited.

Firstly, it is clear that one cannot map from unbound relational structures into the fixed-size vectors or tensors without (unwanted) loss of information. This obvious limitation is commonly addressed by bounding the number of domain elements, seemingly restricting the maximum size of the resulting (neural) computation [53]. However, even if we restrict ourselves to such bounded structures, designing a suitable learning representation in the form of a numeric vector or tensor is still deeply problematic. For example, let us take even just graph structures – a restricted form of relational data. If there was a definite way to map a graph into the standard learning form of a (fixed-size) numeric vector (or tensor), it would trivially solve the graph isomorphism problem, since to test if two graphs are isomorphic or not, it would suffice to turn them into such vectors and compare these for equality instead. Of course, one can simply decide to ignore this problem and choose one of the plethora of the (NSI) approximations [16]. However, any such vector (tensor) mapping that ignores the isomorphism symmetry will naturally break the underlying logical semantics that is inherently invariant to it. Therefore, to address this problem properly, it is necessary to leave the space of fixed-size vector (tensor) transformations and revisit the original space of symbolic logic.

3.2.Inductive logic programming

Much out of the lights of the ML mainstream, there has been a community of Inductive Logic Programming (ILP) [9], concerned with proper ways of learning (interpretable) models from exactly such relational representations. For illustration, let us see how the graph-structured learning problems can be approached with the relational logic representations of ILP. To represent a graph, we simply define a binary “edge” relation, with a set of instantiations edge(x,y) for all the adjacent nodes x, y. Additionally, we may also use other (unary) relations to assign attributes to the sets of nodes, such as red(x), etc.

Fig. 2.

An example learned ILP model of a path (left), being unfolded on a labeled graph sample encoded in relational logic (middle), resulting into two different computation graphs for the same target query “path(d, a)” (right).

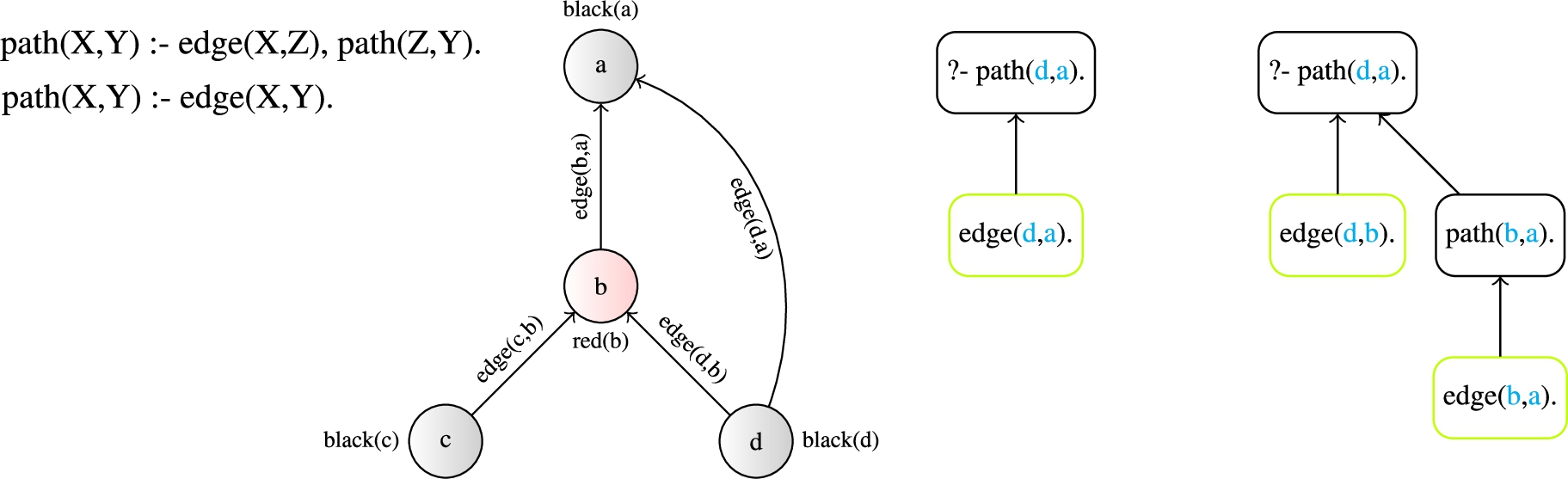
The models then take the form of relational logic rules, enabling to capture an unbound variety of structures, from characteristic motifs in molecules to paths in a network (Fig. 2). For instance, a (learned) relational model correctly capturing paths in a graph, can be easily learned with a basic ILP system from but a few examples. The simplicity of this problem within the relational representation formalism of ILP is then in direct contrast to the neural models operating on the propositional foundation of fixed-size vectors (tensors). There, in order to properly embed the same problem into the hypothesis space of a classic, fixed neural architecture, we would generally need to restrict ourselves to fixed-size graphs, design an exponentially large network to capture all the possible (inference) paths, in which it would be close to impossible for gradient descent to find the correct solution, and we would still not be able to properly generalize to different (larger) graphs. Moreover, the learning difficulties remain even if we move to theoretically expressive (Turing-complete) neural architectures, such as the (DeepMind’s) “Differentiable Neural Computer” [22], which required an extreme number of examples and additional hacking (e.g., pruning out invalid path predictions) to approximate the very same path-finding task through the (propositional) tensor representation, emulating a “differentiable memory” [21].

While ILP is able to correctly capture the expressiveness of relational logic, it is not well suited for dealing with noise and uncertainty, commonly present in real-world learning tasks. To address that issue, a number of methods arose to merge ILP with statistical learning under the notion of Statistical Relational Learning (SRL) [20], such as the “graphicalization”55 approach of [17], transforming the relational domains into graphs on top of which kernel methods were utilized. Generally, there have been two major streams of approaches in SRL – (i) probabilistic logic programs [11] and (ii) lifted graphical models [31]. While the former builds heavily on the classic, symbolic ILP formalism, the latter is much closer to standard statistical models, the expressiveness of which it “lifts” from the propositional into the relational setting, while retaining proper logical semantics. Naturally, this is highly relevant to the aforementioned problem of propositional fixation of neural networks and relational-level NSI (Section 2.3).

3.3.Lifted graphical models

As opposed to standard (“ground”) machine learning models, such as neural networks, lifted models do not specify a particular computation structure, but rather a logical “template” from which the standard models are being unfolded as part of the inference (evaluation) process, given the varying context of the relational input data. For instance, the (arguably) most popular lifted model – a Markov Logic Network (MLN) [42] may be seen as such a template for the classic Markov networks. For example, such an MLN template may express a general prior that “friends of smokers tend to be smokers” and “smoking may lead to cancer”. The learning data may then describe a social network of people with a subset of smokers labeled as such. The lifted modeling paradigm of MLNs then allows to induce the smoking probabilities of all the other people based on their social relationships, as if modeled by a regular Markov network, yet correctly generalizing over social networks of diverse structures and sizes, overcoming the propositional fixation of the base Markov model (Fig. 3).

The crucial ability to capture the unbound variability of the relational computation structures with a bounded computation template necessarily induces some form of repeated regularities, i.e. symmetries, within any such unfolded computation. In relational logic, these symmetries stem from the use of logical variables within the relations, i.e. subsets of the Cartesian products defined over the respective sets of objects. That is, unless the computation is effectively propositional as a corner case, one should be able to observe these repeated computational substructures, including shared parameterization, in the unfolded computation of the (ground) model. And while the, relational logic-based, lifted graphical models make this observation very explicit, we can actually observe the same principle being effectively exploited in many successful DL architectures, too, such as the popular CNNs, exploiting the symmetry of translational equivariance.66 From this computational view, the CNNs can thus be seen as a particular instance of an (implicit) relational modeling template (Fig. 3).

Fig. 3.

Illustration of two forms of relational expressiveness, with CNNs (right) capturing a spatial pattern of a 3-neighborhood, and an MLN (left) capturing a social pattern of smoking habits amongst friends, both reflected by the symmetries in the respective ground model computations.

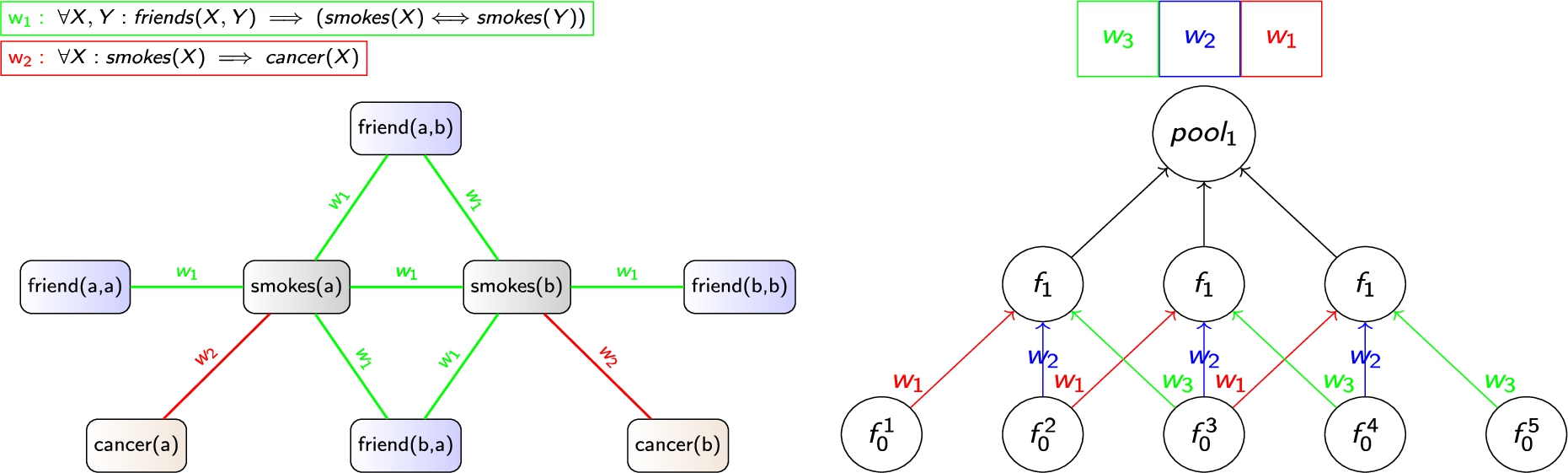
The proper logical semantics of the lifted graphical models is, however, redeemed by computational difficulties. Due to the explicit treatment of the logic variable binding, these models are commonly viewed as computationally expensive. Nevertheless, from the perspective of a general NSI system, this view is somewhat misleading since the computation is exactly as complex as necessary to properly capture the respective relational (logic) expressiveness.77 However, the problematic factor is the structure of the resulting computation.

4.1.Basic deep learning

By far the most common computation paradigm in deep learning is to structure the computation graphs regularly into homogeneous “layers”, which are used to refer to the sets of neurons {N|depthG(N)=k} residing at the same depth k in G. An input layer k=0 is then commonly used to represent the feature values x of the input data samples (xi,yi) themselves. An output layer k=depth(G) then corresponds to the target values y. The arguably most popular computation structure is then a “fully-connected” design pattern, where the interconnections between nodes in subsequent layers k and k+1 follow Nk,Nk+1:(Nk,Nk+1)∈E, forming a complete bipartite graph. Moreover, each edge here is associated with a unique weight as E⟶1:1W. Consequently, assuming the common vector form of the input data samples xi, the computation can be efficiently reduced to a linear series of full (dense) matrix Wkk+1 multiplications, each followed by an element-wise application of some non-linear function fk+1.

4.2.Relational neural models

The regular, dense, and homogeneous structure of the computation graph G, mapping to the basic matrix (tensor) operations, is a salient feature of the basic neural models. Note that from the aforementioned perspective of the lifted (graphical) models from SRL (Section 3.3) such computation, lacking any symmetries, is effectively propositional. However, there are also neural models designed to operate with some forms of relational data structures, such as sequences, trees, and graphs, which necessarily need to reflect some level of relational expressiveness. As a consequence, following the SRL reasoning from Section 3.3, their computations will, in contrast to the basic neural models, need to reflect some type of sparsity, heterogeneity, or irregularity, within the scope of the necessary symmetries reflected by some form of regular weight-sharing patterns within their computation graphs. Let us now inspect some common representatives of these neural models.

Fig. 4.

The symmetric weight-sharing patterns in the structured computation graphs of recurrent (left) and recursive (right) neural models.

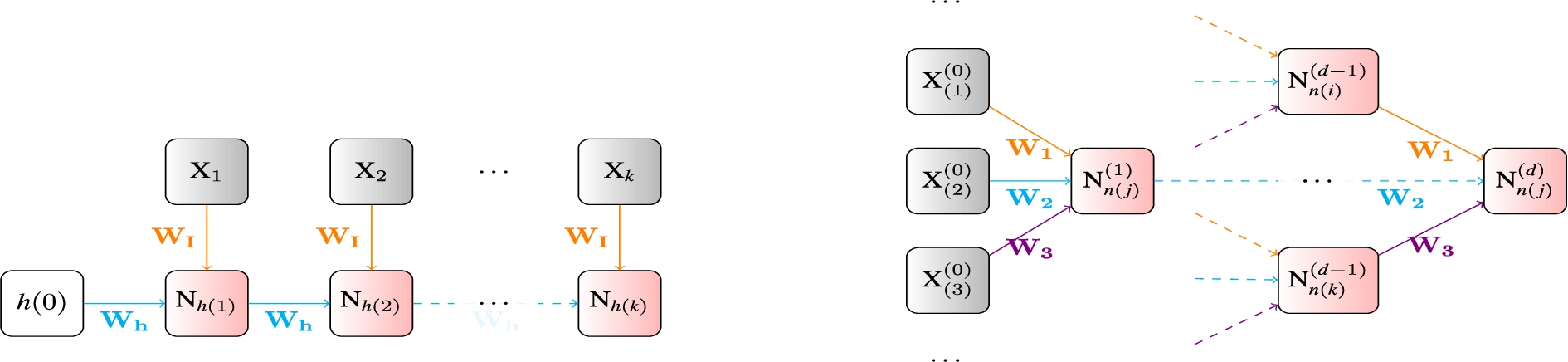
A Recursive Neural Network (RecNN) [41,46] is a neural architecture the computation graphs Gi of which directly follow the structure of each input example xi, which takes the form of a k-regular tree. This enables to learn neural networks directly from differently-structured regular tree examples xi, as opposed to using some transformation into the fixed-size tensors x (Section 3.1).88 Here, the (vector) representations of every c leaf nodes xj,…,xj+c with the same parent node Nj1 in the respective computation tree Gi are consequently combined by a given c-parameterized operation c, such as a c-weighted dot-product, to compute the representation of the parent Nj1. This combining operation c then continues recursively for all the interior nodes, until the representation for the root node Nk=d is computed, which forms the output of the model for xi. Similarly to the convolution in CNNs, this parameterized combining operation c over the children nodes is shared across the tree [45] however, differently from CNNs, the resulting computation graph can be highly and irregularly sparse (Fig. 4).

Note that the basic form of the more common Recurrent Neural Networks (RNNs) [34] can then be seen as a restriction of the RecNN computation to sequential structures xi (Fig. 4). There, the computation graph G in the form of a linear binary tree is successively unfolded along the input sequence to compute the hidden representation for each node Ni based on the previous node’s Ni−1 representation, and the current input features xi.

The most popular recent addition in this category are then Graph Neural Networks (GNN) [5,43] which, in contrast to the RNNs, can be seen as an extension of RecNNs to completely irregular graph data xi={Ni,Ei}. For that purpose, they unfold the computation graph Gi structure from each input structure xi, similarly to the RecNNs. However, a GNN still follows the standard layered approach (Section 4.1), where the structure of each layer k exactly follows the structure of the whole input graph xi. For computation of the next layer k+1 representations of the nodes in Gi, each node N calculates its own value h(N) by aggregating A (“pooling”) the (vector) values of the nodes M:(N,M)∈Ei adjacent in the input graph xi (“message passing”), transformed by some parametric function CW1 (“convolution”), which is again being reused with the same parameterization W1k within each layer k (Fig. 5). However, in contrast to RecNNs, a different parameterization is typically used at each layer.

Fig. 5.

Compressing a typical GNN model computation (up) based on the contained computation graph symmetries, resulting into a much smaller yet functionally equivalent computation (down), in the spirit of (symbolic) lifted inference [49], as implemented in LRNNs (Section 4.3).

4.3.Lifted relational neural networks

Lifted Relational Neural Networks [47] can be seen as a further generalization of the GNNs to arbitrary relational structures, covering all the previous models as special cases [48]. For that, they transfer the strategy of lifted modeling (Section 3.3) into a deep learning setting, effectively extrapolating the original, direct neuro-symbolic correspondence between deep learning and propositional logic (Section 2.2) straight into fully expressive relational setting.

Similarly to the lifted graphical models (Section 3.3), they adopt the language of weighted relational logic as their foundation, endowing them with explicit variable binding and symbolic reasoning capabilities, as found in the ILP systems (Section 3.2). This covers the sought-after ability to manipulate unbound structures xi, such as correctly resolving various path-finding (planning) problems (Fig. 2). However, differently from ILP and SRL, they introduce a differentiable semantics to the language, endowing them with ability to also directly model various deep learning architectures. Particularly, all the introduced CNN, RNN, RecNN, and GNN examples come directly from trivial differentiable logic programs in the LRNN framework [48]. This is in contrast to the modern (tensorization) NSI systems (Section 2.4) that build on top of the existing static DL compute stack, forcing them to map the logical semantics into fixed-size tensors, losing the relational expressiveness in the process (Section 3.1). Nevertheless, this also means that LRNNs necessarily share the computational difficulties associated with the relational expressiveness, particularly the dynamically structured computation graphs Gi, notoriously incompatible with the GPUs [39].

5.1.Accelerating symbolic computation

The maturity of the existing HW&SW DL ecosystem naturally incentivizes NSI researchers away from the expressive symbolic computation towards further “tensorization” of their systems [19], even in cases where such a choice would otherwise be conceptually inappropriate, which has a self-reinforcing side-effect of regressing to the same models [27]. This is becoming noticeable with more and more NSI methods operating simply as modules on top of existing tensor-based frameworks [2]. However, the symbolic computation, as exploited in the classic (relational) AI tasks, is often inherently sequential, stateful, and conditional, leading to dynamically sized and structured computation graphs, the forms of which are just impossible to properly embed into the common fixed-size tensor processing on GPUs.

For instance, the computation of a relational (lifted) model (Section 3.3) may completely change from sample to sample, making it principally incompatible with the SIMD philosophy of the GPU architecture. Importantly, this does not mean that the relational (symbolic) compute strategy would itself be somehow inferior or impossible to accelerate. On the contrary, akin to batching in DL, one can always naively parallelize in the data dimension across multiple CPU threads, utilizing its “multiple instructions, multiple data” (MIMD) capabilities. Consequently, should the evolution of CPU parallelism have reflected its GPU counterpart, i.e. chips with (hundreds of) thousands of CPU threads be readily available, there would be no need to sacrifice the symbolic capabilities in NSI systems. Moreover, the symbolic model representation also offers a much broader range of interesting acceleration strategies, such as lifted inference [51], in contrast to the comparatively brute-force approach of the GPU-based DL.

5.2.Accelerating graph neural networks

An interesting borderline example between these two, largely separate, worlds of symbolic and neural compute are the aforementioned GNN models, which can be seen as an instance of deep learning evolving in the direction of relational learning. Since the GNNs are able to (partially) capture graph-structured data, they necessarily reflect some level of (symbolic) relational logic expressiveness. Particularly, their expressive power corresponds to a guarded fragment of C2 logic [24,48].1212 Similarly to the other relational models, this increased, albeit still relatively limited (e.g., compared to the LRNNs [48]), expressiveness already takes its toll in their compute structure. Particularly, the variability of the input graph data, reflected in the irregularly sparse interconnection patterns within the GNN layers requiring random access to the underlying tensor indices (through respective gather/scatter operations [14]), is highly detrimental to the classic GPU acceleration.

However, the significant rise in popularity of the GNN-like architectures, driven by the omnipresence of the graph data structures in real-world problems, has come with an interesting paradigm shift in which the SW and HW developers started to actively reflect back on these alternative computing concepts in AI, too. Consequently, there have been new SW frameworks emerging [14,29], and most of the latest GPU cards support some levels of sparsity [8]. This is an interesting step in a direction beneficial for NSI [33], however, it is still far from a proper foundation for the full NSI compute, which can never fully fit the SIMD design of the GPUs. The corresponding low-level optimizations here are still largely incremental, building heavily on the legacy of the matrix-multiplication-based architectural design. Moreover, they tend to be increasingly specific, e.g., enforcing particular, fixed sparsity patterns [8], or even containing hardwired acceleration for particular models, such as the Transformers [7].

In contrast, the high-level, HW-independent, symbolic acceleration techniques are much more principled and reusable. For instance, in the spirit of NSI, the symbolic techniques of lifted inference (Section 3.3) can be transferred into deep learning to effectively accelerate relational neural models, such as the GNNs, by exploiting the inherent symmetries contained in their computation graphs. This results into explicitly smaller neural computation that effectively performs the exact same function (Fig. 5), which was unprecedented in deep learning [49]. Consequently, using this symbolic technique, even a naive CPU implementation of a GNN model can become faster than a specialized GPU-accelerated implementation [49].1313 However, should we completely fixate on the GPU-based deep learning as the foundation for NSI, our possibilities for such a beneficial transfer of symbolic techniques into deep learning (and vice-versa) might gradually become extinct.