1.5 GPa compact double-wall clamp cell for SANS and NSE studies at low temperatures and high magnetic fields
Abstract
We have developed and realised a compact high-pressure clamp cell of the piston-cylinder type for Small Angle Neutron Scattering (SANS) and Neutron Spin Echo (NSE) spectroscopy measurements. The cell can pressurise ⌀5 mm samples up to 1.5 GPa. It is non-magnetic, produces a sufficiently low and flat SANS background with a relatively good neutron transmission and can be used in combination with polarised neutrons. The cell accommodates samples of up to 55 mm3 in volume and adopts a two-layer geometry: a TiZr body (outer layer) and a CuBe2 insert (inner layer). Its design is very compact and can be employed inside cryomagnets featuring a sample bore greater than ⌀30 mm. We present the cell and illustrate its performances with a series of neutron scattering experiments performed on single-crystalline MnSi.
1.Introduction
Pressure is a fundamental thermodynamic variable and therefore plays an important role in condensed matter physics. It has a pronounced influence on the structural, magnetic, electric, chemical and mechanical properties of condensed materials [11]. In addition, the experimental investigation of some of the most fascinating phenomena in condensed matter physics, such as quantum critical points [3,6,15], hidden order [2,15] or non-Fermi liquid behavior [6], often require the combination of low temperatures, high magnetic fields and high pressures. In this field of research, neutron scattering is an invaluable probe as it provides direct microscopic information on both the structural and magnetic correlations. It is therefore important to develop non-magnetic pressure cells optimised for neutron scattering studies which can reach moderate pressures, beyond 1 GPa, whilst being able to accommodate relatively large sample volumes.
These requirements are met using piston-cylinder type clamp cells where the pressure is fixed by two knots. In addition, cells of the piston-cylinder type are compact enough to fit in the cryomagnets and cryostats typically used for neutron scattering experiments. In the following we present a new non-magnetic high pressure double-wall cell, which we have developed for Small Angle Neutron Scattering (SANS) and Neutron Spin Echo Spectroscopy (NSE) experiments. The cell has been successfully tested at the Institute Laue-Langevin (ILL) and the ISIS neutron source. It has been used to investigate the magnetic properties of the archetype helimagnet MnSi beyond the critical pressure of ∼1.4 GPa where a non-Fermi Liquid behaviour sets-in [17]. We show that this pressure cell produces a low-enough and flat neutron background in the Q-range covered by typical SANS instruments and that it can also be used for NSE. The cell can accommodate samples up to 55 mm3 in volume and reaches pressures as high as 1.5 GPa at low temperatures.
2.Choice of materials
The choice of materials is the most important factor determining the performances of high pressure cells. In the specific case of neutron scattering, the materials used should not only have suitable mechanical properties including high tensile strength and hardness, but also be relatively transparent to hot, thermal and cold neutrons. In this way both the attenuation of the intense neutron beam and the activation of the pressure cell are minimised. Furthermore, it is important to choose materials with low coherent and incoherent scattering cross sections to reduce the scattering by the cell, and therefore decrease the (Q-dependent) background, or noise, of the measurement. To be able to apply magnetic fields or use polarised neutron beams (essential for NSE spectroscopy), it is of crucial importance that the chosen materials remain non-magnetic down to the lowest temperatures of interest.
Table 1
Relevant properties for several materials considered for the pressure cell. Data on the scattering length and neutron cross section are adapted from ref. [21]. Hardness data are given in Rockwell units. Ultimate Tensile Stress (UTS) data at 300 K are provided in [16,24]
| Material | Hardness [HRC] | UTS [GPa] | |||||
| Al | 3.449 | 1.495 | 0.0082 | 1.503 | 0.231 | ||
| Be | 7.79 | 7.63 | 0.0018 | 7.63 | 0.0076 | ||
| Cr | 3.635 | 1.66 | 1.83 | 3.49 | 3.05 | ||
| Cu | 7.718 | 7.485 | 0.55 | 8.03 | 3.78 | ||
| Ni | 10.3 | 13.3 | 5.2 | 18.5 | 4.49 | ||
| Ti | −3.438 | 1.485 | 2.87 | 4.35 | 6.09 | ||
| Zr | 7.16 | 6.44 | 0.02 | 6.46 | 0.185 | ||
| TiZr | 0.06 | 0.04 | 314.8 | 314.9 | 32 | 0.86 | |
| CuBe2 | 7.73 | 7.50 | 0.49 | 7.99 | 35 | 1.20 | |
| NiCrAl | 7.36 | 8.31 | 141.1 | 149.4 | 57–59 | 1.90 |
Table 2
Relative mass weight composition of the Russian NiCrAl alloy 40HNU-VI
| C | Si | Mn | Fe | Ni | Cr | Mo | Ti | Al | Nb | Co | S | P |
| ⩽0.03 | ⩽0.1 | ⩽0.1 | ⩽0.6 | balanced | 39–41 | – | – | 3.3–3.8 | – | – | ⩽0.01 | ⩽0.01 |
Table 1 provides an overview of relevant material properties for chemical elements and the alloys considered for the construction of the pressure cell. The CuBe2 (2 wt.% Be), TiZr [22] and NiCrAl [19] alloys are all non-magnetic. Among them, the Russian Ni alloy with designation 40HNU-VI and mass weight composition provided in Table 2 has the highest hardness and has already been used for high-pressure neutron diffraction studies [4,19]. However, this alloy combines relatively high incoherent and coherent cross sections with strong forward scattering likely due to dislocations and/or short range order [18]. It is therefore much less appropriate for SANS than CuBe2 and TiZr.
The null-matrix TiZr alloy has a zero coherent cross-section
3.Design of the cell
Fig. 1.
Schematics of the assembled cylindrical multi-layer clamp cell: 1. NiCrAl piston, 2. hardened Ti nuts (grade VT8), 3. NiCrAl pistons, 4. TiZr body, 5. Teflon cap, 6. hardened CuBe2 rings, 7. Teflon can, 8. hardened CuBe2 insert, 9. sample. At the sample position, the diameter of the cell is reduced to 22.2 mm to improve the signal to background ratio.
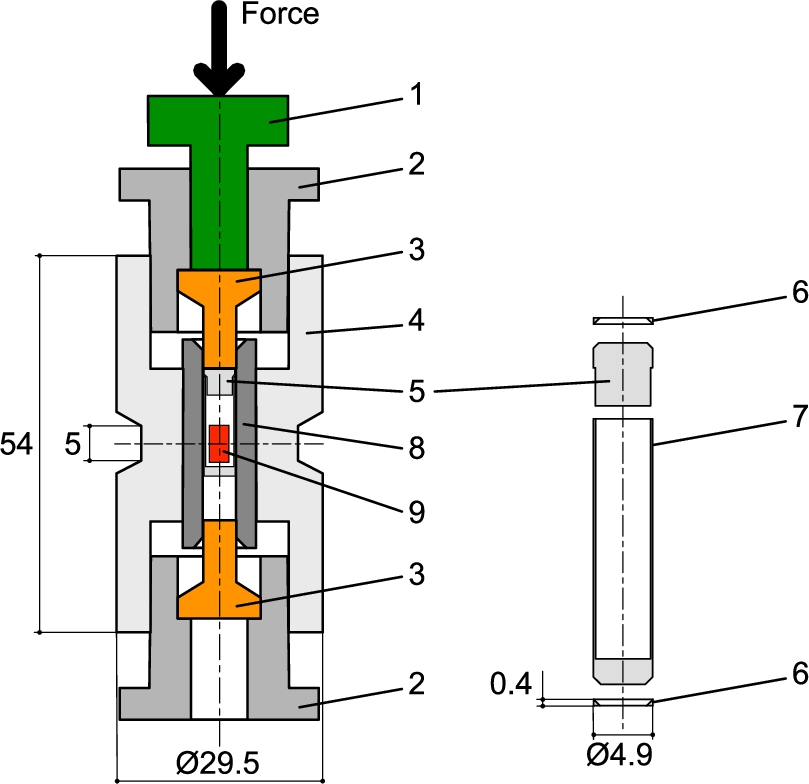
Figures 1, 2 and 3 show drawings and photographs of the double-wall cell and its auxiliary equipment. It consists of a hardened CuBe2 cylindrical insert pressed into a TiZr cylinder. The TiZr body is 54 mm long and has a maximum outer diameter of 29.5 mm. This diameter is reduced to 22.2 mm at the beam height on 5 mm. Flat faces are machined to ease its operation. M20 threads are provided at both ends to lock the NiCrAl pistons. With this design, the clamp cell matches most of the cryomagnets provided by neutron facilities up to fields of 10 Tesla.
The insert, made from hardened CuBe2, has inner and outer diameters of 4.9 and 10 mm respectively. Its length was chosen to match the dimensions of single crystals that are typically available. Before assembly, the inner cylinder of the TiZr body was machined with a conical shape inclined by
Fig. 2.
Photographs of the pressure cell, nuts and pistons.

The sample with a maximum diameter of 3.7 mm and a maximum height of 5 mm is encapsulated in a cylindrical Teflon (PTFE) can placed in the heart of the pressure cell. This Teflon can is topped up with a hydrostatic pressure transmitting liquid, typically Fluorinert [5]. At both ends of the can, the sealing is realised with two hardened CuBe2 rings with an outer diameter of 4.9 mm, only slightly greater than the diameter of the bore. The shape of the internal diameter of each ring is inclined by 45° so that the pressure slightly enlarges the diameter of the ring, ensuring its tightness. The optimum thickness of the rings is ≈0.4 mm.
Nonmagnetic pistons made of NiCrAl alloy are positioned on both sides of the sample can. These pistons have a diameter which is 0.02 mm smaller than the inner diameter of the CuBe2 insert to avoid an excess of friction from the elastic deformation of the pistons at high pressures. Such a deformation ultimately results in “barrel-shaped” pistons leading to an increased contact area with the inner walls of the CuBe2 insert. This increase in friction lowers the effective pressure at the sample area and therefore reduces the effective operating pressure range. Molybdenum sulphide powder can be spread to reduce the friction with the inner surface of the CuBe2 insert but care must be taken because it activates in a neutron beam.
Finally, the pistons are clamped by two non-magnetic titanium (alloy grade VT8) knots positioned at both ends of the pressure cell. An M8 hole threaded in the top knot facilitates the fixation of the high pressure cell to the sample stick of the cryostat or cryomagnet.
Fig. 3.
Photographs of the PTFE sample cans and CuBe2 rings.

4.Tests and operation of the cell
The cell has been used successfully for a series of neutron scattering experiments on the SANS instrument Larmor at ISIS (UK) and the NSE instrument IN15 at the ILL (France) [20]. The measurements were performed on a 110 mg single crystal of MnSi, approximately
At ISIS, we successfully applied pressures up to 2.2 GPa at room temperature. The pressure was applied using a 100 ton press and fixed by tightening the two titanium knots. These knots were tightened stepwise (i.e. first the top, then the bottom, then again the top, etc.) to prevent a displacement of the single crystal. The applied pressure was measured using a Strainstall 20 tons load cell. The press used at the ILL is equipped with an electronic load cell that accurately measures the load force of the press and the displacement sensor of the piston, which makes it possible to determine the friction and the pressure at room temperature by increasing and decreasing the load.
Figure 4 shows the relation between the applied force or the expected pressure in the cell at room temperature, and the effective pressure applied to the sample below 50 K. The pressure at low temperature is estimated from the critical temperature of MnSi as reported in ref [17], where the long range helimagnetic order sets-in at zero field. The figure shows that the pressure losses due to friction and the freezing of Fluorinert amount to about approximately 20%. These losses increase for higher applied pressures, possibly due to plastic instead of elastic deformation of the pistons.
Fig. 4.
Relation between the applied force or the expected pressure in the cell at room temperature, and the effective pressure applied to the sample below 50 K as deduced from the critical temperature of MnSi. The pressure at low temperatures is estimated from the critical temperature of the helimagnetic order at zero field as reported in [17].
![Relation between the applied force or the expected pressure in the cell at room temperature, and the effective pressure applied to the sample below 50 K as deduced from the critical temperature of MnSi. The pressure at low temperatures is estimated from the critical temperature of the helimagnetic order at zero field as reported in [17].](https://content.iospress.com:443/media/jnr/2018/20-1-2/jnr-20-1-2-jnr056/jnr-20-jnr056-g004.jpg)
Fig. 5.
Transmission of the empty cell as a function of the wavelength λ measured on Larmor using a
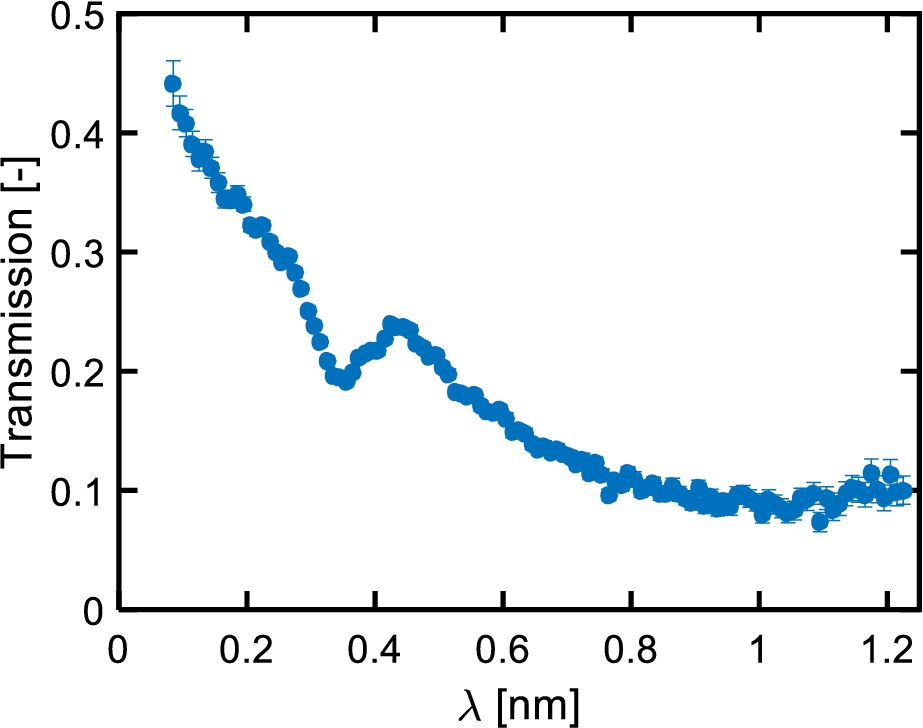
Figure 5 presents the neutron transmission of the high pressure cell measured as a function of neutron wavelength at the time-of-flight instrument Larmor. The transmission decreases with increasing wavelength, from about 40% at
The neutrons absorbed by the cell activate its constituents. We note that although Cu and Mn activate under neutron irradiation (both β-emitters), the activity outside the cell stayed below 2 μSv/h despite the long exposure time to the intense neutron beams of Larmor and IN15 (typically a week). The TiZr outer layer shields the activity originating from the decay of the irradiated Cu and Mn atoms. The resulting low activity measured outside the cell is a major advantage as it allows one to handle the cell and change the pressure directly immediately exposition to neutrons.
5.SANS and NSE experiments
The SANS measurements were performed on the time-of-flight instrument Larmor. The sample was illuminated by a
Figure 6 presents the scattering function
Fig. 6.
Scattering function
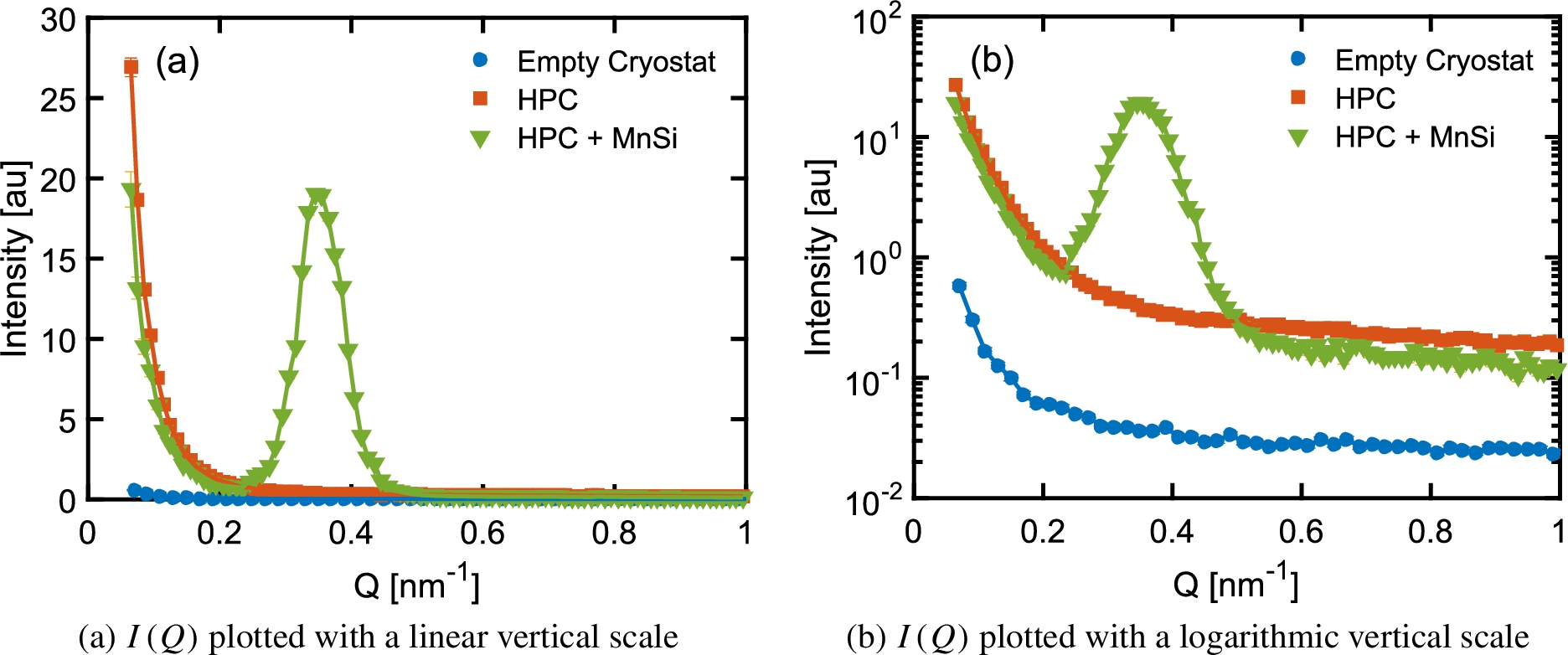
Fig. 7.
Typical SANS patterns of MnSi at 1.3 GPa (1.7 GPa at room temperature) and T = 8.3 K. A magnetic field of (a) B = 0 T and (b) 0.28 T was applied along the incident neutron beam. The SANS patterns are background corrected using a high-temperature measurement at 50 K where the magnetic contributions to the scattering are negligible.
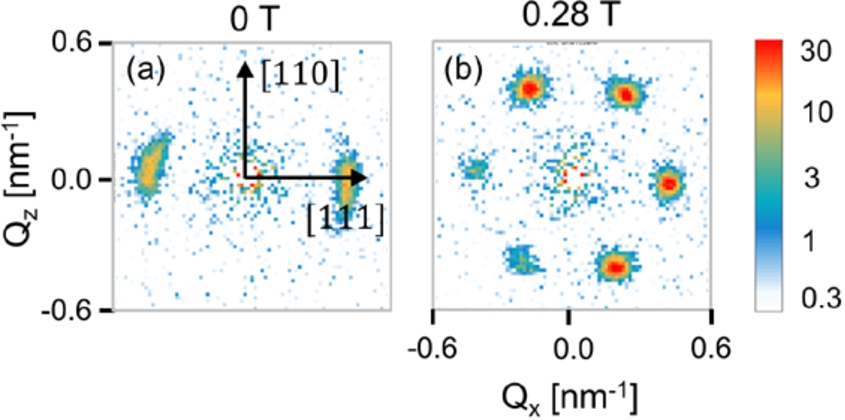
Fig. 8.
Neutron spin echo spectroscopy results obtained on MnSi at a pressure of 1.3 GPa at zero magnetic field. The intermediate scattering function
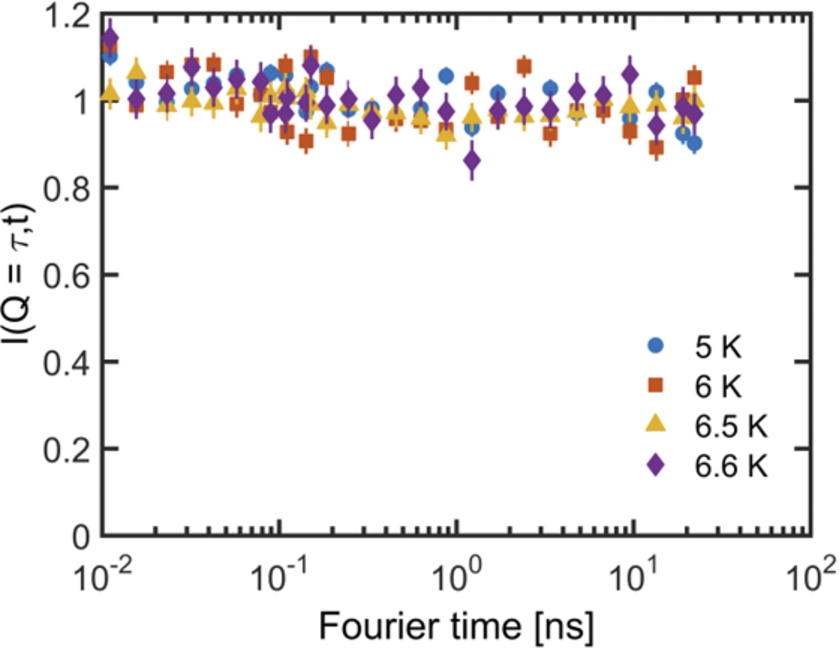
To further illustrate the performance of the clamp cell, we present in Fig. 7 two SANS patterns of MnSi at 1.3 GPa and 8.3 K. Pattern (a) reveals two Bragg peaks indicative of the helimagnetic ordering at zero field. The SANS pattern (b) collected with a field 0.28 T applied along the incident neutron beam reveals six Bragg peaks, characteristic of skyrmion lattice correlations [7,12].
The NSE experiments were performed in the paramagnetic configuration on the NSE spectrometer IN15 using a 95% polarised incident neutron beam with a wavelength of
6.Conclusion
We have successfully designed, constructed and operated a compact high pressure cell of the piston-cylinder type with a relatively high transmission and sufficiently low background, adapted for neutron small angle scattering investigations at low temperatures and high magnetic fields. The high pressure cell is non-magnetic and can be used for investigations with polarised neutrons and NSE spectroscopy. The cell has a two-layer construction with a TiZr outer layer and a CuBe2 insert with an inner diameter of almost 5 mm. It can accommodate samples up to 55 mm3 in volume and is compatible with the cryomagnets typically used in neutron scattering. The high pressure cell can be pressurised up to 1.5 GPa and has been successfully used for SANS and NSE spectroscopy experiments on single-crystal MnSi.
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement N°654000. The work of L.J. Bannenberg and C. Pappas is financially supported by the Netherlands Organisation for Scientific Research through the project 721.012.102.
References
[1] | L.J. Bannenberg, F. Qian, R.M. Dalgliesh, N. Martin, G. Chaboussant, M. Schmidt, D.L. Schlagel, T.A. Lograsso, H. Wilhelm and C. Pappas, Reorientations, relaxations, metastabilities, and multidomains of skyrmion lattices, Phys. Rev. B 96: ((2017) ), 184416. doi:10.1103/PhysRevB.96.184416. |
[2] | P. Chandra, P. Coleman, J.A. Mydosh and V. Tripathi, Hidden orbital order in the heavy fermion metal URu2Si2, Nature 417: ((2002) ), 831. doi:10.1038/nature00795. |
[3] | J. Custers, P. Gegenwart, H. Wilhelm, K. Neumaier, Y. Tokiwa, O. Trovarelli, C. Geibel, F. Steglich, C. Pépin and P. Coleman, The break-up of heavy electrons at a quantum critical point, Nature 424: ((2003) ), 524. doi:10.1038/nature01774. |
[4] | B. Fåk, R.A. Sadykov, J. Flouquet and G. Lapertot, Pressure dependence of the magnetic structure of the itinerant electron magnet MnSi, Journal of Physics: Condensed Matter 17: (10) ((2005) ), 1635, ISBN 0953-8984, http://stacks.iop.org/0953-8984/17/i=10/a=018. |
[5] | |
[6] | L. Forró, R. Gaál, H. Berger, P. Fazekas, K. Penc, I. Kézsmárki and G. Mihály, Pressure induced quantum critical point and non-Fermi-liquid behavior in |
[7] | S.V. Grigoriev, S.V. Maleyev, A.I. Okorokov, Y.O. Chetverikov, R. Georgii, P. Böni, D. Lamago, H. Eckerlebe and K. Pranzas, Critical fluctuations in MnSi near |
[8] | Horizon 2020, SINE2020 Poject, WP7 Task 3 High Pressure, https://www.sine2020.eu/randd-activities/sample-environment.html. |
[9] | S. Klotz, High tensile aluminium alloys, in: Techniques in High Pressure Neutron Scattering, T. Francis, ed., CRC Press, Boca Raton, (2013) . |
[10] | S. Klotz, J.-C. Chervin, P. Munsch and G.L. Marchand, Hydrostatic limits of 11 pressure transmitting media, Journal of Physics D: Applied Physics 42: (7) ((2009) ), 075413, ISBN 0022-3727, http://stacks.iop.org/0022-3727/42/i=7/a=075413. doi:10.1088/0022-3727/42/7/075413. |
[11] | H.-K. Mao, X.-J. Chen, Y. Ding, B. Li and L. Wang, Solids, liquids, and gases under high pressure, Rev. Mod. Phys. 90: ((2018) ), 015007. doi:10.1103/RevModPhys.90.015007. |
[12] | S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Skyrmion lattice in a chiral magnet, Science 323: (5916) ((2009) ), 915, http://science.sciencemag.org/content/323/5916/915.abstract. doi:10.1126/science.1166767. |
[13] | C. Pappas, L.J. Bannenberg, E. Lelièvre-Berna, F. Qian, C.D. Dewhurst, R.M. Dalgliesh, D.L. Schlagel, T.A. Lograsso and P. Falus, Magnetic fluctuations, precursor phenomena, and phase transition in MnSi under a magnetic field, Phys. Rev. Lett. 119: ((2017) ), 047203. doi:10.1103/PhysRevLett.119.047203. |
[14] | C. Pappas, E. Lelièvre-Berna, P. Falus, P.M. Bentley, E. Moskvin, S. Grigoriev, P. Fouquet and B. Farago, Chiral paramagnetic skyrmion-like phase in MnSi, Phys. Rev. Lett. 102: ((2009) ), 197202. doi:10.1103/PhysRevLett.102.197202. |
[15] | T. Park, F. Ronning, H.Q. Yuan, M.B. Salamon, R. Movshovich, J.L. Sarrao and J.D. Thompson, Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5, Nature 440: ((2006) ), 65. doi:10.1038/nature04571. |
[16] | J. Peters, M. Golub, B. Demé, J. Gonthier, J. Maurice, C. Payre, R. Sadykov and E. Lelièvre-Berna, New pressure cells for membrane layers and systems in solutions up to 100°C, Journal of Neutron Research 20(1–2) (2018). |
[17] | C. Pfleiderer, S.R. Julian and G.G. Lonzarich, Non-Fermi-liquid nature of the normal state of itinerant-electron ferromagnets, Nature 414: ((2001) ), 427. doi:10.1038/35106527. |
[18] | R. Sadykov, V. Litvin, S. Axenov, D. Trunov, A. Gulutin, A. Kharkovskii, V. Glazkov, P. Borisova, M.-S. Appavou, A.I. Ioffe and R. Khasanov, Neutron diffraction studies of the hardness of the 40HNU (NiCrAl) alloy from the phase composition and size, formed nanoparticles solid phase bulk samples, to be published. |
[19] | R.A. Sadykov, T. Strassle, A. Podlesnyak, L. Keller, B. Fak and J. Mesot, High-pressure cells for study of condensed matter by diffraction and inelastic neutron scattering at low temperatures and in strong magnetic fields, Journal of Physics: Conference Series 941: (1) ((2017) ), 012082, ISBN 1742-6596, http://stacks.iop.org/1742-6596/941/i=1/a=012082. |
[20] | P. Schleger, G. Ehlers, A. Kollmar, B. Alefeld, J.F. Barthelemy, H. Casalta, B. Farago, P. Giraud, C. Hayes, C. Lartigue, F. Mezei and D. Richter, The sub-neV resolution NSE spectrometer IN15 at the Institute Laue–Langevin, Physica B: Condensed Matter 266: (1) ((1999) ), 49–55, ISBN 0921-4526, http://www.sciencedirect.com/science/article/pii/S0921452698014914. doi:10.1016/S0921-4526(98)01491-4. |
[21] | V.F. Sears, Neutron scattering lengths and cross sections, Neutron News 3: (3) ((1992) ), 26–37. doi:10.1080/10448639208218770. |
[22] | S.S. Sidhu, L. Heaton, D.D. Zauberis and F.P. Campos, Neutron diffraction study of titanium–zirconium system, Journal of Applied Physics 27: (9) ((1956) ), 1040–1042. doi:10.1063/1.1722538. |
[23] | V.A. Sidorov and R.A. Sadykov, Hydrostatic limits of fluorinert liquids used for neutron and transport studies at high pressure, Journal of Physics: Condensed Matter 17: (40) ((2005) ), 3005, ISBN 0953-8984, http://stacks.iop.org/0953-8984/17/i=40/a=002. |
[24] | Y. Uwatoko, S. Todo, K. Ueda, A. Uchida, M. Kosaka, N. Mori and T. Matsumoto, Material properties of Ni Cr Al alloy and design of a 4 GPa class non-magnetic high-pressure cell, Journal of Physics: Condensed Matter 14: (44) ((2002) ), 11291–11296. |




