Hand pose estimation based on fish skeleton CNN: application in gesture recognition
Abstract
The modern world contains a significant number of applications based on computer vision, in which human-computer interaction plays a crucial role, pose estimation of the hand is a crucial approach in the field of human-computer interaction. However, previous approaches suffer from the inability to accurately measure position in real-world scenes, difficulty in obtaining targets of different sizes, the structure of complex network, and the lack of applications. In recent years, deep learning techniques have produced state-of-the-art outcomes but there are still challenges that need to be overcome to fully exploit this technology. In this research, a fish skeleton CNN (FS-HandNet) is proposed for hand posture estimation from a monocular RGB image. To obtain hand pose information, a fish skeleton network structure is used for the first time. Particularly, bidirectional pyramid structures (BiPS) can effectively reduce the loss of feature information during downsampling and can be used to extract features from targets of different sizes. It is more effective at solving problems of different sizes. Then a distribution-aware coordinate representation is employed to adjust the position information of the hand, and finally, a convex hull algorithm and hand pose information are applied to recognize multiple gestures. Extensive studies on three publicly available hand position benchmarks demonstrate that our method performs nearly as well as the state-of-the-art in hand pose estimation. Additionally, we have implemented hand pose estimation for the application of gesture recognition.
1Introduction
As the development of computer technology has accelerated, human-computer interaction has become an increasingly important aspect of life. Particularly under the background of epidemic situation, human-computer interaction has become increasingly important. In addition to human-computer interaction (HCI), hand pose estimation and gesture recognition [1–3] have applications in virtual reality (VR) and augmented reality (AR). During gesture recognition, the finger curvature characteristic is utilized based on the keypoint coordinates obtained by hand pose estimation. It was found that hand pose estimation is not only useful in gesture recognition but plays an important part in gesture tracking [4]. The severe self-occlusion, flexible hand finger movements, appearance ambiguities, wide range of perspectives, self-similarity of fingers, and other factors make hand pose estimate a very difficult challenge even today.
In recently, the rapid development of deep learning has made the technology increasingly significant in a wide variety of fields. For example, product quality estimation [5]; battery state monitoring [6]; multi-animal pose tracking [7]; palmprint recognition [8]; pose estimation [9], etc. Among them, deep learning have been used to make significant advancements in the field of hand pose estimation. Especially, as depth sensors have been developed, from a hardware-based synchronization solution based on data gloves, hand pose estimation technology has evolved into a computer vision-based solution. Based on the type of data, hand pose estimation from a single depth image is separated from hand pose estimation from a single RGB image. The increasing number of depth image datasets has stimulated research into hand pose estimation technology [10–13]. While depth sensors have limited resolution and range, they are also affected by ambient lighting [14]. Nonetheless, they remain uncommon compared to RGB cameras. Hand pose estimation based on a single RGB image is one of the hottest topics in current research, some of the reasons it is more representative of real-life application scenarios [15–17]. In such works, research tends to focus on the estimation of hand poses based on RGB images. However, the current hand pose estimation technique has the following disadvantages:
(1) As a result of the loss of excessive feature information, obtaining targets of different sizes is more difficult.
(2) The structure of complex networks and the lack of applications.
(3) The inability to measure position accurately.
In view of these above problems, we propose a hypothesis that effective gesture feature extraction has an impact on hand pose estimation. Standard coordinate encoding plays an important role in the accuracy of keypoint location information. According to the above assumptions, a fish skeleton CNN (FS-HandNet) is proposed for hand pose estimation from a monocular RGB image. The proposed framework is composed mainly of three parts: Fish head using an efficient bidirectional pyramid structure(BiPS), which can effectively alleviate the loss of feature information downsampling and small target feature extraction; Fish body using high-resolution retention with an asymmetric convolution structure(HRACS), its ability to maintain high resolution, in addition, it is possible to improve the network’s robustness to image flipping, and it can be enhanced in its ability to extract features; Fish tail using a simple deconvolution head structure(DcHS). The network structure does not need to be complicated. To obtain hand pose information, a fish skeleton network structure is used first, then a distribution-aware coordinate representation is employed to adjust the position information of the hand, and finally, a convex hull algorithm and hand pose information are applied to recognize multiple gestures. We evaluate the performance of FS-HandNet using three publicly available hand pose benchmarks [18–20]. With experimental verification, our method has achieved the best performance. Among them, the ablation experiments demonstrate our method’s ability to extract features successfully while ensuring the accuracy of the location information of keypoints. The main contributions of this article are as follows:
• We propose a fish skeleton CNN model called FS-HandNet that is composed mainly of three parts: BiPS, HRACS, and DcHS.
• A distribution-aware coordinate representation is employed to adjust the position information of the hand.
• Using the affine transform of the image and random blocking of squares(ATaRBS) to improve the prediction performance.
• FS-HandNet is better than the other models on three popular hand pose benchmarks.
• A convex hull algorithm and hand pose information are applied to recognize multiple gestures.
2Related work
Hand pose estimation. The primary focus of skeleton-based gesture recognition is the examination of distinct patterns derived from hand joint position. Individually, skeleton data can be utilized for efficient gesture recognition. Rastgoo [21] demonstrate a complex deep learning-based pipeline architecture employing multimodal capabilities for effective automatic hand sign language recognition from RGB videos. In order to project the hand skeleton features, the model utilized a multi-view representation of the features. Jiang [22] employ a skeleton-aware multimodal SLR framework (SAM-SLR) to exploit multi-modal data. This framework incorporates RGB and depth modalities in addition to the skeleton-based methods SL-GCN and SSTCN for providing global information. And it requires no additional effort to annotate skeletons using this approach. Neverova [23] proposed a method to estimate hand poses that combine raw depth input with an intermediate representation. For reasoning about joint location, this intermediate representation provides useful topological information. Smedt [24] introduced a new skeleton-based method for 3D gesture recognition. It extracts an effective descriptor based on the hand’s geometric shape from the hand skeleton joints returned by the Intel RealSense depth camera. Using the SVM classification method for classification. Shin [25] used the mediapipe tool for estimating hand joints from RGB images. The support vector machine (SVM) and the light gradient boosting machine (GBM) were used as classifiers.
Gesture recognition using the convex hull algorithm. The convex hull for object detection is often used in the recognition of objects, gestures, and boundaries. Convex hulls and convexity defects are used to recognize the hand as an input to the system. Additionally, The functionality of the technology was verified by testing it in three scenarios involving variable lighting, background color, and indoor or outdoor conditions [26]. The convex hull and convexity defect algorithms have been successfully put into Android phones, the research shows. Ganokratanaa [27] proposed a method for recognizing gestures using contour detection, the extraction of convex hull features, and rule-based classification. As part of the lingual description, six gestures are classified based on vision-based gesture recognition. Using a segmentation algorithm that combines depth and color information, it is first necessary to segment the gesture region. Afterward, the eigenvectors are extracted by using the circularity of the static potential profile, the convex hull points, the convex defect points, and the 7Hu-moment features. Finally, static gestures can be recognized using SVMs [28]. The HSV color space skin color segmentation algorithm is used to segment the skin color region, while the gesture region is segmented based on its geometric features. After the fingertips are detected using the convex hull algorithm, the number of fingertips, inter-finger angle features, and contour aspect ratio features are combined to build a decision tree for classifying the 12 different gestures [29].
Video image processing was implemented with a multi-modal and multi-processing process [21, 22]. Hand pose estimation is implemented using the mediapipe tool [25]. Depth-based gesture image processing is implemented [22–24]. [24, 25, 28] implements image classification with SVM. [26, 28] used convexity defects and convexity hulls to extract features, while [26] implemented a variety of scenarios, and [28] segmented data before feature extraction. [27, 29] only implements the recognition of specific gestures. In our algorithm, gesture keypoints are obtained by applying a fish skeleton network structure and using distribution-aware coordinates to improve keypoint location accuracy. We also implement multiple gesture recognition using convex hulls and hand pose information.
3Method
3.1Overview
To estimate the 2D locations of K = 21 keypoints of the hand from a single RGB image. A fish skeleton CNN(FS-HandNet) for hand pose estimation is proposed. The 2D pixel coordinate of the k-th keypoint in image I is used to estimate the 2D hand pose. The order of these keypoints is defined as follows [18]. The k-th keypoint is described using a heatmap. According to [30], regressing a heatmap is more advantageous than regressing pixel coordinates.
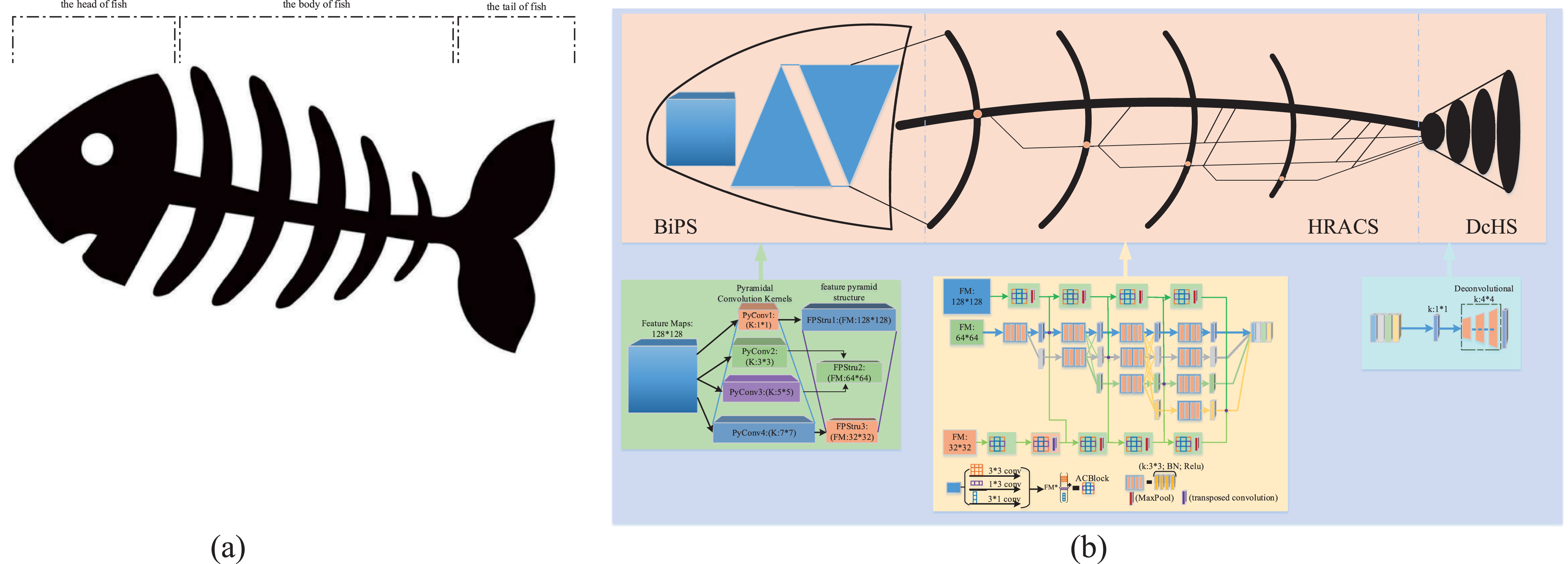
The fish skeleton structure can be divided into three parts: The head of fish; the body of fish; the tail of fish. Figure 1a depicts the overall architecture as a diagram. We will introduce these parts in Section 3.2.
Fig. 1
Overview of the proposed a fish skeleton CNN for hand pose estimation. (a) The fish skeleton structure: The head of fish; the body of fish; the tail of fish. (b) A detailed view of FS-HandNet. The three colored boxes represent BiPS, HRACS, and DcHS, respectively.
3.2Fish skeleton CNN for hand pose estimation
The fish skeleton CNN(FS-HandNet) for hand pose estimation is composed of three parts: Fish head using an efficient bidirectional pyramid structure(BiPS); Fish body using high-resolution retention with an asymmetric convolution structure(HRACS); Fish tail using a simple deconvolution head structure(DcHS). Also, the three parts can work together to achieve global optimization and improve the accuracy of estimating the position of a 2D hand. As shown in Fig. 1b, the above series of operations define the FS-HandNet.
3.2.1Fish head using an efficient bidirectional pyramid structure
In the fish head using an efficient bidirectional pyramid structure(BiPS), there are two pyramidal structures. Pyramidal convolution(PyConv) and feature pyramid structure(FPStru), which can effectively alleviate the loss of feature information downsampling, and small target feature extraction [31].
The PyConv model utilizes convolution operations of 1 × 1, 3 × 3, 5 × 5, and 7 × 7, respectively. It contains a pyramid with n levels of different types of kernels. The perceptual fields of different convolution kernels enable them to extract feature information with different sizes effectively. It seeks to process input at various kernel scales while minimizing computational cost [31]. The convolution blocks of 1 × 1 are used to obtain 128 × 128 feature maps, which maintain the input feature size and effectively mitigate the loss of image information. Convolution blocks of 3 × 3 and 5 × 5 are used to extract 64 × 64 feature maps, improving feature extraction. The convolution blocks of 7 × 7 are utilized to obtain 32 × 32 feature maps. The obtained feature maps of varying sizes are fed into the HRACS’s three-way network structure. In Fig. 1b, the BiPS section illustrates the network structure. The BiPS can be formulated as:
(1)
(2)
(3)
3.2.2Fish body using high-resolution retention with an asymmetric convolution structure
An asymmetric convolution method and high-resolution retention technique are used in this fish body. Due to its ability to maintain high resolution, the predicted heatmap is more accurate spatially than one that recovers resolution by moving from low to high. In addition, it is possible to improve the network’s robustness to image flipping, and it can be enhanced in its ability to extract features [33, 34].
The HRACS is divided into three main branches: Its main stem branches use a structure similar to that of a fish’s spine, which is maintained from head to tail by fusing tiny spines. The principal stem branches consist of a number of elements: Parallel repeated multi-resolution fusions in conjunction with multi-resolution convolutions. The multi-resolution convolution process consists of parallel streams with high-to-low resolution. The multi-resolution convolution consists of four stages with parallel convolution streams. The resolutions are 1/4, 1/8, 1/16, and 1/32, while the channel counts are C, 2C, 4C, and 8C, respectively. Four residual units, each with 3 × 3 convolutions, make up these stages. After each convolution comes batch normalization and nonlinear activation ReLU. As a result, the resolutions for a later stage consist of the previous stage’s resolutions and an extra lower resolution. The repeated multi-resolution fusions are mainly an alignment and feature fusion operation for parallel resolution. Specifically, upsampling and downsampling are used for alignment, while 1 × 1 convolution is used for channel consistency.
Two other branches use asymmetric convolution structures, and their input feature maps correspond to the bottom and top of the feature pyramid, respectively. In the top branch, four asymmetric convolution blocks (ACBlock) are utilized, each consisting of three parallel layers with kernel sizes of 3 × 3, 1 × 3, and 3 × 1, respectively. In standard CNN, each layer is followed by batch normalization, also known as a branch, and the outputs of three branches are added together to produce the output of ACBlock. Following the ACBlock, maximum pooling operations are connected to ensure subsequent alignment of feature sizes [34]. To implement the feature size alignment operation, a deconvolution algorithm is connected after the second ACBlock similarly to the top branch. The top and bottom branches can be formulated as:
(4)
(5)
(6)
Where fa ×b,j/k(·) denotes a mapping function learned by a × b asymmetric convolutional, j/k denotes the corresponding j or k layer, Fn/m indicates the size of the input feature map is n × n/m × m. MaxPj/k(·) denotes the maximum pooling corresponding to each layer, TraC(·) is a deconvolution function. Ftop (j) /Fdown (k) denote the intermediate features resulted from the top and bottom branches.
The main stem branches are fused with the top and bottom branches to obtain more information about the characteristics. Four parallel branches of the main stem branches have resolutions of 64 × 64, 32 × 32, 16 × 16, and 8 × 8. The branches with different resolutions fuse the top and bottom branches corresponding to the irregular convolution respectively. To achieve this, each main stem branch’s resolution is matched by up-sampling or down-sampling operations after the top and bottom branch ACBlocks. Finally, each resolution of the main stem branch is fused. The HRACS is shown in Fig. 2. This HRACS can be formulated as:
Fig. 2
Gesture recognize using the convex hull algorithm and hand pose information.
(7)
(8)
Where Ftop (i), Fdown (i +1) and Fhr (i,1) is the intermediate features resulted from three main branches, i denotes the corresponding layer. Fn,hr (a,b) indicates the size of the main stem branches is n × n, hr(a,b) denotes the bth module of the ath branch of the four parallel branches of the main stem branches. TraCn(·) is a deconvolution function, and n denotes the resolutions of n × n. ⊕ refers to the concatenation of feature maps. where Ffuse (i,1) denotes the intermediate features resulting from the fusion of three main branches.
3.2.3Fish tail using a simple deconvolution head structure
The tail of fish uses a deconvolution head structure as the upsampling method and does not use a skip connection. The tail of fish is based on literature [35], it proposes that the network structure does not need to be complicated, and it is straightforward to get better results capturing the main points, outputting a larger heatmap.
First, On perform feature fusion using 1 × 1 convolution and then input into the deconvolution head structure that defaults to the following: Utilization of deconvolutional layers with batch normalization and ReLU activation. Each layer contains 256 filters, each with a 4 × 4 kernel. Finally, for all k keypoints, a 1 x 1 convolutional layer is added to generate predicted heatmaps [H1...Hk]. Using Mean Squared Error(MSE), the average loss of posture estimation is computed by comparing the predicted and targeted heatmaps (MSE). To generate a targeted heatmap for joint k, a 2D Gaussian centered on the kth joint’s ground truth location is applied. The loss function for hand posture estimation can be obtained as:
(9)
3.3Distribution-aware coordinate representation for hand pose estimation
Based on the performance of the model, the standard coordinate decoding method is designed empirically [36]. The highest activation in the projected heatmap does not match the precise location of the joint in the original coordinate space, but rather to its approximate location. Using the Distribution-Aware Coordinate Representation of Keypoint (DARK) approach [37], we offer a principled method for shifting estimations and then evaluate more precise hand position estimations. The method investigates the distribution structure of the anticipated heatmap to deduce the highest activation underlying the heatmap. There are a total of three steps in a sequence:
Heatmap distribution modulation- Due to the assumption of Gaussian distribution in the coordinate decoding method. When compared to the training heatmap data, the predictive heatmaps do not have an ideal Gaussian structure, presenting multiple peaks phenomena near the maximum activation [37]. It could hinder the performance of the decoding process. It tackles this problem by changing the distribution of heat maps beforehand.
For smoothing out the effects of multiple peaks in the heatmap H, we utilize a Gaussian kernel K with the same variance as the training data, formally as:
(10)
(11)
Distribution-aware joint localisation by taylor expansion at sub-pixel accuracy- Obtaining accurate location information at the subpixel level, we assume that the predicted heatmap follows the same 2D Gaussian distribution as the real heatmap [37]. It represents the predicted heatmap as:
(12)
(13)
To simplify inference, we logarithmize h while preserving the original site of greatest activation:
(14)
(15)
(16)
(17)
Combining Equations (15) (16), and (17), ,we ultimately obtain:
(18)
Recovery of the coordinate system’s original resolution- Using Eq. (19), when we get y, we can guess the coordinate in the original image space.
(19)
3.4Gesture recognition using the convex hull algorithm and hand pose information
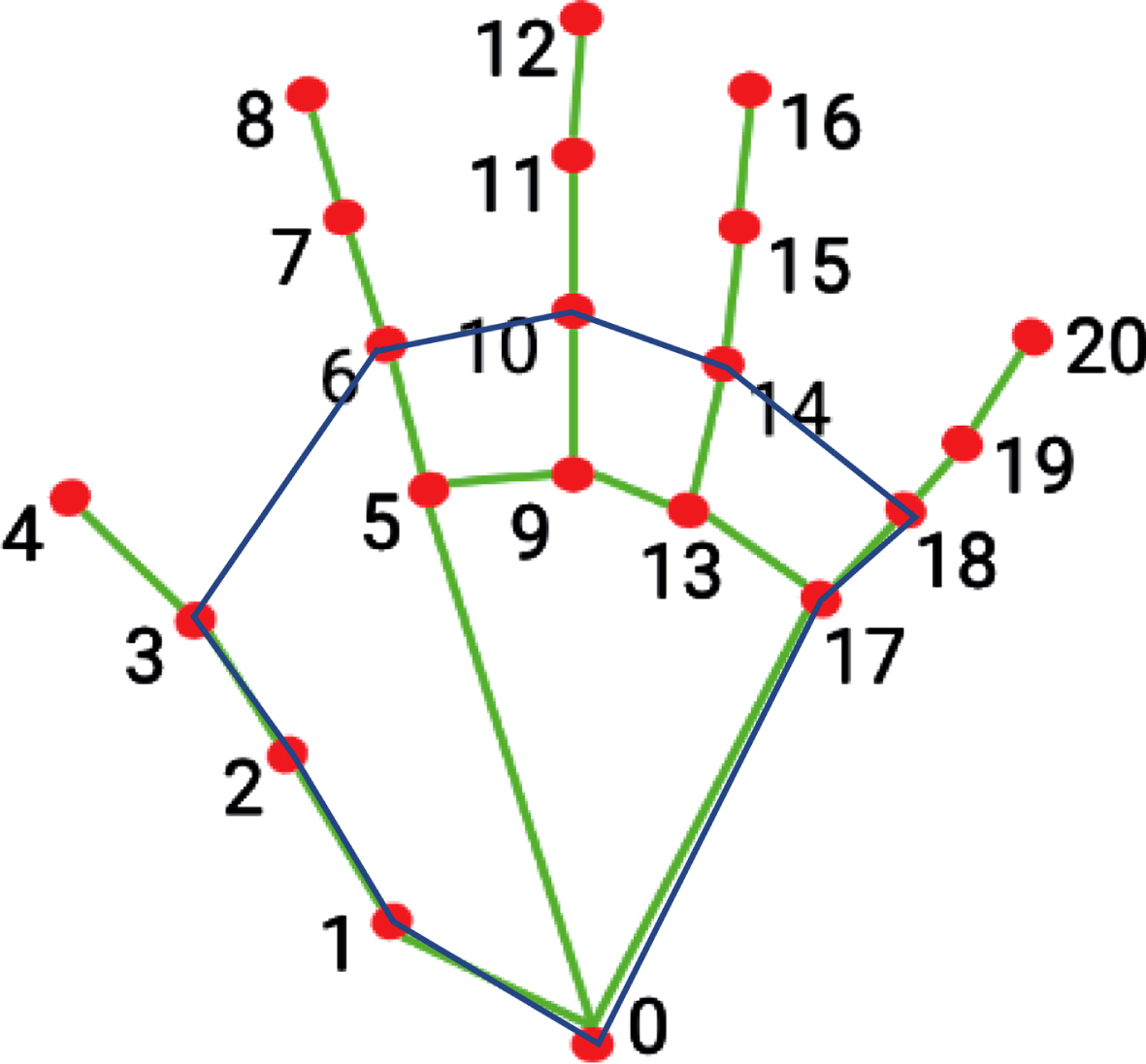
As a gesture, the fingertips of different fingers have a particular distance from the palm, and the gesture can be determined by analyzing this relationship. The situation is analyzed using mathematical models of the convex hull. To form a convex polygon, the gesture keypoints (0,1,2,3,6,10,14,19,18,17) are connected by the convex hull algorithm. The convex hull of the detected hand is depicted by the blue line in Fig. 2. The fingertips correspond to the keypoints (4,8,12,16,20). It is possible to recognize gestures by determining that the fingertip is within the convex hull.
Whether the vertical coordinate Ty of the point under test is within the range of the vertical coordinates of the two adjacent points tested in this loop.
(20)
(21)
If both of these conditions are satisfied simultaneously, we determine that the fingertips are inside a convex hull.
4Experiments
4.1Dataset and evaluation metrics
In this research, we assess our method using three publically accessible datasets: The OneHand 10k dataset [18] (OneHand 10k), the CMU Panoptic Hand dataset [19] (Panoptic), and the Rendered Hand Pose Dataset [20] (RHD). OneHand 10k online collection has issues relating to occlusion, light variation, and shadowed backgrounds. OneHand 10k is a real-world dataset comprised of 11703 images containing the ground truth coordinates of 21 hand joint sites. The dataset is divided into 10,000 training samples and 1,703 testing samples. With 480 VGA cameras, 30+ HD cameras, and 10 Kinnect sensors, CMU’s Panoptic collected the dataset. The Panoptic dataset is made up of 14,817 pictures of people. These pictures have been randomly split into two groups: training (80%), and testing (20%). There are 21 key points annotated with 2D labels for each image. RHD is a synthetic dataset including 41258 images for training and 2728 for testing. This dataset is difficult to examine due to the numerous viewpoint alterations and low image quality.
Four common metrics are used to evaluate the performance of 2D hand position estimation: (i) AUC: AUC provides a measure of a learner’s strengths and weaknesses, indicating the likelihood that the positive predicted case will rank ahead of the negative predicted case. The area under the PCK curve for various error thresholds [39]. (ii) EPE: The overall pixel-average error rate is obtained by using endpoint error (EPE), which is the average of the Euclidean distance between predicted and true values [20]. (iii-iv) GFLOPs and #Params: GFLOPs and #Params indicate the complexity of the network, according to its design and the GPU and CPU that are being utilized. In computing, GFLOPs refer to the number of floating-point operations, which can be thought of as the amount of computation. #Params measure the number of parameters in the model. They are used to determine the complexity of an algorithm or model. Evaluation metrics mainly include AUC, EPE, GFLOPs, and #Params. Our goal is to improve AUC by increasing them and to decrease EPE, GFLOPs, and #Params by decreasing them.
4.2Implementation details
Our method is implemented in Pytorch framework. The networks are trained with 32-element mini-batches and a 5 × 10-4 learning rate using the Adam optimizer [40]. In this paper, We set the epoch as 200. The OneHand10K, Panoptic, and RHD datasets are used to train the FS-HandNet, which is trained end-to-end. The image is scaled to 256 × 256 pixels. For training and testing, all experiments are conducted on a single server with GPU.
4.3Data augmentation
To enhance the robustness of the algorithms, data enhancement strategies are implemented. We used strategies of data enhancement mainly include: Random shift of the box center, random image flip, random scaling & rotating [41], affine transform of the image [42], random blocking of squares, and Normalize.
To ensure rotational invariance, the collected dataset is transformed using affine transformations. According to geometry, an affine transformation is a linear transformation and a translation that converts one vector space to another. Due to the partial occlusion of the gesture, we propose the random blocking of squares to effectively alleviate the existing deficiencies. A gesture detection box with labels is used as a filled area for random squares, and a fixed size square is continuously filled into the area so that the gesture area can be simulated for masking operations. It makes the model more robust in this way.
4.4Performance comparison
4.4.1Experiment results
We analyze our proposed FS-HandNet using three publicly available datasets: OneHand 10k, Panoptic, and RHD. Our proposed FS-HandNet is compared to DeepPose, the CPM baseline, Mobilev2, and the MSPN. It is common to use these methods for pose estimation. Quantitative and qualitative comparisons were the primary focus of the experiments.
1) Comparison of OneHand10K: The purpose of our comparison of OneHand10K is to demonstrate that the proposed method behaves better than the four types of pose estimation methods. We use the commonly used evaluation metrics the area under the curve(AUC) [39], the endpoint error(EPE) [20], GFLOPs, and #Params to evaluate our method. Table 1 summarizes the detailed numerical results. Our model behaves better than four types of pose estimation methods, this is especially evident in the AUC and EPE indicators. In terms of #Params metrics, our method is second only to the Mobilev2 methods in terms of performance, and comprehensive analysis will reveal that we achieve better results with our approach. Figure 3 illustrates the contrast of performance.
Table 1
Detailed numerical evaluations of AUC, EPE, GFLOPs, and #Params using the OneHand 10k test data
| Method | AUC↑ | EPE↓ | GFLOPs↓ | #Params(M)↓ |
| DeepPose [43] | 0.483 | 34.48 | 5.38 | 23.59 |
| CPM [44] | 0.525 | 29.56 | 85.4 | 31.62 |
| Mobilev2 [45] | 0.530 | 30.34 | 2.12 | 9.57 |
| MSPN [46] | 0.546 | 27.28 | 21.72 | 83.4 |
| Ours | 0.572 | 23.87 | 23.39 | 16.95 |
Fig. 3
Comparison results on OneHand 10k dataset. (a) DeepPose [43], (b) CPM [44], (c) Mobilev2 [45], (d) MSPN [46], (e) Our method.
![Comparison results on OneHand 10k dataset. (a) DeepPose [43], (b) CPM [44], (c) Mobilev2 [45], (d) MSPN [46], (e) Our method.](https://content.iospress.com:443/media/ifs/2023/44-5/ifs-44-5-ifs224271/ifs-44-ifs224271-g003.jpg)
2) Comparison of Panoptic: The Panoptic is used to test our method. It has 11853 training images and 2964 testing images. The input image is resized to 256 × 256 on the Panoptic [47]. We evaluate our method using the area under the curve(AUC) [39], the endpoint error(EPE) [20], GFLOPs, and #Params metric. Table 2 provides a summary of the numerical results. On the Panoptic dataset, our model exhibits a substantial improvement in AUC and EPE over the CPM baseline. As a combined analysis of GFLOPs and #Params metrics display results, our approach is second only to the Mobilev2 methods. Figure 4 demonstrates the performance of FS-HandNet, DeepPose, the CPM baseline, Mobilev2, and MSPN.
Table 2
Detailed numerical evaluations of AUC, EPE, GFLOPs, and #Params based on Panoptic testing data
| Method | AUC↑ | EPE↓ | GFLOPs↓ | #Params(M)↓ |
| DeepPose [43] | 0.686 | 9.35 | 5.38 | 23.59 |
| CPM [44] | 0.699 | 9.60 | 85.4 | 31.62 |
| Mobilev2 [45] | 0.698 | 9.55 | 2.12 | 9.57 |
| MSPN [46] | 0.685 | 10.16 | 21.72 | 83.4 |
| Ours | 0.747 | 7.56 | 23.39 | 16.95 |
Fig. 4
Comparison results on Panoptic dataset. (a) DeepPose [43], (b) CPM [44], (c) Mobilev2 [45], (d) MSPN [46], (e) Our method.
![Comparison results on Panoptic dataset. (a) DeepPose [43], (b) CPM [44], (c) Mobilev2 [45], (d) MSPN [46], (e) Our method.](https://content.iospress.com:443/media/ifs/2023/44-5/ifs-44-5-ifs224271/ifs-44-ifs224271-g004.jpg)
Figure 4 visualizes the predictive results of FS-HandNet, the DeepPose, the baseline of CPM, the Mobilev2, and the MSPN on the Panoptic test data. An analysis of the left and right hand pose estimation problem for the same image that illustrates the effectiveness of our method from another perspective. Our model significantly reduces ambiguity in inferences and reinforces structure consistency.
3) Comparison of RHD: We have implemented our method on the RHD which is a synthetic dataset containing 41258 training images and 2728 testing images. Considering the RHD dataset is larger than both OneHand10K and Panoptic, we achieve better results when estimating hand gestures from the RHD dataset. Table 3 analyzes the RHD dataset performance of several network designs, Our method behaves better than four types of pose estimation methods, this is especially evident in the AUC and EPE indicators. Our method is second only to the Mobilev2 in terms of #Params metrics, and an in-depth analysis of our performance will reveal that our approach achieves better results. As shown in Fig. 5, there is a comparison of performance.
4.4.2Ablation study
In this section, we conducted an ablation research on the OneHand 10k dataset to examine the following three aspects: 1) the influence of the bidirectional pyramid structure (BiPS); 2) the influence of the Distribution-Aware coordinate Representation of Keypoints (DARK) [37] to hand pose estimation. 3) The impact of the affine transform of the image and random blocking of squares(ATaRBS) to enhance the robustness of the algorithms. To do this, we did the ablation study by comparing the following FSNet variations.
FSNet Baseline: In this experiment, we only retain the basic structural model. removing the BiPS, DARK, and ATaRBS from FS-HandNet.
FSNet+BiPS: We only keep the FSNet baseline and BiPS from the FS-HandNet. removing the DARK and ATaRBS from FS-HandNet.
FSNet+BiPS+ATaRBS: Only keep the FSNet baseline and BiPS, jointly the affine transform of the image and random blocking of squares(ATaRBS) to enhance the robustness of the algorithms. the DARK is removed.
Table 4 displays the quantitative comparison findings of various versions on the OneHand 10k test set. It can be observed that the FSNet + BiPS outperforms the FSNet Baseline, which means that joint the Bidirectional Pyramid Structure(BiPS) can effectively improve the performance. Using the affine transform of the image and random blocking of squares (ATaRBS) gets even better results, so the best performance is achieved by our suggested method.
Table 4
The hand pose estimation ablation study’s numbers showed how the different types of ablation worked on the OneHand 10k testing data
| Method | AUC↑ | EPE↓ | GFLOPs↓ | #Params(M)↓ |
| FSNet Baseline | 0.552 | 26.91 | 22.75 | 16.49 |
| FSNet+BiPS | 0.561 | 25.73 | 23.39 | 16.95 |
| FSNet+BiPS+ATaRBS | 0.565 | 25.05 | 23.39 | 16.95 |
| Ours | 0.572 | 23.87 | 23.39 | 16.95 |
4.5Applying hand pose estimation for gesture recognition
Hand pose estimate can be used in the gesture recognition process, and the gesture recognition results can be obtained by analyzing the coordinates of each keypoint, which can be obtained by using the hand pose estimation algorithm. Figure 6 depicts the application of hand pose estimation to gesture recognition.
Fig. 6
Hand pose estimation is applied to gesture recognition.

The gesture recognition task is usually performed using image classification methods, which require only a few samples to achieve satisfactory results. However, adding new gestures later requires recollecting and retraining samples according to current common methods. Hand pose estimation algorithms can address the shortcomings of classification algorithms for gesture recognition. However, hand pose estimation algorithms also have weak performance in gesture recognition tasks, due to its low recognition accuracy and complicated modeling.
5Conclusion and future work
In conclusion, this article developed a fish skeleton CNN for hand pose estimation from single color images, referred to as “FS-HandNet”. To obtain hand pose information, the FS-HandNet is used for the first time, then a distribution-aware coordinate representation is employed to adjust the position information of the hand, and finally, a convex hull algorithm and hand pose information are applied to recognize multiple gestures. In addition, to improve the resilience of the algorithms, we applied an efficient data augmentation method. We analyze the performance of FS-HandNet using three publicly available hand posture benchmarks. The experimental results demonstrate that our proposed strategy is superior and progressive. Future work includes improving the hand position information for gesture recognition and designing a lightweight model for hand pose estimation.
Acknowledgements
National Key Research and Development Program of China (No. 2022YFF0607000); National Natural Science Foundation of China (61871188); Guangdong Provincial Key Laboratory of Human Digital Twin (2022B1212010004); Guangzhou city science and technology research projects (201902020008).
Conflict of interest
The authors declare that they have no conflict of interest.
References
[1] | Ren G. and Li W. , Towards the design of effective freehand gesturalinteraction for interactive tv, Journal of Intelligent & Fuzzy Systems 31: ((2016) ), 2659–2674. |
[2] | Wan J. , Gesture recognition and information recommendation based onmachine learning and virtual reality in distance educatio, Journal of Intelligent & Fuzzy Systems 40: ((2021) ), 7509–7519. |
[3] | Huang X. , Tsai M. 3d virtual-reality interaction system, in: 2019 IEEE International Conference on Consumer Electronics –Taiwan (ICCE-TW) (2019), 1–2. |
[4] | Zhou Y. , Jiang G. and Lin Y. , A novel finger and hand poseestimation technique for real-time hand gesture recognition, Pattern Recognition 49: ((2016) ), 102–114. |
[5] | Wu H. , Lei R. and Peng Y. , Pcbnet: A lightweight convolutional neuralnetwork for defect inspection in surface mount technology, IEEE Transactions on Instrumentation and Measurement 71: ((2022) ), 1–14. |
[6] | Su S. , Li W. , Mou J. , Garg A. , Gao L. and Liu J. , A hybrid battery equivalent circuit model, deep learning, and transfer learning for battery state monitoring, IEEE Transactions on Transportation Electrification ((2022) ), 1–16. |
[7] | Pereira T. , Tabris N. and Matsliah A. , Sleap: A deep learning systemfor multi-animal pose tracking, Nature Methods 19: ((2022) ), 486–495. |
[8] | Jia W. , Ren Q. , Zhao Y. , Li S. , Min H. and Chen Y. , Eepnet: An efficient and effective convolutional neural network for palmprint recognition, Pattern Recognition Letters 159: ((2022) ), 140–149. |
[9] | Liu T. , Sun J. and Zhao L. , View-invariant, occlusion-robust probabilistic embedding for human pose, International Journalof Computer Vision 130: ((2022) ), 111–135. |
[10] | Yuan S. , Ye Q. , Stenger B. , Jain S. , Kim T. Bighand2.2m benchmark: Hand pose dataset and state of the art analysis, in: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017), 2605–2613. |
[11] | Tompson J. , Stein M. , Lecun Y. and Perlin K. , Real-time continuouspose recovery of human hands using convolutional networks, ACM Transactions on Graphics (ToG) 33: ((2014) ), 1–10. |
[12] | Sun X. Wei, Y. Liang S. Tang X Sun J. Cascaded hand pose regression, in: Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR) (2015), 824–832. |
[13] | Wan C. , Yao A. , Van Gool L. Hand pose estimation from local surface normals, in: European conference on computer vision (ECCV) (2016), 554–569. |
[14] | Mehta D. , Sridhar S. and Sotnychenko O. , Vnect: Real-time 3d humanpose estimation with a single rgb camera, ACM Transactions on Graphics (TOG) 36: ((2017) ), 1–14. |
[15] | Cai Y. , Ge L. , Cai J. , Yuan J. Weakly-supervised 3d hand pose estimation from monocular rgb images, in: Proceedings of the European Conference on Computer Vision (ECCV) (2018), 678–694. |
[16] | Panteleris P. , Oikonomidis I. , Argyros A. Using a single rgb frame for real time 3d hand pose estimation in the wild, in: IEEE Winter Conference on Applications of Computer Vision (WACV) (2018), 436–445. |
[17] | Simon T. , Joo H. , Matthews I. , Sheikh Y. Hand keypoint detection in single images using multiview bootstrapping, in: Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (CVPR) (2017), 4645–4653. |
[18] | Wang Y. , Peng C. and Liu Y. , Mask-pose cascaded cnn for 2d hand poseestimation from single color image, IEEE Transactions on Circuits and Systems for Video Technology 29: ((2018) ), 3258–3268. |
[19] | Joo H. , Simon T. and Li X. , Panoptic studio: A massively multiview system for social interaction capture, IEEE Transactions on Pattern Analysis and Machine Intelligence 41: ((2019) ), 190–204. |
[20] | Zimmermann C. , Brox T. Learning to estimate 3d hand pose from single rgb images, in: IEEE International Conference on Computer Vision (ICCV) (2017), 4913–4921. |
[21] | Rastgoo R. , Kiani K. and Escalera S. , Hand sign language recognition using multi-view hand skeleton, Expert Systems with Applications 150: ((2020) ), 113336–113348. |
[22] | Jiang S. , Sun B. Skeleton aware multi-modal sign language recognition, in: Proceedings of the IEEE/CV Conference on Computer Vision and Pattern Recognition (CVPR) (2021), 3413–3423. |
[23] | Neverova C. and Wolf N. , Hand pose estimation through semisupervised and weakly-supervised learning, Computer Vision and Image Understanding 164: ((2017) ), 56–67. |
[24] | De Smedt Q. Wannous H. Vandeborre J. Skeleton based dynamic hand gesture recognition, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2016), 1–9. |
[25] | Shin J. and Matsuoka A. , American sign language alphabet recognition by extracting feature from hand pose estimation, Sensors 21: ((2021) ), 5856–5875. |
[26] | Anshary M. , Hidayat E. and Amalia T. , Prototype program hand gesture recognize using the convex hull method and convexity defect on android, Journal Online Informatika 5: ((2020) ), 205–211. |
[27] | Ganokratanaa T. , Pumrin S. The algorithm of static hand gesture recognition using rule-based classification, in: International Symposium on Natural Language Processing (2016), 173–184. |
[28] | Wen F. , Kang C. Static hand gesture recognition based on rgbd data, Computer and Modernization (2018), 74–77. |
[29] | Sun H. and Liao L. , Real-time gesture recognition with multiple cues based on opencv, Electronic Science and Technology 28: ((2015) ), 145–148. |
[30] | Pfister T. , Charles J. , Zisserman A. Flowing convnets for human pose estimation in videos, in: IEEE International Conference on ComputerVision (ICCV) (2015), 1913–1921. |
[31] | Duta I. , Liu L. , Zhu F. , Shao L. Pyramidal convolution: rethinking convolutional neural networks for visual recognition, in: arXiv preprint arXiv:2006.11538, 2020. |
[32] | Loffe C. , Szegedy S. Batch normalization: Accelerating deep network training by reducing internal covariate shift, in: International Conference on Machine Learning (2015), 448–456. |
[33] | Wang J. , Sun K. and Cheng T. , Deep high-resolution representation learning for visual recognition, IEEE Transactions on PatternAnalysis and Machine Intelligence (TPAMI) 43: ((2020) ), 3349–3364. |
[34] | Ding X. , Guo Y. , Ding G. Acnet: Strengthening the kernel skeletons for powerful cnn via asymmetric convolution blocks, in: IEEE/CVF International Conference on Computer Vision (ICCV) (2019), 1911–1920. |
[35] | Xiao B. , Wu H. , Wei Y. Simple baselines for human pose estimation and tracking, in: Proceedings of the European conference on computer vision (ECCV) (2018), 466–481. |
[36] | Newell A. , Yang K. , Deng J. Stacked hourglass networks for human pose estimation, in: European conference on computer vision (ECCV) (2016), 483–499. |
[37] | Zhang F. , Zhu X. , Dai H. Distribution-aware coordinate representation for human pose estimation, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020), 7093–7102. |
[38] | Franklin W.R. ,https://www.ecse.rpi.edu/homepages/wrf/research/shortnotes/pnpoly.html ((2006) ). |
[39] | Ge L. , Ren Z. , Li Y. 3d hand shape and pose estimation from a single rgb image, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019), 10833–10842. |
[40] | Yi J. and Ji S. , An effective optimization method for machine learning based on adam, Applied Sciences 10: ((2020) ), 1073–1093. |
[41] | Sun K. , Xiao B. , Liu D. Deep high-resolution representation learning for human pose estimation, in: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019), 5693–5703. |
[42] | Liu L. , Jiang X. , Saerbeck M. , Dauwels J. Ead-gan: A generative adversarial network for disentangling affine transforms in images, IEEE Transaction on Neural Networks and Learning Systems (2022), 1–11. |
[43] | Toshev A. , Szegedy C. Deeppose: Human pose estimation via deep neural networks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2014), 1653–1660. |
[44] | Wei S. , Ramakrishna V. , Kanade T. , Sheikh Y. Convolutional pose machines, in: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2016), 4724–4732. |
[45] | Sandler M. , Howard A. , Zhu M. , Zhmoginov A. , Chen L. Mobilenetv2: Inverted residuals and linear bottlenecks, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2018), 4510–4520. |
[46] | Li W. , Wang Z. , Yin B. Rethinking on multi-stage networks for human pose estimation, in: arXiv preprint arXiv:1901.00148, 2019. |
[47] | Chen Y. , Ma H. , Kong D. Nonparametric structure reg-ularization machine for 2d hand pose estimation, in: IEEE Winter Conference on Applications of Computer Vision (WACV) (2020), 370–379. |

![Comparison results on RHD dataset. (a) DeepPose [43], (b) CPM [44], (c) Mobilev2 [45], (d) MSPN [46], (e) Our method.](https://content.iospress.com:443/media/ifs/2023/44-5/ifs-44-5-ifs224271/ifs-44-ifs224271-g005.jpg)



