Fuzzy logic-based multi-factor aided multiple-model filter for general aviation target tracking

Wang, Quanhui; Huang, Jianjun; Huang, Jingxiong

doi:10.3233/IFS-151963

Fuzzy logic-based multi-factor aided multiple-model filter for general aviation target tracking

Issue title: The fuzzy system and its application in East Asia

Guest editors: Ildar Batyrshin, Dragan S. Pamučar, Paolo Crippa and Feng Liu

Article type: Research Article

Authors: Wang, Quanhui^a | Huang, Jianjun^{a; *} | Huang, Jingxiong^b

Affiliations: [a] College of Information Engineering, Shenzhen University, Shenzhen, China | [b] Air Defense Forces Command Academy, Zhengzhou, China

Correspondence: [*] Corresponding author. Jianjun Huang, College of Information Engineering, Shenzhen University, Nanshan district, Shenzhen 518060, China. Tel.: +8613600447234; Fax: +86075526732049; E-mail: [email protected]

Keywords: General aviation target tracking, multi-factor Aided, IMM algorithm, model transition probability matrix, fuzzy inference

DOI: 10.3233/IFS-151963

Journal: Journal of Intelligent & Fuzzy Systems, vol. 29, no. 6, pp. 2603-2609, 2015

Published: 2015

Get PDF

Abstract

A fuzzy logic-based multi-factor aided multiple-model filter (FLMAMMF) for General aviation (GA) maneuvering target tracking (MTT) is presented. The target category and meteorological information are introduced into the interacting multiple model (IMM) filter to perform GA target tracking. Fuzzy logic inference is employed in the proposed algorithm to reflect the complicated relationship between these two factors and the transition probability matrix (TPM). Both the number of models in model set and the transition probabilities between models are adjusted through fuzzy inference. Simulation results show that the proposed method is efficient and effective.

1Introduction

For flight safety, an uninterrupted, reliable, accurate and effective monitoring of air traffic is crucial, especially for GA flights. Target tracking technology is the key to the GA aircraft monitoring system [12]. Over the years, many tracking methods have been developed, such as the differential polynomials, CV (constant velocity) and CA (constant acceleration) models, semi-Markov tracking filters, the “current” statistic models [9, 10]. These methods meet the tracking need of transport aviation ATC system but not that of GA, since there are a wide variety of GA aircrafts. GA aircrafts vary from ultra-light aircraft to small aircraft, powered to un-powered, manned to unmanned, etc. These wide variety of aircrafts have great difference in performance and flight mode. Furthermore, they flight at low altitude and are more influenced by meteorological environment. As a result, their flight trajectories show a strong maneuvering.

For maneuvering target tracking, Bar-Shalom and Blom proposed an algorithm called interactive multiple model (IMM) method, which is based on Generalized Pseudo-Bayesian algorithm (GPB) [3, 4]. The IMM uses a set of models to reflect different modes of maneuvering target and combines the output of multiple parallel filters (each with a different model) to get the global estimate. This filter has been successfully used in an ATC system [12]. However, flight model design is vital to the IMM algorithm and has a direct influence on the tracking result [1, 11]. This design should answer two basic questions: a) how many models are adequate to reflect such wide variety of GA targets, and b) how often does a flight change from one model to another.

The first question can be easily solved when the type of GA aircraft is known. For example, an aircraft with ADS-B equipment can broadcasting its type along with its position to ATC system. The model set for each type can be predefined. When the aircraft type is known, the corresponding model set can be employed by the IMM. When the type is unknown, one can identify the type by some target recognition methods or he has to use an over-fitted model set that will result in a bad global estimation.

The second one is the problem of how to setting transition probability matrix (TPM), which is obviously depend on the model set, i.e. the result of the first question. IMM algorithm commonly uses two methods to set the TPM when model set is determined, the off-line and the online methods. The off-line design method sets the TPM a priori as a design parameter. In the online method, the TPM is adaptable and is set by the process of quasi Bayesian estimator while filtering for tracking [6]. The existing TPM setting methods perform well when the affect of meteorological environment can be neglect, which is not the case in GA target tracking.

For better tracking of GA targets, the identified target type and the meteorological environment should be introduced into IMM. Since target recognition usually outputs the possibility of target types, the output is fuzzy in nature. Furthermore, meteorology (such as airflow) influence the flight in a complicated way, which can be modeled by fuzzy relations [2, 5, 7]. Considering of the above situations, a novel fuzzy logic-based multi-factor aided multiple-model filter (FLMAMMF) is proposed which employs the above influencing factors to adjust TPM. A set of fuzzy rules is designed according to the relationship of TPM with target category and meteorological environment. It gives a beneficial attempt to acquire better GA target tracking performance.

2Problem formulation

In the IMM algorithm, the system of state equation and observation equation are given by

(1)

xk=Fk(mk,xk-1)+wk(mk)

(2)

zk=Hk(mk,xk)+vk

where k is the time index, x _k and z _k represent the state and measurement vectors, respectively. F _k and H _k are the transition matrix and the observation matrix, respectively. The Gaussian white noise w _k and v _k are independent and their covariance are Q _k and R _k, respectively. The parallel filtering system preset r models work and mk is the model at time k.

IMM algorithm assumes the transition of the flight mode has homogeneous Markovian property. The probability of model i at time k transition to model j at time k + 1 is given by

(3)

pij=p(mk+1j|mki)=[p11⋯p1j⋯p1r⋮⋱⋮⋯⋮pi1⋯pii⋯pir⋮⋯⋮⋱⋮pr1⋯prj⋯prr]

where mki is the filter model using at k time, mk+1j is that at time k + 1.

The diagonal elements of the TPM between the model depend on the sojourn time in each motion model. The transition probability p _ii depends on the expected sojourn time τ _i is given by

(4)

τi=T1-Pii

where τ _i is the expected sojourn time of the ith model, P _ii is the probability of transition from ith model to the same model, and T is the sampling interval.

P _ii are calculated using

(5)

Pii=min{hi,max(li,1-Tτi)}

where l _i = 0.1 and h _i = 0.95 are the lower and upper limits, respectively, for the ith model transition probability. The selection of the off-diagonal elements of the TPM depends on the switching characteristics [8].

3Selection of TPM

GA targets are diverse in category, and their performance differs greatly and is vulnerable to be influenced by meteorological environment. To achieve better GA target tracking this paper introduces the target category and meteorological information to adjust TPM.

3.1Multi-factor aided adjust TPM

TPM in the IMM algorithm is given by

(6)

Pij=P(mk+1j|mki)=P(mk+1j,mki)P(mki)

When influence factor F _n is considered, it becomes

(7)

Pij=∑nP(mk+1j,Fn|mki)

According to Bayesian law,

(8)

P(mk+1j,Fn|mki)=P(mk+1j,Fn,mki)P(mki)⋯⋯=P(mk+1j|mki,Fn)P(mki,Fn)P(mki)⋯

⋯=P(mk+1j|mki,Fn)P(Fn|mki)

Target motion model has no relevance to F _n. So P(Fn|mki)=P(Fn),the TPM P _ij is thus given by

(9)

Pij=∑RnP(mk+1j|mki,Fn)P(Fn)

The influence factor mainly has two types: one for target category c _i and one for meteorology g _i. The introduction of the target category information will first reduce the number of corresponding models and then be utilized to adjust TPM. It will improve the filtering accuracy and increase the speed of filter computation.

In GA target tracking, if the category of target exhibits weak maneuvering ability, the probability of keeping in “current motion state” is large while that of transition to “other motion state” is small. If the category of target has strong maneuvering ability, the probability of staying in “current motion state” is small, and the transition probability to “other motion state” is large. But one thing remains the same, the sum of the transition probability of the target from one state to others and itself is always 1.

When airspace meteorological information g _i changes, TPM needs to change accordingly. If a target is in good meteorological environment, then its maneuvering frequency will be relatively low, which suggests large diagonal elements of TPM and small off-diagonal elements. If a target is in bad meteorological environment, then its maneuvering frequency will be relatively high, thus the diagonal elements of TPM should be smaller and the off-diagonal elements be larger.

Considering these facts, target category and meteorological environment information can be used to determine TPM.Following the above relationship, the proposed algorithm adopt the fuzzy system to adjust the TPM for GA tracking.

3.2The fuzzy system design

The target category and meteorology of GA assigned airspace can be employed to determine the expected sojourn time τ _i of the ith model. The τ _i can be calculated by the fuzzy system. Its main functions are given as follows:

– map the relationship of the τ _i with c _i and g _i into a set of fuzzy rules.
– take c _i and g _i as the input variable and τ _i as the output variable of the fuzzy system.

The fuzzy system consists of four blocks, as shown in Fig. 1.

– block 1: utilize singleton fuzzifier.
– block 2: implement the fuzzy law between the input and output. Map the spaces of all variable into the fuzzy spaces.
– block 3: defuzzify the fuzzy output.
– block 4: estimate the target state by using τ _i.

Δc _i, Δg _i and Δτ _i are necessary to be normalized with the following forms: Δc′_i = Δc _i/Δc _max, Δg′_i = Δg _i/Δg _max and Δτ′_i = Δτ _i/τ _max. Here Δc _max, Δg _max and Δτ _max are their corresponding maximum values. The two input variables Δc′_i and Δg′_i which are expressed as A˜m and B˜n (m, n = 1, 2, 3, 4) and are usually relate with the target category and the meteorological environment.

These fuzzy sets are labeled in the linguistic terms of zero (ZE), small positive (SP), medium positive (MP), and large positive (LP). Triangular functions can simplify the calculation of a fuzzy reference engine and suppress noise of the inputs. They are used to define the membership functions of antecedent fuzzy sets for each fuzzy rule. As shown in Fig. 2. The output consequence of the fuzzy system is Δτ′_i. To obtain optimum Δτ′_i, the region of Δτ _max is divided into six different fuzzy sets, ZE, SP, MP, VP, large positive (LP), and extremely large positive (EP), expressed as C˜s, s = 1, 2, ⋯ , 6. As shown in Fig. 3.

The membership function in each fuzzy set is determined in the following:

(10)

μA˜ml(Δc′i)=1-|Δc′i-dil|bil

where Δc′i∈[dil-bil,dil+bil]. Use the fuzzy IF-THEN rules to establish the fuzzy model of the relationship of Δτ′_i with Δc′_i and Δg′_i:

(11)

Rl:IFΔc′i∈A˜mlANDΔg′i∈B˜nlTHENΔτ′i∈C˜sl

where l = 1, 2, ⋯ , M, and M = 16. The designed fuzzy rule base is shown in Table 1.

As a result, the fuzzy system output is given asfollows:

(12)

Δτ′i=∑l=1Mλsl[min(μA˜il(Δc′i),μB˜jl(Δg′i))]∑l=1M[min(μA˜il(Δc′i),μB˜jl(Δg′i))]

Δτ′_i can be applied to estimate TPM by usingEquation (5).

4FLMAMMF for hybrid estimation

FLMAMMF based on the original IMM algorithm adds the influence factors. A recursive cycle diagram of the algorithm is as shown in Fig. 4.

In this process, first using the current influence factor information (target category, meteorological environment information) to adaptively adjust TPM elements P _ij to P _ij′. The next step is interactive filtering, which is the same as in traditional IMM. Calculation of all the quantities is shown in Table 2.

5Experimental results and analysis

5.1Simulation setup

The simulational experiment is conducted by using a computer with a dual-core CPU of Pentium D 2.93 GHz, 2GB RAM. The programs are performed by using the Matlab 2013a version software. The simulation results are derived from 100 Monte Carlo runs.

The first part: Simulated target motion trajectory is shown in Fig. 5. The simulation assumed that the target flight models be CV linear motion model and coordinated turn (CT) curvilinear motion model. Target initial state is (200 m, 40 m/s, 200 m, 40 m/s), the flight lasts for 100 seconds with a sampling rate of 1 point per second. The observation data are corrupted by a Gaussian white noise with a variance of 2500 m ². The motion trajectory of the simulation target is divided into seven phases: CT motion with turn rate +3°/s between 15–30 seconds, CT motion with turn rate -3°/s between 35–50 seconds, CT motion with turn rate +5°/s between 55–70 seconds, CT motion with turn rate -5°/s between 75–90 seconds, and constant velocity motion at the rest time. Simulation assumed that the target type information be unknown in the first 50 seconds. Filter initial model set is selected as follows: model 1: CV; model 2: CA; model 3: CT with turn rate +3°/s; model 4: with turn rate -3°/s CT; model 5: CT with turn rate +5°/s; model 6: CT with turn rate -5°/s; model 7: CT with turn rate +7°/s; model 8: CT with turn rate -7°/s; model 9: CT with turn rate +10°/s; model 10: CT with turn rate -10°/s. The initialization of TPM is selected as the 10 × 10 matrix:

(13)

Pij=[0.82⋯0.02⋮⋱⋮0.02⋯0.82]

After 50 seconds, target type information F ₁ came, the fuzzy system adjusted the TPM to a 5 × 5 matrix and the model sets to the following: model 1: CV; model 2: CT with turn rate +3°/s; model 3: CT with turn rate -3°/s; model 4: CT with turn rate +5°/s; model 5: CT with turn rate -5°/s. The original models that do not conform to the target were abandoned.

(14)

Pij=P(mkj|mk-1i,F1)=⋯⋯[0.900.0250.0250.0250.0250.030.900.030.020.020.030.030.900.020.020.030.030.020.900.020.030.020.030.020.90]

The second part: To simulate the GA target under the meteorological conditions of the dramatic changes in the air flight.

The initial state of target is (50 m, 20 m/s, 50 m,20 m/s, 50 m, 20 m/s), the observation is obtained at a data rate of 1 second. A Gaussian white noise was added to the observation. Its variance is set to be 2500 m ². Target motion trajectory in simulation is shown in Fig. 6. The target keeps CV motion in horizontal plane, while in the vertical direction (i.e. the altitude axis) target is affected by a severe turbulence and exhibits constant ups and downs of movement. The simulation assumes that the undulating motion can be regarded as the synthesis movement of cycle +5°/s and -5°/s of CT motions.

The filter initial model set remained unchanged and the TPM was continuously adapted as Equation (14) in the simulation. FLMAMMF adopting Equation (12) to calculate Δτ′_i and then got τ _i. At last the TPM is calculated by using Equation (5). The TPM is given by

(15)

P(mkj|mk-1i)=[0.70.100.100.050.050.150.600.050.150.050.150.050.600.050.150.150.150.150.500.050.150.150.150.050.50]

5.2Simulation results

After 100 Monte Carlo simulation runs, the average computation time for trajectory 1 at each time step is shown in Fig. 7. Since the target type information is not the arrival, at the first 50 seconds the computation time of the proposed algorithm and that of IMM algorithm are basically the equal. From the 51 second, after the target type information comes up, the computation time of the proposed algorithm is obviously reduced. The position root mean square error (RMSE) and velocity RMSE during track process are shown in Fig. 8. The proposed algorithm and IMM algorithm have similar precision.

The filtering results target motion trajectory 2 are shown in Fig. 9. It can be seen that FLMAMMF shows a superior performance to the fixed structure IMM algorithm, especially at the beginning of each maneuver, where the position and velocity RMSEs of the proposed algorithm is significantly reduced compared to the IMM algorithm.

6Conclusion

The wide diverse categories of GA aircrafts are easily affected by meteorological environment in flight, which leads to the difficult problem of effectively track. This paper proposed a FLMAMMF for maneuvering GA target tracking. The relationship of target category and meteorological environment with the TPM is mapped into a set of fuzzy rules. By applying fuzzy logic in the standard IMM and designing the fuzzy system, the proposed algorithm introduces the target classification information and the meteorological environment information into the auxiliary filtering. Adjusting the model TPM by these two factors makes it more close to the actual flight mode, thus improves the tracking precision of the GA target, and reduce the computation time. Simulation experiments show that the estimation performance of the algorithm is better than that of the IMM algorithm. Future works may include introducing more influence factors and to quantify the influencing factors in further studies on the TPM.

Acknowledgments

This work was support by the Research Fund for Doctoral Program of Higher Education of China (20124408110002), the Science and Technology Project of Shenzhen (JCYJ20150324141711674).

References

1	Averbuch , Itzikowitz S, Kapon T (1991) Radar target tracking-Viterbi versus IMM IEEE Transactions on Aerospace and Electronic Systems 27: 3 550 563
2	Jwo D, Wang S (2007) Adaptive fuzzy strong tracking extended Kalman filtering for GPS Navigation IEEE Sensors Journal 7: 5 778 789
3	Blom HAP, Bar Shalom Y (1988) The Interacting multiple model algorithm for systems with Markovian switching coefficients IEEE Transactions on Automatic Control 38: 8 780 783
4	Chen HD, Chang KC (2008) Novel nonliner filtering & prediction method for maneuvering target tracking IEEE Transactions on Aerospace and Electronic Systems 45: 1 237 243
5	Kim H, Kim I (2007) Design of adaptive fuzzy IMM algorithm for tracking the maneuvering target with time-varying measurement noise International Journal of Control Automation System 5: 3 307 316
6	Jilkov VP, Li XR (2004) Online Bayesian estimation of transition probabilities for markovian jump systems IEEE Transactions on Signal Processing 52: 6 1620 1630
7	Barhari MH, Karsaz A, Pariz N (2011) High maneuvering target tracking using a novel hybrid Kalman filter-fuzzy logic architecture International Journal of Innovative Computing Information & Control 7: 5 501 510
8	Kirubarajan T, Bar Shalom Y (1998) IMMPDAF for radar management and tracking benchmark with ECM IEEE Transactions on Aerospace and Electronic Systems 34: 4 1115 1134
9	Li XR, Jilkov VP (2003) Survey of maneuvering target tracking Part I: Dynamic models IEEE Transactions on Aerospace and Electronic Systems 39: 4 1333 1364
10	Li XR, Jilkov VP (2010) Survey of maneuvering target tracking Part II: Motion models of ballistic and space targets IEEE Transactions on Aerospace and Electronic Systems 46: 1 96 119
11	Li XR, Jilkov VP (2005) Survey of maneuvering target tracking Part V: multiple-model methods IEEE Transactions on Aerospace and Electronic Systems 41: 4 1255 1321
12	Li XR, Shalom YB (1993) Design of an interacting multiple model algorithm for air traffic control tracking IEEE Transactions on Control Systems Technology 1: 3 186 194

Figures and Tables

Fig.1

Design procedure of the fuzzy system.

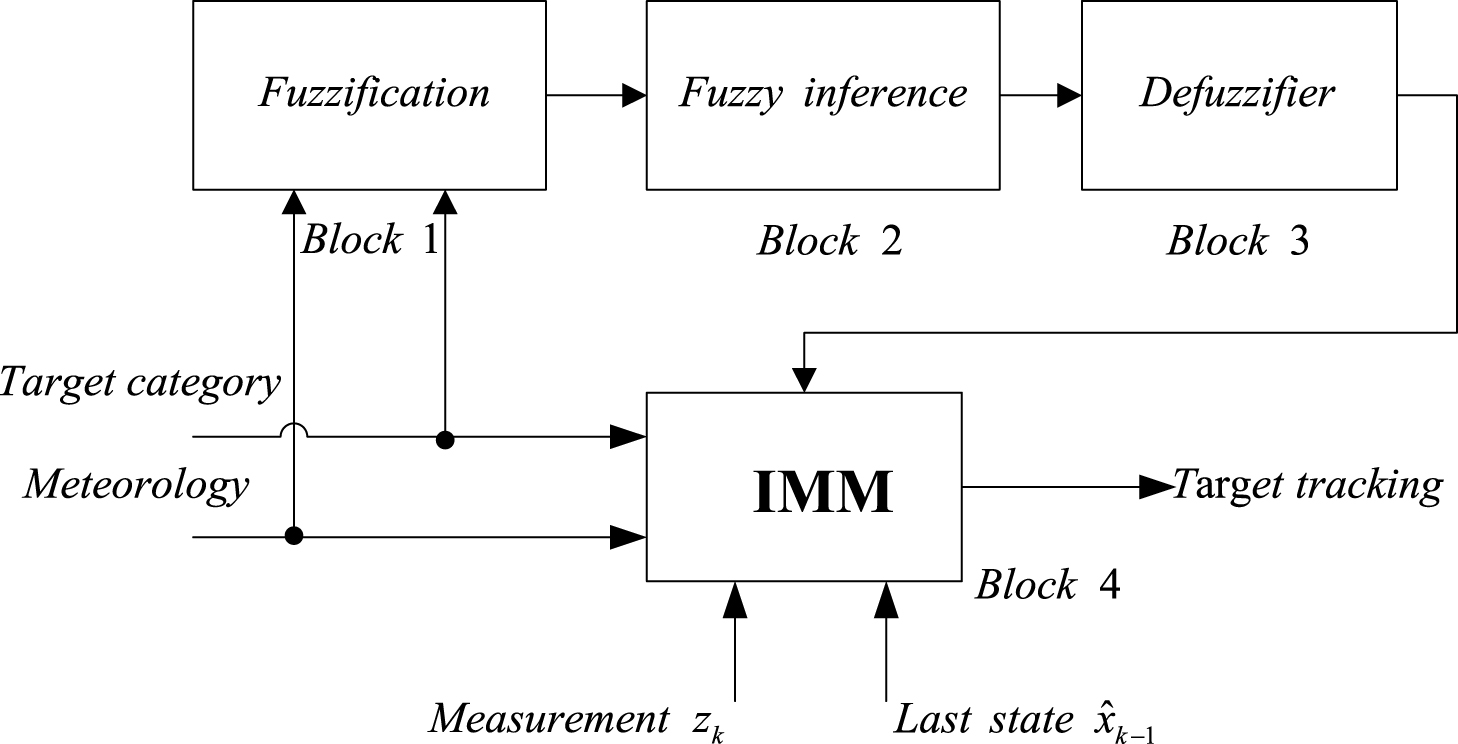
Fig.2

Membership function of Δc′_i or Δg′_i.

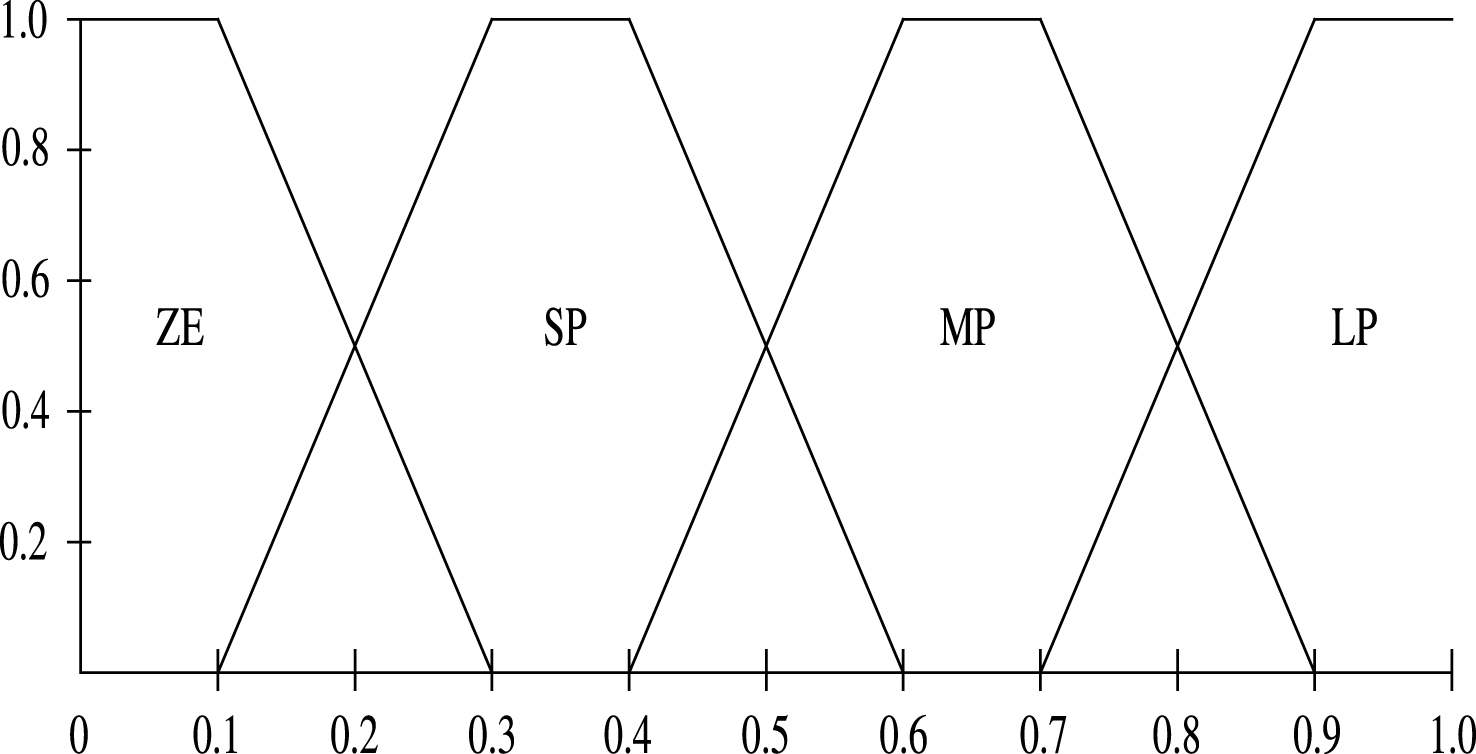
Fig.3

Membership function of Δτ′_i.

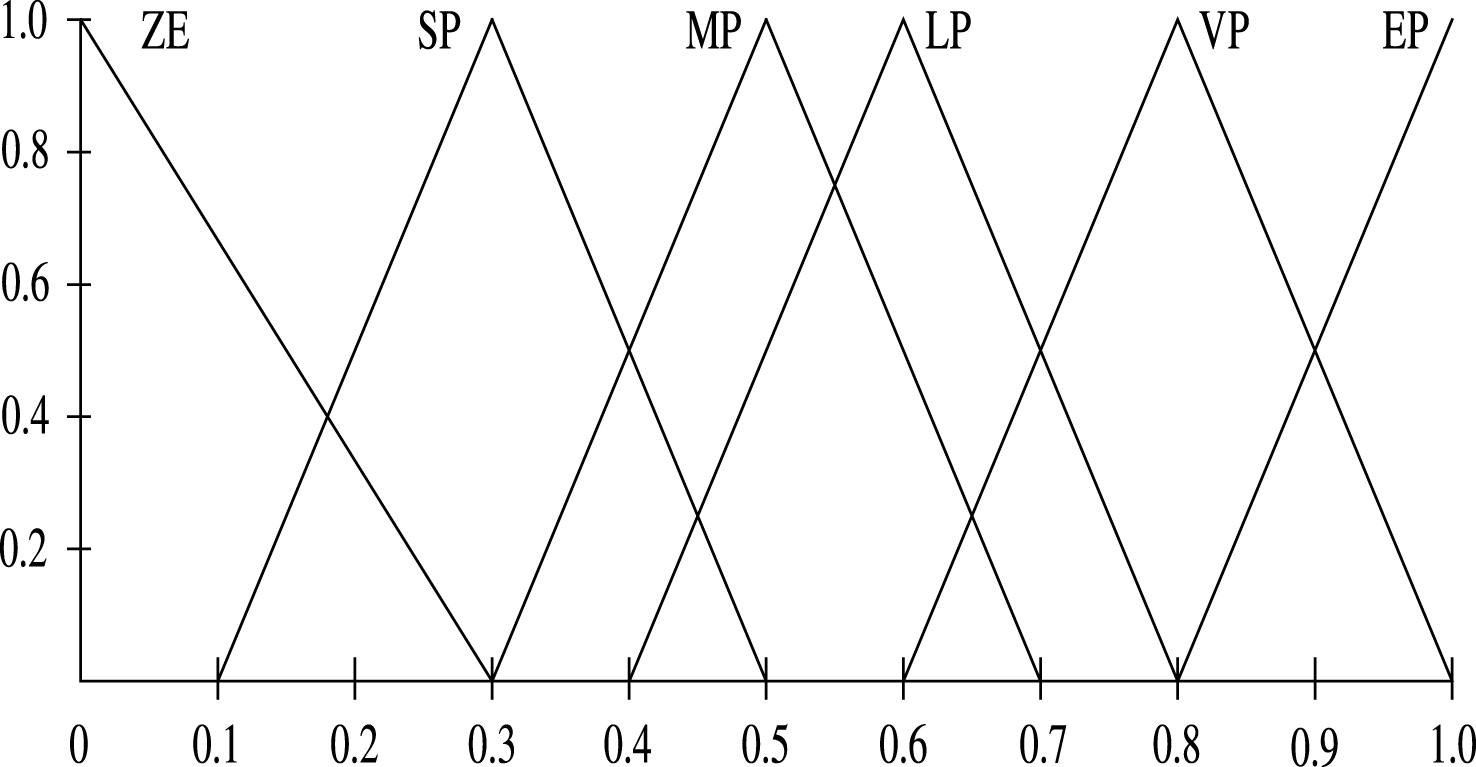
Fig.4

FLMAMMF schematic diagram.

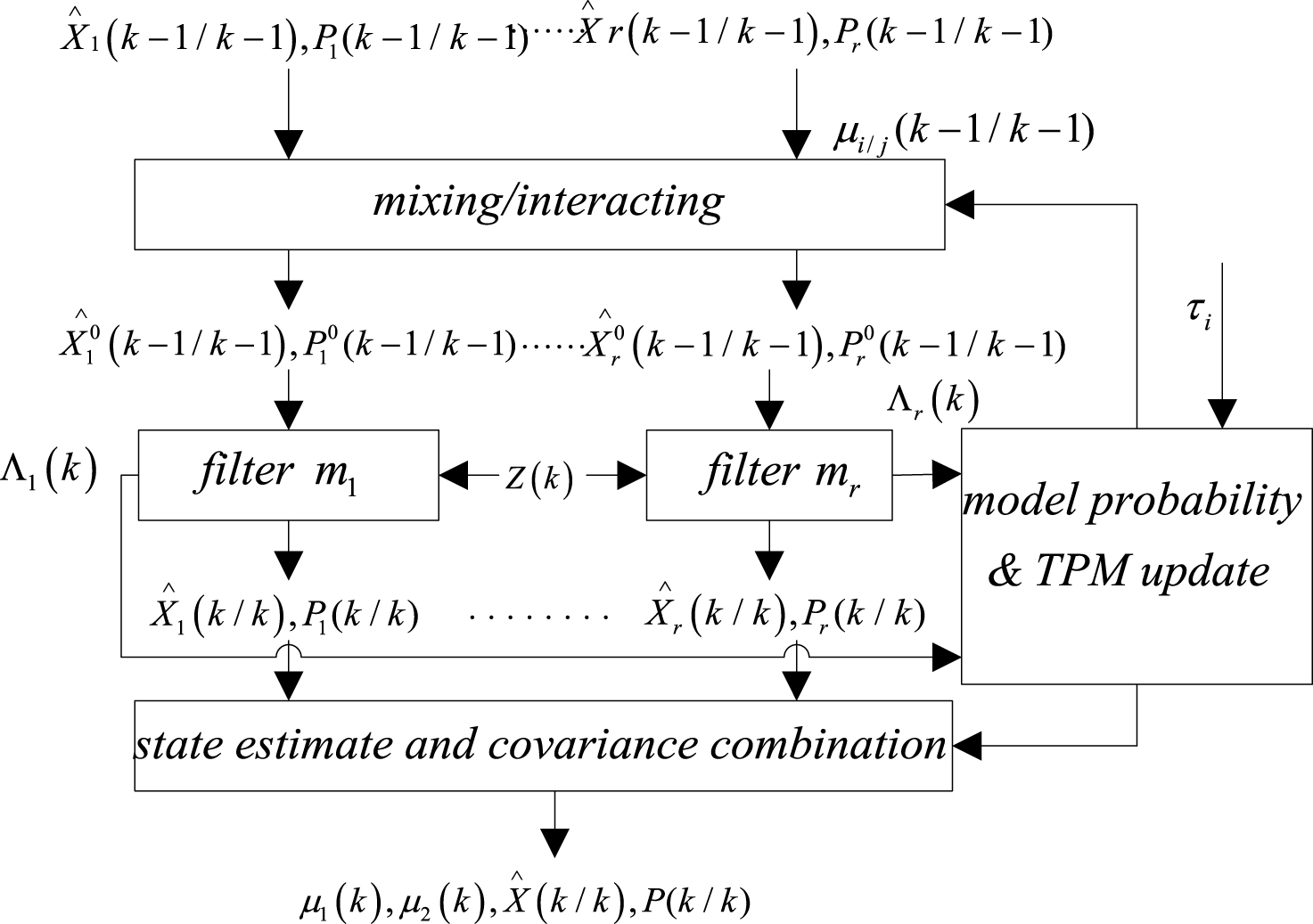
Fig.5

The target trajectory 1.

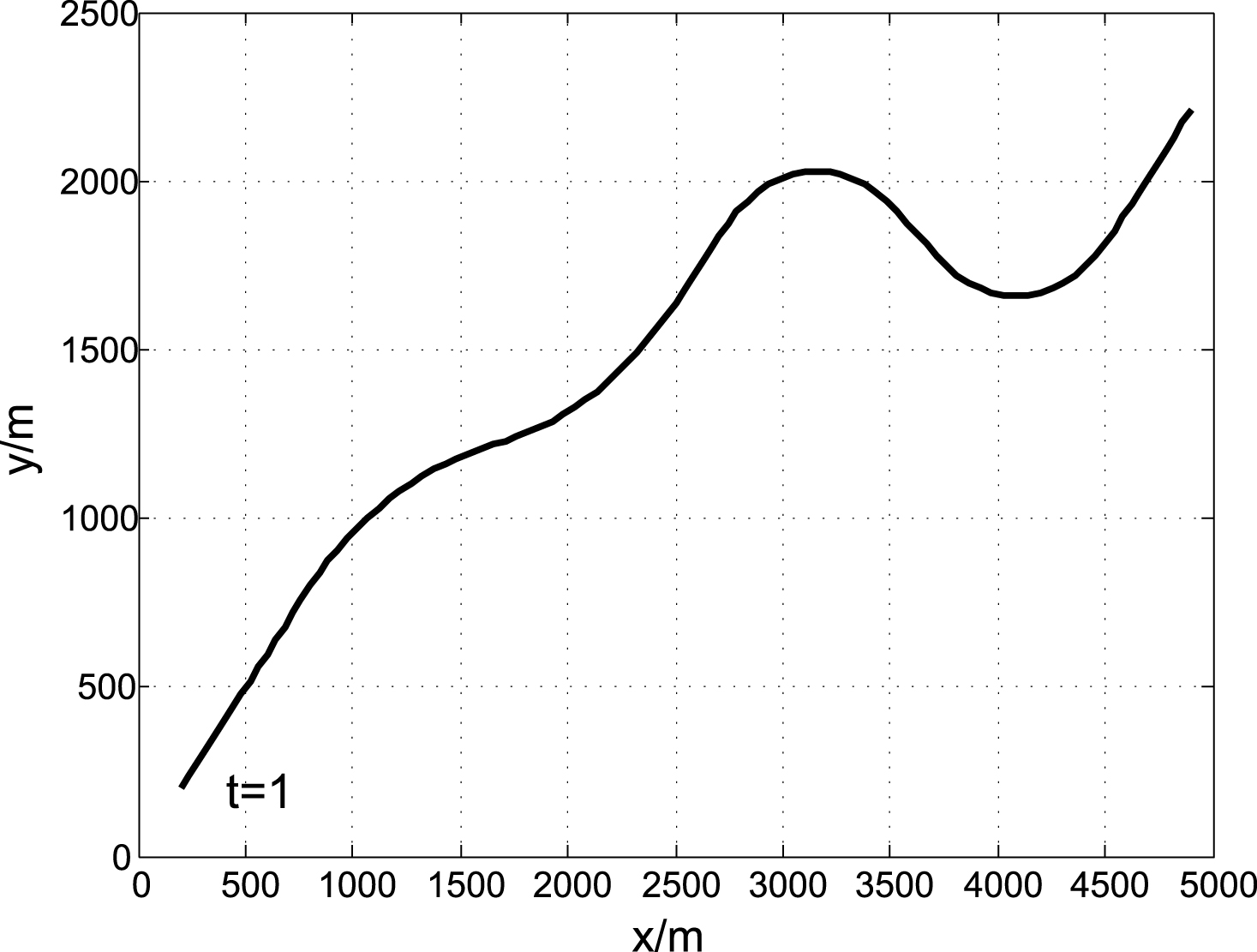
Fig.6

The target trajectory 2.

Fig.7

The comparison of algorithm calculation time.

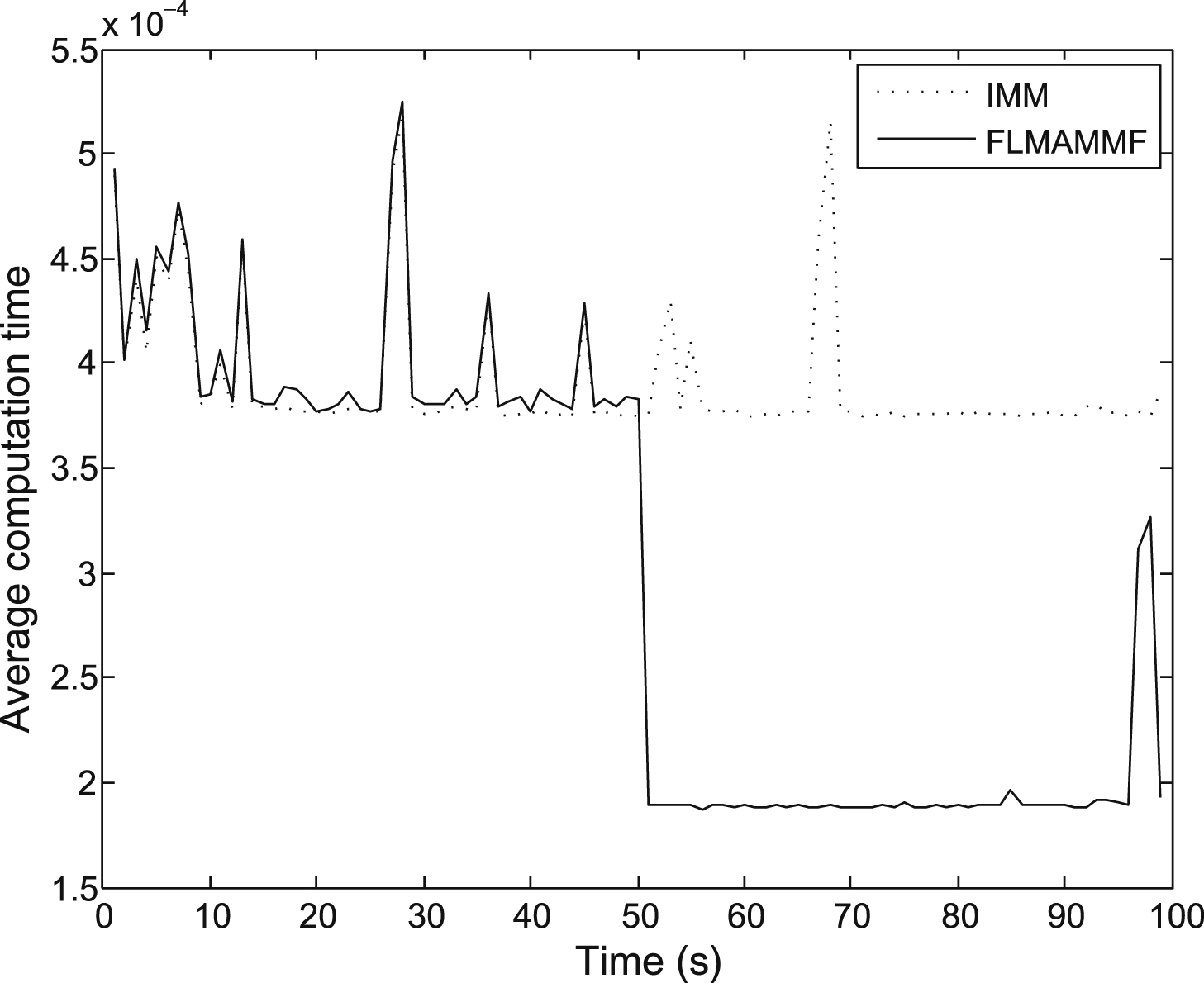
Fig.8

The RMSE of Position and velocity of trajectory 1.

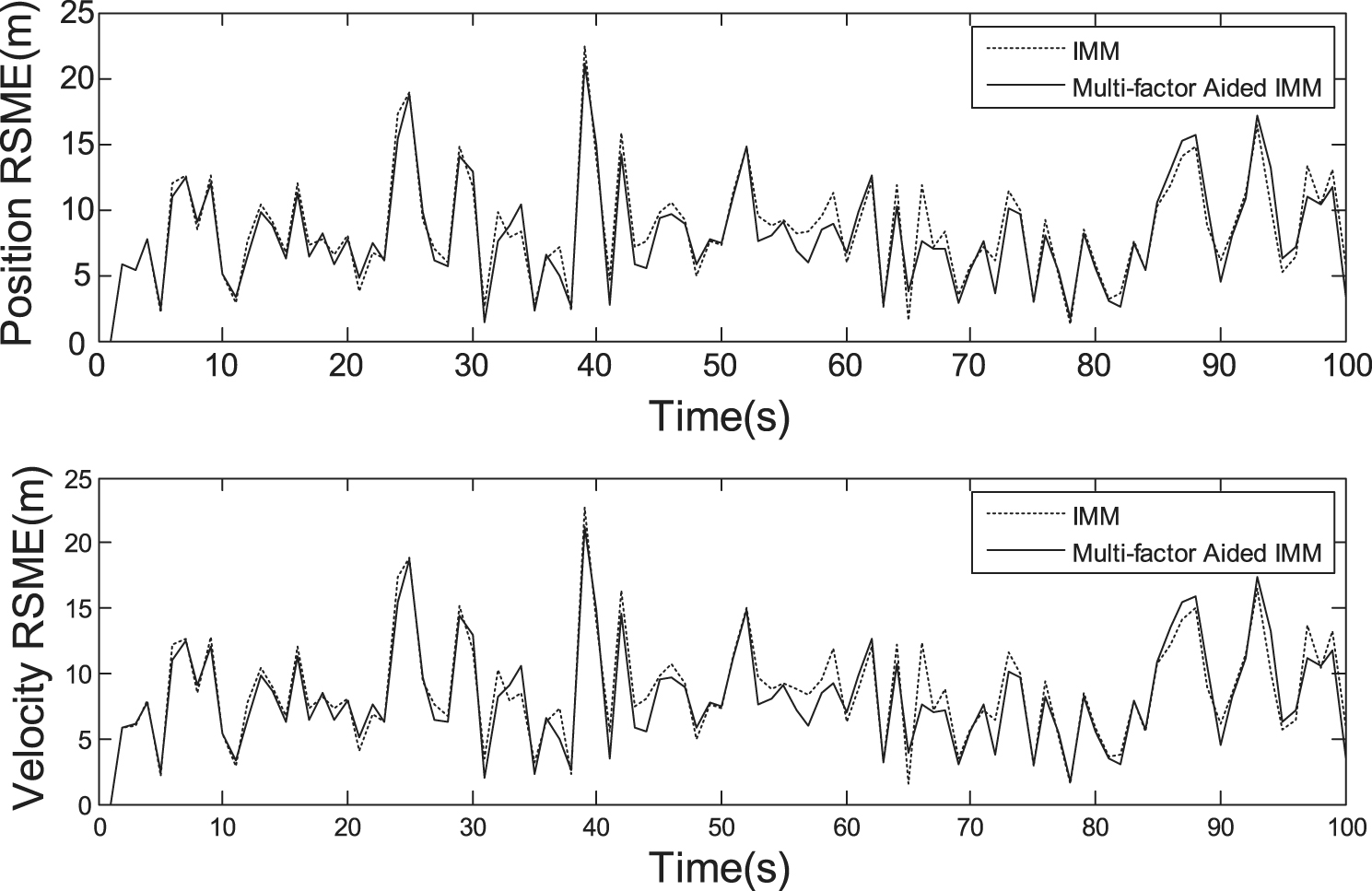
Fig.9

The RMSE of Position and velocity of trajectory 2.

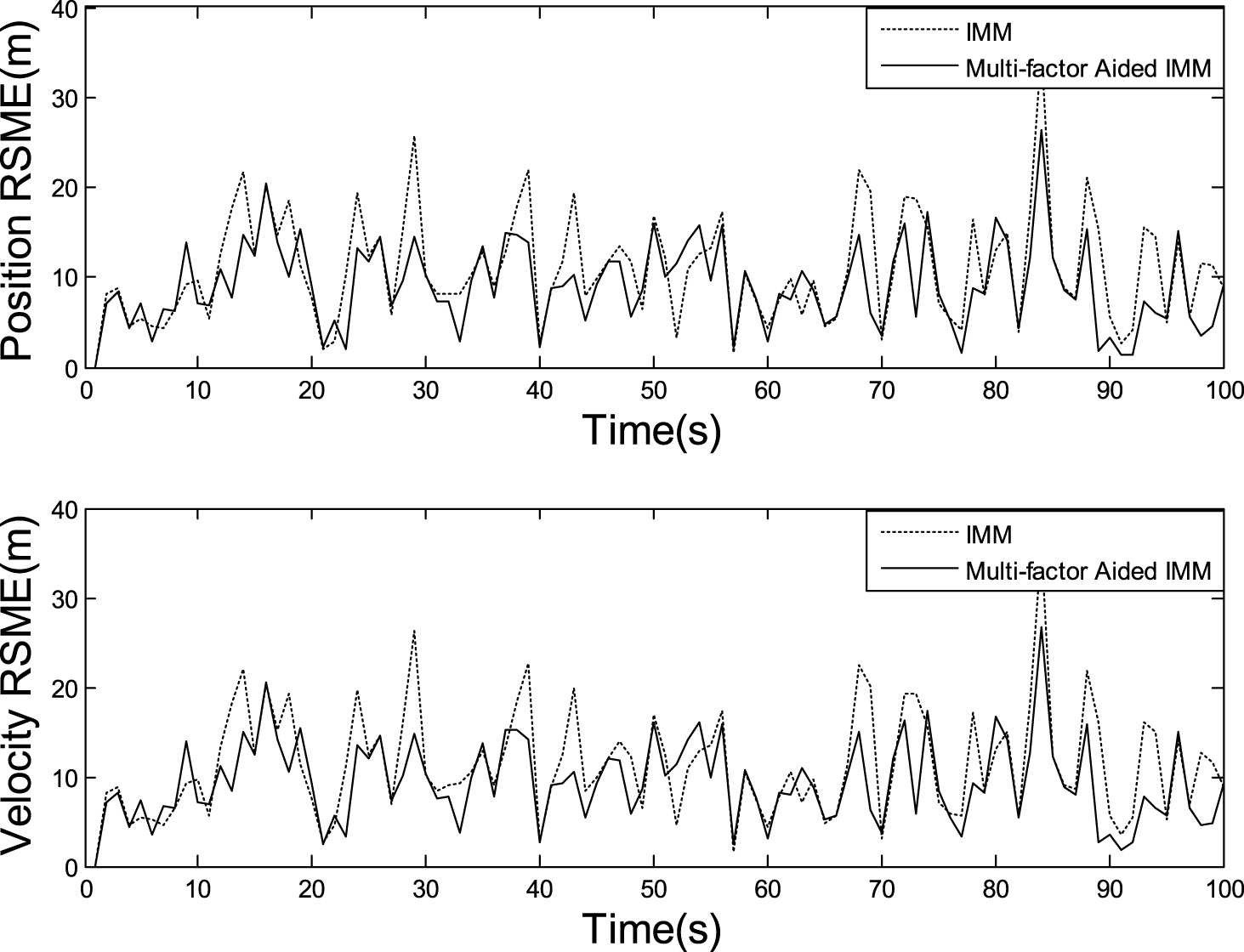
Table 1

Fuzzy rules on Δc′_i, Δg′_i and Δτ′_i

Δτ′_i	Δg′_i
		ZE	SP	MP	LP
	ZE	ZE	SP	MP	LP
Δc′_i	SP	ZE	MP	MP	LP
	MP	MP	MP	LP	VP
	LP	MP	LP	VP	EP

Table 2

FLMAMMF process table

Model-set and TPM (re)initialization:	Pij′=∑RkP(mk+1j\|mki,Fn)P(Fn)
Model probability prediction:	μk-1\|k-1ij=1cjpij′μk-1icj=∑1rpij′μk-1i
mixing estimate and covariance:	xˆk-1\|k-1j(o)=∑1rxˆk-1\|k-1iμk-1\|k-1ij
	Pk-1\|k-1j(o)=∑1rμk-1\|k-1ij{Pk-1\|k-1i+…
	…[xˆk-1\|k-1i-xˆk-1\|k-1i(o)][xˆk-1\|k-1i-xˆk-1\|k-1i(o)]T}
Model-conditioned filtering
predicted state and covariance:	xˆk\|k-1j=Fk-1jxˆk-1\|k-1j(o)
	Pk\|k-1j=Fk-1j(Fk-1j)T+Qk-1j
measurement residual and residual covariance:	vj=zk-Hkxˆk\|k-1j
	Sj=HkPk\|k-1jHkT+Rkj
filter gain:	Wj=Pk\|k-1jHkT(Sj)T
updated state and covariance:	xˆk\|kj=xˆk\|k-1j+Wjvj
	Pk\|kj=Pk\|k-1j-WjSj(Wj)T
Mode probability update
model likelihood:	Λkj=N[vj;0,Sj]=\|2πSj\|-1/2exp(-12(vj)T(Sj)-1vj)
model probability:	μkj=P(mkj\|zk)=1cΛkjcjc=∑j=1rΛkjcjcj=∑j=1rPij′μk-1i
Fusion
overall estimate and covariance:	xˆk\|k=∑j=1rxˆk\|kjμkj
	Pˆk\|k=∑j=1rμkj{Pk\|kj+[xˆk\|kj-xˆk\|k][xˆk\|kj-xˆk\|k]T}

Model-set and TPM (re)initialization:	Pij′=∑RkP(mk+1j\|mki,Fn)P(Fn)
Model probability prediction:	μk-1\|k-1ij=1cjpij′μk-1icj=∑1rpij′μk-1i
mixing estimate and covariance:	xˆk-1\|k-1j(o)=∑1rxˆk-1\|k-1iμk-1\|k-1ij
	Pk-1\|k-1j(o)=∑1rμk-1\|k-1ij{Pk-1\|k-1i+…
	…[xˆk-1\|k-1i-xˆk-1\|k-1i(o)][xˆk-1\|k-1i-xˆk-1\|k-1i(o)]T}
Model-conditioned filtering
predicted state and covariance:	xˆk\|k-1j=Fk-1jxˆk-1\|k-1j(o)
	Pk\|k-1j=Fk-1j(Fk-1j)T+Qk-1j
measurement residual and residual covariance:	vj=zk-Hkxˆk\|k-1j
	Sj=HkPk\|k-1jHkT+Rkj
filter gain:	Wj=Pk\|k-1jHkT(Sj)T
updated state and covariance:	xˆk\|kj=xˆk\|k-1j+Wjvj
	Pk\|kj=Pk\|k-1j-WjSj(Wj)T
Mode probability update
model likelihood:	Λkj=N[vj;0,Sj]=\|2πSj\|-1/2exp(-12(vj)T(Sj)-1vj)
model probability:	μkj=P(mkj\|zk)=1cΛkjcjc=∑j=1rΛkjcjcj=∑j=1rPij′μk-1i
Fusion
overall estimate and covariance:	xˆk\|k=∑j=1rxˆk\|kjμkj
	Pˆk\|k=∑j=1rμkj{Pk\|kj+[xˆk\|kj-xˆk\|k][xˆk\|kj-xˆk\|k]T}