On the Clinimetrics of the Montreal Cognitive Assessment: Cutoff Analysis in Patients with Mild Cognitive Impairment due to Alzheimer’s Disease
Abstract
Background:
In the era of disease-modifying therapies, empowering the clinical neuropsychologist’s toolkit for timely identification of mild cognitive impairment (MCI) is crucial.
Objective:
Here we examine the clinimetric properties of the Montreal Cognitive Assessment (MoCA) for the early diagnosis of MCI due to Alzheimer’s disease (MCI-AD).
Methods:
Data from 48 patients with MCI-AD and 47 healthy controls were retrospectively analyzed. Raw MoCA scores were corrected according to the conventional Nasreddine’s 1-point correction and demographic adjustments derived from three normative studies. Optimal cutoffs were determined while previously established cutoffs were diagnostically reevaluated.
Results:
The original Nasreddine’s cutoff of 26 and normative cutoffs (non-parametric outer tolerance limit on the 5th percentile of demographically-adjusted score distributions) were overly imbalanced in terms of Sensitivity (Se) and Specificity (Sp). The optimal cutoff for Nasreddine’s adjustment showed adequate clinimetric properties (≤23.50, Se = 0.75, Sp = 0.70). However, the optimal cutoff for Santangelo’s adjustment (≤22.85, Se = 0.65, Sp = 0.87) proved to be the most effective for both screening and diagnostic purposes according to Larner’s metrics. The results of post-probability analyses revealed that an individual testing positive using Santangelo’s adjustment combined with a cutoff of 22.85 would have 84% post-test probability of receiving a diagnosis of MCI-AD (LR+ = 5.06).
Conclusions:
We found a common (mal)practice of bypassing the applicability of normative cutoffs in diagnosis-oriented clinical practice. In this study, we identified optimal cutoffs for MoCA to be allocated in secondary care settings for supporting MCI-AD diagnosis. Methodological and psychometric issues are discussed.
INTRODUCTION
Every 3 seconds, someone in the world develops dementia. Every year, almost 10 million new cases are recorded. Nowadays, over 55 million people are living with dementia. Among older people, dementia is one of the primary causes of disability and dependency, and the seventh leading cause of death.1–3 This scenario is further compounded by the dramatic congestion of healthcare and socio-assistance services, as well as by the significant financial impact of the disease. The annual cost of dementia, including both direct and indirect expenses, exceeds cumulatively 1 trillion dollars.2,3
Alzheimer’s disease (AD) is the most prevalent cause of dementia, contributing to 60–80% of cases.1 Amyloidogenesis, namely, the process leading to abnormal aggregation of amyloid proteins resulting in the formation of insoluble fibrils, represents a pivotal pathophysiological mechanism in AD. Consequently, in the fervent pursuit of disease-modifying therapies, most of AD-related drugs currently undergoing clinical trials aim to weaken amyloid protein aggregates.4 With this in mind, the imperative for early identification of individuals at risk of conversion towards AD has never been more critical. Particularly, those diagnosed with Mild Cognitive Impairment (MCI) warrant special mention.
MCI is traditionally considered a boundary stage between healthy aging and overt dementia. It is characterized by a slight cognitive decline with minimal or no functional impairment in daily activities.5 The amnestic phenotype, which predominantly affects memory domains, is a major risk factor for the subsequent onset of AD dementia (ADD), with a conversion rate ranging from 8% to 15% within 1 year, reaching 80% at 6 years.6 However, MCI can stabilize over time and demonstrates reversibility in 26% of cases.5,7 Although the clinical phenotype is relevant, conversion towards ADD is primarily related to the etiopathogenic profile. Therefore, it is crucial to detect MCI patients with a biological diagnosis of AD (i.e., MCI due to AD).8
According to the National Institute on Aging-Alzheimer’s Association (NIA-AA), an accurate evaluation of patients with suspected MCI due to AD (MCI-AD) should involve a comprehensive neurocognitive assessment combined with gathering evidence of AD-like pathophysiology.8 In particular, based on the AT(N) paradigm (amyloid-β deposition, pathologic tau, and neurodegeneration), a patient with MCI is classified as being on the AD continuum if they exhibit biomarker evidence of Aβ deposition (abnormal amyloid PET scan, low cerebrospinal fluid Aβ42, or low Aβ42/Aβ40 ratio), with pathologic phosphorylated tau strengthening the diagnostic likelihood.9 Interestingly, relying solely on biomarkers seems to reduce the predictive value of the diagnosis.10
While acknowledging the importance of integrated approaches that combine etiological and clinical diagnosis, the management of patients with dementia faces limitations in terms of time, costs, and availability of experienced staff. To give a few examples, waiting times for undergoing instrumental examinations can be quite long. Additionally, significant logistical resources are required for administering extensive neuropsychological batteries, which is particularly problematic in outpatient settings where time constraints are rigid. Moreover, the costs associated with procedures like the amyloid PET scan can be notably high, as can those of neuropsychological assessments performed by private providers rather than through the public healthcare system. Finally, those actively practicing clinical neuropsychology in Europe have a very heterogeneous educational background and skill level, compounded by the scarcity of academic training programs and/or clinical training opportunities.11,12 In light of this, there is a pressing need for brief, flexible tools with high diagnostic power, particularly in secondary care settings, where the objective is to skim patients and, when necessary, direct them towards furtherinvestigations.13
Among the tests used in memory clinics, the Mini-Mental State Examination (MMSE) is widely acknowledged as the gold standard neuropsychological battery for assessing global cognitive functioning in moderate/advanced stages of dementia.14 Instead, the Montreal Cognitive Assessment (MoCA) has been specifically designed to evaluate general cognition in patients with MCI and mild ADD.15 As compared to MMSE, MoCA covers a wider range of cognitive domains, including sustained attention, visuospatial, and visuoconstructive abilities. Furthermore, MoCA is less affected by patient’s linguistic capabilities and has demonstrated utility in predicting conversion from MCI towards dementia. In particular, some studies have shown that patients with MCI exhibiting low MoCA scores at baseline were more likely to convert to ADD within a timeframe of 1.5 to 3.5 years.16,17 In addition to providing an overview of general cognitive functioning, it is of particular interest to inquire whether MoCA holds sufficient diagnostic value. To address this inquiry, one should interrogate the architecture of diagnosticresearch.
The architecture of diagnostic research: key questions
Let us imagine that a young researcher has devised a long-term visuospatial memory task requiring the examinee to memorize, and then recall, the spatial arrangement of tokens placed on a chessboard, namely, the ‘Chessboard Test’ (CBT). In particular, the researcher is interested in determining whether CBT could be considered a reliable marker for AD. To establish this, the researcher refers to one interesting chapter within the seminal manual by Knottnerus and Buntinx titled ‘The Evidence Base of Clinical Diagnosis’,18 so as to identify the appropriate research questions to pose.
• Phase 1 question: Do patients with AD achieve significantly lower scores on CBT than healthy individuals?
• Phase 2 question: Are individuals getting lower CBT scores more likely to be diagnosed with AD than individuals getting a higher CBT score?
• Phase 3 question: Among individuals for whom there is a clinical suspicion of AD, can CBT score effectively discriminate between those with and without AD?
• Phase 4 question: Do patients tested with CBT have better health outcomes, such as functional autonomies, quality of life, or mortality rate, compared to those who do not undergo the test?
Here we focus on Phase 1 and 2 questions. This choice is prompted by the presence of several threats to validity in Phase 3 studies and limitations in their applicability to clinical research. As for the Phase 4 question, interventions for AD remain currently confined to cognitive stimulation and palliative pharmacological therapies.19
Consider once more our enterprising researcher. Picture them now, eager to delve into a Phase 1 question. To determine whether CBT may be clinically meaningful, the test should be administered to demographically-matched samples of patients with AD and healthy controls. If a significant difference is detected in CBT score’s distribution between the two groups, the researcher may conclude that CBT is a useful diagnostic tool. Regrettably, this finding does not really ensure that CBT can be confidently translated into clinical practice for diagnostic purposes. Indeed, if the Phase 1 question receives an affirmative response, the next step is conducting a clinimetric study to address a Phase 2 question.19 Here, clinimetrics refers to that branch of psychometrics encompassing statistical algorithms for disease classification and diagnosis.
To answer a Phase 2 question, the researcher set up a supplementary study. This time, CBT is administered under standardized (ideal) conditions. Furthermore, to discern the presence of AD, the researcher relies on established gold standard references, e.g., cerebrospinal fluid (CSF) Aβ levels and performance on the Rey Auditory Verbal Learning Test (RAVLT).20,21 Upon collecting CBT scores, its discriminative capability is estimated, typically using Receiver Operating Characteristic (ROC) curve analysis. Still, indexes of diagnostic power, such as sensitivity and specificity, are computed with respect to a specified cutoff point.19 The study results suggest that CBT exhibits adequate discriminatory power. Moreover, the identified optimal cutoff appears to strike a well-balanced equilibrium between sensitivity and specificity. Also, CBT demonstrates excellent convergent validity, showing strong correlations with CSF markers and RAVLT. The young researcher is now satisfied: CBT can be employed in diagnostic-oriented clinical practice.
Stopping at the first rung: the normative studies
Phase 1 studies are relatively simple, quick, and cost-effective. These advantages have captivated researchers in neuropsychology, leading to an oversimplification of the aforementioned diagnostic architecture: normative studies are born.
The diagnostic significance of a test relies on its ability to discriminate between ‘normal’ and ‘abnormal’ conditions. Accordingly, the definition of normality is pivotal. In normative studies, the interpretation of an individual’s test score involves comparing it with scores from a normative/healthy sample, assumed to be representative of the population from which the individual comes. There are different methods to quantify the relative standing of an individual’s score within a normative distribution. For instance, one may use the percentile rank, but it only indicates the score’s ordinal position within the distribution, without assuming univariate normality. Instead, if one posits that scores follow the normal/gaussian distribution, it is possible to proceed in terms of equal intervals using measures of central tendency and dispersion. Specifically, the individual’s raw score may be converted into z or t standardized scores.22 An alternative approach, rooted in the Italian tradition, is the regression-based Equivalent Score (ES) method.23–25
As sociodemographic variables, such as age and education, can affect cognitive performance, the ES method entails statistically weighing their contributions to score variability using linear regression. Subsequently, correction coefficients are derived. Upon application of these correction factors, it becomes possible to easily compare individuals with different age and education levels. For instance, the performance of a young university student can be compared with that of a septuagenarian with only primary education. Following this, the demographically-adjusted normative distribution is standardized using a 5-point ordinal scale, from ES0 to ES4. Conventionally, ES0 corresponds to an adjusted score that is equal to or lower than the outer non-parametric tolerance limit on the 5th percentile with 95% confidence. ES4, conversely, corresponds to performance equal to or better than the median value. ES1, ES2, and ES3 are obtained by dividing the distribution between ES0 and ES4 into three parts.24,26 The outer non-parametric tolerance limit on the 5th percentile aligns with z=–1.88 deviations on a normal distribution curve, given, for example, 300 sample units, and represents the so-called nominal normative cutoff. Theoretically, this cut-point should separate the 3% of individuals getting a deficient performance from the 97% classified as ‘normal’.25 ESs provide a straightforward interpretation and minimize individual differences. Furthermore, such an ordinal scale might allow us to compare an individual’s performance across different neuropsychological tests. However, this method presents some weaknesses.
On the one hand, it may represent a step backward compared to standardized scores, resulting in a loss of information. On the other hand, only the tolerance region around the 5th percentile holds potentially inferential value. Indeed, while it is reasonable to use the median as a designated measure of central tendency due to the self-styled non-parametric nature of the method, the portion of the distribution between ES0 and ES4 remains a black hole. Assuming that the left tail of the adjusted score distribution is comparable to that of the normal distribution, the ES0-ES4 interval is divided into three sections using the space between z = –1.88 and z = 0 (median) as a reference (i.e., using z = –1.25 and z = –0.63 as anchor points for N = 300).26,27 Alternatively, one might consider using other pre-defined tolerance limits, such as the 10th and 20th percentiles.24,25 In any case, the setting of tolerance limits and ESs is governed by ‘z’ logic and is solely contingent upon sample size, which may appear counterintuitive. Adopting a parametric approach to determine the intermediate ESs introduces a methodological inconsistency with the non-parametric approach used to define the fixed ES0 and ES4. In this regard, it has been recently proposed that intermediate ESs should be calculated independently from assumptions about the distribution’s shape, and instead based on a non-parametric rank subdivision of the adjusted scores distribution.28 Similar algorithms, already silently used in the literature,29–32 allow for partitioning the region between ES0 and ES4 into three equal parts with the same density, likely improving classification accuracy.
From a diagnostic perspective, an additional flaw of the ES method concerns the establishment of the nominal cutoff. Now it is clear that using ESs to compare an individual’s score to normative data is traditionally grounded in the idea that normative distributions approximate a Gaussian distribution. In healthy individuals, some psychological test scores fit the normal distribution. Conversely, many neuropsychological scores typically show negatively skewed and leptokurtic distributions in normative datasets, as a result of a significant ceiling effect. Consequently, scores are condensed into a limited set of discrete values at the upper extreme of the score range, with only a few observations at the left tail of the distribution.18 In such instances, setting nominal cutoffs at the 5th percentile may be a procedure devoid of meaning.
Also, it is crucial to emphasize that even in the presence of a normal distribution, using such a ‘low’ cutoff may be disadvantageous for several reasons. It is customary to classify as not normal those scores that fall within the lower 5% of the population, accepting an error risk < 5%. This approach stems from inferential statistics, where it is common practice to assume a nominal alpha level equal to 0.05 to mitigate type 1 error inflation, namely, the rejection of the null hypothesis when it is true. In diagnostic terms, this implies maximizing the test specificity, decreasing the risk of false positives, i.e., the risk of mistakenly rejecting the null hypothesis that an individual is free from cognitive impairment. Concurrently, this entails a decrease in the test sensitivity, which is a crucial diagnostic parameter.33 This is especially true in the context of serious health conditions that can be delayed (or treated) if correctly managed in the early stages.34 Ultimately, the test may become primarily beneficial for general screening purposes.
To conclude, the crux of the matter lies in the stark contrast between the statistical and diagnostic definitions of normality. According to Bayes’ theorem, the probability (P) that an individual suffering from a disease (D) tests positive (T), i.e., the positive predictive value P(D|T), is equal to
In the clinical neuropsychology literature, there is the habit of omitting the investigation of normative thresholds’ diagnostic applicability to target conditions. As previously outlined, the extent of neuropsychological deficits may be differently captured by normative data, depending on how they are handled psychometrically. Furthermore, their diagnostic significance may be negligible. However, it is important to stress that a great deal of work has been done recently within the Italian scenario to identify disease-specific cut-offs on demographically-adjusted scores. This is particularly the case for tests conceived originally for cognitive screening purposes.33,35–39 As a general rule, following Phase 1 and/or normative studies, it should be imperative to conduct robust clinimetric studies answering the Phase 2 question. The best algorithm is still to administer the test to be validated to a large normative sample, adjust the score distribution, and then calculate optimal cutoffs for sensitivity and specificity based on a specific target clinical population.40
Aims
The MoCA is the designated character of this paper. Several normative studies on the MoCA exist, involving cognitively intact individuals with different geographic backgrounds, e.g., Czechoslovakia,41 Italy,42 Japan,43 Norway,44 Portugal,45 and Sweden.46 As many clinimetric studies on the MCI population have been conducted.13,47–57 However, in these studies, patients were selected based on different algorithms for clinical diagnosis only, i.e., using Petersen’s criteria, the Diagnostic and Statistical Manual of Mental Disorders (DSM), or NIA-AA 2011 guidelines.8,58–61 This approach, on the one hand, guarantees less conservative inclusion criteria, hence allowing the enrollment of large patient cohorts in line with the prevailing big data ‘culture’. On the other hand, however, it exposes to risks of misdiagnosis, false positives, and limited generalizability to individuals with a biologically confirmed diagnosis of neurogenerative disease. This may represent a significant methodological flaw. Surprisingly, only one Czech study investigated the clinimetric properties of MoCA in patients with MCI-AD, thus addressing such a crucial issue.62
Recently, some of us devised a study that highlighted how the historic overconfidence in the effectiveness of normative data among Italian neuropsychologists may constitute a significant challenge in diagnostic settings.33 Specifically, the study included patients with MCI and early dementia of mixed etiology (i.e., AD, mixed AD, cerebrovascular disease, frontotemporal degeneration, dementia with Lewy bodies). This cohort was compared with a control group consisting of healthy participants matched for sociodemographic characteristics. Regardless of correction factors and geographic extraction of normative datasets, we demonstrated that the available Italian normative cutoffs exhibited excellent specificity.42,63,64 However, these cutoffs showed very poor sensitivity, ranging from 0.09 to 0.24, in distinguishing between individuals with mild neurodegeneration and normal cognition.33 Moreover, we determined the optimal cutoffs for each of the Italian normative adjustments, as well as for the conventional Nasreddine’s 1-point adjustment method.15 In this replication study, we aimed to assess the clinimetric properties of MoCA in a sample of patients with MCI-AD. In particular, we (i) tested the diagnostic properties of previously identified cutoffs, and (ii) computed new optimal cutoffs, weighted for sensitivity and specificity.
METHODS
Retrospective data collection was performed for a consecutive series of patients of either sex with suspected MCI who were referred to the Memory Centre of Trieste University Hospital (Neurological Unit, Azienda Sanitaria Universitaria Integrata Giuliano Isontina, ASUGI, Trieste, Italy) and the Dementia Clinic of C.T.O. Hospital (Neurological Unit, AORN Ospedali ‘Dei Colli’, Naples, Italy). All eligible patients underwent a comprehensive neurological and neuropsychological examination by experienced clinicians. Patients were included in the study if received a clinical diagnosis of MCI according to Petersen’s algorithm,60 and a concurrent biomarker-driven diagnosis of MCI-AD. The latter was performed by harmonizing the NIA-AA 2011 criteria with the AT(N) framework.8,9 Specifically, the diagnosis of MCI-AD was supported by neurobiological evidence indicating ongoing AD-like pathophysiological mechanisms. This evidence encompasses markers of Aβ deposition (e.g., lower CSF Aβ42 levels, lower CSF Aβ42/Aβ40 ratio, positive results at amyloid PET imaging). In addition, pathologic tau biomarkers (i.e., elevated CSF phosphorylated tau levels) and markers of neuronal injury (e.g., hippocampal and medial temporal lobe atrophy detected in MRI, hypometabolic clusters affecting the temporoparietal and/or the posteromedial parietal cortex highlighted in FDG-PET, elevated CSF total tau levels) were taken into account. Patients were thus classified according to both diagnostic categories outlined in the NIA-AA 2011 guidelines (i.e., low, intermediate, and high diagnostic likelihood) and AT(N) profiles. The minimum inclusion criterion was set at intermediate likelihood in combination with an A + T– N– profile, indicating that biomarker evidence of Aβ deposition was deemed critical for diagnosis.
A group of participants with normal cognition (normal controls, NCs) was assembled by recruiting, on a voluntary basis, individuals from various districts in Friuli-Venezia Giulia, Veneto, Trentino-Alto Adige, and Campania regions, ensuring demographic comparability with the patient group. None of the control participants reported cognitive complaints. Exclusion criteria for both patient and control groups were age > 75 years, <5 years of formal education according to the Italian schooling system, history of learning disabilities, acquired brain injuries, psychiatric disorders (e.g., major depression), other major health conditions (e.g., cancer, severe obesity), alcohol/drug abuse, and ongoing treatments with psychoactive medications (e.g., antidepressants, neuroleptics, anxiolytics). Furthermore, while patients showing chronic cerebrovascular lesions (Fazekas grade≤2) were retained, those with severe vascular encephalopathy (Fazekas grade = 3) or multi-infarct dementia, which may justify the clinical picture, were excluded.65 Note that participants over 75 years of age were excluded in accordance with Italian consensus recommendations for biomarker-based etiological diagnosis in patients with MCI,66 owning to the high variability of the potential clinical impact of amyloid biomarkers assessment in this population (e.g., to minimize unnecessary investigations and age-related false positives in amyloid biomarkers). Participants with well-pharmacologically compensated chronic medical illnesses (e.g., hypertension, type II diabetes, gastrointestinal diseases) were included to minimize the risk of a ‘hyper-normality’. All participants had normal or corrected-to-normal vision. All participants were Caucasian and native Italian speakers.
Both patients and controls completed the Italian version of the MoCA. This was not used within the diagnostic process. In particular, the clinicians involved in the diagnostic process were uninformed about the individual’s MoCA score. Additionally, the neuropsychologists administering the MoCA were unaware of the presence of a clear diagnostic suspicion. Finally, data analysis was performed in a blinded fashion concerning group membership (dummy: 0 = Group A, 1 = Group B). Raw MoCA scores were adjusted according to (i) Nasreddine’s 1-point correction, entailing the addition of 1 point for individuals with≤12 years of education15 and (ii) age-and-education correction factors derived from the three available Italian normative studies.42,63,64 Therefore, four distinct MoCA scores, each subjected to independent adjustments, were achieved. Subsequently, we examined whether these adjusted scores fell below or exceeded the reference threshold values. Specifically, as concerns Nasreddine’s method, the conventional cutoff of 26 was employed as the gold standard,15 in combination with the cut-point of 23.50 proposed by Ilardi et al.33 Regarding Italian normative data, adjusted MoCA scores were compared with the respective nominal cutoffs (Conti = 17.36, Santangelo = 15.50, Aiello = 18.58), i.e., the upper limits of ES0.23–25 In addition, for each of the three Italian adjustment methods, the cutoffs proposed by Ilardi et al. were reassessed (Conti = 20.97, Santangelo = 22.85, Aiello = 22.29).33 Optimal cutoffs for MCI-AD were finally calculated.
The current study was approved by the Comitato Etico Unico Regionale of Friuli-Venezia Giulia (CEUR-FVG; decree n. 438 of 8 June 2018; study protocol n.95/2018) and performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki and its later amendments. Informed consent was obtained from all participants included in this study. Based on the EQUATOR (Enhancing the QUAlity and Transparency Of health Research) network library, the STARD 2015 guidelines for reporting diagnostic accuracy studies were followed.
Statistical analyses
For descriptive purposes, nominal variables were presented as frequency while quantitative ones as mean (M)±standard deviation. Between-group comparisons were conducted using two-way chi-squared test (χ2) and independent samples t-test for nominal and quantitative variables, respectively. Four conditional nonparametric models based on ROC curve analysis were run to assess the extent to which the adjusted MoCA scores (test variables: MoCA-Nasreddine, MoCA-Conti, MoCA-Santangelo, MoCA-Aiello) could discriminate between patients with MCI-AD and NCs. According to agreed conventions, an area under the ROC curve (AUC) greater than 0.70 is suggestive of adequate diagnostic accuracy.67 Concurrently, the optimal cutoffs for MCI-AD were identified based on a simultaneous assessment of sensitivity (Se) and specificity (Sp). Any optimal cutoff was determined by integrating different metrics: the Youden index (J),68 concordance probability method (CZ),69 and Closest to (0, 1) Criteria (ER).70 Also, for each adjustment method, these metrics were used to evaluate the adequacy of Se/Sp balance for both the conventional/normative cutoffs and the decision thresholds proposed by Ilardi et al.33 Finally, additional metrics of diagnostic accuracy were calculated, namely, positive and negative predictive values (PPV, NPV), false positive and false negative rates (FPR, FNR), diagnostic accuracy (ACC), positive and negative likelihood ratios (LR+, LR–) and related post-test probability, Larner’s number needed for screening utility (NNSU), and Larner’s likelihood to be diagnosed or misdiagnosed (LDM) 71. Table 1 presents an overview of each clinimetric index employed in the current study. A p-value < 0.05 was considered statistically significant. Bonferroni’s correction for multiple comparisons was performed, as appropriate. No missing data were detected. Statistical analyses were performed by means of IBM SPSS Statistics for Windows v. 27 (IBM, Armonk, 204 NY, USA) and Stata Statistical Software r. 15 (StataCorp LLC, College Station, TX).
Table 1
Summary measures of diagnostic accuracy employed in this study
| Measure | Formula | Description |
| Sensitivity (Se) |
| The proportion of true positive results, indicating the test’s ability in correctly identifying individuals with the target condition. |
| Specificity (Sp) |
| The proportion of true negative results, indicating the test’s ability in correctly identifying individuals without the target condition. |
| Positive predictive value (PPV) |
| The probability that a positive test result correctly indicates the presence of the target condition. The more specific the test, the greater the PPV. |
| Negative predictive value (NPV) |
| The probability that a negative test result correctly indicates the absence of the target condition. The more sensitive the test, the greater the NPV. |
| False positive rate (FPR) |
| The proportion of individuals with a confirmed negative condition who receive a positive test result (fall-out). The more specific the test, the lower the FPR. |
| False negative rate (FNR) |
| The proportion of individuals with a confirmed positive condition who receive a negative test result (miss rate). The more sensitive the test, the lower the FNR. |
| Accuracy (ACC) |
| The proportion of correctly classified individuals. |
| Positive likelihood ratio (LR+) |
| The ratio of Se to FPR, indicating the probability of having a diagnosis in individuals with a confirmed positive condition testing positive compared with individuals with a confirmed negative condition testing positive. Values greater than 1 suggest an increase in the probability of disease. The larger the LR+, the more informative the test. |
| Negative likelihood ratio (LR–) |
| The ratio of FNR to Sp, indicating the probability of having a diagnosis in individuals with a confirmed positive condition testing negative compared with individuals with a confirmed negative condition testing negative. Values lower than 1 suggest a decrease in the probability of disease. The smaller the LR–, the more informative the test. |
| Youden index (J) | Se + Sp - 1 | This method defines the optimal cutoff as the point maximizing the difference between Se and FPR, corresponding to the vertical distance between the 45 degree line and the point on the ROC curve. Higher values of J are better than lower values. |
| Concordance probability method (CZ) | Se × Sp | This method defines the optimal cutoff as the point maximizing the product of Se and Sp. CZ can be expressed as the area beneath the ROC curve, represented geometrically as a rectangle. Its height corresponds to Se and its width to Sp. The cutoff maximizing CZ is the one that maximizes the area of the rectangle. Higher values of CZ are better than lower values. |
| Closest to (0, 1) criteria (ER) |
| This method defines the optimal cutoff as the point minimizing the Euclidean distance between the ROC curve and the (0, 1) point/top-left corner. Lower values of ER are better than higher values. |
| Number needed for screening utility (NNSU) |
| The reciprocal of the so called ‘Summary utility index’. NNSU values lower than 1.02 are desirable, suggesting that the test is suitable for ruling in and ruling out diagnosis. |
| Likelihood to be diagnosed or misdiagnosed (LDM) |
| This is the ratio between the reciprocal of the proportion of incorrectly classified individuals and the reciprocal of the Youden index (J). Higher values of LDM (>1) indicate a test more likely to diagnose than misdiagnose. |
TP, true positive; TN, true negative; FP, false positive; FN, false negative.
RESULTS
Power analysis
The results of a priori power analysis indicated that, at a nominal alpha level of 0.05, statistical power set to 0.80, minimum expected AUC of 0.70, and an allocation ratio equal to 1, the required total sample size was 48, i.e., 24 patients with MCI-AD and 24 NCs.72
Sample characteristics
Forty-eight patients with MCI-AD (23 females, 36 from northern Italy, M age = 71.25±4.99 years, M education = 11.96±4.63 years) and 47 NCs (24 females, 26 from northern Italy, M age = 71.08±4.59 years, M education = 11.43±4.72 years) were included in this study. All patients were classified as having a high biomarker likelihood of MCI-AD diagnosis according to NIA-AA 2011 criteria. Furthermore, they fell within the AD continuum according to the AT(N) framework (see Table 2). The two groups were matched for sex (χ2 = 0.273, df = 1, p > 0.05), age (t = –0.837, df = 93, p > 0.05), education (t = –0.555, df = 93, p > 0.05), and geographical background (χ2 =3.236, df = 1, p > 0.05). As expected, NCs outperformed patients with MCI-AD in the MoCA score (NCs: M MoCA = 24.77±3.53; patients: M MoCA = 20.52±3.58; t = 5.816, df = 93, p < 0.001, Cohen’s d = 1.19).
Table 2
Descriptive statistics in patient and control groups
| Sociodemographic and clinical variables | MCI-AD patients | Healthy controls | p | Effect size |
| (n = 48) | (n = 47) | |||
| Demographics and global cognitive status | ||||
| Sex (f/m) | 23/25 | 24/23 | nsa | |
| Location (northern Italy/southern Italy) | 36/12 | 26/21 | nsa | |
| Age, years, M±SD | 71.25±4.99 | 71.08±4.59 | nsb | |
| Education, years, M±SD | 11.96±4.63 | 11.43±4.72 | nsb | |
| MoCA score, raw, M±SD | 20.52±3.58 | 24.77±3.53 | <0.001b | 1.19c |
| Diagnostic criteria incorporating biomarkers | ||||
| NIA-AA 2011 | ||||
| High likelihood, n (%) | 48 (100.00) | |||
| AT(N) framework | ||||
| A+T+N+, n (%) | 28 (58.33) | |||
| A+T– N+, n (%) | 9 (18.75) | |||
| A+T*N+, n (%) | 11 (22.91) |
MCI-AD, Mild cognitive impairment due to Alzheimer’s disease; MoCA, Montreal Cognitive Assessment; NIA-AA, National Institute on Aging and Alzheimer’s Association; AT(N), ATN classification system (Amyloid, Tau, Neurodegeneration). Among the AT(N) profiles, the asterisk (*) indicates that the biomarker group was untested. aChi-squared test. bStudent’s t-test. cCohen’s d.
ROC curve analysis
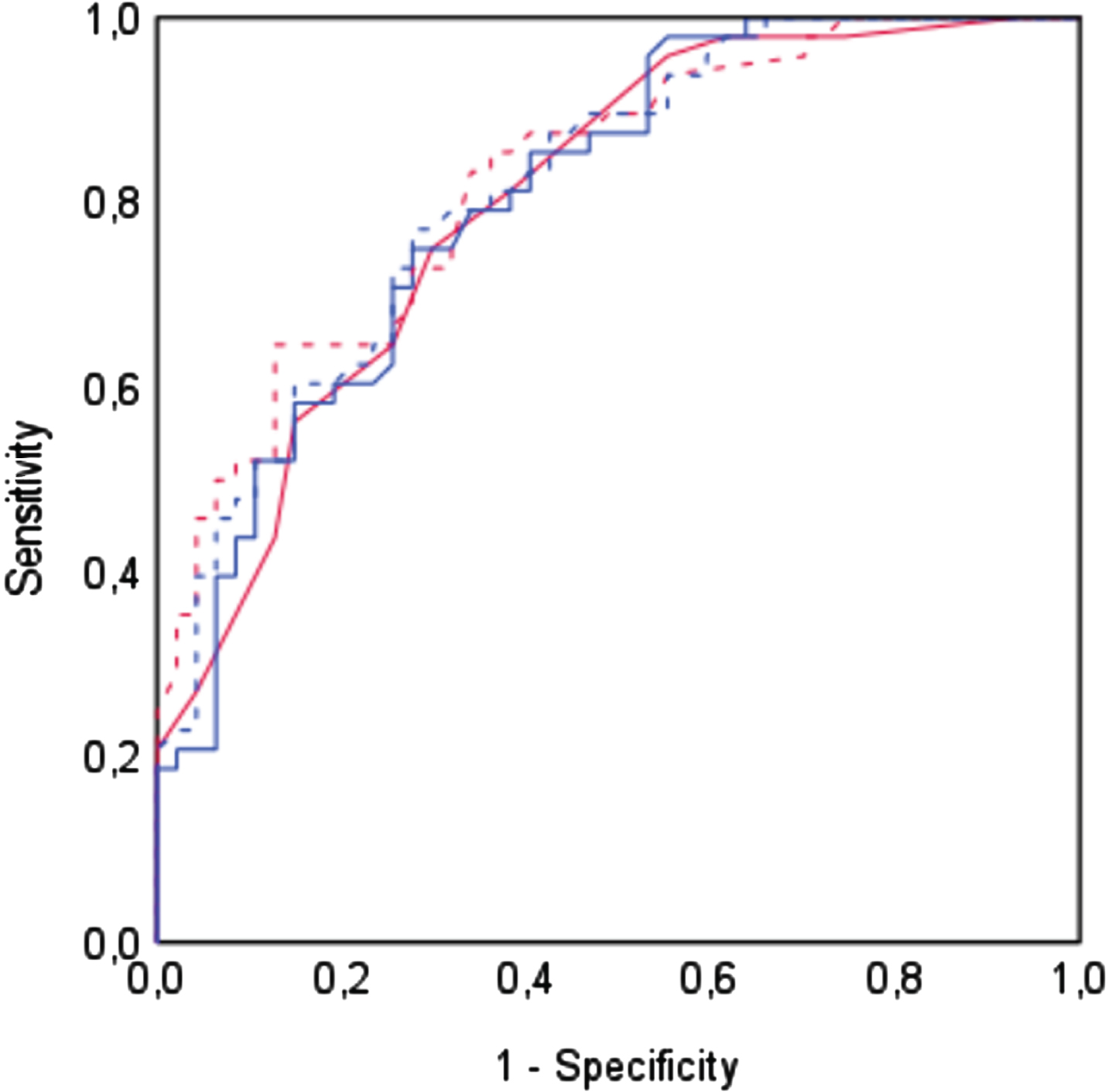
Regardless of the adjustment method, the MoCA demonstrated an adequate discriminative capability (MoCA-Nasreddine: AUC = 0.802, SE = 0.04, p < 0.001; MoCA-Conti: AUC = 0.807, SE = 0.04, p < 0.001; MoCA-Santangelo: AUC = 0.826, SE = 0.04, p < 0.001; MoCA-Aiello: AUC = 0.817, SE = 0.04, p < 0.001). No significant differences were detected among the four AUCs, as indicated by the overall equality test (DeLong test: p = 0.60). The four ROC curves are depicted in Fig. 1.
Fig. 1
Receiver Operating Characteristic (ROC) curves for each adjustment method. ROC curves depicting the trade-off between sensitivity and false positive rate (1 – specificity) across different adjustment methods. Each curve visually represents the MoCA’s ability to distinguish between patients with MCI-AD and healthy controls. The curves are represented as follows: solid red line for Nasreddine’s adjustment, solid blue line for Conti’s adjustment, dashed red line for Santangelo’s adjustment, and dashed blue line for Aiello’s Adjustment.
Cutoff analysis
The results of cutoff analysis are summarized in Table 3. According to J, CZ, and ER metrics, the three optimal cutoffs for the Italian normative adjustments offered the best balance between Se and Sp. However, Santangelo’s and Aiello’s cutoffs exhibited the highest J and CZ values (MoCA-Contioptimal = 22.53, Se = 0.75, Sp = 0.72, J = 0.47, CZ = 0.54, ER = 0.37; MoCA-Santangelooptimal = 22.85, Se = 0.65, Sp = 0.87, J = 0.52, CZ = 0.56, ER = 0.38; MoCA-Aiellooptimal = 23.35, Se = 0.77, Sp = 0.72, J = 0.49, CZ = 56, ER = 0.36). The optimal cutoff for Santangelo’s adjustment– – which corresponded to the one previously identified by Ilardi et al. in patients with MCI and early dementia of mixed etiology– – demonstrated higher specificity than that of Aiello, along with higher PPV and lower FPR. Conversely, the optimal cutoff for Aiello’s adjustment– – which was higher compared to the one previously proposed by Ilardi et al. (MoCA-AielloIlardi = 22.29)– – was more sensitive, thus showing lower FNR than Santangelo’s (MoCA-Santangelooptimal, PPV = 0.84, NPV = 0.71, FPR = 0.13, FNR = 0.35; MoCA-Aiellooptimal, PPV = 0.74, NPV = 0.76, FPR = 0.28, FNR = 0.23). Given a prior probability of disease at 50%, Santangelo’s adjustment outperformed Aiello’s in increasing the post-test probability of disease in individuals testing positive (MoCA-Santangelooptimal =∼30%, MoCA-Aiellooptimal =∼20%). Nevertheless, in terms of LR–, the two cutoffs performed quite similarly (MoCA-Santangelooptimal, LR+ = 5.06, post-test probability of MCI-AD = +84%, LR– = 0.41, post-test probability of MCI-AD = –70%; MoCA-Aiellooptimal, LR+ = 2.79, post-test probability of MCI-AD = +74%, LR– = 0.32, post-test probability of MCI-AD = –75%). For both adjustment methods, post-test probability is depicted as Fagan’s nomograms in Fig. 2.
Fig. 2
Fagan’s nomograms representing post-test probability for Santangelo’s (left) and Aiello’s (right) optimal cutoffs. The Fagan’s nomogram is used to graphically illustrate how the likelihood ratio (LR) mediates the relationship between pre- and post-test probability of disease. The pre-test probability is represented on the left vertical line, the LR on the middle vertical line, and the post-test probability on the right vertical line. The resulting predicted increase or decrease in post-test probability is calculated by tracing a line connecting the values of pre-test probability and LR (LR+, blue line; LR–, red line) until it reaches the right vertical line. On the left, the nomogram representing the performance of the optimal cutoff according to Santangelo’s adjustment (LR+ = 5.06, CI 95% [2.33–11.00], post-test probability = 84%, CI 95% [70–92]; LR– = 0.41, CI 95% [0.27–0.60], post-test probability = 30%, CI 95% [22–38]); on the right that of the optimal cutoff according to Aiello’s adjustment (LR+ = 2.79, CI 95% [1.71–4.54], post-test probability = 74%, CI 95% [64–82]; LR– =0.32, CI 95% [0.18–0.55], post-test probability = 25%, CI 95% [16–36]). These graphs were generated using Diagnostic Test Calculator (version 2010042101) accessed at http://araw.mede.uic.edu/cgi-bin/testcalc.pl (07 Jan 2024). This calculator is a free software available under the Clarified Artistic License.
![Fagan’s nomograms representing post-test probability for Santangelo’s (left) and Aiello’s (right) optimal cutoffs. The Fagan’s nomogram is used to graphically illustrate how the likelihood ratio (LR) mediates the relationship between pre- and post-test probability of disease. The pre-test probability is represented on the left vertical line, the LR on the middle vertical line, and the post-test probability on the right vertical line. The resulting predicted increase or decrease in post-test probability is calculated by tracing a line connecting the values of pre-test probability and LR (LR+, blue line; LR–, red line) until it reaches the right vertical line. On the left, the nomogram representing the performance of the optimal cutoff according to Santangelo’s adjustment (LR+ = 5.06, CI 95% [2.33–11.00], post-test probability = 84%, CI 95% [70–92]; LR– = 0.41, CI 95% [0.27–0.60], post-test probability = 30%, CI 95% [22–38]); on the right that of the optimal cutoff according to Aiello’s adjustment (LR+ = 2.79, CI 95% [1.71–4.54], post-test probability = 74%, CI 95% [64–82]; LR– =0.32, CI 95% [0.18–0.55], post-test probability = 25%, CI 95% [16–36]). These graphs were generated using Diagnostic Test Calculator (version 2010042101) accessed at http://araw.mede.uic.edu/cgi-bin/testcalc.pl (07 Jan 2024). This calculator is a free software available under the Clarified Artistic License.](https://content.iospress.com:443/media/jad/2024/101-1/jad-101-1-jad240339/jad-101-jad240339-g002.jpg)
Table 3
Results of cutoff analyses for diagnosis of MCI due to AD
| Adjustment methods | Cutoffs | MCI-AD patients (n = 48) | Healthy controls (n = 47) | Additional metrics for diagnostic accuracy | |||||||||||
| T+/T– | Sensitivity (95% CI) | T+/T– | Specificity (95% CI) | PPV | NPV | FPR | FNR | ACC | LR+ | LR– | J | CZ | ER | ||
| Nasreddine et al.15 | <26a | 46/2 | 0.96 (0.89–0.99) | 26/21 | 0.45 (0.35–0.55) | 0.64 | 0.91 | 0.55 | 0.04 | 0.70 | 1.73 | 0.09 | 0.41 | 0.43 | 0.55 |
| ≤23.50c,d | 36/12 | 0.75 (0.65–0.83) | 14/33 | 0.70 (0.60–0.79) | 0.72 | 0.73 | 0.30 | 0.25 | 0.73 | 2.52 | 0.36 | 0.45 | 0.53 | 0.39 | |
| Conti et al.64 | ≤17.36b | 9/39 | 0.19 (0.12–0.28) | 1/46 | 0.98 (0.92–1.00) | 0.90 | 0.54 | 0.02 | 0.81 | 0.58 | 8.81 | 0.83 | 0.17 | 0.18 | 0.81 |
| ≤20.97c | 28/20 | 0.58 (0.49–0.68) | 7/40 | 0.85 (0.76–0.91) | 0.80 | 0.67 | 0.15 | 0.42 | 0.71 | 3.92 | 0.49 | 0.43 | 0.50 | 0.44 | |
| ≤22.53d | 36/12 | 0.75 (0.65–0.83) | 13/34 | 0.72 (0.62–0.81) | 0.73 | 0.74 | 0.28 | 0.25 | 0.74 | 2.71 | 0.35 | 0.47 | 0.54 | 0.37 | |
| Santangelo et al.42 | ≤15.50b | 3/45 | 0.06 (0.03–0.13) | 0/47 | 1.00 (0.95–1.00) | 1.00 | 0.51 | 0.00 | 0.94 | 0.52 | ■ | 0.94 | 0.06 | 0.06 | 0.94 |
| ≤22.85c,d | 31/17 | 0.65 (0.54–0.74) | 6/41 | 0.87 (0.78–0.93) | 0.84 | 0.71 | 0.13 | 0.35 | 0.76 | 5.06 | 0.41 | 0.52 | 0.56 | 0.38 | |
| Aiello et al.63 | ≤18.58b | 11/37 | 0.23 (0.15–0.33) | 2/45 | 0.96 (0.89–0.99) | 0.85 | 0.55 | 0.04 | 0.77 | 0.59 | 5.38 | 0.80 | 0.19 | 0.22 | 0.77 |
| ≤22.29c | 29/19 | 0.60 (0.50–0.70) | 7/40 | 0.85 (0.76–0.91) | 0.81 | 0.68 | 0.15 | 0.39 | 0.73 | 4.06 | 0.46 | 0.45 | 0.51 | 0.42 | |
| ≤23.35d | 37/11 | 0.77 (0.67–0.85) | 13/34 | 0.72 (0.62–0.81) | 0.74 | 0.76 | 0.28 | 0.23 | 0.75 | 2.79 | 0.32 | 0.49 | 0.56 | 0.36 | |
T+, positive test results; T–, negative test result; MCI-AD, mild cognitive impairment due to Alzheimer’s disease; PPV, positive predictive value; NPV, negative predictive value; FPR, false positive rate; FNR, false negative rate; ACC, overall accuracy; LR+, positive likelihood ratio; LR–, negative likelihood ratio; J, Youden index; CZ, concordance probability method; ER, Closest to (0, 1) criteria. aConventional MoCA’s cutoff. bNominal normative cutoffs. cCutoffs from Ilardi et al. (2023). dOptimal cutoffs for MCI due to AD. ■ Not computable.
Although originally set on a more heterogeneous clinical population, Ilardi’s cutoff for Aiello’s adjustment maintained good diagnostic performance in MCI-AD. In comparison to the optimal cutoff for MCI-AD, Ilardi’s cutoff for Aiello’s adjustment demonstrated increased Sp, higher PPV, lower FPR, and higher LR+, while sustaining comparable ACC (MoCA-AielloIlardi = 22.29, Sp = 0.85, PPV = 0.81, FPR = 0.15, LR+ = 4.06, post-test probability of MCI-AD = +81%, ACC = 0.73). Congruently with Ilardi et al., the optimal cutoff for Nasreddine’s adjustment was notably lower than the conventional cut-point (MoCA-Nasreddineoptimal = 23.50). Overall, Nasreddine’s optimal cutoff showed acceptable clinimetric properties (Se = 0.75, Sp = 0.70, PPV = 0.72, NPV = 0.73, FPR = 0.30, FNR = 0.25, ACC = 0.73, LR– =0.36, post-test probability of MCI-AD=–73%). The Italian nominal normative cutoffs and the original Nasreddine’s cutoff of 26 were excessively skewed in Se and Sp.
Table 4 shows the NNSU and LDM values for each examined cutoff. These newly-developed metrics express the utility of MoCA for screening and the rate of diagnosis versus misdiagnosis of MCI-AD. In line with the canonical cutoff analysis results, the presented optimal cutoffs demonstrated acceptable performance in both screening and diagnosis (NNSU values < 1.02, LDM values > 1), with Santangelo’s and Aiello’s adjustments showing a certain superiority over Conti’s. However, a dissociation persisted between Santangelo’s and Aiello’s adjustments. While they behaved similarly when measuring MoCA’s screening utility, the former surpassed the latter in terms of diagnoses over misdiagnoses (MoCA-Santangelooptimal, NNSU = 0.86, LDM = 2.17; MoCA-Aiellooptimal, NNSU = 0.89, LDM = 1.96). Ilardi’s cutoffs for Conti’s and Aiello’s adjustments performed comparably to Nasreddine’s cutoffs. The Italian nominal normative cutoffs were found to be unsatisfactory for both screening and diagnostic aims.
Table 4
‘Number needed for screening utility’ and ‘likelihood to be diagnosed or misdiagnosed’ for each cutoff
| Adjustment methods | Cutoffs | NNSU | LDM |
| Nasreddine et al.15 | <26a | 0.98* | 1.37** |
| ≤23.50c,d | 0.95* | 1.67** | |
| Conti et al.64 | ≤17.36b | 1.43 | 0.40 |
| ≤20.97c | 0.97* | 1.48** | |
| ≤22.53d | 0.95* | 1.81** | |
| Santangelo et al.42 | ≤15.50b | 1.75 | 0.12 |
| ≤22.85c,d | 0.86* | 2.17** | |
| Aiello et al.63 | ≤18.58b | 1.38 | 0.46 |
| ≤22.29c | 0.94* | 1.67** | |
| ≤23.35d | 0.89* | 1.96** |
NNSU, Number Needed for Screening Utility; LDM, Likelihood to be Diagnosed or Misdiagnosed. *Screening utility for ruling in and ruling out diagnosis. **Diagnosis prevails over misdiagnosis. aConventional MoCA’s cutoff. bNominal normative cutoffs. cCutoffs from Ilardi et al. (2023). dOptimal cutoffs for MCI due to AD.
DISCUSSION
Clinical neuropsychology is a discipline marked by considerable ‘volatility’. This likely stems from the lack of universally agreed-upon standards in diagnostic clinical practices. Neuropsychological examinations may be strongly affected by the clinician’s subjectivity, especially when their ‘style’ or professional experience collides with a standardized approach. Neuropsychologists may introduce biases in the selection of appropriate psychometric tools because of time constraints and overworking. In addition, differences in demographic profile, sociocultural and financial backgrounds, educational quality, language/communication style, cognitive reserve, emotional and personality factors may significantly moderate patients’ performance at cognitive testing.73,74 However, even considering these limitations, the utility of clinical neuropsychology should not be questioned, and this is certainly true in the framework of AD.
In 2018, the AT(N) paradigm attempted to exclude clinical expertise from AD diagnosis.9 Nevertheless, it has been demonstrated that a mere biological definition of AD has poor predictive accuracy. Likely, AD does not align with an at-risk model, such as that of prostate cancer, where screening and treating an asymptomatic patient can ensure a better prognosis.10 Here, neuropsychology comes into play. It can outperform neuroradiology in predictive power for MCI and AD diagnoses.75 Also, it covers methods and techniques to quantify the therapeutic outcomes in terms of cognitive and functional performance. The contribution of neuropsychology is highly relevant in the context of MCI due to AD (MCI-AD), especially in view of future disease-modifying treatments.
MoCA is a brief pencil-and-paper neuropsychological battery originally devised to identify patients with MCI and early-stage dementia.15 Over time, its application has extended to exploring cognitive deficits and monitoring rehabilitation/treatment outcomes across different clinical populations, ranging from Parkinson’s disease to chronic obstructive pulmonary disease.16 MoCA has been translated into over 50 languages, and normative data are available for many countries.44,46 Regrettably, a common (mal)practice in the interpretation of neuropsychological test scores involves primarily relying on normative data, without delving into whether the designated normative ‘pathological’ ranges truly hold diagnostic significance. In fact, the conventional psychometric approaches to extract normative cutoffs render neuropsychological tools highly specific but inadequately sensitive for MCI. This applies to both short cognitive batteries like MoCA and more elaborate, domain-specific tests. Paradoxically, it may be hypothesized that irrespective of the length or comprehensiveness of cognitive assessment, neuropsychological clinical practice leans heavily towards screening rather than diagnosis. This would be appropriate if, for instance, neuropsychological tools were used by general practitioners in their clinics for a preliminary neurocognitive evaluation.76 However, if the assessment is intended for diagnostic framing and orientation within neurological outpatient or secondary care settings, this is to be considered unacceptable.
In this study, we examined the diagnostic properties of MoCA in patients with MCI-AD. Particularly, we aimed at identifying optimal cutoffs, balanced for sensitivity and specificity, when four demographic adjustments were applied: the conventional 1-point correction by Nasreddine et al.15 and correction factors derived from three Italian normative studies.42,63,64 To our best knowledge, only one previous study shared a similar goal,62 wherein a cutoff of 24 was found to be the optimal threshold for differentiating patients with MCI-AD from healthy controls sampled from the Czech population.62 Consistently, our optimal cutoffs ranged from 22.53 to 23.50. The slight discrepancy between the Czech study’s results and ours might be attributed to differences in sampling procedures or geographic extraction of participants.
In accordance with previous research,33,77 we highlighted that the original Nasreddine cutoff of 26 led to an increased false positive rate due to high sensitivity but poor specificity. Instead, the optimal Nasreddine’s cutoff we proposed, at 23.50, is close to that recommended in a recent meta-analysis on the matter,77 and demonstrated adequate clinimetric outcomes.
As concerns normative adjustments, among the optimal cutoffs we identified, those related to Santangelo’s42 and Aiello’s63 demographic adjustments demonstrated the highest diagnostic performance. Aiello’s cutoff of 23.35 was more sensitive while Santangelo’s of 22.85 was more specific. Furthermore, according to the ‘Number Needed for Screening Utility’ (NNSU) and ‘Likelihood to be Diagnosed or Misdiagnosed’ (LDM) metrics, Santangelo’s adjustment, combined with our optimal cutoff, restores robust performance to MoCA when used as a screener and even more so as a diagnostic-oriented tool. Still, it is crucial to emphasize that, based on our estimates of the likelihood ratio, an individual testing positive on MoCA with Santangelo’s adjustment and a cutoff of 22.85 will have, in the presence of a diagnostic suspicion, 84% post-test probability of being diagnosed with MCI-AD.
In a recent clinimetric study by Ilardi et al., MoCA’s discriminatory power was assessed in patients with MCI and early dementia of mixed etiology compared to individuals with normal cognitive functioning. Sensitivity- and specificity-weighted cutoffs were also computed.33 Here, we tested the generalizability of these cutoffs in the MCI-AD population. Interestingly, the optimal cutoffs for Nasreddine’s and Santangelo’s adjustments coincided between the two studies. This evidence suggests a certain degree of MoCA’s clinimetric flexibility along the continuum of dementia, independently of the underlying pathology. In comparison to the earlier study, here all cutoffs suffered from a loss of diagnostic sensitivity (including those related to Nasreddine’s and Santangelo’s methods), likely stemming from the inclusion of patients with mild dementia, who scored ∼1.5 points lower on MoCA than patients with MCI. However, it is worth noting that the diagnostic performance of Santangelo’s cutoff remained largely unchanged.33
In light of the above considerations, we advocate for the preferential adoption of Santangelo’s demographic adjustment alongside an optimal cutoff of 22.85 for a comprehensive evaluation of cognitive functioning in patients with suspected amnestic MCI-AD. However, despite its limitation in controlling the covariance of sociodemographic variables,77 one should ponder the idea of using the rapid Nasreddine’s procedure to correct MoCA scores, and interpreting them with a cutoff of 23.50. This may represent a valuable resource in memory clinics with high attendance in the earlier steps.33
As previously shown,33 we found that cutoffs extracted from normative datasets exhibited very low sensitivity, despite excellent specificity, revealing their limited utility in diagnosis-oriented clinical settings for dementia. This finding is further corroborated by poor LDM values. Given the equally poor NNSU values, normative cutoffs demonstrate limited relevance, even for screening purposes. If clinical decisions must rely on normative data, it would be akin to flipping a coin. To sum up, we confirm the constraints of solely depending on normative data when correcting and interpreting neuropsychological test scores for clinical purposes. Their usefulness in gauging the degree of possible cognitive impairments along the dementia continuum is a different matter, though a lot relies on how reliable the psychometric extraction technique is.
The present study has some limits. Even considering the favorable a priori power analysis results, the sample size was relatively small, potentially undermining the external validity of the study. Additionally, the demographic attributes of the clinical and control samples (e.g., income, employment status, occupation, parental status) were not sufficiently specified. Lastly, although this paper exclusively centers on the MoCA, the latter serves merely as a pretext. The theoretical and methodological aspects expounded upon herein can be extended to all neuropsychological tests grounded in a quantitative framework. Clearly, tests relying on qualitative assessment, such as cancellation tasks, where a single error is deemed symptomatic, are exempt from our considerations.
Conclusions
Italy is leading the debate on the need for extra efforts to define disease-specific cutoffs for routinely used tools in clinical neuropsychology practice. These endeavors should prioritize the accurate classification of patients with a variety of clinical conditions. One major challenge is the significant fluctuation of cutoffs across different diseases (e.g., MoCA cutoff of 22.82 for patients with stroke or 19.94 for patients with extra-pyramidal disorders).35,36 This highlights the importance of conducting methodologically sound clinimetric research that carefully considers intergroup homogeneity from as many perspectives as possible, including age, education, and number of comorbidities, and that ideally involves different clinical cohorts in addition to healthy controls.
In this study, we started by identifying optimal MoCA cutoffs for the early detection of patients with MCI-AD. The imperative of enhancing the diagnostic properties of neuropsychological tests should remain a focus in future research, as neuroimaging techniques are unlikely to ever completely replace a comprehensive and sensitive neuropsychological assessment performed by an expert clinician.
AUTHOR CONTRIBUTIONS
Ciro Rosario Ilardi (Conceptualization; Formal analysis; Methodology; Validation; Visualization; Writing – original draft); Alina Menichelli (Conceptualization; Data curation; Investigation; Resources; Writing – review & editing); Marco Michelutti (Data curation; Investigation; Resources); Tatiana Cattaruzza (Data curation; Investigation; Resources; Writing – review & editing); Giovanni Federico (Conceptualization; Methodology; Writing – review & editing); Marco Salvatore (Funding acquisition; Project administration); Alessandro Iavarone (Resources; Writing – review & editing); Paolo Manganotti (Resources; Supervision).
ACKNOWLEDGMENTS
The authors have no acknowledgments to report.
FUNDING
This work was funded by the Italian Ministry of Health by “Progetti di Ricerca Corrente”.
CONFLICT OF INTEREST
The authors have no conflict of interest to report.
DATA AVAILABILITY
The data supporting the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
REFERENCES
1. | Alzheimer’s Association. 2023 Alzheimer’s disease facts and figures. Alzheimers Dement (2023) ; 19: : 1598–1695. |
2. | World Health Organization. Global action plan on the public health response to dementia 2017–2015, https://apps.who.int/iris/bitstream/handle/10665/259615/?sequence=1 (2017, accessed 28 January 2024). |
3. | World Health Organization. Towards a dementia plan: A WHO guide, https://apps.who.int/iris/bitstream/handle/10665/272642/9789241514132-eng.pdf (2018, accessed 28 January 2024). |
4. | Cummings J , Lee G , Zhong K , et al. Alzheimer’s disease drug development pipeline: 2021. Alzheimers Dement (N Y) (2021) ; 7: : e12179. |
5. | Petersen RC , Lopez O , Armstrong MJ , et al. Practice guideline update summary: Mild cognitive impairment: Report of the Guideline Development, Dissemination, and Implementation Subcommittee of the American Academy of Neurology. Neurology (2018) ; 90: : 126–135. |
6. | Petersen RC , Doody R , Kurz A , et al. Current concepts in mild cognitive impairment. Arch Neurol (2001) ; 58: : 1985–1992. |
7. | Canevelli M , Grande G , Lacorte E , et al. Spontaneous reversion of mild cognitive impairment to normal cognition: A systematic review of literature and meta-analysis. J Am Med Dir Assoc (2016) ; 17: : 943–948. |
8. | Albert MS , DeKosky ST , Dickson D , et al. The diagnosis of mild cognitive impairment due to Alzheimer’s disease: Recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimers Dement (2011) ; 7: : 270–279. |
9. | Jack CR , Bennett DA , Blennow K , et al. NIA-AA Research Framework: Toward a biological definition of Alzheimer’s disease. Alzheimers Dement (2018) ; 14: : 535–562. |
10. | Dubois B , Villain N , Frisoni GB , et al. Clinical diagnosis of Alzheimer’s disease: Recommendations of the International Working Group. Lancet Neurol (2021) ; 20: : 484–496. |
11. | Onida A , Di Vita A , Bianchini F , et al. Neuropsychology as a profession in Italy. Appl Neuropsychol Adult (2019) ; 26: : 543–557. |
12. | Hokkanen L , Lettner S , Barbosa F , et al. Training models and status of clinical neuropsychologists in Europe: Results of a survey on 30 countries. Clin Neuropsychol (2019) ; 33: : 32–56. |
13. | Ng TP , Feng L , Lim WS , et al. Montreal Cognitive Assessment for screening mild cognitive impairment: Variations in test performance and scores by education in Singapore. Dement Geriatr Cogn Disord (2015) ; 39: : 176–185. |
14. | Folstein MF , Folstein SE , McHugh PR . “Mini-mental state”: A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res (1975) ; 12: : 189–198. |
15. | Nasreddine ZS , Phillips NA , Bédirian V , et al. The Montreal Cognitive Assessment, MoCA: A brief screening tool for mild cognitive impairment. J Am Geriatr Soc (2005) ; 53: : 695–699. |
16. | Julayanont P , Brousseau M , Chertkow H , et al. Montreal Cognitive Assessment Memory Index Score (MoCA-MIS) as a predictor of conversion from mild cognitive impairment to Alzheimer’s disease. J Am Geriatr Soc (2014) ; 62: : 679–684. |
17. | Krishnan K , Rossetti H , Hynan LS , et al. Changes in Montreal Cognitive Assessment scores over time. Assessment (2017) ; 24: : 772–777. |
18. | Haynes RB , You JJ . The architecture of diagnostic research. In: Knottnerus JA, Buntinx F (eds) The Evidence Base of Clinical Diagnosis. Theory and Methods of Diagnostic Research. 2nd ed. Oxford: BMJ Books, (2009) , pp. 20–41. |
19. | Sackett DL and Haynes RB . The architecture of diagnostic research. BMJ (2002) ; 324: : 539–541. |
20. | Dubois B , Feldman HH , Jacova C , et al. Advancing research diagnostic criteria for Alzheimer’s disease: The IWG-2 criteria. Lancet Neurol (2014) ; 13: : 614–629. |
21. | Ricci M , Graef S , Blundo C , et al. Using the Rey Auditory Verbal Learning Test (RAVLT) to differentiate Alzheimer’s dementia and behavioural variant fronto-temporal dementia. Clin Neuropsychol (2012) ; 26: : 926–941. |
22. | Mitrushina M , Boone KB , Razani J , et al. Handbook of Normative Data for Neuropsychological Assessment. Oxford University Press, 2005. |
23. | Capitani E . Normative data and neuropsychological assessment. Common problems in clinical practice and research. Neuropsychol Rehabil (1997) ; 7: : 295–310. |
24. | Capitani E , Laiacona M . Aging and psychometric diagnosis of intellectual impairment: Some considerations on test scores and their use. Dev Neuropsychol (1988) ; 4: : 325–330. |
25. | Spinnler H , Tognoni G . Standardizzazione e Taratura Italiana di Test Neuropsicologici. Milano: Masson Italia, 1987. |
26. | Capitani E , Laiacona M . Outer and inner tolerance limits: Their usefulness for the construction of norms and the standardization of neuropsychological tests. Clin Neuropsychol (2017) ; 31: : 1219–1230. |
27. | Aiello EN , Depaoli EG . Norms and standardizations in neuropsychology via equivalent scores: Software solutions and practical guides. Neurol Sci (2022) ; 43: : 961–966. |
28. | Facchin A , Rizzi E , Vezzoli M . A rank subdivision of equivalent score for enhancing neuropsychological test norms. Neurol Sci (2022) ; 43: : 5243–5249. |
29. | Bianchi A , Dai Prà M . Twenty years after Spinnler and Tognoni: New instruments in the Italian neuropsychologist’s toolbox. Neurol Sci (2008) ; 29: : 209–217. |
30. | Ilardi CR , Chieffi S , Scuotto C , et al. The Frontal Assessment Battery 20 years later: Normative data for a shortened version (FAB15). Neurol Sci (2022) ; 43: : 1709–1719. |
31. | Ilardi CR , La Marra M , Amato R , et al. The “Little Circles Test” (LCT): A dusted-off tool for assessing fine visuomotor function. Aging Clin Exp Res (2023) ; 35: : 2807–2820. |
32. | Rizzi E , Vezzoli M , Pegoraro S , et al. Teleneuropsychology: Normative data for the assessment of memory in online settings. Neurol Sci (2023) ; 44: : 529–538. |
33. | Ilardi CR , Menichelli A , Michelutti M , et al. Optimal MoCA cutoffs for detecting biologically-defined patients with MCI and early dementia. Neurol Sci (2023) ; 44: : 159–170. |
34. | Trevethan R . Sensitivity, specificity, and predictive values: Foundations, pliabilities, and pitfalls in research and practice. Front Public Health (2017) ; 5: : 307. |
35. | Salvadori E , Cova I , Mele F , et al. Prediction of post-stroke cognitive impairment by Montreal Cognitive Assessment (MoCA) performances in acute stroke: Comparison of three normative datasets. Aging Clin Exp Res (2022) ; 34: : 1855–1863. |
36. | D’Iorio A , Aiello EN , Trinchillo A , et al. Clinimetrics of the Italian version of the Montreal Cognitive Assessment (MoCA) in adult-onset idiopathic focal dystonia. J Neural Transm (2023) ; 130: : 1571–1578. |
37. | Aiello EN , Solca F , Torre S , et al. Validity, diagnostics and feasibility of the Italian version of the Montreal Cognitive Assessment (MoCA) in Huntington’s disease. Neurol Sci (2024) ; 45: : 1079–1086. |
38. | Ilardi CR , di Maio G , Villano I , et al. The assessment of executive functions to test the integrity of the nigrostriatal network: A pilot study. Front Psychol (2023) ; 14: : 1121251. |
39. | Solca F , Aiello EN , Migliore S , et al. Diagnostic properties of the Frontal Assessment Battery (FAB) in Huntington’s disease. Front Psychol (2022) ; 13: : 1031871. |
40. | Gasparini M , Scandola M , Amato S , et al. Normative data beyond the total scores: A process score analysis of the Rey’s 15 word test in healthy aging and Alzheimer’s Disease. Neurol Sci (2024) ; 45: : 2605–2613. |
41. | Kopecek M , Stepankova H , Lukavsky J , et al. Montreal Cognitive Assessment (MoCA): Normative data for old and very old Czech adults. Appl Neuropsychol Adult (2017) ; 24: : 23–29. |
42. | Santangelo G , Siciliano M , Pedone R , et al. Normative data for the Montreal Cognitive Assessment in an Italian population sample. Neurol Sci (2015) ; 36: : 585–591. |
43. | Narazaki K , Nofuji Y , Honda T , et al. Normative data for the Montreal Cognitive Assessment in a Japanese community-dwelling older population. Neuroepidemiology (2012) ; 40: : 23–29. |
44. | Engedal K , Gjøra L , Benth JŠ , et al. The Montreal Cognitive Assessment: Normative data from a large, population-based sample of cognitive healthy older adults in Norway— The HUNT Study. J Alzheimers Dis (2022) ; 86: : 589–599. |
45. | Gonçalves J , Gerardo B , Nogueira J , et al. Montreal Cognitive Assessment (MoCA): An update normative study for the Portuguese population. Appl Neuropsychol Adult (2023) ; doi: 10.1080/23279095.2023.2252949. |
46. | Classon E , van den Hurk W , Lyth J , et al. Montreal Cognitive Assessment: Normative data for cognitively healthy Swedish 80-to 94-year-olds. J Alzheimers Dis (2022) ; 87: : 1335–1344. |
47. | Bello-Lepe S , Alonso-Sánchez MF , Ortega A , et al. Montreal cognitive assessment as screening measure for mild and major neurocognitive disorder in a Chilean population. Dement Geriatr Cogn Disord Extra (2021) ; 10: : 105–114. |
48. | Dong Y , Lee WY , Basri NA , et al. The Montreal Cognitive Assessment is superior to the Mini– Mental State Examination in detecting patients at higher risk of dementia. Int Psychogeriatr (2012) ; 24: : 1749–1755. |
49. | Lu J , Li D , Li F , et al. Montreal Cognitive Assessment in Detecting cognitive impairment in Chinese elderly individuals: A population-based study. J Geriatr Psychiatry Neurol (2011) ; 24: : 184–190. |
50. | Ng A , Chew I , Narasimhalu K , et al. Effectiveness of Montreal Cognitive Assessment for the diagnosis of mild cognitive impairment and mild Alzheimer’s disease in Singapore. Singap Med J (2013) ; 54: : 616–619. |
51. | Pinto TC , Machado L , Costa MLG , et al. Accuracy and psychometric properties of the Brazilian version of the Montreal cognitive assessment as a brief screening tool for mild cognitive impairment and Alzheimer’s disease in the initial stages in the elderly. Dement Geriatr Cogn Disord (2019) ; 47: : 366–374. |
52. | Poptsi E , Moraitou D , Eleftheriou M , et al. Normative data for the Montreal Cognitive Assessment in Greek older adults with subjective cognitive decline, mild cognitive impairment and dementia. J Geriatr Psychiatry Neurol (2019) ; 32: : 265–274. |
53. | Pugh EA , Kemp EC , van Dyck CH , et al. Effects of normative adjustments to the Montreal Cognitive Assessment. Am J Geriatr Psychiatry (2018) ; 26: : 1258–1267. |
54. | Tan J , Li N , Gao J , et al. Optimal cutoff scores for dementia and mild cognitive impairment of the Montreal Cognitive Assessment among elderly and oldest-old Chinese population. J Alzheimers Dis (2015) ; 43: : 1403–1412. |
55. | Tsai C-F , Lee W-J , Wang S-J , et al. Psychometrics of the Montreal Cognitive Assessment (MoCA) and its subscales: Validation of the Taiwanese version of the MoCA and an item response theory analysis. Int Psychogeriatr (2012) ; 24: : 651–658. |
56. | Tsai J-C , Chen C-W , Chu H , et al. Comparing the sensitivity, specificity, and predictive values of the Montreal Cognitive Assessment and Mini-Mental State Examination when screening people for mild cognitive impairment and dementia in Chinese population. Arch Psychiatr Nurs (2016) ; 30: : 486–491. |
57. | Zhang S , Qiu Q , Qian S , et al. Determining appropriate screening tools and cutoffs for cognitive impairment in the Chinese elderly. Front Psychiatry (2021) ; 12: : 773281. |
58. | American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 4th Edition. 2006. |
59. | American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th Edition 2013. |
60. | Petersen RC . Mild cognitive impairment as a diagnostic entity. J Intern Med (2004) ; 256: : 183–194. |
61. | Petersen RC , Smith GE , Waring SC , et al. Mild cognitive impairment: Clinical characterization and outcome. Arch Neurol (1999) ; 56: : 303–308. |
62. | Bartos A and Fayette D . Validation of the Czech Montreal cognitive assessment for mild cognitive impairment due to Alzheimer disease and Czech norms in 1,552 elderly persons. Dement Geriatr Cogn Disord (2019) ; 46: : 335–345. |
63. | Aiello EN , Gramegna C , Esposito A , et al. The Montreal Cognitive Assessment (MoCA): Updated norms and psychometric insights into adaptive testing from healthy individuals in Northern Italy. Aging Clin Exp Res (2022) ; 34: : 375–382. |
64. | Conti S , Bonazzi S , Laiacona M , et al. Montreal Cognitive Assessment (MoCA)-Italian version: Regression based norms and equivalent scores. Neurol Sci (2015) ; 36: : 209–214. |
65. | Fazekas F , Chawluk JB , Alavi A , et al. MR signal abnormalities at 1.5 T in Alzheimer’s dementia and normal aging. AJR Am J Roentgenol (1987) ; 149: : 351–356. |
1. | Boccardi M , Nicolosi V , Festari C , et al. Italian consensus recommendations for a biomarker-based aetiological diagnosis in mild cognitive impairment patients. Eur J Neurol (2020) ; 27: : 475–483. |
67. | Mandrekar JN . Receiver operating characteristic curve in diagnostic test assessment. J Thorac Oncol (2010) ; 5: : 1315–1316. |
68. | Youden WJ . Index for rating diagnostic tests. Cancer (1950) ; 3: : 32–35. |
69. | Liu X . Classification accuracy and cut point selection. Stat Med (2012) ; 31: : 2676–2686. |
70. | Perkins NJ , Schisterman EF . The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve. Am J Epidemiol (2006) ; 163: : 670–675. |
71. | Larner AJ . New unitary metrics for dementia test accuracy studies. Prog Neurol Psychiatry (2019) ; 23: : 21–25. |
72. | Obuchowski NA . ROC analysis. Am J Roentgenol (2005) ; 184: : 364–372. |
73. | Franzen S , European Consortium on Cross-Cultural Neuropsychology (ECCroN) , Watermeyer TJ , et al. Cross-cultural neuropsychological assessment in Europe: Position statement of the European Consortium on Cross-Cultural Neuropsychology (ECCroN). Clin Neuropsychol (2022) ; 36: : 546–557. |
74. | Manly JJ . Critical issues in cultural neuropsychology: Profit from diversity. Neuropsychol Rev (2008) ; 18: : 179–183. |
75. | Kurbalija V , Geler Z , Stankov TV , et al. Analysis of neuropsychological and neuroradiological features for diagnosis of Alzheimer’s disease and mild cognitive impairment. Int J Med Inf (2023) ; 178: : 105195. |
76. | Williams BW , Flanders P , Welindt D , et al. Importance of neuropsychological screening in physicians referred for performance concerns. PLoS One (2018) ; 13: : e0207874. |
77 | Carson N , Leach L , Murphy KJ . A re-examination of Montreal Cognitive Assessment (MoCA) cutoff scores. Int J Geriatr Psychiatry (2018) ; 33: : 379–388. |




