A recommendation model for college majors based on deep learning and clustering algorithms
Abstract
Many colleges in China have adopted the policy of recruiting students by academic subject categories in order to optimize the talent training mode. To solve the problems in major selection after enrollment, this paper has designed an intelligent algorithm model for recommending college majors. Compared with existing methods for assigning college majors, the model uses deep neural networks and clustering algorithms to simulate complex calculations in the human brain. It uses historical learning data from senior students or graduates to predict the future grades of freshmen, judge their adaptability to various college majors, reduce human interference in the college major selection process, recommend the most suitable college major to students.
1.Introduction
At present, many colleges only offer subject categories for selection when recruiting students, without specifying specific college majors. After a year of general education and basic courses, students can determine college majors to continue their studies based on their learning situation. The major selection is generally based on factors such as students’ preferences and academic performance, and students with high scores usually have priority choices. The academic performance is calculated comprehensively based on the quantification of course scores, practical courses, competition awards, and other factors.
Recruiting students by academic subject categories can reduce the risk of students blindly filling out their preferences after the college entrance examination, providing students with a buffer period for their understanding and selection of college majors. However, students enrolled in subject categories still face problems such as low flexibility, unreasonable curriculum, unclear standards, and strong human operability when selecting college major. Especially, students with lower comprehensive scores have lower autonomy in choosing college majors, which to some extent affects the subsequent learning outcomes.
With the advent of intelligent Chatbot ChatGPT (Chat Generic Pre Trained Transformer), Baidu ERNIE Bot and other projects, AI technology has attracted widespread and rapid attention of the public, and gradually applied to all aspects of people’s daily life. Artificial intelligence is relative to human natural intelligence, which refers to the use of artificial methods and technologies to develop intelligent machines or systems to imitate, extend, and expand human intelligence. Deep learning based on neural network algorithms is a method of artificial intelligence that deepens traditional machine learning algorithms. It allows machines to learn from massive data and large-scale knowledge simultaneously, resulting in better results and higher efficiency [1]. The analysis and utilization of educational data have also undergone revolutionary changes with the progress of AI technology, especially machine learning and deep learning technology. Educational data mining (EDM) [2] technology is the application of theories and technologies from multiple disciplines such as education, computer science, psychology, and statistics to solve problems in educational research and teaching practice. In the process of building educational informatization, various types of educational data have been accumulated, among which student performance data is an important component. The educational administration management system simply records and stores the achievement data, and lacks mining, analysis and application of student achievement data. Every year, a certain number of students in colleges fail exams, repeat grades, or even drop out due to major issues. Therefore, constructing an efficient student performance prediction and major recommendation model has important application value and practical significance [3–5].
Predicting the academic performance of college students is one of the key areas of educational data mining research, many scholars have conducted similar research in the field of educational data mining [6]. Roy [7] proposed artificial intelligence (AI)-based models to predict the academic results and recommend study plan accordingly to improve the students’ performance. Khemakhem [8] proposed a novel education level state system to determine the student engagement level in an e-learning environment. Liu [9] used the Multi-Agent System (MAS) idea to propose an Agent-based Modeling Feature Selection (ABMFS) model, the model selects the targeted features and improved performance noticeably across different classifiers, and better prediction results are achieved when the proposed approach was used for student performance prediction. In this paper, we have designed a comprehensive model based on the experience of previous researchers to predict academic performance and recommend majors for college students. The machine learning based model for predicting college students’ academic performance and assigning majors aims to analyze and explore the inherent laws through the massive data resources accumulated in the field of education, and through relevant technologies and methods such as machine learning, data mining, and statistical analysis, in order to solve various potential problems in the teaching process and improve teaching quality and students’ academic level.
2.Model architecture and module design
In order to make the logical structure of the model clearer, we have divided the overall architecture of the model into five modules, including data collection module, data preprocessing module, clustering analysis module, deep learning module, and recommendation module. Among them, the clustering analysis module includes two sub modules: the clustering module and the analysis calculation module.
2.1.Data collection module
The data collection module is responsible for collecting and summarizing source data, and the nature of the source dataset determines which intelligent algorithm is used for prediction. In machine learning and deep learning, the size and quality of data largely determine the prediction results. Even if the algorithm is good, if the data volume is small and unevenly distributed, it will not produce good prediction results. Therefore, the data collection module should collect various relevant data as comprehensively and meticulously as possible. For example, in this system, the data collection module may collect course scores, competition awards, practical learning, and other information of students (including senior students who have already chosen their college majors and freshmen who are preparing to select majors), and saves it as a table of students’ learning data.
One row of the table contains information about a student, and different columns of the table store the student’s various courses, competitions, and practical learning achievements. Each column has a weight, which can be determined based on course credits or competition levels. The structure of the learning data table can be as Table 1:
Table 1
Students’ learning data
| Student ID | Name | Mathematics: weight 4 | Data structure: weight 3 | Physical experiment: weight 2 | ACM competition: weight 10 | …… |
| 2022001 | Zhang | 90 | 85 | Excellent | Second prize | …… |
| 2022002 | Li | 85 | 90 | Good | First prize | …… |
| …… | …… | …… | …… | …… | …… | …… |
2.2.Data preprocessing module
The data preprocessing module completes operations such as denoising, quantifying and weighting the collected data, making the processed data easy to calculate. For example, GPA of each course is obtained by multiplying the exam scores by credits. The experimental course is scored as 100 for excellence, 80 for good, 60 for pass, and 0 for others. For subject competitions, the first prize is scored as 100, the second prize is scored as 80, and then multiplied by a weight. In addition, if some students’ scores are obtained through make-up exams or retakes, we need to remove such data rows. After processing the above learning data in Table 1, it becomes the following form, as Table 2:
Table 2
Processed students’ learning data
| Student ID | Name | Mathematics GPA | Data structure GPA | Physical experiment GPA | ACM competition GPA | …… |
| 2022001 | Zhang | 360 | 255 | 200 | 800 | …… |
| 2022002 | Li | 340 | 270 | 160 | 1000 | …… |
| …… | …… | …… | …… | …… | …… | …… |
2.3.Clustering analysis module
2.3.1.Clustering module
The clustering module uses various clustering algorithms to divide students into several categories based on processed student data, with students in each category having similar learning interests and situations. First, encapsulate student data into vectors, and then input these vectors (the content participating in the calculation only includes the students’ learning data before the major assigning) into the clustering algorithm to divide the students into categories, and the students in each category have similar learning interests and situations. For example, the above two student data are packaged into a vector of [2022001, Zhang, 360, 255, 200, 800, ...] and [2022002, Li, 340, 270, 160, 1000, ...].
In order to classify students more accurately, we have chosen multiple clustering algorithms, including K-means, Mini-Batch K-means, DBSCAN algorithm, BIRCH algorithm [10,11]. They are used to divide students into categories with the same number of majors, and store the category numbers in a table, for example, the following Table 3 divides students into three categories: 01, 02, and 03.
Table 3
An example of clustering result
| Student ID | Name | …… | K-means | Mini-Batch K-means | DBSCAN | BIRCH |
| 2022001 | Liu | …… | 02 | 02 | 01 | 02 |
| 2022002 | Chen | …… | 01 | 02 | 02 | 02 |
| 2022003 | Zhang | …… | 02 | 01 | 03 | 01 |
| 2022004 | Li | …… | 03 | 03 | 03 | 03 |
| 2022005 | Wang | …… | 01 | 02 | 02 | 01 |
| 2022006 | Zhao | …… | 02 | 01 | 03 | 02 |
| …… | …… | …… | …… | …… | …… | …… |
The goal of the K-means clustering algorithm is to specify the number of cluster classes or cluster centers first, and through repeated iteration, make the points in the cluster close enough, and the points between the clusters far enough. Here, students’ scores in various subjects are packed into multi-dimensional points, first randomly selecting K points as the center of classification (initial centroid), and then calculating the distance between each data point and the centroid when the classification of any other data point is determined or changed. Assign the data points to the closest class, recalculate the mean of the points in each class and select a new centroid. Assuming that xi(i =1,2, …, n) is the data point and 𝜇j(j =1,2, …, k) is the initialized centroid, then the objective function can be written as follows:
(1)
The Mini-Batch K-means algorithm is a modified version of the K-means algorithm that updates the cluster centroid using a small batch of samples instead of the entire data set, which can make large data sets update faster and potentially more robust to statistical noise.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm is a density-based spatial clustering algorithm. The algorithm divides regions with sufficient density into clusters and finds arbitrarily shaped clusters in a noisy spatial database, which defines clusters as the largest set of densely connected points. The K-means algorithm can only deal with spherical clusters, because the algorithm is based on the limitation of calculating the average distance, and the DBSCAN algorithm can cluster for specially distributed point sets.
The BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies) algorithm uses clustering features to represent a cluster and a clustering feature tree (CF-tree) to represent the hierarchy of clusters.
These algorithms use different ideas such as segmented clustering method, density-based method and hierarchical clustering method to classify the students’ multidimensional data vectors, which effectively avoids the shortcomings of a single algorithm [12,13].
2.3.2.Analysis calculation module
The analysis and calculation module is used to compare the division effects of the above clustering algorithms, select the most suitable clustering algorithm by counting the excellent rate of graduates of each major in each classification, and take the N categories divided by the clustering algorithm as the N directions of college major selection. For example, it is now necessary to divide the freshmen with a total number of Sn into d majors, and the learning data of graduates with the number of So is currently collected, so the total number of students for clustering is S = Sn + So, where the amount of graduate data So is much greater than the amount of freshman data Sn. First, K-mean clustering algorithm is used to divide S students into d categories, and the total number of students in category i is Si, of which the number of freshmen is Sni and the number of graduates is Soi, that is, Si = Sni + Soi and
Similarly, the overall excellent rate Sg of Mini-Batch K-Means Algorithm, DBSCAN Clustering and BIRCH Clustering are calculated, and the algorithm with the highest Sg is selected for use. All students (including freshmen and graduates) are clustered according to the selected clustering algorithm, and the major of divided categories are determined according to the above algorithm, and the major is recommended to freshmen in that category.
2.4.Deep learning module
The deep learning module predicts the academic performance of students to recommend suitable majors to students. First, training graduates’ learning data from different majors, and the performance prediction model of N majors is established. Inputting learning data of freshmen into N models to predict the learning performance of their professional courses, and the major with the best performance result is selected as the recommended major.
In this system model, the freshmen course includes general basic courses, professional basic courses, practical courses, and the courses after assigning major include professional core courses, professional degree courses, etc., and the learning data of these courses is processed and divided into training sets, verification sets, and test sets. By default, the training set is composed of 80% of the graduates’ learning data, which is used to train the model and find a way to predict the scores of professional courses from the scores of freshmen courses; The validation set consists of 20% of the graduate’s learning data for validating and correcting the parameters of the model; The test set consists of scores from freshmen and is used to predict the scores of professional courses using the trained model. The continuous iterative optimization is used to obtain the final model, so as to predict the scores of their major courses and choose the most suitable major [14,15].
Specifically, a three-layer BP neural network is used here to implement this model: input layer, hidden layer, output layer. Assuming the neurons number of the input layer is m, the neurons number of the output layer is n, and the neurons of the hidden layer is p, then the input vector of the BP neural network is X = (x1, x2, …, xi, …, xm)T, the output vector is O = (o1, o2, …, oj, …, on)T, the expected output vector is D = (d1, d2, …, dj, …, dn)T, the output error is defined as:
(2)
By default, the activation function is the Hyperbolic Tangent Function (Tanh Function), which converts the input value of the training sample into the interval (−1,1), and the input variable can have a large threshold range. In addition to Tanh Function, we will compare the effects of several common activation functions on the predicted results in the experimental section. The formula of the Tanh Function is:
(3)
According to the training of graduates’ learning data in different majors, prediction models of different majors can be obtained. Input the freshmen’s learning data into these models separately for prediction, and the model with the highest prediction score is the recommended major model.
2.5.Recommendation module
The recommendation module is mainly used for comparing the recommendation results of the clustering analysis module and deep learning module. If the results are the same, recommend it to the students. Otherwise, recommend both results to the students. The recommendation module will also collect the learning data of students after they determine their major, and pass the data to the data collection module to update the students’ data set so that the system model can be iteratively optimized.
3.Key algorithms
3.1.Dataset definition
The input data is packaged into two different data sets, namely the clustering datasets and the deep learning datasets. Clustering datasets include: complete dataset (including learning data of freshmen and graduates), graduate dataset (including only learning data of graduates), freshman dataset (including only learning data of freshmen); The deep learning dataset (multiple sets of datasets need to be prepared by different majors) includes: training set (including 80% of graduate learning data), validation set (including 20% of graduate learning data), and test set (including all freshman learning data). Among them, the learning data of graduates includes general basic courses, professional basic courses, professional core courses, professional degree courses, other compulsory credit scores, etc. throughout the college, and the learning data of freshmen only includes score information such as general basic courses and professional basic courses before major selection. For example, a college has 4 majors: Computer Science (CS), Software Engineering (SE), Electronic Design Automation (EDA), Internet of Things (IOT), and the learning data of graduates needs to be divided into 4 groups according to major numbers, and each group contains training sets, verification sets, and test sets. So the training set for Computer Science major includes 80% graduates’ learning data in Computer Science department, the verification set includes 20% graduates’ learning data in Computer Science department, and the test set includes all freshmen’s learning data who are ready to choose a major.
3.2.Cluster calculation algorithm
We use multiple algorithms to cluster the complete dataset in the clustering datasets separately, and the number of clusters is the number of majors to be assigned. For example, if a college has four majors: CS, SE, EDA, and IOT, then the K-means algorithm is first used to cluster the “complete dataset (including the learning data of freshmen and graduates)”, and 4 categories are produced, which are labeled as A, B, C, and D.
The number of graduates in A is calculated to be a_grd, and the number of graduates belonging to the four majors of CS, SE, EDA, and IOT is a_grd_cs, a_grd_se, a_grd_eda, and a_grd_iot, and the number of excellent students in these four majors is a_grd_cs_good, a_grd_se_good, a_grd_eda_good, and a_ grd_iot_good, choose the major with the largest number of excellent students. If the number of excellent students in two majors is the same, we will compare the proportion of the two and choose the one with higher proportion.
For example, the current category A has 110 students, which includes 100 graduates, so a_grd=100, 100 graduates include 30 CS students with 15 excellent (a_grd_cs=30 and a_grd_cs_good=15), 25 SE students with 12 excellent (a_grd_se=25 and a_grd_se_good=12), 24 EDA students with 10 excellent (a_grd_eda=24 and a_grd_eda_good=10), 21 IOT students with 13 excellent (a_grd_iot=21 and a_grd_iot_good=13). Then the number of excellent CS students is the most, and the major of category A is set as CS, and the excellent rate of the current category is
Then three other algorithms were used to cluster the complete dataset, and the overall classification excellence rates were similarly calculated as Sg2, Sg3, and Sg4. The algorithm with the highest Sg value is the one we choose. Since the complete dataset includes information for graduates and freshmen, the recommended major corresponding to the category in which the freshman is located is the first major to be recommended.
3.3.Neural network training algorithm
The neural network training process is as follows:
(1) Set the weights and biases in the neural network to random numbers between −1 and 1. Due to the low efficiency of the random initialization algorithm, we use genetic algorithm to initialize the parameters of the neural network. The weights and biases in the neural network are encoded to generate the initial population, and then the initial population is selected, crossed, and mutated, and the optimal initial values of the weights and biases are iteratively selected. Firstly, all parameters (including the weights from the input layer to the hidden layer, the weights between the hidden layers, the weights from the hidden layer to the output layer, the biases of each hidden layer, the biases of the output layer and others) are encoded in real numbers and generate an initial population, and then the adaptive function is used to allow the initial population to carry out evolutionary operations such as selection, crossover, and mutation, so that the error of the neural network algorithm is minimized. The adaptability function can be set to the reciprocal of the neural network calculation error, as follows:
(4)
The method of selection operations is: calculate the fitness value fi of the individual i of the current population, and then calculate the proportion of fi in the total fitness of all individuals in the population, which is the probability that the individual is selected, that is
The method of crossover operation is to select several individuals from the population and cross their codes to obtain new individuals. For example, the formula for crossing the x and y chromosomes is: xi = xi(1 −𝛼) + 𝛼yi , yi = yi(1 −𝛼) + 𝛼xi, where i is the number of chromosomal crossings and 𝛼 is the probability of crossovers, which is a random number between [0,1].
The method of mutation operation is to select an individual from the population and randomly change one of its bits to become a new individual. For example, for the i-th position variant of chromosome x, the formula is xi = xi + 𝛼 , where 𝛼 is a random variation, and the value range is [xmin − xi, xmax − xi], xmin is the smallest bit of chromosome x, xmax is the largest of chromosome x.
(2) By default, set hidden layer activation function to Tanh Function, set output layer activation function to purelinlinear function. The training target is set to 0.001, learning rate is 0.01, number of iterations is 1000. The input layer of the model includes 20 neurons, corresponding to the input of 10 general basic courses, 8 professional basic courses, 1 practical course and 1 competition score; The output layer includes only one neuron, corresponding to the average score of professional courses; The hidden layer is set to 2 layers, and the number of neurons is determined according to the formula
(3) Normalize the collected graduate data and map it to the range of [0,1], so as to improve the convergence efficiency of the algorithm. The formula for normalization is
(4) Let the input data after normalization be X = (x1, x2, …, xi, …, xm)T, then the input to the neuron j of the first hidden layer is
(5) Let the output of each neuron after r hidden layers is Or, j, which is the input of the output layer. So the input of the neuron j in the output layer is
(6) The output of neuron i of the output layer is
(7) To calculate the error between the desired output D and the actual output O, we use the mean squared error formula as follows:
(5)
(8) Use gradient descent algorithm to correct the weights and biases in the model, the correction value of weight is
(9) Determine whether the output error meets the requirements or whether the number of training iterations reaches the preset value, and if the condition is met, end the training; Otherwise, modify the model parameters according to the values calculated in step (7). After multiple trainings, an ideal neural network model can be obtained, and the model is used to predict the freshmen ’s professional course scores on the test set (freshmen’s learning data).
4.Model testing
This paper uses Python 3.9 to implement the system model, running on a virtual server based on the VMware ESXi 6.7 platform. The physical server is configured with 24 CPUs x Intel Xeon Silver 4310 [email protected] GHz and 256 GB of memory. The configuration of virtual machine used for testing was as follows: Windows Server 2012 64-bit operating system, a virtual Intel Xeon Silver 4310 [email protected] GHz, and 32 GB of memory.
This experiment uses a trained model to predict the students’ average score of core courses after major assigning, and compares it with the actual average score to test the accuracy of the model. We randomly selected 20%, 40%, 60% of 200 graduates’ learning data as test samples, and the rest as training samples, and recorded the MAE predicted by the model after 50 rounds of training. The final test results are shown in Table 4. In addition to the default activation function Tanh, we also tested two other activation functions, LeakyReLU and Sigmoid, to train the model. The error changes in the training process are shown in Fig. 1.
Table 4
Training loss of different test samples
| Epochs | 10 | 20 | 30 | 40 | 50 |
| 20% Test set | 0.317808 | 0.010675 | 0.005963 | 0.006152 | 0.010309 |
| 40% Test set | 1.538737 | 0.025595 | 0.009872 | 0.005259 | 0.005194 |
| 60% Test set | 0.682434 | 0.014444 | 0.003208 | 0.003374 | 0.002932 |
Fig. 1.
Training Loss of three different activation functions.
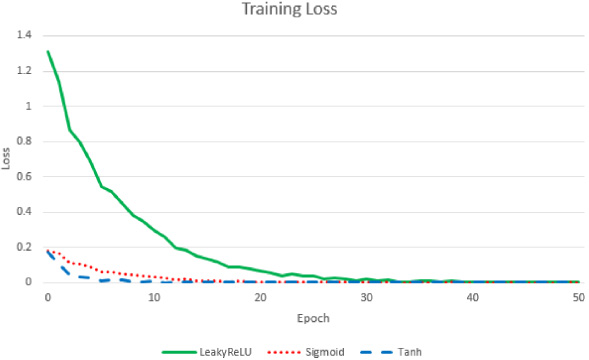
The horizontal coordinates in Fig. 1 represent the training rounds of the model, while the vertical coordinates represent the current error of the prediction model. The experimental results validate the hypothesis that there is a potential connection between freshman course scores and professional scores, and indicate that neural networks have high practicality, stability, and accuracy in predicting scores. The three activation functions used in the model, Tanh, LeakyReLU and Sigmoid, can train stable prediction results after different rounds.
In addition, the experimental results showed that as the number of training samples and testing samples changed, the error showed a floating nature, and the training error did not significantly decrease with the increase of training samples. This phenomenon indicates that the BP algorithm has the advantage of not requiring too many training samples and being less affected by the number of samples in score prediction, making it possible to construct score prediction models based on the BP algorithm with fewer samples and competent for score prediction work in colleges with fewer students. Secondly, the final error of the training samples is basically stable below 0.05, which means the error is less than 5 points in the percentage system. Finally, after evaluating the model using test samples, the prediction error remained stable at around 0.05. If converted to a percentage system, the error would be between [−5,5] points. Stable prediction results can help students choose suitable majors, promote their learning and continuous progress, and effectively improve the achievement of talent cultivation goals. Therefore, the score prediction and college major recommendation model proposed in this paper can effectively utilize freshman scores to predict major scores, provide reference basis for students to choose majors, and play a greater role in talent cultivation.
5.Conclusion
This algorithm model utilizes machine learning and neural network technologies in the field of artificial intelligence, based on historical learning data of college students, to provide suggestions for professional courses selection of college freshmen, and assist students in selecting appropriate major directions. This solution can avoid blind choices made by students due to lack of information, subjective experience, and other reasons during major selection. It gives low scoring students the opportunity to choose majors as well, thereby improving the scientificity, effectiveness, and credibility of major selection, optimizing the direction of talent cultivation, and improving the quality of talent cultivation. However, further research can consider optimizing the model to achieve better prediction performance on smaller datasets. For example, quantifying more relevant factors into the model and processing noise data instead of simply deleting them.
Acknowledgements
The authors acknowledge the Hubei Province Education Science Planning Key Topics in 2019 (Grant: 2019GA043).
References
[1] | E. Adamopoulou and L. Moussiades, An Overview of Chatbot Technology. Springer Science and Business Media Deutschland GmbH, Neos Marmaras, Greece, (2020) . |
[2] | J. Yu, Design of an algorithm for recommending elective courses based on collaborative filtering, Journal of Computational Methods in Sciences and Engineering 22: (6) ((2022) ), 2173–2184. |
[3] | L. Ma and J. Li, Influence of educational informatization based on machine learning on teaching mode, International Transactions on Electrical Energy Systems 2022: : ((2022) ), 1–7. |
[4] | B. Lin, Intelligent system for educational informatization based on bp neural network, Engineering Intelligent Systems 31: (1) ((2023) ), 21–31. |
[5] | S. Liu and J. Wang, Ice and snow talent training based on construction and analysis of artificial intelligence education informatization teaching model, Journal of Intelligent and Fuzzy Systems 40: (2) ((2021) ), 3421–3431. |
[6] | K. Zhang and L. Chen, Student Score Prediction Based on Deep Learning. Institute of Electrical and Electronics Engineers Inc, China, (2022) , Virtual, Online. |
[7] | C. Yijun, L. Guo and C. Zhang, Score prediction model based on neural network, Optical Memory and Neural Networks (Information Optics) 29: (1) ((2020) ), 37–43. |
[8] | J. ZhuGaussian Mixture Model Based Prediction Method of Movie Rating. Institute of Electrical and Electronics Engineers Inc, Chengdu, China, (2016) . |
[9] | C. Yijun, L. Guo and C. Zhang, Score prediction model based on neural network, Optical Memory and Neural Networks 29: (1) ((2020) ), 37–43. |
[10] | V.P. Patel, M.K. Rawat and A.S. Patel, Local neighbour spider monkey optimization algorithm for data clustering, Evolutionary Intelligence 16: (1) ((2023) ), 133–151. |
[11] | J. Yu, Research on the Improvement of Data Mining Algorithm Based on ‘Internet +’ System in Cloud Computing. Institute of Electrical and Electronics Engineers Inc, Harbin, China, (2020) . |
[12] | S. Wang, An overview of advanced deep graph node clustering, IEEE Transactions on Computational Social Systems 2023: : ((2023) ), 1–13. |
[13] | L. Fu, An overview of recent multi-view clustering, Neuro Computing 402: : ((2020) ), 148–161. |
[14] | H. MaImage Recognition Algorithms Based on Deep Learning. IOP Publishing Ltd, Xi’an, Virtual, China, (2021) . |
[15] | B.P. Rusyn, O.A. Lutsyk and R.Y. Kosarevych, Evaluating the informativity of a training sample for image classification by deep learning methods, Cybernetics and Systems Analysis 57: (6) ((2021) ), 853–863. |




