MRI Brain Tumour Segmentation Using Multiscale Attention U-Net
Abstract
Focusing on the problems of failing to make full use of spatial context information and limited local receptive field when U-Net is utilized to solve MRI brain tumour segmentation, a novel 3D multi-scale attention U-Net method, i.e. MAU-Net, is proposed in this paper. Firstly, a Mixed Depth-wise Convolution (MDConv) module is introduced in the encoder and decoder, which leverages various convolution kernels to extract the multi-scale features of brain tumour images, and effectively strengthens the feature expression of the brain tumour lesion region in the up and down sampling. Secondly, a Context Pyramid Module (CPM) combining multi-scale and attention is embedded in the skip connection position to achieve the combination of local feature enhancement at multi-scale with global feature correlation. Finally, MAU-Net adopts Self-ensemble in the decoding process to achieve complementary detailed features of sampled brain tumour images at different scales, thereby further improving segmentation performance. Ablation and comparison experiment results on the publicly available BraTS 2019/2020 datasets well validate its effectiveness. It respectively achieves the Dice Similarity Coefficients (DSC) of 90.6%/90.2%, 82.7%/82.8%, and 77.9%/78.5% on the whole tumour (WT), tumour core (TC) and enhanced tumour (ET) segmentation. Additionally, on the BraTS 2021 training set, the DSC for WT, TC, and ET reached 93.7%, 93.2%, and 88.9%, respectively.
1Introduction
Gliomas are the most common primary intracranial tumours and are also a class of tumours refractory to neurosurgical treatment (Herholz, 2017). Since the tumour area is located in the cranial cavity and cannot be observed directly, magnetic resonance imaging (MRI), with its ability to produce high-quality and non-invasive brain images, has become a major technique for doctors to clinically diagnose and treat brain tumours (van Dijken et al., 2017). For the precise execution of brain tumour surgeries, the necessity often arises for radiologists to manually delineate the tumour region, thereby affording clinicians with diagnostic benchmarks. However, this technology is afflicted by substantial subjectivity and diminished efficiency, making it challenging to fulfill the demands of extensive tumour image segmentation (Işın et al., 2016). Therefore, automatic segmentation of lesion regions from magnetic resonance images of brain tumours, aimed at aiding medical practitioners in treatment, emerges as a prominent research area within the realm of medical imaging (Hussain et al., 2018).
In recent years, owing to the remarkable success of Convolutional Neural Networks (CNNs) in various computer vision tasks, the community of brain tumour segmentation has witnessed a gradual shift towards CNN-based approaches as the prevailing methodology. During its early stages, this approach predominantly embraced the concept of classifying small-scale image blocks, initially partitioning brain tumour MRI images into smaller segments. Subsequently, these small image blocks were channeled into the CNN classification network, and the resultant classifications of all image blocks were amalgamated to achieve comprehensive tumour segmentation (Zikic et al., 2014; Urban et al., 2014; Kamnitsas et al., 2017). Despite the substantial performance enhancements achieved by the CNN method compared to traditional brain tumour segmentation techniques, it grapples with challenges such as extensive computational requirements and diminished operational efficiency (Rao et al., 2015).
The introduction of the Fully Convolutional Network (FCN) by Long et al. (2015) marked a pivotal advancement in addressing the brain tumour segmentation challenge, enabling end-to-end semantic segmentation of brain tumour images. Subsequently, Ronneberger et al. (2015) presented U-Net, a significant variant of FCN that has progressively established itself as the predominant method for numerous medical image segmentation tasks, owing to its benefits of minimal sample requirements, high segmentation precision and speed. Concurrently, the remarkable progress in computer hardware capabilities has given rise to 3D segmentation networks, which excels in capturing the contextual information of brain tumours, thereby gradually exhibiting heightened performance advantages. Leveraging the 3D U-Net (Çiçek et al., 2016) segmentation model as a foundation, researchers have introduced advanced modelling techniques, including residual models (Russakovsky et al., 2015; Chen et al., 2018), attention mechanisms (Hu et al., 2018; Wang et al., 2018), multi-scale fusion (Kirillov et al., 2019; Bao and Chung, 2018), and Transformers (Dosovitskiy et al., 2020; Liu et al., 2021b). These augmentations enhance the capability to express coded features and fuse coded features, thereby improving brain tumour segmentation precision further. Consequently, they make a valuable contribution to the evolution of the 3D U-Net brain tumour segmentation model, solidifying its position as the predominant method for brain tumour segmentation tasks. Although these methods have achieved satisfactory results, they do not specifically target small-sized brain tumours, so there is still potential for improvement in the accurate segmentation of brain tumours.
Therefore, this paper employs the 3D U-Net as the base model, and focuses on enhancing the multi-scale features and feature attention expression in MRI brain tumour images to extract small-scale tumour spatial information. We introduce the multi-scale approach at three levels, including network coding and decoding feature extraction, coding and decoding feature skip connections, and decoding and segmentation result output. Simultaneously, within the coding and decoding feature skip connections, we integrate the attention mechanism to emphasize the segmentation of small-scale tumours. Consequently, a novel method is proposed, termed the Multiple Attention U-Net (MAU-Net), to address the MRI brain tumour segmentation task. The contributions of this paper can be summarized as follows:
(1) In this paper, we propose a novel brain tumour segmentation method called MAU-Net, which effectively captures spatial contextual information by employing convolutional kernels of varying scales with attention mechanism, thereby improving small size tumour location details and tumour segmentation accuracy.
(2) MAU-Net introduces Mixed Depth-wise Convolutions in the encoder and decoder to extract multi-scale brain tumour features, and leverage Context Pyramid Modules combining multi-scale with attention embedded in the skip connection position to combine local features and global features. Besides, it also adopts Self-ensemble in the decoding process to further improve segmentation performance.
(3) We comprehensively evaluated MAU-Net on the publicly available BraTS 2019, BraTS2020 and BraTS 2021 brain tumour image datasets. Ablation experiments, visualization results alongside comparisons with representative methods effectively demonstrate the effectiveness of MAU-Net for MRI brain tumour segmentation.
The rest of the paper is organized as follows. Section 2 reviews the theoretical foundation and recent studies. Section 3 describes the methodology. Section 4 describes the dataset processing and experimental configuration. Section 5 discusses the experimental results. Section 6 concludes the paper.
2Related Work
2.1Brain Tumour Segmentation
In the realm of medical image segmentation tasks, the continual advancement of deep learning has given rise to numerous methods for brain tumour segmentation. These segmentation approaches, rooted in deep learning, autonomously acquire image features, yielding commendable segmentation outcomes. Notably, U-Net variant methods, founded upon the U-Net architecture, have gained considerable attention and prominence. Zhou et al. (2019) introduced Unet++, a U-Net variant incorporating multi-scale feature fusion and more efficient skip connections. This modification aims to augment the model’s capacity for extracting and fusing features at varied scales, thereby diminishing redundant features in the skip connections and enhancing the model’s efficiency and performance. Milletari et al. (2016) proposed V-Net, which fine-tunes the U-Net structure on 3D MRI data. The model employs the Dice coefficient as a loss function, calculating the similarity between predicted images and the Ground Truth. Subsequently, the Dice loss has become a prevalent choice for loss functions in medical image segmentation tasks. Akbar et al. (2022) presented a shallow 3D U-Net model featuring a distinctive downsampling strategy. This streamlined architecture utilizes a multipath convolutional block, incorporating residual modules and atrous convolution to mitigate gradient instability. Attention gates are integrated into the skip connections, amplifying the segmentation target features. González et al. (2021) employed an asymmetric U-Net, enhancing feature extraction and reconstruction capabilities for improved brain tumour segmentation results. Moreover, Guo et al. (2020) cascaded multiple segmentation networks using U-Nets within a single network. This approach segments different regions of brain tumours sequentially, with each U-Net incorporating a global context block to capture long-range dependencies, inter-channel dependencies, and depth supervision. This enables the network to finely segment brain tumours in a stage-wise manner. Cirillo et al. (2021) proposed a GAN-based brain tumour segmentation method employing a U-Net generative model and the same discriminative model as the encoder in the U-Net. This configuration enables the network to generate realistic segmentation results from MRIs through a zero-sum game.
2.2Attention Mechanism
In vision tasks, attention mechanisms play a pivotal role in the selection of key information and the deliberate exclusion of extraneous details. SENet (Hu et al., 2018) places emphasis on channels with noteworthy contributions to optimize the selection of feature maps. Concurrently, CBAM (Woo et al., 2018) attains superior results by incorporating considerations for both channels and spatial dimensions. The Non-Local (Wang et al., 2018) method introduces a global receptive field into the network by computing interactions between any two positions in the feature map. This facilitates the direct capture of long-range dependencies, effectively substantiating the visual task importance of such dependencies.
In the brain tumour segmentation task, the attention mechanism is similarly able to assign different weights to the input information, effectively suppressing uninteresting features and focusing the network on more discriminative features. For example, Jun et al. (2021) introduced attention gates into the skip connections of U-Net to suppress features irrelevant to the task, enhancing the performance of brain tumour segmentation. Liu et al. (2021a) introduced a context-guided attention network proficient in capturing high-dimensional and high-temporal resolution features by leveraging contextual information within the convolutional space and the feature interaction graph. This approach adeptly discriminates brain tumour features. Moreover, they introduced a context-guided conditional random field for selective feature aggregation, refining the segmentation of brain tumours. Wang et al. (2020) proposed a global aggregation block serving as an encoder and decoder based on self-attention, enabling the network to aggregate global information without necessitating a deep encoder. Additionally, Wang et al. (2021) introduced the self-attention-based Transformer into the bottleneck layer in U-Net, presenting TransBTS. This model exhibits exceptional brain tumour segmentation performance attributed to the potent remote modelling capabilities of the Transformer.
3Proposed Model: MAU-Net
3.1Overall Structure
MAU-Net adopts the 3D brain tumour segmentation U-Net as the base network, primarily incorporating a down-sampled coding layer module, an up-sampled decoding layer module, a skip connection module interconnecting coding and decoding layers, and a decoder feature map integration module within its structure. Notably, both the number of encoders and decoders is established at four, as depicted in Fig. 1. To facilitate the understanding of MAU-Net, the network structure table is given Table 1. Figure 1 illustrates the specific structure of the MAU-Net. Each encoder incorporating one Mixed Depth-wise Convolution (MDConv) Block and one max pooling. Within this context, MDConv Block comprises one regular convolutional unit and one MDConv unit connected sequentially. The regular convolutional unit serves the initial extraction of network features, while the mixed convolutional unit is employed for capturing feature maps with differing receptive field sizes. The max pooling is utilized for size reduction in the feature maps, thereby lowering computational resource consumption and mitigating network overfitting. After four layers of encoding, the feature map dimensions of the brain tumour image are ultimately reduced from
The skip connections merge the shallow features, imbued with valuable location information in the encoder, with the corresponding deep features in the decoder, within the channel dimension. Nevertheless, it is relevant to note that the shallow features also incorporate redundant original information. To address this concern, a Context Pyramid Module (CPM) has been introduced to mitigate feature responses in irrelevant regions and enhance overall performance. Considering the computational resources needed for network training, the CPM is exclusively integrated within the fourth skip connection, while the remaining layers 1–3 utilize basic skip connections. Finally, a self-ensemble operation is included to facilitate the gradual fusion of feature maps from the upper three levels of the decoder, which enhances the robustness of the model for brain tumour segmentation.
Fig. 1
Structure of the proposed MAU-Net.
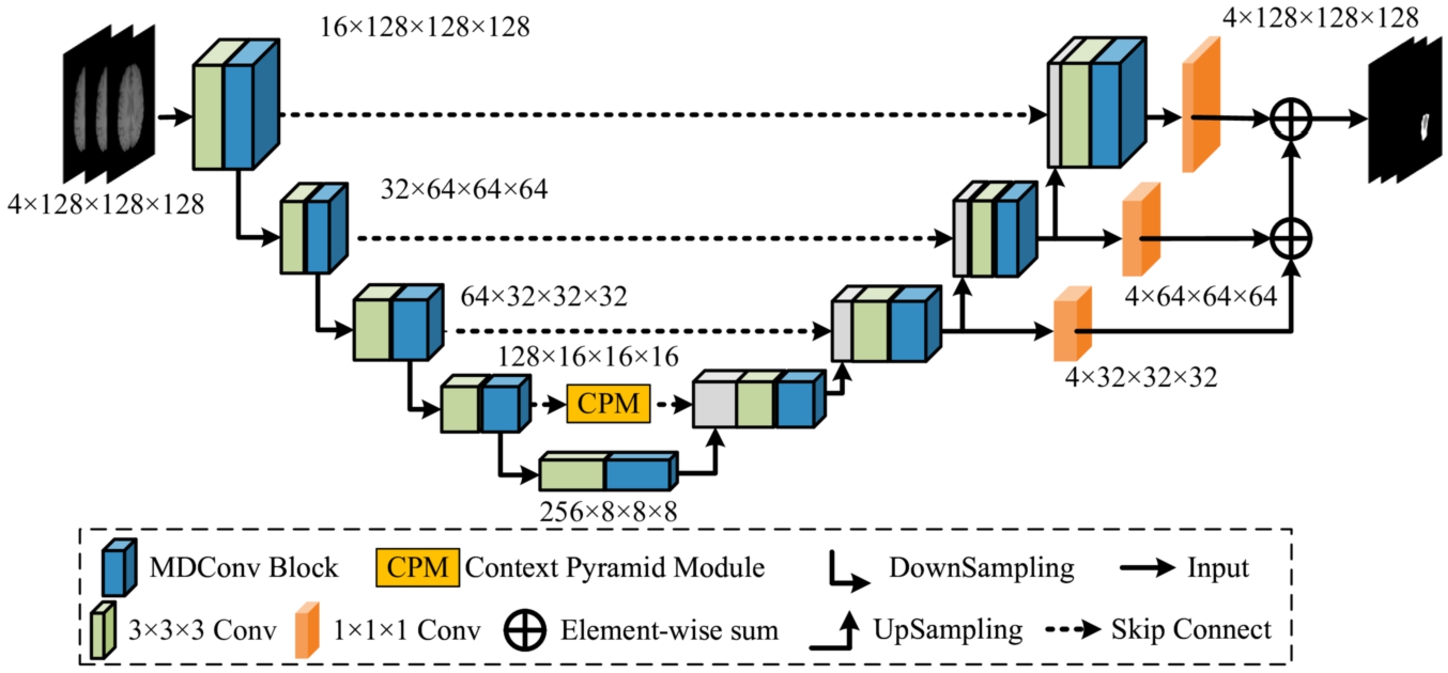
Table 1
MAU-Net network structure table. Square brackets indicate the MDConv structure.
| Output size | Encoder | Decoder |
| Trilinear Interpolation | ||
| Conv3d, | ||
| Max Pooling | ||
| Conv3d, | Trilinear Interpolation | |
| Conv3d, | ||
| Max Pooling | ||
| Conv3d, | Trilinear Interpolation | |
| Conv3d, | ||
| Max Pooling | Trilinear Interpolation | |
| Conv3d, | ||
| Context Pyramid Module (CPM) | ||
| Max Pooling | ||
3.2Mixed Depth-Wise Convolution (MDConv)
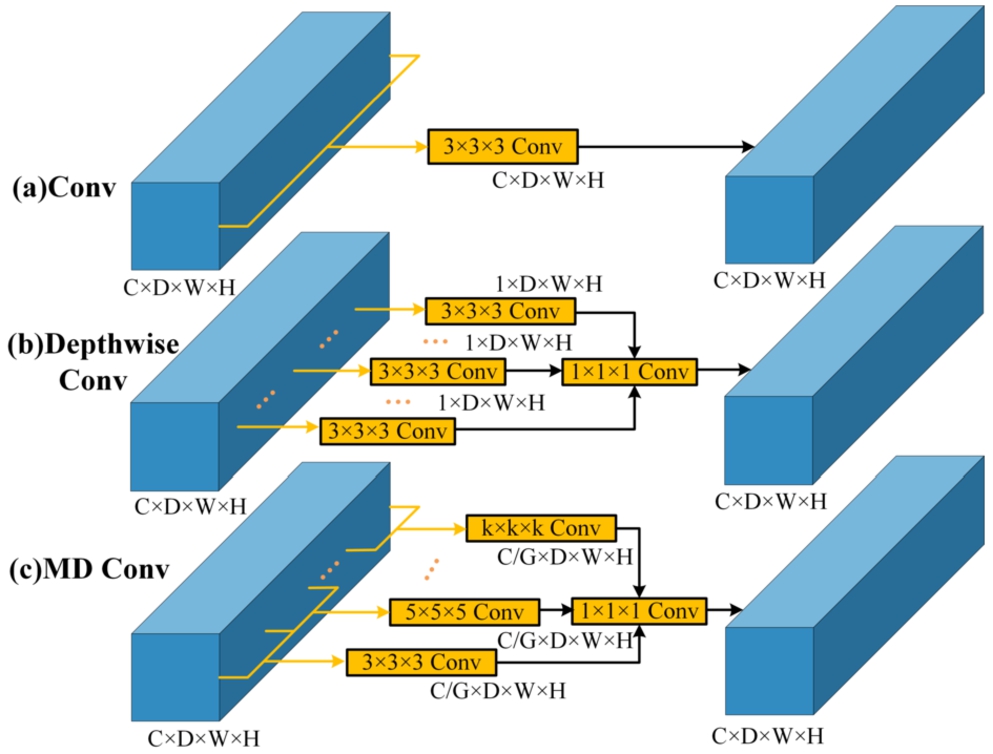
In recent convolutional neural networks, Depth-wise Convolution (DConv) is often used instead of conventional convolution to reduce the amount of computation and the number of parameters, e.g. MobileNets (Sandler et al., 2018), ShuffleNets (Zhang et al., 2018), and MnasNet (Tan et al., 2019), but this type of DConv also extracts features using a fixed-size convolution kernel similarly to the conventional convolution, which results in a fixed convolutional sensory field and makes it difficult to capture spatial information of different sizes. To this end, Tan and Le (2019) combined different sized convolution kernels to construct a new Mixed Depth-wise Convolution (MDConv), which can use a large convolution kernel to capture high-resolution information, and a small convolution kernel to capture low-resolution information, which effectively improves the performance of convolution to extract spatial features.
In the context of specific implementation, MDConv differs somewhat from conventional convolution and DConv. The number of channels within each convolution kernel in the standard convolution aligns with the number of channels in the input feature map, while the count of channels in the output feature map corresponds to the quantity of convolution kernels used. In DConv, each convolution kernel possesses a channel count of 1 with each kernel responsible for computing a single channel in the feature map. Consequently, the number of convolution kernels aligns with the number of channels in both the input and output feature maps. Based on DConv, MDConv organizes convolution kernels of diverse sizes into groups for each channel. Different groups employ convolution kernels with a channel count of 1 and it should be noted that MDConv is equivalent to DConv when the grouping is set to 1. Since the number of output channels in both DConv and MDConv matches the number of input channels, a modification of channel count is implemented using a
Fig. 2
Differences among (a) Convolution, (b) Depth-wise Convolution and (c) Mixed Depth-wise Convolution.
3.3Context Pyramid Module (CPM)
Global information plays a pivotal role in image analysis and comprehension. The incorporation of non-local attention mechanisms to capture long-range dependencies and acquire global information represents a typical approach. To overcome the limitations of calculating non-local attention solely at a single scale, Zhang et al. (2021) introduced an Attention-Guided Context Block (AGCB). This AGCB amalgamates both local and non-local attention and integrates it with the original feature maps in a multi-scale configuration, constituting a Context Pyramid Module (CPM). This approach has demonstrated robust performance in the detection of small infrared targets. Given the distinct morphological variations in brain tumour images and the presence of numerous small tumour regions that pose challenges for accurate segmentation, this paper endeavours to extend the CPM module from 2D to its 3D counterpart. The aim is to improve network segmentation performance by introducing this extension module within the framework of a 3D brain tumour segmentation.
Fig. 3
Structure of Attention-Guided Context Block.
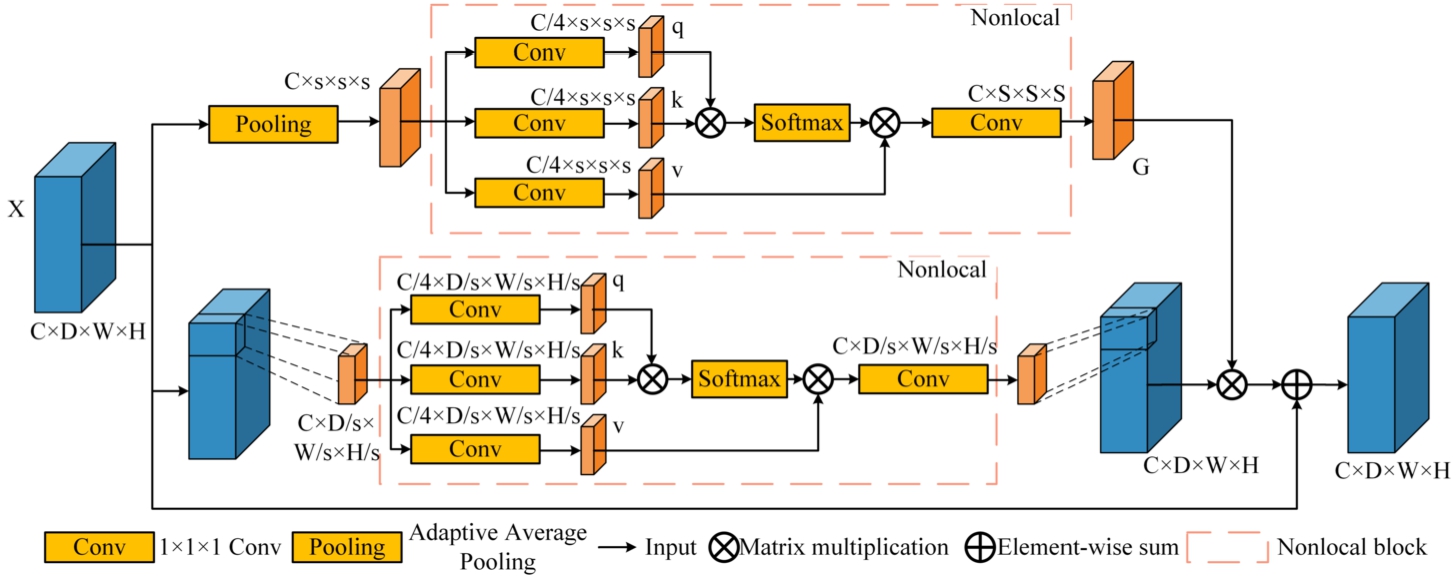
The AGCB module primarily comprises two branches. In the upper branch, global context module attention is employed to compute global correlations, enabling the network to differentiate small targets through the utilization of global information. In the lower branch, the input feature map is partitioned into non-overlapping segments, facilitating the computation of voxel correlations within each segment. This process enhances local feature extraction capabilities, as depicted in Fig. 3. The top branch applies adaptive average pooling to the input feature map
(1)
(2)
(3)
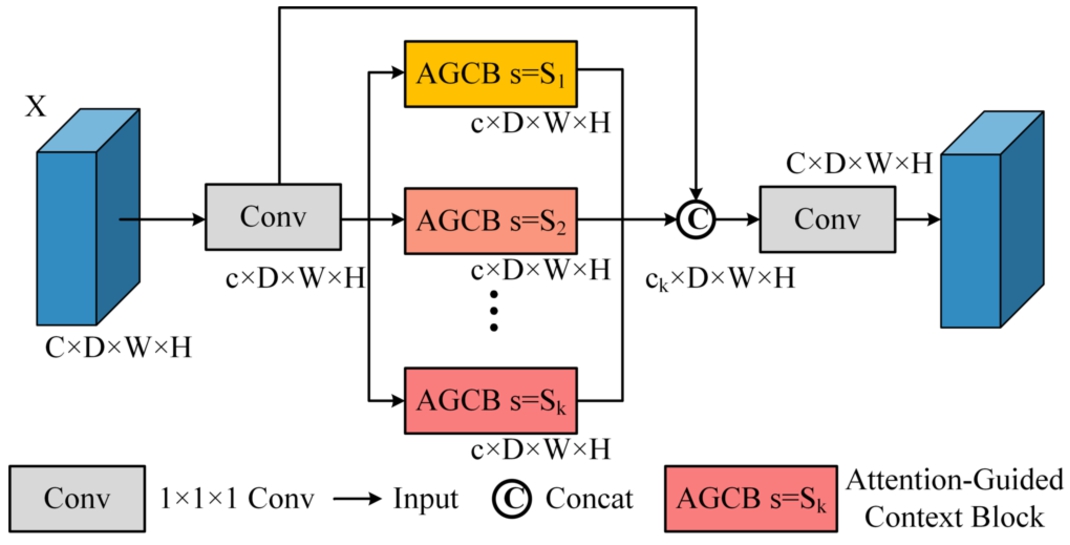
The CPM module comprises multiple AGCB modules of varying scales, thereby amalgamating multi-scale features to augment network performance. The CPM structure is visually depicted in Fig. 4. The feature map
The computational load of the CPM module escalates as it is required to compute non-local attention on the 3D feature maps multiple times, causing a size difference of
Fig. 4
Structure of context pyramid module.
3.4Self-Ensemble
Although U-Net uses skip connection to enhance the decoder ability to recover high-resolution spatial information, it falls short for fine segmentation of brain tumours with blurred edges. For this reason, Zhao et al. (2020) fused features from different layers in a serial structure to form a Self-ensemble (S.E) module, which reduces the loss of spatial information during up-sampling and enables the network to segment finer tumour edges. In the specific implementation, the decoders of the first to the third layers in the 3D U-Net are reduced to the number of channels to the number of categories using
4Experiments
4.1Experimental Environment
In our study, the experiments were conducted using a single Nvidia RTX 3090 GPU with 24 GB of memory, and the PyTorch deep learning framework was employed. The model was trained using the Adam optimizer, with a momentum value of 0.95 and a weight decay factor of
4.2Datasets and Data Processing
4.2.1Datasets
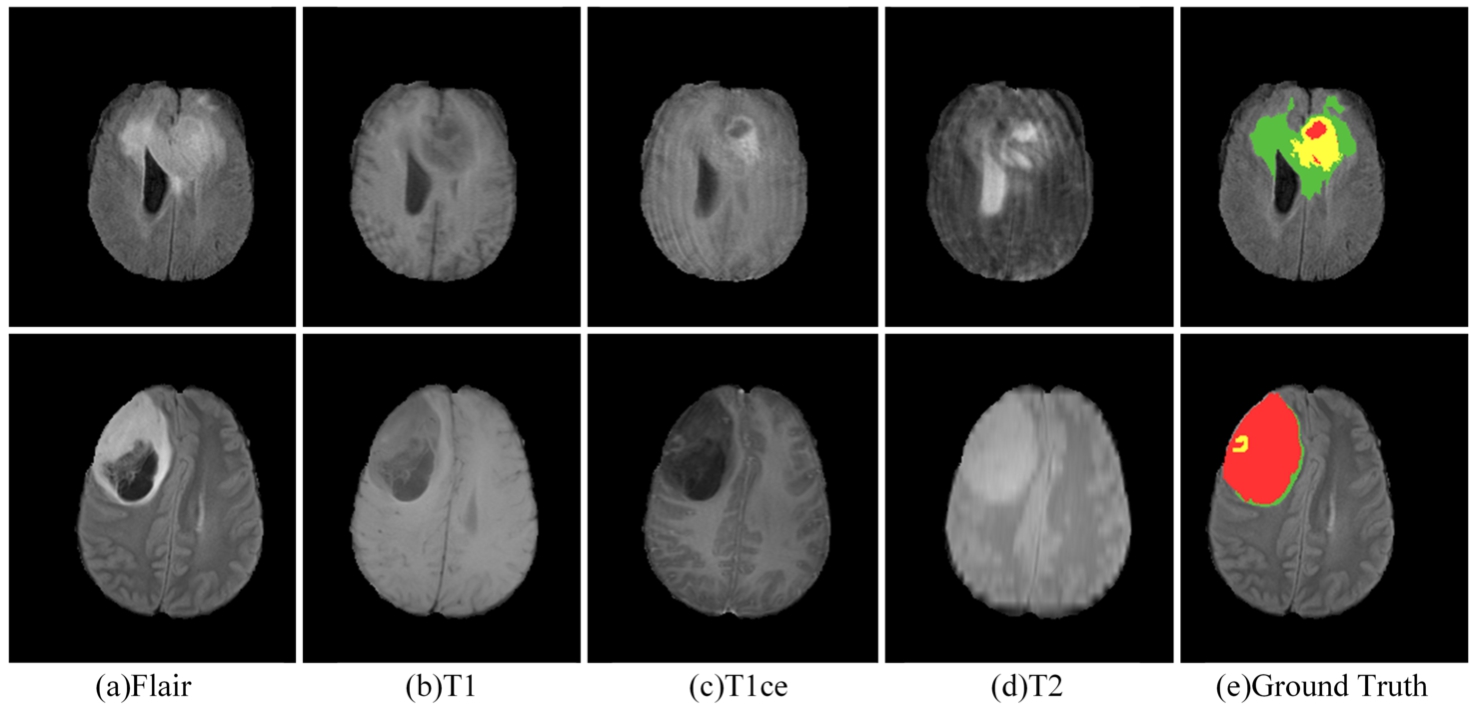
Three publicly available datasets were used for the experiments, namely BraTS 2019, BraTS 2020 and BraTS 2021 (Bakas et al., 2017; Menze et al., 2014; Baid et al., 2021). The BraTS 2019 dataset consists of 335 glioma patient cases for training and 125 samples of unknown tumour types for validation. The BraTS 2020 dataset training set consists of 369 glioma patient cases and the validation set consists of 125 cases of unknown tumour types. Due to the closure of the official validation process for BraTS 2021, we conducted a five-fold cross-validation using the BraTS 2021 training set, which includes 1251 glioma patient cases. Each sample in the dataset consists of four modalities: T1-weight (T1), post-contrast T1-weighted (T1ce), T2-weighted (T2), and T2 Fluid Attenuated Inversion Recovery (FLARE), as depicted in Fig. 5. The image size for each modality is
Fig. 5
MRI in different modes and ground truth.
4.2.2Data Preprocessing
Given that the BraTS dataset includes four modalities per case, resulting in varying image contrasts, we employed z-score normalization independently for each case. The mean and standard deviation were calculated based on the non-zero voxels within the brain region defined by the corresponding segmentation mask. This approach ensures that the normalization process closely aligns with the unique characteristics of each case while maintaining consistency across modalities within the same case, thereby improving the focus on relevant brain tissue regions. During the training phase, each case was randomly cropped to dimensions of
4.2.3Data Postprocessing
In the prediction stage, to prevent downsampling dimension mismatches, the original image is padded with zeros. Consequently, the original image size of
4.3Evaluation Metrics
In our study, we employed two key metrics, namely the Dice Similarity Coefficient (DSC) and the Hausdorff Distance (HD), for the evaluation of brain tumour segmentation across the regions of WT, TC, and ET. The DSC quantifies the degree of similarity between two samples, with values ranging from 0 to 1. A value closer to 1 indicates a higher degree of similarity. Meanwhile, the HD measures the maximum distance between any two sets within an array in the spatial domain. To mitigate the impact of potential outliers within the dataset, the final result is adjusted by a factor of
4.4Loss Function
To address the substantial class imbalance issue inherent in brain tumour segmentation, we employ a hybrid loss function represented as L. This function combines the Cross Entropy (CE) loss, represented as
(4)
(5)
(6)
5Results
In this study, we aim to demonstrate the effectiveness and competitiveness of the proposed MAU-Net. We conducted experiments using the BraTS2019 and BraTS2020 datasets to validate the performance of the model. First, a 5-fold cross-validation experiment was performed on the BraTS2019 and BraTS2020 training set, and the segmentation results were visualized. Second, ablation experiments were carried out on the BraTS2019 and BraTS2020 validation sets to demonstrate the effectiveness of the proposed method. Finally, comparisons were made with other representative methods on the BraTS 2019 and BraTS 2020 validation sets. Additionally, five-fold cross-validation experiments were conducted on the BraTS 2021 training set. The extensive comparative experiments demonstrate the advanced performance and competitiveness of the proposed method.
5.1Ablation Experiment
To comprehensively assess the effectiveness of the incorporated modules, we conducted ablation experiments on the BraTS 2019 dataset and BraTS 2020 dataset. These experiments involved using the 3D U-Net as the baseline method and separately adding MDConv and CPM to the 3D U-Net. We initially examined the performance of incorporating both the MDConv and CPM modules. Subsequently, we verified the validity of the final method, MAU-Net, by introducing the self-ensemble module. To facilitate comparisons, we use “Mix”, “CPM” to denote the experimental results when incorporating MDConv and CPM, respectively.
Table 2
Ablation experiments on BraTS training set.
| Dataset | Methods | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | ||
| BraTS2019 | U-Net (baseline) | 77.3 | 90.0 | 82.3 | 6.48 | 5.34 | 8.54 |
| U-Net+Mix | 78.1* | 90.3 | 83.1* | 4.39* | 4.32* | 7.35 | |
| U-Net+CPM | 78.3* | 90.5 | 83.5* | 4.51* | 4.51 | 6.78* | |
| U-Net+Mix+CPM | 78.9* | 90.7* | 84.0* | 3.78* | 4.01* | 6.03* | |
| MAU-Net | 79.5* | 90.8* | 84.3* | 3.45* | 3.79* | 5.43* | |
| BraTS2020 | U-Net (baseline) | 79.4 | 90.5 | 82.6 | 26.60 | 5.14 | 8.73 |
| U-Net+Mix | 79.6 | 91.1* | 84.0* | 25.48* | 4.97 | 10.47 | |
| U-Net+CPM | 79.5 | 91.5* | 83.2* | 26.61 | 4.64 | 6.84* | |
| U-Net+Mix+CPM | 80.4* | 91.1* | 84.4* | 28.01 | 4.48* | 8.48 | |
| MAU-Net | 80.7* | 91.3* | 85.1* | 26.31 | 4.35* | 6.16* | |
* Denotes comparison with U-Net by Wilcoxon signed rank test (p-value < 0.05).
First, we implemented a five-fold cross-validation strategy on the BraTS 2019 and BraTS 2020 training sets. The datasets were randomly divided into five subsets, with each iteration reserving one subset as the validation set and using the remaining subsets for training. This approach ensured comprehensive and stable evaluation. The results of the ablation experiments, averaged over the five iterations, are presented in Table 2. The experiments demonstrated that the MAU-Net model, which integrates MixConv, CPM, and S.E modules within a 3D U-Net architecture, achieved optimal performance across both datasets. Compared to the baseline U-Net model, MAU-Net showed significant improvements in DSC and reductions in Hausdorff95 distance. Specifically, in BraTS 2019, DSC improvements were observed for ET, WT, and TC, with increases of 2.2%, 0.8%, and 2%, respectively, while Hausdorff95 was reduced by 3.03 mm, 1.55 mm, and 3.11 mm. In BraTS 2020, DSC improvements were 1.3% for ET, 0.8% for WT, and 2.5% for TC, with corresponding reductions in Hausdorff95 by 0.29 mm, 0.79 mm, and 2.57 mm.
To further validate the effectiveness of the individual modules, we conducted additional ablation experiments on the validation sets of BraTS 2019 and BraTS 2020. The segmentation models trained on the training sets were used to predict the validation sets, with the results submitted to an online evaluation platform to enhance the reliability and impartiality of the findings. The results are shown in Table 3. In the BraTS 2019 validation set, incremental introduction of the MixConv and CPM modules into the 3D U-Net resulted in notable increases in DSC values for ET, WT, and TC, particularly for TC, where the inclusion of MixConv and CPM led to a 1.5% improvement. This highlights their effectiveness in segmenting small-volume targets. When both modules were integrated into U-Net, further improvements of 0.7% for ET and 1.8% for TC were observed. To further optimize brain tumour segmentation performance, MAU-Net incorporated a self-assembly module, achieving DSC values of 77.9%, 90.6%, and 82.7% for ET, WT, and TC, respectively. Compared to U-Net, MAU-Net demonstrated substantial performance advantages, with DSC improvements of 1.4% for ET and 2.4% for TC, validating the positive impact of the embedded modules in brain tumour segmentation tasks. Additionally, MAU-Net significantly reduced Hausdorff95 distance, with reductions of 0.89 mm for ET, 0.61 mm for WT, and 1.42 mm for TC, further confirming the effectiveness of MixConv, CPM, and the self-assembly mechanism in enhancing segmentation accuracy. In the BraTS 2020 validation set, MAU-Net achieved outstanding DSC values of 78.5% for ET, 90.2% for WT, and 82.8% for TC, surpassing the 3D U-Net by 1.6%, 0.9%, and 2.9%, respectively, thus affirming the efficacy of the MAU-Net model. Similarly, in terms of Hausdorff95 distance, MAU-Net exhibited significant advantages, with values of 26.96 mm for ET, 7.61 mm for WT, and 8.61 mm for TC, representing reductions of 5.6 mm, 0.09 mm, and 3.5 mm compared to U-Net. The superior performance of MAU-Net, particularly for ET and TC, further underscores its excellence in brain tumour segmentation tasks.
Table 3
Ablation experiments on BraTS validation set.
| Dataset | Methods | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | ||
| BraTS2019 | U-Net (baseline) | 76.5 | 90.6 | 80.3 | 3.94 | 4.68 | 6.82 |
| U-Net+Mix | 76.8 | 90.8 | 81.8* | 2.81* | 4.40 | 5.95 * | |
| U-Net+CPM | 76.7 | 90.5 | 81.8* | 3.97 | 4.56 | 6.55 | |
| U-Net+Mix+CPM | 77.2* | 90.6 | 82.1* | 3.14* | 4.30* | 6.14 | |
| MAU-Net | 77.9* | 90.6 | 82.7* | 3.05* | 4.07* | 5.40* | |
| BraTS2020 | U-Net(baseline) | 76.9 | 89.3 | 79.9 | 32.56 | 7.70 | 12.11 |
| U-Net+Mix | 77.4* | 90.0* | 81.5* | 33.00 | 8.26 | 15.61 | |
| U-Net+CPM | 77.4* | 89.9 | 81.4* | 31.08* | 7.41 | 12.28 | |
| U-Net+Mix+CPM | 77.4* | 90.0* | 82.3* | 32.11 | 7.09* | 11.49 | |
| MAU-Net | 78.5* | 90.2* | 82.8* | 26.96* | 7.61 | 8.61* | |
* Denotes comparison with U-Net by Wilcoxon signed rank test (p-value < 0.05).
Table 4
Ablation experiments on MAU-Net training hyper-parameters on BraTS 2020 training set.
| MAU-Net | DSC (%)↑ | Hausdorff95 (mm)↓ | |||||
| Batch size | Learning rate | ET | WT | TC | ET | WT | TC |
| 2 | 0.005 | 79.7 | 90.9 | 84.4 | 27.04 | 4.87 | 6.91 |
| 0.001 | 80.3 | 91.2 | 84.9 | 26.24 | 4.55 | 6.71 | |
| 0.0005 | 78.1 | 90.4 | 83.4 | 29.33 | 5.84 | 7.32 | |
| 0.0001 | 77.4 | 89.9 | 83.5 | 29.97 | 6.32 | 7.94 | |
| 4 | 0.005 | 79.3 | 90.7 | 84.6 | 27.51 | 4.79 | 6.94 |
| 0.001 | 80.7 | 91.3 | 85.1 | 26.31 | 4.35 | 6.16 | |
| 0.0005 | 78.3 | 90.1 | 83.9 | 28.77 | 5.32 | 6.47 | |
| 0.0001 | 77.6 | 90.2 | 84.2 | 30.21 | 6.33 | 7.56 | |
Fig. 6
Training loss for the BraTS2020 training set.
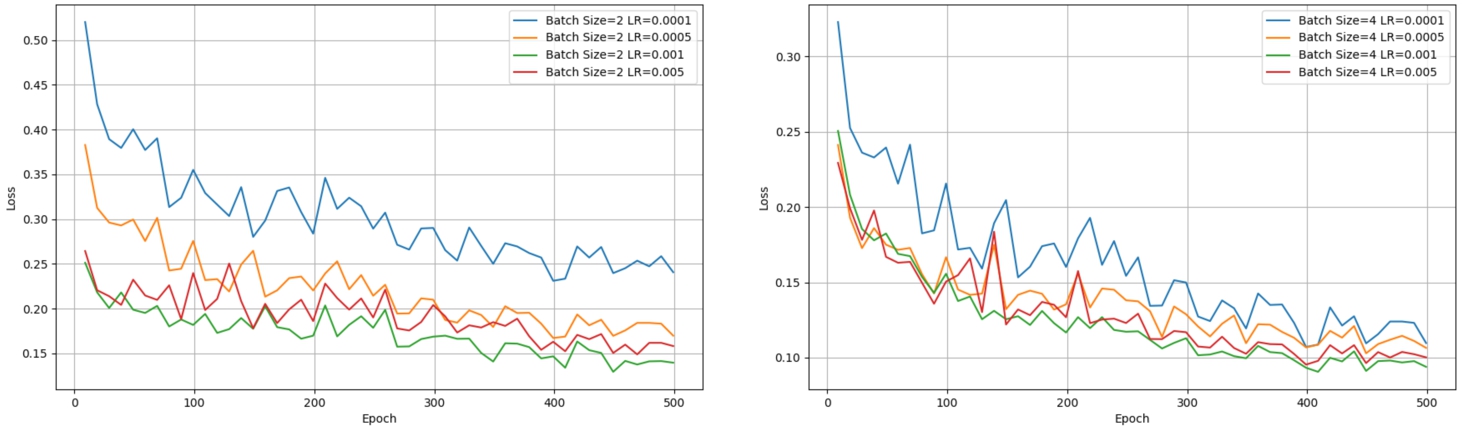
To validate the reasonableness of the training hyper-parameter settings, we systematically conducted ablation experiments on learning rate (LR) and batch size. The results of these experiments are summarized in Table 4, and visually represented by the training loss curves (Fig. 6). First, under the condition of a consistent learning rate, we explored the effect of different batch sizes on brain tumour segmentation accuracy. Through detailed comparative analysis, we found that moderately increasing the batch size can slightly improve segmentation accuracy. This finding suggests that, when resources permit, increasing the batch size helps the model better capture statistical characteristics of the data, thereby optimizing segmentation outcomes. Next, with the batch size fixed, we thoroughly examined the effect of learning rate on segmentation accuracy. Specifically, we tested several learning rates, including 0.005, 0.001, 0.0005, and 0.0001, to comprehensively evaluate their impact on the training process and final performance. The results indicated that a learning rate of 0.001 yielded the best segmentation performance, a conclusion visually supported by Fig. 6, which shows a smooth decline in training loss and successful convergence before 500 epochs at this learning rate. In contrast, when the learning rate was set to 0.0001, the training process was slower and failed to fully converge. This observation is clearly reflected in the loss curve in Fig. 6, and the quantitative data in Table 4 further confirm that the model’s segmentation performance was suboptimal with a lower learning rate.
Table 5
Ablation experiments on loss function hyper-parameter on BraTS 2020 training set.
| Hyper-parameter | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | |
| 79.3 | 90.8 | 84.2 | 27.48 | 5.09 | 7.33 | |
| 80.7* | 91.3* | 85.1* | 26.31 | 4.35* | 6.16* | |
| 80.1* | 90.4 | 84.5 | 25.47* | 4.55 | 6.74 | |
| 80.4* | 91.1 | 84.7 | 26.11 | 4.78 | 6.14* | |
| 78.8 | 91.0 | 83.9 | 27.14 | 5.51 | 7.07 | |
* Denotes comparison with the loss function hyper-parameter (
As shown in Table 5, we conducted a series of experiments on the BraTS 2020 training set to determine the optimal value of the hyper-parameter α in the loss function. Notably,
Table 6
Ablation experiments on the BraTS 2020 validation set for MAU-Net’s padding method and different noises.
| MAU-Net | DSC (%)↑ | Hausdorff95 (mm)↓ | |||||
| ET | WT | TC | ET | WT | TC | ||
| Padding methods | Zero padding | 78.5 | 90.2 | 82.8 | 26.96 | 7.61 | 8.61 |
| Reflection padding | 78.7 | 90.4 | 83.0 | 25.31* | 6.45* | 7.44* | |
| Replication padding | 78.5 | 90.3 | 82.7 | 26.23 | 7.34 | 7.96 | |
| Noise type | – | 78.5 | 90.2 | 82.8 | 26.96 | 7.61 | 8.61 |
| Gaussian noise | 78.5 | 90.1 | 82.6 | 27.14 | 8.10 | 8.94 | |
| Salt-and-pepper noise | 78.3 | 89.5 | 82.3 | 27.54 | 7.94 | 9.01 | |
| Rayleigh noise | 78.0 | 90.2 | 82.4 | 28.04* | 7.84 | 8.73 | |
* Denotes comparison with zero padding methods by Wilcoxon signed rank test (p-value < 0.05).
To evaluate the impact of different padding methods on segmentation performance, we compared Zero Padding, Reflection Padding, and Replication Padding. Our results, as summarized in the Table 6, reveal that zero padding tends to introduce edge artifacts, which negatively affect performance, especially in the Hausdorff95 metric. In contrast, reflection padding offers a more natural treatment of image edges, leading to a significant improvement in Hausdorff95. While replication padding also prevents edge artifacts, it was slightly outperformed by reflection padding, likely due to the latter’s better ability to preserve edge information. Therefore, we decided to use MAU-Net with added reflection padding in subsequent comparison experiments with other methods. Additionally, we validated the robustness of the model by introducing different types of noise, as shown in Table 6. We added three common types of noise to the data, Gaussian noise, Pretzel noise, and Rayleigh noise. The experimental results indicate that while MAU-Net exhibited a significant increase in the Hausdorff95 metric for ET under Rayleigh noise, no significant differences were observed in any other evaluation metrics. This further demonstrates the stability and reliability of the MAU-Net model across different noisy.
5.2Visualization
Fig. 7
Visualization of segmentation results on the BraTS 2020 training set. WT contains red (labels 1), green (labels 2) and yellow (labels 4); TC contains red (labels 1) and yellow (labels 4); ET contains yellow (labels 4).
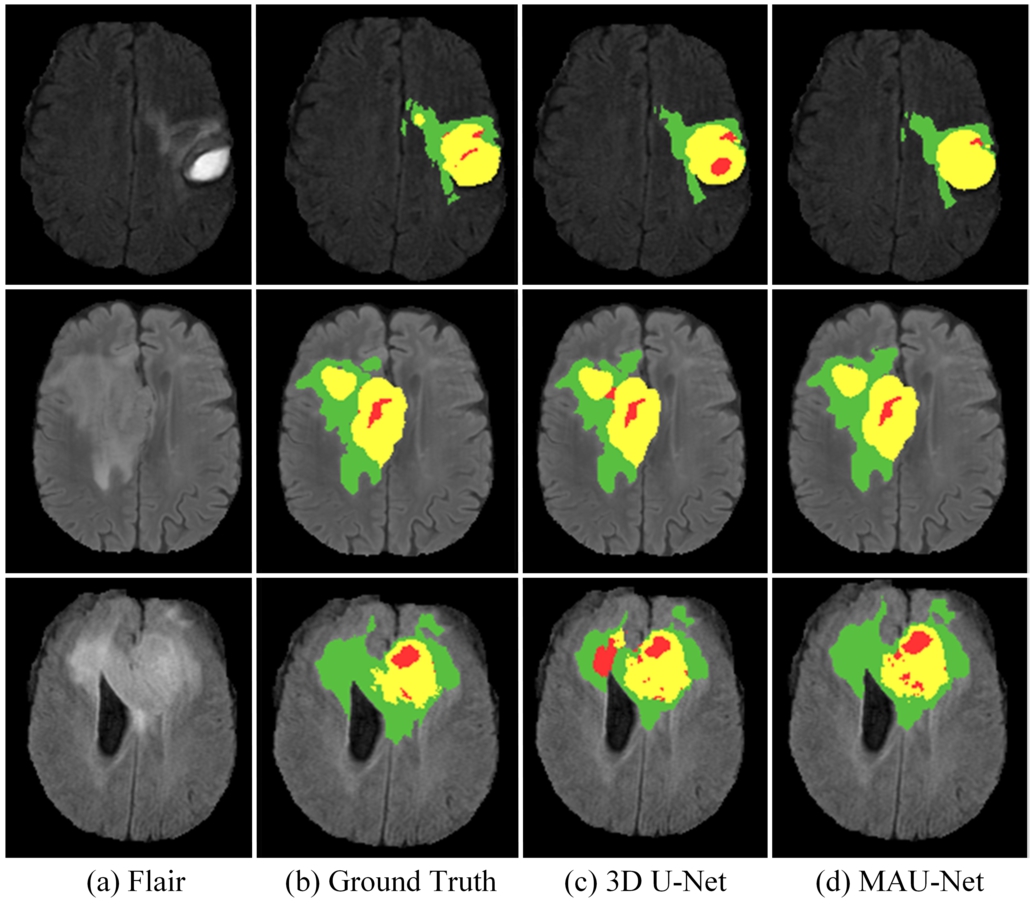
To better demonstrate the results of the method, Fig. 7 provides visual representations of select samples within the BraTS 2020 training set. Distinct colours correspond to varying label, with red signifying areas of necrotic and non-enhanced regions (label 1), green signifying areas of edema (label 2), and yellow signifying areas of enhancing tumour (label 4). The images describe the segmentation results of Flair, Ground Truth, 3D U-Net, and MAU-Net, respectively. In contrast to the 3D U-Net model, the figure underscores that MAU-Net excels in the segmentation of whole tumour (WT), tumour core (TC) and enhancing tumuor (ET) region.
Table 7
Comparisons with typical methods on the BraTS 2019 validation set.
| Methods | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | |
| Jun et al. (2021) | 76.0* | 88.8* | 77.2* | 5.20* | 7.76* | 8.26* |
| Milletari et al. (2016) | 70.9* | 87.4* | 81.2* | 5.06* | 9.43* | 8.72* |
| Akbar et al. (2022) | 74.2* | 88.5* | 81.0* | 6.67* | 10.83* | 10.25* |
| Liu et al. (2021a) | 75.9* | 88.5* | 85.1 | 4.80* | 5.89* | 6.56* |
| Zhao et al. (2020) | 75.4* | 91.0 | 83.5 | 3.84* | 4.57 | 5.58 |
| Guo et al. (2020) | 77.3* | 90.3 | 83.3 | 4.44* | 7.10* | 7.68* |
| Wang et al. (2021) | 73.7* | 89.4* | 80.7* | 5.99* | 5.68* | 7.36* |
| Chang et al. (2023) | 78.2 | 89.0* | 81.2* | 3.82* | 8.53* | 7.43* |
| MAU-Net (Ours) | 78.0 | 90.6 | 82.8 | 3.04 | 4.05 | 5.37 |
* Represent the significance of other methods compared to MAU-Net by Wilcoxon signed rank test (p-value < 0.05).
5.3Comparison with Representative Methods
To validate the effectiveness and competitiveness of the proposed method, we conducted comparisons with representative brain tumour segmentation approaches using the BraTS 2019 and BraTS 2020 validation sets, with results uploaded to the online platform. Additionally, we performed five-fold cross-validation on the BraTS 2021 training set to further confirm its performance.
The comparative experiments on the BraTS2019 and BraTS2020 validation sets are presented in Table 7 and Table 8. To demonstrate the superiority of MAU-Net among similar methods, we first compared it with various 3D U-Net variants, including V-Net (Milletari et al., 2016), Attention U-Net (Jun et al., 2021; Zhao et al., 2020), CANet (Liu et al., 2021a; Akbar et al., 2022; González et al., 2021), and (Vu et al., 2021). The experimental results clearly show that MAU-Net outperforms these methods, particularly in segmenting small tumours like the ET, with significant improvements. Additionally, we compared MAU-Net with the more recent dual-path attention fusion network proposed by Chang et al. (2023), which also employs attention mechanisms. MAU-Net demonstrated a marked advantage over this method across multiple brain tumour regions, further underscoring its effectiveness and competitiveness.
Table 8
Comparisons with typical methods on the BraTS 2020 validation set.
| Methods | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | |
| Jun et al. (2021) | 75.2* | 87.8* | 77.9* | 30.65* | 6.30 | 11.02* |
| Milletari et al. (2016) | 68.8* | 84.1* | 79.1* | 50.98* | 13.37* | 13.61* |
| Akbar et al. (2022) | 72.9* | 88.9* | 80.2* | 31.97* | 10.26* | 13.58 * |
| González et al. (2021) | 77.3* | 90.2 | 81.5* | 21.80 | 6.16 | 7.55 |
| Vu et al. (2021) | 77.2* | 90.6 | 82.7 | 27.04* | 4.99 | 8.63 |
| Cirillo et al. (2021) | 75.0* | 89.3* | 79.2* | 36.00* | 6.39 | 14.07* |
| Jiang et al. (2022) | 77.4* | 89.1* | 80.3* | 26.84 | 8.56* | 15.78 * |
| Wang et al. (2021) | 78.7 | 90.1 | 81.7* | 17.95 | 4.96 | 9.77* |
| Li et al. (2024b) | 75.4* | 89.9 | 83.0 | 22.07 | 6.64 | 6.09 |
| MAU-Net (Ours) | 78.7 | 90.4 | 83.0 | 25.31 | 6.45 | 7.44 |
* Represent the significance of other methods compared to MAU-Net by Wilcoxon signed rank test (p-value < 0.05).
Additionally, we compared MAU-Net with brain tumour segmentation networks based on different architectures to further establish its competitiveness. Guo et al. (2020) introduced a cascaded global semantic convolutional network, which uses multiple U-Nets to sequentially segment WT, TC, and ET. Compared to this method, MAU-Net significantly reduced the Hausdorff95 distance for ET, WT, and TC by 1.39 mm, 3.03 mm, and 2.28 mm, respectively, demonstrating superior performance. MAU-Net also shows strong competitiveness compared to the 3D CNN proposed by González et al. (2021), the multi-encoder network with multiple denoising inputs proposed by Vu et al. (2021), and the GAN-based method proposed by Cirillo et al. (2021). We further evaluated MAU-Net against U-Net models incorporating Transformers, such as TransBTS (Wang et al., 2021) and SwinBTS (Jiang et al., 2022). While TransBTS and SwinBTS expand the receptive field at a single scale by replacing the bottleneck layer with transformers, MAU-Net effectively enhances segmentation accuracy by extracting features with different receptive fields across multiple scales, highlighting its advanced capabilities. Finally, Li et al. (2024b) proposed a multi-level fusion brain tumour segmentation method within a hybrid architecture, where MAU-Net demonstrated a clear advantage in DSC, further validating the competitiveness of our approach.
In the BraTS 2021 training set, we employed five-fold cross-validation, with the results presented in Table 9. The rationale for selecting comparative methods is consistent with that used in BraTS 2019 and BraTS 2020. Compared to the dual-branch network proposed by Jia et al. (2023)., which integrates attention mechanisms with super-resolution reconstruction techniques, MAU-Net achieved significant improvements in the DSC evaluation metric, particularly with a 3.8% lead in the ET region, a 1.6% lead in the WT region, and a 3.1% lead in the TC region. Furthermore, when compared to the residual spatial pyramid pooling-enhanced 3D U-Net employed by Vijay et al. (2023), MAU-Net demonstrated clear advantages across all metrics, validating the superiority of the MAU-Net architecture. Additionally, in comparison to Transformer-based architectures like UNETR (Hatamizadeh et al., 2022) and VTU-Net (Peiris et al., 2022), MAU-Net also exhibited superior performance, further proving its advanced capabilities. Finally, compared to the multi-scale residual U-Net proposed by Li et al. (2024a), MAU-Net maintained a lead in segmentation accuracy for both the WT and TC regions, further confirming its effectiveness and competitiveness.
Table 9
Comparisons with typical methods on the BraTS 2021 training set.
| Methods | DSC (%)↑ | Hausdorff95 (mm)↓ | ||||
| ET | WT | TC | ET | WT | TC | |
| Jia et al. (2023) | 85.1* | 92.1* | 90.1* | – | – | – |
| Vijay et al. (2023) | 85.0* | 90.0* | 90.0* | 6.30* | 9.43* | 7.78* |
| Hatamizadeh et al. (2022) | 86.2* | 92.5* | 91.8* | 11.28* | 7.74* | 7.85* |
| Peiris et al. (2022) | 85.3* | 93.1 | 90.2* | 10.78* | 6.76* | 7.56* |
| Li et al. (2024a) | 89.7 | 92.8* | 92.9 | 2.29 | 5.12 | 4.16 |
| MAU-Net (Ours) | 88.9 | 93.7 | 93.2 | 3.75 | 4.68 | 4.03 |
* Represent the significance of other methods compared to MAU-Net by Wilcoxon signed rank test (p-value < 0.05).
6Conclusions
This paper introduces a novel MAU-Net method for MRI brain tumour segmentation, which intricately integrates mixed depth-wise convolution, context pyramid module, and self-ensemble module into the 3D U-Net architecture. The primary objective is to enhance brain tumour segmentation accuracy by bolstering the multi-scale features of tumour images with local feature expression. Extensive ablation and comparative experiments conducted on three public brain tumour datasets have validated the effectiveness and competitiveness of the proposed segmentation method. Among them, on the three regions of ET, WT and TC, the DSC is 78.0%, 90.6% and 82.8% in the BraTS 2019 validation set, and 3.04 mm, 4.05 mm and 5.37 mm in Hausdorff95; in the BraTS 2020 validation set, the DSC is 78.7%, 90.4% and 83.0%, and the 25.31 mm, 6.45 mm and 7.44 mm for Hausdorff95; and 88.9%, 93.7% and 93.2% for DSC and 3.75 mm, 4.68 mm and 4.03 mm for Hausdorff95 in the BraTS2021 training set. Although MAU-Net has achieved promising segmentation results, certain limitations remain. In future work, we will explore the use of CPM across different semantic levels to maximize the interaction of multi-scale semantic information. Additionally, we will investigate the impact of larger convolutional kernels on brain tumour segmentation and explore more advanced structures for feature extraction. Finally, we will experiment with graph-based or Conditional Random Fields strategies to enhance the post-processing phase.
References
1 | Akbar, A.S., Fatichah, C., Suciati, N. ((2022) ). Single level UNet3D with multipath residual attention block for brain tumor segmentation. Journal of King Saud University-Computer and Information Sciences, 34: (6), 3247–3258. |
2 | Baid, U., Ghodasara, S., Mohan, S., Bilello, M., Calabrese, E., Colak, E., Farahani, K., Kalpathy-Cramer, J., Kitamura, F.C., Pati, S., Prevedello, L.M., Rudie, J.D., Sako, C., Shinohara, R.T., Bergquist, T., Chai, R., Eddy, J., Elliott, J., Reade, W., Schaffter, T., Yu, T., Zheng, J., Moawad, A.W., Otavio, C.L., McDonnell, O., Miller, E., Moron, F.E., Oswood, M.C., Shih, R.Y., Siakallis, L., Bronstein, Y., Mason, J.R., Miller, A.F., Choudhary, G., Agarwal, A., Besada, C.H., Derakhshan, J.J., Diogo, M.C., Do-Dai, D.D., Farage, L., Go, J.L., Hadi, M., Hill, V.B., Michael, I., Joyner, D., Lincoln, C., Lotan, E., Miyakoshi, A., Sanchez-Montano, M., Nath, J., Nguyen, X.V., Nicolas-Jilwan, M., Ortiz, J.J., Ozturk, K., Petrovic, B.D., Shah, C., Shah, L.M., Sharma, M., Simsek, O., Singh, A.K., Soman, S., Statsevych, V., Weinberg, B.D., Young, R.J., Ikuta, I., Agarwal, A.K., Cambron, S.C., Silbergleit, R., Dusoi, A., Postma, A.A., et al. (2021). The RSNA-ASNR-MICCAI BraTS 2021 benchmark on brain tumor segmentation and radiogenomic classification. arXiv preprint arXiv:2107.02314. |
3 | Bakas, S., Akbari, H., Sotiras, A., Bilello, M., Rozycki, M., Kirby, J.S., Freymann, J.B., Farahani, K., Davatzikos, C. ((2017) ). Advancing the Cancer Genome Atlas glioma MRI collections with expert segmentation labels and radiomic features. Scientific Data, 4: , 170117. |
4 | Bao, S., Chung, A.C. ((2018) ). Multi-scale structured CNN with label consistency for brain MR image segmentation. Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, 6: (1), 113–117. |
5 | Chang, Y., Zheng, Z., Sun, Y., Zhao, M., Lu, Y., Zhang, Y. ((2023) ). DPAFNet: a residual dual-path attention-fusion convolutional neural network for multimodal brain tumor segmentation. Biomedical Signal Processing and Control, 79: , 104037. |
6 | Chen, H., Dou, Q., Yu, L., Qin, J., Heng, P.-A. ((2018) ). VoxResNet: deep voxelwise residual networks for brain segmentation from 3D MR images. NeuroImage, 170: , 446–455. |
7 | Çiçek, Ö., Abdulkadir, A., Lienkamp, S.S., Brox, T., Ronneberger, O. ((2016) ). 3D U-Net: learning dense volumetric segmentation from sparse annotation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016, Lecture Notes in Computer Science, vol. 9901: . Springer, Cham, pp. 424–432. |
8 | Cirillo, M.D., Abramian, D., Eklund, A. ((2021) ). Vox2Vox: 3D-GAN for brain tumour segmentation. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Lecture Notes in Computer Science, vol. 12658: . Springer, Cham, pp. 274–284. |
9 | Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., Houlsby, N. et al. ((2020) ). An image is worth 16 x 16 words: transformers for image recognition at scale. In: International Conference on Learning Representations. |
10 | González, S.R., Zemmoura, I., Tauber, C. ((2021) ). 3D brain tumor segmentation and survival prediction using ensembles of convolutional neural networks. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Lecture Notes in Computer Science, vol. 12659: . Springer, Cham, pp. 241–254. |
11 | Guo, D., Wang, L., Song, T., Wang, G. ((2020) ). Cascaded global context convolutional neural network for brain tumor segmentation. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Lecture Notes in Computer Science, vol. 11992: . Springer, Cham, pp. 315–326. |
12 | Hatamizadeh, A., Tang, Y., Nath, V., Yang, D., Myronenko, A., Landman, B., Roth, H.R., Xu, D. ((2022) ). UNETR: transformers for 3D medical image segmentation. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pp. 574–584. |
13 | Herholz, K. ((2017) ). Brain tumors: an update on clinical PET research in gliomas. Seminars in Nuclear Medicine, 47: (1), 5–17. |
14 | Hu, J., Shen, L., Sun, G. ((2018) ). Squeeze-and-excitation networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7132–7141. |
15 | Hussain, S., Anwar, S.M., Majid, M. ((2018) ). Segmentation of glioma tumors in brain using deep convolutional neural network. Neurocomputing, 282: , 248–261. |
16 | Işın, A., Direkoğlu, C., Şah, M. ((2016) ). Review of MRI-based brain tumor image segmentation using deep learning methods. Procedia Computer Science, 102: , 317–324. |
17 | Jia, Z., Zhu, H., Zhu, J., Ma, P. ((2023) ). Two-branch network for brain tumor segmentation using attention mechanism and super-resolution reconstruction. Computers in Biology and Medicine, 157: , 106751. |
18 | Jiang, Y., Zhang, Y., Lin, X., Dong, J., Cheng, T., Liang, J. ((2022) ). SwinBTS: a method for 3D multimodal brain tumor segmentation using swin transformer. Brain Sciences, 12: (6), 797. |
19 | Jun, W., Haoxiang, X., Wang, Z. ((2021) ). Brain tumor segmentation using dual-path attention U-Net in 3D MRI images, Lecture Notes in Computer Science, vol. 12658: . Springer, Cham, pp. 183–193. |
20 | Kamnitsas, K., Ledig, C., Newcombe, V.F., Simpson, J.P., Kane, A.D., Menon, D.K., Rueckert, D., Glocker, B. ((2017) ). Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Medical Image Analysis, 36: , 61–78. |
21 | Kirillov, A., Girshick, R., He, K., Dollár, P. ((2019) ). Panoptic feature pyramid networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 6399–6408. |
22 | Li, P., Li, Z., Wang, Z., Li, C., Wang, M. ((2024) a). mResU-Net: multi-scale residual U-Net-based brain tumor segmentation from multimodal MRI. Medical & Biological Engineering & Computing, 62: (3), 641–651. |
23 | Li, Z., Chen, Z., Huang, H., Chen, C. ((2024) b). Multi-level fusion in a hybrid architecture for 3D image segmentation. In: 2024 39th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Dalian, China, 2024, pp. 373–380. |
24 | Liu, Z., Tong, L., Chen, L., Zhou, F., Jiang, Z., Zhang, Q., Wang, Y., Shan, C., Li, L., Zhou, H. ((2021) a). CANet: context aware network for brain glioma segmentation. IEEE Transactions on Medical Imaging, 40: (7), 1763–1777. |
25 | Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., Lin, S., Guo, B. ((2021) b). Swin transformer: hierarchical vision transformer using shifted windows. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 10012–10022. |
26 | Long, J., Shelhamer, E., Darrell, T. ((2015) ). Fully convolutional networks for semantic segmentation. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3431–3440. |
27 | Menze, B.H., Jakab, A., Bauer, S., Kalpathy-Cramer, J., Farahani, K., Kirby, J., Burren, Y., Porz, N., Slotboom, J., Wiest, R., et al. ((2014) ). The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Transactions on Medical Imaging, 34: (10), 1993–2024. |
28 | Milletari, F., Navab, N., Ahmadi, S.-A. ((2016) ). V-Net: fully convolutional neural networks for volumetric medical image segmentation. In: 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 2016, pp. 565–571. |
29 | Peiris, H., Hayat, M., Chen, Z., Egan, G., Harandi, M. ((2022) ). A robust volumetric transformer for accurate 3D tumor segmentation. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, Lecture Notes in Computer Science, vol. 13435: . Springer, Cham, pp. 162–172. |
30 | Rao, V., Sarabi, M.S., Jaiswal, A. ((2015) ). Brain tumor segmentation with deep learning. In: MICCAI Multimodal Brain Tumor Segmentation Challenge (BraTS), pp. 56–59. |
31 | Ronneberger, O., Fischer, P., Brox, T. ((2015) ). U-Net: convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Lecture Notes in Computer Science, vol. 9351: . Springer, Cham, pp. 234–241. |
32 | Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., Berg, A.C., Fei-Fei, L. ((2015) ). Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115: , 211–252. |
33 | Sandler, M., Howard, A., Zhu, M., Zhmoginov, A., Chen, L.-C. ((2018) ). MobileNetV2: inverted residuals and linear bottlenecks. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 4510–4520. |
34 | Tan, M., Le, Q.V. (2019). MixConv: mixed depthwise convolutional kernels. arXiv preprint arXiv:1907.09595. |
35 | Tan, M., Chen, B., Pang, R., Vasudevan, V., Sandler, M., Howard, A., Le, Q.V. ((2019) ). MnasNet: platform-aware neural architecture search for mobile. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2820–2828. |
36 | Urban, G., Bendszus, M., Hamprecht, F., Kleesiek, J. ((2014) ). Multi-modal brain tumor segmentation using deep convolutional neural networks. In: MICCAI BraTS (Brain Tumor Segmentation) Challenge. Proceedings, Winning Contribution, pp. 31–35. |
37 | van Dijken, B.R., van Laar, P.J., Holtman, G.A., van der Hoorn, A. ((2017) ). Diagnostic accuracy of magnetic resonance imaging techniques for treatment response evaluation in patients with high-grade glioma, a systematic review and meta-analysis. European Radiology, 27: (10), 4129–4144. |
38 | Vijay, S., Guhan, T., Srinivasan, K., Vincent, P.D.R., Chang, C.-Y. ((2023) ). MRI brain tumor segmentation using residual Spatial Pyramid Pooling-powered 3D U-Net. Frontiers in Public Health, 11: , 1091850. |
39 | Vu, M.H., Nyholm, T., Löfstedt, T. ((2021) ). Multi-decoder networks with multi-denoising inputs for tumor segmentation. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Lecture Notes in Computer Science, vol. 12658: . Springer, Cham, pp. 412–423. |
40 | Wang, G., Li, W., Aertsen, M., Deprest, J., Ourselin, S., Vercauteren, T. ((2019) ). Aleatoric uncertainty estimation with test-time augmentation for medical image segmentation with convolutional neural networks. Neurocomputing, 338: , 34–45. |
41 | Wang, W., Chen, C., Ding, M., Yu, H., Zha, S., Li, J. ((2021) ). TransBTS: multimodal brain tumor segmentation using transformer. In: Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part I 24. Springer, pp. 109–119. |
42 | Wang, X., Girshick, R., Gupta, A., He, K. ((2018) ). Non-local neural networks. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 2018, pp. 7794–7803. |
43 | Wang, Z., Zou, N., Shen, D., Ji, S. ((2020) ). Non-local U-Nets for biomedical image segmentation. Proceedings of the AAAI Conference on Artificial Intelligence, 34: (4), 6315–6322. |
44 | Woo, S., Park, J., Lee, J.-Y., Kweon, I.S. ((2018) ). CBAM: convolutional block attention module. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 3–19. |
45 | Zhang, T., Cao, S., Pu, T., Peng, Z. (2021). AGPCNet: attention-guided pyramid context networks for infrared small target detection. arXiv preprint arXiv:2111.03580. |
46 | Zhang, X., Zhou, X., Lin, M., Sun, J. ((2018) ). ShuffleNet: an extremely efficient convolutional neural network for mobile devices. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 6848–6856. |
47 | Zhao, Y.-X., Zhang, Y.-M., Liu, C.-L. ((2020) ). Bag of tricks for 3D MRI brain tumor segmentation. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Lecture Notes in Computer Science, vol. 11992: . Springer, Cham, pp. 210–220. |
48 | Zhou, Z., Siddiquee, M.M.R., Tajbakhsh, N., Liang, J. ((2019) ). UNet++: redesigning skip connections to exploit multiscale features in image segmentation. IEEE Transactions on Medical Imaging, 39: (6), 1856–1867. |
49 | Zikic, D., Ioannou, Y., Brown, M., Criminisi, A. ((2014) ). Segmentation of brain tumor tissues with convolutional neural networks. Proceedings MICCAI-BRATS, 36: (2014), 36–39. |



