Assessing the clinical utility of biomarkers using the intervention probability curve (IPC)

Paez, Rafael; Rowe, Dianna J.; Deppen, Stephen A.; Grogan, Eric L.; Kaizer, Alexander; Bornhop, Darryl J.; Kussrow, Amanda K.; Barón, Anna E.; Maldonado, Fabien; Kammer, Michael N.

doi:10.3233/CBM-230054

Assessing the clinical utility of biomarkers using the intervention probability curve (IPC)

Article type: Research Article

Authors: Paez, Rafael^{a; b} | Rowe, Dianna J.^{a; b} | Deppen, Stephen A.^{b; c; d} | Grogan, Eric L.^{b; c; d} | Kaizer, Alexander^e | Bornhop, Darryl J.^f | Kussrow, Amanda K.^f | Barón, Anna E.^e | Maldonado, Fabien^{a; b; d} | Kammer, Michael N.^{a; b; *}

Affiliations: [a] Department of Medicine, Division of Allergy, Pulmonary and Critical Care Medicine, Vanderbilt University Medical Center, Nashville, TN, USA | [b] Multidisciplinary Approach to Stratification of Lung Cancer with Biomarkers, MASLAB, Vanderbilt University Medical Center, Nashville, TN, USA | [c] Tennessee Valley Healthcare System, Nashville, TN, USA | [d] Department of Thoracic Surgery, Vanderbilt University Medical Center, Nashville, TN, USA | [e] Department of Biostatistics and Informatics, Colorado School of Public Health, University of Colorado Anschutz Medical Campus, Aurora, CO, USA | [f] Department of Chemistry, and The Vanderbilt Institute of Chemical Biology, Vanderbilt University, Nashville, TN, USA

Correspondence: [*] Corresponding author: Michael N. Kammer, PRB 638B, 2220 Pierce Ave, Nashville, TN 37232, USA. E-mail: [email protected].

Keywords: Biomarkers, clinical utility, Intervention Probability Curve, indeterminate pulmonary nodule, net reclassification index

DOI: 10.3233/CBM-230054

Journal: Cancer Biomarkers, vol. Pre-press, no. Pre-press, pp. 1-8, 2023

Received 10 February 2023

Accepted 1 September 2023

Published: 28 October 2023

Get PDF

Supplementary Materials:

Supplementary table and Figure

Abstract

BACKGROUND:

Assessing the clinical utility of biomarkers is a critical step before clinical implementation. The reclassification of patients across clinically relevant subgroups is considered one of the best methods to estimate clinical utility. However, there are important limitations with this methodology. We recently proposed the intervention probability curve (IPC) which models the likelihood that a provider will choose an intervention as a continuous function of the probability, or risk, of disease.

OBJECTIVE:

To assess the potential impact of a new biomarker for lung cancer using the IPC.

METHODS:

The IPC derived from the National Lung Screening Trial was used to assess the potential clinical utility of a biomarker for suspected lung cancer. The summary statistics of the change in likelihood of intervention over the population can be interpreted as the expected clinical impact of the added biomarker.

RESULTS:

The IPC analysis of the novel biomarker estimated that 8% of the benign nodules could avoid an invasive procedure while the cancer nodules would largely remain unchanged (0.1%). We showed the benefits of this approach compared to traditional reclassification methods based on thresholds.

CONCLUSIONS:

The IPC methodology can be a valuable tool for assessing biomarkers prior to clinical implementation.

1.Introduction

Indeterminate pulmonary nodules (IPNs) are a common clinical problem with over 1.6 million detected in the United States annually [1]. Management of IPNs depends on the pretest probability of cancer [2, 3, 4]. Several clinical prediction models have been developed and validated to help estimate this pretest probability [5, 6, 7]. Improving prediction models through the addition of novel biomarkers is the focus of much research. Most methods used to assess the combination of new biomarkers and prediction models focus on accuracy, improvements in the receiver operator characteristic (ROC) area under the curve (AUC), positive and negative predictive values, and likelihood ratios [8, 9, 10]. However, improving diagnostic accuracy does not necessarily translate into improving clinical utility [11].

The reclassification of patients across clinically relevant subgroups is a method used to estimate the potential clinical utility of biomarkers [12, 13]. This approach summarizes the number of patients who are correctly and incorrectly moved between actionable subgroups defined by probability thresholds. For example, in the management of IPNs, patients in the low probability subgroup should undergo CT surveillance, patients in the intermediate probability subgroup should undergo further diagnostic testing, and patients in the high probability subgroup should undergo biopsy or definite surgical resection. A patient with a benign nodule moved from the intermediate to the low probability group would represent a correct reclassification. The bias-corrected net reclassification index (cNRI) is the most robust and commonly used method. This approach accounts for both correct and incorrect movements of intermediate probability patients into high- or low-probability groups, accounting for random movements between groups to correct for overly optimistic results [14].

There are important limitations with this methodology, however. Small changes in probability close to decision thresholds can result in reclassification interpreted as a potential change in management that is unlikely to happen clinically. Conversely, large changes that do not cross thresholds are likely to affect patient management yet would not be captured as such. This “all-or-nothing” approach to threshold-based decisions might be, in practice, inaccurate. Additionally, there are several disconnects between the mathematical derivation of these methods and the clinical reality. First, the thresholds that define risk groups are often based on the likelihood of disease and the potential for cure, but do not consider patients’ preferences or the ability to provide the recommended intervention. For example, in the management of IPNs, a physician at a well-equipped tertiary care center might be more likely to suggest a complex intervention than a physician at a community clinic that does not have dedicated specialists [15]. Second, thresholds are not hard rules, but rather estimates that physicians could use within the clinical context, and physician’s judgement is often more accurate than validated clinical prediction models [16]. Finally, reclassification depends on the model used and the prevalence of cancer in the intended population [7].

Recently, we proposed the Intervention Probability Curve (IPC) as a model for the likelihood of an intervention as a function of the probability of cancer. We showed its use in assessing clinical decision making in lung, prostate, and ovarian cancer [17]. The IPC can be estimated using professional society guidelines or can be obtained by using historical data on past interventions. In this work, we take the next step and present a novel approach to assessing the potential clinical utility of biomarkers, the cumulative change in intervention probability curve (CCIP). To assess the impact of new biomarkers, we calculated the change in the likelihood of intervention for each patient based on their change in probability from pre-test to post-test. The summary statistics of the change in likelihood of intervention over the population represents the potential clinical utility of the added biomarker. We show this application using a recently published biomarker data.

2.Methods

2.1Datasets

The National Lung Screening Trial (NLST) dataset was used to derive the IPC for this analysis and was obtained from the National Cancer Institute. The NLST dataset has been previously described [17, 18]. Briefly, the NLST is a multicenter, randomized controlled trial (RCT) comparing low-dose helical CT with chest radiography for lung cancer screening in current and former smokers. CT images were reviewed by radiologists for the presence of lung nodules, masses, or other abnormalities suspicious for lung cancer. Diagnostic evaluations in response to a positive screening result were collected. Diagnostic invasive procedures included transthoracic CT-guided, bronchoscopic or surgical lung biopsy. Data from nodules detected in the CT arm of the trial was used to calculate the probability of cancer using the Mayo Clinic Model. The data from the screening visit immediately prior the diagnosis of cancer was used in subjects diagnosed with a lung cancer. For patients with benign nodules, the first screening visit with a reported CT abnormality was used.

The combined biomarker model (CBM) dataset was used to show the potential clinical utility of this biomarker combination using the IPC. This dataset has been previously described [19]. Briefly, the dataset includes 457 adult subjects 18–80 years old with incidental or screening detected IPNs 6–30 mm in size (Table S1). Subjects were enrolled across multiple centers in the United States including: Vanderbilt University Medical Center and the Tennessee Valley VA Healthcare System Nashville Campus (N= 171), University of Pittsburgh Medical Center (UPMC, N= 99), the Detection of Early Cancer Among Military Personnel (DECAMP, N= 99) consortium involving 12 clinical centers, and the University of Colorado Denver Hospital and the Rocky Mountain Regional VA Medical Center (UC Denver, N= 88). Participants had prospectively collected serum samples and CT scans with a slice thickness of 3 mm or less at the initial detection of the nodule. Disease outcome was biopsy proven cancer, biopsy proven benign, or two years longitudinal follow-up for benign nodules that were not biopsied (at least 3 years for subsolid nodules). The CBM includes clinical variables, and two biomarkers: a radiomic model derived from chest CTs, and the hs-CYFRA 21-1 assay.

Data obtained from the National Cancer Institute is publicly available. The NLST data use was approved by ECOG-ACRIN (NCI Protocol number A6654T4). Subjects enrolled in the CBM study were prospectively consented, and the study was approved by the IRB. Only deidentified data was used for the purpose of this study. All studies were conducted in accordance with the declaration of Helsinki.

2.2Derivation of IPC curve and statistical methods

The intervention probability curve (IPC) has been previously described. It models the likelihood that an intervention was chosen in practice based on the pretest probability of a cancer calculated using a validated clinical prediction model [17]. Briefly, the cumulative distribution function was used as the IPC curve, and the NLST dataset was used to fit the curve.

𝐼𝑃x=(1-C0-C1)σ⁢2⁢π⁢∫-∞xe-(x-μ)22⁢σ2⁢𝑑x+C0

Patients were grouped into equal width bins based on their pre-test probability of cancer (estimated using the Mayo model) using 20 bins ranging from 0 to 1. In each bin, the number of patients with interventions was divided by the total number of patients in that bin. The binning process was iterated 100 times, using bootstrap sampling (repeated sampling with replacement) in each of the 100 rounds. In each repetition, a 1% Gaussian noise was introduced to the probability associated with each patient, effectively introducing small variations in the signal. This noise was generated by drawing a random number from a Gaussian distribution with a mean of 0 and a standard deviation of 1, which was then multiplied by 0.01 and added to the cancer probability. The average proportion for each bin across these 100 iterations was used to fit the IPC function. These operations, including histogram binning, repeated sampling, and the addition of noise, were carried out using MATLAB R2020b (MathWorks, Natwik MA, USA), while the fitting of the IPC was performed using GraphPad Prism (GraphPad Software, San Diego, CA, USA). All R2 presented are approximate, as calculated according to Kvalseth’s method [20].

The IPC derived from the NLST dataset was applied to the clinical decision of performing a biopsy to obtain a diagnosis for an IPN in the CBM dataset. The pretest probability of cancer was estimated using the Mayo Clinic Model as originally published [5]. The posttest probability of cancer was estimated using the CBM as published, which is derived using a combination of clinical variables, a 10-feature radiomic model, and the hs CYFRA 21-1 [19]. Performance of the CBM and each individual component is illustrated in Figure S1. For each patient, we calculated the difference in probability by subtracting the pre- from the posttest probability of cancer. The intervention probability (IP) was estimated for each patient using the pretest probability (IP𝑃𝑟𝑒) and posttest probability (IP𝑃𝑜𝑠𝑡) in the IPC function fit to the NLST dataset. Then, the change in probability of intervention (ΔIP) was calculated for each patient by subtracting the pretest probability of intervention from the posttest probability of intervention. To construct 95% confidence intervals for all outcomes, the IPC reclassification analysis was performed 1000 times with bootstrap sampling, then the 2.5th and 97.5th percentile of outcomes across the 1000 folds was reported.

3.Results

A histogram of the change in probability of cancer across the patient population is presented in Fig. 1A, with benign (blue) and cancer (red) separate. The median change in probability of cancer for benign nodules was -0.067 (95% CI: -0.091 to -0.049), and for cancers was 0.000 (95% CI: -0.026 to 0.036). To determine the change in the probability of intervention (ΔIP) for each patient, the intervention probability at the pretest score (IP𝑃𝑟𝑒) was subtracted from the intervention probability at the posttest score (IP𝑃𝑜𝑠𝑡). Distribution plots of the ΔIP values are shown in Fig. 1B, for benign (left, blue) and cancer (right, red).

Figure 1.

Population-based assessment of changes in intervention probability. While the mean of the distributions is similar, the spread of distributions shows the change in probability is more tightly clustered around zero in the cancer population than the change in probability.

To capture the effect of the posttest probability on the population, we averaged the ΔIP for all cancers and obtained the population intervention probability for cases (PΔIP𝐶𝑎𝑠𝑒), determined to be 0.1019. Similarly, the ΔIP for all controls is averaged to obtain the population intervention probability (PΔIP𝐶𝑜𝑛𝑡𝑟𝑜𝑙𝑠), determined to be -0.0359. These suggest that in general, patients with cancer are more likely to undergo the intervention after applying the biomarker test, while benign patients are less likely to undergo the intervention.

Figure 2.

Cumulative change in the Intervention Probability for benign and malignant nodules. Panel A shows the Cumulative Change in Intervention Probability for benign nodules. Blue shaded area represents the correct movement of controls with ΔIP < 0. Panel B shows the Cumulative Change in Intervention Probability for malignant nodules. Red shaded area represents the correct movement of cases with ΔIP > 0. AAC: area above the curve, AUC: area under the curve, ΔIP: change in probability of intervention.

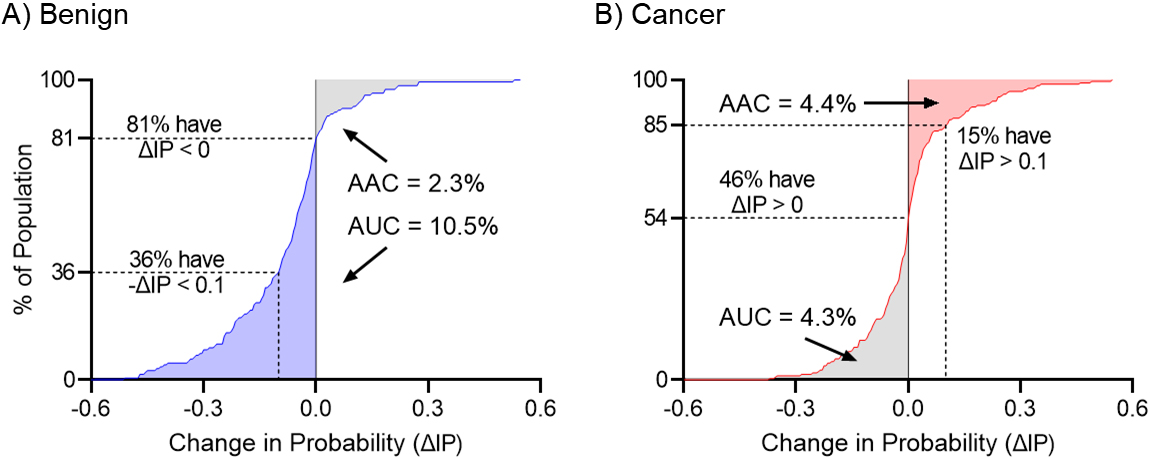
Figure 3.

Graphical representation of the total estimated clinical utility of the biomarker for the (A) IPC and (B) cNRI analysis. The CCIP curve shows where patients were moved in their probability of cancer estimate, and by how much, while the cNRI shows only changes between defined groups. CCIP: Cumulative Change in Intervention Probability, NRI: Net Reclassification Index.

Figure 2 shows the cumulative distribution (CD) of ΔIP for cases and controls. A shift of the CD to the left of ΔIP = 0 represents an overall improvement in the classification for controls (benign nodules). The area under the curve (AUC) is therefore a summary statistic of overall shift. The AUC from -∞ to 0 captures the correct movement of controls (blue shaded area, Fig. 2A), calculated to be 0.105 (95% CI: 0.091–0.131). The area above the curve (AAC) from 0 to ∞ captures the incorrect movement (grey shaded area, Fig. 2A), calculated to be 0.023 (95% CI: 0.016–0.035). A perfect posttest would result in an AAC of 0, meaning no benign patients were more likely to receive an intervention after receiving the biomarker. Subtracting the AAC from the AUC provides the shift in the net probability of intervention equal to 0.082 (95% CI: 0.062–0.109). We performed the same analysis in cases. The correct movement is 1 – AAC from 0 to ∞ (red shaded area, Fig. 2B), calculated to be 0.044 (95% CI: 0.033–0.059). The incorrect movement is the AUC from -∞ to 0 (grey shaded area, Fig. 2B), calculated to be 0.043 (0.034–0.056). The shift in the net probability of intervention for cases is therefore 0.044–0.043 = 0.001 (95% CI: -0.019–0.020). These results suggest a potential decrease in interventions by 8.2% in patients with benign nodules and a potential increase in interventions by 0.1% in patients with cancer after applying the CBM.

The magnitude of the net change in the probability of intervention will depend on the number of true-positives who did not get the intervention and true-negatives who did get the intervention. Therefore, a biomarker with high accuracy may show a small improvement if applied to a clinical situation where patients are already managed appropriately, while a biomarker with moderate accuracy may show a relatively larger improvement if applied to a clinical situation with high rates of over or undertreatment. In the management of IPNs in the NLST setting, the larger benefit of the CBM is seen in benign nodules as many of these patients undergo unnecessary invasive procedures given how similar these nodules look to cancer.

From the cumulative change in the intervention probability curve (CCIP) we can also assess the proportion of subjects that had a change in the ΔIP by a certain amount. For example, the CCIP for controls (Fig. 2A) cross ΔIP = 0 at 0.81 (95% CI: 0.74–0.86), meaning that 81% of controls are moved down (ΔIP < 0). Similarly, the CCIP for cases (red line) crosses ΔIP = 0 at 0.46 (95% CI: 0.43–0.57), meaning that 54% (95% CI 43–57%) of cases were moved up (ΔIP > 0). The proportion of the population that is moved by a certain amount will depend on the clinical context and the nature of the intervention. In many cases, however, only shifts greater than a specified amount may be clinically relevant. For example, let’s assume that only a change greater than 10% in either direction (|ΔIP|> 0.1) is clinically significant. We can see that 36% of controls and 15% of the cases will have this selected clinically relevant change, Fig. 2.

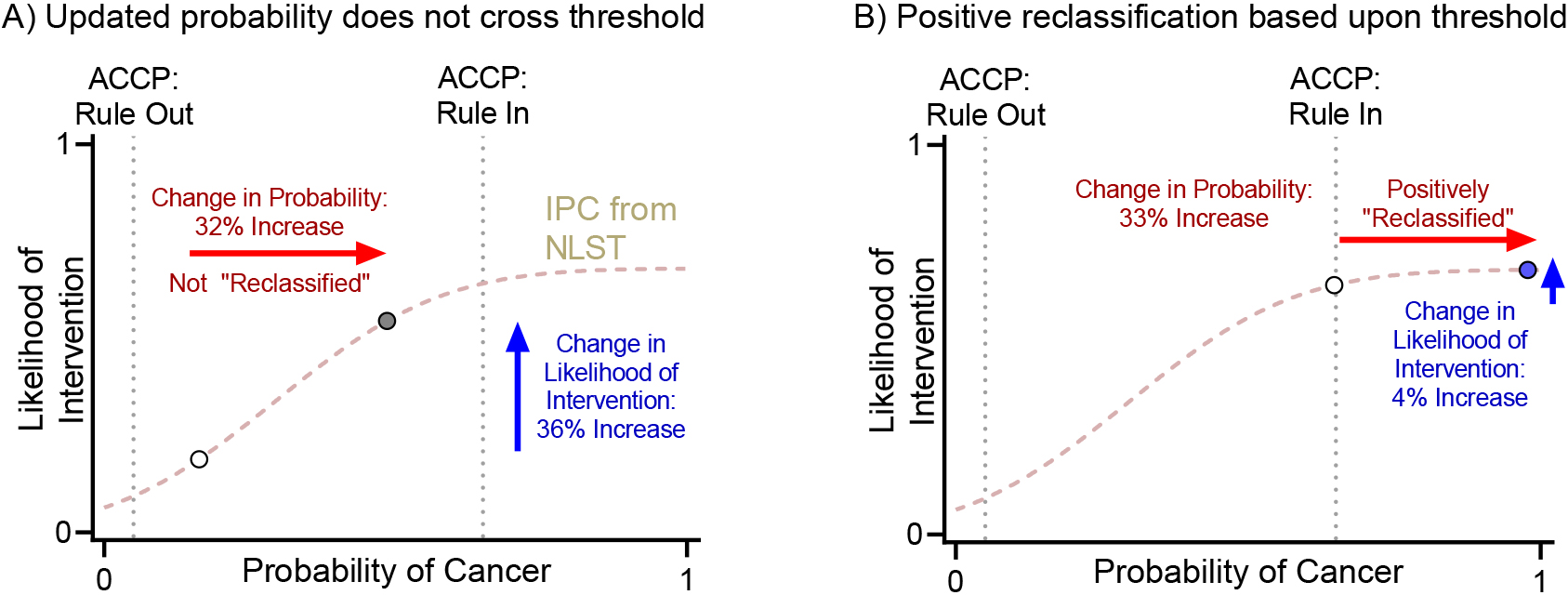
Figure 4.

Reclassification based on clinical thresholds from ACCP guidelines vs change in probability of intervention. ACCP: American College of Chest Physician, NLST: National Lung Cancer Screening Trial.

On a more summary level, we can estimate the impact of total downward movements (ΔIP < 0, blue shaded for benign, and grey shaded for cancer) or upward movements (ΔIP > 0 red shaded for cancer, grey shaded for benign), Fig. 3A. The grey shaded area therefore represents all incorrect movements, and the blue/red shaded area represents all correct movements. When these two plots are overlaid, we can arrive at a simplified representation of the total movement of probability of intervention across cases and controls. On the left side of Fig. 3A (ΔIP < 0), the incorrect movement of cases (grey area from Fig. 2B, AUC = 4.3%, 95% CI 3.5% to 5.6%) is subtracted from the correct movement of controls (blue area in Fig. 2A, AUC = 10.5%, 95% CI 9.0% to 13.0%), resulting in an area between the curves (ABC) = 6.2% (95% CI 4.2% to 8.8%). Similarly, on the right side of the graph in Fig. 3A (ΔIP > 0), the incorrect movement of controls (grey area from Fig. 2A, AUC = 2.3%, 95% CI 1.6% to 3.5%) is subtracted from the correct movement of cases (red area in Fig. 2B, AUC = 4.4%, 95% CI 3.3% to 5.9%), resulting in an ABC = 2.1% (95% CI 0.4% to 3.7%) for improvement in positive changes in probability of intervention.

3.1IPC versus cNRI

From the previous study evaluating the CBM in the context of IPN management, the reclassification of patients across risk groups was tabulated, and the bias-corrected cNRI was calculated [19]. The two-way confusion matrix showing the total number of controls and cases and their classification is shown in Fig. 3B. Here, we used the ACCP risk thresholds of 0.05 for low probability and 0.65 for high probability of cancer. There were 167 benign nodules in the intermediate probability group based on the Mayo Clinic Model. A total of 46 of these were correctly reclassified as low probability and 4 were incorrectly reclassified as high probability after applying the CBM. Likewise, there were 153 malignant nodules in the intermediate probability group, of which 50 were correctly reclassified as high risk and 1 incorrectly reclassified as low risk. The cNRI was 0.148 for the control population and 0.211 for the case population. Here, the cNRI provides an optimistic interpretation of how many cancer patients would benefit from the biomarker test compared to the CCIP analysis. In fact, most of the 50 cases that moved from intermediate probability based on the Mayo Clinic Model (between 5% and 65% probability of cancer, according to American College of Chest Physician guidelines) to high probability (greater than 65% probability of cancer) based on the CBM received the intervention (biopsy) based on an intermediate to high pretest probability of cancer.

4.Discussion

We previously described the IPC, which models the likelihood of an intervention as a function of the probability of cancer and showed its use in assessing clinical decisions in lung, prostate, and ovarian cancer [17]. In this work, we demonstrate that the IPC could also provide a method to estimate the potential clinical utility of biomarkers. Like the cNRI, it provides information regarding the possible clinical benefit of biomarkers but in a continuous rather than a binary way. We highlighted this benefit using data from a recently published CBM that includes clinical information, hs CYFRA-21-1 and a radiomic signature.

Management of IPNs depends on the pretest probability of cancer. Clinical guidelines make recommendations based on probability thresholds. The American College of Chest Physician (ACCP) guidelines define low and high probability thresholds at 0.05 and 0.65 [2]. A mathematical consequence of threshold-based-reclassification is that a change in probability is not counted unless it crosses the threshold, regardless of the absolute magnitude of the change. For example, if a biomarker changes the posttest probability from 0.16 to 0.48, it is not counted as a reclassification, even though this change is large enough to potentially cause a shift in clinical management (increase in probability of intervention from 16% to 48%). Likewise, a biomarker that changes the posttest probability from 0.64 to 0.97 would be counted even though this change is unlikely to impact clinical care (increase in probability of intervention from 64% to 97%). These scenarios are highlighted in Fig. 4.

The IPC illustrates the benefits of analyzing data as continuous rather than using cutoffs. As shown a Fig. 4, the cNRI does not account for large changes in posttest probability within the intermediate probability group that would lead to a change in management. Conversely, small changes around the cutoffs would lead to “reclassification” into low or high probability groups, although these movements would not result in a change in clinical management.

The IPC analysis of the CBM estimated that 8% of the benign nodules could avoid an invasive procedure while the cancer nodules would largely remain unchanged (0.1%). This contrasts with the cNRI analysis which suggests a net reclassification index of 0.148 for the benign population and 0.211 for the cancer population. The reason for this difference, particularly in the malignant population, is the nature of management patterns among moderate-to-high risk patients and low risk patients. Based upon analysis of management decisions within the NLST study, the likelihood of intervention did not increase much once the pretest probability was approximately 55% or higher [17]. Therefore, a biomarker that changes a patient from a 50% to an 70% posttest probability would likely not change management. The cNRI assumes that every cancer patient moved above the high probability threshold will have an increase in intervention, while in practice, that intervention had already occurred in many given the moderately high probability of cancer. This phenomenon can be quantitatively captured by the IPC analysis using empirical data as the foundation for the IPC curve.

One limitation of using the IPC to assess the potential clinical utility of biomarkers is the assumption that the IPC will not change over time. In practice, it is possible that providers might alter their practice pattern as they gain experience with the new biomarker, which would change the IPC. This limitation, however, is common to any method used to assess possible clinical utility. Another potential limitation is the use of NLST and the CBM datasets. All the centers in the CBM study were expert centers and might not reflect common practice in community care settings. Further analysis may reveal that the IPC differs between community clinics and tertiary care centers. Lastly, while this approach provides an estimation of the possible clinical utility of a biomarker, it is not a substitute for real world data collected within the context of a randomized controlled trial.

5.Conclusion

The intervention probability curve is a novel method that could provide useful insights when assessing the potential clinical utility of novel biomarkers. It provides a continuous evaluation that can overcome some of the quantization errors inherent in reclassification analysis. While the IPC is not a substitute for a prospective clinical trial, it can be a valuable tool for assessing biomarkers prior to clinical implementation.

Funding

This work was funded by the NIH (EDRN U01CA15 2662 to ELG, R01CA252964 to ELG and AEB, SPORE 51P50CA058187) and the Gift of Life and Breathe Foundation.

Authors contributions

Conception: RP, MNK, AEB, and FM made substantial contributions to the conception or design of the work.

Interpretation or analysis of data: All authors contributed to the analysis or interpretation of the data.

Preparation of the manuscript: RP and MNK prepared and drafted the manuscript.

Revision for important intellectual content: All authors reviewed the manuscript for important intellectual content and provided final approval of the manuscript.

Supervision: ELG, AEB, FM and MNK.

Supplementary data

The supplementary files are available to download from http://dx.doi.org/10.3233/CBM-230054.

References

[1]	M.K. Gould, T. Tang, I.L. Liu, J. Lee, C. Zheng, K.N. Danforth et al., Recent Trends in the Identification of Incidental Pulmonary Nodules, Am J Respir Crit Care Med 192: (10) ((2015) ), 1208–14.
[2]	M.K. Gould, J. Donington, W.R. Lynch, P.J. Mazzone, D.E. Midthun, D.P. Naidich et al., Evaluation of individuals with pulmonary nodules: when is it lung cancer? Diagnosis and management of lung cancer, 3rd ed: American College of Chest Physicians evidence-based clinical practice guidelines, Chest 143: (5 Suppl) ((2013) ), e93S–e120S.
[3]	M.E. Callister, D.R. Baldwin, A.R. Akram, S. Barnard, P. Cane, J. Draffan et al., British Thoracic Society guidelines for the investigation and management of pulmonary nodules, Thorax 70: (Suppl 2) ((2015) ), ii1–ii54.
[4]	H. MacMahon, D.P. Naidich, J.M. Goo, K.S. Lee, A.N.C. Leung, J.R. Mayo et al., Guidelines for Management of Incidental Pulmonary Nodules Detected on CT Images: From the Fleischner Society, Radiology 284: (1) ((2017) ), 228–43.
[5]	S.J. Swensen, M.D. Silverstein, D.M. Ilstrup, C.D. Schleck and E.S. Edell, The probability of malignancy in solitary pulmonary nodules. Application to small radiologically indeterminate nodules, Arch Intern Med 157: (8) ((1997) ), 849–55.
[6]	A. McWilliams, M.C. Tammemagi, J.R. Mayo, H. Roberts, G. Liu, K. Soghrati et al., Probability of cancer in pulmonary nodules detected on first screening CT, N Engl J Med 369: (10) ((2013) ), 910–9.
[7]	H.K. Choi, M. Ghobrial and P.J. Mazzone, Models to Estimate the Probability of Malignancy in Patients with Pulmonary Nodules, Ann Am Thorac Soc 15: (10) ((2018) ), 1117–26.
[8]	M.S. Pepe, K.F. Kerr, G. Longton and Z. Wang, Testing for improvement in prediction model performance, Stat Med 32: (9) ((2013) ), 1467–82.
[9]	E.W. Steyerberg, A.J. Vickers, N.R. Cook, T. Gerds, M. Gonen, N. Obuchowski et al., Assessing the performance of prediction models: a framework for traditional and novel measures, Epidemiology 21: (1) ((2010) ), 128–38.
[10]	Y. Huang and M.S. Pepe, Assessing risk prediction models in case-control studies using semiparametric and nonparametric methods, Stat Med 29: (13) ((2010) ), 1391–410.
[11]	N.R. Cook, Use and misuse of the receiver operating characteristic curve in risk prediction, Circulation 115: (7) ((2007) ), 928–35.
[12]	N.R. Cook and P.M. Ridker, Advances in measuring the effect of individual predictors of cardiovascular risk: the role of reclassification measures, Ann Intern Med 150: (11) ((2009) ), 795–802.
[13]	M.J. Pencina, R.B. D’Agostino Sr., R.B. D’Agostino, Jr. and R.S. Vasan, Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond, Stat Med 27: (2) ((2008) ), 157–72; discussion 207-12.
[14]	N.P. Paynter and N.R. Cook, A bias-corrected net reclassification improvement for clinical subgroups, Med Decis Making 33: (2) ((2013) ), 154–62.
[15]	N.T. Tanner, J. Aggarwal, M.K. Gould, P. Kearney, G. Diette, A. Vachani et al., Management of Pulmonary Nodules by Community Pulmonologists: A Multicenter Observational Study, Chest 148: (6) ((2015) ), 1405–14.
[16]	N.T. Tanner, A. Porter, M.K. Gould, X.J. Li, A. Vachani and G.A. Silvestri, Physician Assessment of Pretest Probability of Malignancy and Adherence With Guidelines for Pulmonary Nodule Evaluation, Chest 152: (2) ((2017) ), 263–70.
[17]	M.N. Kammer, D.J. Rowe, S.A. Deppen, E.L. Grogan, A.M. Kaizer, A.E. Baron et al., The Intervention Probability Curve: Modeling the practical application of threshold-guided decision making, evaluated in Lung, Prostate, and Ovarian Cancers, Cancer Epidemiol Biomarkers Prev 31: (9) ((2022) ), 1752–1759.
[18]	D.R. Aberle, A.M. Adams, C.D. Berg, W.C. Black, J.D. Clapp, R.M. Fagerstrom et al., Reduced lung-cancer mortality with low-dose computed tomographic screening, N Engl J Med 365: (5) ((2011) ), 395–409.
[19]	M.N. Kammer, D.A. Lakhani, A.B. Balar, S.L. Antic, A.K. Kussrow, R.L. Webster et al., Integrated Biomarkers for the Management of Indeterminate Pulmonary Nodules, Am J Respir Crit Care Med 204: (11) ((2021) ), 1306–1316.
[20]	T.O. Kvalseth, Cautionary Note About R2, Am Stat 39: (4) ((1985) ), 279–285.