Myocardial ischemia simulation based on a multi-scale heart electrophysiology model

1.Introduction

Myocardial ischemia, the leading cause of death worldwide according to the World Health Organization (WHO) [1], significantly affects the normal functioning of the heart due to the occurrence of myocardial ischemia and hypoxia. In clinical practice, electrocardiography (ECG) is widely used to diagnose and monitor various cardiovascular diseases, including arrhythmias, ischemia, and myocardial infarction [2, 3]. Abnormal ECG manifestations of myocardial ischemia are classified into three grades [2, 3]: Grade 1 ischemia (G1I) shows T wave changes, Grade 2 ischemia (G2I) exhibits ST segment changes, and Grade 3 ischemia (G3I) displays terminal QRS distortions. The severity of ischemia increases with the higher grades. The T wave to R wave amplitude ratio and the Q wave and S wave cut-off values are essential indicators to evaluate the normalcy of T waves and ST segments in ECG. The ECG changes resulting from myocardial ischemia hold significant clinical value in terms of early diagnosis, treatment guidance, and prognosis assessment.

Over the past few decades, mathematical models have been extensively applied in the study of cardiac electrophysiology [4]. There has been much progress in the study of the underlying mechanisms of myocardial ischemia. Researchers have explored potential causes of myocardial ischemia using established cell models such as LR91 [5], TNNP06 [6], and Ord [7]. They have demonstrated that hyperkalemia, acidosis, and hypoxia [8, 9] are biochemical factors that contribute to ischemic changes observed on ECG. Through investigation, researchers have found that myocardial ischemia leads to a reduction in inter-cellular electrical coupling [10], an increase in inter-cellular electrical heterogeneity [8], and a slowing down of intertissued conduction [11] in surrounding tissues. These abnormal changes may result in phenomena such as superconductivity, inhibition of conduction, and conduction blocking [12, 13]. Researchers have used multi-scale heart electrophysiological models to simulate Electrocardiographs that are consistent with clinical ischemic Electrocardiographs [14]. They were able to simulate elevation or depression of ST-segments [15] and terminal QRS distortion [16] in areas [17] where myocardial ischemia occurred, as well as the degree of myocardial ischemia [11, 18].

Previous studies on the leading pathological causes of myocardial ischaemia [8, 9, 15, 19] have shown that, in contrast to acidosis and hypoxia, hyperkalaemia is a decisive factor affecting the performance of myocardial ischemia on the ECG. This is because hyperkalemia reduces the ability of sodium ion channels to pass through the cell membrane and the potassium equilibrium potential. This leads to changes in the action potential and decreased excitability of myocardial cells. The changes in the action potential can be transmitted to the body surface via fluid conduction and recorded by ECG. Therefore, changes in the action potential of cells can cause corresponding ECG changes. However, there is no quantitative analysis of the relationship between extracellular potassium concentration ([K ⁺ ]_o) and the grade of myocardial ischemia.

The goal of the present study is to explore the relationship between [K ⁺ ]_o and ECG ischaemic grade. A multi-scale heart electrophysiological model was established. Using this model, we simulated action potentials and Electrocardiographs under various [K ⁺ ]_o conditions and analyzed the relationship between [K ⁺ ]_o and the grade of myocardial ischemia based on established clinical diagnostic criteria.

2.Method

2.1The algorithm of multi-scale heart electrophysiological modelling

This study utilized a multi-scale cardiac electrophysiological model to simulate abnormal ECG resulting from myocardial ischemia. The multi-scale model comprises cell-scale, tissue-scale, and torso-scale models [20].

2.1.1The cellular-scale model

The electrical circuit, as shown in Fig. 1, represents the physical structure of the electrophysiological model of the myocardial membrane [21]. The ionic current in the myocardial membrane is determined by the driving force, which can be measured as an electrical potential difference, and a permeability coefficient with the dimensions of a conductance. The equation of the potassium ion channel of the cell membrane is

(1)

IK=GK⁢(Vm-EK)

Figure 1.

The equivalent circuit of the cell membrane. All values are constant except for RN⁢a, RK and Rl, which are related to the Vm.

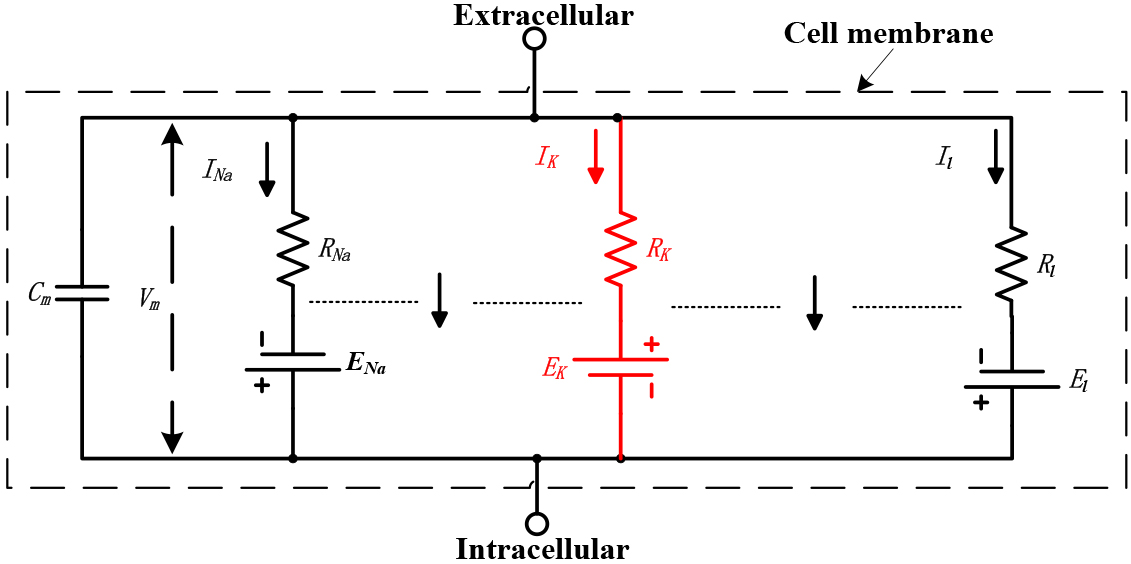
Where, IK is potassium current, GK is potassium conductance, Vm is membrane potential, and EK is equilibrium potential of the Potassium ion.

Ion channels enable the movement of ions between the cell’s interior and exterior, causing alterations in the potential difference across the cell membrane. The homogenized equation of the ion exchange [21] of the cell membrane is

(2)

I=CM⁢d⁢Vd⁢t+Ii

Where, I is the total membrane current density (inward current positive), Ii is the ionic current density, Vm is the displacement of the membrane potential from resting value (depolarization negative), CM is the membrane capacity per unit area, t is time.

The atrial myocyte model used in this article is the CRN model [22]. The total membrane ionic current of the CRN model is given by

(3)

Ii=IN⁢a+It⁢o+I𝐶𝑎𝐿+I𝐶𝑎𝑁𝑎+IK⁢r+IK⁢s+IK⁢1+I𝑁𝑎𝐾+I𝑁𝑎𝑏+IK⁢b+I𝑝𝐶𝑎+I𝐶𝑎𝑏

The ventricle myocyte model used in this article is the ORd model [7]. Endo, M and Epi are three sub-models of the ORd model that differ in their membrane conductances. The total membrane ionic current of the CRN model is given by

(4)

Ii=IN⁢a+I𝑁𝑎𝐿+It⁢o+I𝐶𝑎𝐿+I𝐶𝑎𝑁𝑎+I𝐶𝑎𝐾+IK⁢r+IK⁢s+IK⁢1+INaCa_i+INaCa_ss+I𝑁𝑎𝐾+I𝑁𝑎𝑏+IK⁢b+I𝑝𝐶𝑎+I𝐶𝑎𝑏

Where, Ii is the total membrane current density, It⁢o is the transient outward K ⁺ current, I𝐶𝑎𝐿 is the Ca^{2 +} current through the L-type Ca^{2 +} channel, I𝐶𝑎𝑁𝑎 is the Na ⁺ current through the L-type Ca^{2 +} channel, I𝐶𝑎𝐾 is the K ⁺ current through the L-type Ca^{2 +} channel, IK⁢r is the rapid delayed rectifier K ⁺ current, IK⁢s is the slow delayed rectifier K ⁺ current, IK⁢1 is the inward rectifier K ⁺ current, INaCa_i is the myoplasmic component of Na ⁺ /Ca^{2 +} exchange current, INaCa_ss is the subspace component of Na ⁺ /Ca^{2 +} exchange current, I𝑁𝑎𝐾 is the Na ⁺ /K ⁺ ATPase current, I𝑁𝑎𝑏 is the Na ⁺ background current, I𝐶𝑎𝑏 is the Ca^{2 +} background current, IK⁢b is the K ⁺ background current, I𝑝𝐶𝑎 is the sarcolemmal Ca^{2 +} pump current.

2.1.2The tissue-scale model

The cardiac tissue electrophysiological model can simulate the propagation of action potentials among different regions of the tissue. A new tissue model was developed based on the existing one [23]. This new model includes the heart’s four-chamber structure, different types of cardiomyocytes, and an algorithm for action potential propagation.

Figure 2.

Simplified two-dimensional cross-sectional structure of the heart, with non-cardiomyocytes occupying the white part and cardiomyocytes in the colored part. Each integer coordinate (x,y) within the colored part represents a cell, and cells of the same color belong to the same type. There are ten types of cells, including common cells such as left atrial cells, right atrial cells, Endo cells, ventricular cells, M cells, and Epi cells, as well as conduction cells like sinus node cells, Bachmann-bundle cells, His-bundle cells, and atrioventricular node cells. P represents the virtual electrode.

The four-chamber structure in Fig. 2 represents the frontal view of the heart [24] and contains a total of 103,786 cardiomyocytes, divided into ten different types.

The chosen AP propagation algorithm in this study is the cellular automaton (CA) [25]. In this model, the individual cells serve as the fundamental units of the system, and their states evolve in a spatially distributed manner over time according to the locally defined rules [26]. The AP propagation algorithm is given by

(5)

Ω⁢(t+1,x,y,R)={(Ω⁢(x,y,t,R)+1)modnΩ⁢(x,y,t)<n1,Ω⁢(x,y,t)=0⁢ and ⁢θ⁢(R)≥δt⁢h0,Ω⁢(x,y,t)=0⁢ and ⁢θ⁢(R)<δt⁢h

Where, Ω⁢(t,x,y) is the state of the cell at coordinates (x,y) in Fig. 2 at time t, and Ω⁢(t,x,y) belongs to {0,1,2,…,n-1}. Ω⁢(t,x,y) equals zero, which indicates the cell is resting; Ω⁢(t,x,y) equals 1, which indicates the cell is excited; Ω⁢(t,x,y) belongs to {2,3,…,n-1} which indicates the cell is non-excited; n is the number of the cell states and indicates the duration of the cell AP; θ⁢(R) is the number of activated cells in the neighbourhood range of radius R; δt⁢h is the excitation threshold.

2.1.3The torso-scale model

The aim of the troso-scale model is to calculate the electric potential at a specific location on the surface of the body, which is then represented as a time series known ECG. The unipolar electrogram is a simplified model of ECG computation wich assumes that the human body is a conductor with a constant conductivity [26]. It is based on the concept that the electrical potential difference between a single point on the body surface and a virtual point at the center of the heart is proportional to the activation wavefront of the heart. The model utilizes only one electrode, denoted as P, with coordinates (P⁢x,P⁢y) that indicate the position of the clinical lead. The potential of P is computed by

(6)

ϕP⁢(t)=S0π⁢∑CC⁢s∑i=18(VC-Vi)⁢σi⁢n⁢cos⁡θiσi⁢rP,C2

Where σi is the average conductivity from the ith cell to the P, S0 is a dimensionless constant, C⁢s is the coordinate set of all cells, C is one of the C⁢s with integer coordinates (x,y), VC is the membrane potential of C, Vi is the membrane potential of the ith neighbour of C, σi⁢n is the conductivity of the intracellular fluid, θi is the angle between the vector of C to P and the vector of the C to ith neighbour, rP,C is the distance from P to C.

2.1.4The model for the multi-scale heart electrophysiological model

After developing models at the cellular, tissue, and torso scales, they were integrated to form a multiscale cardiac electrophysiological model. This model establishes a connection between ECG signals and the electrical activity of myocardial cells. The multi-scale heart electrophysiological modelling algorithm can be broken down into four steps: parameter initialization, computation of the four action potentials, simulation of action potential propagation, and computation of virtual electrocardiogram.

1) Parameters initialization.

The main parameters of the computational models such as Table 1.

Table 1

The main parameters

Parameters	Value
Parameters of cell-scale model
CL: Action potential duration of the cell	500 ms
Nao: Extracellular sodion concentration	140 mM
Cao: Extracellular calcium concentration	1.8 mM
Ko: Extracellular potassium concentration	5.4 mM
Paramaters of tissue-scale model
Moore_SN: Moore radius of sinus node cells	0.05 m⋅s - 1
Moore_Atr: Moore radius of left and right atrial cells	1 m⋅s - 1
Moore_BB: Moore radius of Bachmann-bundle cells	1.7 m⋅s - 1
Moore_HB: Moore radius of His-bundle cells	1.7 m⋅s - 1
Moore_AVN: Moore radius of atrioventricular node cells	0.05 m⋅s - 1
Moore_VS: Moore radius of ventricular septum cells	1 m⋅s - 1
Moore_Endo: Moore radius of Endo cells	4 m⋅s - 1
Moore_M: Moore radius of M cells	1.5 m⋅s - 1
Moore_Epi: Moore radius of Epi cells	1 m⋅s - 1
δt⁢h: Excitation threshold	2 pieces
T_VP: Ventricular septum activation time	190 ms
Parameters of torso-scale model
P: Coordinates of the virtual electrode	[26 cm, 5 cm]
σi: Average conductivity of all substances outside the cell	0.74 S⋅m - 1
σi⁢n: Conductivity of the intracellular fluid	1.28 S⋅m - 1
S0: Dimensionless constant	100
Cells: A coordinate set of all cardiomyocytes	Coloured in Fig. 3b
HB_Period: Duration of a single heartbeat	700 ms

2) Computation of the four action potentials.

We stimulated the CRN and the ORd models with an external current of -80 μA/μF for a duration of 0.5 ms and solved them using the forward Euler algorithm. The resulting solutions were then discretized at intervals of ten to obtain the action potentials Atr_ap, Endo_ap, M_ap, and Epi_ap for for their respective cell types.

3) Simulation of the AP propagation.

To simulate the propagation of action potentials (AP), two three-dimensional matrices are defined: State [t, x, y] and MP [t, x, y]. The State matrix represents the cell states at time t, and the MP matrix reflects the membrane potential of each cell at time t. These matrices are initialized as a zero matrix. Over time, they are updated to simulate the propagation of the AP through the tissue. The initial value of t is set to 0 and its unit is defined as a step, where one step is equivalent to 10 ms. The state of the myocardial cells at coordinate (x, y) is updated according to Eq. (5).

4) Computation of virtual ECG.

Since an ECG is essentially a time series, the sequence Virtual_ECG is represented by [φP⁢(0),φP⁢(1),…,φP (HB_Period)] where each ϕP⁢(t) value is computed using Eq. (6) and corresponding M⁢P [t,x,y].

3.Results

3.1Normal model

Using the algorithm of multi-scale heart electrophysiological modeling, we performed simulations to capture the occurrence and propagation of AP, as well as the corresponding virtual ECG.

Figure 3.

The simulation of normal conditions. (a) Four action potentials; (b) AP propagation in the heart; (c) virtual ECG.

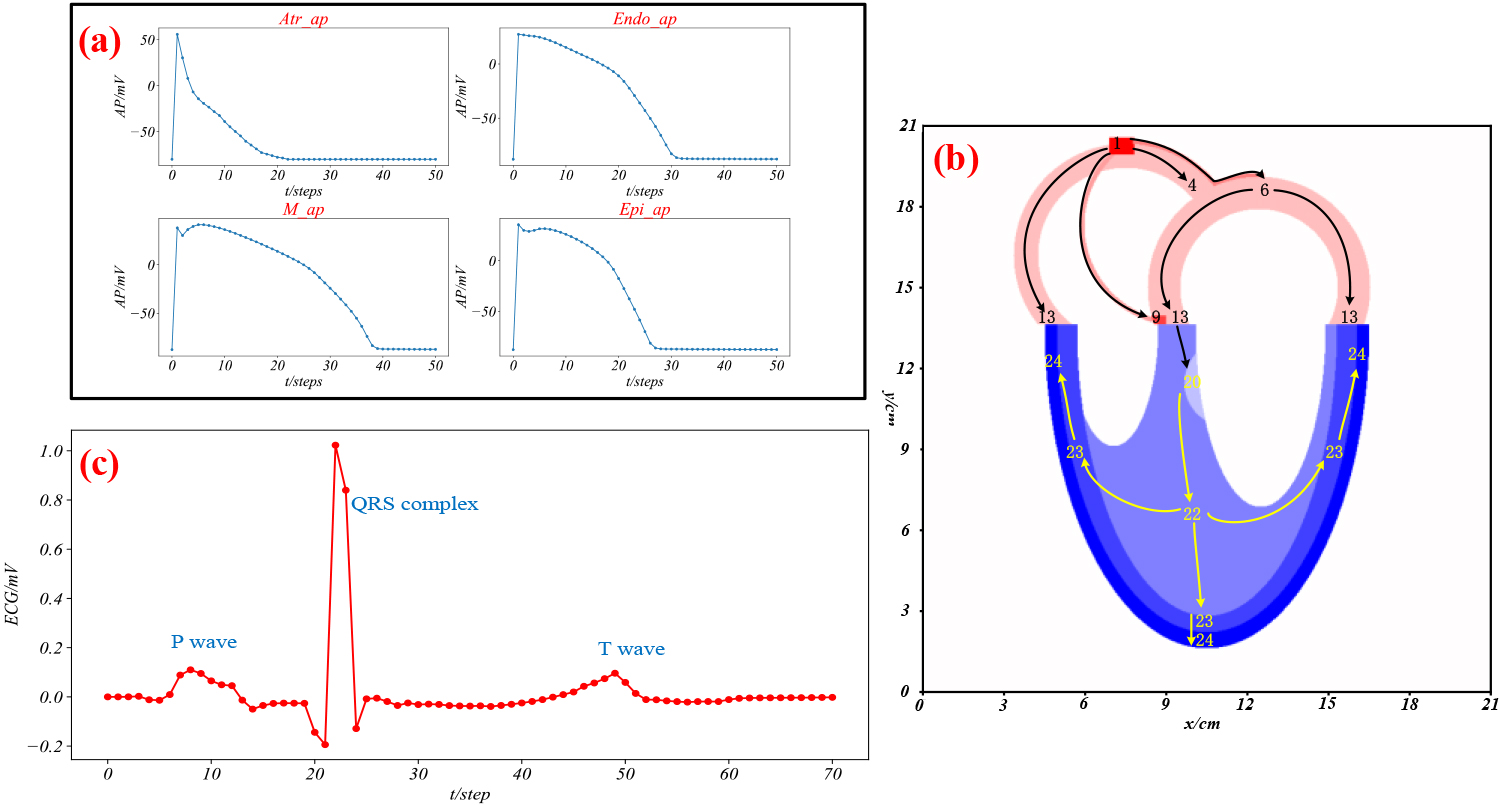
Figure 3a represents the action potentials generated in the atrium, Endo, M, and Epi when stimulated. Figure 3b illustrates the spatiotemporal dynamics of the AP propagation, where the arrows represent the direction of propagation, and the numbers indicate the time in steps when the cells at that location start to depolarize in a single heartbeat cycle. Figure 3c shows a simulated ECG in lead V6, exhibiting P, QRS, and T waves.

3.2Ventricular ischemia

Next, we simulated the action potentials and ECG of ventricular ischemia by adjusting the values of Epi_Ko or Endo_Ko. The results are shown in Fig. 4.

Figure 4a displays the trends of Epi_AP and ECG for different values of Epi_Ko.

As Epi_Ko increases from 3.3 to 11.0, APD90 decreases, RP increases, CV_SQ and AV_TR increase. The duration of Epi_AP shortens, resting potential of Epi_AP elevates, and ST-T of ECG elevates. As Epi_Ko increases from 3.3 to 11.0, the 90% repolarization time (APD90) of steps drops, RP (resting potential) increases, S wave and Q wave cutoff value (CV_SQ) and amplitude ratio of the T wave to the R wave (AV_TR) increase. The duration of Epi_AP shortens, the resting potential of Epi_AP elevates, and ST-T of ECG elevates. However, when Epi_Ko equals 11.1, there is a significant decrease in APD90 and PP, an increase in CV_SQ, and AV_TR becomes non-existent. The Epi_AP depolarization potential decreases, and ECG shows elevated ST-segment and terminal QRS. As Epi_Ko increases from 11.1 to 12.0, the APD90 shortens, PP decreases, CV_SQ slowly increases, and AV_TR is non-existent. Simultaneously, the ST-segment of ECG elevates, and terminal QRS of ECG distorts. Figure 4b shows the general changes trend of Endo_AP and ECG when Endo_Ko increases from 3.3 to 12.0. The changes trend of Endo_AP is the same as that of the Epi_AP, while the changes trend of ECG is the opposite. Based on the simulation results of Epi_Ko or Endo_Ko at different values, we have summarized the ischemia grades in Table 3.

Table 3

The Relationship between Epi_Ko, Endo_Ko and the ischemia grade

Ischemia grade	Endo_Ko/mM	Epi_Ko/mM
G1I	3.3∼4.9	5.4
	5.4	3.3∼3.6
Normal	5.0∼7.5	5.4
	5.4	3.7∼5.9
G2I	7.6∼11.0	5.4
	5.4	6.0∼10.4
G3I	11.1∼12.0	5.4
	5.4	10.5∼12.0

Figure 4.

The simulation of Ventricular ischemia. (a) Epi ischemia; (b) Endo ischemia. The arrows illustrate the general trend of changes in action potentials and ECGs when Epi_Ko and Endo_Ko range from 3.3 to 12.0. Both the AP graph and the ECG graph have the horizontal axis representing time in milliseconds (ms), and the vertical axis representing membrane potential and electrode potential in millivolts (mV), respectively. The APD90 graph and the Rp, PP graph have Epi_Ko (mM) on the horizontal axis and 90% repolarization time in steps (ms), resting potential, and peak potential (mV) on the vertical axis, respectively. The CV_SQ graph and the AV_TR graph have Epi_Ko (mM) on the horizontal axis and the cutoff value at the end of the S wave and the start of the Q wave (mV) and the amplitude ratio of the T wave to the R wave (unitless) on the vertical axis, respectively. The axes of (b) are the same as those in (a).

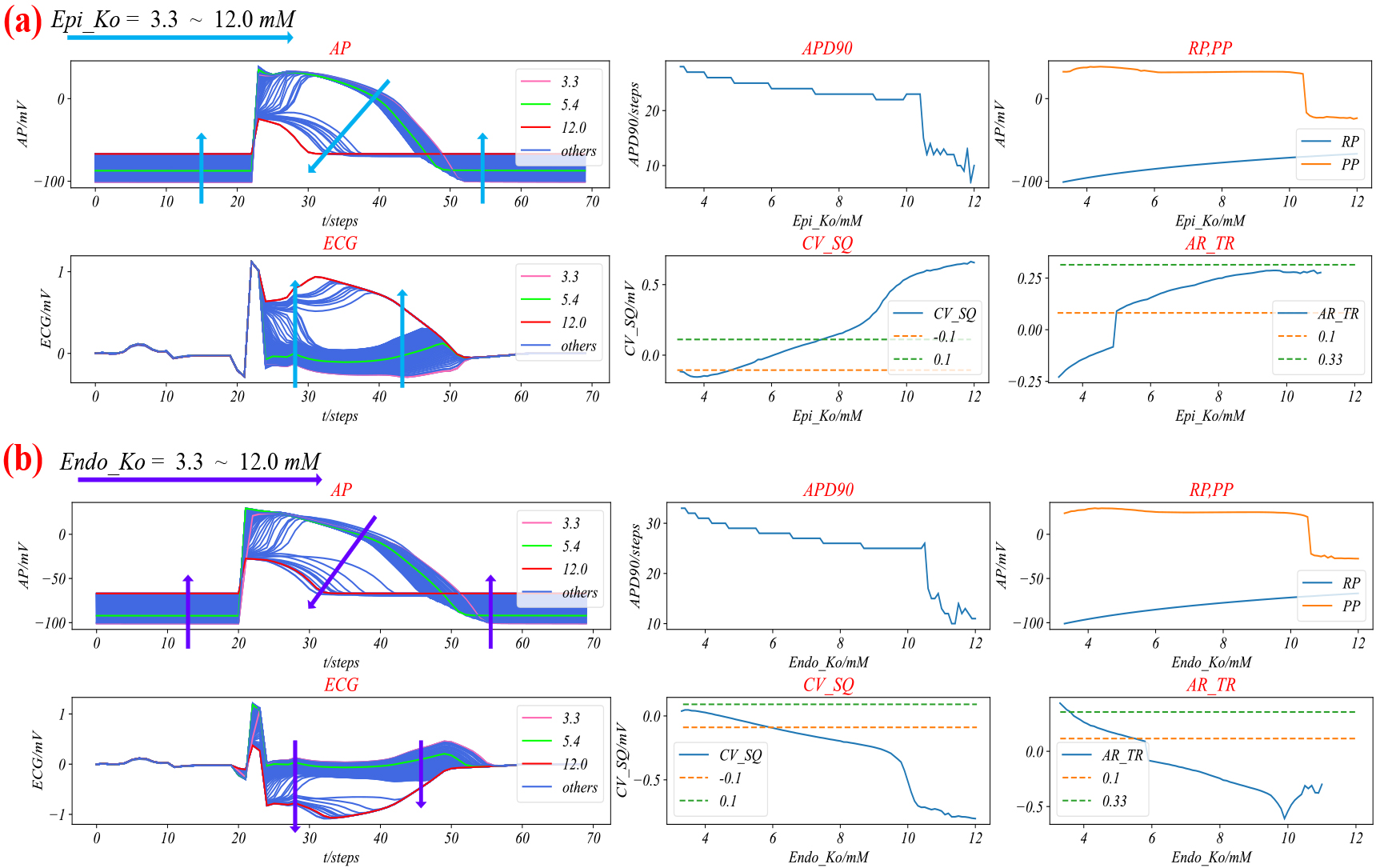
Figure 5.

Three grades of Epi or Endo ischemia. (a) Three grades of Epi ischemia, where Endo_Ko is equal to 5.4 always, and that Epi_Ko is equal to 5.4, 3.3, 8.0 and 12.0, respectively; (b) Three grades of Endo ischemia, where Epi_Ko is equal to 5.4 always, Endo_Ko is equal to 5.4, 3.3, 8.0 and 12.0, respectively.

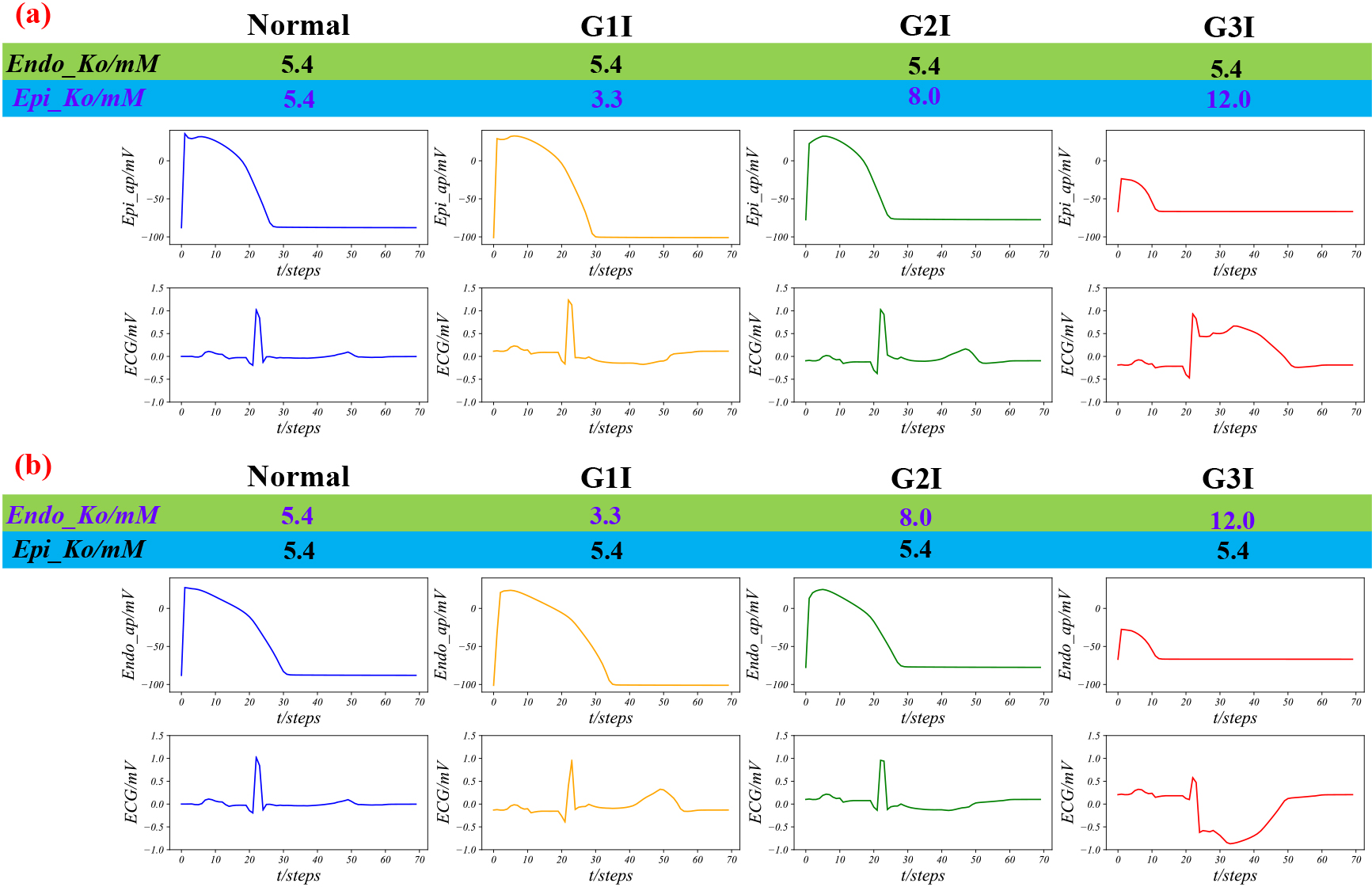
We simulated three grades of Epi ischaemia and Endo ischaemia, by adjusting suitable Epi_Ko and Endo_Ko based on Table 3, as shown in Fig. 5. As shown in Fig. 5a, from left to right, the duration of AP slowly extends and then abruptly shortens with the decrease of depolarizing potential from left to right. Meanwhile, the T wave and the ST-segment of the ECG first elevate and then decrease, and finally, the terminal QRS shows low distortion. Similarly, in Fig. 5b, the variation of AP is the same as that of Fig. 5a, while the trend of changes in the ECG is opposite. The T wave and the ST-segment of the ECG are depressed and elevated, respectively, and finally, the terminal QRS shows high distortion.

4.Discussions

In this study, we used the established multi-scale cardiac electrophysiological model to simulate the process of generating ECG under normal conditions. The action potentials depicted in Fig. 3a are consistent with experimental data [7]. Figure 3b illustrates the AP the propagation of the action potential (AP) in the heart [27]. The virtual ECG shown in Fig. 3c displays trends of the Q wave, QRS complex, and T wave consistent with real ECG recordings.

Next, we used the model to simulate abnormal ECG resulting from myocardial ischemia. As shown in Fig. 4, as [K ⁺ ]_o increases, the APD90 for Epi_AP and Endo_AP decreases, RP increases. When Epi_Ko equals 10.5 or Endo_Ko equals 11.1, the APD90 and PP decrease dramatically. This is due to the massive inactivation [28] of sodium ion channels in the Epi and Endo cell membranes. Despite their physiological similarities, the conductivity of [K ⁺ ]_o ion channels in Epi cells is 1.3 times higher than that of Endo cells [7], leading to distinct electrical properties and responses to stimuli.

Furthermore, with increasing Epi_Ko, the CV_SQ and AV_TR of the ECG increase, while with increasing Endo_Ko, the CV_SQ and AV_TR of the ECG decrease. This is due to the V6 lead used in the ECG simulation. The distance between Endo, M and Epi cells to V6 increases sequentially. When Epi cells are ischemic, t their low membrane potential creates a positive potential between them and M cells, resulting in an elevated ST-T segment of the ECG. When Endo cells are ischemic, a negative potential is formed between them and M cells, depressing the ST-T segment of the ECG. This is consistent with findings based on data from clinical trials [29, 30].

The study results indicate that the degree of ischemia can be classified into three categories: G1I, G2I, and G3I, depending on the level of [K ⁺ ]_o. Specifically, G1I occurred when [K ⁺ ]_o was lower than normal, G2I occurred when [K ⁺ ]_o was slightly higher than normal, and G3I occurred when there was significant inactivation of sodium channels. The present discovery establishes a direct relationship between [K ⁺ ]_o levels and the severity of ischemia. The study results reveal that [K ⁺ ]_o levels decrease initially and then gradually increase during the ischemic process, which challenges the common belief that ischemia is primarily caused by elevated [K ⁺ ]_o levels [15, 29]. One reason for the difference in our findings from what is commonly believed about the role of [K ⁺ ]_o in ischemia could be that [K ⁺ ]_o levels are not regularly monitored in the early stages of acute heart problems. Additionally, the T wave in ECG is not commonly regarded as a direct marker of myocardial ischemia, which may lead to the underestimation of [K ⁺ ]_o levels and the oversight of their relationship with the severity of ischemia [30, 31]. As a result, [K ⁺ ]_o levels may go undetected, and their relationship with the severity of ischemia may be overlooked.

5.Conclusions

The finding that the abnormal [K ⁺ ]_o levels can lead to ischemia, and that the more [K ⁺ ]_o deviates from normal, the more severe the ischemia. We classified the grade of ischemia into three categories based on [K ⁺ ]_o levels: G1I, G2I, and G3I. In particular, we propose a new viewpoint that [K ⁺ ]_o levels may be lower than normal during grade 1 ischemia, which differs from the commonly held belief that myocardial ischemia is caused by an increase in extracellular potassium concentration. This unusual finding provides a new perspective on the mechanisms underlying myocardial ischemia and has the potential to lead to the development of new diagnostic and treatment strategies.