Application of translation wavelet transform with new threshold function in pulse wave signal denoising

1.Introduction

The pressure sensor is widely used for pulse wave collection because it simulates the pulse manipulation of traditional Chinese medicine and collects pulse wave information under manual, air bag or mechanical pressurization techniques. By applying different pressure to the pressure sensor, the intensity of the pulse wave first increases to a maximum point and then fades. The pulse wave corresponding to the strongest point is called the pulse wave under the optimal pulse pressure. It is usually used to assess human body’s physiological and pathological information. Pulse wave signal de-noising is the first and a critical step in physiological characteristics analysis.

The noise carried by the pulse wave mainly includes the power frequency noise, EMG noise and respiratory noise. Power frequency noise can be removed by 50 Hz notch filter. EMG noise removal methods mainly include traditional filtering, adaptive filtering, mathematical morphology filtering, Kalman filtering, ICA filtering, artificial neural network algorithm, wavelet filtering, etc. In the traditional filtering methods, FIR filtering and smooth filtering are the most commonly used. FIR filtering method is usually designed as a low-pass filter to remove high-frequency noise. However, the processing accuracy of the band boundary is low so the useful information of the pulse wave signal is often filtered out [1, 2, 3]. The smoothing filter is actually a linear filter whose window size affects the filtering effect and the general window width has an empirical value. If the window is too wide, it will roughly be too smooth on the other hand, when the window is too narrow, the denoising effect is not ideal [4]. The filter used in the adaptive method has an automatic updating mechanism of filter coefficients. Based on minimum mean square error (MSE) of the filtering result and the reference signal, a new set of filter coefficients are generated by continuously superimposing and updating the adaptive updating algorithm, so as to obtain the theoretically optimal filter. It can be seen from the principle of adaptive filter that the selection of reference signal is an important aspect to determine the merits of the adaptive filter. However, in practice it is difficult to use adaptive filtering directly, since the signal characteristics cannot be ascertained in advance and then select a suitable reference signal [5, 6, 7]. The mathematical morphology filtering method is derived from the image filtering algorithm, which is mainly used to expand and erode the signal, and the open-close operation completes the pulse wave filtering. However, the processed pulse wave produces a spike pulse phenomenon, introduces additional noise, and brings errors in the subsequent pulse detection [8, 9, 10, 11]. Kalman filter usually uses input and output signals to evaluate the system state and realize filtering.. The parameters of Kalman filter change with time, and the optimal filter can be obtained only when the prior statistical characteristics of the signal and noise are known [12, 13, 14]. ICA filtering was first applied in the separation of sound signals however, it requires either less or equal number of signal sources of the observation channels. For one-dimensional signal pulse waves, it is necessary to establish multiple virtual channels and expand them into a matrix. In addition, solving the optimal solution of the mixed matrix requires a large number of iterations with high complexity [15, 16]. The artificial neural network method can be regarded as an optimal filter however, the parameters of the filter need a lot of memory training. At times, the effect of noise removal for the pulse wave without training is not very good.

Since the wavelet transform can be used to decompose the signals at different scales, wavelet decomposition has become one of the most popular methods used for pulse wave denoising in recent research. The wavelet filtering algorithm mainly includes three processes: wavelet decomposition, filtering and signal reconstruction. Wavelet decomposition mainly decomposes the signal through wavelet transform to obtain wavelet coefficients. Filtering mainly uses one threshold functions (soft threshold, hard threshold and others) to get the processed wavelet coefficients. Whereas, signal reconstruction uses the processed wavelet coefficients to get the filtered signal. The hard threshold function can highlight the detailed features l, but it introduces the Gibbs phenomenon. The soft threshold smoothens the signal as a whole, but may result in losing the detailed features of the signal [17, 18, 19, 20].

In this paper, a new wavelet denoising method based on the translation invariant wavelet with new threshold function is proposed. According to the soft threshold function and the hard threshold function’s characteristics and combine the hyperbolic tangent function and the exponential function’s characteristics, a new threshold function.is constructed. The TIWT method is used to attenuate the pseudo-Gibbs phenomenon and highlight the detailed characteristics of the pulse wave. As compared to the traditional wavelet filtering algorithm, the experiments show that the novel algorithm can better maintain the pulse wave geometric characteristics and has a higher signal to noise ratio (SNR).

The paper is divided in four parts: (1) Introduction: This section describes the current research progress of pulse wave denoising at home and abroad, outlines the significance and the innovative aspect of the present work. (2) Materials and Methods: In this section, the pulse wave acquisition method is introduced and the optimal pulse wave is obtained through the preprocessing method. Subsequently, the derivation process of the new threshold function, the process of the TIWT denoising method and the method of evaluating the algorithm are elaborated. (3) Algorithm results: By introducing the selection method of wavelet basis and the decomposition level, the results are obtained. By comparing the soft threshold and the hard threshold, the effectiveness of the algorithm is proved (4) Conclusion: Based on the findings, this section summarizes the process and significance of the entire algorithm and the application value of the algorithm.

2.Method

2.1Pulse wave signal acquisition

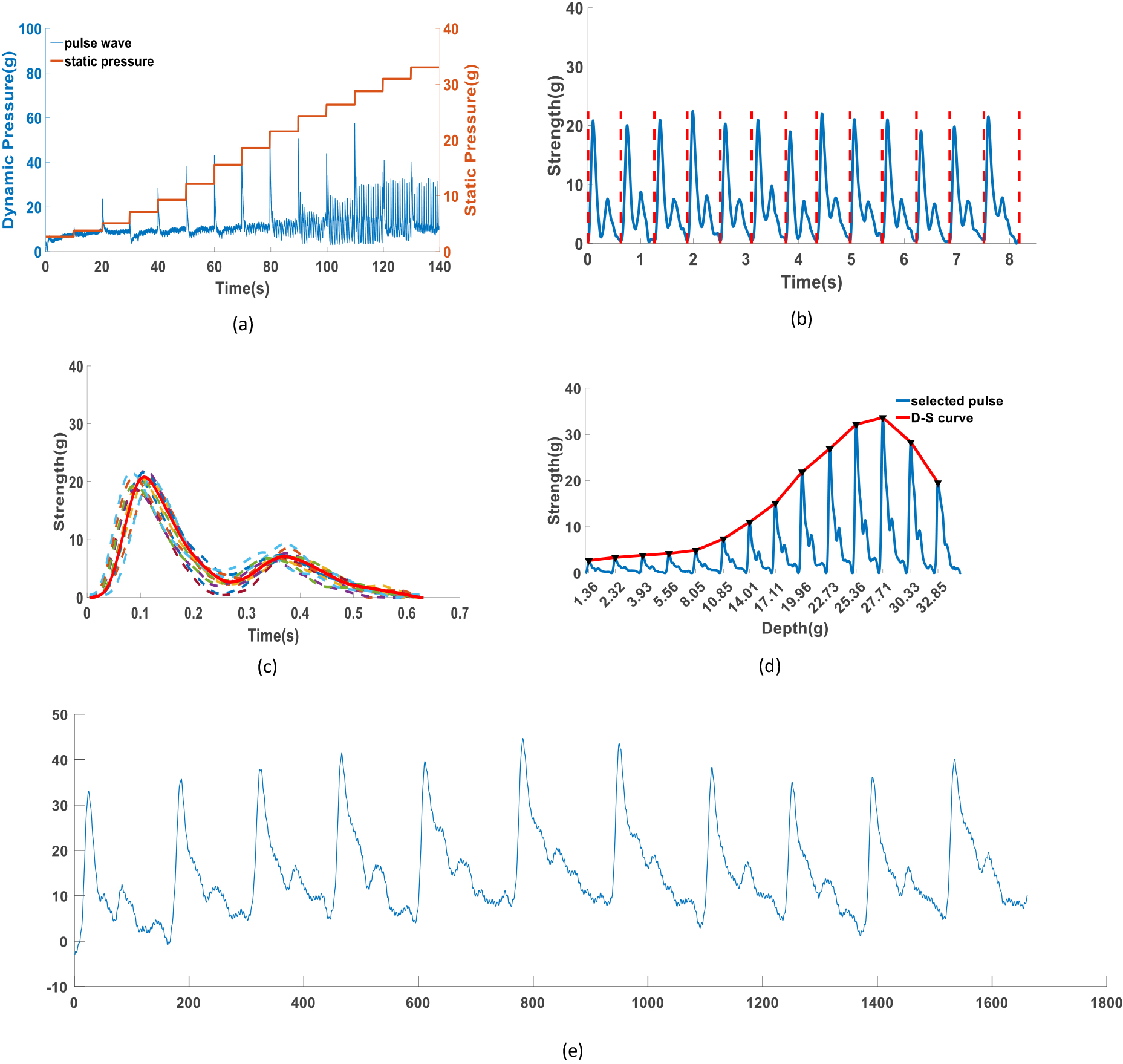
Figure 1a depicts the self-developed multi-channel Chinese medicine pulse detector equipment to complete the acquisition of pulse wave signals. The acquisition probe of the pulse detector has a built-in coincidence sensor, which simulates the pulse manipulation of traditional Chinese medicine by applying 10–150 mm Hg pressure through the air bag to collect the pulse wave information under different gradients of pressure as shown in Fig. 1b. The pulse wave data acquisition time is 10 seconds at each air pressure. Figure 2a shows the pulse wave data collected during the completion process.

Figure 1.

(a) The self-developed multi-channel Chinese medicine pulse detector equipment. (b) Composite sensor built in the acquisition probe.

Figure 2.

(a) Single channel pulse sensor signal. (b) Period division of pulse wave. (c) Obtain single-cycle pulse wave. (d) Obtain D-S curve (e) Optimal pulse wave sequence.

2.3New threshold wavelet filtering

2.3.1Derivation process of new threshold function

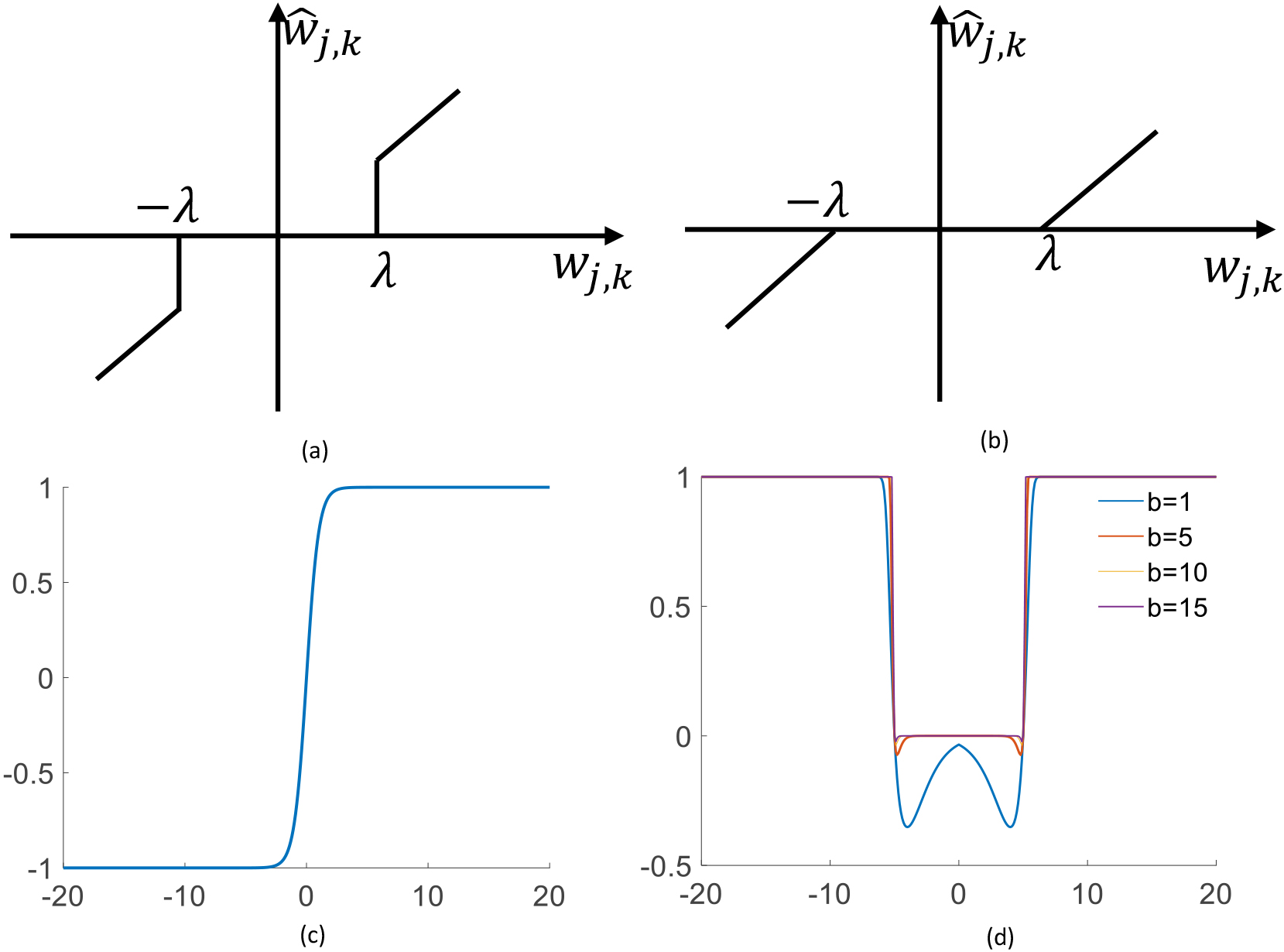
The hard threshold function and soft threshold function’s schematic diagrams are shown in Fig. 2a and b respectively. From the graphics analysis, we find that the threshold and the hard threshold functions have their inherent shortcomings. In the hard threshold method, discontinuities (the expression ω^j,k) exist at λ point and -λ point, which cause the pulse wave signal to oscillate at the mutation point namely, the pseudo-Gibbs phenomenon. However, the soft threshold method can overcome this defect but from the perspective of graphics and expressions, although the value of ωj,k^ and its relative value of ωj,k are continuous, there is a constant deviation, which leads to the weakening or even disappearance of the detailed features of the de-noised pulse wave.

(1)

wj,k^={wj,k,|wj,k|⩾λ0,|wj,k|<λ

Equation (1) is the hard threshold function expression. Where, wj,k is the wavelet coefficient.

(2)

wj,k^={𝑠𝑖𝑔𝑛⁢(wj,k)⁢(|wj,k|-λ),|wj,k|⩾λ0,|wj,k|<λ

Equation (2) is the soft threshold function expression. Where, sign⁢() is a symbolic function, threshold value λ=δ⁢2⁢ln⁢N/ln⁢(j+1) and δ=median⁢(abs⁢(wj,k))/0.6745.

In order to retain the de-noised pulse wave’s detail characteristics, and weaken the pseudo-Gibbs phenomenon, and improve SNR, according to the characteristics of soft and hard threshold functions, we need to build a new threshold function. This function should be proposed based on the following points: (1) Ensure that the wavelet threshold value is continuous at ±λ and (2) The deviation of wavelet coefficients of useful signals can be minimized.

From the analysis of Eqs (1) and (2), we replace these by the following formula:

(3)

f⁢(wj,k)=𝑠𝑖𝑔𝑛⁢(wj,k)⁢(|wj,k|-λ∗a)

Where, a is the real number with a value range [0,1]. When a= 0, the above formula is evolved into the hard threshold function. When a= 1, the above formula is evolved into the hard threshold function.

Figure 3.

(a) Schematic diagram of hard threshold function. (b) Schematic diagram of soft threshold function. (c) Schematic diagram of hyperbolic tangent function. (d) g⁢(wj,k) function curve under different b values.

When a ∈ (0,1), the zero position of the abscissa is wj,k=±λ∗a. Here we introduce a function g⁢(wj,k), so that Eq. (3) can make wj,k^ tend to zero when wj,k∈(-λ,+λ), and keep wj,k^ linear when wj,k∈(-∞,-λ)⁢U⁢(+λ+∞). Here, it is necessary for g⁢(wj,k) to have a value that tends to zero at (-λ,+λ) and 1 at (-∞,-λ)⁢U⁢(+λ+∞). As shown in the Fig. 3a, the tangent function is an odd function and ranges in (-1, +1).

(4)

𝑙𝑖𝑚wj,k→+∞tanh⁢(wj,k)=1

(5)

𝑙𝑖𝑚wj,k→-∞tanh⁢(wj,k)=-1

In order to make the hyperbolic function meet the requirements, we introduce an exponential function and add a regulating factor to the exponential function. The expression of g⁢(wj,k) is as follows:

(6)

g(wj,k)=tanh(e∧(b∗(|wj,k|-λ))∗(|wj,k|-λ))

Where, b is an adjustable factor, b⩾1.

Thus, the novel wavelet threshold function can be expressed as follows:

(7)

wj,k^=𝑠𝑖𝑔𝑛(wj,k)(|wj,k|-λ∗a)∗tanh(e∧(b∗(|wj,k|-λ))∗(|wj,k|-λ))

In Eq. (7), since g⁢(wj,k) function is a continuous function, the expression has a continuous property at ±λ, and when |wj,k|⩾λ, the function has a higher derivative property.

When wj,k>0:

(8)

𝑙𝑖𝑚wj,k→+∞wj,k^wj,k=𝑙𝑖𝑚wj,k→+∞𝑠𝑖𝑔𝑛⁢(wj,k)⁢(|wj,k|-λ∗a)∗tanh⁡(e(b∗(|wj,k|-λ))∗(|wj,k|-λ))wj,k=𝑙𝑖𝑚wj,k→+∞𝑠𝑖𝑔𝑛⁢(wj,k)⁢(1-λ∗a∗tanh⁡(e(b∗(|wj,k|-λ))∗(|wj,k|-λ))wj,k)=1-λ∗a

When wj,k<0:

(9)

𝑙𝑖𝑚wj,k→-∞wj,k^wj,k=𝑙𝑖𝑚wj,k→-∞𝑠𝑖𝑔𝑛⁢(wj,k)⁢(|wj,k|-λ∗a)∗tanh⁡(e(b∗(|wj,k|-λ))∗(|wj,k|-λ))wj,k=𝑙𝑖𝑚wj,k→-∞-(1+λ∗a∗tanh⁡(e(b∗(|wj,k|-λ))∗(|wj,k|-λ))wj,k)=-1+λ∗a

In Fig. 4, when a= 0, the function tends to small soft threshold discriminant function while when a= 1, the function tends to wavelet hard threshold discriminant function. When a ∈ (0,1), the function is between soft threshold and hard threshold.

Figure 4.

The change curve of the new threshold function under different a values.

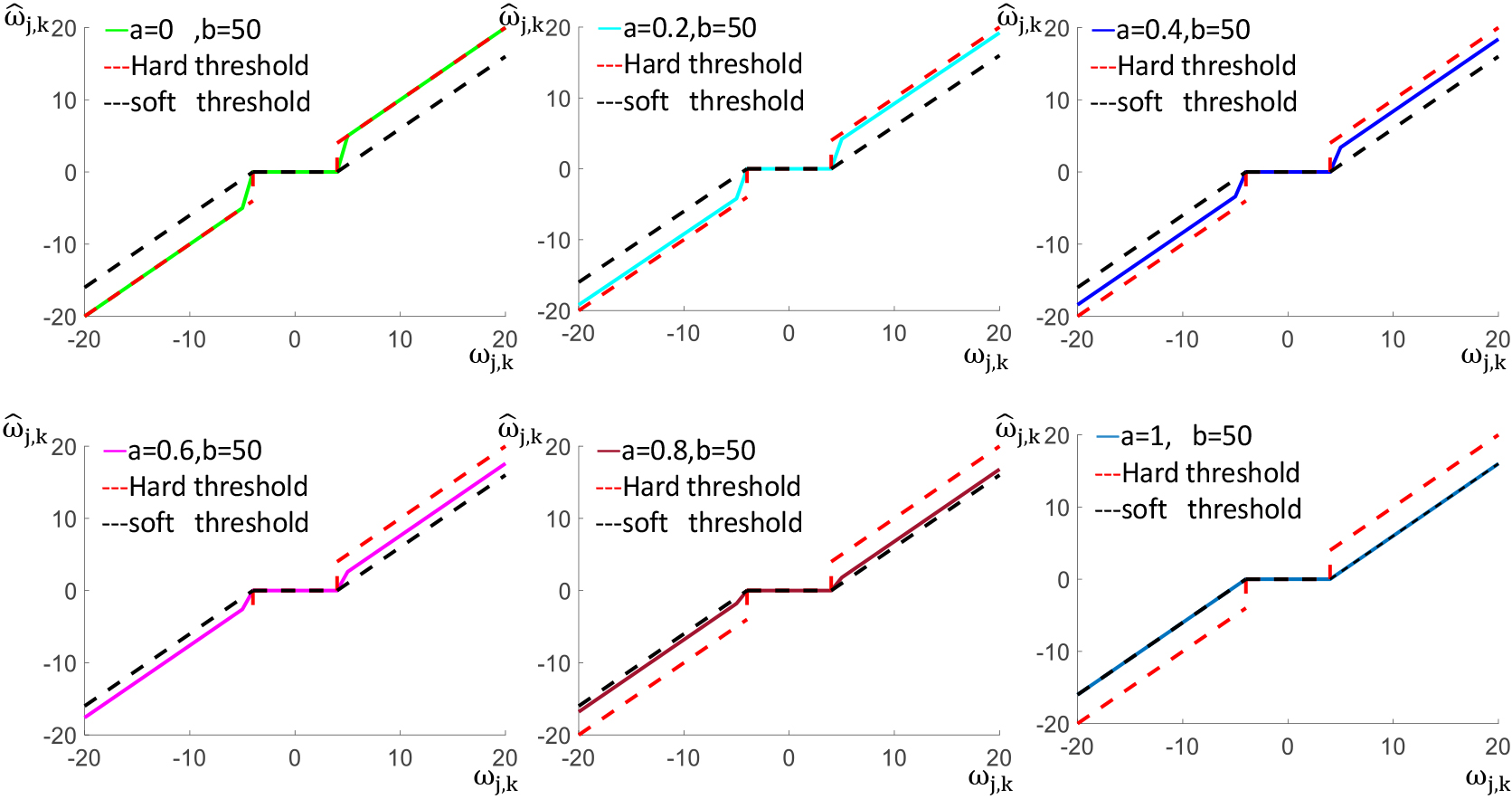
Figure 5.

Flow chart of denoising algorithm.

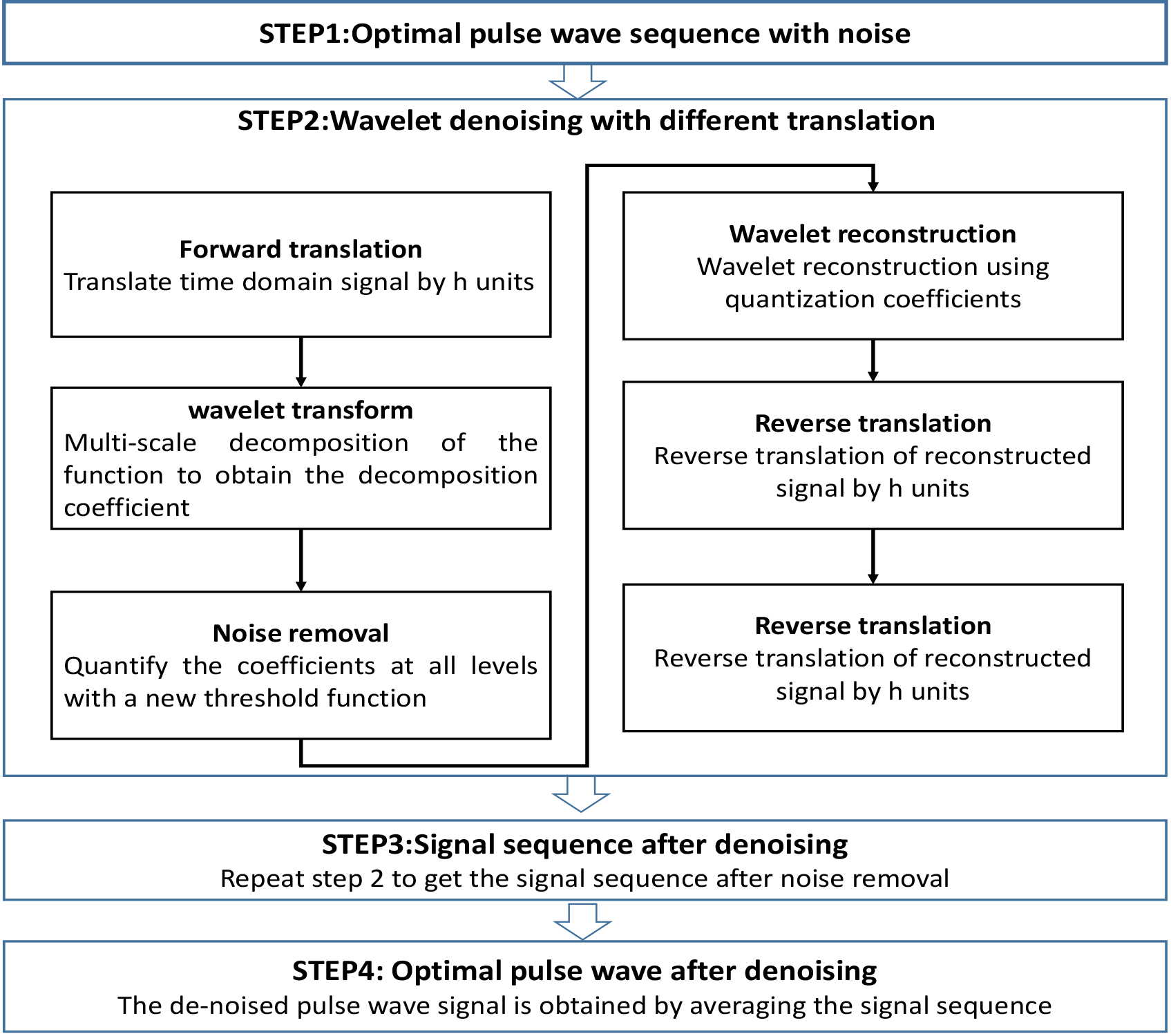
2.3.2Specific process of translation wavelet transforms

The flow chart of denoising algorithm is shown in Fig. 5. Set the vector input signal after preprocessing as s0,n(0<n⩽N). The cyclic translation operator is Th. Note that Th⁢(s0,n) is the time domain translation of s0,n. The translation range is 0<n⩽N. The following expression can be obtained:

(10)

Th⁢(s0,n)=s0⁢(n+h)

The new signals with a certain phase difference corresponding to the vector input signal s0,n can be obtained. Its cyclic anti-translation operator T-h is its inverse operation.

(11)

T-h=(Th)-1

Let Cj,k and Dj,k correspond to the low-frequency component (scale coefficient) and high-frequency component (wavelet coefficient) of the one-dimensional signal S transformation into the wavelet domain, respectively, j represents the wavelet decomposition series, and k represents the number of bits of cyclic translation. G and H represent down-sampling high-pass and low-pass operators respectively, C0,0=S, then the decomposition formulae are given by:

(12)

Dj+1,2⁢k=𝐺𝑇0⁢Cj,k,Dj+1,2⁢k+1=𝐺𝑇1⁢Cj,k

(13)

Cj+1,2⁢k=𝐻𝑇0⁢Cj,k,Cj+1,2⁢k+1=𝐻𝑇1⁢Cj,k

The reconstruction formulae are:

(14)

αj-1,k=T0⁢(G~⁢Cj,2⁢k+H~⁢Dj,2⁢k)

(15)

βj-1,k=T-1⁢(G~⁢Cj,2⁢k+1+H~⁢Dj,2⁢k+1)

(16)

Cj-1,k=(αj-1,k+βj-1,k)/2

The reconstruction process is actually the inverse process of decomposition. At each level of the wavelet reconstruction, multiple low-frequency components can be generated, which require the inverse translation and averaging of scale coefficients. Finally, the vector output is post-processed to obtain one-dimensional output signals y(h), 0<h⩽H, and then the translation invariant multi-wavelet reconstruction signal is obtained by averaging:

(17)

fr=∑h=1Hy(h)/H

In order to prove the effectiveness of the translation invariance, we make the following assumption:

(18)

y(h)=s⁢(n)+bh⁢(n)

Where, s⁢(n) is the clean pulse wave signal that appears repeatedly, b⁢(n) is the Gibbs oscillation signal caused by the threshold function when other noise signals not removed. According to Eq. (18, (17) can be re-expressed as follows:

(19)

fr=1H⁢∑h=1Hy(h)⁢(n)=1H⁢∑h=1H[s⁢(n)+bh⁢(n)]=s⁢(n)+1N⁢∑h=1N[bh⁢(n)]

The SNR of pure signal and noise can be derived as follows by assuming that P is the power of s⁢(n), σ2 is the variance of bi⁢(n):

(20)

𝑆𝑁𝑅=Pσ2

Equation (19) shows that the TIWT algorithm can reduce the noise by N times while, Eq. (20) shows that the algorithm can improve the SNR of pulse wave by N times.

3.Algorithm results

3.1The Choice of wavelet basis and wavelet decomposition level number

In wavelet threshold denoising, wavelet bases and wavelet decomposition layers are to be determined first. At present, the common discrete wavelet families include DB (Daubechies) wavelet family, SYM (Symlets) wavelet family and COIF (Coiflet) wavelet family. The pulse wave signal data is used for DTW transformation, and after the wavelet threshold function processing, the wavelet coefficients are reconstructed. The optimal wavelet basis function is selected by using the three parameters of SNR: MSE, filter length two cases are considered to analyze SNR and the peak error results (unified use of full threshold processing, decomposition scale bit is 4, SNR is 25, and the threshold function is hard threshold).

Figure 6.

(a) Filter length and output SNR. (b) Filter length and MSE output.

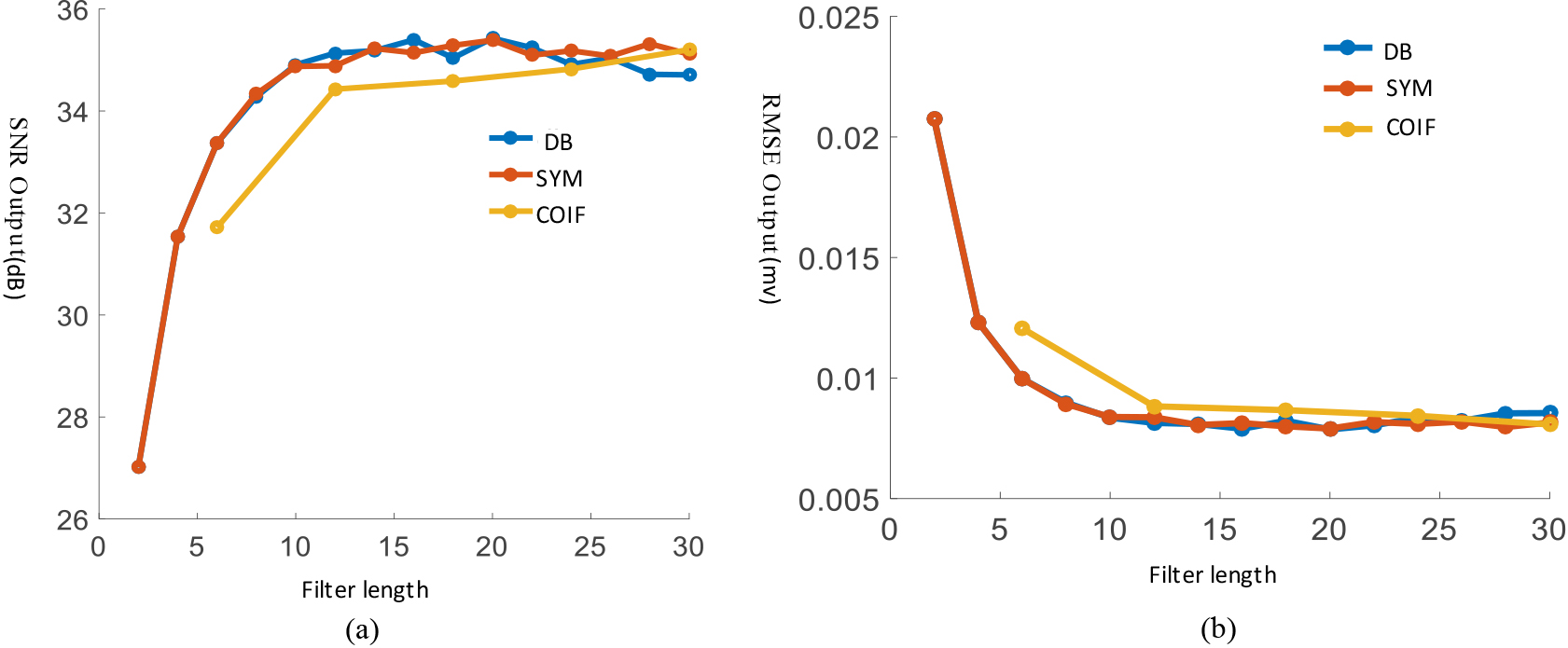
It is observed from Fig. 6 that when the filter length exceeds 10, SNR of the output signal tends to be stable. The output SNR of DB wavelet system and SYM wavelet system is 2 dB higher than that of COIF series wavelet system. From the perspective of the MSE of the output signal, when the filter length exceeds 12, the MSE of the output signal tends to a fixed value. The MSE of da wavelet system and SYM wavelet system is less than that of COIF system. Taking into consideration the influence of vanishing distance on data, we choose DB6 wavelet for pulse wave filtering. After selecting the wavelet, we need to consider the influence of decomposition level on wavelet denoising. Here, SNR and MSE of the output signal are used to evaluate the number of decomposition layers. (Full threshold processing is used uniformly, SNR is 25, and the threshold function is hard threshold).

Figure 7.

(a) Number of decomposition layers and output SNR. (b) Number of decomposition layers and MSE of output signal.

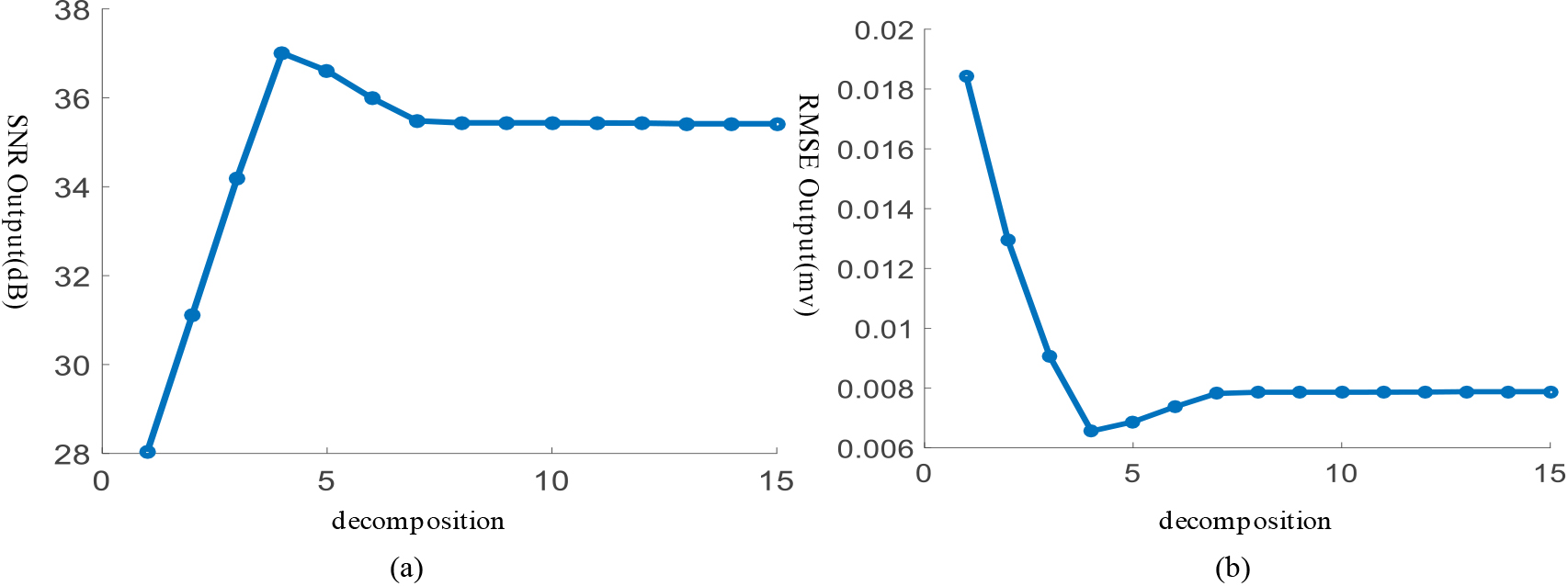
It can be seen from Fig. 7 that when the number of decomposition layers lev = 4, the maximum SNR of the output signal is 37 dB, and the MSE of the output signal reaches the minimum 0.0066 (mv), so the number of wavelet decomposition layers selected is 4.

3.2Evaluation of algorithm effectiveness

The standard pulse wave signal is added with zero-mean Gaussian white noise (20 dB). The comparison of hard threshold, soft threshold, new threshold and new threshold methods is done with translation invariant wavelet transform to denoise the pulse wave signal. Table 1 shows the denoised γ𝑜𝑢𝑡 and RMSE values in the traditional threshold denoising methods where, the hard threshold de-noising method’s MSE is slightly lower, and SNR is 1.26 times of the soft threshold de-noising method. The improved new threshold de-noising method’s SNR is 1.32 times of the hard threshold de-noising method.

Table 1

Comparison of different wavelet denoising methods

Wavelet denoising method	r𝑜𝑢𝑡/d⁢B	RMSE
Hard threshold	34.31	0.0089
Soft threshold	27.37	0.0199
New Threshold	36.22	0.0072
Translation invariance with new threshold	37.48	0.0062

Figure 8.

(a) The cures of γ𝑖𝑛 and γ𝑜𝑢𝑡. (b) The cures of γ𝑖𝑛 and RMSE.

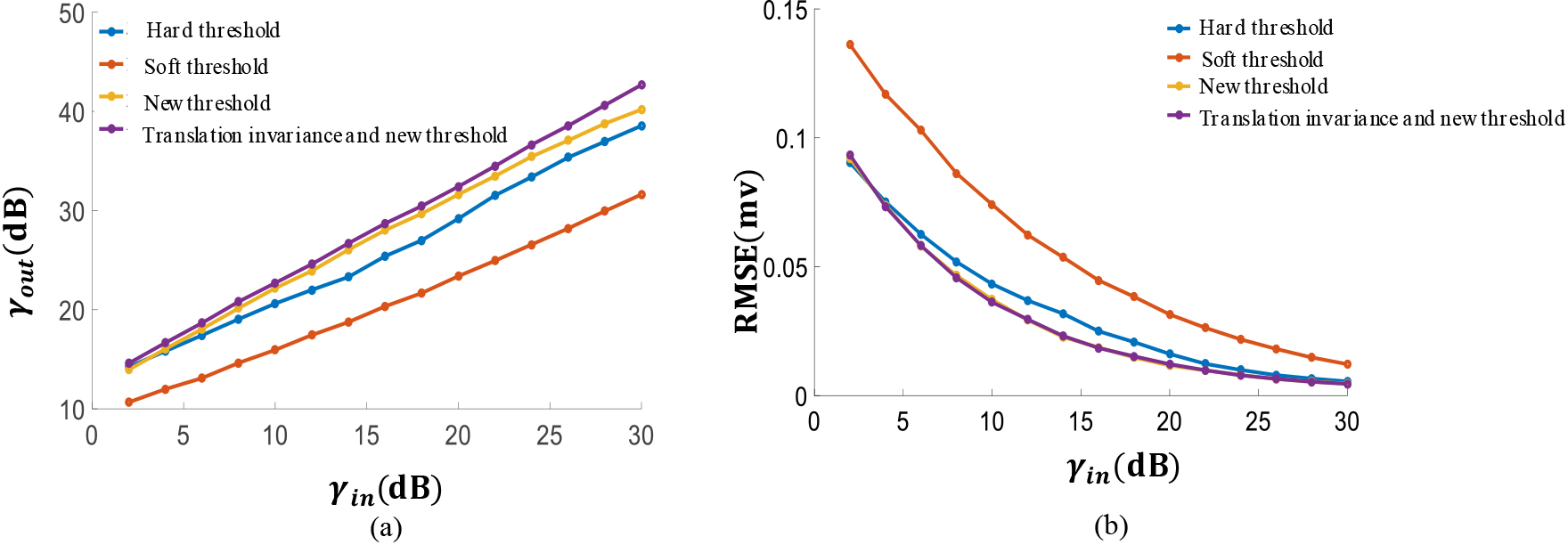
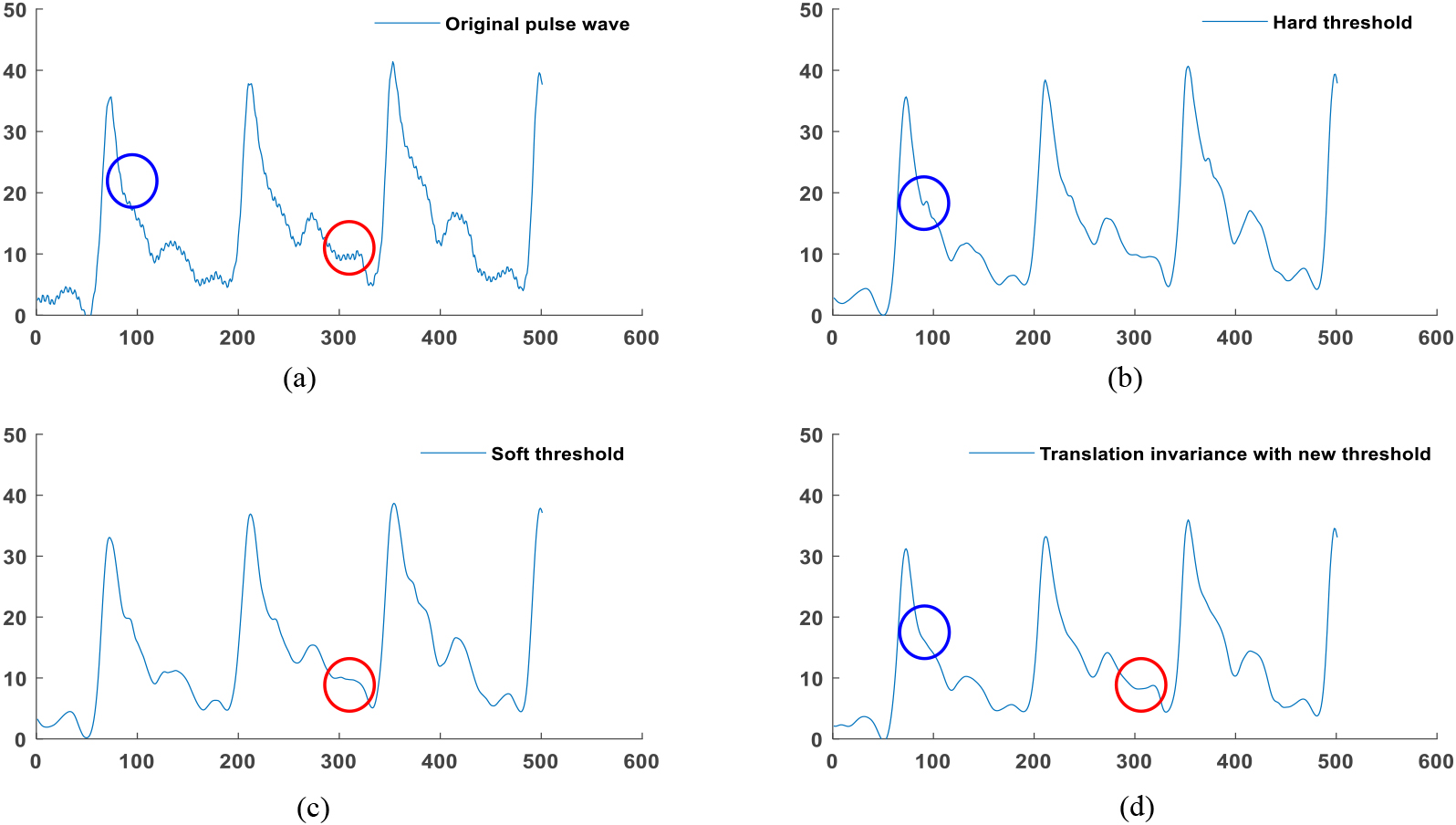
Figure 9.

(a) Original pulse wave. (b) wavelet hard threshold denoising. (c) wavelet soft threshold denoising. (d) Translation invariance with new threshold denoising.

An attempt is also made to verify the stability of the algorithm under different noises. Different zero mean Gaussian white noise is added to the noiseless pulse wave signal to generate noisy pulse signals with different SNRs. The wavelet hard threshold, the wavelet soft threshold, the new wavelet threshold and the algorithm in this paper are used to denoise the noisy pulse signal. The SNR and MSE before and after denoising are shown in Fig. 8. It is noticed that the new threshold increases SNR and reduces the MSE. The translation invariant new threshold wavelet denoising further improves SNR and reduces the MSE.

Figure 9b shows the effect of using the hard threshold wavelet de-noising algorithm to de-noise the original signal in Fig. 9a. The hard threshold can highlight the detailed characteristics of the pulse wave, but additional mutation points are introduced by some detail feature points (shown in the blue area). Figure 9c shows the effect of using the soft threshold wavelet denoising algorithm to denoise the original signal in Fig. 9a. From the overall view of the figure, the soft threshold can smoothen the pulse wave as a whole, and the smooth transition leads to the detailed characteristics of the pulse wave (shown in the red area). Figure 9d shows the effect of denoising the original signal in Fig. 9a using the algorithm proposed in this paper. It is evident that the algorithm in this paper is smooth as a whole and retains the detailed characteristics of the pulse wave.

4.Conclusion

The pressure pulse wave signal is weak and gets easily affected by EMG noise, which makes it difficult to extract the signal features. Compared with the traditional methods, the translation invariant wavelet denoising method proposed in this paper is more suitable for pulse wave signal denoising. The improved new threshold shifts invariant wavelet transform method and compensates the shortcomings of the traditional wavelet threshold denoising methods in a better way. This method discards the traditional threshold function, uses a new wavelet threshold function, and further combines the translation invariant wavelet transform on this basis, which not only improves the denoising effect to a greater extent but also effectively suppresses the pseudo-Gibbs phenomenon. In addition, through simulation experiments, it is further verified that applying translation invariant wavelet transform to the processing of pulse wave can obtain better denoising effect. Thus, it is verified that this method can improve the SNR and reduce the root MSE of the signal. The preprocessing method mentioned in this paper can support the feature extraction and recognition of subsequent pulse wave signals, and has good practical significance and reference value.

Author contributions

Jun Zhang: Methodology, software; Xingguang Geng and Yitao Zhang: Data curation, investigation; Fei Yao: Visualization, writing-original draft preparation, validation and writing-reviewing, conceptualization; Haiying Zhang and Yunfeng Wang: Supervision, editing. All authors participated in the study and read and approved the final version of this manuscript.

Funding

Financial support for data acquisition and algorithm verification was provided by the Key Research Program of the Chinese Academy of Sciences (ZDRW-ZS-2021-1).