Suppression of acoustic reflection artifact in endoscopic photoacoustic tomographic images based on approximation of ideal signals

1.Introduction

Photoacoustic tomography (PAT) is a rapidly developing functional imaging modality in recent years. It provides good optical contrast and ultrasonic resolution as well as high imaging depth compared with pure optical imaging technologies [1]. Endoscopic PAT (EPAT) combines noninvasive PAT with endoscopic detection, which has a great potential in the early diagnosis of diseased tissues in a tubular object such as digestive tract and coronary vessels.

In practical applications, it is usually difficult to achieve the theoretical imaging depth because of acoustic reflection. When the PA wave propagates in different tissue types in all directions, partial wave far away from the detector may be reflected by the acoustically dense deep tissue and then propagates back to the detector which is similar to a virtual acoustic source, resulting in reflection artifacts (RAs) in the reconstructed images [2]. The RAs usually appear at a deeper depth than actual optical absorbing structures and they are easily confused with the optical absorbers to be imaged [3]. Further, RAs at a certain depth are stronger than weak PA signals generated by deep tissues, leading to the reduced imaging depth [4]. In addition, the strongly reflected clutter arising from the acoustic sources outside the imaging plane is another contributing factor leading to the limited imaging depth [5].

Early researches on RA reduction focused on clutter decorrelation. For example, Jaeger et al. [5] designed a deformation compensated averaging (DCA) approach basing on tissue palpation with the imaging probe. It requires special training for operators to control the probe motion. Moreover, it can only be employed in the epi-mode of PA imaging for easily deformable tissues such as forearm and neck, but unsuitable for EPAT. To overcome the shortcomings of DCA, Jaeger et al. [6] developed a single-focus localized vibration tagging (LOVIT) method without the need for tissue palpation. The localized tissue displacement was induced by the acoustic radiation force (ARF) generated by a focused ultrasonic beam at its focus. Different from DCA, LOVIT does not require considerable practice and training for operators. It can only be employed in the imaging system equipped with an detector which can transmit ARF beam satisfying the ultrasonic safety rules. Moreover, it takes a long time to scan the entire imaging plane since it eliminates the clutter at one focal region at a time. Later, to shorten the signal acquisition time, Petrosyan et al. [7] improved the single-focus LOVIT by creating multiple foci in parallel forming the comb-shaped ARF patterns.

The clutter decorrelation requires additional devices to acquire pulse-echo images recording tissue deformation, which prolongs the process of data acquisition. Alles et al. [8] distinguished reflected clutters and PA signals based on the difference in their spatial coherence expressed by the short-lag spatial coherence (SLSC). Compared with clutter decorrelation, SLSC needs only a single scan, which shortens the acquisition process. However, it has difficulties in distinguishing the clutter from the incoherent signal produced by dense microvascular tissues whose spatial coherence is similar to or lower than that of the clutter. Moreover, SLSC relies on time measurement of the geometric path associated with beamforming, so the reduced accuracy is observed in the case of hyperechoic reflection or strong reflection.

Recently, deep learning with convolutional neural networks (CNNs) has been widely used in medical image processing and analysis. CNN has shown its potential in recognition and removal of RAs in PA imaging [9]. The main concern is that public data sets for PAT has not been available, and the clinical case data are seriously insufficient. The data sets used in current studies are usually constructed by computer simulation. The validity of CNNs trained by such simulation data may not be guaranteed in in vivo imaging of human tissues.

This paper presents a simple method to suppress in-plane RAs in EPAT. The method recovers the approximation of ideal PA signals from acoustic measurements and numerically generated planar ultrasound. It does not require additional devices to record tissue deformation, and it is computationally efficient in comparison with CNN which requires a large amount of image data for training.

2.Method

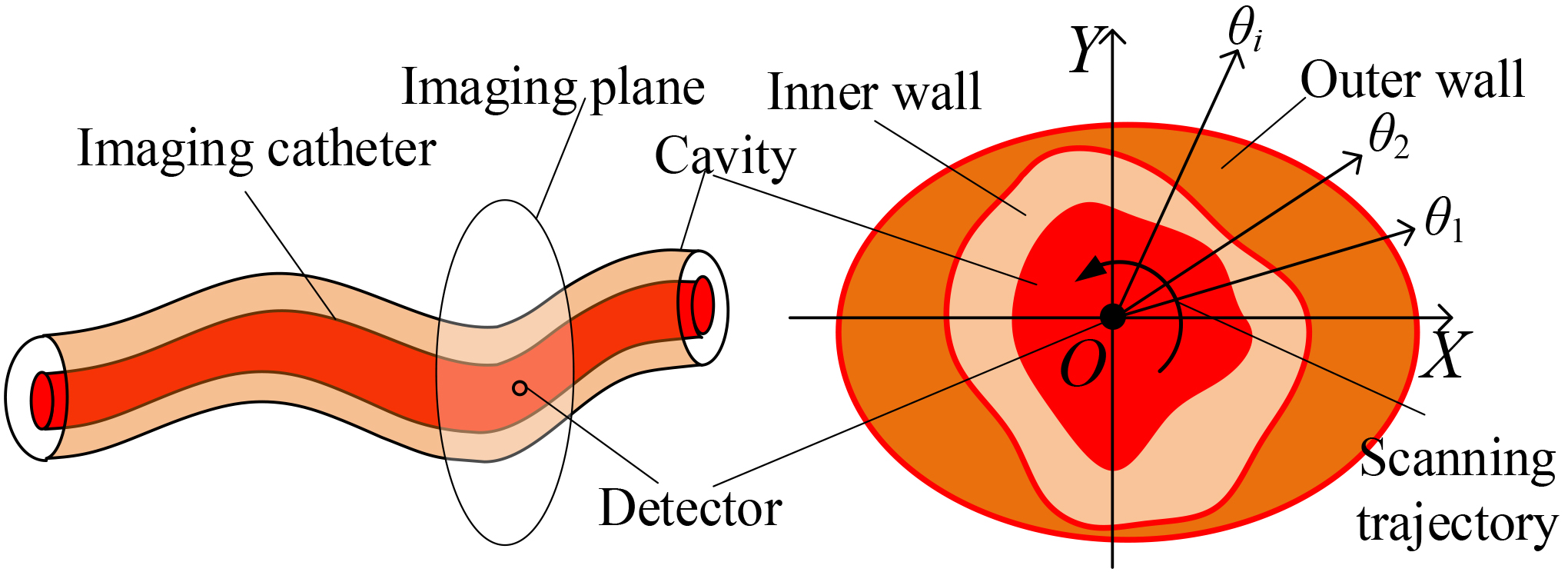
As shown in Fig. 1, an imaging catheter is inserted into the object cavity. The detector at the catheter tip circumferentially scans surrounding tissues and collects time-dependent series of acoustic pressure photoacoustically generated by optical absorbing structures. The imaging plane is perpendicular to the catheter, and the detector is located in the image center. A XOY rectangular coordinate system and a θ-l polar coordinate system are established on the imaging plane with the detector as the origin.

Figure 1.

Schematic diagram of acquiring PA signal from inside a tubular object. Left: axial view. Right: transverse view.

The probe emits short laser pulses (∼ ns) radially to illuminate the surrounding tissues. Ignoring the wave aspect of light, the laser induced irradiation in the multilayered wall is regarded as the interaction between a large number of photons and tissues. We model light transportation in tissues with Monte Carlo (MC) simulation to obtain the numerical solution of the spatially distributed absorbed optical energy density (AOED) [10].

The photoacoustic pressure propagating in acoustically heterogeneous lossy medium satisfies the following wave equation considering both absorption and dispersion [11],

where 𝒓∈Ω and Ω∈ℝ2 is the imaging plane, ∇ is Hamiltonian operator, p⁢(𝒓,t) is the pressure at r and time t, c⁢(𝒓) is the speed of sound (SoS), A⁢(𝒓) is the AOED, βe is the isobaric volume expansion coefficient, CP is the specific heat, a is the power law exponent typically in the range of 1⩽a⩽1.5 for biological tissues [11] (here it is set as 1.5), I⁢(t) is the time-domain function describing the instantaneous irradiation pulse, which can be further expressed as I⁢(t)=δ⁢(t) for impulse heating, and I′⁢(t) is the first derivative of I⁢(t) versus time. τ⁢(𝒓) and η⁢(𝒓) denote the acoustic absorption and dispersion proportionality coefficients, respectively [11],

where μ≈(10-7/2⁢π) cm-1rad-1s is the absorption coefficient [12].

Assume that the PA wave is reflected only once during propagation. Based on the Born approximation, the pressure reaching the detector is determined by [13, 14]

where

and

Here, pp⁢a⁢(𝒓,t) is the pressure reaching the detector, γρ⁢(𝒓) and γκ⁢(𝒓) are the acoustic heterogeneity parameters regarding the density and compressibility, g⁢(𝒓) is the Green’s function, ρ0⁢(𝒓) and κ0⁢(𝒓) are the ambient density and compressibility, ρ⁢(𝒓) and κ⁢(𝒓) are the density and compressibility of the inhomogeneous medium, st is the wave number, ‘*’ denotes convolution, j is the imaginary unit, H0(2)⁢(⋅) is the Bessel function of the third kind, and |𝒓| is the distance between the position r and the detector.

The planar ultrasonic wave is numerically generated as follow,

where

and

Here, σ∈ [0, 360∘) is the incident angle of a single planar ultrasonic wave relative to the positive X-axis, kt=ω/c0 is the wave number, ω is the angular frequency, c0 is the ambient SoS, pu⁢s⁢(𝒓,kt,σ) is the pressure at r with the incident angle σ and wave number kt, and kx is the spatial wave number along the positive X-axis with |kx|<kt.

where pr⁢c⁢(𝒓,kt) is the pressure of the reflected clutter at r with the wave number kt, kx,σ=kt⁢cos⁡σ, ph⁢(-kx,σ,-kt) is the pressure of the ideal PA signal, and ε< 0 is the dimension factor. ε is an empirical constant being used to balance the amplitude of the PA signal and planar ultrasound. It is independent of image structures and is needed to be finely tuned according to the results.

The matrix form of Eq. (10) in frequency domain is

where 𝑷u⁢s⁢(𝒓n,σ) is the M×M diagonal matrix composed of the time-dependent planar ultrasound,

Here, M is the length of the time series of the pressure collected by the detector at each measuring position and pu⁢s⁢(𝒓n,σ,ktm) is the pressure of the planar ultrasonic wave with the wave number ktm and the incident angle σ at 𝒓n. 𝑷r⁢ctn and 𝑷htn are the nth row vectors in 𝑷r⁢c and 𝑷h, respectively. 𝑷h and 𝑷r⁢c are the ideal signal matrix and reflected clutter matrix with the dimension of N×M, respectively,

where N is the number of the measuring locations and ph⁢(𝒓n,ktm) and pr⁢c⁢(𝒓n,ktm) denote the pressure of the ideal signal and reflected clutter with the wave number ktm at 𝒓n.

The measured acoustic signal is the superposition of the ideal signal and reflected clutter,

where pp⁢a⁢(𝒓,t), ph⁢(𝒓,t), and pr⁢c⁢(𝒓,t) are the pressure of the measured signal, ideal signal, and reflected clutter, respectively. In frequency domain, Eq. (15) is rewritten as

where 𝑷p⁢a is the N×M matrix of the measured signal

and pp⁢a⁢(𝒓n,ktm) is the pressure of the measured signal with the wave number ktm at 𝒓n. Substitute Eq. (11) into Eq. (16) obtaining

where 𝑷p⁢atn is the nth row vector in 𝑷p⁢a. Finally, the ideal signal is recovered from 𝑷p⁢atn and 𝑷u⁢s⁢(𝒓n,σ) as follow,

where I is the identity matrix.

The AOED is finally recovered from the ideal signal by back projection (BP) [15] as follow,

Figure 2.

Geometry of computer-simulated phantoms. From left to right, the phantoms are numbered as I, II, III, and IV.

where z0 is the distance between the position r and the tissue surface.

3.Results

Figure 2 shows the cross-sectional geometry of the computer-simulated coronary vessel and cavity phantoms. Table 1 lists their parameters by referring to [16]. The SoS and density of each tissue layer are set as the Gauss distribution with the mean of the values in the table and the variance of 5 and 0.05, respectively.

Figure 3.

Images of AOED (top) and initial pressure (bottom) by forward simulation.

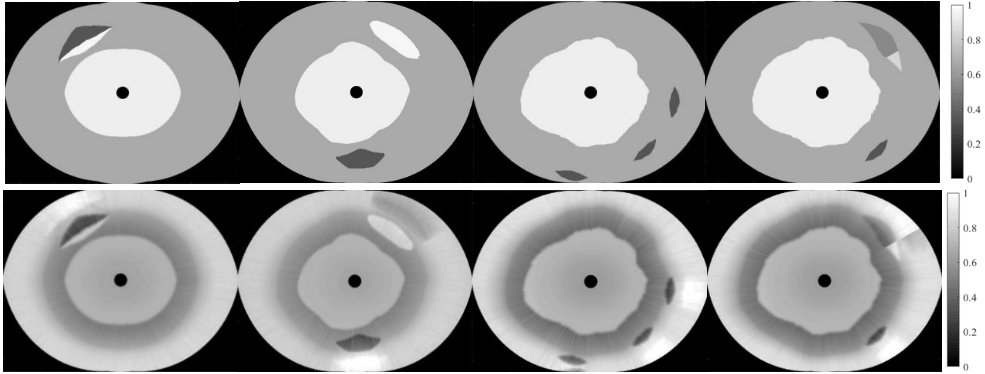
Figure 4.

Images of AOED reconstructed by using BP (top) and our method (bottom).

Figure 5.

Evaluation indexes of reconstructed images before and after suppression of RAs.

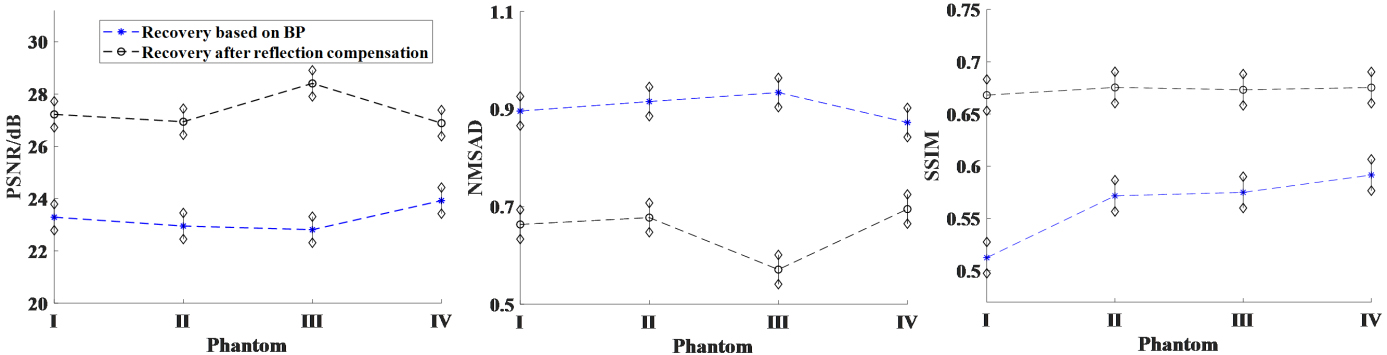
Figure 6.

Images of AOED reconstructed by SLSC (top) and CNN (bottom).

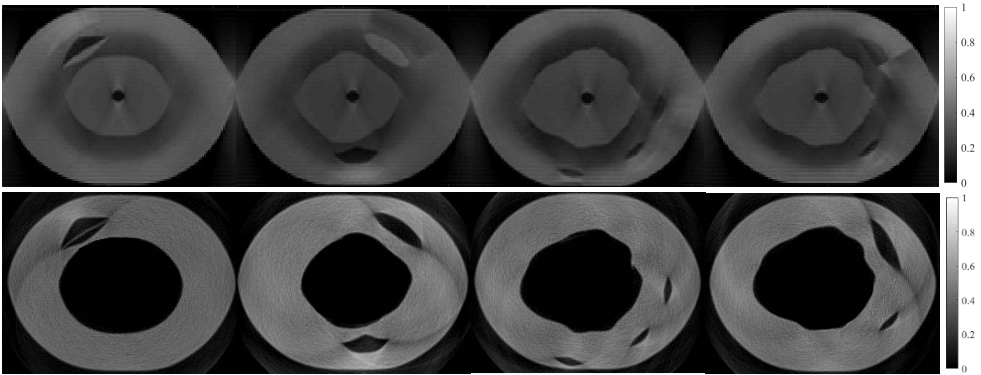
Figure 7.

Evaluation indexes of reconstructed images by using our method, SLSC and CNN.

Figure 3 shows the forward simulation results of the AOED and PA signal which contains the additive Gaussian white noise with the signal-to-noise ratio (SNR) of 30 dB. The exciting wavelength and pulse duration are 1.7 μm and 20 ns, respectively. In AOED images, different tissue types can be distinguished from each other due to their specific optical properties. The three-layered structures of the arterial wall cannot be identified because of their similar optical parameters. In images of the initial pressure, the tissue boundaries can be identified, but obvious RAs are observed around the lesions.

Figure 8.

Reconstructed images of AOED. (a) From top to bottom, σ= 0∘, 90∘, 180∘, 270∘, and equals to the measuring angle of the detector; (b) From top to bottom, ε= -2e-7, -2e-8, -2e-9, -2e-10, and -2e-11, respectively.

Figure 8.

Continued.

Figure 9.

Evaluation indexes of images regarding different (a) σ and (b) ε.

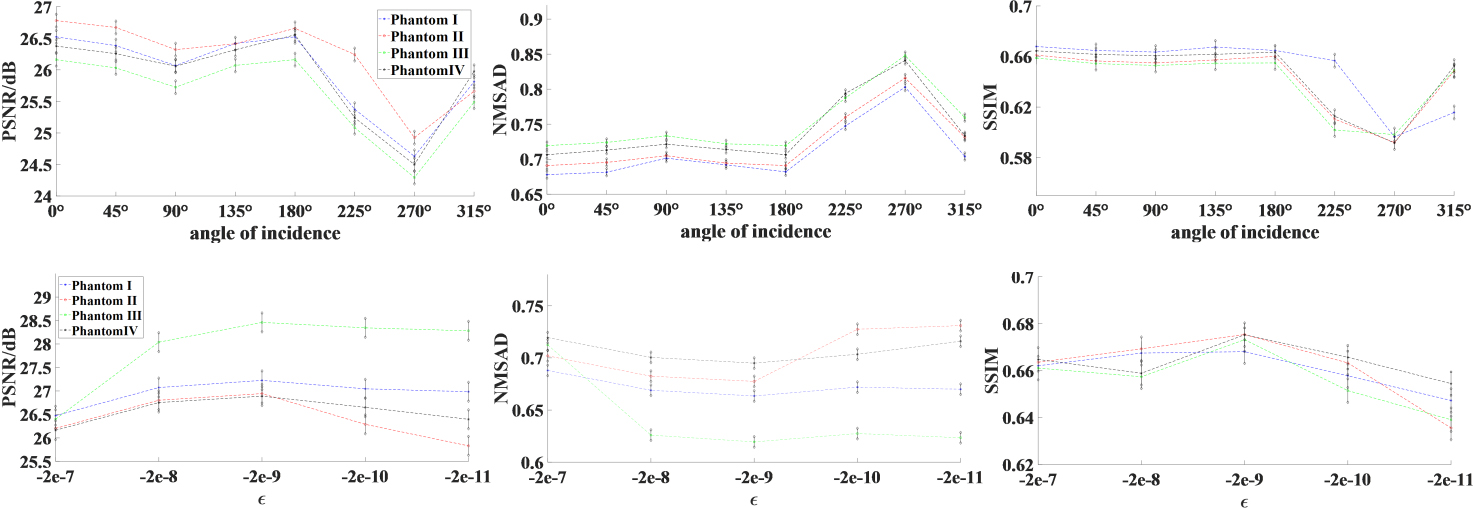
Figure 4 presents the images reconstructed by using our method and BP [15]. We utilized k-wave toolbox in MATLAB to generate the planar ultrasonic wave where ε= -2e-9 and the incident angle σ is equal to the measuring angle of the detector θ. The blurred boundaries, artifacts, and distortions are observed around the plaques and lesions in BP reconstructions. In contrast, the quality of the images obtained with our method is significantly improved and the contrast of different tissue types are enhanced.

We adopted peak signal to noise ratio (PSNR), normalized mean square absolute distance (NMSAD), and structural similarity (SSIM) [17] as quantitative indices to evaluate the reconstruction quality. From Fig. 5, we concluded that the quality of the images after RA suppression is improved in comparison with that of BP reconstructions. These convincing results demonstrate the effectiveness of our method in reducing RAs and the improvement in the contrast of different tissue types.

We compared our method with the SLSC approach [8] and a CNN method of our previous work [18]. SLSC is used as a weighting factor of different signals in reconstructing images to suppress clutters and preserve PA signals as well. As stated in Introduction, the SLSC approach is unable to effectively distinguish incoherent signals generated by dense tissues from the clutters because of their similar spatial coherence. Severe artifacts are observed around the cavity wall in Fig. 6. Figure 7 reveals the improvement in the quantitative indices of our method in comparison with SLSC.

The CNN method constructs and trains a neural network based on a U-net. The network is used to optimize the time-reversal reconstructions. We constructed the data set by computer simulation which contains 5000 pairs of sample images. We trained and tested the network on a GPU configured with NVIDIA geforce 1080ti. Figures 6 and 7 reveal that the quality of CNN reconstructions is similar to that of our method. CNN has the advantages of strong learning ability and good portability. However, its performance in reconstructing high-quality images depends on the data set used for training. It can only provide application scenarios with limited amount of data, and it is time-consuming to train the network with a high requirement for hardware.

4.Discussion

We discussed the influence of the incident angle of the planar ultrasound denoted as σ on the reconstruction quality based on the results by setting σ at 45∘ intervals within the range of [0∘, 360∘) while other parameters remained unchanged. The results in Figs 8a and 9a, and Table 2 reveal that the image quality obtained when σ equals to the measuring angle θ of the detector is better than that of a fixed incident angle. Then, we set ε as -2e-7, -2e-8, -2e-9, -2e-10, and -2e-11, respectively, by referring to [19] while σ=θ. The results in Figs 8b and 9b indicate that the best reconstruction quality is achieved when ε= -2e-9.

5.Conclusion

This work developed a method to suppress RAs in EPAT images with low requirements for equipment and operators. The results of simulated phantoms demonstrate its validity in improving the image quality. The best quality is obtained when ε= -2e-9 and the incident angle equals to the measuring angle of the detector. Compared with BP reconstructions, the PSNR, NMSAD, and SSIM are improved by up to 18.8%, 27.7%, and 14%, respectively. Compared with SLSC, the indexes are improved by up to 8%, 20%, and 5%.

This study focused on removal of in-plane RAs which are produced by the acoustic scatterers and optical absorbers inside the imaging plane. As for out-of-plane reflection, a highly focused ultrasonic transducer is needed to achieve high-quality imaging, where the out-of-plane clutter can be neglected.

Deep learning has shown great potential in real-time imaging with the development of high-performance processor, big data technology, and the continuous increase of open source databases. In the future work, we plan to design a model-based strategy to suppress RAs in EPAT by combining the approximation of ideal PA signals with CNN training.