Direct 3D model extraction method for color volume images

Liu, Bin; Liu, Shujun; Shang, Guanning; Chen, Yanjie; Wang, Qifeng; Niu, Xiaolei; Yang, Liang; Zhang, Jianxin

doi:10.3233/THC-218014

Direct 3D model extraction method for color volume images

Article type: Research Article

Authors: Liu, Bin^{a; b; c} | Liu, Shujun^a | Shang, Guanning^d | Chen, Yanjie^a | Wang, Qifeng^a | Niu, Xiaolei^a | Yang, Liang^e | Zhang, Jianxin^{f; *}

Affiliations: [a] International School of Information Science and Engineering (DUT-RUISE), Dalian University of Technology, Dalian, Liaoning 116620, China | [b] DUT-RU Co-Research Center of Advanced ICT for Active Life, Dalian University of Technology, Dalian, Liaoning 116620, China | [c] Key Lab of Ubiquitous Network and Service Software of Liaoning Province, Dalian University of Technology, Dalian, Liaoning 116620, China | [d] Department of Orthopedic Surgery, ShengJing Hospital, China Medical University, Shengyang, Liaoning 110004, China | [e] The Second Hospital of Dalian Medical University, Dalian Medical University, Dalian, Liaoning 116023, China | [f] School of Computer Science and Engineering, Dalian Minzu University, Dalian, Liaoning 116600, China

Correspondence: [*] Corresponding author: Jianxin Zhang, School of Computer Science and Engineering, Dalian Minzu University, Dalian, Liaoning 116600, China. E-mail: [email protected].

Keywords: Virtual human, 3D organ models, volume data segmentation, matting components

DOI: 10.3233/THC-218014

Journal: Technology and Health Care, vol. 29, no. S1, pp. 133-140, 2021

Published: 25 March 2021

Get PDF

Abstract

BACKGROUND:

There is a great demand for the extraction of organ models from three-dimensional (3D) medical images in clinical medicine diagnosis and treatment.

OBJECTIVE:

We aimed to aid doctors in seeing the real shape of human organs more clearly and vividly.

METHODS:

The method uses the minimum eigenvectors of Laplacian matrix to automatically calculate a group of basic matting components that can properly define the volume image. These matting components can then be used to build foreground images with the help of a few user marks.

RESULTS:

We propose a direct 3D model segmentation method for volume images. This is a process of extracting foreground objects from volume images and estimating the opacity of the voxels covered by the objects.

CONCLUSIONS:

The results of segmentation experiments on different parts of human body prove the applicability of this method.

1.Introduction

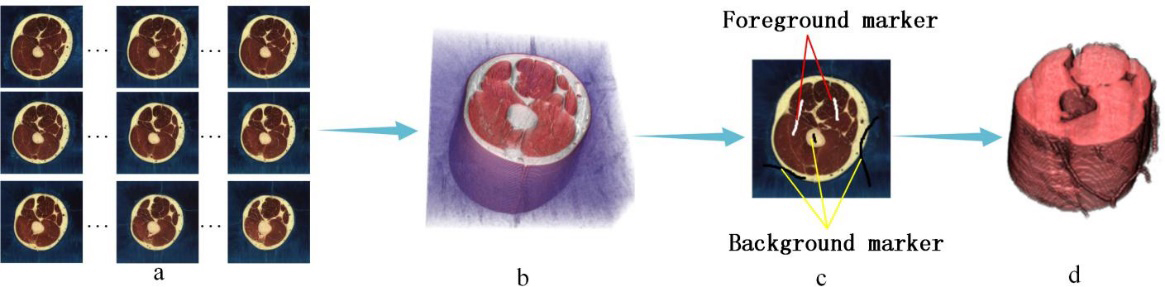
Extracting three-dimensional (3D) regions of interest (ROIs) from color volume images is an interesting and challenging topic. It is an issue that must be solved urgently for particular fields, e.g., the Virtual Human Project (VHP). The VHP was proposed by the United States National Library of Medicine (NLM). The ultimate research aim of the VHP is establishing a cellular-level virtual human tissue digitized human body, which would be very useful for new drug development, sports medicine, and industrial design, and so on. As the first step of the VHP, human body organ 3D visualization via massive cadaver cross-section images is essential. In past research, it was necessary to manually sketch the contours of human body organs on the images slice by slice. The process requires a lot of energy and time. With the development of image processing, we can extract the regions of interest via a small quantity of interactive using image matting technology. However, currently published methods [1, 4] are all designed for two-dimensional (2D) images. Therefore, we still need to complete the segmentation slice by slice. If there is a 3D color volume image matting method, the extraction efficiency will be highly enhanced. In this paper, we propose a method to directly segment 3D color volume image data. As shown in Fig. 1, we use the serial color slice images provided by VHP to construct volume data, and makes simple marks on the image to assist segmentation, so as to directly obtain the 3D organ model.

Figure 1.

Segmentation for 3D medical images: (a) Serialized human body cross-section images, (b) 3D volume image data, (c) Manual markers on image and (d) Extracted target organ.

2.Proposed method

2.1Voxel decomposition

In our method, we consider each voxel as a convex combination of K volume image blocks (components) F1⁢…⁢Fk. Then, the i-th voxel in the volume image can be expressed as

(1)

Ii=∑k=1Kαik⁢Fik

where Fik denotes the k-th block, αik denotes the opacity (matting component) of the k-th block, and αik denotes the proportion of the actual color contribution per voxel. This matting component is non-negative, and the sum of components for each voxel is 1.

2.2Spectral analysis

The eigenvectors of the Laplacian matrix (L = D - A) capture most of the image structures. Levin et al. introduced the matting Laplacian, which can accurately evaluate the effect of matting when the color distribution of foreground and background is uncertain [7]. If the colors of foreground and background in the local volume image window w are linearly distributed in RGB space the α value in w can be expressed as a linear combination of color channels:

(2)

αi=aR⁢IiR+aG⁢IiG+aB⁢IiB+b ∀i∈w

where a=1/(F-B), b=-B/(F-B) and F and B are the foreground and background components of the local image window. Therefore, this foreground and background separation problem can transforme into finding the alpha value with the minimum deviation in all image windows wq:

(3)

J⁢(α,a,b)=∑q∈I∑i∈wq(αi-aR⁢IiR-aG⁢IiG-aB⁢IiB-bq)2+ε⁢∥aq∥2

where ε⁢∥aq∥ is a regularization term on a. After simplifying this formula, we can obtain

(4)

J⁢(α)=αT⁢L⁢α

where L represents the matting Laplacian matrix, whose terms are functions of the input images in the local window and are independent of the foreground or background. The calculation is as follows:

(5)

where δi⁢j is the Kronecker delta, wq is a 3×3×3 window, ∑q is the covariance matrix in the window, Ii is color vector of i-th voxel, μq is the mean vector of color, I3 is a unit matrix, Ij is color vector of j-th voxel, and ε is a constant parameter (generally its value is 10-7). To build the Laplacian matrix L for volume image, a local window moves through the volume image, and voxel traversal is implemented in this local window. This process is shown in Fig. 2.

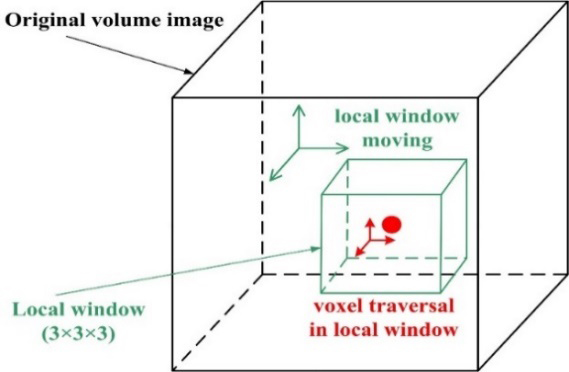
Figure 2.

Traversing all voxels to build the Laplacian matrix.

2.3Matting components

After obtaining L, the key to solve this segmentation issue is to find a reasonable set of vector α values. It can be proven that the actual matting components belongs to the null space of Laplacian matrix under reasonable situation [8]. In our experimental images, the Laplacian matrices usually have few eigenvectors with zero eigenvalues but the minimum eigenvectors of L is close to being stable. Therefore, we can extract the matting component from the minimum eigenvectors of matting Laplacian matrix. The reconstruction of the matting components of the volume data is equivalent to finding the linear transformation of the smallest eigenvectors of the Laplacian matrix. The sum of the matting components for each voxel is 1. In addition, because most of the voxels are usually opaque, we hope most voxels’ matting component value is 0 or 1. Therefore, we can utilize the Newton iteration method to obtain a set of approximate binary vectors (matting components).

More formally, we calculate and obtain a set of minimum eigenvectors of L:e1,…,en. Let the matrix E=[e1,…,en]. Our goal is to find a set of linear combination vectors yn and obtain

(6)

min⁢∑i,n|αin|γ+|1-αin|γ,where ⁢αn=E⁢yn⁢ subject to ⁢∑nαin=1

where γ is a constant between 0 and 1 (in this paper, γ= 0.9).

Since cost of Eq. (6) is not convex, the result of Newton’s method largely depends on the selection of the initial value of iteration. Therefore, we use k-means clustering method to cluster the minimum eigenvector of L defined by Eq. (5), and then set the initial value of Newton method as the clustering result. Namely, we cluster the eigenvectors e1,…,en into m(m⩽n) classes to obtain e′⁣1,…,e′⁣m. Substitute the matrix E=[e′⁣1,…,e′⁣m] into Eq. (6) and let n=m. By judging the convergence condition of ∑i,m|αim|γ+|1-αim|γ, we can obtain the matting components, as shown in Fig. 3.

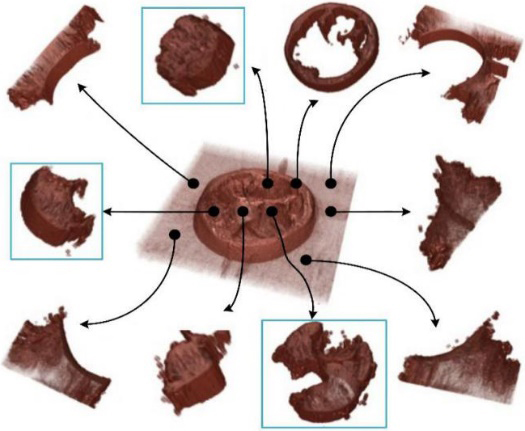
Figure 3.

Matting components decomposition for volume image.

In the process of clustering feature vectors using k-means algorithm, an important problem is to select the number of clustering K. Setting a fixed value cannot adapt to different images to be segmented. Therefore, we use the eigen gap method to set the adaptive K value. According to the matrix perturbation theory, the larger the eigen gap (difference between two adjacent eigenvalues) is, the more stable the subspace composed of the selected K eigenvectors. Therefore, we set the number of clusters as the parameter corresponding to the maximum value of feature gap sequence. Specifically, we calculate a set of minimum eigenvalues of the Matting Laplace λ1<λ2<…<λn, and calculate the difference value to its eigengap sequence {g1,g2,…,gn|gi=λi+1-λi}. Then set the number of clusters as the number of subscripts in the maximum sequence plus 1. As shown in Fig. 4, it is the schematic diagram of the eigenspace sequence calculated at the thigh. We will select 25 as the number of clusters for k-means clustering. Through this method, we can automatically select a reasonable number of clusters K according to the characteristics of each volume image, and also avoid the calculation waste caused by too large selection of K value.

Figure 4.

Eigengap sequence.

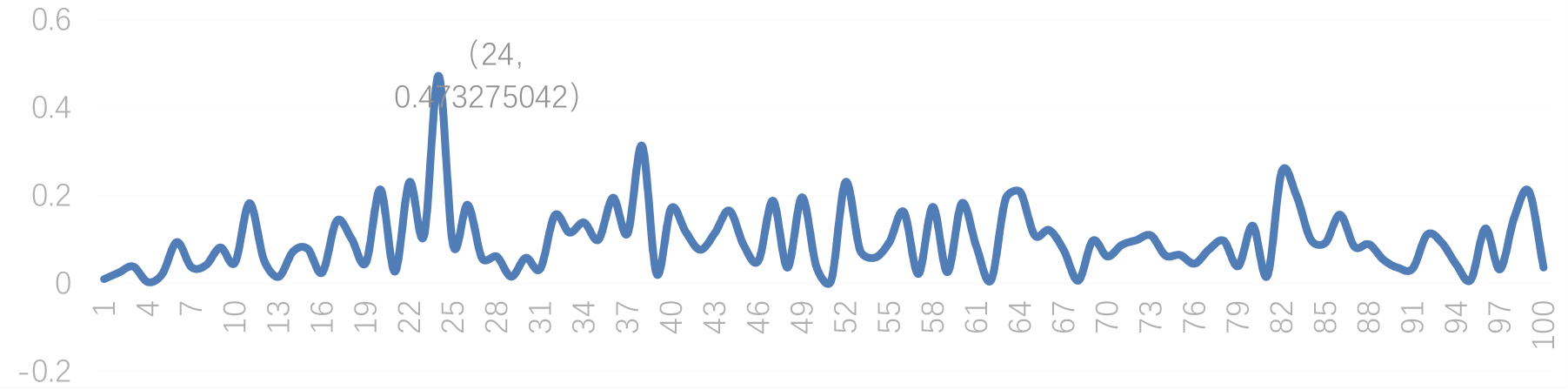
Figure 5.

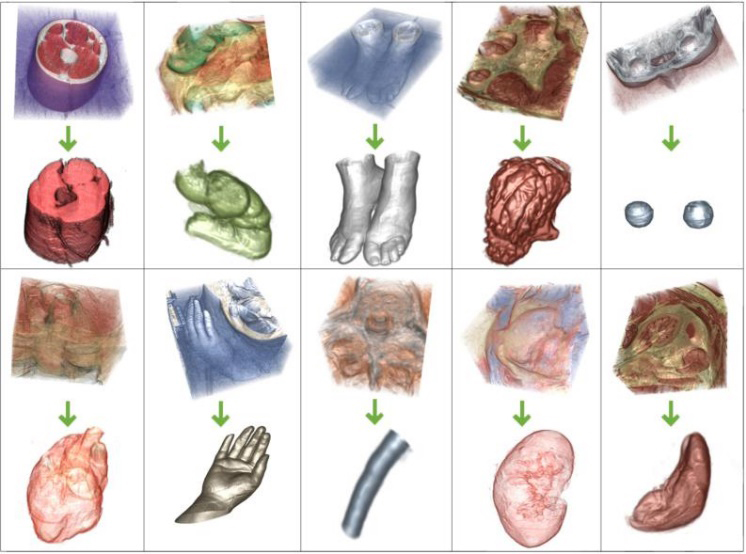
3D human organ models extraction from color volume images. From the upper left to low right (row-major order), the images show respectively extraction experiments for the thigh muscles model (by 10 matting components), large intestine model (by 14 matting components), feet model (by 9 matting components), stomach model (by 15 matting components), eyes model (14 matting components), heart model (by 17 matting components), hand model (by 10 matting components), medulla spinalis model (by 8 matting components), kidney model (by 19 matting components) and spleen model (by 16 matting components).

2.4User-supervised matting

For the obtained matting components, we use brushes to mark the volume image (a white brush for the foreground and a black brush for the background). In this manner, most of the matting elements can be classified into foreground or background. For x image matting components without marked, we give 2x hypotheses and calculate the values of energy Eq. (4) for each hypothesis. We obtain a hypothesis when the energy function is minimized, and its corresponding matting component belongs to the foreground. The final segmentation result can be obtained by adding all the matting components corresponding to foreground images. In Fig. 3, the matting elements in the blue box are regarded as foreground (target model) components by our method.

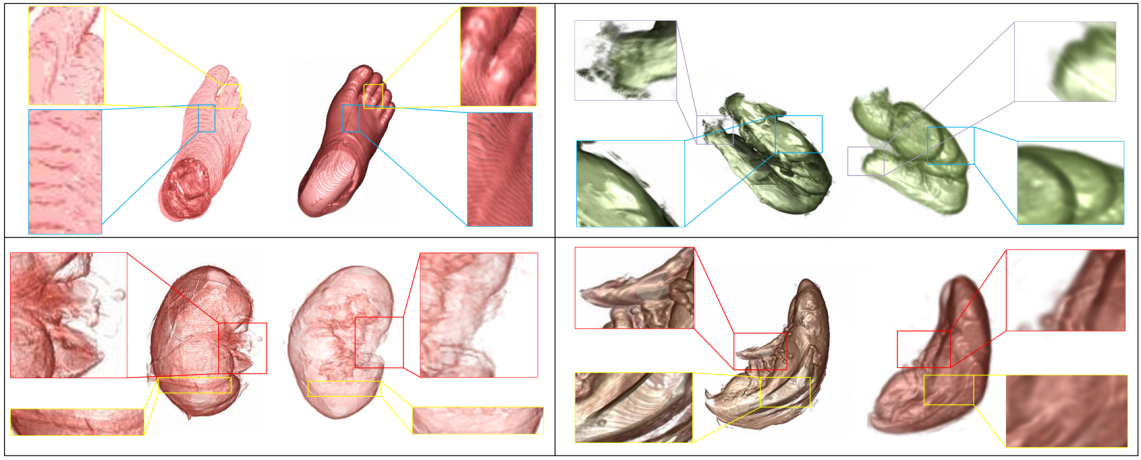
3.Experiment results

In this paper, we used volume images from the VHP as experimental material. The images used are BMP and JPG, ranging in size from 200 × 180 to 110 × 120. We selected several organs located in different positions of the human body with different colors as the segmentation objects. In Fig. 5, for each segmentation object, the upper subfigure is the original volume image, and the lower subfigure is the extracted organ model. In our experiments, different organ models are extracted with different number of matting components. We also designed comparative experiments between our method and the 2D slice segmentation and rendering method. This method needs to mark all sequential slice images to be segmented in turn, and then draw a single segmentation result into a 3D model. Using our method, only scribbling on a slice image can get the result, which greatly reduces the workload. And our method also has some advantages in the segmentation effect. As shown in Fig. 6, the left image is the organ model obtained by the method of 2D slice segmentation and rendering method. In the results, there is a fault phenomenon (marked with yellow box) between single 2D slice images, the segmentation results are not complete (marked with red box), and the edge of the organ model is rough (marked with purple box). The image on the right is the organ model obtained by our method. The organ model is complete and smooth, which can better retain details, such as the blood vessels in the instep (marked with blue box). The experimental results show that our method is effective for color volume image segmentation.

Figure 6.

Comparative experiment diagram.

4.Discussion

Medical image segmentation has always been an important research topic in the field of image processing. Traditional segmentation methods can be divided into two categories: 2D segmentation and 3D segmentation. In the 2D segmentation method, threshold segmentation methods [9, 11] are susceptible to noise, and the effect at the edge of the image is not good. Some horizontal set-based methods [12, 14] solve the image segmentation problems of uneven gray scale and fuzzy boundary, but they have the disadvantage of slow segmentation speed. 3D image segmentation methods can be divided into two kinds. The first is single 2D image segmentation and then rendering into volume [16]. The second is to segment the 3D image directly [18, 6]. These methods are based on specific parts of the 3D model segmentation methods, and the segmentation objects are gray-scale images. From the above analysis, the segmentation method for 2D medical image has achieved some results, but there are still some problems, such as the complexity of calculation and the slow speed of segmentation. For 3D image with more data and more complex image structure, the data structure and algorithm processing of these methods will inevitably lead to greater complexity, and some problems such as low accuracy and slow computing speed will further appear. Besides, there is no general method for 3D color medical image segmentation except for the research based on specific parts. Compared with previous similar studies, the method proposed in this paper is a user-oriented direct segmentation method for 3D medical images, which not only improves the segmentation efficiency, but also ensures the segmentation accuracy.

5.Conclusion

In this paper, we present a semi-automatic and direct segmentation method for creating 3D target models from color volume images. In this method, we construct original 3D volume image data by using serialized corpse section images. Via constructing the Laplace matrix and linear transformation with eigenvectors, we obtain a set of matting components. We use an energy function to select components belonging to the target region. This method can achieve interested model direct extraction by using a small number of user markers. In addition, by comparing with current used 2D segmentation method, our method can generate more accurate result.

Acknowledgments

The authors thank the U.S. National Library of Medicine and Southern Medical University of China for providing the virtual human image data sets. This study was supported by the National Natural Science Foundation of China (Nos 61972440, 61572101 and 61300085), the Fundamental Research Funds for the Central Universities (Nos DUT20YG108 and DUT20TD107) and the Scientific Research Project of Educational Department of Liaoning Province of China (No. LZ2020031).

Conflict of interest

None to report.

References

[1]	Karacan L, Erdem A, Erdem E. Image Matting with KL-Divergence Based Sparse Sampling. IEEE International Conference on Computer Vision. (2015) ; pp. 424-432.
[2]	Gastal ESL, Oliveira MM. Shared sampling for RealTime alpha matting. Computer Graphics Forum. (2010) ; 29: (2): 575-584.
[3]	Wang L, Xia T, Guo Y, et al. Confidence-driven image co-matting. Computers & Graphics. (2013) ; 38: (2): 131-139.
[4]	Feng X, Liang X, Zhang Z. A Cluster Sampling Method for Image Matting via Sparse Coding. European Conference on Computer Vision. (2016) ; 204-219.
[5]	Levin A, Lischinski D, Weiss Y. A closed form solution to natural image matting. IEEE Transactions on Pattern Analysis & Machine Intelligence (2007) ; 30: (2): 228-242.
[6]	Levin A, Rav-Acha A, Lischinski D. Spectral matting. IEEE Transactions on Pattern Analysis & Machine Intelligence. (2008) ; 30: (10): 1699-1712.
[7]	Varga-Szemes A, et al. Clinical feasibility of a myocardial signal intensity threshold-based semi-automated cardiac magnetic resonance segmentation method. European Radiology. (2016) ; 26: (5): 1503-1511.
[8]	Geng L, Shao YT, Xiao ZT, et al. Fundus optic disc localization and segmentation method based on phase congruency. Bio-medical Materials and Engineering. (2014) ; 24: (6): 3223-3229.
[9]	Wang R, Zhou Y, et al. A hybrid flower pollination algorithm based modified randomized location for multi-threshold medical image segmentation. Bio-medical Materials and Engineering. (2015) ; 26: (s1).
[10]	Zhou S, Wang J, Zhang S, et al. Active contour model based on local and global intensity information for medical image segmentation. NEUROCOMPUTING. (2016) ; 186: (C): 107-118.
[11]	Huang J, Jian F, Wu H, et al. An improved level set method for vertebra CT image segmentation. BioMedical Engineering OnLine. (2013) ; 12: (1): 48.
[12]	Khadidos A, Sanchez V, Li CT. Weighted level set evolution based on local edge features for medical image segmentation. IEEE Transactions on Image Processing. (2017) ; 26: (4): 1979-1991.
[13]	Zhao SY, Ding S. Medical image registration based on hidden markov model and multi wavelet threshold algorithm. Journal of Computational and Theoretical Nanoscience. (2016) ; 13: (11): 7978-7983.
[14]	Dong E, Zheng Q, Sun W, et al. Constrained multiplicative graph cuts based active contour model for magnetic resonance brain image series segmentation. Signal Processing. (2014) ; 104: : 59-69.
[15]	Li L, Yang R, Huang Y, et al. Registration-based automatic 3D segmentation of cardiac CT images. IFMBE Proceedings. (2013) ; 39: (3): 908-911.
[16]	Chen H, Dou Q, Wang X, et al. 3D Fully Convolutional Networks for Intervertebral Disc Localization and Segmentation. Medical Imaging and Augmented Reality. (2016) ; 375-382.
[17]	Pazos M, Dyrda AA, Marc B, et al. Diagnostic accuracy of spectralis SD OCT automated macular layers segmentation to discriminate normal from early glaucomatous eyes. Ophthalmology. (2017) ; 124: (8): 1218-1228.
[18]	Rashno A, Parhi KK, Nazari B, et al. Automated intra-retinal, sub-retinal and sub-RPE cyst regions segmentation in age-related macular degeneration (AMD) subjects. Investigative Ophthalmology & Visual Ence. (2017) ; 58: : 397-397.
[19]	Qiu W, Yuan J, Kishimoto J, et al. 3D MR Ventricle Segmentation in Pre-term Infants with Post-Hemorrhagic Ventricle Dilation. Medical Imaging 2015: Image Processing. (2015) ; 9413.
[20]	Ballerini L, Lovreglio R, Valdés H, Maria del C, et al. Perivascular spaces segmentation in brain MRI using optimal 3D filtering. Scientific Reports. (2018) ; 8: (1): 2132.