RF ablation thermal simulation model: Parameter sensitivity analysis

1.Introduction

RFA technology is to apply the AC electric field to the tumor tissue, thus achieving tumor coagulation necrosis by the resistance heating. This technique has been widely used in the treatment of liver tumors due to its minimal invasiveness. However, the ablation quality still depends on the experiences of clinicians. Some studies [1, 2, 3] have shown that RFA outcomes mainly rely on the lesion volume size, shape of the ablation zone and its internal temperature distribution. Thence, the precise characterization of the RFA temperature field is particularly important.

Computer modeling and simulation technology can not only obtain the temperature changes in the ablation zone, but also help doctors to make a reasonable surgical plan before surgery. Zhang [4] established the temperature field models based on the Pennes and Hyperbolic heat transfer equations and discussed the effects of different heat transfer models on the temperature distributions. Nie [5] studied the temperature field of RFA in the spinal tumor conformal therapy. Jin et al. [6] found a RFA model of thyroid treatment based on MRI. Huang et al. [7] attempted to adjust the electrode needle voltage based on the proportional integral feedback control method, to build temperature-controlled RFA simulation model, but did not consider the parameter changes over time. In these literatures, however, the electro-thermal parameters were regarded as fixed values, and the specificity of the biological tissue parameters was not considered. Actually, these parameters will vary with temperature. Rossmann and Haemmerich [8] presented a review of temperature dependence of tissue electro-thermal properties. The study also suggested that all these parameters were necessary for determining absorption of electromagnetic energy (e.g. microwaves or RF current), and estimating the temperature profile. Trujillo and Berjano [9] also investigated the mathematical functions used to describe temperature dependence of electrical and thermal conductivities in RFA models. Thus, using a single reference value in RFA simulation model is not sufficiently accurate. In order to improve the accuracy of the simulation model of liver tumor temperature field, it is necessary to research the influence of changes of tissue parameters on the lesion volume in RFA.

In view of the above, a sensitivity analysis method is required to precisely characterize how the temperature dependence of parameters will influence the simulation temperature and lesion volume. Sensitivity analysis is a quantitative description of the input parameters on the output response [10], and its quantitative index is the variance contribution rate of error. The greater the SS% is, the higher the effects of the parameter on the model responses will be [11]. The purpose of this paper is to achieve the sensitivity of each characteristic parameter by sensitivity analysis method. In the feedback application, the less sensitive parameters can be removed, so as to effectively reduce the complexity of the model, simplify data operations, and further improve the accuracy of the simulation model. This paper mainly analyzes the characteristic parameters of the temperature distribution model by variance analysis method, and obtains the sensitivity parameters which have significant influences on the ablation temperature and lesion volume.

In clinical RF thermal ablation surgery, the temperature-controlled ablation instrument is commonly used. The working principle is to adjust the output power in real time according to the set parameters (center temperature, temperature-raising rate, etc.), acquire a constant central temperature by power compensation, and finally achieve the required thermal coagulation effects. Temperature-controlled RFA model was established based on the ablation instrument RFA-I (Blade Co., Ltd., Beijing, China) and the liver tissue phantom. The temperature field modeling was performed using COMSOL Multiphysics software version 5.1 (COMSOL Inc., Palo Alto, CA, USA). The sensitivity of each characteristic parameter was studied by factor analysis (DOE) in Minitab (State College, PA, USA).

2.Materials and methods

2.1Geometric modeling of RFA

The RFA simulation model was established and solved by the finite element method (FEM) in Comsol software. FEM was used to solve the diffusion equation numerically [12, 13], which offered advantages in speed and flexibility.

Due to the symmetry of the electrode, only half of the model needed to be considered to save computation time. The symmetrical model was constructed into a semi-cylinder of homogenized tissue (50 mm * 25 mm * 70 mm), and a clinical multi-polar electrode was embedded in the tissue as shown in Fig. 1. The shapes and dimensions of the electrode were designed based on the real multi-polar electrode used in the experiments (Fig. 2). Six sub-electrodes were distributed on one side of the multi-polar electrode uniformly. Therefore, the angle between two sub-electrodes was about 55∘. Each sub-electrode had a different degree of deflection, and the deflections of the adjacent two sub-electrodes were 104∘ and 57∘.

Figure 1.

Geometry model of the tissue and multi-polar electrode.

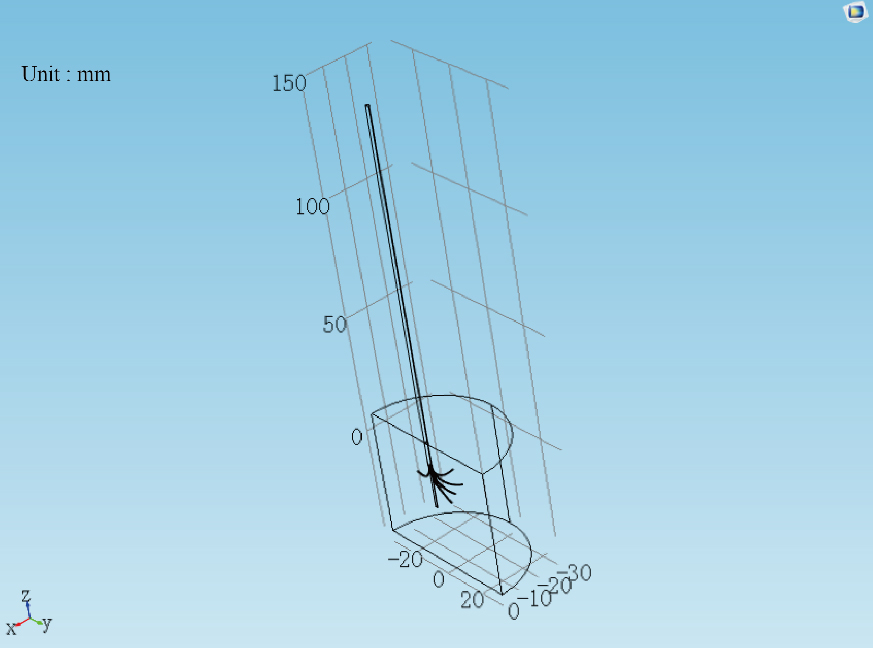
Figure 2.

The shape and distributing range of the electrode.

To obtain the solution of FEM model, the boundary conditions and initial conditions of the simulation model were set. For the current field, the boundary of the multi-polar RF electrode was set as the voltage source, and the boundary of the liver tissue was set as the ground; for the bio-heat transfer physical field, the initial temperature of the model was 28∘C, the external thermal boundary condition was 28∘C. At the same time, we assumed that the tissue perfusion rate ω had no effect on the simulated temperature in the liver phantom.

3.Results

Some representative points including the far field point (0 mm, 15 mm, -19 mm) and the near field point (0 mm, -5 mm, -19 mm) as well as the 54∘C isothermal surface volume of the ablation zone were analyzed, so as to study the effects of the characteristic parameters on the temperature distributions in RFA model. 54∘C isothermal surface volume here represents the voulme enclosed by the 54∘C isotherm around the electrode and is used interchangeably with the term “ablation volume” or “lesion volume”. Figure 3 showed the positions of representative points in simulation model.

According to the 54 runs in Table 2, the temperature field simulation was implemented in Comsol software, and the simulation time was 360 s. Figures 4 and 5 showed the main effects of the parameters R, Cp, Sigma, rho and Epsilon on the far field temperature and near field temperature, respectively at t= 50 s and t= 360 s. As could be seen in Figs 4 and 5, the influences of Cp and rho on the far field temperature were getting smaller and smaller over time, and these parameters were negatively correlated with the simulation temperature. The effects of R and Sigma on the far field temperature were always obvious, so R and Sigma were significant influencing factors. With regard to Epsilon, there was no effect on ablation temperature. Besides, the SS% trendlines of the parameter k in the near field and far field were different.

Figure 3.

The position of representative points in RFA model.

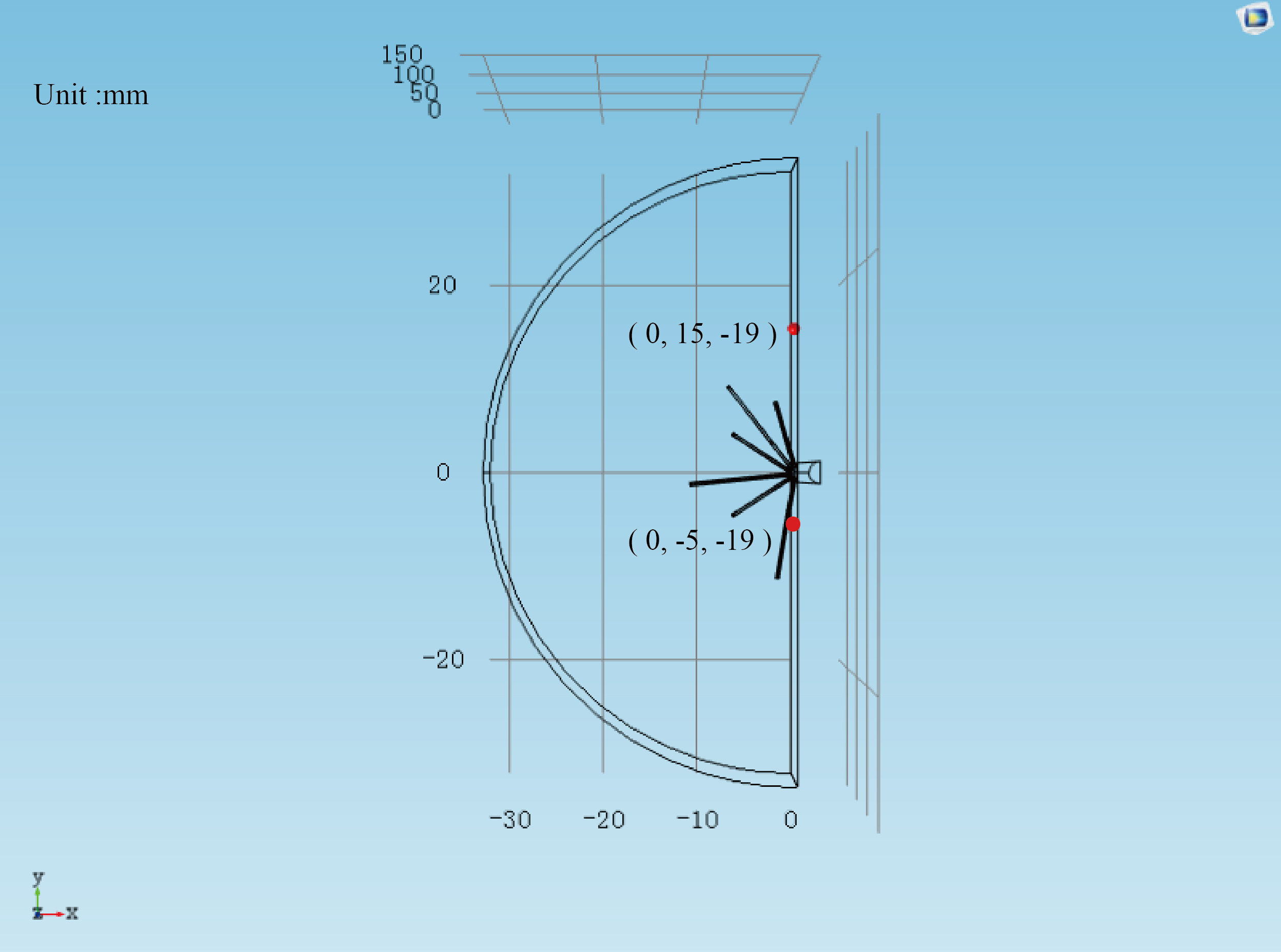
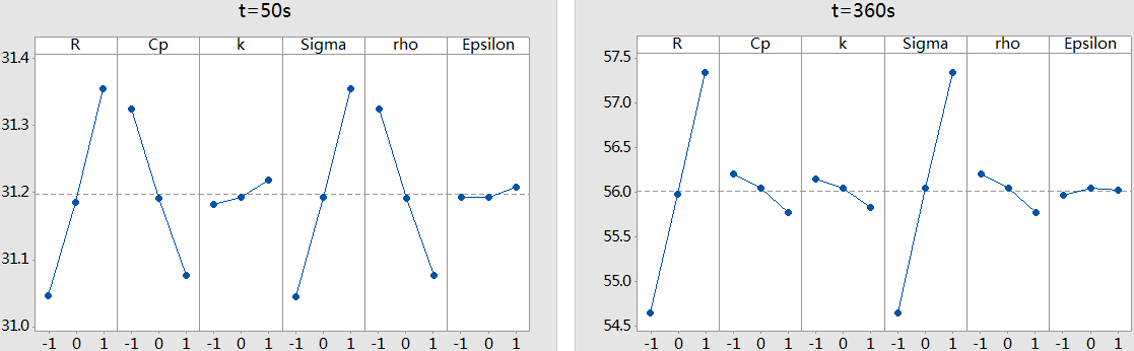
Figure 4.

The main effect of each parameter at t= 50 s and t= 360 s on the far field temperature.

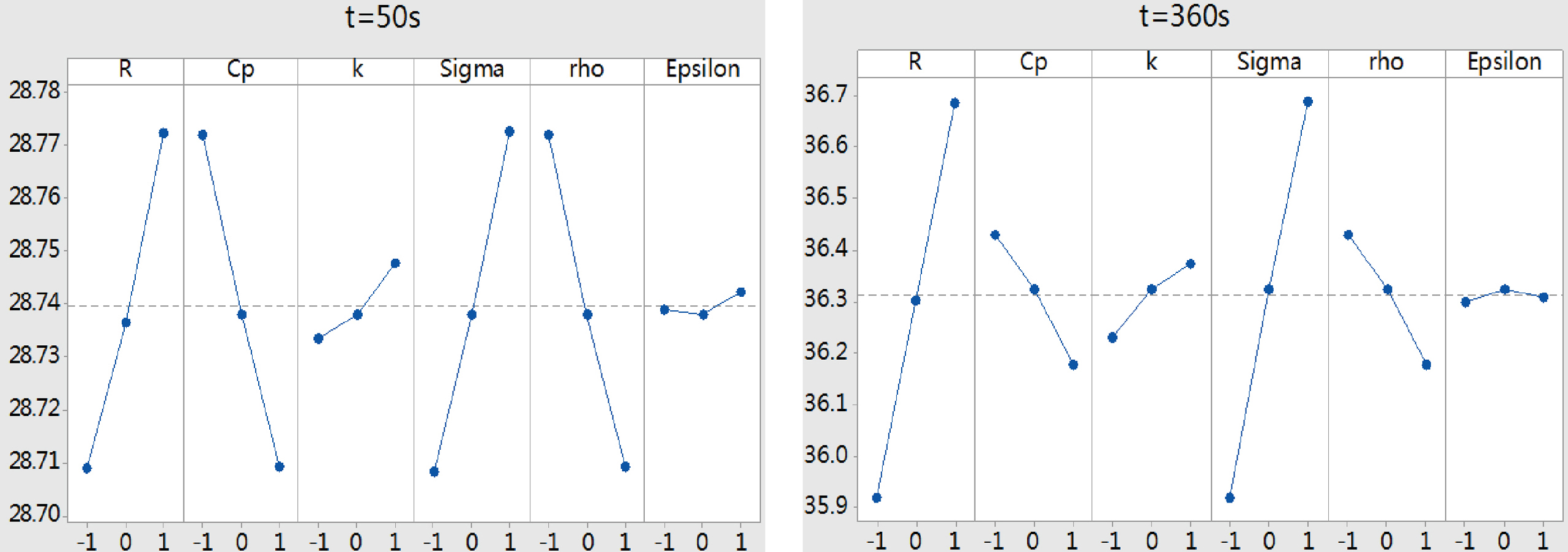
Figure 5.

The main effect of each parameter at t= 50 s and t= 360 s on the near field temperature.

In order to acquire the quantitative analysis of the influences of the parameters on the ablation temperature, the variance analysis was carried out. As shown in Table 3, the F-value is the variance of the mean of the test data. The larger the value is, the more significant the parameter is. The P-value is used to determine the result of the hypothesis test [10]. If the P-value < 0.05, the parameter is significant. DOF represents the degree of freedom; Adj_MS represents the mean of the variance of the parameters; SS% represents the square sum of the variance deviations from the mean, and its value quantitatively reflects the significance of the parameters on the ablation temperature, as shown in Eq. (7):

where i can take A, B, C, D, E, and F; 𝐴𝑑𝑗⁢_⁢S⁢Si represents the variance of the ith parameter.

Figure 6.

The SS% trendlines for each parameter at far field point.

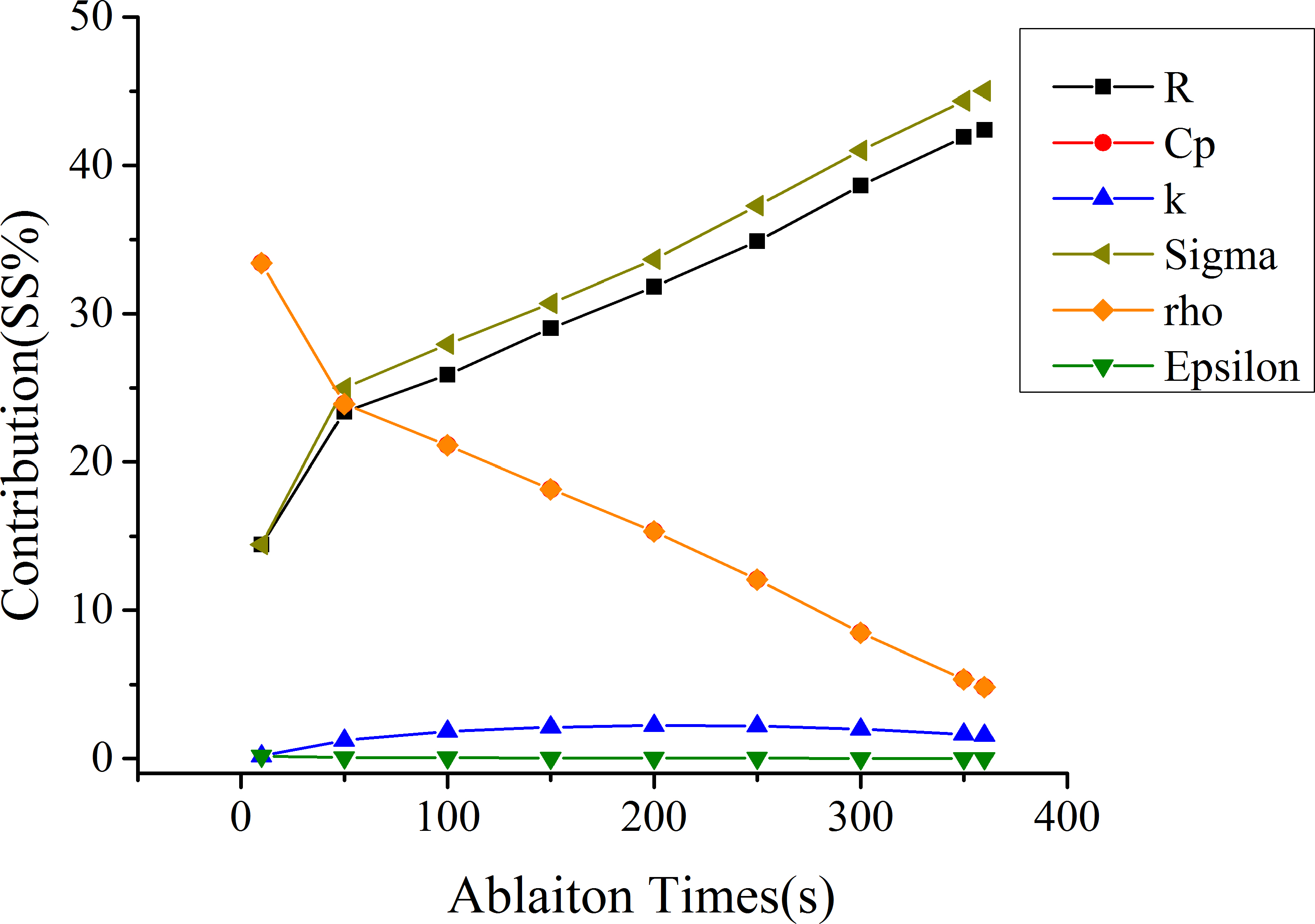
Figure 7.

The SS% trendlines for each parameter at near field point.

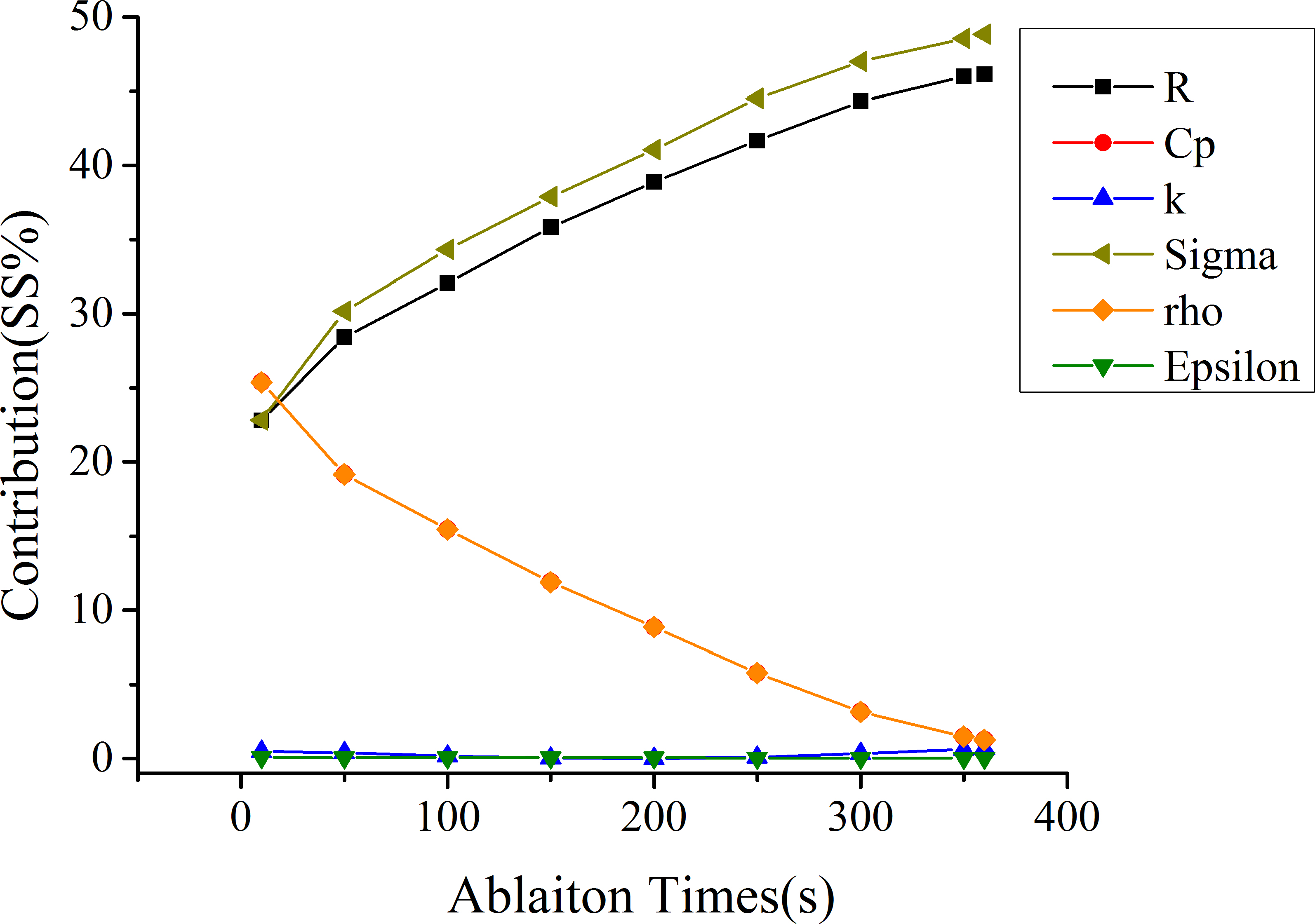
Figure 8.

The main effect of different parameters on the volume of 54∘C isothermal surface volume.

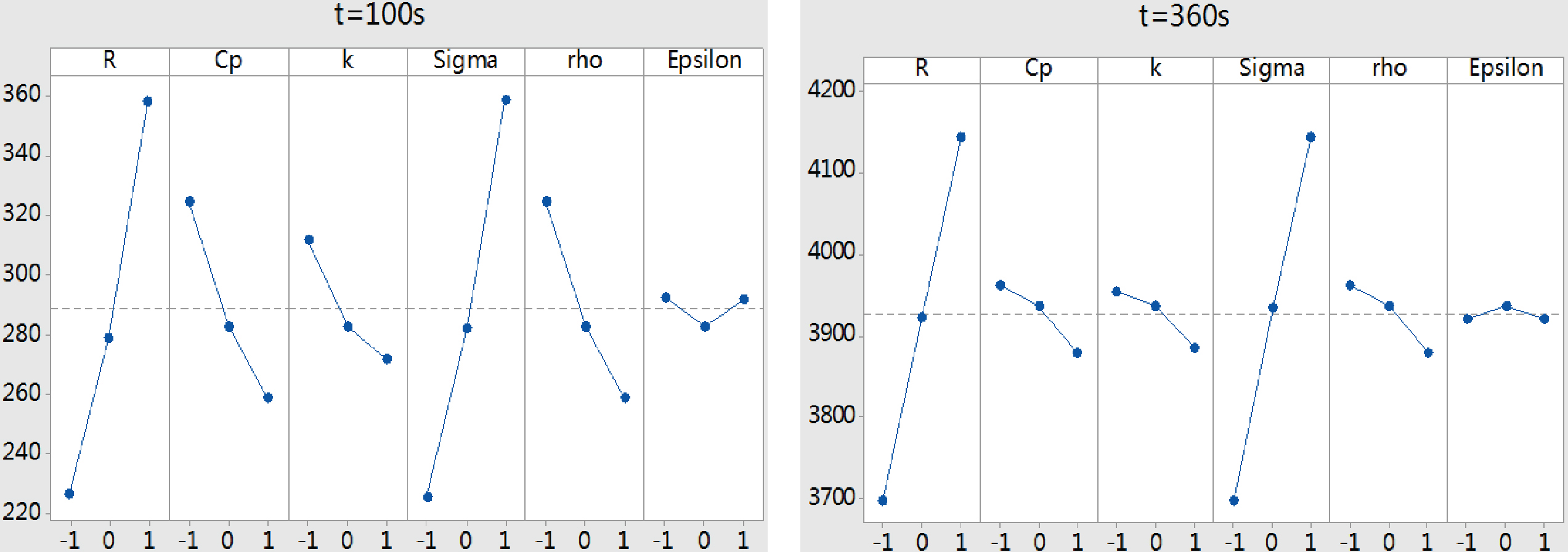
Figure 9.

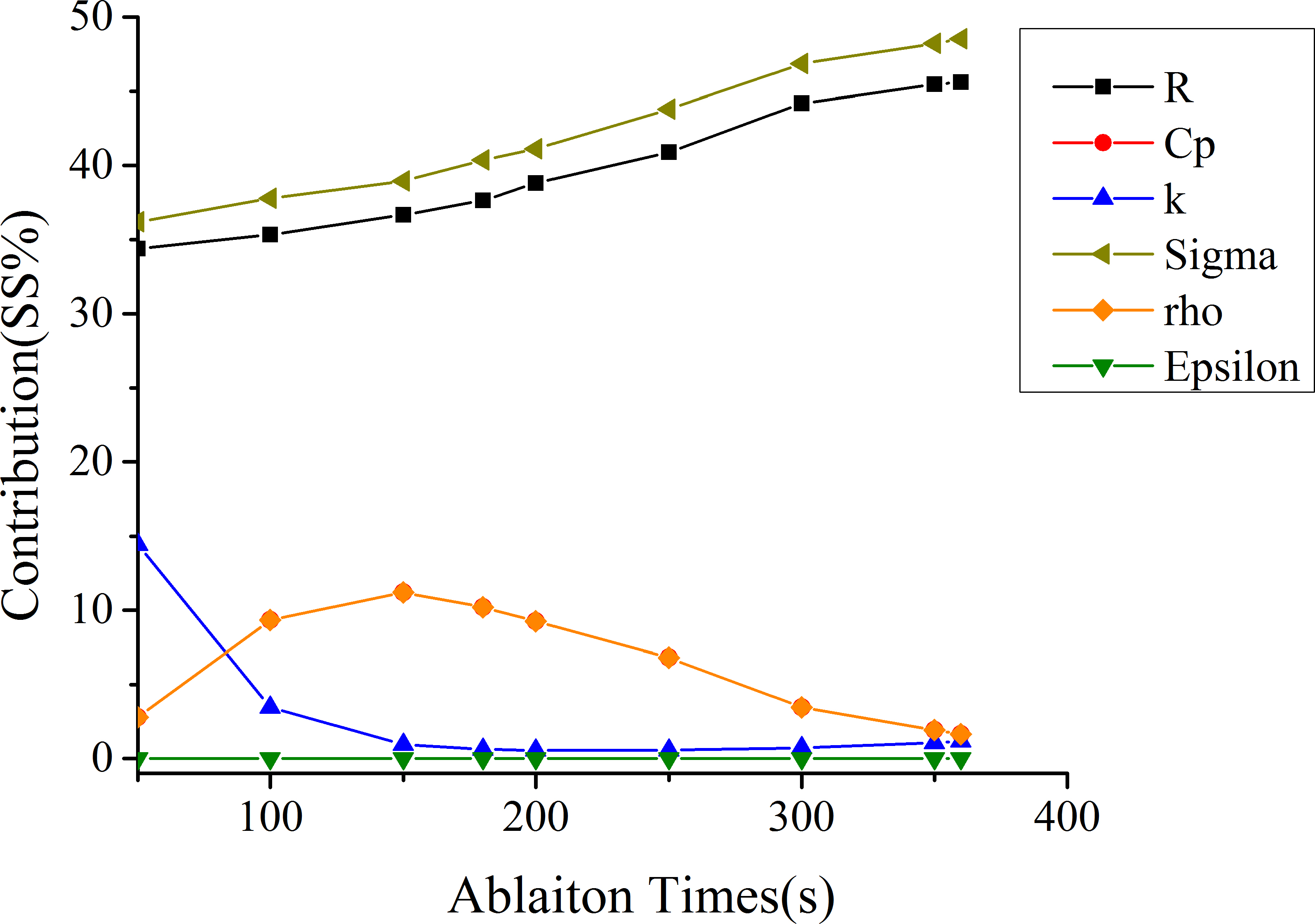
The contribution rate of each parameter to 54∘C isothermal surface volume.

The SS% values of single parameter in the far field and near field were shown in Tables 3 and 4. The Interaction and Square results between mentioned parameters were also listed. The sensitivity of single parameter, interaction and square item at t= 50 s was: Sigma>Cp (rho) >R>k> Interaction > Square >Epsilon and at t= 360 s was: Sigma> R>Cp (rho) >k> Interaction >Epsilon> Square; where Epsilon and its Interaction and Square item had little influence on RFA temperature.

This paper also showed the SS% trendlines to more clearly illustrate the changes of the parameter sensitivity during the RFA period. As could be seen in Figs 6 and 7, in the far field, the SS% of Cp and rho ranged from 33.4% to 4.8%; the SS% of Sigma and R ranged from 14.4% to 45%; in the near field, the SS% of Cp and rho ranged from 23% to 3.2%; the SS% of Sigma and R ranged from 22.8% to 48.8%. Therefore, the ablation temperature was sensitive to Cp and rho at early ablation stage; Sigma and R had important effects on ablation temperature at the middle and later period.

However, the sensitivity analysis merely based on individual points had some particularity. This study further discussed the sensitivity of the parameters on thermal coagulation zone, which was the main output of RFA. 50∘C isothermal surface [9, 15, 16] and 60∘C isothermal surface [17, 18] were usually used as the ablation zone boundary during the RFA. In another word, 50∘C isothermal surface volume or 60∘C isothermal surface volume could be regarded as the thermal damage volume. In order to highlight the effects of the parameters on the lesion volume, the zone with the temperature more than 54∘C was considered as the ablation volume.

Figure 8 illustrated the main effects of the parameters on 54∘C isothermal surface volume during the ablation period. The results showed that the influences of R and Sigma on the 54∘C isothermal surface volume were significant. Epsilon had little effect on the isothermal surface volume. With the passing of time, the sensitivity of Cp and rho to the isothermal surface volume became inconspicuous. These conclusions were consistent with the results of single-point sensitivity analysis. Table 5 also showed the variance analysis results of 54∘C isothermal surface volume.

As shown in Fig. 9, the SS% trendlines of 54∘C isothermal surface volume were plotted. The SS% trendlines of parameters Cp and rho were consistent. Figure 8 indicated that the lesion volume was significantly sensitive to Sigma and R during RFA period. Their contribution rate was about 35% at early ablation stage, and was above 46% at the middle and later period of RFA.

4.Discussion

Based on the RFA experiment and FEM model of vitro phantom, the parameters that have a significant influence on ablation zone size of the liver tissue were analyzed. There are two primary contributions: (1) this study has established an accurate RFA model based on the actual power profile and equivalent resistance; (2) because the non-linearity variation of the liver tissue parameters during RFA process, six parameters with three levels each were selected to analyze the sensitivity to ablation temperature and lesion volume. Parameter sensitivity analysis results, presented in this study, could provide a priori information for clinical practitioners and simplify the finite element modeling of liver tumor RFA.

Although many methods can carry out parameter sensitivity analysis, the efficiency of different methods varies widely. In order to estimate the effects of tissue parameters to ablation zone, full factorial experimental design can be used to provide the optimum results by testing all the possible combinations of the parameters. Johansson et al. [19] used a 24-factorial design to investigate the influences of tissue parameters on lesion zone of the brain. Nevertheless, the authors did not consider the non-linearity effects of the parameters during RFA. Furthermore, the more experimental combinations will be performed with increasing input parameters. For instance, with regard to 5 parameters each having three levels, 3=5 243 experimental combinations are required to be performed. Considering this disadvantage, CCD method was taken into account in the present study to improve efficiency of sensitivity analysis. For example, as for 5 parameters each having 3 levels, 54 experimental combinations will be required using the CCD method. For purpose of improving the experimental efficiency, more and more researchers have used Taguchi orthogonal arrays (OA) to design an experiment. Compared with the full factorial experimental design and RSM experiment methodology, this technique can acquire minimal number of experiments and greatly improve experimental efficiency. Jamil and Ng [20] have utilized Taguchi’s L27 orthogonal array that requires only 27 experiments (simulations) to determine the effect of 6 parameters with 3-levels each during RFA of liver tumor.

At present, some scholars have conducted sensitivity analysis on the parameters during RFA process. However, there are still some differences between the present sensitivity analysis results. Hall et al. [21] indicated that blood perfusion, electrical conductivity and the cell death model were the most important factors for estimating the ablation zone size in liver RFA models. Similarly, our results obviously demonstrated that electric conductivity was one of the important parameters. Monsalvo et al. [22] analyzed how the variations of the different parameters influenced the temperature in liver tissue through using the complex Taylor series expansion (CTSE) finite element method. The authors have found that the thermal and electrical conductivity of the healthy liver tissue have extremely important influence on the final temperature of RFA simulation models. According to what we has mentioned above, it is clear that electric conductivity is one of the most important parameters, thus confirming the results of our study. Moreover, the insensitivity parameters of the lesion size cannot be focused to simplify the RFA model of liver tumor. However, due to RFA model differences, analysis parameter differences and experimental environment differences (e.g. in vitro experiments or in vivo experiments) during sensitivity analysis, there are a few differences between our results and the previous studies.

Although some important discoveries have been revealed in this paper, there are also limitations. Firstly, the proposed RFA model for predicting the temperature did not consider the cooling effects of large blood vessels. Actually, during RFA of liver tumor, the cooling influence of the large blood vessel (i.e., the blood vessel with the diameter larger than 3 mm) has a remarkable impact on lesion volume [23]. This issue will be taken into account in the future work. Secondly, CCD experimental design needed complex experimental combinations in contrast with the Taguchi’s orthogonal array design. Thirdly, 54∘C isotherm contours was used to assess the extent of the ablation zone in the RFA computer models. However, the death of tissue during RFA depends on the local temperature as well as the RF ablation time [24]. Therefore, Arrhenius [25] models ought to be used in further study. Finally, due to the variability between in vitro and vivoexperiment, the subsequent step is to establish the RF finite element simulation model with blood vessels for sensitivity analysis.

5.Conclusions

In this paper, based on the temperature-controlled RFA simulation model, the influences of the electro-thermal parameters on the temperature distributions and ablation volume were analyzed. According to the main effects and the SS% values, the sensitive parameters were obtained. It can be concluded that the size of the RFA zone was mainly dependent on Sigma and R, and these parameters were positively correlated with ablation zone. The sensitivity of Cp and rho on the ablation zone was reduced over time, and these parameters were negatively correlated with the ablation zone; Epsilon had little effect on the ablation zone during the RFA period. There was no good agreement for the parameter k on the temperature changes. In the near field, the heat was absorbed by the heat exchange at the beginning of RFA, so the temperature will increase with the increase of the k. At the later stage of ablation, heat is released by heat exchange, so k was negatively correlated with temperature. In the far field, heat was mainly absorbed by heat conduction and, as a result, was positively correlated with k. The sensitivity of the parameter k on some points and 54∘C isothermal surface volume was slightly different in the early stage of ablation, and the trends of change in the later ablation session were basically the same.

In conclusion, the most important parameters in predicting the RFA volume are electric conductivity and bioelectric impedance. These results can provide a scientific basis for the feedback regulation of the sensitivity parameters. These extended applications would be the topic of our future study.