Differential barometric-based positioning technique for indoor elevation measurement in IoT medical applications

1.Introduction

Emerging IoT technology, such as interconnected medical devices and sensors, has played an important role in next-generation medical technology [1].The wearable medical devices are the typical IoT sensor nodes that are able to continuously monitor, actuate, and record patient bio-signal data, which can be used by medical personnel to diagnose, prevent, and respond to various illnesses [2, 3]. Wireless sensor network (WSN) is a critical part to the actualization of the IoT paradigm. In addition, indoor localization has become increasingly vital to today’s pervasive wireless technology as add-ons [4]. Together, WSNs and indoor localization can be used to achieve a variety of location-based services, such as patient tracking, health care monitoring, and domotic automations. Due to growing demands for indoor location-based applications, high-accuracy indoor localization has a vast market prospect.

Accurate localization can be achieved using Indoor Positioning Systems (IPS). IPSs can measure the positions (x-, y-, and z-coordinates) of object in indoor environments. Several localization approaches can be applied to medical problems [5]. One of the most important tasks in intensive care can monitor vital signs, such as the blood pressure, oxygen saturation, and pulse rate of a patient. Figure 1 shows a measurement setup for invasive arterial blood pressure. Invasive arterial blood monitoring systems are particularly useful clinical tools that provide beat-to-beat blood pressure measurements and visible waveforms, allowing for a more detailed analysis of a patient’s cardiovascular status [6]. The arterial pressure is directly measured by inserting cannula needle into a suitable artery. Intra-arterial monitoring systems include a measuring apparatus, transducer, and monitor. The measuring apparatus, which consists of an arterial cannula connected to tubing containing a continuous column of saline, transmits the blood pressure to the transducer [7]. The transducer then converts the measured pressure into an electrical signal. The monitor amplify the output signal from the transducer, filter noise, and display the arterial waveform in real time on a screen [7].

Figure 1.

Components of an arterial monitoring system [6, 7].

Changes in location and orientation can affect pressure parameters inside the body where the body needs to react accordingly. For example, the pressure parameters in the lungs and limbs of a patient sitting upright are different from a patient lying horizontally. A localizing sensor node, called a “tag”, can be fixed to the patient’s body to improve the accuracy of the monitoring system. For our medical applications, tag localization is achieved by updating the elevation estimation when the tag moves to a new elevation.

One method used to perform indoor elevation measurement is barometric altimetry. Barometric altimetry is a traditional method for altitude measurement that is based on the decrease in atmosphere pressure as the altitude increases [8, 9]. Hence, elevation estimation can be performed using measured pressures and a height-pressure model. WSNs enable data transfer among barometric sensors.

This study focuses on the development of an IPS that can precisely measure the z-coordinate of a tag rather than the x- or y-coordinates of the tag. This work consists of the following general features.

The rest of this paper is organized as follows. In Section 2, previous IPSs research is discussed. In Section 3, our proposed system structure for accurate elevation measurement in medical applications is presented. In Section 4, the differential barometric altimetry model, Gaussian filter, and calibration steps are introduced. In Section 5, a comparative evaluation is performed, and the effects of environmental factors on the elevation measurements are discussed. The conclusions and opportunities for future studies are presented in Section 6.

2.Related work

This study focuses on the indoor altitude estimation of a tag. Several IPSs could be applied to this medical application. Liu et al. [10] provide a survey of the existing IPS and classified them based on the used technology. A comprehensive performance comparisons including accuracy, precision, complexity, scalability, robustness, and cost is given. However, these IPSs systems have not been compared from a medical application perspective.

Systems that integrate additional sensors have been designed for improving altitude estimation precision. Evennou and Marx introduced a system employing inertial sensors for WLAN [11]. Wang et al. developed a system by utilizing additional air pressure sensors [12]. Both of these systems yielded estimation accuracies within one meter. However, these systems are still insufficient for the medical applications discussed herein. Furthermore, measurements obtained from inertial sensors can be easily drifted, which must be corrected.

In [13], pressure sensors were employed for improving the accuracy of altitude estimation in satellite navigation systems. The authors indicated that local interference must be considered when performing altitude estimation. In [14] a method based on barometric sensors was developed for Body Sensor Networks (BSNs). In this method, one barometric sensor acts as a reference object, while the other sensor is attached to the patient’s body. However, the transmission may be not direct, if the nodes are in remote range or via multi-hop. Obviously, there is an air pressure measurement delay. Thus, these systems are not suitable for the real-time requirements of medical applications.

Medical applications have additional hardware requirements. For example, hardware must be small and easy to use. The aging population and nursing staff shortages necessitate the development of advanced systems. However, although many IPSs have been proposed, most have only been evaluated in the non-representative measurement.

In this study, the air atmosphere pressures were collected to calculate altitude, according to the idea of differential measurement. The proposed method is based on the decrease in barometric pressure that occurs with increasing altitude. The effects of local disturbance are prevented with the differential barometric altimetry model and a Gaussian filter.

3.System architecture

The Crossbow® TelosB sensor node was used herein due to its ready-to-use. The high precision and low power pressure sensor, Bosch BMP180, was also used. The operation of the TelosB nodes is made by user programs written in the NesC language and linked to TinyOS libraries.

The IEEE 802.15.4 compliant protocol was implemented in order to transmit the barometric pressure measurements. One node, which was fitted on the floor, acted as the reference node and sent the measured pressure measurements to the base station. The other node, which was placed at different altitudes, acted as the localizing tag and sent the measured pressure values to the base station. The difference in altitudes between the reference and the sensors measured the altitude, was calculated by using the differential barometric altimetry formula.

4.Differential barometric altimetry system

In this section, the accurate altitude measurement system for medical applications is presented. The proposed differential barometric-based positioning system implements three strategies to improve the accuracy of elevation estimation:

4.3Calibration

Generally, a principle of “uncertainty” is reflected in air pressure measurement. During the initial stages of the experiment, the sensors placed near one another yielded different air pressure values at the same altitude. The sensors still yielded different values after being moved the same distance vertically. This indicated that the differences in pressure readings resulted from inaccurate factory calibration coefficients are unique to each sensor. The differences did not change over time. Therefore, a constant offset calibration procedure is significant to enable a reliable and accurate elevation estimation system.

The proposed system was calibrated by obtaining a number of samples at a reference position (elevation h = 0 m). The offset was determined by using the pressure differences between sensors. This offset was stored for further elevation measurement. Because the deviation in pressures between sensors was found to be nonlinear, the calibration process was repeated at different pressure measurement in order to improve the accuracy of the elevation estimation.

The flow diagram of the proposed system is shown in Fig. 2.

Figure 2.

Flow diagram of the differential barometric altimetry system.

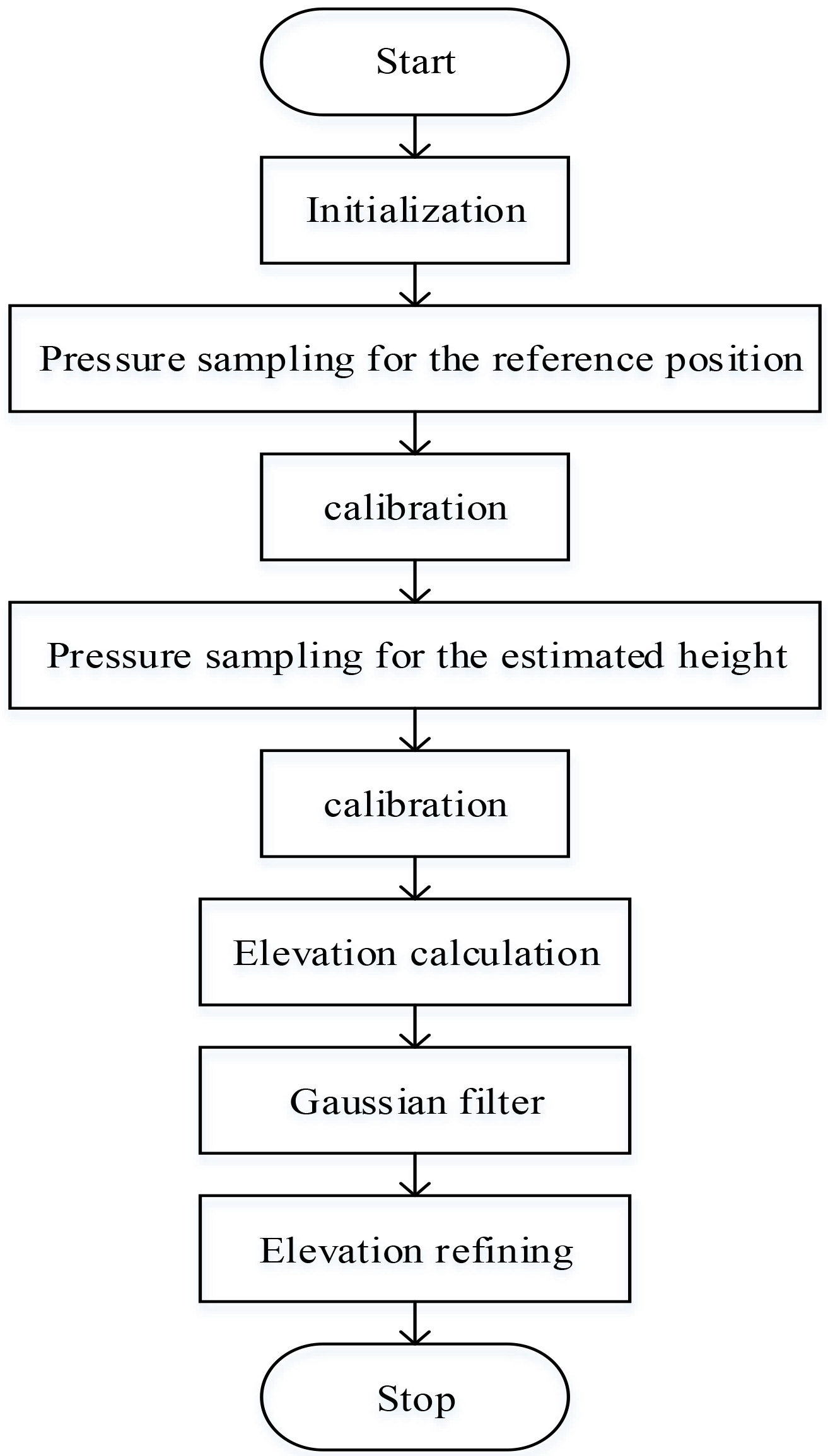
5.Results and discussion

In this section, a comparative experimental evaluation is performed, and the effects of environmental factors on the elevation measurements are discussed.

5.1Results and analysis

First, the system was calibrated by placing the two sensors in the same room at the reference position h = 0 m. The software requires 200 samples of atmospheric pressure data from each device. The pressure data obtained from the reference sensor and localizing sensor were denoted SENSOR1 and SENSOR2 herein, respectively. Figure 3a displays the measurement results obtained at the reference position, including the deviation errors that occurred between sensors. In Fig. 3b, the average pressure difference between two sensors is calculated, and a deviation correction of the SENSOR1 and SENSOR2 measurement data is performed.

The distribution of the calibrated elevation measurement samples, obtained when the localizing sensor was positioned at elevations of h = 10, 20, 30, and 40 cm, was also investigated in order to evaluate the performance of the system. In each trial, 200 measurements were collected at each elevation. In the proposed system, the differences in air pressure between two sensors were utilized to calculate the elevation in space. The pressure readings were obtained simultaneously from air pressure sensors. Furthermore, the offsets in each trial were corrected via the calibration process. Therefore, the Gaussian distributions of the elevation measurements were used to examine the accuracy of the system.

Figure 3.

(a) Air pressure measurements obtained at the same reference position. (b) Deviation correction of the measurements.

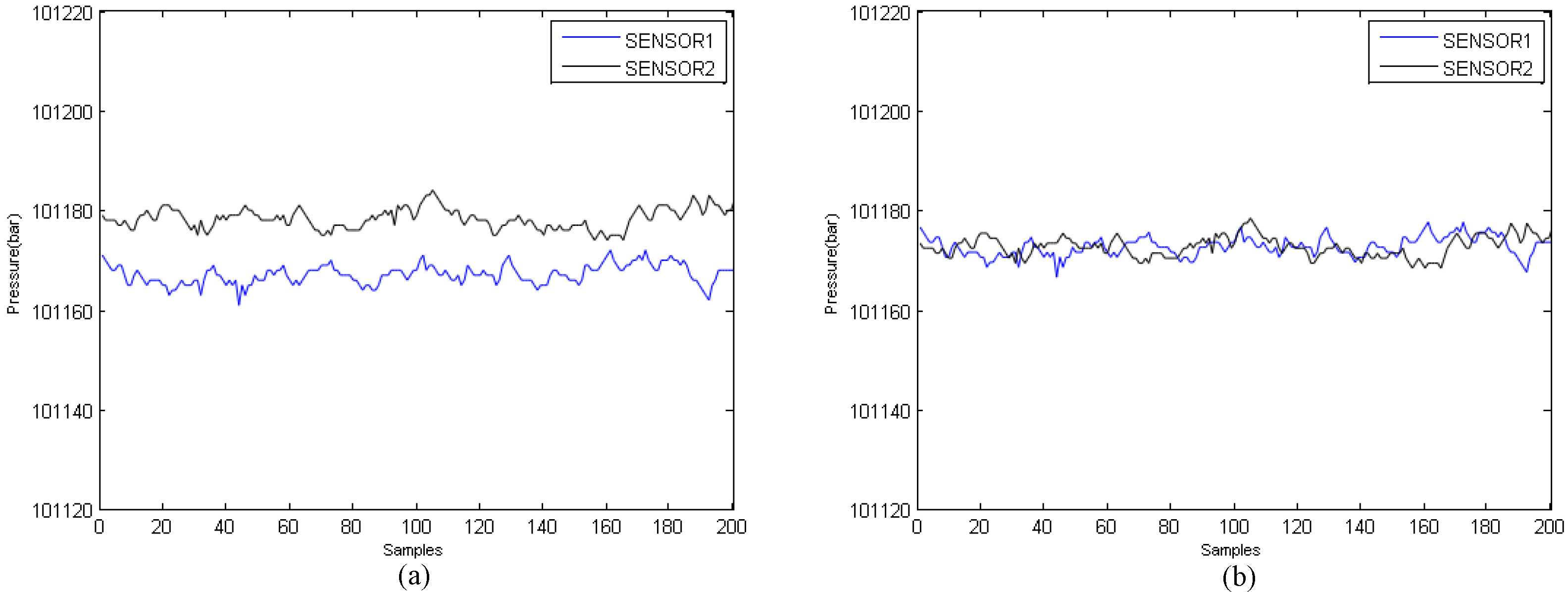
Figure 4.

Normally distributed dataset of the differential altimetry.

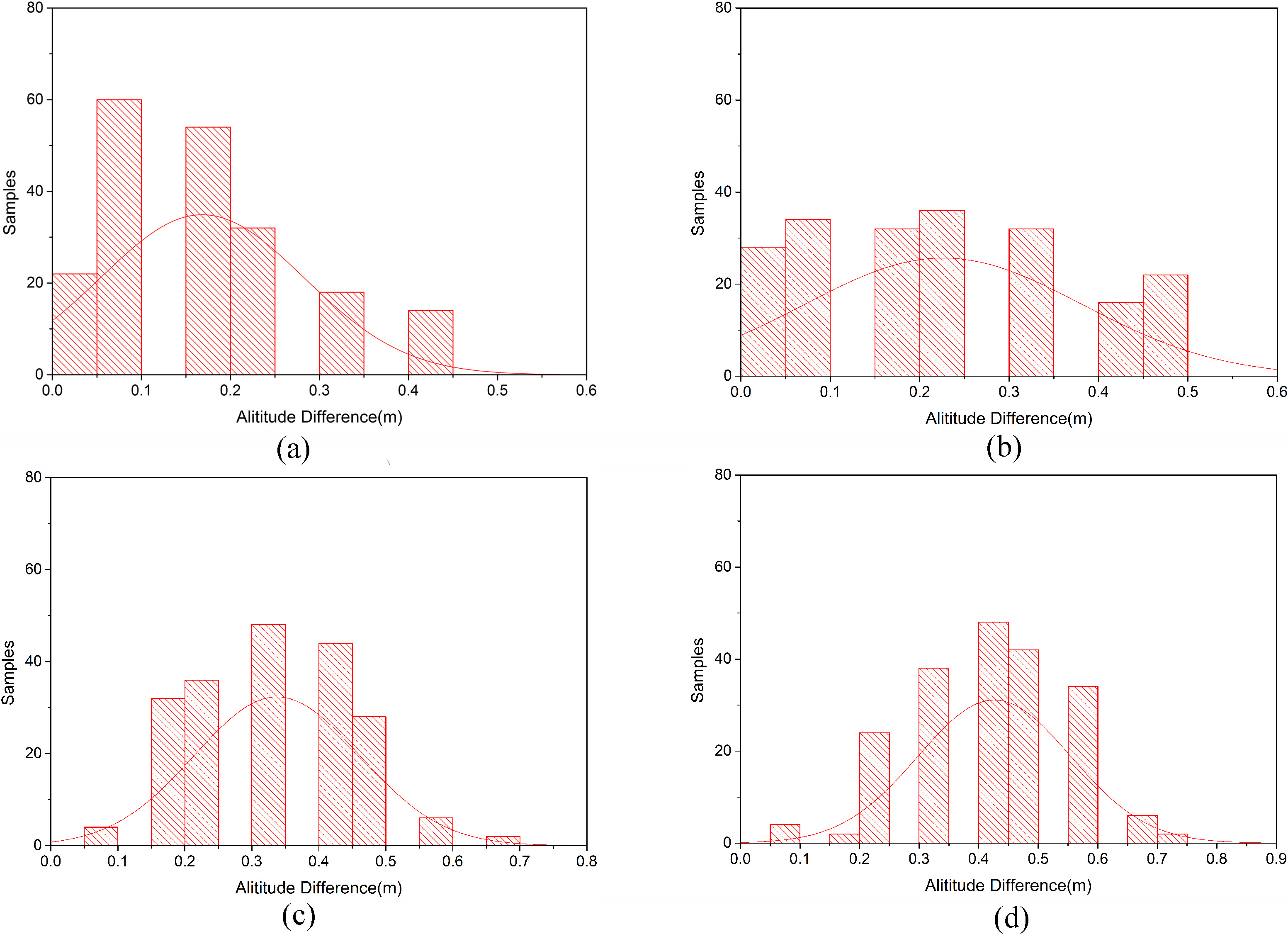
Since the derived elevation is calculated in terms of pressure conversions, the noise in this particular case is normally distributed. Figure 4 depicts the Gaussian distribution of the unfiltered measurements at heights of 10, 20, 30, and 40 cm, respectively. The red bar graphs represent the absolute frequency of the elevation difference values in m with 0.05 m spacing. The red curve denotes the corresponding calculated Gaussian distribution. These graphs illustrate the raw elevation measurements. Consequently, the filtered measurements followed a normal distribution. As shown in this figure, most of the 200 measurements obtained at each height were distinguishable.

Furthermore, the errors introduced into the proposed system were estimated according to the differences between the actual and the calculated elevation. Four statistical criteria were used to determine the stability, accuracy, and precision of the proposed system, including the Mean, Standard Deviation, Average Error (AE), and Root Mean Square Error (RMSE), defined in Eqs (5) and (6):

(5)

𝐴𝐸=1n⁢∑i=1n|D-Di|

(6)

𝑅𝑀𝑆𝐸=∑i=1n(D-Di)2n

where n is the number of samples (200 samples), D is the actual elevation, and Di is the elevation measurements obtained from sensors. Four statistical criteria can be used to determine the variation in the elevation accuracy. Table 1 displays the calculated Mean, Standard Deviation, AE, and RMSE values of the unfiltered and filtered measurements for each height.

Table 1

Error statistics (Unit: m)

Actual	Unfiltered elevation measurements				Filtered elevation measurements
elevation (m)	Mean (m)	Standard deviation	AE	RMSE	Mean (m)	Standard deviation	AE	RMSE
0.1	0.17	0.11	0.1	0.13	0.15	0.06	0.08	0.06
0.2	0.23	0.16	0.13	0.16	0.21	0.09	0.09	0.08
0.3	0.34	0.12	0.11	0.13	0.34	0.07	0.08	0.07
0.4	0.43	0.13	0.11	0.13	0.42	0.07	0.07	0.06

Table 1 indicates that the filtered measurements yielded lower errors than the unfiltered measurements. Points with large fluctuations were eliminated by the Gaussian filter processing. For example, the standard deviations of the unfiltered and filtered measurements were less than 0.16 m and 0.09 m, respectively. In addition, the AE values of the unfiltered and filtered measurements were 0.1–0.13 m and 0.07–0.09 m, respectively. The RMSE values of the unfiltered and filtered measurements were 0.13–0.16 m and 0.06–0.08 m, respectively. The stability, accuracy, and precision of the filtered elevation measurements were clearly better than the unfiltered measurements. So, the filtered measurements can be used to solve the indoor elevation estimation problem for medical applications.

6.Conclusions and future work

Accurate, reliable, real-time indoor positioning and position-based services are needed for medical applications, such as blood pressure monitoring and wireless elevation measurement. In this paper, a differential barometric-based positioning system was proposed for indoor elevation measurement in medical applications. Although environmental changes are very unstable, they could influence on the elevation measurements. The proposed system was resilient to environmental effects that alter air pressures, such as air conditioners and changes in weather. The differential altimetry model demonstrated that the environmental changes did not influence the elevation measurements. Meanwhile, the Gaussian filter processing was used to reduce noise. The stability, accuracy, and precision of the filtered elevation measurements were approximately 40%, 30% and 50% greater than those of the unfiltered measurements, respectively. Thus, the proposed system could be effectively applied to elevation measurement, even when many obstacles are present. Using IEEE802.15.4, the entire prototype system could be easily extended with additional sensors.

In future studies, the long-term stability of the system will be investigated. In addition, use of more than two sensors as the localizing or reference sensor will be discussed. Furthermore, the Standard Deviation, AE, and RMSE values of the elevation measurements should be further reduced.

Conflict of interest

None to report.