Statistical data integration models to bridge health official statistics

1.Introduction

Government programs use geography-specific health official statistics to allocate funds or make decisions. For this, reliable health estimates at fine levels of aggregation serve as key data. In addition, health estimates available from different sources need to be in agreement so that the decisions made by different groups be consistent. In the United States, there are at least two sources of health insurance coverage estimates: the Behavioral Risk Factor Surveillance System (BRFSS) and the Small Area Health Insurance Estimates (SAHIE) program. Since 2008, data from these two sources are released on a yearly basis and documented as having important policy implications.

As the nation’s premier system collecting health data from individuals in the U.S. using telephone surveys, the BRFSS is considered an important source of survey data used to inform health-related policy decisions. The BRFSS was initiated in 1984 by the U.S. Centers for Disease Control and Prevention (CDC). Throughout the years, the BRFSS methodology has been subject to changes. For example, [1] report on adding cellular telephone households to the BRFSS survey samples in order to maintain coverage and validity and on revising the BRFSS survey weights adjustments to account for declining response rates. At the end of each year, the respondent data collected throughout the year are released to the public along with documentation. In particular, the 2018 BRFSS codebook describes the many health variables for which data were released in 2018, including health insurance coverage [2].

County-level model-based estimates of health insurance coverage are produced by the U.S. Census Bureau as part of the SAHIE program. These estimates result from combining data from multiple sources, including survey data from the American Community Survey (ACS), administrative records, postcensal population estimates, and decennial census estimates. The first two sets of SAHIE estimates were released in 2000 and 2001 and were deemed experimental. Subsequently, from 2005 to 2007, SAHIE estimates were released as official statistics of health insurance coverage. The main survey data used to produce these initial sets of SAHIE estimates were data from the Current Population Survey. Since 2008, the main survey data used in the SAHIE program are health insurance coverage data from the American Community Survey. More details on the early SAHIE data releases are available in [3]. For the 2018 SAHIE report we refer to [4].

In this paper, we integrate BRFSS and SAHIE public-use health data for the reference year 2018. First, we address comparability of estimates at the finest level at which data from both sources are publicly available, i.e., state. When summarized at the state level, the BRFSS and the SAHIE estimates of health insurance coverage differ. As a result, policy decisions made using one set of estimates over the other could have different consequences; not to mention the possible confusion induced by these differences in the decision-making process. Using models that account for the error in both sources, we bridge the two sets of health insurance coverage estimates. Then, we address estimation at the finest level at which data from at least one source are publicly available, i.e., county. The SAHIE estimates are published for all-but-one counties in the United States on a yearly basis. On the other hand, the BRFSS data released on a yearly basis contain suppressed county identifiers, making it impossible to produce county-level estimates using public-use data. Using models that include a bridging level, county-level model estimates are produced on both the BRFSS and SAHIE scales.

We are not assuming one of the two sources is the gold standard. Rather, we acknowledge that each of the BRFSS and the SAHIE estimates are subject to corresponding errors. The SAHIE scale corresponds to county-level estimates of low uncertainty. On the other hand, the BRFSS scale corresponds to state-level estimates of low uncertainty. Producing estimates on both the BRFSS and SAHIE scales using data from the corresponding sources and accounting for its uncertainty provides a way to construct estimates of lower uncertainty and to construct BRFSS estimates at lower levels of aggregation. If additional information becomes available and deems sufficient to consider one source as the gold standard, then simply the model-based estimates on that scale could be used as official statistics.

The bridging problem and the estimation at finer levels problem have been recently considered in [5]. In this study, data from one survey are available at the census division level, while data from another survey are available at the state level. Participation in recreational sports is estimated using data from the two sources and observed to differ at the census division level (a common level of aggregation). The authors present a bridging model that reconciles the participation estimates at the census division level and produces estimates at the state level on the scales of both surveys. Similarly, we develop a model that integrates the health insurance coverage estimates at the state level and produces estimates at the county level on the scales of both BRFSS and SAHIE. Unlike the scenario in [5], only one of the sources is a survey, the other being the result of model-based estimation and estimates from both sources are publicly available as health official statistics at distinct levels of aggregation.

The rest of the paper is organized as follows. In Section 2, we introduce the motivation for this work, including a description of the available data, the process of constructing initial estimates, and selected results motivating the need for statistical data integration. The statistical data integration models are presented in Section 3, along with a Bayesian framework for model fit and prediction. Results for bridging health insurance coverage estimates are provided Section 4. Public-use data from BRFSS and SAHIE are used for the application. Similarities between the models presented in this paper and small area estimation models and measurement error models are discussed in Section 5.

2.Background and motivation

The data sources for this study are the public-use files containing record-level BRFSS data and county-level SAHIE data for the reference year 2018. The BRFSS data contain geography identifiers, survey design information and final survey weights, which can be used to produce survey estimates at state, census division, and nation levels; county identifiers are not available in the public-use file. Population totals are available in the SAHIE data, which allow for aggregation of the county-level estimates to state, census division, and nation levels; the population totals serve as aggregation weights. The Kalawoa County in Hawaii is excluded from the SAHIE data and noted as not applicable, hence will not be used in this study. Lacking county identifiers in the BRFSS data, we are unable to identify this county and remove its potential corresponding data. However, its contribution to BRFSS estimation at higher levels of aggregation would not be noticeable due to its very small population size [6]. On the other hand, BRFSS data include Guam and Puerto Rico, unlike the SAHIE data which only include information on the 50 contiguous states and the District of Columbia. Therefore, we set aside the BRFSS data in the additional U.S. territories.

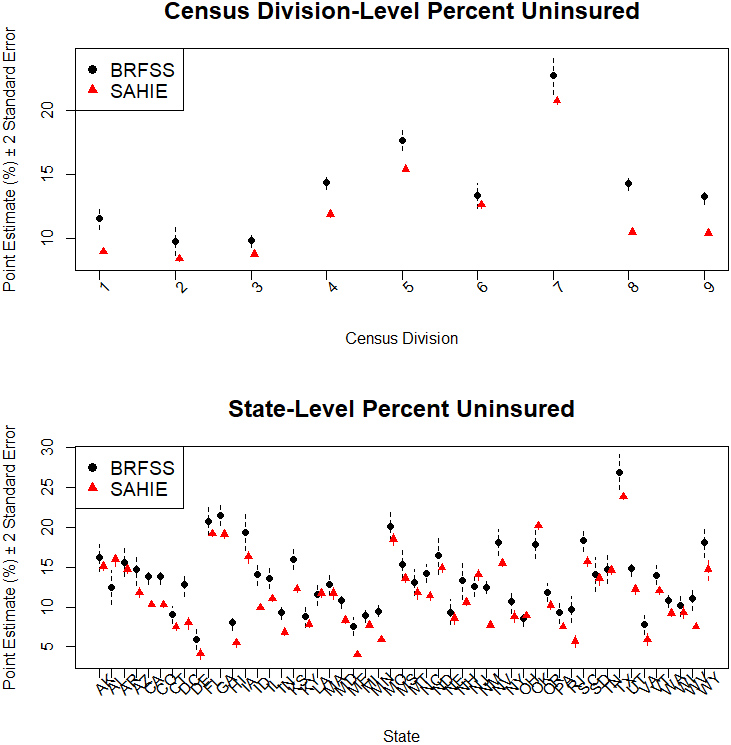
Figure 1.

Initial estimates of percent uninsured 18–64 years old individuals.

The BRFSS target population is the U.S. noninstitutionalized adult population 18 years of age and older. On the other hand, SAHIE estimates are available for age category 0–64. To align the target populations for the two sources (BRFSS and SAHIE) more closely, we restrict our attention to the adult individuals with age between 18 and 64. For this, the BRFSS data corresponding to individuals 65 years old and older and the SAHIE data corresponding to individuals 17 years old and younger are discarded. In addition, to align the health care coverage quantity of interest more closely, we identify the BRFSS quantity corresponding to the SAHIE quantity describing the health insurance coverage as “any kind of health insurance coverage, including health insurance, prepaid plans such as HMOs, or government plans such as Medicare, or Indian Health Services.” When aligning the target population and the quantity of interest more closely, the most complete (i.e., after possible imputation) BRFSS data are used. Any incomplete BRFSS data are discarded, and the BRFSS survey weights are raked to state population totals available from the SAHIE data and treated as fixed and known. This step completes the initial data processing steps, necessary to align the public-use data from BRFSS and SAHIE.

Figure 2.

Relationship between the initial estimates of percent uninsured 18–64 years old individuals.

3.Statistical data integration models

We develop a multilevel model with two initial levels to model the estimates available from the two sources, a bridging level to link the pairs of estimates from the two sources, and a smoothing level to improve the uncertainty of the final model estimates. The SAHIE county estimates and the BRFSS state estimates are assumed unbiased for the underlying population target, but with respect to the corresponding model/design. The first two levels of each of the multilevel models reflect this assumption:

The quantities of interest are the county population targets (health insurance coverage rates), which can be measured in either the SAHIE or the BRFSS scale. At this fine level (county), direct measurements are available for these quantities from SAHIE, but there are no available measurements for these quantities from BRFSS. Using a bridging level, we assume a latent linear relationship between the SAHIE and the BRFSS county-level quantities of interest:

The bridging level and the data level for SAHIE data are directly linked because county-level SAHIE initial estimates are available, as measurements of the quantity of interest on the SAHIE scale. Since there are no county-level BRFSS measurements for the quantity of interest on the BRFSS scale, we include an identity level in the model to create a link between county-level and state-level quantities:

Finally, three types of smoothing levels are investigated, depending on the latent effects included: county, or county and state, or county, state, and census division. The three full models are hereafter denoted by M12, M121, and M122, corresponding to the three versions of smoothing levels, respectively.

Smoothing level for M12:

Smoothing level for M121:

Smoothing level for M122:

The models are specified as hierarchical Bayes models. For this, we adopt the following independent, weakly-informative priors for the model parameters: γ0∼N⁢(0,104), γ1∼N⁢(0,104), μ∼N⁢(0,104), σd∼Uniform⁢(0,105), σs∼Uniform⁢(0,105), and σc∼Uniform⁢(0,105). We fit the models in R JAGS using Markov chain Monte Carlo (MCMC). Three chains are used, each consisting of 20,000 draws with the first 5,000 as burn-in and with the remaining 15,000 thinned to every 10th draw to reduce dependence. The remaining R= 4,500 draws from the three chains combined are used to approximate the joint posterior distribution of all unknown parameters. Mixing and convergence diagnostics for the MCMC sampler ensure that the posterior samples are valid for inference.

Let ζ=1,…,R index the posterior samples. Then, county-level predictions are constructed using the county-level posterior samples on both scales, μ𝑖𝑗𝑘B/S,ζ. State-level and census division-level predictions are constructed by aggregating the county-level posterior samples:

where ni is the number of counties in census division i and ni⁢j is the number of counties in state j and census division i. In the next section we present results for the following posterior statistics: mean and standard deviation.

4.Results

The plots in Fig. 3 illustrate the relationship between the state-level model predictions and the initial estimates. The model predictions represent smoothed versions of the initial estimates. As expected, the model predictions on the BRFSS scale are closer to the BRFSS initial estimates and higher than the SAHIE initial estimates, and the model predictions on the SAHIE scale are closer to the SAHIE initial estimates. The model predictions have lower uncertainty than the initial estimates when compared on the same scale. There are no noticeable differences between the model predictions based on the three models. Similar findings hold at the census division level; see Fig. 4.

Figure 3.

State-level initial estimates and model predictions of percent uninsured 18–64 years old individuals on the SAHIE and BRFSS scales.

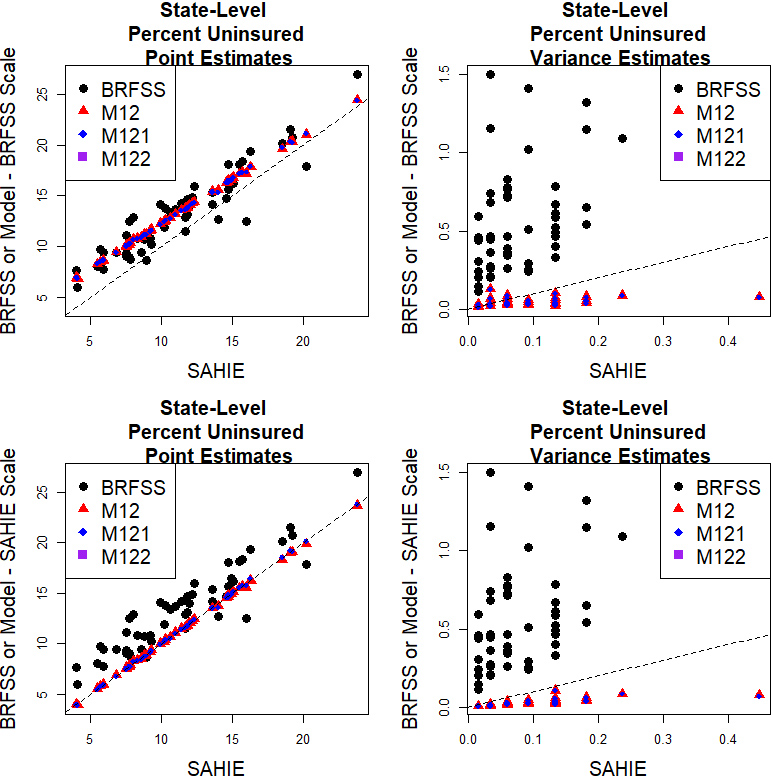
Figure 4.

Census division-level initial estimates and model predictions of percent uninsured 18–64 years old individuals on the SAHIE and BRFSS scales.

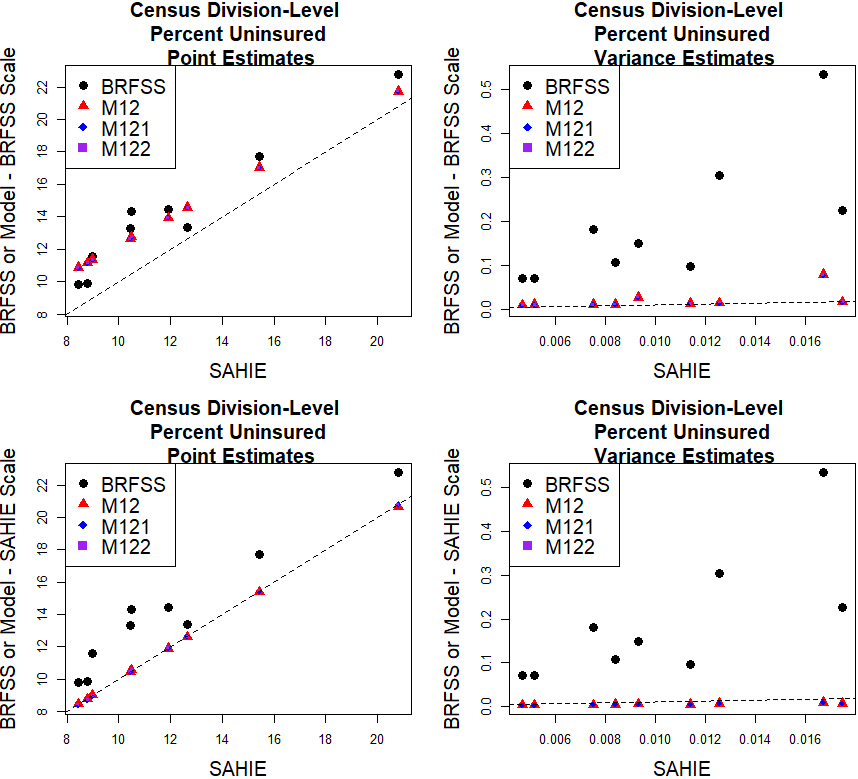
Figure 5.

County-level initial estimates and model predictions of percent uninsured 18–64 years old individuals on the SAHIE and BRFSS scales.

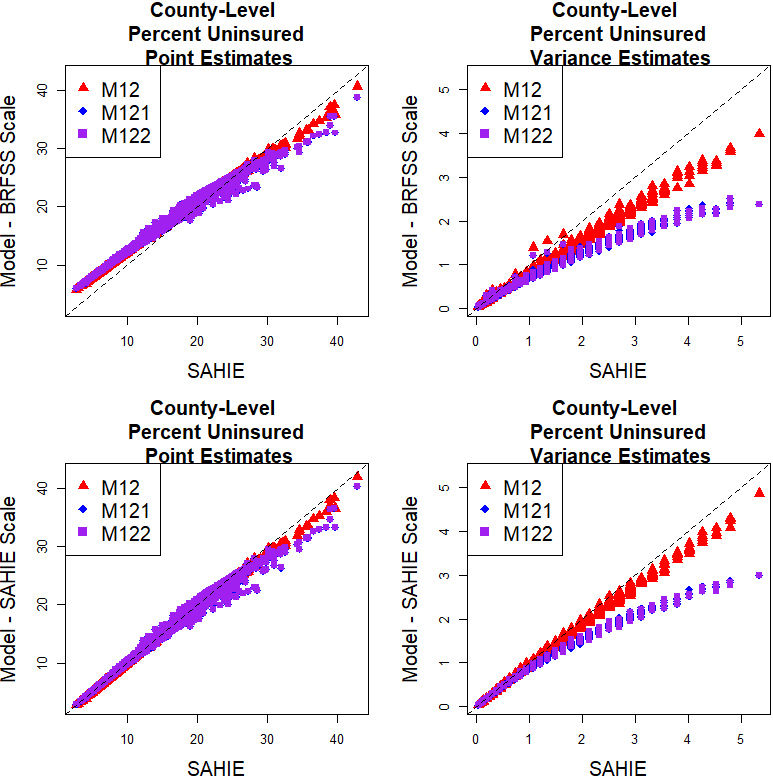
Figure 6.

County-level model predictions of percent uninsured 18–64 years old individuals on the SAHIE and BRFSS scales relative to the SAHIE initial estimates of percent uninsured 18–64 years old individuals.

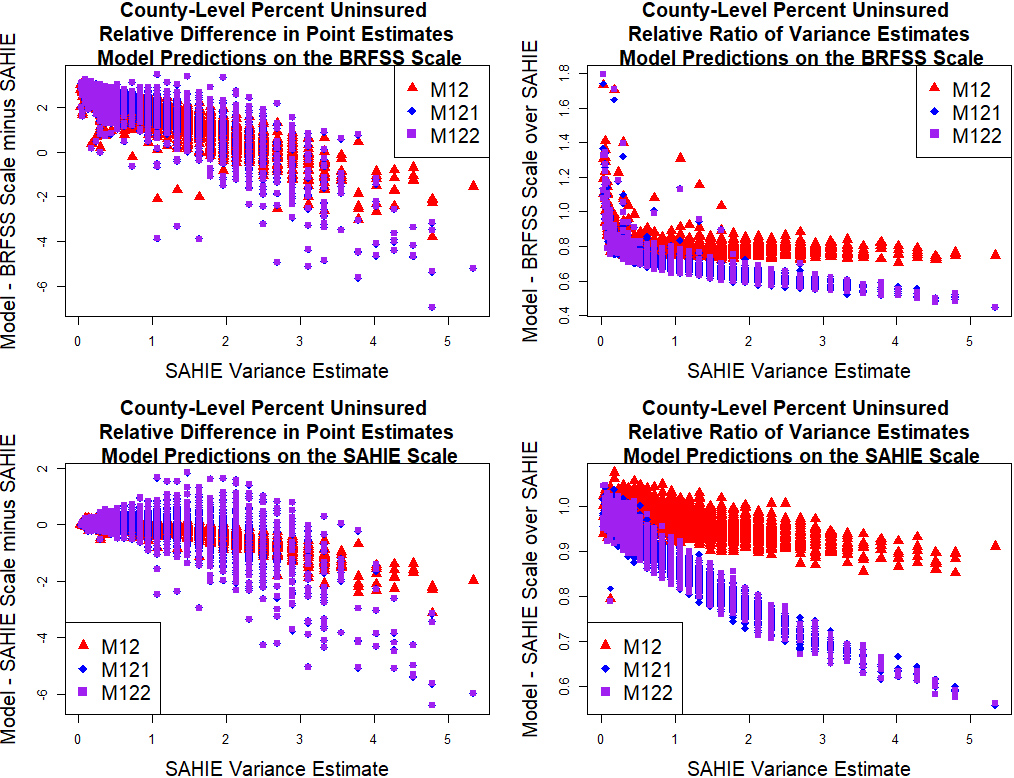
Figure 7.

Initial estimates and M122 model predictions of percent uninsured 18–64 years old individuals.

At the county level, we present comparisons between the model predictions and the SAHIE initial estimates in Fig. 5. The plots in this figure are closely following the structure of the plots in Figs 3 and 4, the only exception being the omission of BRFSS initial estimates because they are not available at the county level. The results indicate that the model predictions on the BRFSS scale deviate more from the SAHIE initial estimates than the model predictions on the SAHIE scale do, and there are no noticeable differences between the model predictions based on M12, M121, and M122. The differences between the county-level M12 and M122 model predictions range from -1.67 to 2.60 M122 model prediction standard errors, and the differences between the county-level M121 and M122 model predictions range from -0.07 to 0.08 M122 model prediction standard errors. Despite the overall mild deviations from the SAHIE initial estimates, the model predictions have lower uncertainty (posterior variance) than the SAHIE initial estimates, with the M121 and M122 model predictions having lower uncertainty than the M12 model predictions. The improvement in uncertainty based on the M121 and M122 models is expected because these models include two and three nested latent levels, respectively.

To further assess the quality of the county-level model predictions, we constructed differences in model predictions and SAHIE initial estimates and ratios of the model variances to the SAHIE initial variance estimates. These are plotted against the SAHIE initial variance estimates in Fig. 6. The results indicate that the model predictions deviate more from, and have lower uncertainty then, the SAHIE initial estimates for counties where the SAHIE initial estimates have larger uncertainty. These results do not present a concern because the larger uncertainty in the SAHIE initial estimates gives these latter estimates less weight in the combination of information comprising the model predictions. Finally, we update Fig. 1 to include model predictions based on model M122, on both scales. The results are consistent with the results presented above.

5.Discussion

We addressed the issue of integrating multiple official statistics on the same quantity of interest subject to error. None of the two sources was considered gold standard. Specifically, we integrated BRFSS and SAHIE measurements of health insurance coverage at the state level (and higher geographies) and produced reliable county-level estimates on both BRFSS and SAHIE scales. For this, we modeled initial estimates from the two sources at different levels of aggregation and subject to different error. Producing estimates on both the BRFSS and SAHIE scales using data from the corresponding sources and accounting for its uncertainty provides a way to construct estimates of lower uncertainty and to construct BRFSS estimates at lower levels of aggregation. If additional information becomes available and deems sufficient to consider one source as the gold standard, then simply the model-based estimates on that scale could be used as official statistics. This scenario is also known as a random benchmarking problem, the gold standard estimates being the random controls to which the other estimates need to be benchmarked to.

Three multilevel models were presented, building on each other, depending on the nested data structure accounted for. There were small differences between a model containing a two-fold smoothing level and a model containing a three-fold smoothing level, with more noticeable differences between these models and a model containing a one-fold smoothing level. The model predictions based on models with two or three latent effects had lower uncertainty than model predictions with one latent effect.

Extensions to more than two sources of initial estimates available at distinct levels of aggregation are straightforward. Estimating other BRFSS quantities could also be investigated in future research. For example, suppose flu vaccination coverage estimates would be of interest. Then, state-level flu vaccination coverage could be estimated using the relationship between the state-level flu vaccination coverage and health insurance coverage, estimated using the BRFSS data, and the state-level model predictions on either the BRFSS or the SAHIE scale. Estimation of county-level flu vaccination coverage would be based on a further assumption between the county-level and the state-level BRFSS estimates; for example the same relationship between the flu vaccination coverage and health insurance coverage at both county and state levels. This additional assumption would not be necessary if county-level BRFSS survey estimates would be available at the county-level as initial estimates.