Small area estimation of non-monetary poverty with geospatial data

2.1Constructing measures of non-monetary welfare and poverty in the census

The first step of the analysis is to construct measures of non-monetary poverty based on the Sri Lankan and Tanzanian censuses, which were each conducted in 2012. Non-monetary poverty, unlike monetary poverty, is directly observed in the census population and can therefore provide a benchmark for evaluation. For each country, we identified a set of household assets (e.g., ownership of TVs, computers, housing materials) and demographic proxies (e.g., gender of household heads, household size, literacy, sector of work) for welfare. We then carried out a principal component analysis, weighted according to household size, to estimate a loading factor for each proxy welfare indicator.88 The principal component analysis is based on the correlation matrix, weighted by household size, and the first principal component was retained. Each household’s non-monetary welfare measure was obtained by summing the product of each loading factor and the household’s value of the associated variable. We then set a poverty threshold at the 4th percentile of non-monetary welfare in Sri Lanka and the 20th percentile in Tanzania, to reflect prevailing national monetary poverty rates.99 Households were classified as non-monetarily poor if their non-monetary welfare, defined as the score of the first principal component, fell under the poverty thresholds mentioned above.

2.2Constructing synthetic household surveys

The previous section discussed the measure of non-monetary welfare and poverty, defined as the share of the population for which the non-monetary welfare measure is below the respective poverty line for Sri Lanka and Tanzania. With these in hand, we turn to drawing a synthetic household survey from each country’s census. The synthetic survey, along with the auxiliary geospatial data, are key inputs into the small area estimation procedures. To draw the synthetic survey, we utilized the actual two-stage sample conducted by the National Statistics Offices for two household budget surveys: The 2018 Tanzania Household Budget Survey, and the 2016 Sri Lanka Household income and Expenditure Survey. These surveys were merged with the census at the village level, which is the GN Division in Sri Lanka and the village in Tanzania1010 After retaining the GN Divisions and EAs present in the household survey, we randomly selected census households in each matching EA to match the number of households in each EA for each survey. Finally, we merged the sample weights from the household budget surveys for each village. Essentially, this procedure drew synthetic surveys that mimicked as much as possible the sample drawn by the NSO for the household surveys.

2.3Remote sensing data

The auxiliary data for the small area estimation exercise were drawn from a large candidate pool of satellite-derived information. Most of these geospatial data are derived from publicly available layers and imagery, including, but not limited to, night-time lights from the Visible Infrared Imaging Remote Sensor (VIIRS); precipitation data from the Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) and [22]; elevation and slope taken from [23] and the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) satellite; global forest cover change from [24] estimates of built-up area from the Global Human Settlement Layer (GHSL), population estimates (WorldPop); climactic region1111 from [25]; and lastly, crop yield estimates for Maize, Sorghum, and Rice [26].1212

The Sri Lanka indicators were also supplemented by a variety of spatial “contextual” features derived from a cloud-free mosaic of 2017–2018 Sentinel-2 imagery, which is collected every 5 days by Sentinel 2 sensors on board two satellites, Sentinel 2A and 2B.1313 These contextual features have been shown to be strongly correlated with poverty, population density and building and road characteristics [4, 33, 34]. These contextual features were calculated by comparing pixels with their neighbors and then reporting this value back to the individual pixel (in this case 10m). The number of neighboring pixels considered in the comparison is the scale, which varies by the feature being calculated.1414 Since these contextual features are derived from Sentinel 2, they are available at 10 m spatial resolution and are theoretically available for free for the entire world. Cloud free Sentinel 2 mosaics can be made in Google Earth Engine and the code to calculate the contextual features is written in Python (SpFeas package). Therefore, all that is required to calculate the features is computer processing time. While the majority of remote sensing data used for Tanzania were largely derived from publicly available imagery, it was supplemented by proprietary data on building footprints produced by Ecopia and Maxar based on very fine spatial resolution imagery.1515 While these data are more costly and difficult to create than the contextual features, with these data we are able to capture the spatial patterns of buildings and roads, their density, and the general neighborhood structure that is indicative of relative differences in poverty over space [4, 33]. The building footprint data was proprietary when we first did this study and costly to create. However, the costs are rapidly decreasing as satellite imagery becomes cheaper, more ubiquitous and computing power becomes less expensive and recently Google released a similar data set covering the majority of the African continent.1616 Also, additional data sources such as Open Street Map are rapidly increasing in spatial coverage. Together, the open source nature of the contextual features, and the increasing availability of satellite derived data going forward, makes using these types of data in studies such as this in the future very feasible.

2.4Geographic structure of Sri Lanka and Tanzanias

Before describing the methodology used in the study, we briefly review the geographic structure of the two countries. Villages are the lowest level for which shapefiles were obtained and are therefore the most disaggregated level for which geospatial data could be linked with the survey. Small areas are the target domains for the small area estimates, which are at a higher level than the villages, but below the level at which the survey is considered to be representative. For Sri Lanka, there are 13,978 villages1717 (GN divisions), 331 areas (DS divisions), and 25 regions (districts); while Tanzania contains 14,981 villages, 159 areas (districts), and 25 regions.1818

3.1Direct survey estimates

Direct estimates obtained from the survey serve both as a benchmark against which to assess the increase in precision from incorporating satellite data, and as an input into the Fay-Herriot area-level models. The most common method of obtaining variance estimates clusters the residuals by enumeration area, which accounts for positive correlation within clusters but assumes that disturbances across clusters are independent [35, 36]. As an alternative, we also applied the Horvitz-Thompson (H-T) approximation, which offers an alternative approach to estimate the variance of the small area poverty rates [37]. The H-T approximation also underestimates the variance, but in these contexts by less than clustered standard errors, and therefore yield less biased variance estimates. The H-T approximation underestimates the variance by assuming that the joint inclusion probabilities are the product of the marginal inclusion probabilities, which holds only for Poisson sampling.1919

3.2Fay-Herriot area-level model

The Fay-Herriot model was introduced by Fay and Herriot [18] to model incomes for small areas of fewer than 1,000 persons in the United States, and is perhaps the best-known and widely used small area-level estimator. It was derived as an application of the James-Stein estimator [38] using data aggregated to the small area level, and is also the Empirical Best Linear Unbiased Predictor (EBLUP) of the small area level regression. It is an “empirical” best linear unbiased predictor because the survey error variance is assumed to be known. The small area estimates are a weighted average of the synthetic regression prediction and the direct survey estimate, with the weights inversely related to the estimated variance of the direct and synthetic estimates. Many variants of the Fay-Herriot estimator have been developed that employ transformations and account for spatial and intertemporal correlation, among other refinements. We estimate a basic area-level Fay-Herriot model, using the Horvitz-Thompson approximation to calculate the variance of the direct survey estimate, as recommended by [39].

The Fay-Herriot estimator, unfortunately, has several limitations for the purposes of generating small area estimates of poverty using spatial auxiliary data. The main shortcoming is that the Fay-Herriot model requires aggregating the auxiliary data to the small area level, which discards variation in the auxiliary data at the village level that would increase the precision of the estimates. This is consistent with the strand of the small area estimation literature that emphasizes the importance of including cluster-level “auxiliary data” from censuses to control area-specific bias, reduce uncertainty, and estimate uncertainty more accurately [40, 41]. Implementing a sub-area model that adapts the Fay-Herriot model to address this issue, such as the one proposed by [42] can incorporate auxiliary data at the village level but is currently constrained by the lack of available software. Another limitation is that, because the Fay-Herriot model is based on direct estimate of poverty rates, it discards information on the variation in welfare within the poor and non-poor portions of the welfare distribution. In addition, when no transformation is applied, as is the case below, the poverty rate is assumed to be a linear function of the predictors, which can lead to predictions that are negative or greater than one. The Fay-Herriot model also faces challenges when no households are poor in a significant number of small areas, as is the case in Sri Lanka.2020 For these small areas, either the prediction from the auxiliary data must be ignored, the sample must be ignored, or they must be dropped from the estimation. Finally, the Fay-Herriot model does not account for uncertainty in the survey-based estimates of variance, which tends to underestimate the variance of the prediction.

Despite these limitations, the Fay-Herriot model is much simpler to apply and explain than a unit level model. It generally provides credible estimates and is a standard workhorse when using area level models for small area estimation. We estimate a Fay-Herriot model by aggregating all indicators to the small area level, weighting by population. The Fay-Herriot models are estimated using the Stata FHSAE command [43]. We utilize the “Chandra method”, which estimates the prediction model using Feasible Generalized Least Squares [44].

3.3Household-level model

In contrast to area level models, unit level models are specified at the level of the individual unit, which in this case is the household.2121 Although the auxiliary data only varies at the village level, predicting welfare at the household level fully utilizes the information in the sample survey on the level and variability of household welfare. Unit-level models are more convenient to estimate than sub-area models, because of the availability of well-established software packages that utilize empirical best methods with conditional random effects specified at the level of the small area.

The EBP model can be written as follows:2222

where Y𝑟𝑎𝑣𝑖 is the non-monetary welfare for household i, living in village v, small area a, and region r. In each country, Y𝑟𝑎𝑣𝑖 is the principal component score constructed using the loading factors in Table 1 and G⁢(Y𝑟𝑎𝑣𝑖) is a transformed version of this welfare measure. Traditionally, ELL uses the log function to transform welfare, but any monotonic transformation can be used. As described in greater detail below, we use an ordered quantile normal transformation for the primary set of results. X𝑟𝑎𝑣𝑖 is a set of satellite-derived indicators that vary at the village level. X𝑟𝑎 is a set of satellite-derived indicators that vary at the small area level. These predictors are important to include to reduce the variance of the small area random effect and thereby mitigate bias in the estimated mean squared error [41]. Ir corresponds to a set of regional dummy variables indicating regions for which the survey is considered to be representative. The Sri Lanka specification also includes dummies for the rural and estate sectors, while the Tanzania specification includes a rural dummy.2323η𝑟𝑎 is a conditional random effect specified at the small area level, assumed to be distributed normally. η𝑟𝑎 is conditioned on the sample values of observed welfare, denoted y𝑟𝑎𝑣𝑖. Lastly, ε𝑟𝑎𝑣𝑖 denotes a household level idiosyncratic error term, also assumed to be distributed normally and assumed to be independent of η𝑟𝑎. The conditional random effects regression is weighted using population weights, equal to the product of the household sample weights and household size.

A key feature of the EBP framework is that the random small area effect ηr⁢a is conditioned on the sample values of observed welfare ys. This, along with the assumption that σ2⁢η is normal, allows for the use of the following model for generating simulated welfare:

Where η𝑟𝑎 is the area random effect from Eq. (1) and

is the shrinkage factor due to conditioning the random effect on the sample mean for small area a. N𝑟𝑎 is the number of sample observations for small area a.

EBP estimation has proven to offer a large efficiency improvement compared to other methods such as the traditional ELL. This efficiency gain comes from the fact that the EB method conditions on the sample and thereby makes more efficient use of the information given, while ELL does not. When the auxiliary data are specified at an aggregate geographic level, such as a village or small area in the EBP framework described above, the use of predictors aggregated to the village level increases the variance of the small area effect σ2⁢η, which also represents the covariance of unexplained welfare across households within the same small area. The increase in σ2⁢η due to the use of regionally aggregated predictors in turn increases the shrinkage factor γ𝑟𝑎, leading to a greater increase in precision when using an EBP model versus the traditional ELL synthetic estimator. Additional empirical evidence to support this point is provided below in Section 5.

The assumption of normality is critical in the EBP framework, as a distributional assumption is required to condition the small area level random effect on the average residual of the regression in that small area. The normality assumption is consequently also necessary for the Monte-Carlo simulations of the parameters, which are required because headcount poverty is a non-linear function of welfare. Violations of the normality assumption can therefore lead to biased estimates. Below, we discuss a monotonic transformation to the welfare measure that makes the assumptions that the small area effect and the household error term are distributed normally more palatable.

3.4Normalizing transformation

Welfare typically follows a right-skewed distribution, and it is therefore standard practice to transform the welfare indicator before implementing small area estimation models based on simulated welfare. The most common transformation is to take the logarithm of welfare, following [6].2424 More recently, Box-Cox or Log-shift transformations h ave become more popular [47]. However, our preferred estimates utilize a monotonic transformation called the “ordered quantile normalization” to transform welfare, which transforms the scaled rank of the welfare variable to conform with a normal distribution. Among several methods proposed in the literature, the ordered quantile normalization most consistently transforms an underlying variable to follow a normal distribution [48]. While a normally distributed outcome variable does not guarantee normality of the residuals, in these cases it helps make the distribution of residuals closer to normal, and leads to smaller discrepancies between the official national poverty rate estimated from the survey and the weighted mean of the small area estimates.2525

3.5Model selection using Lasso

Model selection in small area estimation remains an unsettled issue and has traditionally been treated as both art and science.2626 In recent years, the least absolute shrinkage and selection operator (LASSO) has become an increasingly popular tool for selecting prediction models. The post-lasso procedure, in particular, offers the benefit of a convenient and data-driven approach to model selection that, in its most popular variant, maximizes out-of-sample predictive accuracy, while roughly equalizing in and out of sample R2 to prevent overfitting the model to the sample.2727 We show in the robustness checks below that the results are robust to the implementation of stepwise regression, an alternative model selection model.

3.6Benchmarking

Calibrating the small area estimates to match the direct sample estimates for regions can be desirable to ensure that the population-weighted average of small area poverty estimates, when aggregated to regions, match official published statistics derived from the survey [19, 20]. We therefore apply a simple ratio benchmarking procedure by multiplying the estimated headcount rate in each small area by a scaling factor unique to each region,2828 for both the Fay-Herriot and household level model estimates.2929 Below, we report results without benchmarking as a robustness check to assess whether and to what extent the procedure improves the accuracy of the estimates.

3.7Criteria for evaluating estimates

To evaluate the performance of the above-mentioned different SAE methods, we examine seven summary statistics, averaged across areas: non-monetary poverty rates; Mean Squared Error (MSE); Coefficient of variation (CV);3030 Relative Bias;3131 correlation between estimated and census non-monetary poverty rates; Root Mean Squared Error3232 (RMSE); and lastly coverage rate or the share of small areas for which the estimated 95 percent confidence intervals for the small area non-monetary poverty rate contains the census non-monetary poverty rate.3333

4.1Predictive power of geospatial variables

In both the area-level (Fay-Harriot) and unit-level (EBP) models, geospatial variables perform reasonably well in explaining variation in poverty or consumption. The small area-level predictor variables were selected using the lasso plugin method, to prevent overfitting the model to the sample. The set of candidate variables included all small area-level remote sensing indicators as well as regional dummies. For the Fay Harriot models, which is used as a reference point for comparison with the direct estimates and the unit level model, the lasso selected a small number of predictor variables, only 3 in Tanzania and 8 in Sri Lanka. Despite containing only three variables, the Tanzania model explains half of the variation in non-monetary poverty rates. Meanwhile, the eight Sri Lanka variables explain 6 percent of the variation in headcount poverty across subdistricts. Overall, the results suggest that the Fay-Herriot estimates, despite using predictors that only vary across small areas, can significantly improve on the efficiency of the direct estimates, particularly in Tanzania where the model fit is especially good.3434

Figure 1.

Quantile vs. Quantile plots of household error terms and small area random effects. Notes: Figures report normal quantile-quantile plots of estimated household welfare residuals (error term) and small area random effects (random effect).

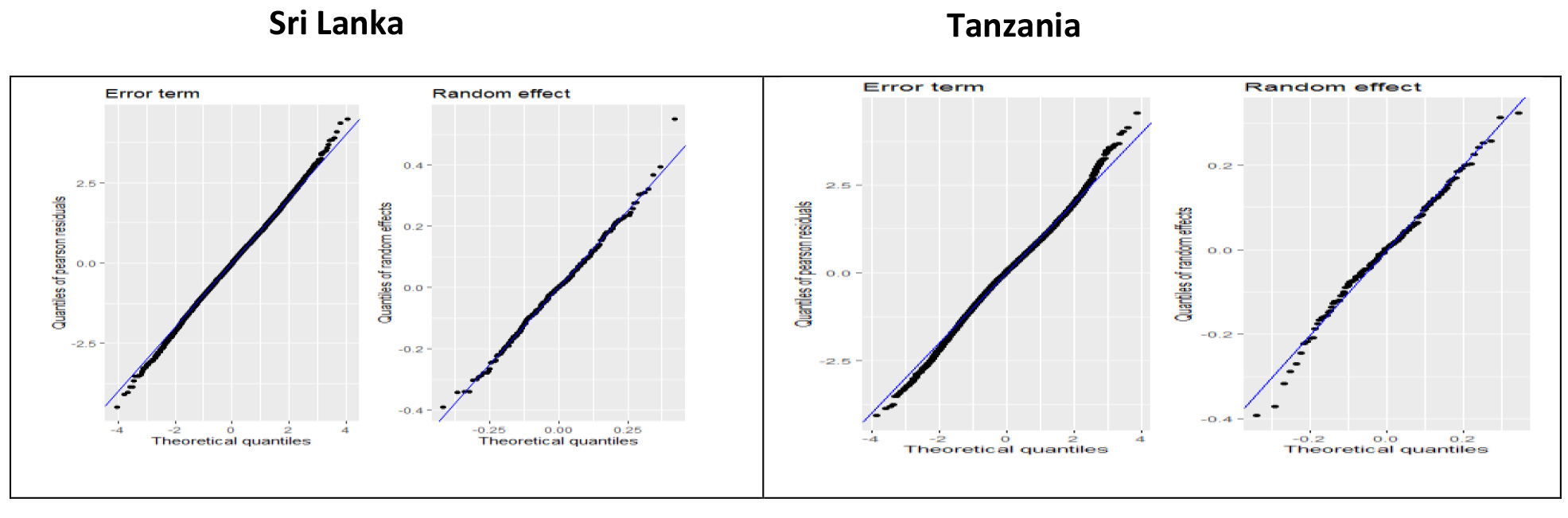
Turning to the results from the unit-level EBP models, the first striking result is the overall predictive power of the models. Tabke 1 summarizes the results from the model specifications employed for Sri Lanka and Tanzania. The marginal R2 from the model is 0.30 in Tanzania and 0.27 in Sri Lanka, which is notable given that the explanatory variable, non-monetary welfare, is measured at the household level while all the independent variables vary only at the village level. At the village level, the satellite indicators explain a large amount of the variation in average non-monetary welfare. In village level regressions, predictor variables explain 73 percent of the variation in average non-monetary welfare in Tanzania and 59 percent in Sri Lanka.3535 The village level model R2 of 0.73 for Tanzania is substantially higher than the estimates presented in [2] which find that features derived from satellite data explain 58 percent of the DHS asset index in Tanzania. The stronger predictive power of the model for Tanzania may result from using a welfare measure based on a smaller number of household welfare proxies, as well as the use of interpretable features derived from imagery such as building footprints, rather than features optimized to predict night-time lights.3636

For Tanzania, the lasso model selected several building footprints and built-up area measures, as well as measures of night-time lights that capture building and population density. Building counts, night- time lights, and built-up area are all positively associated with welfare. Several climactic variables were also selected, reflecting the dependence of rural areas on favorable rainfall patterns. Higher variance in the NDVI vegetation index, reflecting areas that contain a mix of built-up area and green space, is also positively related to welfare. The Sri Lanka model contains measures of built-up area, rainfall, as well as texture features such as the Fourier Transform and Line Support Region Mean at the village level, and other features such as the standard deviation of the Gabor filter and Histogram of Ordered Gradients at the small area level. This is consistent with previous research showing that these texture algorithms or contextual features reflect spatial variability in building and road patterns, as well as poverty [56, 57, 58].

4.2Evaluation results

The previous section demonstrated that remote sensing indicators are predictive of both small area-level poverty and household non-monetary welfare. This section turns to evaluating the small area estimates generated by different methods. The distribution of both the small area effect and the household error term is close to normal, as seen in both Fig. 1 and the skewness and kurtosis statistics reported in Table 1, reflecting the success of the normalizing transformation.

Table 2 begins by presenting the (unweighted) mean poverty rates and uncertainty of the small area estimates, as measured by the mean squared error, multiplied by ten thousand, and the mean coefficient of variation. The table presents the results for direct survey estimates for both the standard method and the Horvitz-Thompson estimates, as well as the Fay-Herriot area model and the unit-level model estimated with the modified EMDI package. All are simple unweighted averages across small areas.

The results for the mean poverty predictions in Table 2 show that the Fay-Herriot estimates (prior to benchmarking) underestimate poverty, by a slight amount in Sri Lanka but by a more significant amount in Tanzania. The difference in precision is more striking. The Fay-Herriot estimators are significantly more precise than the Horvitz-Thompson direct estimates in both countries. Relative to these more conservative direct estimates, the Fay-Herriot procedure reduces the mean square error by nearly half in both countries. However, the household level model, compared with the Horvitz-Thompson estimates, reduces the average mean squared error of the small area estimates substantially more, by 70 percent in Sri Lanka and 85 percent in Tanzania.

Table 3 shows the evaluation results against the small area poverty rates derived from the census. Average relative bias is highest for the Fay-Herriot estimator in both countries, and lowest for the direct estimates. Of greater interest for evaluating accuracy, however, are the results for rank correlation and root mean squared error. In both countries, the small area estimates are far more accurate than the direct estimates, with the household model performing at least as well as the area level model. In Sri Lanka, the household level model is significantly more accurate than the area level model (rank correlation of 92.6 vs 85.4). Meanwhile, in Tanzania the household level model estimates have a slightly higher rank correlation than the area-level model estimates (85.7 vs. 84.7), and a real mean squared error that is negligibly worse (0.053 vs 0.052).

The last column of Table 3 shows the coverage rate, which for the household model in Sri Lanka is 84.3%. This is slightly higher than the Horvitz-Thompson estimates (82.2%), moderately higher than the clustered direct estimates (76.1%) but substantially lower than the Fay-Herriot estimates (91.8%). For Tanzania, the coverage rate for the household level model is 74.8%. This is the lowest of the four estimators but only modestly lower than that of the standard enumeration-area clustered estimates (76.1%). The Horvitz-Thompson and Fay-Herriot estimators achieve much higher coverage rates of 85.5% and 91.8%, respectively.

Figure 2.

Comparison of area poverty estimates by method for Sri Lanka (left) and Tanzania (right). Notes: Figures show predicted asset-based poverty rates generated by household-level model, Fay-Herriot model, and Direct Survey estimates, in comparison with actual asset-based poverty rates calculated from the census.

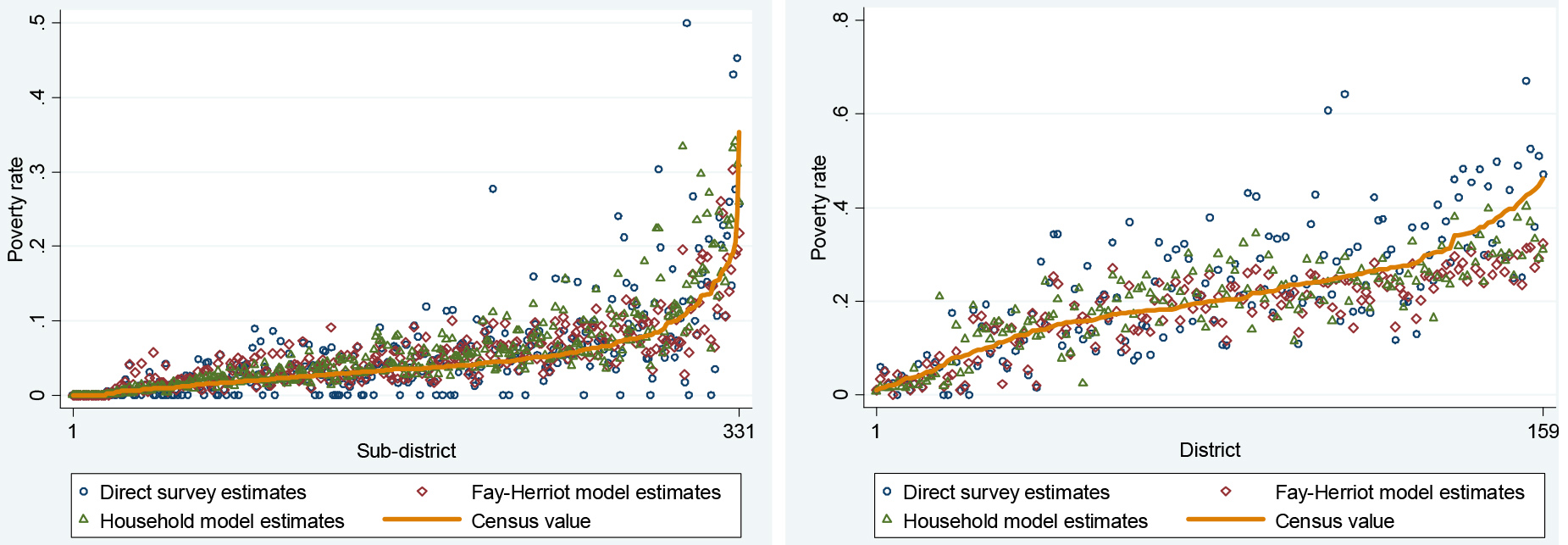
Figure 3.

Comparison of estimated Relative Mean Square Error by area and method for Sri Lanka (left) and Tanzania (right). Notes: Figures show mean squared errors of predicted asset-based poverty rates generated by household-level model, Fay-Herriot model, and Direct Survey estimates. Direct survey estimate MSEs top-coded at 0.015.

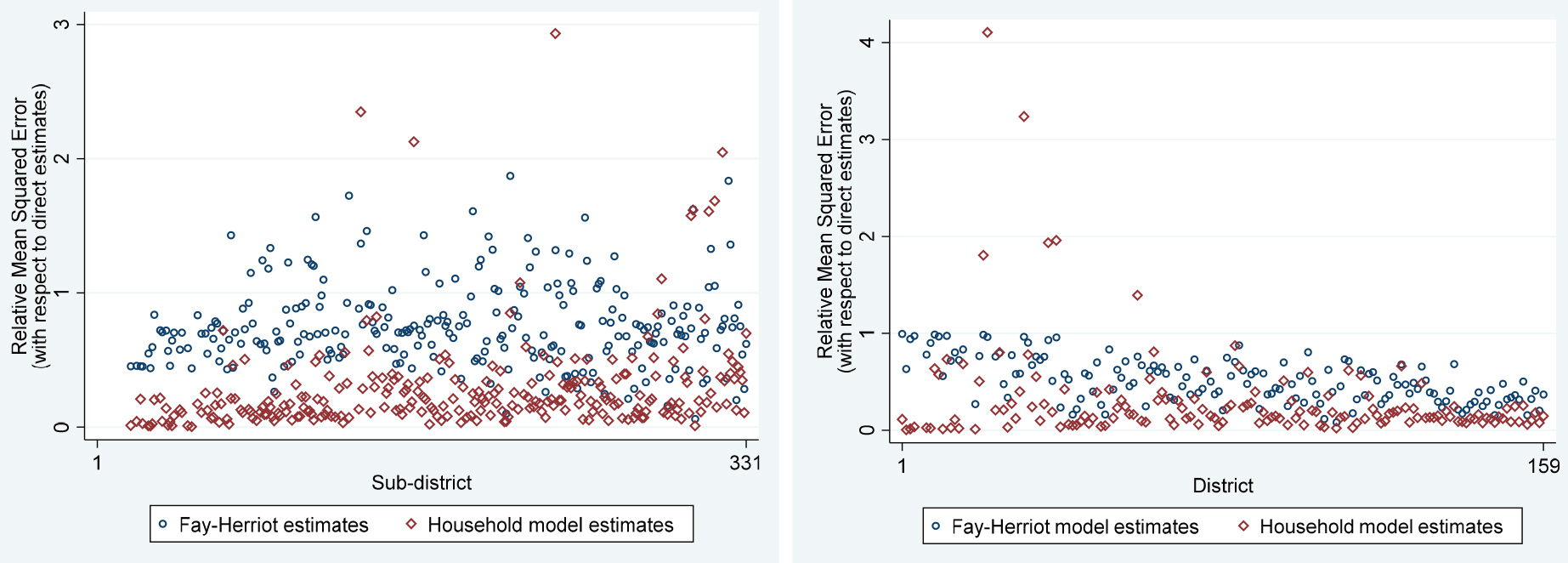
Figures 2 and 3 give a detailed look at the point estimates and mean squared errors for the area poverty estimates for each method. Sri Lanka is shown on the left panel and Tanzania on the right, and in each country the areas are ordered according to their non-monetary poverty rate in the census. The results clearly show that both Fay-Herriot and Household-level models greatly improve on the accuracy of the direct estimates, especially in areas with higher poverty rates. In Sri Lanka, many of the direct estimates are zero, even in high-poverty areas. The comparison between household models and Fay-Herriot models is less clear, but the Fay-Herriot estimates appear to be more prone to overestimate poverty for low-poverty areas and underestimate poverty for high-poverty areas.3737 Figure 3 presents the relative mean squared errors produced by the Fay-Herriot and Household model, relative to the direct estimates. It clearly demonstrates that the household model estimates are substantially more precise than both the Fay-Herriot estimates and the direct estimates for most target areas in both countries.

Finally, Table 4 compares the precision of the unit level model with the direct survey estimates for regions, which are districts in Sri Lanka and regions in Tanzania. The regions are levels for which the household survey is considered reliable and direct survey estimates of monetary poverty rates are published. In Sri Lanka, where there are 331 target areas, the mean squared errors for the subdistrict estimates are about sixty percent larger than the direct survey estimates for districts. In Tanzania, meanwhile, there are only 159 areas and the same number as regions as Sri Lanka. In this case, the average mean squared error of the small area district estimates is slightly lower than the direct estimates for regions, while the mean CV is modestly higher. This type of comparisons is useful to inform decisions by national statistics offices of whether small area estimates are sufficiently precise to publish.