Temporal relevance for representing learning over temporal knowledge graphs

Song, Bowen; Amouzouvi, Kossi; Xu, Chengjin; Wang, Maocai; Lehmann, Jens; Vahdati, Sahar

doi:10.3233/SW-243699

Temporal relevance for representing learning over temporal knowledge graphs

Article type: Research Article

Authors: Song, Bowen^{a; e} | Amouzouvi, Kossi^{b; e; f} | Xu, Chengjin^c | Wang, Maocai^{a; *} | Lehmann, Jens^{b; d; e; **} | Vahdati, Sahar^{e; g}

Affiliations: [a] School of Computer, China University of Geosciences, Wuhan, China | [b] Faculty of Computer Science, TU Dresden, Dresden, Germany | [c] International Digital Economy Academy, China | [d] Amazon, Germany | [e] Institute for Applied Informatics (InfAI), Dresden, Germany | [f] Department of Mathematics, KNUST, Kumasi, Ghana | [g] Leibniz Information Centre for Science and Technology, TIB, Hannover, Germany

Correspondence: [*] Corresponding author. E-mail: [email protected].

Note: [**] The work is done outside Amazon.

Keywords: Temporal knowledge graph, representation learning, knowledge graph embedding, link prediction

DOI: 10.3233/SW-243699

Journal: Semantic Web, vol. Pre-press, no. Pre-press, pp. 1-17, 2024

Published: 22 November 2024

Get PDF

Abstract

Representation learning for link prediction is one of the leading approaches to deal with incompleteness problem of real world knowledge graphs. Such methods are often called knowledge graph embedding models which represent entities and relationships in knowledge graphs in continuous vector spaces. By doing this, semantic relationships and patterns can be captured in the form of compact vectors. In temporal knowledge graphs, the connection of temporal and relational information is crucial for representing facts accurately. Relations provide the semantic context for facts, while timestamps indicate the temporal validity of facts. The importance of time is different for the semantics of different facts. Some relations in some temporal facts are time-insensitive, while others are highly time-dependent. However, existing embedding models often overlook the time sensitivity of different facts in temporal knowledge graphs. These models tend to focus on effectively representing connection between individual components of quadruples, consequently capturing only a fraction of the overall knowledge. Ignoring importance of temporal properties reduces the ability of temporal knowledge graph embedding models in accurately capturing these characteristics. To address these challenges, we propose a novel embedding model based on temporal relevance, which can effectively capture the time sensitivity of semantics and better represent facts. This model operates within a complex space with real and imaginary parts to effectively embed temporal knowledge graphs. Specifically, the real part of the final embedding of our proposed model captures semantic characteristic with temporal sensitivity by learning the relational information and temporal information through transformation and attention mechanism. Simultaneously, the imaginary part of the embeddings learns the connections between different elements in the fact without predefined weights. Our approach is evaluated through extensive experiments on the link prediction task, where it majorly outperforms state-of-the-art models. The proposed model also demonstrates remarkable effectiveness in capturing the complexities of temporal knowledge graphs.

1.Introduction

Knowledge graphs (KGs) as a formalism for knowledge representation and management, have emerged as underlying technology of many downstream AI tasks, including recommendation systems and question-answering systems, and so on [6,25]. Example of such KGs are DBPedia [23], YAGO [33], and NELL [12]. Generally, knowledge graphs consist of a collection of triples representing real world facts, in the form of (s,r,o), where s and o are subject and object entities respectively, r is the relation between them. Despite the large quantities of triples in KGs, they often suffer from incompleteness problem [3]. One of the most popular methods to deal with this problem is by Knowledge Graph Embedding (KGE) models that are based on technique for predicting missing links between existing entities. KGEs operate by representing entities and relations from the symbolic KG into a low-dimensional vector space [2,7], and then measure the plausibility of possible links. Performing link prediction is mainly to complete queries in the form of (s,r,?) or (?,r,o) according to the score of the potential entity in the object position.

Facts in the real world, often involve time, for which the representation in KGs need to be extended beyond triples (e.g., quadruples, quintuples), to include the temporal knowledge [11]. These type of KGS are called temporal knowledge graphs (TKGs) such as ICEWS [9], GDELT [22] and Wikidata [37]. In TKGs designed with quadruples, the facts are represented with one timestamp in the form (s,r,o,τ). In this representation, τ refers to the timestamp for the (s,r,o) fact. Similar to the static KGs, TKGs also have incompleteness problem which could be found by embedding models design to represent TKGs in vector space [32]. These models are called Temporal Knowledge Graph Embedding (TKGE) and perform link prediction by posing queries (s,r,?,τ) or (?,r,o,τ). These cases belong to the facts in real world such that potential subject or object entities are changing with time. TKG reasoning is a process of inferring new facts from known facts, which can be divided into two types, interpolation [19,39] and extrapolation [31,45]. In our work, we mainly focus on interpolation tasks, which complete the missing facts at the timestamp in the past.

Among different types of TKGEs, Tensor-based models which employ tensor decomposition techniques, have demonstrated remarkable efficacy in representing temporal facts [30,46]. As a remark, relations in TKGs serve as the connectors linking entities to form a fact, and time constitutes the temporal validity attribute of the fact. By decomposing the facts into tensors, quadruples are transformed into lower-dimensional embeddings, effectively mitigating complexity, and information from diverse attributes can be integrated to achieve comprehensive representations [24]. Different tensor decomposition methods, such as Canonical Polyadic (CP) decomposition [35] and Tucker decomposition [4], are leveraged in KGEs such as [4,20,30]. In these models, associations between entities, relations and timestamps are established through multiplication operations directly, thereby subject entities, relations, timestamps, object entities have the same status, and there is no clear distinction between them. However, generally in temporal facts, the connection between relations and semantics fundamentally diverges from the connection between time and semantics imposed by relations. As one relation constitutes the main part of a fact that represents the main semantics, the timestamp only gives the semantics an attribute about time. Therefore, when learning over temporal facts, it is important to not only account for the semantic aspects of these facts but also recognize the importance of the temporal attribute for each individual fact. For example, some relations, such as “parents of”, “brother of in” and so on, do not have obvious time dependence, therefore, the facts composed of these relations do not have significant characteristics about time in the temporal knowledge graph. In contrast, some relations exhibit significant temporal properties. However, those tensor-based models often prioritize considerations regarding how to accurately represent timestamps or the entirety of quadruples. The methods to derive connections among these three components through straightforward multiplication fail to align with the authentic meaning of some temporal facts. Consequently, they tend to overlook the intricate interplay between time and semantics inherent in real-world facts.

We introduce a novel model dubbed TRKGE, considering temporal relevance in temporal knowledge graph, which leverages the tensor decomposition method but facilitated to be aware of time importance. Temporal relevance is used to judge the importance of time in facts when learning their representation. For example, the semantics of facts formed by “visit” and “daughter of” have different temporal attributes, one is temporary and the other is permanent. Similar to other tensor decomposition models, our model is also built in the complex space. But the real and imaginary parts of our model represent different information. The real part learns the semantic features of facts with a bias based on temporal relevance, while the imaginary part learns characteristics without a bias. The real part of our model focuses on capturing temporal relevance within the facts. To ensure consistency between the transformation in the real part and complex multiplication, we employ rotation matrices in this part. These matrices effectively adjust entities based on relations and timestamps, facilitating a specific understanding of timestamps and semantics. Furthermore, we introduce attention mechanisms in the real part to learn the temporal relevance within the facts. This attention mechanism allows the model to learn the relational and temporal information of facts in a certain weighting to make them more relevant to the actual meaning. On the other hand, the imaginary part of our model utilizes half of the embeddings to learn the connections among diverse elements through direct multiplication. Then the imaginary part complements the real part in capturing complex relationships within temporal knowledge graphs. Experimental results underscore its performance in comparison to state-of-the-art baselines, thereby illustrating the ability of the proposed method in learning temporal relevance when representing temporal facts.

In this work, the main contributions include:

– Defining a Novel Problem Statement: We introduce a novel problem statement focused on preserving temporal information within knowledge graph embedding models.
– Introducing Temporal Relevance: We propose a new concept called Temporal Relevance, which can serve as a foundational principle for future models to effectively incorporate temporal dynamics.
– Presenting a New Model: We propose a novel model that leverages the power of complex numbers to enhance knowledge graph embeddings.
– Evaluating the Model: We conduct several evaluations of the proposed model to demonstrate its effectiveness in preserving temporal information.

The following sections will dive into these contributions in detail.

2.Related work

In this section, we review the existing literature on knowledge graph embedding methods, categorizing them into two main areas: Static KGE and Temporal KGE. Static KGE methods focus on representing the entities and relationships of knowledge graphs that remain constant over time. These models embed the nodes and edges into a fixed, continuous vector space, effectively capturing the structure and semantics of the graph. However, real-world knowledge graphs often include a temporal dimension, where each fact is associated with a specific time point or interval. This necessitates the development of Temporal KGE methods. These approaches extend static models by incorporating temporal information into the embeddings, capturing the evolution of facts across different time points. Below is a more detailed discussion on these two categories.

Static Knowledge Graph Embedding. In the last decade, various KGE models have been proposed for static knowledge graph completion. These models can generally be categorized into translation-based models, tensor decomposition models and neural models. Translation-based models treat a relation as a translation from the subject entity to the object entity. The scores in these models are typically calculated based on the distance or angle between the translated subject entity embeddings and object embeddings. TransE [8] treats relations as translations from subject entities to object entities, then calculates the distance between translated subject and object entities. RotatE [34] represents each entity and relation as an embedding in complex space, with a real part and an imaginary part. Relations are represented as angles, and subject entities are rotated by relations, the angles between them is the score of the model. Additionally, some researchers proposed models that embed entities and relations in non-Euclidean spaces. MURP [5] first use hyperbolic space to model hierarchical structures in KGs, which brought a big improvement. Later, AttH [13] bring both rotation and reflection into hyperbolic spaces to model various relational patterns. These models focus on capturing the translation relationship between entities and relations and perform well in capturing one-to-one and one-to-many relationships. Tensor decomposition models assume entities as vectors and relations as matrices, such as RESCAL [29], whose scores are calculated based on the product between these embeddings. But RESCAL cannot model complex structures, so ComplEx [35] was proposed, it represents entities and relations as complex embeddings consisting of both real and imaginary parts. The use of complex embeddings can capture both symmetric and asymmetric relationships in KGs. Compared with translation-based models, these models can capture more complex relationships. Besides, neural models employ neural architectures to train embeddings for entities and relationships for KG modeling, such as ConvKB [28], ConvE [16], and KBGAT [27]. While static knowledge graph embedding models have received significant attention over the years, they do not fully correspond to real-life situations. In real life, many facts are often time-dependent and static KGE models can not perform well in TKGs, therefore, there is a need for research on the temporal knowledge graph embedding model.

Temporal Knowledge Graph Embedding. Similar to the static KGs, temporal knowledge graphs are also modeled by the embeddings of entities, relations and timestamps. Many TKGE models are built following existing static KGE models [10]. For example, TTransE [21], is an extension of TransE model, which translates entities by both relations and timestamps. HyTE [15] also borrowed the idea from TransH [40], but it projects entities and relations to different time-dependent planes rather than relation-dependent planes. Based on the static KGE model BoxE [1], BoxTE [26] extends the box embedding model to temporal knowledge graph. RotateQVS [14] models the temporal changes with rotation in quaternion vector space and uses a score function that is similar to TransE. Inspired by RotatE, TeRo [42] defines the temporal evolution of entity embedding as a rotation from the initial time to the current time in the complex space. TComplEx and TNTComplEx [20] are both developed based on the static KGE model ComplEx, which use additional tensors to represent timestamps, and then the score is obtained by complex multiplication of embeddings of entities, relations and timestamps. In addition, many new temporal knowledge graph embedding models have been proposed. ChronoR [30] treat relations and timestamps as rotation and scale. Rich information between temporal and multi-relational features in TKGs are captured by using high-dimensional rotations as transformation operators. TeLM [41] uses multivector representation and the geometric product to model entities, relations and timestamps. TLT-KGE [46] treats semantic and temporal information as different axes in complex or quaternion spaces, and a shared time window as well as a temporal-relational binding module are designed to establish the connection between different parts and timestamps. TASTER [38] regards a TKG as a static knowledge graph when ignoring the time dimension, and then learns global embeddings based on static knowledge graph to capture global information. Then TASTER evolves local embeddings from global embeddings based on the corresponding subgraph to capture the local information. However, most of these works only focus on how to represent the flow of time or how to model timestamps, they ignore the real relationships between time and real facts. In our work, we propose the temporal relevance of entities and relations in facts. Temporal facts are represented by a method that is closer to the actual semantics, thereby improving the ability to learn features in temporal facts.

3.The TRKGE model: Time relevance in temporal knowledge graph embedding

In this section, we introduce the proposed model for which we first set the foundation by defining the mathematical notation and terms that will be consistently used throughout the discussion. Next, we explain the core concept of Temporal Relevance that represents temporal dynamics within data. Finally, we introduce the model itself, termed TRKGE (Temporal Relevance Knowledge Graph Embedding).

3.1.Notation and background for model formulation

As a lead-in to the model formulation, Table 1 provides an overview of the notations employed throughout this section. Now, let us consider a temporal knowledge graph in which the facts are represented as quadruples (s,r,o,τ), where s and o represent subject and object entities respectively, r represents the relation, and τ represents the timestamp. We define E, R and T as the sets of entities, relations and timestamps, then s,o∈E, r∈R and τ∈T.

Table 1

An overview of the symbols used in TRKGE model formulation, along with their corresponding meanings

Symbol	Meaning	Symbol	Meaning
E	Entity set	Im()	Imaginary part
R	Relation set	⟨,⟩	Hermitian inner product
T	Timestamp set	sim()	Real part of Hermitian inner product
s	Subject entity	R()	Rotation operation
o	Object entity	Θ	Angle set
r	Relation	R	Real number
τ	Timestamp	rsem	Additional relation embedding for semantics
V	Vector space	α	Attention vector
C	Complex space	⊙	Element wise complex multiplication
Re()	Real part	⊕	Element wise complex addition

Temporal knowledge graph embedding models aim at completing such TKGs by learning embeddings of entities, relations, and timestamps. The score function of a TKGE model measures the likelihoods of quadruples, hence, new quadruples can be inferred, and their plausibility can be judged to complete the TKG. For temporal facts, relations have different time sensitivities. Therefore, when learning temporal information, the proportion of time information versus relational information in different facts is also needed to be considered. The proposed TRKGE model is capable of capturing these complexities of time relevance with rereads to relations. The rest of this section focuses on the mathematical concepts required to understand, details theories and development of our model TRKGE.

As all geometric TKGE models, our model embeds entities in a continuous vector space and uses geometric transformation to preserve information between subject and object entities.

A vector space V over a field K is a set endowed with two operations, namely addition and scalar product, denoted by + and · respectively. These two operations must satisfy some axioms such as associativity, commutativity, existence identity and inverse elements, compatibility, and distributivity. In this work, we consider the 2 dimension complex vector space C2 over the field of real numbers R. Vectors s∈C2 are in the form s=(s1,s2) where sj=xj+iyj∈C, for j=1,2, and i2=−1. We define and denote by Re(s)=(x1,x2) the real part of s and by Im(s)=(y1,y2) its imaginary part. Embeddings in high dimensional vector space are obtained by considering the Cartesian product of C2. We use ⟨s,s′⟩ to denote the Hermitian inner product of two vectors s and s′. Its real part Re(⟨s,s′⟩), denoted by sim(s,s′), is a positive real vector, which can also represent the similarity of two vector.

Interaction between subject and object entities is done via a variety of geometric transformations. In the literature, many KGE models are built upon the rotation transformation. Similarly, our model uses rotation. However, there is a systematic difference between how the rotation transformation was used by other models. In fact a two-dimensional representation of a rotation of angle θ is defined by the two-dimensional matrix R(θ)=(cosθ−sinθsinθcosθ) or the unit complex number eiθ. In the previous models, a vector s∈C2 is rotated through the product eiθjsj or R(θj)(xjyj),j=1,2. In our model, the rotation is achieved through R(θ1)(x1x2) and R(θ2)(y1y2). In other words, rotation transformations act on the real or imaginary parts (Re(s),Im(s)) of vectors in C2 instead of acting on its projections (s1,s2) onto the complex plane C. We extend this formalism into d dimensional vector space V=(C2)d by considering the Cartesian product of C2. The matrices R(θj) are combined to form block diagonal matrices R(Θ)=diag(R(θ1),…,R(θd) which represent rotation transformations in high dimension. In this case, Θ is the set of rotation angles θj.

3.2.Our approach: The TRKGE model

The proposed model is designed to capture temporal information in knowledge graphs by incorporating Temporal Relevance concept into its architecture.

The concept of Temporal Relevance. We embed subject and object entities, relations, and timestamps in the TKG by d-dimensional vectors s,o,r,τ∈V, respectively. More explicitly, any embedding has two embeddings Re(z) and Im(z) in (R2)d, and so can be expressed as z=Re(z)⊕iIm(z). By z, we refer to the embeddings s,o,r,τ, and by ⊕, we refer to the element wise addition. Similarly, we will use ⊙ to refer to element wise complex multiplication. Since entity embeddings need to be rotated according to relations and timestamps, relation embeddings r and time embeddings τ are transformed into high dimensional block diagonal rotation matrices R(Θr) and R(Θτ) where Θr,Θτ,∈Rd. Thus, relations and timestamps are firstly embedded in V, and then they are projected into block diagonal matrix vector space.

To allow the model to selectively learn relational and temporal information based on temporal relevance, we transform subject entities according to relation and time embeddings, respectively. In order to gain the temporal relevance, subject entity embeddings need to be transformed simultaneously by time and relation embedding. In our model, when calculating the scores, the real part of final transformed embeddings includes the temporal relevance, and the imaginary part is the original imaginary part. And when learning the temporal relevance, both real and imaginary part of subject entity embedding should be considered, The transformation is defined as

(1)sτ=R(Θτ)Re(s)+iR(Θτ)Im(s)(2)sr=R(Θr)Re(s)+iR(Θr)Im(s).

We thereafter use the attention mechanism to quantify the proportion of temporal information and relational information in facts.

The attention mechanism is proven to have a very significant role in deep learning models [13,36]. Since the semantics of facts is intrinsically related to relations, the temporal relevance of the facts is also determined by the relations. The attention mechanism allows TRKGE to use relation-specific attention vector, defined as α, to compute two (positive real) attention coefficients, αr and ατ. The former is dedicated to capture relational information and the latter is focused on learning temporal information. Higher is ατ associated to a relation, more relevant is the temporal information that relation conveys. As the imaginary part of subject entity embeddings are used for both temporal relevance and imaginary part of final transformed embeddings, real parts and imaginary parts of sr and sτ need to be trained separately. For the interaction of the information in both two parts, the same attention vector α is used. The attention vector and coefficients are related by the equation below:

(3)(αrRe,ατRe)=softmax((αTsrRe,αTsτRe)d),(4)(αrIm,ατIm)=softmax((αTsrIm,αTsτIm)d).

We recall that d is the dimension of the embedding vector space V.

Then, the transformed embedding, aware of temporal relevance, can be obtained by

(5)sTR=αrResrRe⊕ατResτRe⊕i(αrImsrIm⊕ατImsτIm).

However, as sTR is used in the real number space, it should be transformed from the complex space. Here, (1,i) is used to do the transformation.

(6)sfinal=⟨αrResrRe⊕ατResτRe⊕i(αrImsrIm⊕ατImsτIm),1⊖i1⟩(7)=αrResrRe⊕ατResτRe−(αrImsrIm⊕ατImsτIm)

where 1∈(R2)d is a vector of ones.

Score Function. The embeddings with temporal relevance, defined in the previous subsection, constitute the real part of the transformed subject entity embeddings, sf. Due to the biased learning of the attention mechanism, some relational or temporal information in the original facts may be lost. Thus, we select the imaginary part of the original subject embedding as the imaginary part of sf. The transformed subject entity embeddings are then defined as follows:

(8)sf=sfinal⊕iIm(s).

The score function of the TRKGE model is defined as the real part of the Hermitian inner product of embeddings of transformed subject entities, relations, timestamps, and object entities. This is obtained as follows

(9)f(s,r,o,τ)=sim((r⊙τ)⊙sf,o).

Figure 1 shows how the TRKGE model framework is benefiting from complex space and the concept of temporal relevance in its score design.

Fig. 1.

A layered visualization of the TRKGE model and its scoring function and framework.

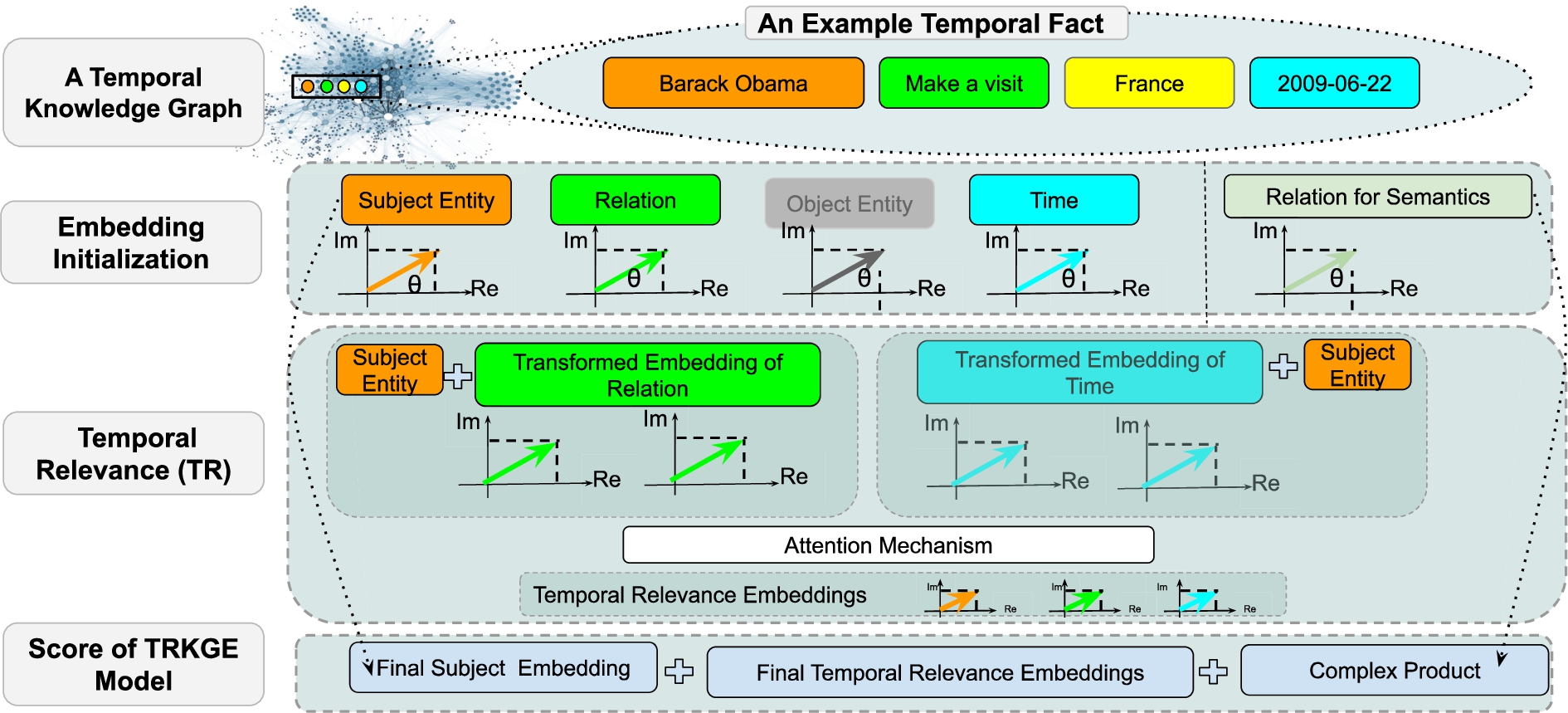
In Eq. (9), the real part of embeddings focus on the temporal relevance, and the imaginary part is used to learn the relationships between different elements in quadruples. However, both the real and imaginary parts of embeddings are involved in the part of temporal relevance, during training the original semantic information gradually loses, which is mainly composed of relations. Therefore, inspired by TNTComplEx [35] that design an extra embedding for time property, we also design an additional relation embedding to represent original semantic information of facts, and use addition to combine it with the relation and time embeddings to enhance the learning of original semantics. Therefore the final score function is

(10)f(s,r,o,τ)=sim((r⊙τ)⊙sf,o)⊕sim(rsem⊙sf,o)=sim((r⊙τ⊕rsem)⊙sf,o)

where rsem∈V is the additional relation embeddings.

Loss Function. In our work, cross entropy loss is used to train the model with uniform negative sampling, where negative examples for (s,r,o,τ) are sampled from all possible quadruples generated by replacing subject or object entities. The loss function to be minimized is

(11)loss(G;Φ)=∑(s,r,o,τ)∈G(−log(f(s,r,o,τ)∑o′∈εf(s,r,o′,τ))−log(f(s,r,o,τ)∑s′∈εf(s′,r,o,τ)))

where Φ is the set of all the model parameters. o′ is the object entity of the negative quadruple(s,r,o′,τ), and s′ is the subject entity of the negative quadruple(s′,r,o,τ).

Besides, a regularization term is added to the loss function to limit the complexity of the model, thus reducing the overfitting of the model. It can also improve the generalization ability of the model, so that the model can be better generalized to unknown data. Regularization is used separately for all embeddings. Because the relational part in the model is divided into two parts, and scores of two relation embeddings are calculated separately, we propose the following regularization.

(12)Ω4(s,r,o)=14(‖s‖44+‖r‖44+‖rsem‖44+‖o‖44)

During training, timestamp embeddings should behave smoothly over time to facilitate a better representation, and the embeddings of adjacent timestamps should be close together. For this, a temporal smoothness objective is used in the loss function.

(13)Λτ=1|T|−1∑i=1|T|−1‖τi+1−τi‖44

Therefore, the final loss function is:

(14)loss(G;Φ)=∑(s,r,o,τ)∈G(−log(f(s,r,o)∑o′∈εf(s,r,o′))−log(f(s,r,o)∑s′∈εf(s′,r,o)))+λ1Ω4+λ2Λτ

where λ1 and λ2 are hyperparameters.

4.Experimental setup

4.1.Datasets and baseline models, and evaluation methodology

We compare our model with other baselines through temporal knowledge graph completion on three popular benchmarks namely ICEWS14, ICEWS05-15 and GDELT. The first two datasets are subsets of Integrated Crisis Early Warning System(ICEWS) dataset that contains information about international events. ICEWS14 collects the facts that occurred between January 1, 2014 and December 31, 2014, and ICEWS05-15 contain events from January 1, 2005 to December 31, 2015. GDELT is a subset of the The Global Database of Events, Language, and Tone (GDELT) that captures events and news coverage from around the world. This dataset includes conflict, cooperation, diplomatic, economic, humanitarian events and so on. GDELT is a very dense TKG, it has 3.4 million quadruples but only 500 entities and 20 relations. Table 2 is the statics of these three datasets.

Table 2

Statistics for ICEWS14, Yago15k and GDELT

	\|E\|	\|R\|	\|T\|	Ntrain	Nvalid	Ntest	Ntotal
ICEWS14	7128	230	365	72826	8963	8941	90730
ICEWS05-15	10488	251	4017	386962	46092	46275	479329
GDELT	500	20	366	2735685	341961	341961	3419607

In the experiments, baselines are chosen from both static KGE models and TKGE models. From the static KGE models, we use TransE [8], DisMult [44], QuatE [47]. We also compare our model with some state-of-the-art TKGE models, such as TTransE [21], HyTE [15], TA-DistMult [17], ATiSE [43], TeRo [42], RotateQVS [14], TCompleEx [20], TNTComplEx [20], BoxTE [26], TLT-KGE(Complex) [46] and TLT-KGE(Quaternion) [46], TASTER [38].

In this work, we perform the evaluations with a focus on link prediction task. This means to replace s and o with all entities in E for each quadruple in the test set. Then the model scores all generated quadruples. In addition, the time-wise filter is used in experiments, which removes all the candidate entities that yield correct quadruples. Following metrics are used for comparison: Mean Reciprocal Rank (MRR), and H@n where n∈{1,3,10}. MRR is measured by ∑j=1nt1rj, where rj is the rank of the j-the test quadruple and nt is the number of triples in the test set. H@n is the number of test quadruples ranked less than n.

In our experiments, we utilize time-aware filters [18], which are also employed by the baseline models. This filter differs from the static models as it incorporates timestamps during the process of filtering out entities, which is meaningful for temporal knowledge graph representation.

4.2.Implementation details

Main experiment In this experiment, temporal knowledge graph completion is done for three datasets. On ICEWS14 and ICEWS05-15, we tune λ1 and λ2 from [0.005, 0.05]. And on GDELT, they are tuned from [0.0000005, 0.00005]. Our model is training with a learning rate 0.1, and it is optimized by Adagrad. The dimensions used on three datasets are all set as 1500 and 2000. We compare the best performance of our model with others’ best results reported in their papers. The hyperparameters we used in the experiments are shown in Table 3.

Table 3

Hyperparameters of TRKGE for ICEWS14, Yago15k and GDELT

	Dimension	Epoch	Batch size	λ1	λ2
ICEWS14	2000(1500)	200	500	0.01	0.5
ICEWS05-15	2000(1500)	200	1000	0.01	2.5
GDELT	2000(1500)	400	2000	1e-6	1e-5

Ablation study In this section, to demonstrate the representation capabilities of temporal and relational information in our model on different datasets, we establish two models, denoted as Rel-TR and Time-TR. In both models, we removed the attention mechanism. Rel-TR only use relation embeddings for transformations, while Time-TR solely utilize time embeddings for transformations. Both models are trained and evaluated with the same hyperparameters as the main experiment. In addition, we also evaluate the design of the imaginary part for learning the relationships between different elements and additional relation embeddings for enhancing semantic learning, namely Im-TR and Sem-TR.

Attention value of time In this section, to demonstrate the effect of temporal relevance, attention values of time for some relations in ICEWS05-15 and GDELT is showed to analyze the plausibility of temporal relevance according to the results in the ablation study and the characteristics of the dataset.

Analyse on efficiency In this section, we compare our model with the best-performing baselines, TLT-KGE (Complex and Quaternion) and TNTComplEx. We trained these models in dimensions of 500, 1000, 1500, and 2000. TLT-KGE and TNTComplEx are trained by the optimal hyperparameters provided in their work. The variation of the models’ performance with the number of parameters is shown in the form of a line graph. In addition, we also compare the running times of these models to show the efficiency of our model.

5.Experiment

We performed extensive evaluations ensuring to reflect the strength of the proposed model. First, we report the performance of the TRKGE model and other baselines on the three aforementioned benchmark datasets. The experimental results for these performance evaluations are shown in Table 4. The main result which can be seen in the table is that our model outperforms all other baseline models on 2000 dimensions in all the metrics. While on the ICEWS14 and ICEWS05-15 datasets, the TLT-KGE model performs better that other baseline models, our model still improves the results with a high margin. On the MRR metric, our model outperforms TLT-KGE model by a delta of 1.6%, on the ICEWS14 dataset and with a margin of 0.2% on the ICEWS05-15 dataset. On the GDELT dataset, TNTComplEx model is the best baseline model. But our model TRKGE outperforms TNTComplEx by 4.1% on GDELT. In 1500 dimensions that is the setting used by most of the baseline models, our model is performing better than any other model on the two ICEWS14 and GDELT datasets. Its results are comparative with the best of state-of-the-art results on ICEWS05-15. As a sign of robustness, our proposed model shows a constant performance increase on all these datasets which are challenging for the upfront models.

Table 4

Experimental results on ICEWS14, ICEWS05-15 and GDELT. The results labeled with * are from the paper [14]. The results of TComplEx and TNTComplEx on GDELT are produced from their original code. Other results are reported in their own paper

Model	ICEWS14				ICEWS05-15				GDELT

	MRR	h@1	h@3	h@10	MRR	h@1	h@3	h@10	MRR	h@1	h@3	h@10
TransE*	28.0	9.4	–	63.7	29.4	9.0	–	66.3	11.3	0.0	15.8	31.2
DistMult*	43.9	32.3	–	67.2	45.6	33.7	–	69.1	19.6	11.7	20.8	34.8
QuatE*	47.1	35.3	53.0	71.2	48.2	37.0	52.9	72.7	–	–	–	–
TTransE*	25.5	7.4	–	60.1	27.1	8.4	–	61.6	11.5	0.0	16.0	31.8
HyTE*	29.7	10.8	41.6	65.5	31.6	11.6	44.5	68.1	11.8	0.0	16.5	32.6
TA-DistMult*	47.7	36.3	–	68.6	47.4	34.6	–	72.8	20.6	12.4	21.9	36.5
ATiSE*	55.0	43.6	62.9	75.0	51.9	37.8	60.6	79.4	–	–	–	–
TeRo*	56.2	46.8	62.1	73.2	58.6	46.9	66.8	79.5	24.5	15.4	26.4	42.0
RotateQVS*	59.1	50.7	64.2	75.4	63.3	52.9	70.9	81.3	27.0	17.5	29.3	45.8
TComplEx	61.9	54.2	66.1	76.7	66.5	58.3	71.6	81.1	38.5	30.5	41.2	53.8
TNTComplEx	60.9	52.1	66.0	77.4	66.9	58.4	72.2	82.2	38.9	30.7	41.6	54.6
BoxTE(k=5)	61.3	52.8	66.4	76.3	66.7	58.2	71.9	82.0	35.2	26.9	37.7	51.1
TLT-KGE(Complex)	63.0	54.9	67.8	77.7	68.6	60.7	73.5	83.1	35.6	26.7	38.5	53.2
TLT-KGE(Quaternion)	63.4	55.1	68.4	78.6	69.0	60.9	74.1	83.1	35.8	26.5	38.8	54.3
TASTER	61.1	52.7	–	76.7	65.4	56.2	–	81.8	–	–	–	–
TRKGE(1500)	64.0	56.1	68.8	78.9	68.7	60.6	73.9	83.4	37.1	29.1	39.7	52.5
TRKGE(2000)	64.4	56.6	69.0	79.2	69.2	61.1	74.3	83.8	40.5	32.6	43.3	55.2

Table 4 also shows that most of the baseline models have different representation capabilities on the versions of ICEWS datasets and GDELT. For example, TLT-KGE performs well on both ICEWS14 and ICEWS05-15, but its performance is mediocre on the GDELT dataset. In contrast, the T(NT)ComplEx model performs well on GDELT, but badly on the other two datasets namely ICEWS14 and ICEWS05-15. This observation can be explained based on the significant structural and statistical differences between those datasets and lack of models in handling those differences. We observed three aspects on these differences including:

– Density of Relations – This refers to the distribution of facts among relations. A dataset is considered denser if a higher number of relations have more facts associated with them.
– Temporal Relevance – This is determined by the number of timestamps in the dataset. A dataset with more timestamps indicates richer temporal information.
– Semantic Richness of Relations – This is determined by the number of facts associated with each relation. A dataset where most relations have a high number of facts indicates that the relations have rich semantics.

Fig. 2.

Percentage of existing quadruples per each relations in two datasets.

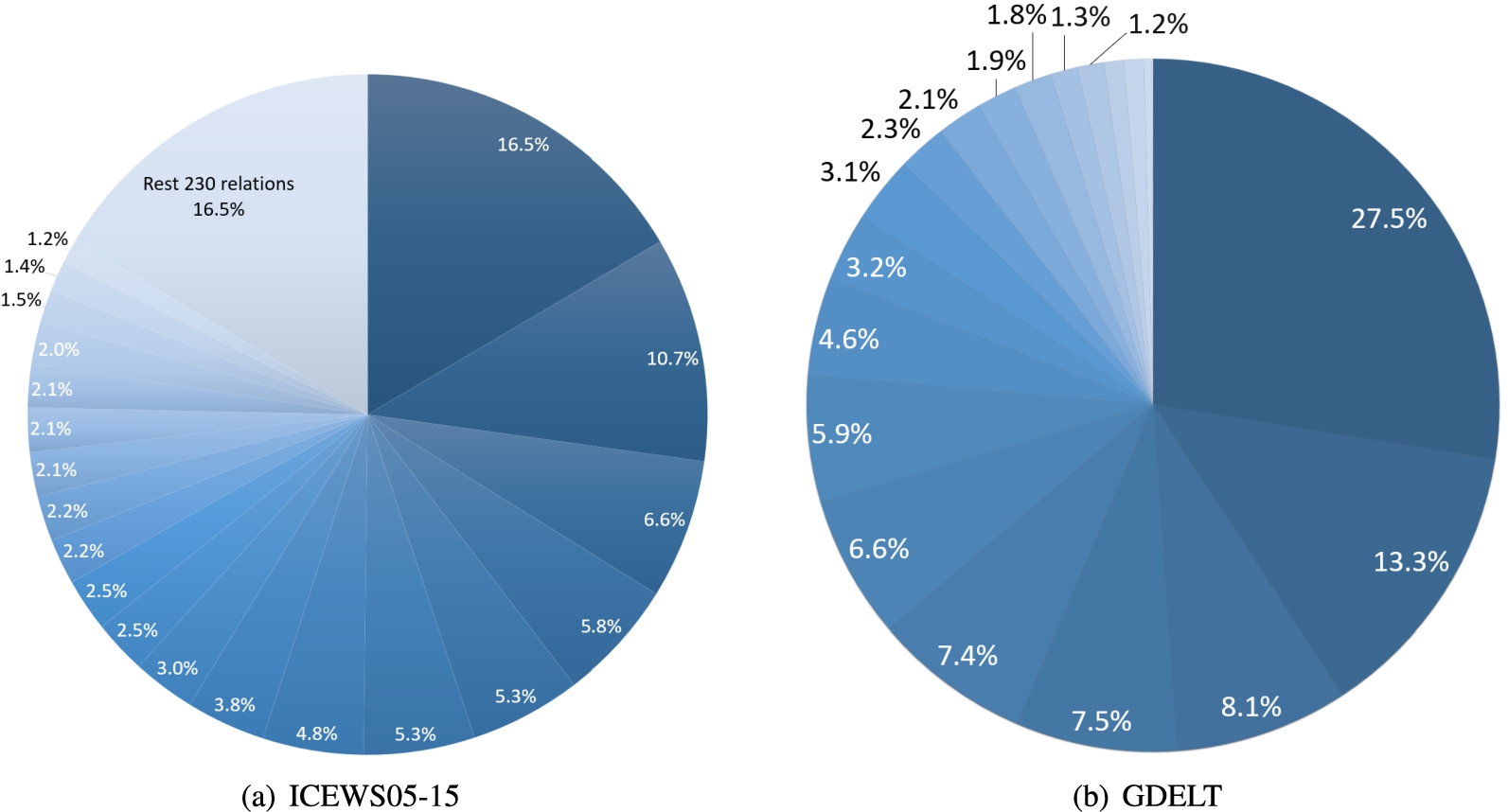
Table 5

Statistics of the number of quadruples associated with relations on ICEWS05-15 and GDELT

Dataset	ICEWS05-15				GDELT
#quadruples	10000<n<100000	1000<n<10000	100<n<1000	n<100	1000000<n<100000	10000<n<100000	n<10000
#relations	12	27	84	128	10	9	1
#quadruples	318168	107146	32200	3815	2982818	434307	2482
Ratio	69.20%	23.30%	7.00%	0.83%	87.23%	12.70%	0.07%

ICEWS14 and ICEWS05-15 have higher number of entities, relation types, and timestamps than GDELT which are shown in Table 2. While the GDELT dataset has only 20 relations, it is way denser than the other two datasets and have much larger data volume in terms of facts. We show the number of quadruples for different relations in Fig. 2, and we also give the information about the number of quadruples formed by each relation in Table 5. As the statistics of the two datasets ICEWS14 and ICEWS05-15 are similar, we only show the case of ICEWS05-15. It is noting that in both ICEWS14 and ICEWS05-15, the top 10 relations in terms of quantity almost construct the 60% of the datasets. In ICEWS05-15, there are 212 relations, among which each relation is present in less than 1000 facts. Only 39 relations out of 212 is present in more than 1000 facts, which leads to less density, resulting in a weak expression ability of most relations. At the same time, this dataset has more than 4000 timestamps that makes the temporal information more relevant. Different from the ICEWS05-15 dataset, in GDELT, there are 10 relations that each of them built more than 100 thousand facts, and 9 relations that each of them built more than 10 thousand facts, so all relations are relatively fully used in different facts. Such a small number of relations and timestamps contribute to a large amount of data, indicating that both relations and time have rich semantics in this dataset.

The baseline models, TNTComplEx and BoxTE, learn the semantics of relations and timestamps equally, allowing them to have good representation capabilities on GDELT. In contrast, TLT-KGE specifically models temporal information by using many extra embeddings related to time, leading to its strong performance on ICEWS05-15, but its normal performance on GDELT shows their design is limited. Based on the best results of our model on three datasets, it can be concluded that our model, by calculating temporal relevance and placing emphasis on learning temporal and relational information, demonstrates good adaptability to different types of datasets. Additionally, with the increase in dimensions, the model’s representational power also improves. The performance of some well-performing baseline models in high dimensions will be discussed in the analysis of the model’s parameter quantity.

5.1.Ablation study

We conducted an ablation experiment on the temporal relevance component. In order to do so, the attention mechanism was removed from the model design with a focus on learning temporal information and relational information. Rel-TR focuses on relational information, while Time-TR focuses on temporal information. Table 6 shows that Time-TR outperforms Rel-TR by 6% on ICEWS14 and 3% on ICEWS05-15, while these two models perform similarly on GDELT.

Table 6

Impact of learning relational and temporal information is evaluated by Rel-TR and Time-TR, where Rel-TR only learns relational information and Time-TR only learns temporal information. Im-TR only learns relational and temporal information with temporal relevance, ignoring the original information of facts. Sem-TR removes the extra relation embedding for learning the semantics of facts

Model	ICEWS14				ICEWS05-15				GDELT

	MRR	h@1	h@3	h@10	MRR	h@1	h@3	h@10	MRR	h@1	h@3	h@10
Rel-TR	60.4	50.7	66.7	77.7	67.7	59.0	73.4	83.3	38.2	30.0	40.9	53.9
Time-TR	64.1	56.3	68.6	78.6	69.0	61.2	73.9	83.3	38.3	30.5	40.9	53.2
Im-TR	63.5	55.5	68.1	78.0	68.4	60.4	73.4	83.2	40.3	32.5	43.0	55.2
Sem-TR	59.3	51.0	64.2	74.3	63.0	54.3	68.2	79.0	40.2	32.3	43.0	55.1
Original	64.4	56.6	69.0	79.2	69.2	61.1	74.3	83.8	40.5	32.6	43.3	55.2

As mentioned in the main experiment, in ICEWS14 and ICEWS05-15, time plays a significant role, and in GDELT, both temporal and relational information are important. The results of Time-TR and Rel-TR align with these characteristics. Furthermore, in order to test the design of the imaginary part in our original model which is used to save the original information of facts, Im-TR is proposed, where both real and imaginary parts learn relational and temporal information with temporal relevance.

On ICEWS14 and ICEWS05-15, Im-TR performs better than Rel-TR but worse than Time-TR., which means that Selectively learning information leads to the improved performance, but it still loses some information when compared with Time-TR and original model. On GDELT it performs better than both Rel-TR and Time-TR and similarly to original model. As facts in GDELT have rich temporal and relational information, the attention mechanism has a weak bias towards these two types of information, which is also shown in Fig. 3(b). Therefore, Im-TR is similar with original one on GDELT.

Sem-TR performs worse on both ICEWS14 and ICEWS05-15. From Fig. 3(a), we can see on ICEWS datasets, the attention mechanism mainly focus on the temporal information, which leads to a massive lack of relational information, so extra relation embedding for enhancing the learning of the semantics of facts is important in our orginal design. Similar with Im-TR, attention mechanism dose not play an important role on GDELT, so the lack of information is less, and its performance is also close to TRKGE.

Overall, the original model TRKGE has the best performance, which demonstrates the meaningfulness of biased learning towards temporal and relational information. It not only improves the model’s performance but also increases its adaptability to different datasets.

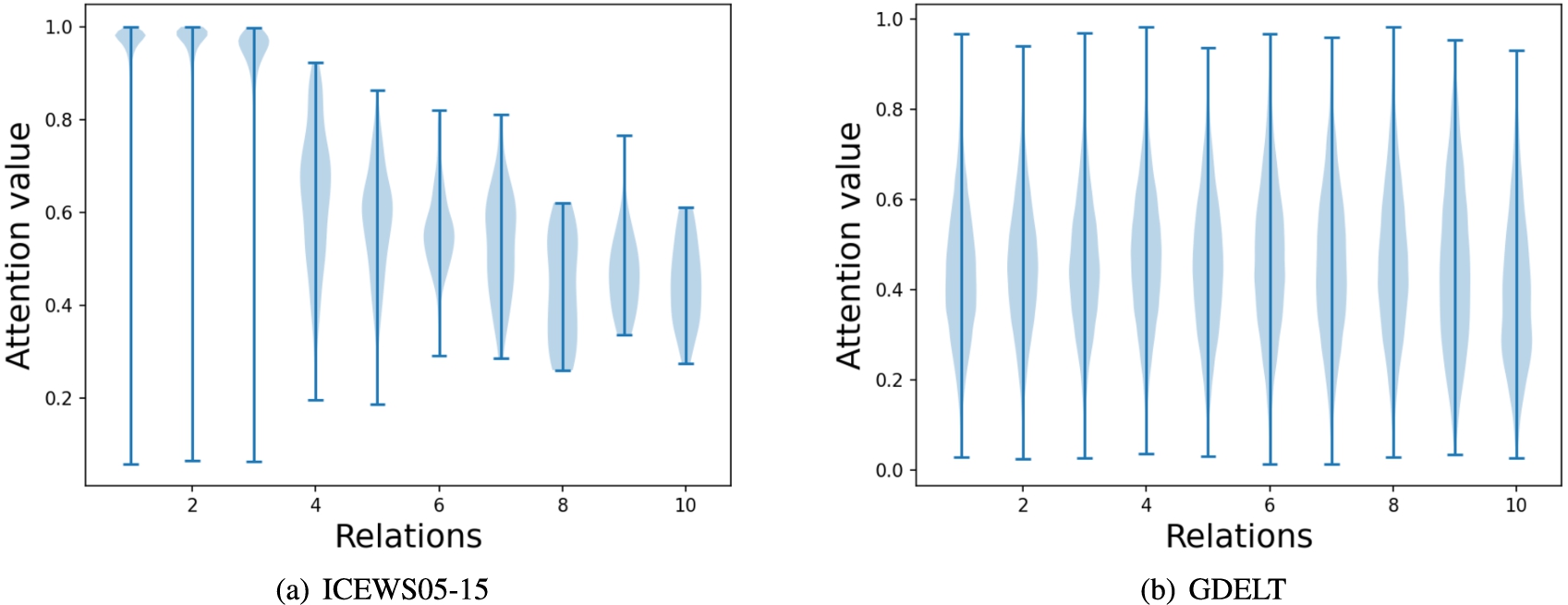
5.2.Attention value of time

In order to visualize the emphasis on time, we show attention values on two datasets of ICEWS05-15 and GDELT in Fig. 3. In the left hand side, the Fig. 3 (a), we can see that the attention values for the frequent three relations on ICEWS05-15 are almost 1. This means the learning is entirely biased towards time, while the attention values for the less frequent relations are evenly distributed around 0.5. However, the most frequent 10 relations constitute 60% of the facts in ICEWS05-15. This indicates that the impact of the less frequent relations is not very high. Therefore, Time-TR model can effectively capture the majority of the facts but cannot represent the remaining facts well, resulting in slightly weaker performance compared to our model, TRKGE. In the case of the GDELT dataset, where both relations and timestamps exhibit rich semantic information, the attention values are centered around 0.5 in the visualization. This aligns with the characteristics of this dataset in terms of time relevance relations which is also consistent with the performance of Rel-TR, Time-TR and Im-TR.

Fig. 3.

Attention values on ICEWS05-15 and GDELT. In the left (a), the first 3 values are from the most frequent 3 relations, the last 4 values are from the least frequent relations, and the middle 3 values are randomly selected. In the right (b), because of the small number of relations and memory limitations, the values are selected from the middle 10 relations.

5.3.Analysis on efficiency

In this section, we performed an experiment to compare TNTComplEx, TLT-KGE and our model in terms of the number of parameters to reflect their efficiency. Table 7 provides a reference for the number of parameters of each model. It is evident that the performance gain of our model is not with higher parameter count than the other leading models, emphasizing its efficiency.

Table 7

Model parameter count for TRKGE, TNTComplEx and TLT-KGE. For TLT-KGE, w is the number of shared time windows

Model	Number of parameters
TNTComplEx	2d(\|E\|+4\|R\|+\|T\|)
TLT-KGE	2d(\|E\|+2\|R\|+3\|T\|+\|T\|w)
TRKGE	2d(\|E\|+5\|R\|+\|T\|)

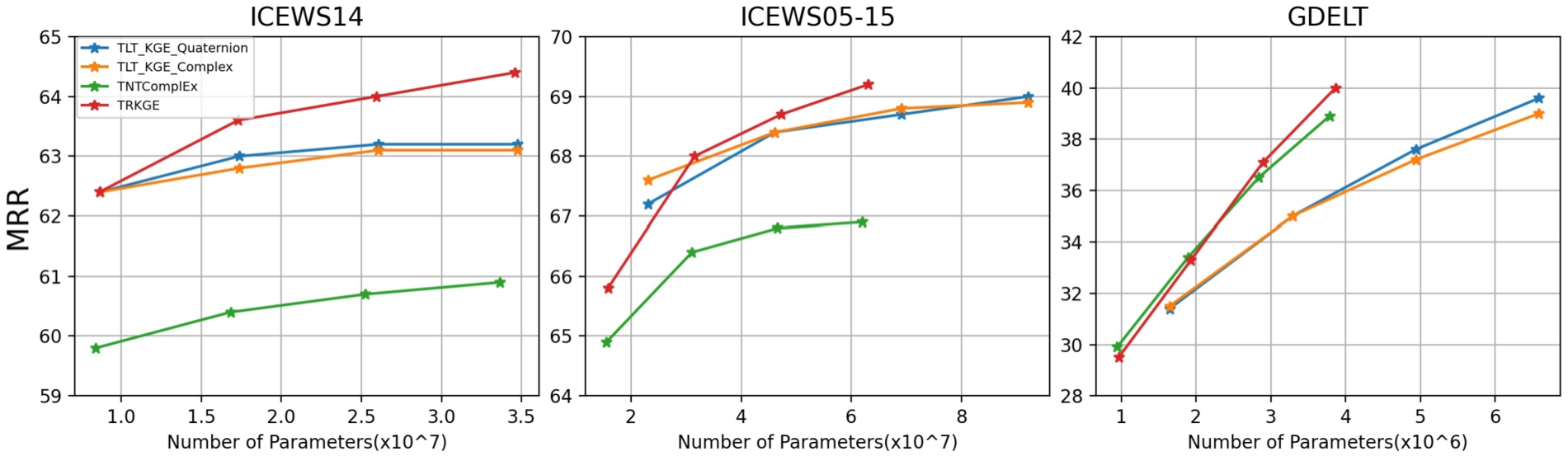
These three models were evaluated on dimensions of 500, 1000, 1500, and 2000, and line graphs were plotted and shown in Fig. 4, to represent the model’s performance with the number of parameters in four dimensions. As the Mean Reciprocal Rank (MRR) can indicate the overall effectiveness of a model, we correlated MRR with the number of parameters in the the graphs to illustrate the performance of different models under varying parameter counts. From Fig. 4, it can be observed that TNTComplEx performed poorly on ICEWS14 and ICEWS05-15 but excelled on GDELT due to its design for simultaneously learning relational and temporal information. TLT-KGE performed well on ICEWS14 and ICEWS05-15 but poorly on GDELT, since it is designed to capture more temporal information, which results in more parameters, especially in the case of ICEWS05-15, where its number of parameters is much more than TNTComplEx and our model. From the graphs, it is obvious that our model achieves better results on ICEWS14 with similar parameter counts. On ICEWS05-15, our model can achieve similar optimal results with only half of parameters of TLT-KGE. On GDELT, both our model and TNTComplEx effectively learn rich information from relations and timestamps and achieve better results with much fewer parameters than TLT-KGE.

Fig. 4.

Performance under different numbers of parameters. Circles represent 500 dimensions, triangles represent 1000 dimensions, stars represent 1500 dimensions, and squares represent 2000 dimensions.

In order to further test the efficiency of our models, we chose three models that performe well to compare the runtimes, TNTComplEx, TLT-KGE(Complex), and TLT-KGE(Quaternion). Although BoxTE also performs well, it takes several days to run, so it was not chosen here. As four models are the tensor decomposition models, they do not need many epochs, so we set the epoch to 100 and the models are tested every 10 epochs, and then the total time of each model is reported. From the Table 8 we can see that the most basic model, TNTComplEx spends the least time on all three datasets. The running time of our models is closer to TNTComplEx on ICEWS14 and ICEWS05-15, while the two models of TLT-KGE need more time. On GDELT, our model requires more time to train, because a small number of entities and relationships and a large number of facts bring complex information, which influences the temporal relevance part and gives a big boost to the performance, but it is still close to the runtime of TLT-KGE(Quaternion).

Table 8

Running time of three model in units of seconds

Model	ICEWS14	ICEWS05-15	GDELT
TNTComplEx	955.30	6571.40	16927.22
TLT-KGE(Complex)	1010.93	11198.65	22258.03
TLT-KGE(Quaternion)	1367.00	13980.95	26660.47
TRKGE	1126.53	7811.36	29832.76

For the task of temporal knowledge graph completion, most tensor decomposition models are efficient, we bring temporal relevance into the model and our model still has better performance with little time cost. Therefore, our model can efficiently and effectively represent temporal facts well in different types of TKGs.

6.Conclusion and future work

By decomposing embeddings into real and imaginary parts, we have ensured that both temporal and relational information in facts are well-represented. The real part plays a crucial role in preserving temporal relevance of relational knowledge, guaranteeing that time-sensitive relations are not marginalized. In contrast, the imaginary component captures the nature of the original information, preventing potential information loss. This distinction and simultaneous handling of these components empower our model to preserve more complex characteristic in TKGs. Our experimental results serve as a testament to the model’s proficiency. By excelling in link prediction tasks and outperforming existing state-of-the-art models, it underscores its capability to cater to the dynamics of TKGs. The novelty presented in this paper is not just in the creation of an advanced embedding model but also the demonstration that understanding and effectively representing the interplay between time and relationships in knowledge graphs can bring significant improvements. This serves as a new direction for future research in refining temporal relevance measures or exploring other complex space representations. In conclusion, as TKGs continue to grow in relevance, models like ours will be instrumental in ensuring that the temporal and relational information they contain is comprehensively captured and utilized. We believe that our proposed model sets a new benchmark in TKG embedding.

In future work, we aim at extending this model to handle more intricate temporal patterns by incorporating advanced time-aware components. Additionally, exploring alternative complex space, like quaternion space, representations may unlock even more efficient ways to represent temporal and relational dynamics in knowledge graphs.

Acknowledgements

We acknowledge the support of the China Scholarship Council for the first author, and contribution of the following Natural Science Foundation of China under Grant No.42271391&No. 62006214, Special Project of Hubei Key Research and Development Program under Grant No.2023BIB015, Joint Funds of Equipment Pre-Research and Ministry of Education of China Grant No. 8091B022148, the 14th Five-year Pre-research Project of Civil Aerospace in China, and Hubei excellent young and middle-aged science and technology innovation team plan project under Grant No.T2021031. We thank the reviewers and editors for their feedback on the submission. We also acknowledge the financial support by the Federal Ministry of Education and Research of Germany and by Sächsisches Staatsministerium für Wissenschaft, Kultur und Tourismus in the programme Center of Excellence for AI-research, Center for Scalable Data Analytics and Artificial Intelligence Dresden/Leipzig” (ScaDS.AI).

References

[1]	R. Abboud, I. Ceylan, T. Lukasiewicz and T. Salvatori, BoxE: A box embedding model for knowledge base completion, in: Advances in Neural Information Processing Systems, H. Larochelle, M. Ranzato, R. Hadsell, M.F. Balcan and H. Lin, eds, Vol. 33: , Curran Associates, Inc., (2020) , pp. 9649–9661, https://proceedings.neurips.cc/paper_files/paper/2020/file/6dbbe6abe5f14af882ff977fc3f35501-Paper.pdf.
[2]	M. Ali, M. Berrendorf, C.T. Hoyt, L. Vermue, M. Galkin, S. Sharifzadeh, A. Fischer, V. Tresp and J. Lehmann, Bringing light into the dark: A large-scale evaluation of knowledge graph embedding models under a unified framework, IEEE Transactions on Pattern Analysis and Machine Intelligence 44: (12) ((2022) ), 8825–8845. doi:10.1109/TPAMI.2021.3124805.
[3]	K. Amouzouvi, B. Song, S. Vahdati and J. Lehmann, Knowledge GeoGebra: Leveraging geometry of relation embeddings in knowledge graph completion, in: Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation (LREC-COLING 2024), N. Calzolari, M.-Y. Kan, V. Hoste, A. Lenci, S. Sakti and N. Xue, eds, ELRA and ICCL, Torino, Italia, (2024) , pp. 9832–9842, https://aclanthology.org/2024.lrec-main.859.
[4]	I. Balazevic, C. Allen and T. Hospedales, TuckER: Tensor factorization for knowledge graph completion, in: Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), K. Inui, J. Jiang, V. Ng and X. Wan, eds, Association for Computational Linguistics, Hong Kong, China, (2019) , pp. 5185–5194, https://aclanthology.org/D19-1522. doi:10.18653/v1/D19-1522.
[5]	I. Balazevic, C. Allen and T. Hospedales, Multi-relational Poincaré graph embeddings, in: Advances in Neural Information Processing Systems, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox and R. Garnett, eds, Vol. 32: , Curran Associates, Inc., (2019) , https://proceedings.neurips.cc/paper_files/paper/2019/file/f8b932c70d0b2e6bf071729a4fa68dfc-Paper.pdf.
[6]	L. Bellomarini, E. Sallinger and S. Vahdati, Knowledge graphs: The layered perspective, in: Knowledge Graphs and Big Data Processing, Springer, Cham, (2020) , pp. 20–34. doi:10.1007/978-3-030-53199-7_2.
[7]	L. Bellomarini, E. Sallinger and S. Vahdati, Reasoning in knowledge graphs: An embeddings spotlight, in: Knowledge Graphs and Big Data Processing, Springer, Cham, (2020) , pp. 87–101. doi:10.1007/978-3-030-53199-7_6.
[8]	A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston and O. Yakhnenko, Translating embeddings for modeling multi-relational data, in: Advances in Neural Information Processing Systems, C.J. Burges, L. Bottou, M. Welling, Z. Ghahramani and K.Q. Weinberger, eds, Vol. 26: , Curran Associates, Inc., (2013) , https://proceedings.neurips.cc/paper_files/paper/2013/file/1cecc7a77928ca8133fa24680a88d2f9-Paper.pdf.
[9]	E. Boschee, J. Lautenschlager, S. O’Brien, S. Shellman, J. Starz, M. Ward, ICEWS Coded Event Data, Harvard Dataverse, (2015) . doi:10.7910/DVN/28075.
[10]	B. Cai, Y. Xiang, L. Gao, H. Zhang, Y. Li and J. Li, Temporal knowledge graph completion: A survey, in: Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI’23, (2023) . ISBN 978-1-956792-03-4. doi:10.24963/ijcai.2023/734.
[11]	L. Cai, K. Janowicz, B. Yan, R. Zhu and G. Mai, Time in a box: Advancing knowledge graph completion with temporal scopes, in: K-CAP’21, Association for Computing Machinery, New York, NY, USA, (2021) , pp. 121–128. ISBN 9781450384575. doi:10.1145/3460210.3493566.
[12]	A. Carlson, J. Betteridge, B. Kisiel, B. Settles, E. Hruschka and T. Mitchell, Toward an architecture for never-ending language learning, in: Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 24: , (2010) , pp. 1306–1313, https://ojs.aaai.org/index.php/AAAI/article/view/7519. doi:10.1609/aaai.v24i1.7519.
[13]	I. Chami, A. Wolf, D.-C. Juan, F. Sala, S. Ravi and C. Ré, Low-dimensional hyperbolic knowledge graph embeddings, in: Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, D. Jurafsky, J. Chai, N. Schluter and J. Tetreault, eds, Association for Computational Linguistics, Online, (2020) , pp. 6901–6914, https://aclanthology.org/2020.acl-main.617. doi:10.18653/v1/2020.acl-main.617.
[14]	K. Chen, Y. Wang, Y. Li and A. Li, RotateQVS: Representing temporal information as rotations in quaternion vector space for temporal knowledge graph completion, in: Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Association for Computational Linguistics, Dublin, Ireland, (2022) , pp. 5843–5857, https://aclanthology.org/2022.acl-long.402. doi:10.18653/v1/2022.acl-long.402.
[15]	S.S. Dasgupta, S.N. Ray and P. Talukdar, HyTE: Hyperplane-based temporally aware knowledge graph embedding, in: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, E. Riloff, D. Chiang, J. Hockenmaier and J. Tsujii, eds, Association for Computational Linguistics, Brussels, Belgium, (2018) , pp. 2001–2011, https://aclanthology.org/D18-1225. doi:10.18653/v1/D18-1225.
[16]	T. Dettmers, P. Minervini, P. Stenetorp and S. Riedel, Convolutional 2D knowledge graph embeddings, in: Proceedings of the AAAI Conference on Artificial Intelligence 32(1), (2018) , https://ojs.aaai.org/index.php/AAAI/article/view/11573. doi:10.1609/aaai.v32i1.11573.
[17]	A. García-Durán, S. Dumančić and M. Niepert, Learning sequence encoders for temporal knowledge graph completion, in: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, E. Riloff, D. Chiang, J. Hockenmaier and J. Tsujii, eds, Association for Computational Linguistics, Brussels, Belgium, (2018) , pp. 4816–4821, https://aclanthology.org/D18-1516. doi:10.18653/v1/D18-1516.
[18]	R. Goel, S.M. Kazemi, M. Brubaker and P. Poupart, Diachronic embedding for temporal knowledge graph completion, in: Proceedings of the AAAI Conference on Artificial Intelligence 34(04), (2020) , pp. 3988–3995, https://ojs.aaai.org/index.php/AAAI/article/view/5815. doi:10.1609/aaai.v34i04.5815.
[19]	M. He, L. Zhu and L. Bai, ConvTKG: A query-aware convolutional neural network-based embedding model for temporal knowledge graph completion, Neurocomputing 588: ((2024) ), 127680, https://www.sciencedirect.com/science/article/pii/S092523122400451X. doi:10.1016/j.neucom.2024.127680.
[20]	T. Lacroix, G. Obozinski and N. Usunier, Tensor decompositions for temporal knowledge base completion, in: International Conference on Learning Representations, (2020) , https://openreview.net/forum?id=rke2P1BFwS.
[21]	J. Leblay and M.W. Chekol, Deriving validity time in knowledge graph, in: Companion Proceedings of the the Web Conference 2018, WWW’18, International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, (2018) , pp. 1771–1776. ISBN 9781450356404. doi:10.1145/3184558.3191639.
[22]	K. Leetaru and P.A. Schrodt, GDELT: Global data on events, location, and tone, 1979–2012, in: ISA Annual Convention, Vol. 2: , Citeseer, (2013) , pp. 1–49.
[23]	J. Lehmann, R. Isele, M. Jakob, A. Jentzsch, D. Kontokostas, P.N. Mendes, S. Hellmann, M. Morsey, P. Van Kleef, S. Auer et al., Dbpedia – a large-scale, multilingual knowledge base extracted from Wikipedia, Semantic web 6: (2) ((2015) ), 167–195. doi:10.3233/SW-140134.
[24]	R. Liu, G. Yin, Z. Liu and L. Zhang, PTKE: Translation-based temporal knowledge graph embedding in polar coordinate system, Neurocomputing 529: ((2023) ), 80–91, https://www.sciencedirect.com/science/article/pii/S092523122300111X. doi:10.1016/j.neucom.2023.01.079.
[25]	M. Ma, P. Xie, F. Teng, B. Wang, S. Ji, J. Zhang and T. Li, HiSTGNN: Hierarchical spatio-temporal graph neural network for weather forecasting, Information Sciences 648: ((2023) ), 119580, https://www.sciencedirect.com/science/article/pii/S0020025523011659. doi:10.1016/j.ins.2023.119580.
[26]	J. Messner, R. Abboud and I.I. Ceylan, Temporal knowledge graph completion using box embeddings, Proceedings of the AAAI Conference on Artificial Intelligence 36: (7) ((2022) ), 7779–7787, https://ojs.aaai.org/index.php/AAAI/article/view/20746. doi:10.1609/aaai.v36i7.20746.
[27]	D. Nathani, J. Chauhan, C. Sharma and M. Kaul, Learning attention-based embeddings for relation prediction in knowledge graphs, in: Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, A. Korhonen, D. Traum and L. Màrquez, eds, Association for Computational Linguistics, Florence, Italy, (2019) , pp. 4710–4723, https://aclanthology.org/P19-1466. doi:10.18653/v1/P19-1466.
[28]	D.Q. Nguyen, T.D. Nguyen, D.Q. Nguyen and D. Phung, A novel embedding model for knowledge base completion based on convolutional neural network, in: Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers), M. Walker, H. Ji and A. Stent, eds, Association for Computational Linguistics, New Orleans, Louisiana, (2018) , pp. 327–333, https://aclanthology.org/N18-2053. doi:10.18653/v1/N18-2053.
[29]	M. Nickel, V. Tresp and H.-P. Kriegel, A three-way model for collective learning on multi-relational data, in: Proceedings of the 28th International Conference on International Conference on Machine Learning, ICML’11, Omnipress, Madison, WI, USA, (2011) , pp. 809–816. ISBN 9781450306195.
[30]	A. Sadeghian, M. Armandpour, A. Colas and D.Z. Wang, ChronoR: Rotation based temporal knowledge graph embedding, Proceedings of the AAAI Conference on Artificial Intelligence 35: (7) ((2021) ), 6471–6479, https://ojs.aaai.org/index.php/AAAI/article/view/16802. doi:10.1609/aaai.v35i7.16802.
[31]	P. Shao, J. He, G. Li, D. Zhang and J. Tao, Hierarchical graph attention network for temporal knowledge graph reasoning, Neurocomputing 550: ((2023) ), 126390, https://www.sciencedirect.com/science/article/pii/S0925231223005131. doi:10.1016/j.neucom.2023.126390.
[32]	B. Song, C. Xu, K. Amouzouvi, M. Wang, J. Lehmann and S. Vahdati, Distinct geometrical representations for temporal and relational structures in knowledge graphs, in: Machine Learning and Knowledge Discovery in Databases: Research Track, D. Koutra, C. Plant, M. Gomez Rodriguez, E. Baralis and F. Bonchi, eds, Springer Nature, Switzerland, Cham, (2023) , pp. 601–616. ISBN 978-3-031-43418-1. doi:10.1007/978-3-031-43418-1_36.
[33]	F.M. Suchanek, G. Kasneci and G. Weikum, Yago: A core of semantic knowledge, in: Proceedings of the 16th International Conference on World Wide Web, WWW’07, Association for Computing Machinery, New York, NY, USA, (2007) , pp. 697–706. ISBN 9781595936547. doi:10.1145/1242572.1242667.
[34]	Z. Sun, Z.-H. Deng, J.-Y. Nie and J. Tang, RotatE: Knowledge graph embedding by relational rotation in complex space, in: International Conference on Learning Representations, (2019) .
[35]	T. Trouillon, J. Welbl, S. Riedel, E. Gaussier and G. Bouchard, Complex embeddings for simple link prediction, in: Proceedings of the 33rd International Conference on Machine Learning, M.F. Balcan and K.Q. Weinberger, eds, Proceedings of Machine Learning Research, Vol. 48: , PMLR, New York, New York, USA, (2016) , pp. 2071–2080, https://proceedings.mlr.press/v48/trouillon16.html.
[36]	A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A.N. Gomez, L. Kaiser and I. Polosukhin, Attention is all you need, in: Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Curran Associates Inc., Red Hook, NY, USA, (2017) , pp. 6000–6010. ISBN 9781510860964.
[37]	D. Vrandečić and M. Krötzsch, Wikidata: A free collaborative knowledgebase, Communications of the ACM 57: (10) ((2014) ), 78–85. doi:10.1145/2629489.
[38]	X. Wang, S. Lyu, X. Wang, X. Wu and H. Chen, Temporal knowledge graph embedding via sparse transfer matrix, Information Sciences 623: ((2023) ), 56–69, https://www.sciencedirect.com/science/article/pii/S0020025522015122. doi:10.1016/j.ins.2022.12.019.
[39]	Z. Wang, D. Ding, M. Ren and M. Conti, TANGO: A temporal spatial dynamic graph model for event prediction, Neurocomputing 542: ((2023) ), 126249, https://www.sciencedirect.com/science/article/pii/S0925231223003727. doi:10.1016/j.neucom.2023.126249.
[40]	Z. Wang, J. Zhang, J. Feng and Z. Chen, Knowledge graph embedding by translating on hyperplanes, in: Proceedings of the AAAI Conference on Artificial Intelligence 28(1), (2014) , https://ojs.aaai.org/index.php/AAAI/article/view/8870. doi:10.1609/aaai.v28i1.8870.
[41]	C. Xu, Y.-Y. Chen, M. Nayyeri and J. Lehmann, Temporal knowledge graph completion using a linear temporal regularizer and multivector embeddings, in: Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, K. Toutanova, A. Rumshisky, L. Zettlemoyer, D. Hakkani-Tur, I. Beltagy, S. Bethard, R. Cotterell, T. Chakraborty and Y. Zhou, eds, Association for Computational Linguistics, Online, (2021) , pp. 2569–2578, https://aclanthology.org/2021.naacl-main.202. doi:10.18653/v1/2021.naacl-main.202.
[42]	C. Xu, M. Nayyeri, F. Alkhoury, H. Shariat Yazdi and J. Lehmann, TeRo: A time-aware knowledge graph embedding via temporal rotation, in: Proceedings of the 28th International Conference on Computational Linguistics, D. Scott, N. Bel and C. Zong, eds, International Committee on Computational Linguistics, Barcelona, Spain (Online), (2020) , pp. 1583–1593, https://aclanthology.org/2020.coling-main.139. doi:10.18653/v1/2020.coling-main.139.
[43]	C. Xu, M. Nayyeri, F. Alkhoury, H. Yazdi and J. Lehmann, Temporal knowledge graph completion based on time series Gaussian embedding, in: The Semantic Web – ISWC 2020, J.Z. Pan, V. Tamma, C. d’Amato, K. Janowicz, B. Fu, A. Polleres, O. Seneviratne and L. Kagal, eds, Springer International Publishing, Cham, (2020) , pp. 654–671. doi:10.1007/978-3-030-62419-4_37.
[44]	B. Yang, S.W.-T. Yih, X. He, J. Gao and L. Deng, Embedding entities and relations for learning and inference in knowledge bases, in: Proceedings of the International Conference on Learning Representations (ICLR) 2015, (2015) , https://www.microsoft.com/en-us/research/publication/embedding-entities-and-relations-for-learning-and-inference-in-knowledge-bases/.
[45]	D. Zhang, W. Feng, Z. Wu, G. Li and B. Ning, CDRGN-SDE: Cross-dimensional recurrent graph network with neural stochastic differential equation for temporal knowledge graph embedding, Expert Systems with Applications 247: ((2024) ), 123295, https://www.sciencedirect.com/science/article/pii/S095741742400160X. doi:10.1016/j.eswa.2024.123295.
[46]	F. Zhang, Z. Zhang, X. Ao, F. Zhuang, Y. Xu and Q. He, Along the time: Timeline-traced embedding for temporal knowledge graph completion, in: Proceedings of the 31st ACM International Conference on Information & Knowledge Management, CIKM’22, Association for Computing Machinery, New York, NY, USA, (2022) , pp. 2529–2538. ISBN 9781450392365. doi:10.1145/3511808.3557233.
[47]	S. Zhang, Y. Tay, L. Yao and Q. Liu, Quaternion knowledge graph embeddings, in: Advances in Neural Information Processing Systems, H. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. Fox and R. Garnett, eds, Vol. 32: , Curran Associates, Inc., (2019) , https://proceedings.neurips.cc/paper_files/paper/2019/file/d961e9f236177d65d21100592edb0769-Paper.pdf.