When one logic is not enough: Integrating first-order annotations in OWL ontologies

1.Introduction

The landscape of applied ontology contains a rift. The vast majority of ontologies that are used in computational systems are written in OWL, more specifically OWL 2 DL or OWL language profiles, which are essentially sublanguages of OWL 2 DL.11 However, the authors who work on the foundational topics of applied ontology, such as upper level entities and their axiomatisations, typically do not use OWL. For example, in 2020 and 2021 the Formal Ontology in Information Systems conferences accepted altogether 19 papers on foundational topics. Of those, none used OWL as a representational language.

The reason for this language rift is easy to explain. The OWL Manchester Syntax is relatively easy to learn for domain experts, and there is an increasing number of widely available tools supporting development of ontologies in the OWL language. Furthermore, OWL is based on the description logic SROIQ and, thus, satisfiability of OWL ontologies and logical inference with OWL ontologies are decidable decision problems. Both factors are major advantages for anybody who develops a domain ontology in cooperation with domain experts and intends to use automatic reasoning (e.g., using consistency checks for quality control). However, the advantages come with a price: in order to improve readability and achieve decidability one needs to sacrifice expressivity. Consequently, many ontological differences that are studied by foundational ontologists are not expressible in OWL. E.g., part-whole relationships are a staple of most ontologies and have been extensively studied by foundational ontologists. However, in OWL 2 DL it is even impossible to axiomatise proper parthood as strict order, let alone represent interesting distinctions between different mereologies [18]. Hence, foundational ontologists typically use first-order logic (FOL) or even more expressive logics as representational languages. Consequently, the vast majority of papers on foundational ontology contain axioms and definitions that cannot be directly reused by the ontologies that are used in practice in information systems. The language rift thus prevents theoretical results and insights from achieving their full impact in benefiting downstream practical applications.

A particularly interesting case are upper level ontologies, which aim to provide a reusable framework for the development of domain ontologies. There are a number of different upper level ontologies [5], which reflect a wide range of philosophical points of view. Most widely used is the Basic Formal Ontology (BFO), which is used by more than 250 ontology projects. BFO is grounded in a rich Aristotelian tradition, is described in numerous publications, a user guide, and a textbook, and most recently it has even been standardised by the International Organization for Standardization as ISO/IEC 21838-2:2021. However, the version of BFO that is actually used in most information systems is BFO 2.0 OWL, which contains exactly 52 axioms, more precisely 18 disjointness axioms and 34 subsumption axioms between atomic classes. Interestingly, BFO 2.0 OWL contains annotations that include additional axioms in the Common Logic Interchange Format (CLIF), a variant of FOL,22 which provide a much richer logical axiomatisation than the OWL axioms. However, since OWL reasoners ignore annotations, these axioms are computationally inert; they only serve as documentation for the human readers. In summary, while there is a rich literature on BFO, almost none of it is materialised in the format that is actually used by domain ontologies. From a logical point of view, BFO 2.0 OWL is just a simple taxonomy with a few additional disjointness axioms. Consequently, the developers of domain ontologies cannot use OWL reasoners or other automatic reasoners to check whether their ontology actually conforms to BFO.

The goal of this paper is to present Gavel33 and its OWL-specific extension Gavel-OWL,44 tools that were developed to bridge the language rift by enabling ontology developers to develop heterogeneous ontologies that contain both FOL and OWL axioms, and supports reasoning with the integrated model. One major benefit of Gavel and Gavel-OWL is that it does not require developers of applied ontologies to make any changes to their established workflow for OWL ontologies: developers can continue to use the same tools (e.g., Protégé) to develop their ontologies, and use standard OWL reasoners to reason with the OWL part of the ontology. Gavel-OWL merely offers the additional option to enhance an OWL ontology with FOL axioms. These additional axioms may be based on a foundational ontology, but they may also be domain-specific axioms that are expressible in FOL but not in OWL.

In Section 2 that follows, we discuss the requirements for Gavel-OWL and our approach for addressing them. The capabilities of Gavel-OWL and its implementation are presented in Section 3. Afterwards, we discuss in Section 4 the merits of the approach by first showing how Gavel-OWL overcomes some limitations of OWL that have been discussed in the literature, and then we consider two case studies. In the first, we will show that BFO CLIF axioms may be used to find errors in an BFO-based OWL domain ontology. In the second, we extend a large domain ontology with FOL axioms and illustrate how automatic theorem proving with the heterogeneous ontology yields new subsumptions that an OWL reasoner on its own is not able to detect. In the remainder of the paper we discuss related work, the significance and potential impact of the approach.

2.Requirements and approach

Our goal is to enable ontology developers to benefit from the advantages of OWL, including its user friendly syntax, decidability, and mature tool chain, without having to forego the ability to use the greater expressivity of FOL when it is required, or when a preexisting FOL ontology is available.

Thus, a FOWL ontology consists of two components, an OWL component and a FOL component, which extends the OWL axioms with additional axioms in FOL. To achieve this goal our solution ideally should meet the following requirements:

Our approach for meeting these requirements is to create a combined OWL and FOL ontology through annotations in OWL ontologies. Thus, in some sense, we follow the precedent set by BFO 2.0 OWL, which is also an OWL file that contains FOL annotations. However, while in BFO 2.0 OWL the FOL annotations are logically inert, Gavel-OWL enables automatic reasoning with the logical theory that is the result of combining the OWL axioms with the FOL axioms.

More specifically, a FOWL ontology is an OWL file where all values of AnnotationAssertion axioms which have a special annotation property are interpreted as FOL axioms. This special annotation property (or a set of such properties) may be customly defined. Hence, the heterogeneous ontology is represented in a syntactically valid OWL file and the OWL part of the ontology may be processed by standard OWL tools, because the FOL annotations do not influence the ontology’s OWL semantics.

Fig. 1.

View of an annotated OWL entity in Protégé.

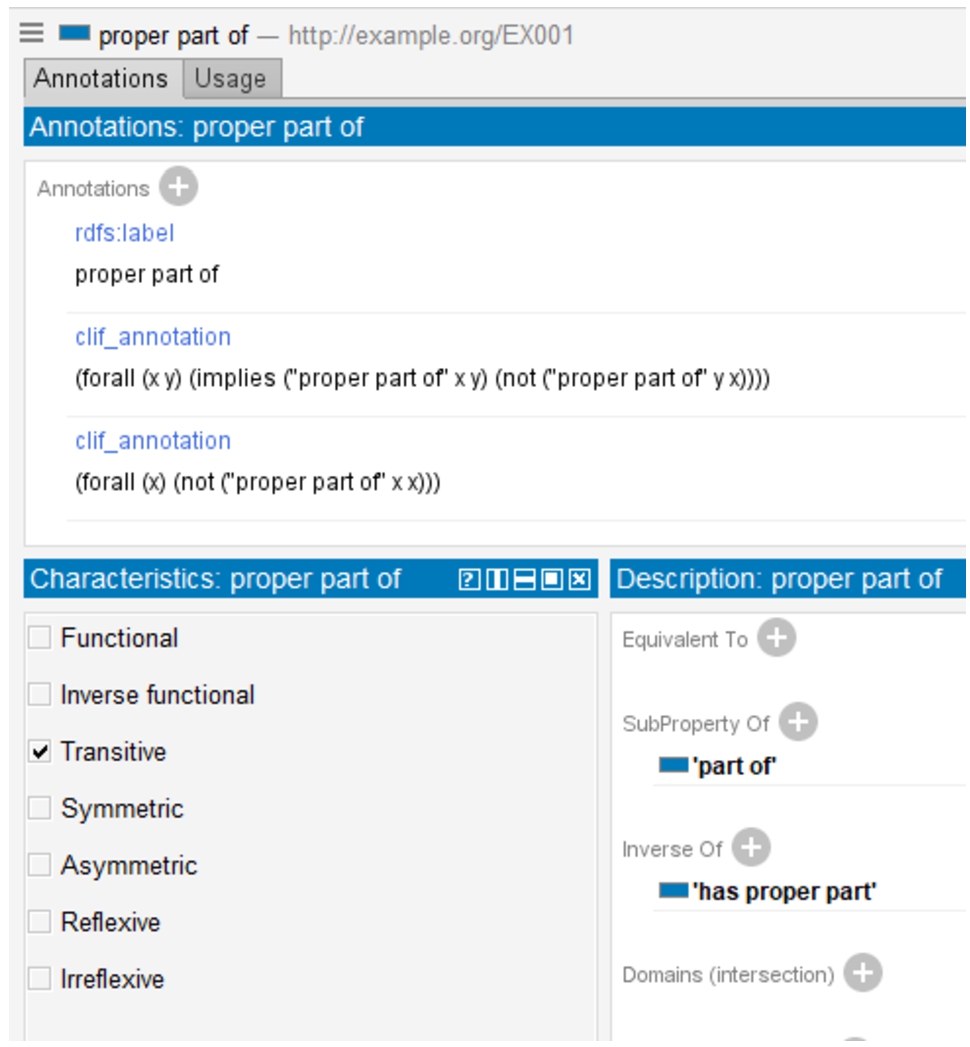
As they are stored in annotation values, the FOL axioms also remain closely connected to the OWL axioms: typically, all axioms for a given subject entity are grouped together. For instance, Fig. 1 shows how Protégé displays annotations and logical OWL axioms for the entity proper part of. The FOL axioms can be seen in the upper part and the OWL axioms in the lower part. Thus, a user is able to view related FOL and OWL axioms on the same screen.

Gavel-OWL supports two different syntaxes for FOL annotations: CLIF and TPTP. CLIF is a human readable syntax for ISO Common Logic [16].55 The TPTP syntax is widely used in the automatic theorem proving community, in particular the TPTP problem library [32,33]. To increase the readability of TPTP, we do not use complete TPTP axioms, but only their formula part. E.g., we write

     ![X] ~ ’proper part of’ (X,X)

instead of the full TPTP expression

    fof(axiom_name, axiom, (![X] ~ ’proper part of’ (X,X))).

Reasoning with a FOWL ontology requires the integration of its OWL component with its FOL component. This is done by translating the OWL axioms into FOL (in TPTP syntax) and integrating them with the FOL axioms from the annotations66 as well as, potentially, additional axioms from a background theory. The result is a FOL ontology in TPTP syntax, which can be used for automatic reasoning and consistency checking. To enable these automated consistency checks, Gavel is able to interact with the theorem prover Vampire [20]. Furthermore, Gavel features a dynamic extension scheme that allows for the integration of other logics through new plugins. We present here Gavel-OWL, which allows the integration of first-order logic and OWL. Other ontologies may also use logics for annotation, such as typed logics or higher order logics. These can then be connected to Gavel by separate plugins similar to Gavel-OWL and to use the same proof pipelines described in this submission.

One obstacle for the integration of OWL axioms and FOL annotations is that it is necessary to map their signatures. E.g., in the example in Fig. 1 an OWL entity, more specifically an object property, is annotated with a CLIF axiom. The OWL and the FOL axioms together specify proper parthood as strict partial order. (This could not be axiomatised in OWL 2 DL, since the axiom would violate its global restrictions.) However, strictly speaking, the OWL axioms are about the entity uniquely identified by a long IRI (namely, http://purl.obolibrary.org/obo/BFO_0000175), which is then annotated with the literal ‘proper part of’^^xsd:string as label, while the CLIF axioms are using neither the OWL IRI nor the exact label of the OWL entity, but the CLIF name “proper_part_of”. This is indicative of a typical problem. IRIs are often too long to be conveniently typed by humans. Thus, one cannot expect the FOL annotations to include the complete IRIs that are used to identify an OWL entity. Further, following recommended best practices [22], many OWL ontologies contain IRIs that consists of arbitrary alpha-numeric identifiers. Thus, they are not human-readable.

Hence, Gavel-OWL attempts to automatically match the OWL and FOL signatures. If a FOL name does not match an IRI exactly, it looks for the IRI-suffix or label which is closest to the FOL symbol (according to the Levenshtein distance). While this enables users to use CLIF names similar to OWL labels in most cases, they can fall back to complete IRIs where resolution fails (e.g., in an ontology where two entities are annotated with the same label).

All in all, our methodology provides a practical, user-friendly approach to combining the advantages of both OWL and FOL: By keeping the main part of the ontology in OWL and only adding FOL axioms as annotations, the ontology can be used as a standard OWL ontology. This means that developers can make use of the existing tools and reasoners, and benefit from their familiarity with the language. The FOL annotations can then be added to extend the ontology with axioms that are not expressible in OWL, increasing the possibilities developers have for modelling their domain as accurately as possible and allowing the integration of FOL upper level ontologies. Reasoning support for the complete ontology is ensured by Gavel-OWL via translating into a unified FOL theory.

3.Capabilities and implementation

To achieve its objective of supporting the development of heterogeneous ontologies that consist of an OWL file with FOL annotations (either in CLIF or TPTP syntax), Gavel-OWL has the following capabilities:

The Gavel-OWL implementation builds on two pre-existing components. First, the OWL API [13]77 is an open source Java library for working with OWL ontologies. It has originally been developed by the University of Manchester and is currently maintained by Matthew Horridge and Ignazio Palmisano. We use it for parsing OWL ontologies and extracting FOL annotations. Since the OWL API is a Java library, Gavel-OWL includes a Java Server that handles the interaction with the OWL API and contains large parts of the OWL-related logic. It is connected to the application’s Python part via Py4J.88 Second, Macleod99 is a Python tool for working with ontologies written in the CLIF syntax, created by Torsten Hahmann [10]. We use it to translate CLIF annotations into TPTP syntax.

Figure 2 illustrates the implementation of the main functionality of Gavel-OWL, namely the translation of an OWL ontology (possibly with FOL annotations) to FOL. In the case of an OWL ontology without any FOL annotations the following things happen: First, it parses the OWL ontology using the OWL API. This includes the content from files imported into the ontology via import-statements. Subsequently, the ontology is translated into FOL. Optionally, IRIs are replaced with more readable names. The translation from OWL to FOL, previously described in [7], is based on the OWL Direct Semantics [14] and uses a mapping []qp between OWL and FOL expressions.1010 This mapping is defined for each basic type of OWL axiom or expression and is then applied recursively on more complex axioms. In doing so, the parameters p and q are used to keep track of substitutions that have to be made and are left out if not needed. E.g., SubclassOf(Fish,Animal) would be translated as follows.

A FOL translation of a complete OWL ontology consists of the translations for each axiom combined with additional background axioms. These capture general assumptions of the Direct Semantics (e.g., the distinction between object and data domains) and the meaning of the OWL reserved vocabulary, such as owl: Nothing. These steps are implemented in the Java Server, because they build upon the OWL API functionality. Therefore, the resulting FOL axioms need to be transferred back to the Python OWL Parser and transformed into Gavel’s internal representation. This representation is then used by Gavel to compile it into a TPTP document, which gets returned to the user.

Fig. 2.

A UML activity diagram illustrating the process of translating an annotated OWL ontology or standard OWL ontology into TPTP. Actions that were newly implemented for the translation tasks are shown in yellow, actions that were reused from existing tools are marked in blue. For green actions, the existing functionality has been extended.

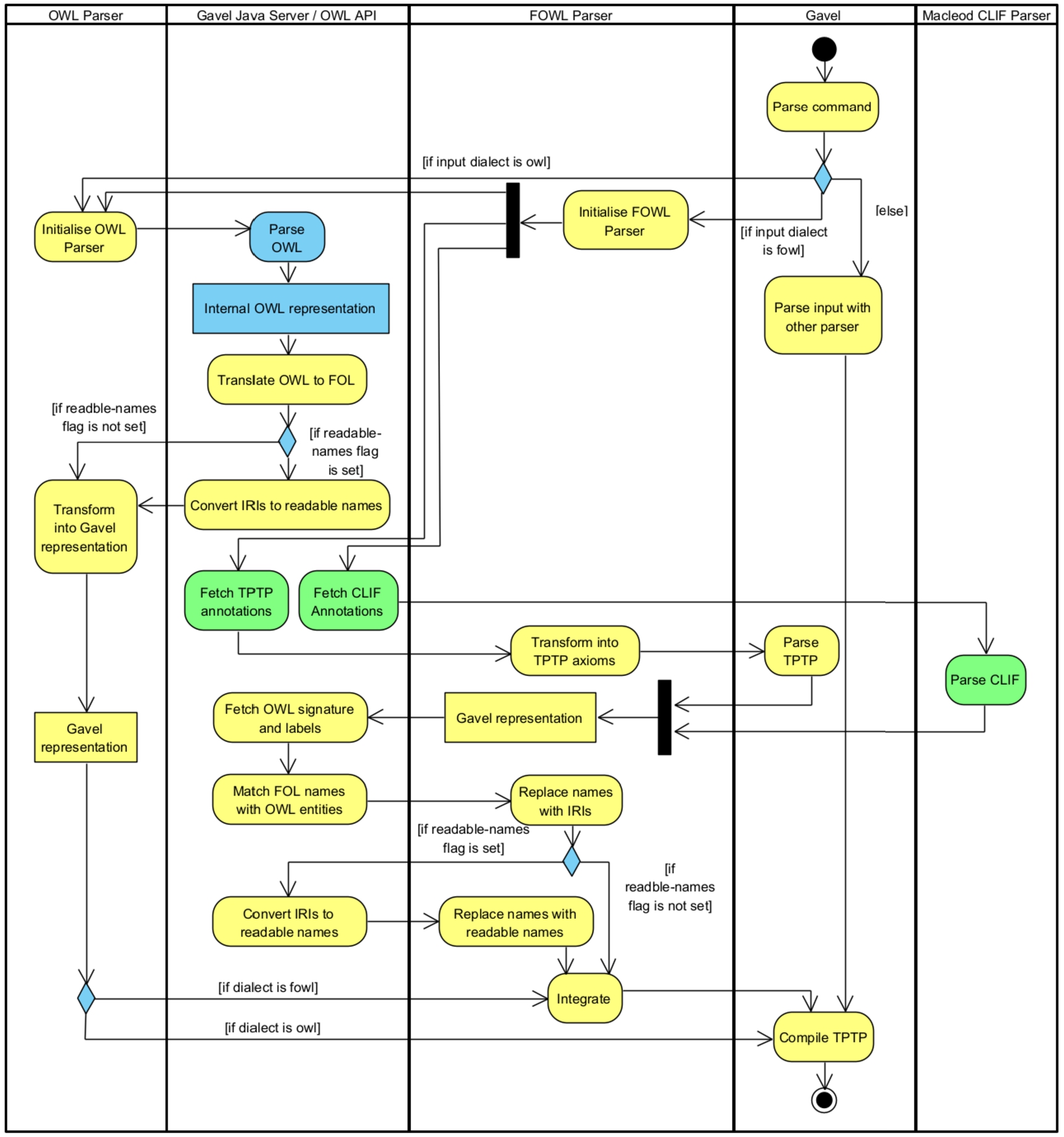
OWL files with FOL annotations are split into three parts. The OWL part of the ontology is translated into the internal FOL representation of Gavel as described above. TPTP annotations are extracted, turned into valid TPTP expressions and then parsed by Gavel. CLIF is parsed with the help of Macleod, which has been modified to return Gavel’s internal representation as well. In order to align the FOL signature with the OWL signature, the Java Server first fetches the OWL signature and rdfs:label-values and then maps them to the FOL names using the Levenshtein distance. If no close match is available, the name will be used as-is, making the assumption that there is no OWL entity to be found and that this name only appears in FOL axioms. Should several equally close matches exist, a warning is issued that the found match might not be the intended one. Based on this mapping FOL names are replaced with IRIs and in a second step, if required, with readable names. Finally, the FOL axioms from annotations are combined with the FOL translation of the OWL part, which also uses either IRIs or readable names, and compiled to TPTP, completing the translation process.

4.Evaluation and use cases

We aim to evaluate Gavel-OWL in use for ontology development. For this purpose, we first evaluate whether Gavel-OWL helps to overcome OWL restrictions that are ontologically significant in the following sense: Since Gavel-OWL enables reasoning with arbitrary FOL axioms, it also enables inferences with FOWL ontologies that an OWL reasoner would not be able to support. However, it is not obvious whether this additional expressivity is also useful for ontology developers. Thus, we evaluate the capability of Gavel-OWL based on examples from the literature in which the authors propose ontologically useful modelling patterns that cannot be expressed in OWL.

As mentioned in the introduction, one motivation for developing Gavel-OWL is to support a better integration of upper level ontologies with domain ontologies. Thus, as a second way to show the benefits of Gavel-OWL, we developed a new version of BFO that integrates OWL and FOL, and used it to check consistency of the Ontology for Biomedical Investigations (OBI) [3], a widely used ontology in the life sciences.

In another case study we show how domain-specific FOL axioms may be used to increase the quality of a domain ontology. For this purpose we extended the Chemical Entities of Biological Interest (ChEBI) ontology [12] with roughly 120 000 FOL axioms. Gavel allowed us to detect errors in ChEBI, which OWL reasoning alone was not able to detect. This example illustrates that even large domain ontologies may benefit from FOL axioms.

In a previous publication [7] we discussed the performance of the translation from OWL to TPTP (e.g., time per translated axiom). We found that even large ontologies may be translated in a reasonable amount of time (e.g., the Gene Ontology is translated in less than 30 minutes on a normal laptop). However, since there is no reason why one would translate the same large ontology regularly, performance may not be the most important metric.

4.1.Evaluation via ontologically useful inferences

For the purpose of this evaluation, we consider modelling patterns that have been identified in the literature as useful for ontology development, but which cannot be expressed in OWL. The first examples are mentioned in a paper by Schneider, Rudolph and Sutcliffe on a version of OWL 2 DL without global restrictions [30]. In order to show the advantages of their unrestricted OWL version, they provide 12 examples of modelling patterns that are useful but are not syntactically valid OWL 2 DL, since they violate its global restrictions. For each example they also provide a conjecture ontology, which is logically entailed according to the OWL Direct Semantics, but cannot be inferred by OWL reasoners because of the global constraint violation. For our purposes we replaced the OWL axioms that violate the DL restrictions with logically equivalent FOL annotations. Thus, the results are twelve pairs of ontologies, each pair consisting of a FOWL premise ontology representing a useful modelling pattern and an OWL conjecture ontology that is entailed by the premise ontology, but cannot be inferred by OWL 2 DL reasoners. In each of the 12 examples, Gavel-OWL is able to prove that the conjecture ontology is logically entailed by the FOWL premise ontology.

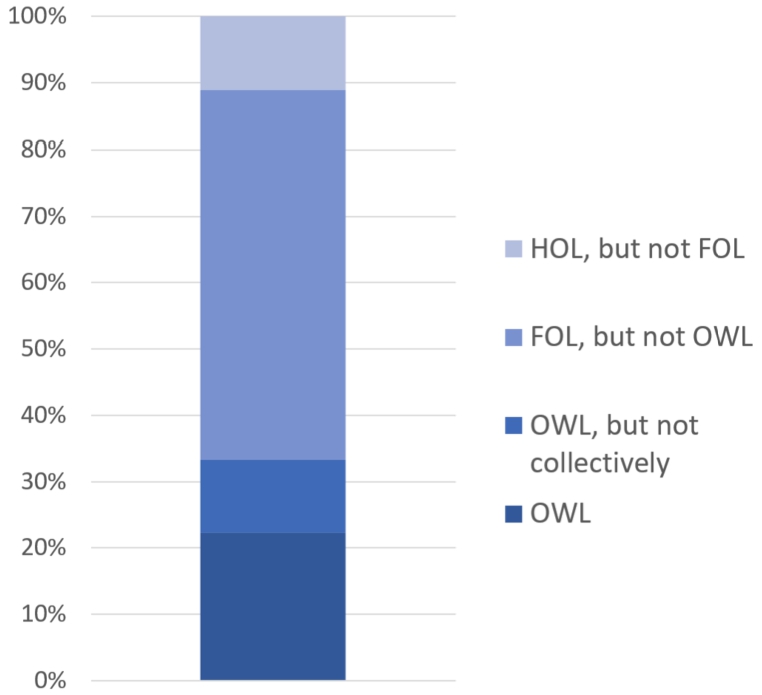
A second set of test cases has been derived from a paper by Keet et al. on mereotopological relations [18], in which the KGEMT mereotopological theory [1] is used to strengthen the axiomatisation of ontologies and thereby improve their accuracy. One of the challenges Keet et al. face is the limited expressiveness of OWL: Of the 27 definitions and axioms they identified in KGEMT only 9 can be fully represented in OWL 2 DL, and three of these can only be represented individually, but not collectively.1111

For the purposes of our evaluation, we can use the set of 27 axioms in [18] as a basis for generating test cases. Out of the 27 axioms, only three are not representable in FOL, instead requiring Higher Order Logic (HOL). Thus, nearly 90% of the axioms are representable in either OWL or FOL (see Fig. 3). The 15 axioms which are representable in FOL, but not in OWL, were used for creating test cases. An additional test case is based on the axioms which cannot be represented collectively in OWL, leading to a total of 16 test cases.

Fig. 3.

The shares of KGEMT axioms which can be represented in OWL, FOL and HOL respectively.

Listing 1.

The premise ontology of a test case based on a KGEMT axiom

Each test case consists of a FOWL premise ontology which consists mostly of OWL axioms but includes one of the KGEMT axioms as a FOL annotation, and an OWL conjecture ontology, which cannot be inferred by OWL reasoning from the premise ontology. For example, the premise ontology in Listing 1 contains OWL axioms that express that every part of OVGU is part of Magdeburg. Further, it includes a KGEMT axiom as a TPTP annotation, which states: for all x and y, if y (e.g., OVGU) is not part of x (e.g., Magdeburg), there has to be an instance z that is part of y, but does not overlap x. The conjecture ontology of this example states that OVGU is part of Magdeburg.

In each of the 16 test cases Gavel-OWL is able to prove that the conjecture ontology is entailed from the premise ontology. This result illustrates that though some axioms had to be left out because they are not representable in FOL, the axiomatisation of an ontology covering mereotopological concepts can become significantly stronger when using FOL annotations. More generally, the results of both test cases indicate our tool is working correctly and that it is able to integrate the FOL annotations and the ontology’s OWL part into a coherent logical theory that can be used for reasoning tasks. Further, they illustrate that the additional expressivity granted by FOL annotations may be used to address some of the limitations of OWL that have been discussed in the literature. All test cases can be found on the project’s GitHub page.1212

(forall (x) (if ("independent continuant" x)
                (exists (r) (and ("spatial region" r) ("located in" x r))))),

(has_specified_input some
    ((tissue and (’located in’ only brain))
        and (’has role’ some ’evaluant role’))),

4.3.Application to the chemistry ontology ChEBI

Sections 4.2 and 4.1 illustrate that FOL annotations enable users to extend OWL ontologies with axioms and reasoning tasks. However, all examples we considered so far involved only small FOWL theories. For the approach to be of benefit in the real world, it needs to scale. In order to evaluate whether large ontologies can benefit from our approach, we extended a widely used OWL ontology, namely the Chemical Entities of Biological Interest (ChEBI) ontology [12], with FOL annotations, which represent the chemical structures of molecules, given by SMILES annotations in ChEBI. In order to explain our process of creating the FOWL version of ChEBI, it is necessary to provide some background information.

ChEBI [12] is a freely accessible, open OWL ontology for biologically relevant chemical entities. This mainly includes substances that occur naturally in biological processes or synthetic substances that interact with these processes. Figure 4 shows an example of a ChEBI class with annotations. In addition to the molecular graph and textual descriptions and definitions, ChEBI contains a representation of the molecular class as SMILES specification. SMILES is a representation language that is specially developed for molecular entities, and it allows the direct linear serialisation of a molecular structure. ChEBI is the largest publicly available ontology for chemical entities and covers, as of March 2023, a total of more than 160,000 classes (across fully and semi-curated content). The maintenance and further development of such an ontology requires a large, heterogeneous team of ontology and domain experts. To facilitate this process, ChEBI allows third-party annotation and uses a special rule-based automatic classifier, ClassyFire [6]. However, ChEBI is generally quite weakly axiomatised and, to our knowledge, no symbolic methods beyond the standard OWL-DL reasoning are currently used to validate ChEBI.

Fig. 4.

The class nitrile as represented on the ChEBI website. The SMILES string [*]C#N specifies a molecule that contains a carbon atom (C) that is connected to nitrogen (N) via a triple bond (#) and some unspecified structure (*).

In initial experiments, we used an extension of ChEBI with an additional ontology that added some chemical background knowledge (e.g., that chemical elements are disjoint). Using Gavel we proved that the current version of ChEBI was, in fact, inconsistent with respect to these disjointness axioms. We therefore decided to investigate further and create a FOWL extension of ChEBI. To this end, we included additional FOL axioms that were automatically generated based on SMILES annotations. In the following, we will describe further how these axioms were generated and report the respective reasoning results thereafter.

For the purpose of this extended case study, we consider two different categories of classes of chemical entities in ChEBI. The first category contains classes that are associated with SMILES strings that contain unspecified parts. These unspecified parts are represented in the SMILES strings as ‘*’ and in the molecular graph as R, representing the attachment at a particular point of a group or sub-structural component. For example, the class Nitrile in Fig. 4 is incompletely specified, because the “*” might be replaced by a range of different structures – nitriles encompass a broad range of different chemical entities.

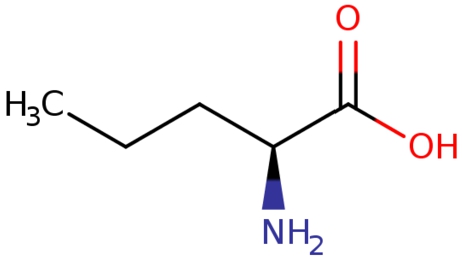
In contrast, there are classes of chemical entities whose structure is completely specified by their SMILES string. These classes occur primarily at the lowest levels of the ontological hierarchy and usually have no subclasses, and if they do, they represent stereoisomers, i.e. the subclasses only differ in spatial orientation around specific bonds and not in constituent structure. For example, L-2-aminopentanoic acid in Fig. 5 is fully specified, i.e. all molecules that instantiate this class have the same molecular structure. The difference between these two categories of classes is important, since they lead to different kinds of FOL axioms.

Fig. 5.

The class L-2-aminopentanoic acid, which had been wrongly axiomatised as a subclass of nitrile (which has now been corrected in ChEBI). It does not feature the required triple bond but a chiral structure in its place.

Classes that are associated with an incompletely specified SMILES specification (i.e. with a ‘*’) are typically classes that are defined via the presence of some substructure or structural part of the molecule. For example, Listing 2 shows part of an axiomatisation for the molecular class nitrile, automatically generated based on its SMILES annotation. (Note that the carbon atom that is bound to the nitrogen is explicitly represented.) Further restrictions have to be introduced for different predicates, like pairwise disjointness of atom classes (c, n, …), formal charges (has_no_charge, has_positive_charge_1, …) and bond types (has_single_bond_to, has_double_bond_to, …). In addition, the SMILES annotations of this category of classes – broader, higher-level classes within the ontology – often only provide an incomplete representation of the textual definitions available in ChEBI. For example, consider medium- and long-chain fatty acids (CHEBI:59554, CHEBI:15904). Their SMILES annotations are identical, but their definitions distinguish them by their respective chain lengths. Medium-chain fatty acids have chains that consist of at least 6 carbon atoms, but not more than 12. Long chains consist of at least 13, but less than 22 carbon atoms. Neither SMILES nor OWL DL can express such definitions. Another example not fully expressible in SMILES is classes that are not just defined by the presence but also by the absence of some substructures, since SMILES has no equivalent of negation. In some cases where we noticed that there were mismatches or omissions in the generated FOL class definitions, we adjusted the FOL axioms manually.

Listing 2.

First order axiomatisation for the molecular class nitrile

The formalisation of the second category of classes, i.e., the fully specified ones, is different in two ways. Since all instances of such a class have the same molecular structure, we represent them as a ‘prototypical instance’. Hence, their formalisations do not involve quantifiers but individuals, as can be seen in Listing 3. Note that the first part of this expression is the skolemised version of the formalisation that has been discussed for underspecified classes before. From a logical point of view, this is not necessary and we could treat fully specified classes like any other class. However, the representation as ‘prototypical instances’ improves the performance of automatic reasoning significantly as it prevents the reasoner from attempting unnecessary, costly unification steps. This may be a problem when a fully specified class has multiple instances, e.g. mixtures, quantities of matter and molecular interactions. In that case, we could not represent the instance of-relation between the instances and the fully specified class. However, these more complex classes are rare in ChEBI, and the potential issues do not affect our use case. In addition, since the SMILES specification is complete, we need to express that the given molecule contains no other parts than the ones explicitly mentioned in the axioms. Hence, the formalisation of these classes contains a formula of the form ![X]:partOf(X, mol) => (X=n1 | X=n2 | ...). For example, the FOL axiom for water (CHEBI:15377) is represented in Listing 3.

Listing 3.

First order axiomatisation for the ‘prototypical instance’ of water

Following these formalisations for our case study we extended ChEBI with more than 129,193 FOL annotations1717 and used these to validate ChEBI’s OWL axioms. For a detailed analysis, we selected a subset of ChEBI consisting of 80 incompletely specified classes and 6569 completely specified classes, each of which is represented by some ‘prototypical individual’. For each of these ‘prototypical individuals’ a and each incompletely specified class B, we created the conjecture B(a). Because a is structurally indistinguishable from all other members of its class, the conjecture is B(a) equivalent to the assertion that the class of a is a subclass of B.

We used Gavel and Vampire to attempt to prove these conjectures and compared the results to the transitive closure of subsumption relations in ChEBI. Assuming that all information in ChEBI is correct, a conjecture B(a) should only be provable from the FOL theory, if a⊑B is true in ChEBI. Furthermore, Vampire should only be able to find a counterexample, if a⊑B is not an axiom or theorem in ChEBI.

The experiments were conducted on a CPU cluster with 80 jobs, using 4 CPUs each. Each job focused on a single molecular class and attempted to prove membership of all 6569 instances individually, limited by a time-out of 30 seconds per proof. Each of the 80 jobs terminated within 24 hours, while 31.06% of all proof attempts were stopped by the time-out. Our experiments showed that the proof complexity scales directly with the complexity of the molecule class. Some complex classes, such as isoflavones (CHEBI:38757), exceeded the time-out of 30 seconds on all instances.

The results of the FOL reasoning can be distinguished into different categories based on expected and actual results (see e.g. [17]). While our findings from FOL reasoning are mostly consistent with the OWL axioms, there are two interesting categories for which this is not the case:

Unexpected proof	a⊑B is not an axiom in ChEBI. Yet, B(a) was provable based on the FOL annotations. This occurred in 10132 proof attempts (0.0279% of all proof attempts).
Unexpected counter-example	a⊑B is an axiom in ChEBI. Yet, Vampire refuted the conjecture B(a). This occurred in 256 proof attempts (0.0007% of all proof attempts).

Unexpected proofs are likely to originate from SMILES annotations that do not specify a class adequately. In these cases the FOL definitions that are automatically generated are too wide, which leads to unexpected proofs. Thus, each of these unexpected proofs is an indication that either a SMILES annotation in ChEBI is erroneous or that SMILES is not expressive enough to represent the definition of the class (for example, as mentioned above, because the class is partially defined by the absence of a feature). As discussed above, in some cases we addressed these unexpected proofs by changing the FOL definitions manually.

Unexpected counter-examples are candidates for inconsistencies in the underlying ontology. For example, the molecule in Fig. 5 was classified in ChEBI as a nitrile even though it has a single bond between the carbon atom and the nitrogen atom and not the triple bond required for nitriles. We reported this finding to the ChEBI developers and it has been acknowledged as an error and fixed in the ontology.1818

This case study illustrates that FOL annotations may be used to represent knowledge in a large domain ontology; and that reasoning with these FOWL ontologies may be successfully used to identify errors. In the future we will study the performance of reasoning with FOWL ontologies more systematically.

5.Related work

There are several approaches on extending the expressivity of OWL ontologies that are closely related to our work. In [30] Schneider et al. present 12 useful modelling patterns that are not expressible in OWL 2 DL, because they violate its global restrictions (e.g., axiomatising an object property as strict partial order). For evaluation purposes these modelling patterns are implemented in OWL ontologies and also translated into FOL. Their experiments show that, while all of the OWL reasoners failed on these test cases, the FOL reasoners were able to draw the desired inferences. Hence, the authors illustrated the feasibility to FOL reasoning for OWL ontologies. However, [30] only considers ontologies that consist of OWL constructs, while our work enables the use of arbitrary FOL annotations as part of OWL ontologies. In that sense our work is more general.

Another important strategy to extend the expressivity of OWL is by adding rules. This is supported by the W3C recommendation Rule Interchange Format (RIF) [19], which supports a variety of dialects based on different logics (e.g., Horn Logic or Datalog), but none of them supports full FOL. Significantly older, but influential is SWRL [15], which combines the OWL and OWL Lite sublanguages with features of the RuleML [4]. It uses Horn-like rules in the form of implications between an antecedent called the body and a consequent called the head. Because OWL with SWRL rules is not decidable, Motik et. al. [27] suggest an alternative, which combines OWL DL with DL-safe rules. These are, roughly speaking, function-free Horn rules, where variables are bound only to named individuals. DL-safe rules have the advantage of decidability and are supported by OWL reasoners such as HermiT. Even though the combination of OWL with SWRL or DL-safe rules has a higher expressivity than OWL, it does not provide the same expressivity as FOL. For this reason it was proposed to extend SWRL by arbitrary FOL axioms [29]. However, as far as we are aware, this proposal has never been implemented.

The Distributed Ontology, Modeling, and Specification Language (DOL) [25,28] is an Object Management Group (OMG) specification, which – among many features – supports the representation of heterogeneous ontologies and translation between ontology languages. DOL is implemented by Hets [24,26] and supports, in particular, OWL, CLIF, and TPTP. Thus, many capabilities of Gavel are also provided by Hets. However, a major difference is the fact that DOL/Hets assumes that a heterogeneous ontology is composed of different sub-ontologies which are written in only one language, e.g., a DOL ontology might import an OWL file and a separate CLIF file. This solution is inconvenient for ontology developers, since the heterogeneous ontology might not be edited by established editors like Protégé and axioms concerning one entity might be spread over different files. Further, Gavel provides the capability to automatically align the signatures of the various ontologies. Another difference is that Gavel is implemented in Python and is more lightweight than Hets.

So far we have discussed approaches that start out with OWL DL and consider possibilities to extend it. In [10] the gap between OWL and FOL ontologies is bridged in a different direction; i.e., based on a given FOL ontology Macleod generates an OWL ontology. This is achieved, roughly speaking, by translating FOL-axioms into a function-free prefix normal form first and then matching the results against templates that correspond to OWL axioms. This process is ‘lossy’ in the sense that a generated OWL ontology will, typically, contain less information than the FOL ontology it is based on. However, the fragment of the FOL ontology that is successfully translated into OWL may be integrated with other OWL ontologies and used for OWL reasoning. This approach is complementary to our work and both could be combined; e.g., by first translating an OWL ontology and its FOL annotations into FOL with FOWL and afterward extracting an OWL ontology with Macleod. However, because Macleod extracts only OWL axioms that correspond to one of its templates, there is no guarantee that the axioms of the original OWL ontology would be preserved in this ‘roundtrip workflow’. For example, axioms with object property cardinality restrictions would be translated to FOL by FOWL, but would not be extracted by Macleod, since Macleod does not support them.

6.Importance, impact and conclusions

As discussed in Section 1, the field of applied ontology is divided by a language barrier. Since ontologists who work on foundational issues typically prefer more expressive languages than OWL, the result of their research cannot be directly applied to ontologies that are written in OWL – which includes the vast majority of all domain ontologies. In particular this is illustrated by the fact that top-level ontologies such as BFO and DOLCE are represented primarily in FOL, but the versions that are actually used by domain ontologies are in OWL. Thus, so far it was not possible to check whether these domain ontologies actually conform to their top-level ontology.

Gavel is designed to help ontology developers to bridge the divide, since it enables the development of FOWL ontologies, i.e., OWL ontologies with FOL annotations. In Section 4 we have illustrated our approach by validating the Ontology for Biomedical Investigations (OBI). OBI is a relatively small (about 5000 entities), but widely used ontology,1919 which uses the (OWL version of) BFO as its top-level ontology. By combining OBI with FOL annotations that were derived from FOL annotations published as part of BFO 2.0 OWL, we were able to detect several inconsistencies.This method of evaluation is not limited to OBI, but is applicable to any of the more than 250 domain ontologies that use BFO as their top-level ontology. By creating analogous FOWL versions of other top-level ontologies, the same strategy may be applied to them as well.

Furthermore, we discussed how Gavel is able to reason with a FOWL ontology that extends an OWL ontology with complex mereological axioms. Mereology is one of the best studied areas in applied ontology, but OWL is not expressive enough to represent many mereological distinctions. This example illustrates that Gavel enables ontology developers to enhance OWL ontologies with the results of research on foundational ontologies.

The benefit of reasoning with FOWL ontologies with Gavel is not limited to the integration of foundational and domain ontologies. As our third use case illustrates, FOL annotations may be fruitfully used to express domain knowledge, which cannot be expressed in OWL – even in the case of very large ontologies such as ChEBI. By applying automatic reasoning we were able to detect a number of potential problems in ChEBI, of which we reported two and these have already been fixed by the ChEBI developers. A surprising result is the fact that FOL reasoning with ChEBI is a viable option, even though ChEBI is a very large ontology. Obviously, there were time-outs, but majority of proof attempts returned a result and, thus, illustrated the usefulness of the approach.

In conclusion, in this paper we have shown the benefits of FOWL ontologies and presented the tool Gavel, which is able to support reasoning with these heterogeneous ontologies. Since these ontologies are syntactically valid OWL ontologies, using these annotations does not break existing tool chains, and, thus, the barrier for using this approach is low.

In the future we are planning to extend our approach from FOL to higher-order logic. This would enable us to cover the mereological axioms in [18] that we had to exclude from our evaluation in Section 4. Further, there are definitions of chemical classes that require monadic second-order logic [21].

Another area we are planning to explore is the development of a more densely axiomatised BFO FOWL ontology. For the purposes of this paper we have mainly considered axioms that have been derived from the FOL annotations that are already present in BFO 2.0 OWL. However, these axioms are relatively sparse and could be significantly improved. In combination with Gavel this would enable a better validation of domain ontologies that are based on BFO.

Further, we are planning to integrate our workflow for a logical evaluation of chemical subclass relationships with our work on automatic ontology extension [8,11,23]. In these works we used machine learning techniques to predict for a given unknown chemical molecule its suitable classification in ChEBI. From a logical point of view, we trained models that – when provided with the structure of a chemical molecule – are able to generate OWL subsumption conjectures. We have already used OWL disjointness axioms to check for some errors in these conjectures. In the future we are planning to use FOL annotations of ChEBI to further automatically validate these conjectures with logical reasoning.