OMTPlan: A Tool for Optimal Planning Modulo Theories

1.Introduction

AI Planning can be defined as the model-based approach to intelligent behaviour, where a model of the world and of possible actions to be performed is used to decide on a sequence of actions, a plan, that brings the world to a desired state [6].

Satisfiability Modulo Theories (SMT) [2] and its extension Optimization Modulo Theories (OMT) [17] are two powerful frameworks that have been used to model, and reason about, expressive planning problems. While SMT technology has long enjoyed popularity within the planning community, the application of OMT to planning has remained unexplored until recently. In [11] we introduced the first domain-independent reduction from optimal planning to OMT solving. More specifically, we presented an OMT-based algorithm to solve optimal numeric planning problems where actions are equipped with unitary (all actions have cost 1), constant (actions have constant costs ⩾1) or state-dependent action costs (SDAC), where the cost of executing an action is a function of the state where it is executed [9]. Notably, no tool support exists for integrated reasoning on problems of the latter class and state-of-the-art (SoA) planners either do not support SDAC upfront, e.g. [14], or solve them with uninformed search, a general class of search algorithms that explore the solution space of a planning problem ignoring domain specific knowledge such as cost structures, e.g. [12].

The present contribution is intended to fill this gap as we introduce OMTPlan, the first planner that leverages state-of-the-art satisfiability techniques to solve optimal planning problems in the presence of rich cost structures. OMTPlan is implemented in Python and presents a modular architecture that can be easily extended with new functionalities. Besides offering solving capabilities, OMTPlan can also act as a translator from PDDL [5], the standard language of planning, to SMT-LIB [1] thus providing a new source of challenging benchmarks for the automated reasoning community – see, e.g. [3] for such an application of the tool. The planner is open-sourced under a GNU General Public License, version 3 (GPL-3.0). Source code and the related documentation are available online at: https://github.com/fraleo/OMTPlan.

2.System Architecture

OMTPlan realises its functionalities through the interaction of the components represented in Fig. 1. Each component takes care of different phases of the planning process as detailed in the following.

Figure 1.

OMTPlan: internal work-flow.

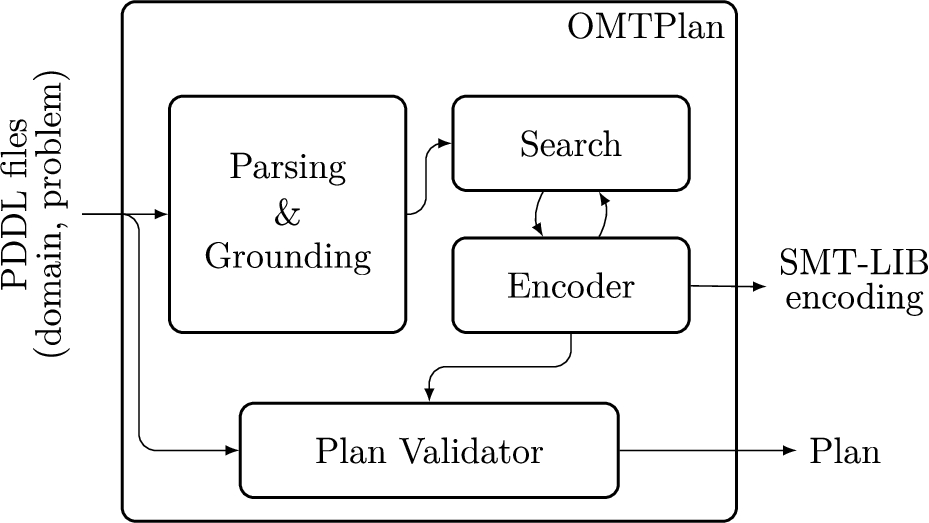
Input Language. OMTPlan accepts problems specified in the Planning Domain Definition Language (PDDL), the de-facto standard language for planning. Dialects of PDDL exist with different expressive power, here we focus on PDDL 2.1 level 2 [5] as it allows to capture rich numeric structures. PDDL describes a planning task by means of: (i) a domain file containing the description of general features of the problem (e.g. the available actions) and, (ii) a problem file defining instance-specific information (e.g. the initial and goal situation, the optimisation metric). We refer to [5] for more details on PDDL.

Parsing and Grounding. We leverage the Python parsing module developed for the Temporal Fast-Downward (TFD) planner.11 The original implementation does not provide support for the specification of arbitrary metrics for plan quality. Hence, we extended it to support metrics expressed in quantifier-free linear real arithmetic (QFLRA), as supported by our approach [11].

Besides parsing operations, this module is also responsible for grounding the first-order representation used in PDDL. The grounding algorithm of TFD makes use of a compilation to a logic program in order to perform reachability analysis and grounding all in one [8]. This compilation is specific to both the set of action schemas and the initial state of the search. The reachability analysis is able to infer if certain ground actions will never be applicable when starting from the given initial state, and that some variables will never actually change their value, i.e. they are seen as static facts. As a result, ground actions that are not applicable are pruned and static variables are compiled away and do not need to be represented with variables in the planning formula.

Search. OMTPlan computes plans by progressively unrolling the transition system induced by the planning problem, as commonly done in Planning as SAT [15]. Given a planning problem Π, we build formulas Πn for unrolling of increasing number of steps n until a plan is found, or a user-defined upper bound is reached. This module is responsible for implementing the logics according to which the unrolling is performed. OMTPlan implements common strategies such as linear (n=1,2,3,…) and exponential (n=1,2,4,…) increment; however custom strategies can be easily implemented.

Once a search strategy has been selected, this module schedules calls to the encoder to produce unrollings of different length. These are dispatched and tested sequentially, although other strategies could be added. The search module is also responsible for feeding the planning formula to the underlying solver, fetching the result of the satisfiability check and act accordingly.

Encoder. The main task of this module is to traverse the parse tree produced by the parsing module and build the planning formula encoding the unrolling for the length selected by the search module. In the current implementation the user can choose between:

Encodings (1) are based on the classical state-based representation of Planning as SAT [15], here extended to numeric variables. Both the parallel and serial execution semantics for actions are supported. The former allows for multiple actions to be executed in parallel provided they act on different subsets of variables; the latter only allows for serial plans where at most one action can be executed per step.

Encodings (2) combine serial encodings with a linear increment strategy to enable optimal planning with unitary costs. An optimal plan in this setting is one which contains the minimum number of actions. If Π0,…,Πn−1 are unsatisfiable and Πn has a solution, then an optimal plan is found and has cost n.

The OMT encodings (3) instead are the most general and extend OMTPlan’s capabilities to perform optimal planning under constant and state-dependent action costs alike. Optimisation objectives are defined as pseudo-boolean expressions for problems with unitary costs and QFLRA expressions for the other cases.

All the encodings above combine elements of the standard Planning as SAT encoding with novel abstraction techniques we presented in [11]. Building on these results, OMTPlan is able to (i) detect efficiently if a goal is not reachable without requiring any unrolling the transition system and (ii) provide a new sufficient condition for determining whether a plan is a global optimum for the planning problem. The latter feature is crucial when dealing with SDAC, as plans with the least number of actions are not necessarily cost-optimal. When a locally optimal solution is found for Πn, proving that this is also a global optimum would require checking that longer unrollings do not yield better plans, for all unrollings of length greater than n. We overcome this challenge by extending the classical encoding with (i) a boolean abstraction that disregards concrete numeric effects and allows to reason on unbounded executions and (ii) loop formulas [13] which enforce a notion of optimality in the abstracted boolean space. Due to space constraint we cannot report all the details of our encoding here; we kindly refer the reader to [11] for that.

Finally, this module also allows to export SMT-LIB encodings [1] of planning formulas. This functionality serves two different purposes:

Validation. When a plan is found, the validation module is called to check its correctness against the PDDL domain and problem files. To this end, a plan is extracted from the model of the planning formula and converted back into PDDL syntax. The validation task is then performed by the plan validator VAL,22 which checks whether the plan complies with the PDDL description of the problem. If a plan is deemed valid, it is passed on to the main routine for subsequent operations. Otherwise, OMTPlan reports a failure.

3.Experimental Evaluation

We demonstrate the capabilities of OMTPlan on optimal numeric planning problems taken from the literature [11,12,16]. The benchmarks include simple domains, where numeric effects of actions are restricted to assignments to constant values, and linear ones, where effects can be described by linear expressions. All instances are satisfiable, i.e. they admit a valid plan.

The current implementation of OMTPlan relies on Z3/νZ [4] to construct and solve planning formulas.33 However other OMT solvers could be used for the latter step via a compilation to SMT-LIB.

We test the three configurations of our planner that support optimal planning, namely:

We compare44 OMTPlan against two state-of-the-art numeric planners: ENHSP [16], based on A∗ search [7], and CSC, based on a reduction to MILP [14]. We report the number of instances solved for each domain (coverage) and the corresponding solving time.

We run our experiments using a 30 minute timeout and 4 GB memory limits on a machine running Debian 3.16 with processor Intel(R) Xeon(R) CPU E5- 2640 v4 @ 2.40 GHz.

Table 1 shows coverage and total solving time for simple numeric domains with unitary costs. CSC appears to be the most effective tool at solving this class of problems, being able to solve the largest number of instances in the least total time. ENHSP and SMT-s follow, with the former yielding better performance on domains that feature long plans (i.e. requiring many actions) that force OMTPlan to construct large encodings (e.g. Sailing). On the other hand, SMT-s outperforms ENHSP on domains admitting shorter solutions. OMT encodings do not show their full potential here: simple numeric problems with unitary costs require limited optimisation capabilities; however, this is not detected by the OMT solver which resorts to expensive optimisation procedures that may result in an unnecessary overhead.

Table 2 shows the results obtained for linear numeric domains with unitary, constant (-Metric) and state-dependent (-SDAC) costs. These experiments show a completely different picture from what is observed for simple domains. The increased expressivity of these problems poses a considerable challenge to CSC and ENHSP. OMTPlan-p, on the other hand, is able to harness the power of the underlying SMT/OMT technology to handle this added expressivity and proves to be effective. This is particularly evident in domains that feature a high-degree of parallelism, which OMTPlan can exploit to build more succinct encodings. Similar results have also been reported by [10], where OMTPlan outperformed SoA planners on linear domains. We highlight that CSC does not support planning with state-dependent costs; ENHSP does not provide admissible heuristics for linear numeric planning. As a result, the planner had to be run using uninformed search that disregards cost structures.

4.Conclusions

We presented OMTPlan, the first domain independent planner based on Optimisation Modulo Theories. Building upon the theoretical results of [11], OMTPlan implements reductions to SMT and OMT to solve expressive planning problems for which tool support was lacking. We discussed the internal work-flow of OMTPlan and explained its main functionalities. Notably, OMTPlan can be used to convert PDDL problems into SMT-LIB format, thus enabling fruitful interactions between the planning and SMT/OMT communities [3]. We reported numeric experiments that demonstrate the capabilities of OMTPlan. Our results, in combination with those already presented in [11], show that OMTPlan offers an efficient solution to solve planning problems that require complex theory reasoning.