Deep Learning Algorithm of 12-Lead Electrocardiogram for Parkinson Disease Screening
Abstract
Background:
Although idiopathic Parkinson’s disease (IPD) is increasing with the aging population, there is no adequate screening test for early diagnosis of IPD. Cardiac autonomic dysfunction begins in the early stages of IPD, and an electrocardiogram (ECG) contains precise information on the heart.
Objective:
This study is to develop an ECG deep learning algorithm that can efficiently screen for IPD.
Methods:
Data were collected from 751 IPD patients (2,138 ECGs), 751 age and sex-matched non-IPD patients (2,673 ECGs) as a control group, and 297 drug-induced Parkinsonism (DPD) patients (875 ECGs) as a disease control group. ECG data were randomly divided into training set, validation set, and test set at a ratio of 6:2:2. We developed a deep-convolutional neural network (CNN) consisting of 16 layers with Bayesian optimization that classified IPD patients by ECG data. The robustness of the deep learning model was verified through 5-fold cross-validation.
Results:
The AUROC of the model for detection of IPD was 0.924 (95% CI, 0.913–0.936) in the test set. That for detecting DPD was 0.473 (95% CI, 0.453–0.504). The sensitivities of the model according to Unified Parkinson’s Disease Rating Scale III and Hoehn & Yahr scale were also similar.
Conclusion:
In conclusion, the CNN-based deep learning model using ECG data showed quite good performance in identifying IPD patients. Standardized 12-lead ECG test could be one of the clinically feasible candidate methods for early screening of IPD in the future.
INTRODUCTION
Idiopathic Parkinson’s disease (IPD) is one of the most common neurodegenerative diseases worldwide, with an incidence of 1 in 1000 during a lifetime [1]. The prevalence is gradually increasing due to the aging of the population and estimated to be about 1% in those over 60 years of age. Motor symptoms including tremor, rigidity, and bradykinesia are known as the main symptoms, and there is still no clear test method for diagnosis yet, and a neurologist makes a diagnosis by combining symptoms and other test results.
Because the diagnosis of IPD relies on the subjective opinion of experts, its diagnosis can sometimes be delayed. Recently, precise imaging tests, such as dopamine transporter (DAT) scan, may be helpful in differentiating from other diseases and diagnosing IPD, but they are not accurate enough to be used as a diagnostic method, require an imaging specialist’s interpretation, and are very expensive. For this reason, recent studies on deep learning algorithms for early screening and diagnosis of IPD using various data modalities have been widely performed.
According to previous studies, the average accuracy of the algorithm to detect IPD using voice recording was approximately 90%, the average accuracy of the algorithm using movement data was 89%, and the average accuracy of the algorithm using hand-writing pattern was 87% [2]. In addition, algorithms using precise image data such as magnetic resonance imaging (MRI) and single-photon emission computed tomography (SPECT), algorithms using various biomarkers obtained from cerebrospinal fluid (CSF), and algorithms integrating data of these various modalities have been also studied [3].
Although IPD is a neurodegenerative disease, it is closely related and affects the heart in a variety of ways. For example, heart rate variability (HRV) is decreased in IPD patients, which is known to be associated with striatal dopaminergic depletion as well as autonomic effects of IPD [4]. In addition, HRV is known to be a major factor in predicting the risk of developing IPD [5], and recently, a pilot study of 35 IPD patients was also reported to predict the risk of IPD with the performance of AUC 0.85 using the features extracted from the R-R interval of the ECG [6]. These findings suggest that ECG can be used to screen or diagnose IPD at an early stage. The present study developed a deep learning model that can distinguish IPD using 5,247 12-lead ECG data including 2,186 ECG data from 756 IPD patients.
METHODS
Study design and dataset
The dataset was extracted from the electronic health record database of Korea University Anam hospital. The IPD group included 1) patients visited at least 4 times with ICD10 diagnostic code for IPD (G20) as primary diagnosis from January 1, 2016 to December 31, 2021 and received IPD medications for more than 90 days, or 2) patients visited one or more with an ICD10 diagnostic code for IPD (G20) over the same period and 18F-N-(3-fluoropropyl)-2β-carbon ethoxy-3β-(4-iodophenyl) nortropane positron emission tomography (18F-FP-CIT PET) showed decreased dopamine transporter (DAT) at posterior putamen. The patients with ICD10 diagnostic codes for multiple system atrophy (G23.2, G23.3, G90.3) or progressive supranuclear ophthalmoplegia (G23.1) were excluded. This study used the 12-lead ECG results after the first diagnosis of IPD. The index date was the date of the first 12-lead ECG after diagnosis of IPD.
We derived a control group from whole population without a history of diagnosis of any type of Parkinson’s disease using a propensity score matching for covariates. Considering the clinical importance of differentiation from other diseases with similar phenotypes in the diagnosis and treatment of IPD, this study added patients with drug-induced Parkinson’s disease (DPD) (ICD 10 code: G21.1) as a disease control. The medical records of all individuals were reviewed to confirm the diagnosis of IPD or DPD. Finally, 751 patients (2,138 ECG test cases) in the IPD group, 751 patients (2,673 ECG test cases) in the Control group and 297 patients (875 ECG test cases) in the DPD group remained for deep learning model development and further analysis.
This study was approved by the Institutional Review Board of Korea University Anam hospital (IRB No. 2022AN0375). Written informed consent was waived considering the retrospective nature of the study using anonymized data with minimal risk to study subjects. The study also complied with the Declaration of Helsinki.
Electrocardiogram (ECG) data
ECG data were composed of general metadata, analyzed parameters, ECG diagnosis, and digital waveform data obtained from the Marquette Universal System for Electrocardiography (MUSE; GE). General metadata included subject id, age, sex, sampling rate and device information. ECG parameters included heart rate, PR interval, QRS duration, QTc interval, P axis, R axis, and T axis. ECG diagnosis consisted of 130 standardized ECG diagnoses mapped from computerized ECG diagnosis [7]. Digital waveform data obtained at a sampling frequency of 500 Hz for 10 s consists of 5000 digits per lead. Data of the first 1 s and the last 1 s were excluded due to relatively higher artifact frequency within these regions. Finally, 2-dimensional data of 12×4000 from each ECG was used in this study.
Deep learning architecture
Convolution neural network (CNN) is a representative feed-forward neural network and is effectively applied in supervised learning models because it extracts useful features from nonlinear relationships between input and output variables. CNN is easy to train compared to other deep and unidirectional neural networks because there are less parameters for optimization. In addition, it has the advantage of being effective in extracting features for various data types, so it is widely used in the study of deep learning [8, 9]. The CNN structure consists of input variables, output variables, convolutional layer, batch normalization layer, pooling layer, flatten and fully-connected layer [10]. Figure 1 represents the architecture of the classification model used in this study, and the classification model was designed with the structure of a deep CNN consisting of 16 layers to classify Parkinson’s disease.
Fig. 1
Deep learning model architecture.
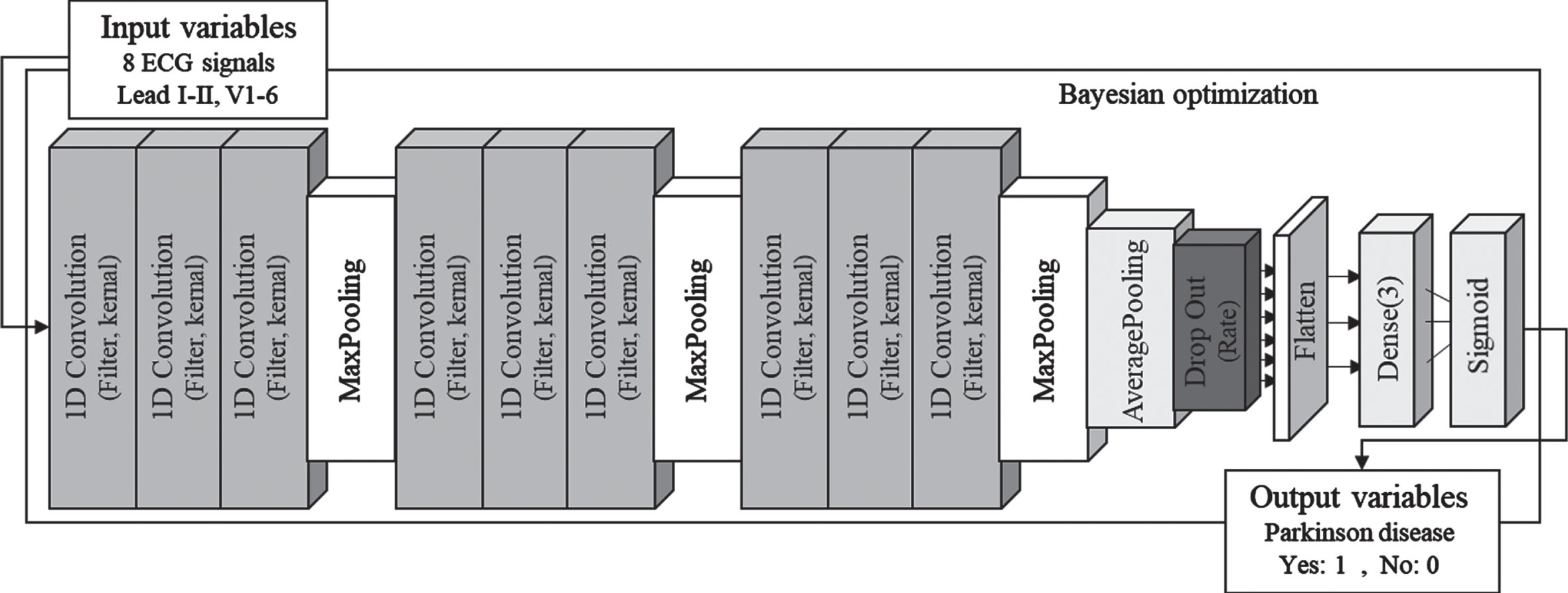
The proposed deep-CNN is built on the basis of 1D CNN and is mainly composed of two types: CNN and fully-connected [8]. The CNN layer provides an output feature map by performing dot-product operation of input variables through convolution kernels. The pooling layer was used in the CNN network to reduce the number of parameters without affecting the features of the input variables. Then, the output of the pooling layer was converted into a one-dimensional vector using flatten to be transmitted to the fully connected layer. In addition, a dropout layer was added between the CNN and the Flatten layer to prevent overfitting after the parameter extraction process by CNN [10]. The feature parameters of the ECG acquired from the CNN network were transmitted to the fully-connected layer to predict disease by sigmoid regression. In addition, a Bayesian optimizer was applied to optimize the hyperparameters of the deep-CNN model. The Bayesian optimizer is a methodology that automatically determines hyperparameters by optimizing the objective function based on prior knowledge using the Gaussian process [9, 11]. The tuning of Hyperparameter can expect high-accuracy results even through manual optimization, but there is a limitation that it should depend on experience. However, Bayesian optimization has advantages in that the number of iterations is small, the convergence speed is fast, and the hyper parameter determination is accurate. Therefore, the deep-CNN model applied Bayesian optimization to determine the correct hyperparameters. The hyperparameters in the deep-CNN model were as follows: The number of CNN filters = 4 to 16; The number of kernel size = 4 to 16; The number of dropout ratio = 0.2 to 0.6; The number of learning rate = 1E–6 to 1E–1; The number of batch size = 4 to 16. The activation function of CNN = ReLU, ELU, SeLU. The Bayesian optimization for hyperparameter selection was run 25 iterations. Eight ECG signals of 4000 frames (lead I, lead II, V1-V6) were used as input variables of the deep-CNN model, and binary values set to 0 and 1 according to disease were used as output variables. As for the data set used for model development, the training set, validation set, and test set were randomly split into 6:2:2, respectively. The proposed model was implemented using python 3.7.13 with Tensorflow 2.3.0 and Keras library. And model was trained on a server with Intel(R) Xeon(R) Silver 4210 R CPU @ 2.40 GHz processor, 256 GB DDR4 memory, and GeForce RTX 3090 GPU.
Statistical analysis
Baseline characteristics are shown as the mean±SD or n (%). Chi-square test were used to compare the categorical variables and ANOVA test or Kruskal-Wallis test was performed for continuous variables between groups after normality test. If the overall p-value was significant, a post hoc test using Bonferroni adjust method was performed. Statistical significance level is 0.05. To control for potential confounding factors that may affect deep learning model performance, we performed 1:1 propensity score matching for IPD group and Control group using caliper 0.2. Covariates included age, sex, alcohol, smoking, hypertension, diabetes, dyslipidemia, chronic kidney disease (CKD), atrial fibrillation (AF), systolic blood pressure, diastolic blood pressure, and medications affecting ECG. The standardized mean difference for all matching variables was less than 0.15, indicating good balance. The baseline characteristics before and after matching between the IPD group and the Control group were provided with supplemental data.
The confusion matrix was analyzed to quantitatively verify the performance of deep-CNN to classify Parkinson’s disease. The confusion matrix is used to evaluate the performance of the classification model by expressing the actual and predicted values as four elements: true positive, false negative, true negative, and false positive. The evaluation indicators derived from the confusion matrix are accuracy, precision, recall, and F1-score. Accuracy is the most common and intuitive indicator as the number of accurate predicted data divided by the total number of predicted data. In addition, the performance evaluation of the binary classifier was performed by calculating the area under receiver operating characteristic (AUROC). The AUROC presents the area under the plot composed of the false positive rate on the x-axis and the true positive rate on the y-axis, and performance analysis of the model is possible for all threshold values. The AUROC is between 1 and 0, and the closer to 1, the better the classifier’s performance. Precision is an indicator that quantifies the ratio of true positives in among the predicted positive value by the model, and the recall is an indicator of the ratio that the model predicts as true among the actual true value. F1-score is an indicator calculated as a harmonic average of precision and recall, and is an effective measure even for models with imbalanced datasets.
In addition, sensitivity specificity, positive predicted value (PPV), and negative predicted value (NPV) were also investigated. Sensitivity and specificity are methods of evaluating a model in terms of actual values. Sensitivity is the probability of a positive test result considering that there is a true value. Specificity is the possibility of negative test results considering that there is negative value. When using a prediction, we need to know how well the test result predicts the actual value. The PPV is the probability that a positive prediction result correctly predicts the true positive value, NPV is the probability that a negative prediction result correctly predicts the true negative value. Also, bootstrapping was performed for computing the 95% confidence interval of a ROC curve with 2000 replicates. Additionally, the k-fold cross-validation (CV) technique was applied to verify the robustness of the Parkinson classification model. In this study, the overfitting problem according to the data set was verified using 5-fold CV, which is most commonly used in the field of machine learning [12]. All variables of the models obtained through 5-fold CV were used for classification model analysis by calculating the average value. All analyses were performed using SAS 9.4 (SAS Institute Inc., Cary, NC, USA) program and R program (Ver 3.6.1).
RESULTS
Baseline characteristics of the study groups are described in Table 1. Since the Control group matched the IPD group, there were no significant variables in baseline demographic characteristics. DPD group was younger and more male than the IPD group and Control group. The DPD group consumed less alcohol, and had lower prevalence of hypertension, and diabetes than the IPD group and Control group. Systolic blood pressure in the DPD group was lower than the Control group and the IPD group (123.9±16.6 mmHg vs. 129.8±17.6 mmHg, p < 0.01 for DPD vs. Control; 123.9±16.6 mmHg vs. 128.7±15.9 mmHg, p < 0.01 for DPD vs. IPD).
Table 1
Baseline demographic characteristics of the study groups
| Total population (n = 1,799) | Control (n = 751) | DPD (n = 297) | IPD (n = 751) | p | Post hoc p (IPD vs. Control) | Post hoc p (IPD vs. DPD) | Post hoc p (DPD vs. Control) | |
| Age (y) | 70.9±14.8 | 74.6±10.2 | 52.5±21.2 | 74.4±9.3 | <0.01 | – | <0.01 | <0.01 |
| Male (n, %) | 983 (54.6) | 358 (47.7) | 114 (38.4) | 344 (45.8) | 0.02 | 0.47 | 0.03 | <0.01 |
| Alcohol (n, %) | 381 (21.2) | 167 (22.2) | 41 (13.8) | 173 (22.9) | <0.01 | 0.71 | <0.01 | <0.01 |
| Smoking (n, %) | 257 (14.3) | 107 (14.3) | 39 (13.1) | 111 (14.8) | 0.79 | – | – | – |
| Hypertension (n, %) | 1,131 (62.9) | 503 (67.0) | 140 (47.1) | 488 (65.0) | <0.01 | 0.41 | <0.01 | <0.01 |
| Diabetes (n, %) | 696 (38.7) | 305 (40.6) | 92 (31.0) | 299 (39.8) | 0.01 | 0.75 | <0.01 | <0.01 |
| Dyslipidemia (n, %) | 956 (53.1) | 405 (53.9) | 146 (49.2) | 405 (53.9) | 0.32 | – | – | – |
| Chronic kidney disease (n, %) | 461 (25.6) | 200 (26.6) | 69 (23.2) | 192 (25.6) | 0.52 | – | – | – |
| Atrial fibrillation (n, %) | 151 (8.4) | 66 (8.8) | 16 (5.4) | 69 (9.2) | 0.12 | – | – | – |
| Hoehn-Yahr stage | – | – | – | 2.5±0.9 | – | – | – | – |
| UPDRS scale I | – | – | – | 2.9±2.8 | – | – | – | – |
| UPDRS scale II | – | – | – | 10.7±9.0 | – | – | – | – |
| UPDRS scale III | – | – | – | 28.5±14.6 | – | – | – | – |
| UPDRS scale IV | – | – | – | 2.7±6.2 | – | – | – | – |
| Schwab and England ADL scale | – | – | – | 77.1±21.2 | – | – | – | – |
| Systolic blood pressure (mmHg) | 128.4±16.8 | 129.8±17.6 | 123.9±16.6 | 128.7±15.9 | <0.01 | 0.31 | <0.01 | <0.01 |
| Diastolic blood pressure (mmHg) | 75.8±12.4 | 75.8±15.7 | 75.2±11.0 | 76.1±9.7 | 0.58 | – | – | – |
| Anti-Parkinson drugs | ||||||||
| Levodopa/COMT inhibitor (n, %) | 170 (9.5) | 0 (0.0) | 4 (1.4) | 166 (22.1) | <0.01 | – | <0.01 | – |
| Dopamine agonist (n, %) | 63 (3.5) | 1 (0.1) | 4 (1.4) | 58 (7.7) | <0.01 | <0.01 | <0.01 | <0.01 |
| MAO-B inhibitor (n, %) | 39 (2.2) | 0 (0.0) | 0 (0.0) | 39 (5.2) | – | – | – | – |
| Amantadine (n, %) | 12 (0.7) | 0 (0.0) | 0 (0.0) | 12 (1.6) | – | – | – | – |
| Anticholinergics (n, %) | 76 (4.2) | 0 (0.0) | 52 (17.5) | 24 (3.2) | <0.01 | – | <0.01 | – |
UPDRS scale I, mental examination; UPDRS scale II activities of daily living; UPDRS scale III, motor examination; UPDRS scale IV, complication of therapy. Schwab and England ADL scale, Activities of Daily Living scale. COMT, catechol-O-methyltransferase; MAO-B, monoamine oxidase type B.
In patients with IPD, Unified Parkinson’s Disease Rating Scale (UPDRS) and modified Hoehn and Yahr (H&Y) stage, Schwab and England Activities of Daily Living (ADL) scale were investigated. The mean of H&Y scale (1–5 scale), which indicates the degree of Parkinson’s disease symptoms, is 2.5, which means mild bilateral disease with recovery on pull test. UPDRS consists of four Parts: part I (mental examination), part II (activity of daily living), part III (motor examination), and part IV (complications of therapy). The higher the score in each item, the higher the severity. Part I can be measured from 0 to 16 points, and the average was 2.9, and part II was found to have an average of 28.5 out of 0–52 points. Part III was found to be 28.5 out of 0 to 108, suggesting that most IPD patients were in motor stage. Part IV, which represents treatment complications, was found to be 2.7 points. The Schwab and England ADL scale, which evaluates the ability to perform daily activities, uses a percentage to score and averages 77.1, which means that it takes more than twice as long to work.
The proportion of anti-Parkinson drugs was low in the IPD group since the initial ECG tests were performed while mainly evaluating Parkinson’s disease. There was 1 patient taking ropinirole for restless legs syndrome in the Control group. In the DPD group, the proportion of patients taking anticholinergics was 17.5%, which was higher than the other two groups, and there were few patients taking the other anti-Parkinson drugs.
Table 2 shows ECG parameters, ECG diagnosis, and medications affecting ECG results exposed at the time of the ECG tests. The heart rate of the IPD group was higher than that of the Control group and less than that of the DPD group. The QRS duration of the IPD group was smaller than that of the Control group. The QTc of the IPD group was higher than that of the Control and DPD group. Among the ECG diagnosis, the percentage of normal sinus rhythm was similar in the IPD group and the Control group, and the DPD group had the highest rate of 37.2% among the 3 groups. In the IPD group, the ranking of abnormal ECG diagnosis rates was in the order of abnormal T wave, AV block, left ventricular hypertrophy (LVH), atrial fibrillation, sinus bradycardia. In the DPD group, it was in the order of abnormal T wave, sinus tachycardia, QT prolongation, LVH, and sinus bradycardia. In the Control group, it was in the order of AV block, abnormal T wave, LVH, sinus bradycardia, and atrial fibrillation.
Table 2
ECG parameters, ECG diagnosis and the exposure to medications affecting ECG results
| Total population (n = 5,686) | Control (n = 2,673) | DPD (n = 875) | IPD (n = 2,138) | p | Post hoc p (IPD vs. Control) | Post hoc p (IPD vs. DPD) | Post hoc p | |
| (DPD vs. Control) | ||||||||
| ECG parameters | ||||||||
| Heart rate (beats/min) | 76.5±17.0 | 74.7±16.5 | 79.5±16.4 | 77.5±17.5 | <0.01 | <0.01 | <0.01 | <0.01 |
| PR interval (ms) | 168.7±29.6 | 171.3±30.7 | 160.5±26.2 | 169.3±28.9 | <0.01 | 0.04 | <0.01 | <0.01 |
| QRS duration (ms) | 94.1±19.9 | 96.8±22.7 | 89.8±12.5 | 92.3±18.0 | <0.01 | <0.01 | <0.01 | 0.19 |
| QTc interval (ms) | 442.5±34.4 | 441.6±36.0 | 439.8±32.3 | 444.8±33.2 | <0.01 | <0.01 | <0.01 | <0.01 |
| ECG diagnosis | ||||||||
| Normal ECG (n, %) | 1,763 (31.0) | 825 (30.9) | 326 (37.2) | 612 (28.6) | <0.01 | 0.09 | <0.01 | <0.01 |
| Top 5 abnormal ECG diagnosis (n, %) | Abnormal T wave (1,054,18.5%), | AV block (482, 18%), | Abnormal T wave (171, 19.5%) | Abnormal T wave (424, 19.8%), | – | – | – | – |
| AV block (920, 16.2%), | Abnormal T wave (459, 17.2%), | Sinus tachycardia (89, 10.2%) | AV block (349, 16.3%), | |||||
| LVH (775, 13.6%), | LVH (401, 15%), | QT prolongation (84, 9.6%) | LVH (300, 14%), | |||||
| Sinus bradycardia (603, 10.5%), | Sinus bradycardia (332, 12.4%), | LVH (74, 8.5%) | Atrial fibrillation (268, 12.5), | |||||
| Atrial fibrillation (547, 9.6%) | Atrial fibrillation (269, 10.1%) | Sinus bradycardia (67, 7.7%) | Sinus bradycardia (204, 9.5%) | |||||
| Medication affecting ECG | ||||||||
| Beta blocker (n, %) | 1,165 (20.9) | 505 (18.9) | 179 (20.5) | 481 (22.5) | <0.01 | <0.01 | 0.12 | 0.31 |
| Non-DHP CCB (n, %) | 207 (3.6) | 109 (4.1) | 18 (2.1) | 80 (3.7) | 0.02 | 0.55 | 0.01 | <0.01 |
| Other medication affecting ECG (n, %) | 1,193 (21.0) | 387 (14.5) | 404 (46.2) | 479 (20.7) | <0.01 | <0.01 | <0.01 | <0.01 |
LVH, left ventricular hypertrophy; RBBB, right bundle branch block. Other medication affecting ECG includes antipsychotics, antiarrhythmics, antidepressants, antihistamines, quinidine, and macrolides.
The proportion of patients taking beta blockers was higher in the IPD group than in the Control group (18.9% vs. 22.5%, p≤0.01), and the proportion of patients taking non-dihydropyridine calcium channel blocker (non-DHP CCB) was higher in the IPD group than in the DPD group (3.7% vs. 2.1%, p = 0.01). The proportion of patients taking other medications affecting ECG results was higher in the IPD group than in the Control group (14.5% vs. 20.7%, p < 0.01), and much lower in the DPD group (46.2% vs. 20.7%, p < 0.01).
The performances of the deep learning model using 12-lead ECG waveform were shown in Table 3 and Fig. 2. The hyperparameter determined by Bayesian optimization was filter size of 8, kernel size of 16, dropout of 0.6, learning rate 0.0000773, and 8 for batch size. The activation function was determined to be ELU. Three test datasets were used to evaluate the IPD and DPD classification performance of the model. The first test set consists of IPD and Control, and evaluates the ability to classify IPD. The second set consists of DPD and Control, and detects DPD. The last set classifies IPD from the data consisting of DPD, and IPD. Performance values were calculated as the average of each CV performance values. In Fig. 2, the sky-blue line is the ROC curve for each CV value, and the deep-blue line is the ROC curve for the average of CVs. The AUROC of the model for detecting IPD was 0.924 (95% CI, 0.913–0.936) in the test set 1. The AUROC of the model for detecting DPD was 0.473 (95% CI, 0.453–0.504) in the test set 2. The AUROC of the model for detecting IPD was 0.946 (95% CI, 0.934–0.959) in the test set 3. The negative predictive value of the model for detecting IPD (test set 1) was more than 80% at the highly sensitive operating point in the test set (Table 4). Subgroup analysis stratifying by age, sex, alcohol, smoking, diabetes, heart rate, the medication affecting ECG and ECG diagnosis showed that AUROC of the model was highest in the patients with a history of diabetes (0.965, 95% CI, 0.948–0.981) and lowest in the patients without a history of diabetes (0.881, 95% CI, 0.850–0.911) (Table 5).
Table 3
Performance of the proposed deep learning model using 12-lead ECG waveform for detecting IPD
| Accuracy (95% CI) | Precision (95% CI) | Recall (95% CI) | F1-Score (95% CI) | AUROC (95% CI) | |
| IPD | 0.869 | 0.842 | 0.892 | 0.801 | 0.924 |
| (Test set 1: Control + IPD) | (0.848–0.889) | (0.815–0.868) | (0.863–0.921) | (0.763–0.836) | (0.913–0.936) |
| DPD | 0.711 | 0.055 | 0.138 | 0.034 | 0.473 |
| (Test set 2: Control + DPD) | (0.694–0.729) | (0.013–0.097) | (0.044–0.253) | (0.010–0.063) | (0.453–0.504) |
| IPD | 0.849 | 0.880 | 0.984 | 0.801 | 0.946 |
| (Test set 3: IPD + DPD) | (0.821–0.875) | (0.821–0.875) | (0.970–0.995) | (0.816–0.837) | (0.934–0.959) |
CI, confidence interval; AUROC, area under the receiver operating characteristics curve.
Fig. 2
ROC curves of the proposed 12-lead ECG deep learning model. A) IPD detection from the IPD group and the control group B) DPD detection from the DPD group and the control group C) IPD detection from the IPD group and DPD group.
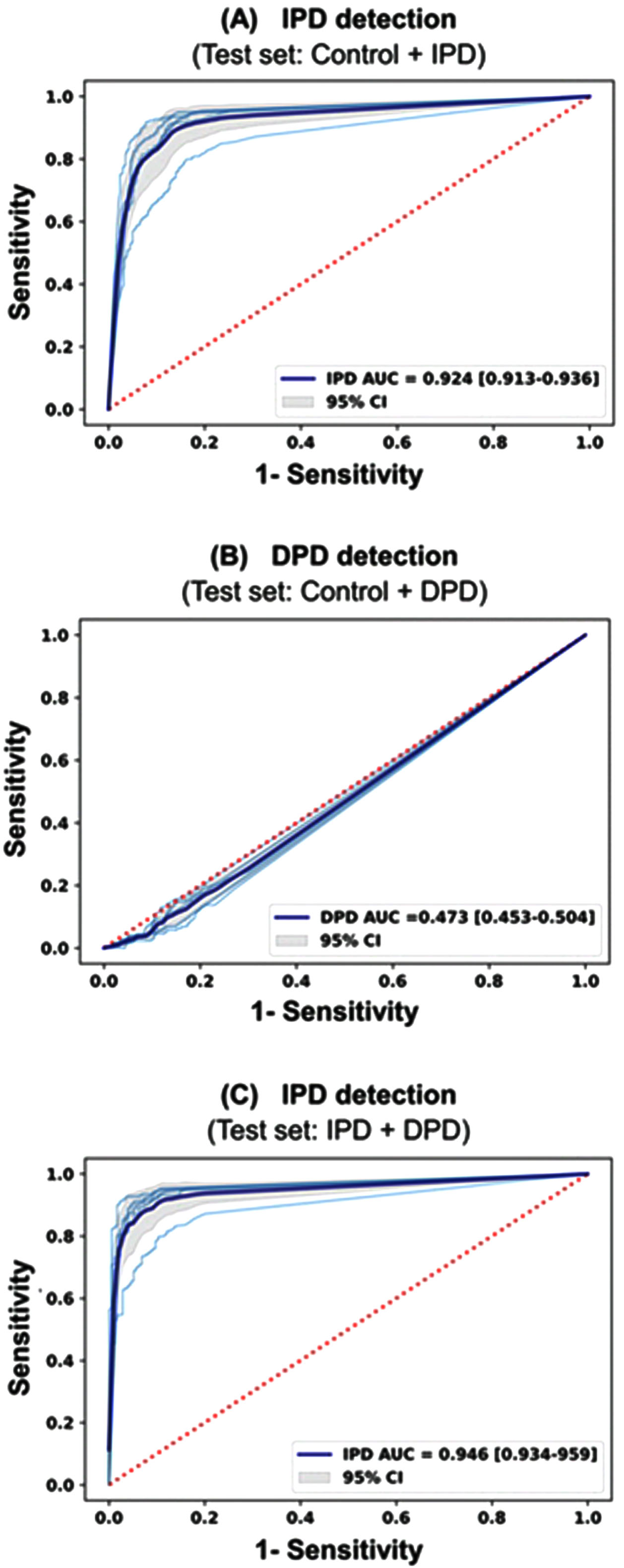
Table 4
Performance of the proposed 12-lead ECG deep learning model for detecting IPD at operating points with high sensitivity in the test set
| Sensitivity (%) | Specificity (%) | NPV (%) | PPV (%) | Accuracy (95% CI) | AUROC (95% CI) |
| 95 | 80.6 | 95.4 | 79.8 | 0.870 (0.847–0.891) | 0.879 (0.855–0.896) |
| 90 | 89.3 | 91.9 | 87.2 | 0.897 (0.876–0.916) | 0.898 (0.878–0.917) |
| 85 | 88.9 | 88.0 | 86.5 | 0.872 (0.849–0.892) | 0.870 (0.849–0.891) |
| 80 | 92.0 | 85.3 | 89.3 | 0.860 (0.845–0.888) | 0.861 (0.839–0.883) |
AUROC, area under the receiver operating characteristic curve; NPV, negative predictive value; PPV, positive predictive value.
Table 5
Subgroup analysis of the performance of the proposed 12-lead deep learning model for detecting IPD
| AUROC | 95% CI | ||
| Age (y) | ≥75 | 0.928 | 0.906–0.949 |
| <75 | 0.919 | 0.908–0.954 | |
| Sex | Men | 0.931 | 0.891–0.943 |
| Women | 0.917 | 0.891–0.943 | |
| Alcohol | No | 0.918 | 0.897–0.938 |
| Yes | 0.944 | 0.915–0.973 | |
| Smoking | No | 0.923 | 0.904–0.942 |
| Yes | 0.933 | 0.894–0.971 | |
| Diabetes | No | 0.881 | 0.850–0.911 |
| Yes | 0.965 | 0.948–0.981 | |
| Heart rate (beats/min) | <100 | 0926 | 0.908–0.943 |
| ≥100 | 0.908 | 0.843–0.973 | |
| Medication affecting ECG | No | 0.914 | 0.892–0.936 |
| Yes | 0.944 | 0.917–0.970 | |
| ECG diagnosis | Normal sinus rhythm | 0.919 | 0.887–0.952 |
| Others | 0.926 | 0.846–0.946 |
UPDRS, unified Parkinson’s disease rating scale; Medication affecting ECG includes beta blockers, non-DHP CCB, antipsychotics, antiarrhythmics, antidepressants, antihistamines, quinidine, and macrolides.
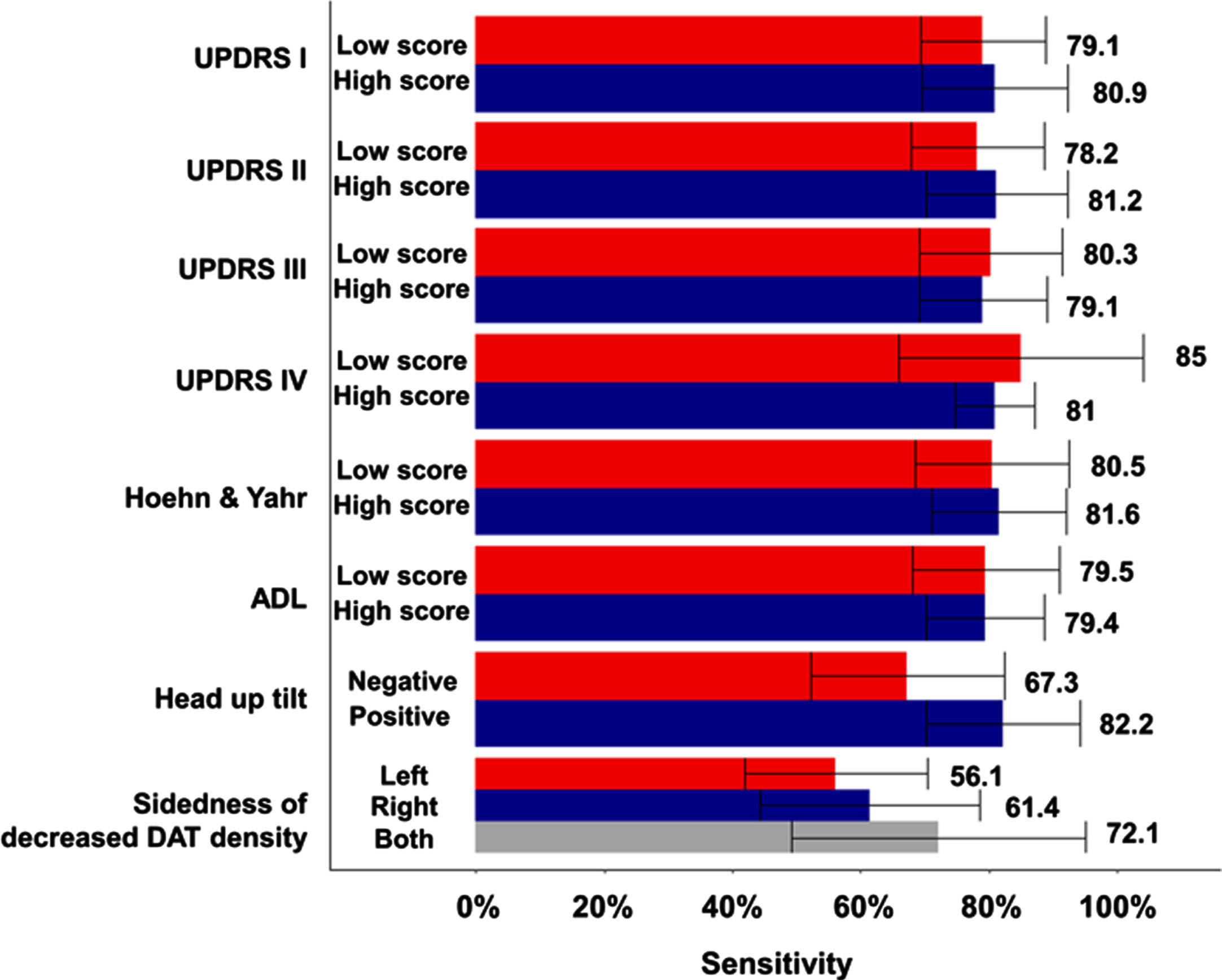
Next, we explored whether the discrimination ability of the deep learning model changes depending on the clinical severity and involvement level of Parkinson’s disease (Fig. 3). Sensitivity analysis was performed on each of the five CV sets, the number of rejections among the five tests was confirmed. In patients with high mental examination and high activity of daily living (UPDRS I & II) the sensitivity of the model was numerically higher than in patients with low score, but there were no statistical difference (the number of rejection is 0 and 1, respectively among 5 times). Sensitivity was higher in patients with low score than those with high UPDRS III & IV, but there was no significant difference (the number of rejection is 0 and 2, respectively among 5 times). There was almost no difference in sensitivity according to the Hoehn & Yahr scale and ADL scale categories (81.6% vs. 80.5%, 79.4% vs. 79.5%). In patients with a positive head-up tilt table test suggesting autonomic nervous system dysfunction, the sensitivity of the model was numerically higher than in patients with a negative result, but there was no statistical difference (82.2% vs. 67.3%, the number of rejection is 2 among 5 times). The performance of the model according to sidedness of decreased DAT density in the 18F-FP-CIT PET was numerically high when the DAT density on the side of the posterior putamen was lowered, but there was also no statistically significant difference (56% for decreased DAT density in left sides vs. 61.4% for that in right side vs. 72.1% for that in both sides, the number of rejection is 1 among 5 times).
Fig. 3
Sensitivity comparison of the deep learning model according to the clinical severity and subtypes of Parkinson’s disease.
Finally, we further developed deep learning models using each single-lead ECG data. The Parkinson’s disease detection performance of the models developed only with single-lead ECG data was inferior to that of the model developed with 12-lead ECG data. The accuracy of a single-lead model for detecting IPD in the test set was highest with V3 (0.763, 95% CI 0.749–0.777) and lowest with V6 (0.730, 95% CI 0.714–0.746) (Table 6). The AUROC of the model was highest with V3 (0.820, 95% CI 0.805–0.835) and lowest with V6 (0.786, 95% CI 0.769–0.803).
Table 6
Performance of a single-lead ECG deep learning model for detecting IPD
| Lead | Accuracy (95% CI) | AUROC (95% CI) |
| V1 | 0.740 (0.724–0.756) | 0.799 (0.783–0.815) |
| V2 | 0.752 (0.737–0.767) | 0.812 (0.795–0.830) |
| V3 | 0.763 (0.749–0.777) | 0.820 (0.805–0.835) |
| V4 | 0.736 (0.721–0.751) | 0.765 (0.747–0.782) |
| V5 | 0.740 (0.725–0.756) | 0.779 (0.762–0.795) |
| V6 | 0.730 (0.714–0.746) | 0.786 (0.769–0.803) |
| I | 0.736 (0.720–0.752) | 0.791 (0.774–0.808) |
| II | 0.740 (0.724–0.756) | 0.799 (0.782–0.816) |
AUROC, area under the receiver operating characteristic curve.
DISCUSSION
Considering that clinical diagnosis of IPD is difficult and the prognosis may be poor if treatment is not started early, it would be important to develop a relatively easy and cost-effective screening tool for detecting IPD patients. This study introduced a CNN-based deep learning model using 12-lead ECG for identifying IPD patients. The novelty of this study in developing a deep learning model for IPD screening are as follows: 1) This is the first deep learning model using 12-lead ECG waveform data to identify IPD patients; 2) This study used the largest number of IPD patients (756 patients) with detailed clinical, imaging and functional information; 3) Considering the clinical importance of differential diagnosis between IPD and DPD, data from DPD patients were included as negative controls; and 4) The deep learning model developed in this study showed robustness without compromising performance in different patient subgroups.
As mentioned earlier, there is no appropriate method to screen IPD patients early. The recommendation guidelines for IPD do not mention how to screen patients with IPD, only suggesting that people with tremor, stiffness, slowness, balance problems, or gait disorder should suspect IPD [13, 14]. Until now, several studies have been attempted to screen and diagnose IPD patients using various methods such as voice, motion video, handwriting, precise imaging tests such as MRI and positron emission tomography (PET), and CSF tests. Apart from their diagnostic accuracy, precise imaging tests are disadvantageous in terms of cost and potential radiation hazard. CSF test is not widely used because it is invasive. Voice, motion video, and handwriting data can be easily obtained, but there is a disadvantage in that it is difficult to standardize the data acquisition and processing. On the other hand, 12-lead ECG is not only non-invasive and radiation-free, but it is also one of the basic routine tests performed in medical institutions. The test method is also standardized, and it can be easily performed. Moreover, considering that IPD patients have a high risk of cardiovascular disease [15], 12-lead ECG may have additional benefits as the most fundamental test for cardiovascular disease.
Several ECG findings have been reported in association with IPD. ECG findings of heart rate variability have been reported to be associated with autonomic dysfunction in patients with IPD [16]. QRS duration was also correlated with disease duration and severity of IPD [17]. QTc prolongation is relatively common in IPD patients, and also correlated with disease duration and severity [18]. Although further studies are still needed, Malkiewicz et al. reported that male gender are potential risk factors for QTc prolongation in patients with IPD [19]. The ECG findings of this study showed that the QTc interval was longer in the IPD group than in the age, sex-matched control group (Table 2). This finding is consistent with previous studies, and interestingly, QT prolongation is also commonly observed in the DPD group. QTc prolongation may also be caused by other causes, such as myocardial ischemia. Additional studies are needed for the clinical significance of QTc prolongation in IPD. In addition, abnormal T wave findings were also more common in both IPD group and DPD group than in Control group. Although DPD patients show ECG characteristics similar to those of IPD patients, IPD has its own pathophysiology that is different from DPD. Cardiac autonomic dysfunction resulting from sympathetic or parasympathetic denervation and postsynaptic receptor upregulation seems to play a role in the cardiac pathology of IPD [20]. Indeed, metaiodobenzylguanidine (123I-MIBG) scintigraphy, which measures postganglionic cardiac autonomic denervation, was included as a supportive criterion for the clinical diagnosis of IPD [21].
Recently, Akbilgic et al. used Probabilistic Symbolic Pattern Recognition (PSPR) method to extract waveform features that can predict the progression of IPD from 12-lead ECG of 35 prodromal or prevalent IPD patients [6]. PSPR features suggested that there were high similarity of ECG waveform features between the prodromal and prevalent IPD groups. The PSPR features representing ECG waveforms of 125 ms in length were significantly different between controls and IPD subjects. This suggests that ECG waveform features in specific frequency bands may help to distinguish IPD patients. The authors conducted a follow-up study using CNN model, and the AUROC of the CNN-based deep learning model was 0.67 (0.54–0.79) between 6 and 12 months before IPD diagnosis [22]. Although our model identifies prevalent IPD patients rather than prodromal IPD patients, it performed better with AUROC of 0.924 (0.913–0.936). In other words, the better performance of our model may be due to the identification of more progressed IPD patients than prodromal IPD patients.
Our study has several limitations. First, this study did not perform external validation using data from other institutes although it was a large-scale study conducted with a total of 5,686 ECG data, including 751 IPD patients. Therefore, if the deep learning model of this study is applied to other datasets, the performance may be degraded compared to the results of this study. However, the deep learning model of this study showed robust performance in various subgroups, and it will be possible to improve the performance of the model by implementing transfer learning in other studies. Second, ECG artifacts, especially motion artifacts generated by Parkinson’s disease, may have affected the performance of the model. Nonetheless, this model showed an excellent performance in distinguishing between DPD and IPD. Therefore, the possibility of bias due to ECG artifacts in this study is estimated to be small. Thus, the effect of ECG artifacts on the model should be considered. Third, it is difficult to explain the decision of our model. The “black box” nature of deep learning makes it difficult to accurately interpret which part of ECG our model focuses on and which information it extracts to identify IPD patients. This may be a subtle or complex ECG feature that humans do not know. It is necessary to overcome these “black box” characteristics of deep learning in the future and increase the possibility of explanation. Forth, this study used the raw ECG signal of 500 Hz, but various features can be extracted from the ECG waveform, and the performance of deep learning can be further improved by using these extracted features. This will be our next research area. Fifth, since IPD patients in this study were in the motor stage, the performance of the deep learning model to screen asymptomatic IPD patients in the prodromal stage would be limited. Finally, machine interpretation was used for ECG diagnosis without cardiologist’s verification in this study. Therefore, the analysis results of ECG diagnosis may not be accurate in this study.
In conclusion, the CNN-based deep learning model using 12-lead ECG had relatively accurate performance in identifying IPD patients.
ACKNOWLEDGMENTS
This research was supported by Young Medical Scientist Research Grant through the Seokchun-nanum Foundation (SCY2106P).
CONFLICT OF INTEREST
The authors have no conflicts of interest to report.
REFERENCES
[1] | Tysnes OB , Storstein A ((2017) ) Epidemiology of Parkinson’s disease. J Neural Transm (Vienna) 124: , 901–905. |
[2] | Mei J , Desrosiers C , Frasnelli J ((2021) ) Machine learning for the diagnosis of Parkinson’s disease: A review of literature. Front Aging Neurosci 13: , 633752. |
[3] | Wang W , Lee J , Harrou F , Sun Y ((2020) ) Early detection of Parkinson’s disease using deep learning and machine learning. IEEE Access 8: , 147635–147646. |
[4] | Heimrich KG , Lehmann T , Schlattmann P , Prell T ((2021) ) Heart rate variability analyses in Parkinson’s disease: A systematic review and meta-analysis. Brain Sci 11: , 959. |
[5] | Alonso A , Huang X , Mosley TH , Heiss G , Chen H ((2015) ) Heart rate variability and the risk of Parkinson disease: The Atherosclerosis Risk in Communities study. Ann Neurol 77: , 877–883. |
[6] | Akbilgic O , Kamaleswaran R , Mohammed A , Ross GW , Masaki K , Petrovitch H , Tanner CM , Davis RL , Goldman SM ((2020) ) Electrocardiographic changes predate Parkinson’s disease onset. Sci Rep 10: , 11319. |
[7] | Yum Y , Shin SY , Yoo H , Kim YH , Kim EJ , Lip GYH , Joo HJ ((2022) ) Development and validation of 3-year atrial fibrillation prediction models using electronic health record with or without standardized electrocardiogram diagnosis and a performance comparison among models. J Am Heart Assoc 11: , e024045. |
[8] | Yıldırım Ö , Pławiak P , Tan RS , Acharya UR ((2018) ) Arrhythmia detection using deep convolutional neural network with long duration ECG signals. Comput Biol Med 102: , 411–420. |
[9] | Yanfei L , Zengyan W , Rui X , Steven L ((2019) ) Bayesian optimized deep convolutional network for electrochemical drilling process. J Manufact Mater Process 3: , 57. |
[10] | Tang S , Zhu Y , Yuan S ((2022) ) Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans 129: , 555–563. |
[11] | Yoo H , Sim T ((2022) ) Automated machine learning (AutoML)-based surface registration methodology for image-guided surgical navigation system. Med Phys 49: , 4845–4860. |
[12] | Wengang Z , Chongzhi W , Haiyi Z , Yongqin L , Lin W ((2021) ) Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci Front 12: , 469–477. |
[13] | Grimes D , Fitzpatrick M , Gordon J , Miyasaki J , Fon EA , Schlossmacher M , Suchowersky O , Rajput A , Lafontaine AL , Mestre T , Appel-Cresswell S , Kalia SK , Schoffer K , Zurowski M , Postuma RB , Udow S , Fox S , Barbeau P , Hutton B ((2019) ) Canadian guideline for Parkinson disease. Cmaj 191: , E989–E1004. |
[14] | National Collaborating Centre for Chronic Conditions ((2006) ) Parkinson’s disease : National clinical guideline for diagnosis and management in primary and secondary care, Royal College of Physicians, London. |
[15] | Park JH , Kim DH , Park YG , Kwon DY , Choi M , Jung JH , Han K ((2020) ) Association of Parkinson disease with risk of cardiovascular disease and all-cause mortality: A nationwide, population-based cohort study. Circulation 141: , 1205–1207. |
[16] | Mochizuki H , Taniguchi A , Nakazato Y , Ishii N , Ebihara Y , Sugiyama T , Shiomi K , Nakazato M ((2016) ) Increased body mass index associated with autonomic dysfunction in Parkinson’s disease. Parkinsonism Relat Disord 24: , 129–131. |
[17] | Mochizuki H , Ishii N , Shiomi K , Nakazato M ((2017) ) Clinical features and electrocardiogram parameters in Parkinson’s disease. Neurol Int 9: , 7356. |
[18] | Zhong LL , Song YQ , Ju KJ , Chen AN , Cao H ((2021) ) Electrocardiogram characteristics of different motor types of Parkinson’s disease. Int J Gen Med 14: , 1057–1061. |
[19] | Malkiewicz JJ , Malkiewicz M , Siuda J ((2021) ) Prevalence of QTc prolongation in patients with Parkinson’s disease. Assessment of the effects of drugs, clinical risk factors and used correction formula. J Clin Med 10: , 1396. |
[20] | Piqueras-Flores J , López-García A , Moreno-Reig Á , González-Martínez A , Hernández-González A , Vaamonde-Gamo J , Jurado-Román A ((2018) ) Structural and functional alterations of the heart in Parkinson’s disease. Neurol Res 40: , 53–61. |
[21] | Postuma RB , Berg D , Stern M , Poewe W , Olanow CW , Oertel W , Obeso J , Marek K , Litvan I , Lang AE , Halliday G , Goetz CG , Gasser T , Dubois B , Chan P , Bloem BR , Adler CH , Deuschl G ((2015) ) MDS clinical diagnostic criteria for Parkinson’s disease. Mov Disord 30: , 1591–1601. |
[22] | Akbilgic O , Karabayir I , Gunturkun F , Goldman S , Kamaleswaran RR , Colletta K , Chinthala L , Jefferies J , Bobay K , Ross G , Petrovitch H , Masaki K , Tanner CM , Externally validated AI model to identify prodromal Parkinson’s disease from ECG, https://www.researchsquare.com/article/rs-1716898/v1, July 6, 2022, Accessed on December 24, 2022. |



