Analysis of SESANS data by numerical Hankel transform implementation in SasView
Abstract
SESANS data analysis has been implemented in the SasView software package, allowing SESANS experiments to be analyzed using a numerical Hankel transformation of isotropic small-angle scattering (SAS) models. The error of the numerical approximation is three orders of magnitude below typical experimental errors. All advanced data fitting features of SasView (multi-model fitting, batch fitting, and simultaneous/constrained fitting) are now also available for SESANS and this is demonstrated by examples of fitting SAS models to SESANS measurements.
1.Introduction
Spin-Echo Small-Angle Neutron Scattering (SESANS) is a small-angle scattering technique for analyzing properties of condensed matter. It was first experimentally demonstrated by Keller et al. [13] and subsequently developed and made useful for analysis of real samples at the Delft University of Technology [6], where it has since been used to characterize many microscopic soft matter structures, such as colloidal suspensions [29], granular materials [1], food structures [31,33], and kinetics of structural changes [34]. The pioneering Delft SESANS instrument extends SANS to length scales reaching 20 μm and has inspired several other instrument development projects, such as a set-up using magnetic Wollaston prisms [19] and two time-of-flight instruments: Offspec [7,20,26] and Larmor [27], collaboratively developed by the Rutherford Appleton Laboratory and Delft University of Technology. Despite the successful design and implementation of these SESANS instruments, user-friendly data analysis tools have remained unavailable to a large extent. Here, we introduce the underlying theory of the numerical Hankel transform, and explain how it has been implemented into the SasView software package. We finally present several examples of successful data analysis, which highlight the capabilities of SESANS and the efficacy of the developed data analysis routines.
SESANS is a variant of the well-established Small-angle neutron scattering technique (SANS), which is itself a form of Small-angle scattering (SAS). The latter has been used over many decades to investigate properties of solids and liquids [10,11] and is a popular technique for material characterization. In a SANS experiment, a sample is placed in a beam of well-collimated neutrons and the small-angle scattering is detected by a position-sensitive detector. SESANS, on the other hand, uses the Larmor precession of polarized neutrons in carefully designed magnetic fields to label the scattering angle. The spin-echo principle can then be used to quantify this labelling to far smaller angles than a SANS instrument of comparable footprint and divergence could detect. Consequently, SESANS uses the available neutron flux far more efficiently than SANS at longer length scales. SESANS however, does not discriminate the scattered neutrons from the direct beam and thus works better in the presence of strong scattering, where multiple scattering corrections become important. Nonetheless, in contrast to SANS, these multiple scattering corrections can be easily accounted for in the SESANS data analysis [24]. Furthermore, the data interpretation is more accessible to non-experts in scattering techniques [4,5,12,22,24] for SESANS than it is for SANS. For the construction of an instrument with the combination of SANS and SEMSANS (Spin-Echo Modulated SANS) the reader is referred to the paper by Kusmin et al. [18].
SasView is an open-source software package for analyzing SAS experimental data written largely in the high-level programming language Python. It has a large, active community of developers from neutron and X-ray facilities and contains an extensive library of SAS model functions and fitting algorithms. As we will explain in the theory section below, for the analysis of the SESANS data the capabilities of SasView have been expanded to include the numerical Hankel transform, which is treated as a SAS resolution function.
2.Theory
In the following, we consider only small-angle scattering. In this case, the wave vector momentum transfer’s modulus Q is fully determined by the neutron wavelength λ and the scattering angle θ:
The measured quantity of a SESANS experiment is the polarization of the neutron beam P as a function of spin-echo length δ [1,13,17,22]. Spin-echo length is an experimental parameter that is determined by the neutron wavelength and the total magnetic field integral experienced by the neutrons.
Fig. 1.
Plot of a scattering function
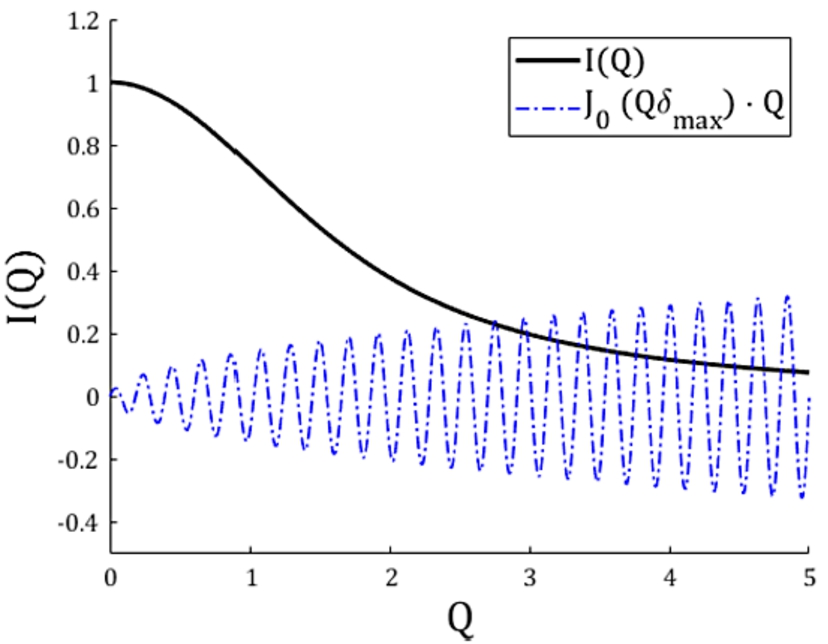
For our numerical approach, integrating Eq. (4) from zero to infinity is not possible. Therefore we must re-write this equation with lower and upper finite integration boundaries
3.Validation and examples
3.1.Validating the numerical approach with an analytical sphere model
The accuracy of the numerically Hankel transformed SAS models was tested on several cases. Here we present a calculation of the point-wise difference between the numerically Hankel transformed SAS model and the analytical (exact) SESANS model of a uniform sphere. The numerical Hankel transform is applied to the following SAS model:
Fig. 2.
Plot of the numerically Hankel transformed SAS model of a sphere in SasView and the analytical projected correlation function of a sphere. Identical parameters were used for both functions (
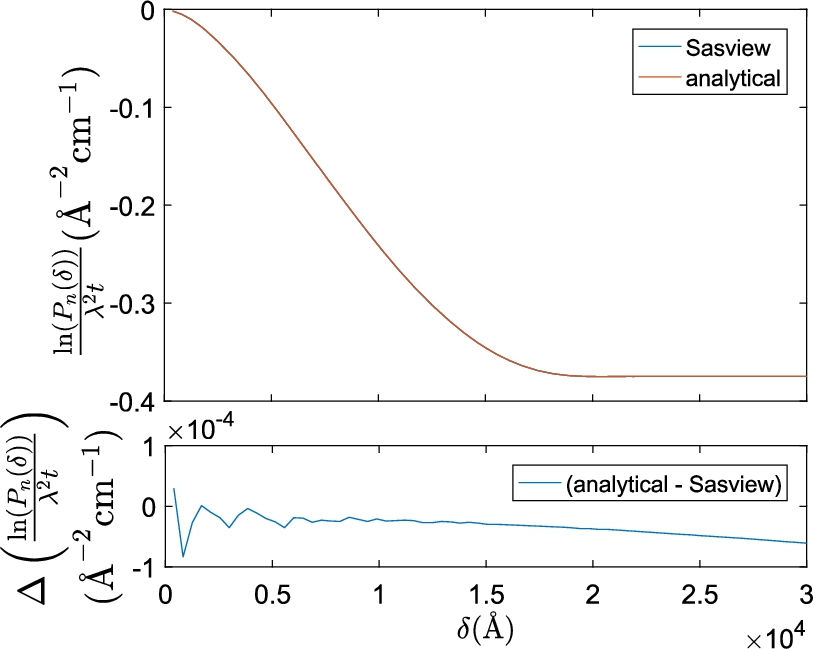
The difference between the analytical equation and SasView’s numerical Hankel transform in Fig. 2 is a factor 1000 smaller than the magnitude of the absolute correlation values of the models themselves and a factor 100 smaller than typical experimental errors (see Figs 3 and 5 for examples). The oscillations in Fig. 2 at small δ are caused by too small
3.2.Examples of fitting a numerical model to a data-set
In the following we validate our approach on experimental data, which have been acquired at the SESANS instrument in Delft [23]. These measurements used neutrons of
Fig. 3.
SESANS data of R=1 μm spherical poly-styrene colloids in D2O. The SAS model used is the solid sphere (Eq. (24)). Fitted values are:
![SESANS data of R=1 μm spherical poly-styrene colloids in D2O. The SAS model used is the solid sphere (Eq. (24)). Fitted values are: R=(1040±10) Å and φ=(3.30±0.03)×10−2. Δρ was fixed at 2×10−6 Å−2. Data from M. Strobl et al. [29].](https://content.iospress.com:443/media/jnr/2020/22-1/jnr-22-1-jnr200154/jnr-22-jnr200154-g003.jpg)
Fig. 4.
SESANS data of Nilac fat-free milk powder in D2O. The SAS model used is the solid sphere (Eq. (24)) with lognormal polydispersity (Eq. (26)) of the radius. Fitted values are:
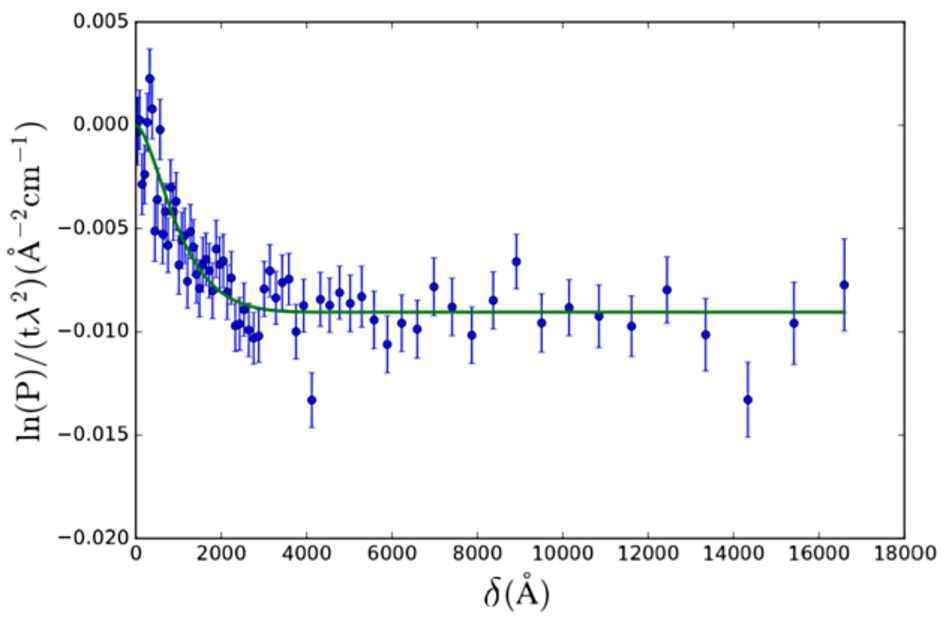
The polymeric gel model (Eq. (27), from [28]) was applied to SESANS data of a gel (yogurt) of NILAC fat-free milk powder in D2O (powder sample provided by NIZO Research, Netherlands) (Fig. 5). This sample is a dispersion of casein micelles in D2O treated with glucono δ-lactone (GDL) to create a yogurt-like substance. The resulting structure has been previously described as a self-affine random medium [2,14,15]. Here we selected a SAS model which approximates the expected structure of the sample (casein micelles connected by a network of gel fibres).
Fig. 5.
SESANS data of Nilac fat-free milk powder in D2O, treated to become yogurt. The SAS model used is the polymeric gel model (Eq. (27)). Fitted values are:

3.3.Example of fitting multiple models to a data-set
Two models were fitted to SESANS data of 70 nm radius spherical core-shell colloids with poly-styrene (PS) core and poly-ethylene oxide (PEO) corona in D2O (data from K. v. Gruijthuijsen et al. [32]).The form factors used were those of solid spheres (Eq. (24)) and core-shell spheres (Eq. (28)),
Fig. 6.
SESANS data of core-shell colloids with a poly-styrene (PS) core and poly-ethylene oxide (PEO) shell in D2O. The data is fitted with the solid sphere (Eq. (24), red) and the core-shell sphere (Eq. (28), green) form factor. Both SAS models were multiplied by the hard sphere structure factor (Eq. (29)). Model fit parameter values are given in Table 1. Data from K. v. Gruijthuijsen et al. [32].
![SESANS data of core-shell colloids with a poly-styrene (PS) core and poly-ethylene oxide (PEO) shell in D2O. The data is fitted with the solid sphere (Eq. (24), red) and the core-shell sphere (Eq. (28), green) form factor. Both SAS models were multiplied by the hard sphere structure factor (Eq. (29)). Model fit parameter values are given in Table 1. Data from K. v. Gruijthuijsen et al. [32].](https://content.iospress.com:443/media/jnr/2020/22-1/jnr-22-1-jnr200154/jnr-22-jnr200154-g006.jpg)
Table 1
Fit parameter values for the multi-model fit (Fig. 6).
| Fit model | Sphere | Core-shell |
| 703 ± 6 | 508 ± 24 | |
| 748 ± 35 | ||
| 2.46 ± 0.01 | 0.28 ± 0.38 | |
| 5.61 ± 0.22 | ||
| 6.4 | ||
| ϕ | 0.377 ± 0.008 | 0.338 ± 0.007 |
Fig. 7.
SANS (top) and SESANS (bottom) data of casein micelles in D2O using the double power law scattering function (Eq. (34)). For this fit, all parameter values of the model, except for the SANS background, were linked between data-sets. The model fit parameter values are given in Table 2. Data from B. Tian [30].
![SANS (top) and SESANS (bottom) data of casein micelles in D2O using the double power law scattering function (Eq. (34)). For this fit, all parameter values of the model, except for the SANS background, were linked between data-sets. The model fit parameter values are given in Table 2. Data from B. Tian [30].](https://content.iospress.com:443/media/jnr/2020/22-1/jnr-22-1-jnr200154/jnr-22-jnr200154-g007.jpg)
3.4.Examples of simultaneous constrained fitting of SANS and SESANS data
A simultaneous constrained fit was performed on SANS and SESANS data of spray-dried calcium caseinate micelles in D2O (data from B. Tian, [30]). The data-sets were fitted with a double power law scattering function (Fig. 7).
USANS and SESANS data of poly-styrene spheres in D2O (data from C. Rehm et al. [21]) were also analyzed using simultaneous/constrained fitting. The data-sets were fitted with a solid sphere form factor (Fig. 8) and the fit parameters are listed in Table 3. It should be noted that the USANS and SESANS measurements were not done on the same sample: 2 samples (1 for USANS, 1 for SESANS) were prepared using the same recipe, but were not taken from the same batch. Also, the SESANS sample was synthesized much longer in advance of the experiment than the USANS one. Due to the size of the particles, this led to significant sedimentation of the SESANS sample. For SESANS, multiple scattering correction is included in the data analysis [2,24]. This is not the case for USANS [25] and SasView does not take multiple scattering into account for SANS. These three factors (different samples, sedimentation, and multiple scattering correction) may explain the factor of 5 difference in φ. The fitted value for R (≈ 21300 Å) agrees well with the published data.
Table 2
Fit parameter values for the simultaneous fit of SANS and SESANS of casein micelles in D2O (Fig. 7), using the double power law scattering function (Eq. (34)). Among the parameters, only
| Fit model | SANS | SESANS |
| A | 23.0 | 18.6 |
| C | 0.0009 | 0.0007 |
| 9 × 10 -4 | ||
| 1.19 | ||
| 2.95 | ||
| bkg ( | 0.05 | 0 |
Fig. 8.
USANS (top) and SESANS (bottom) data of polystyrene micro-spheres in D2O using the solid sphere form factor (Eq. (24)). For this fit, only R is constrained to be the same for both data sets, background (bkg) is only a fit parameter for USANS,
![USANS (top) and SESANS (bottom) data of polystyrene micro-spheres in D2O using the solid sphere form factor (Eq. (24)). For this fit, only R is constrained to be the same for both data sets, background (bkg) is only a fit parameter for USANS, Δρ was fixed and φ was fitted freely. For the USANS fit, a “slit smearing” resolution function with Γ1/2=2×10−5 was used. The derived parameter values are given in Table 3. Data from C. Rehm et al. [21].](https://content.iospress.com:443/media/jnr/2020/22-1/jnr-22-1-jnr200154/jnr-22-jnr200154-g008.jpg)
Table 3
Fit parameter values for the simultaneous fit of USANS and SESANS of poly-styrene spheres in D2O using the solid sphere form factor (Eq. (24)) (Fig. 8). R is linked.
| Fit parameter | USANS | SESANS |
| R (Å) | 21295 ± 22 | |
| 1.3 | ||
| φ | 0.293a | |
| bkg | 500a | 0 |
aSasView was unable to determine errors for these fit parameter values.
4.Conclusion
The validation of the numerical Hankel transform of a solid sphere against its projected correlation function showed excellent agreement and demonstrates that the numerical Hankel transform is, by extension, reliable for other SAS models. Fitting using single and multiple data-sets, in batch mode or with constrained fitting parameters has been proven to work without errors and examples of data analyses have been provided. SasView can now be used to analyze SESANS experimental data.
Acknowledgements
The authors would like to thank the SasView development team for their support in enabling user-friendly SESANS data analysis. Of the members of the SasView team, special thanks go to dr. J.R. (Jeffery) Krzywon for help with understanding the SasView code structure in the early stages of the project, dr. A.J. (Andrew) Jackson for keeping a broad perspective and the brief, yet extremely fruitful discussion leading to the understanding that resolution functions are coordinate transforms, dr. P.A. (Paul) Kienzle for extensive discussions and assistance integrating the SESANS routine into the SasView code-base, and P. Rozyczko and W. Potrzebowski for help with GUI integration and ensuring code stability. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. The USANS data presented in this paper was measured on the BT-5 instrument at NCNR (NIST) and the SANS data was measured on the Larmor instrument at ISIS (RAL).
SasView contains code developed with funding from the European Union’s Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement No 654000. The authors acknowledge Nederlandse Organisatie voor Wetenschappelijk Onderzoek Groot grant no. LARMOR 721.012.102.
References
[1] | R. Andersson, W.G. Bouwman, S. Luding and I.M. De Schepper, Stress, strain, and bulk microstructure in a cohesive powder, Physical Review E – Statistical, Nonlinear, and Soft Matter Physics 77: (5) ((2008) ), 051303. doi:10.1103/PhysRevE.77.051303. |
[2] | R. Andersson, L.F. van Heijkamp, I.M. de Schepper and W.G. Bouwman, Analysis of spin-echo small-angle neutron scattering measurements, Journal of Applied Crystallography 41: (5) ((2008) ), 868–885. doi:10.1107/S0021889808026770. |
[3] | G.V. Bhaskar, O.H. Campanella and P.A. Munro, Effect of agitation on the coagulation time of mineral acid casein curd: Application of Smoluchowski’s orthokinetic aggregation theory, Chemical Engineering Science 48: (24) ((1993) ), 4075–4080. doi:10.1016/0009-2509(93)80252-L. |
[4] | W.G. Bouwman, J. Plomp, V.O. de Haan, W.H. Kraan, A.A. van Well, K. Habicht, T. Keller and M. Theo Rekveldt, Real-space neutron scattering methods, Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 586: (1) ((2008) ), 9–14. doi:10.1016/j.nima.2007.11.045. |
[5] | W.G. Bouwman, R. Pynn and M.T. Rekveldt, Comparison of the performance of SANS and SESANS, Physica B: Condensed Matter 350: (1) ((2004) ), E787–E790. doi:10.1016/j.physb.2004.03.205. |
[6] | W.G. Bouwman, O. Uca, S.V. Grigoriev, W.H. Kraan, J. Plomp and M.T. Rekveldt, First quantitative test of spin-echo small-angle neutron scattering, Applied Physics A: Materials Science and Processing 74: (Suppl. I) ((2002) ), s115–s117. doi:10.1007/s003390101081. |
[7] | R.M. Dalgliesh, S. Langridge, J. Plomp, V.O. De Haan and A.A. Van Well, Offspec, the ISIS spin-echo reflectometer, Physica B: Condensed Matter, 406: ((2011) ), 2346–2349. doi:10.1016/j.physb.2010.11.031. |
[8] | C.G. De Kruif, Casein micelle interactions, International Dairy Journal 9: (3–6) ((1999) ), 183–188. doi:10.1016/S0958-6946(99)00058-8. |
[9] | C.G. de Kruif, Supra-aggregates of casein micelles as a prelude to coagulation, Journal of Dairy Science 81: (11) ((2010) ), 3019–3028. doi:10.3168/jds.s0022-0302(98)75866-7. |
[10] | P. Debye, H.R. Anderson and H. Brumberger, Scattering by an inhomogeneous solid. II. The correlation function and its application, Journal of Applied Physics 28: (6) ((1957) ), 679–683. doi:10.1063/1.1722830. |
[11] | P. Debye and A.M. Bueche, Scattering by an inhomogeneous solid, Journal of Applied Physics 20: (6) ((1949) ), 518–525. doi:10.1063/1.1698419. |
[12] | R. Gähler, R. Golub, K. Habicht, T. Keller and J. Felber, Space-time description of neutron spin echo spectrometry, Physica B: Condensed Matter 229: (1) ((1996) ), 1–17. doi:10.1016/S0921-4526(96)00509-1. |
[13] | T. Keller, R. Gähler, H. Kunze and R. Golub, Features and performance of an NRSE spectrometer at BENSC, Neutron News, 6: (3) ((1995) ), 16–17. doi:10.1080/10448639508217694. |
[14] | L. Klimeš, Estimating the correlation function of a self-affine random medium, Pure and Applied Geophysics 159: (7–8) ((2002) ), 1833–1853. doi:10.1007/s00024-002-8711-1. |
[15] | L. Klimeš, Correlation functions of random media, Pure and Applied Geophysics 159: (7–8) ((2002) ), 1811–1831. doi:10.1007/s00024-002-8710-2. |
[16] | J. Kohlbrecher and A. Studer, Transformation cycle for spherical symmetric correlation functions, projected correlation function and small angle scatteringas implemented in SASfit, Journal of Applied Crystallography 50: ((2017) ), 1395–1403. doi:10.1107/S1600576717011979. |
[17] | T. Krouglov, I.M. De Schepper, W.G. Bouwman and M.T. Rekveld, Real-space interpretation of spin-echo small-angle neutron scattering, Journal of Applied Crystallography 36: (1) ((2003) ), 117–124. doi:10.1107/S0021889802020368. |
[18] | A. Kusmin, W.G. Bouwman, A.A. van Well and C. Pappas, Feasibility and applications of the spin-echo modulation option for a small angle neutron scattering instrument at the European Spallation Source, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 856: ((2017) ), 119–132. doi:10.1016/j.nima.2016.12.013. |
[19] | S.R. Parnell, A.L. Washington, K. Li, H. Yan, P. Stonaha, F. Li, T. Wang, A. Walsh, W.C. Chen, A.J. Parnell, J.P.A. Fairclough, D.V. Baxter, W.M. Snow and R. Pynn, Spin echo small angle neutron scattering using a continuously pumped 3He neutron polarisation analyser, Review of Scientific Instruments 86: (2) ((2015) ), 023902. doi:10.1063/1.4909544. |
[20] | J. Plomp, V.O. de Haan, R.M. Dalgliesh, S. Langridge and A.A. van Well, Neutron spin-echo labelling at OffSpec, an ISIS second target station project, Thin Solid Films 515: (14 Spec. Iss.) ((2007) ), 5732–5735. doi:10.1016/j.tsf.2006.12.129. |
[21] | C. Rehm, J. Barker, W.G. Bouwman and R. Pynn, DCD USANS and SESANS: A comparison of two neutron scattering techniques applicable for the study of large-scale structures, Journal of Applied Crystallography 46: (2) ((2013) ), 354–364. doi:10.1107/S0021889812050029. |
[22] | M.T. Rekveldt, Novel SANS instrument using neutron spin echo, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms 114: (3–4) ((1996) ), 366–370. doi:10.1016/0168-583X(96)00213-3. |
[23] | M.T. Rekveldt, J. Plomp, W.G. Bouwman, W.H. Kraan, S. Grigoriev and M. Blaauw, Spin-echo small angle neutron scattering in Delft, Review of Scientific Instruments 76: (3) ((2005) ), 033901. doi:10.1063/1.1858579. |
[24] | M.Th. Rekveldt, W.G. Bouwman, W.H. Kraan, O. Uca, S.V. Grigoriev, K. Habicht and T. Keller, Elastic neutron scattering measurements using Larmor precession of polarized neutrons, in: Neutron Spin Echo Spectroscopy Viscoelasticity Rheology, F. Mezei, C. Pappas and T. Gutberlet, eds, Lecture Notes in Physics, Vol. 601: , Springer, Berlin, (2007) , pp. 87–99. ISBN 978-3-540-44293-6. doi:10.1007/3-540-45823-9. |
[25] | J. Schelten and W. Schmatz, Multiple-scattering treatment for small-angle scattering problems, Journal of Applied Crystallography 13: (4) ((1980) ), 385–390. doi:10.1107/s0021889880012356. |
[26] | Science and Technology Facilities Council, ISIS Target Station 2 – Offspec, https://www.isis.stfc.ac.uk/Pages/Offspec.aspx, http://www.isis.stfc.ac.uk/instruments/Offspec/. |
[27] | Science and Technology Facilities Council, ISIS Target Station 2 – Larmor, https://www.isis.stfc.ac.uk/Pages/Larmor.aspx. |
[28] | M. Shibayama, T. Tanaka and C.C. Han, Small angle neutron scattering study on poly(N-isopropyl acrylamide) gels near their volume-phase transition temperature, Journal of Chemical Physics 97: (9) ((1992) ), 6829–6841. doi:10.1063/1.463636. |
[29] | M. Strobl, B. Betz, R.P. Harti, A. Hilger, N. Kardjilov, I. Manke and C. Gruenzweig, Wavelength-dispersive dark-field contrast: Micrometre structure resolution in neutron imaging with gratings, Journal of Applied Crystallography 49: (2) ((2016) ), 569–573. doi:10.1107/S1600576716002922. |
[30] | B. Tian, Structure and Dynamics of Fibrous Calcium Caseinate Gels Studied by Neutron Scattering, TU Delft University, Delft, (2020) . ISBN 9789402818857. doi:10.4233/uuid:90ed83af-4eca-45bc-af1a-816db85814d9. |
[31] | R.H. Tromp and W.G. Bouwman, A novel application of neutron scattering on dairy products, Food Hydrocolloids 21: (2) ((2007) ), 154–158. doi:10.1016/j.foodhyd.2006.02.008. |
[32] | K. van Gruijthuijsen, W.G. Bouwman, P. Schurtenberger and A. Stradner, Direct comparison of SESANS and SAXS to measure colloidal interactions, EPL (Europhysics Letters) 106: (2) ((2014) ), 28002. doi:10.1209/0295-5075/106/28002. |
[33] | L.F. Van Heijkamp, I.M. De Schepper, M. Strobl, R. Hans Tromp, J.R. Heringa and W.G. Bouwman, Milk gelation studied with small angle neutron scattering techniques and Monte Carlo simulations, Journal of Physical Chemistry A 114: (7) ((2010) ), 2412–2426. doi:10.1021/jp9067735. |
[34] | L.F. Van Heijkamp, A.M. Sevcenco, D. Abou, R. Van Luik, G.C. Krijger, P.L. Hagedoorn, I.M. De Schepper, B. Wolterbeek, G.A. Koning and W.G. Bouwman, Spin-echo small angle neutron scattering analysis of liposomes and bacteria, Journal of Physics: Conference Series, 247: ((2010) ), 012016. doi:10.1088/1742-6596/247/1/012016. |
[35] | A.L. Washington, X. Li, A.B. Schofield, K. Hong, M.R. Fitzsimmons, R. Dalgliesh and R. Pynn, Inter-particle correlations in a hard-sphere colloidal suspension with polymer additives investigated by Spin Echo Small Angle Neutron Scattering (SESANS), Soft Matter 10: (17) ((2014) ), 3016–3026. doi:10.1039/c3sm53027b. |




