Semi-analytical calculations of intrinsic field magnetic field inhomogeneities for a Neutron Spin Echo spectrometer at the ESS
Abstract
Neutron Spin Echo methods (NSE) use Larmor labelling to measure the precession phase of the neutron beam polarization around well-defined magnetic fields. Scattering by a sample can affect the resulting precession phase providing information on the sample’s structure and dynamics with high accuracy and resolution. A major limitation for the performance of Neutron Spin Echo instruments is the homogeneity of the precession magnetic fields. Here we investigate the influence of the new “pancake” moderator, which is being built at the European Spallation Source, on the design of a Neutron Spin Echo spectrometer. The calculations show clear gains when the height to width ratios of the rectangular beam cross-sections mimic those of the ESS “pancake” moderator beams. In such a case the homogeneity of the magnetic field integrals could improve by at least 30%. However, the calculations show that will not be possible to preserve a high resolution and at the same time reduce the length of the instrument. Consequently, NSE spectrometers will perform better at the ESS but they will not be substantially compacter than at other neutron sources e.g. ILL or FRM2.
1.Introduction
Most neutron scattering spectroscopic techniques determine separately the momentum and energy of the incident (
A neutron beam characterised by the wavelength λ and the energy ϵ, has a velocity of
NSE spectrometers [4,9,10,15] measure the intermediate scattering function
The challenge in reaching the longest possible τ consists in realising high field integrals
A Gauss distribution of magnetic field inhomogeneities will lead to a Gauss distribution of precession angles and to a decrease of
The longest Fourier time depends on the minimum acceptable spin-echo signal for an elastic scatterer. The decrease in the spin-echo signal is given by Eq. (4). As seen from Eq. (5), this decrease depends only on the wavelength and the field integral inhomogeneity,
NSE spectrometers typically use longitudinal magnetic fields that are produced by solenoids, a configuration that reduces the intrinsic magnetic field integral inhomogeneities. Nonetheless, in order to reach Fourier times beyond several ns, Fresnel correction coils must be used, which reduce the magnetic field inhomogeneities by several order of magnitude [8]. However, as the performance of NSE spectrometers is pushed towards longer Fourier times, the Fresnel correction coils (classical circular or Pythagoras design) are often a limiting factor, due to the mechanical precision with which they can be manufactured and positioned in the instrument as well as due to the limited current density that can be used without overheating them. It is thus important to opt for a magnetic field design which reduces the intrinsic field integral inhomogeneities and this has been considered as a primary way to further optimise the NSE spectrometers and increase the accessible Fourier times.
The upgraded IN15 [3] as well as a proposal of a NSE spectrometer at the ESS [11] use coils with reduced intrinsic inhomogeneities based on a optimal field shape (OFS) solution suggested by Zeyen [17]. However, for comparable field integral inhomogeneities, the OFS solution requires the use of longer precession regions than simple solenoids. Indeed, for parallel neutron trajectories, the intrinsic field integral inhomogeneity for a solenoid is: [8]
The magnetic field integral inhomogeneities arise from two sources: i) inhomogeneities of the magnetic field which lead to different precession angles for two parallel trajectories of the same length, and ii) beam divergence, which leads to trajectories with different lengths and thus with different precession angles even in a ideally homogeneous magnetic field. The separation of the effects of these two sources was considered by Zeyen [17] and, recently in more detail, by Pasini et al. [11].
In the following we will consider the separation of those two sources in a more general way and apply the results to assess the implications of the “pancake” moderator which is currently planned for the European Spallation Source (ESS) on an NSE instrument design [1,16]. The novelty of this moderator design is that it will produce high-intensity neutron beams over cross sections that are significantly smaller compared to research reactors. In other words, for the same intensity, averaged over time and the beam cross section, the neutron beams will have much smaller dimensions at the ESS than e.g. at the ILL or FRM2. When it comes to the NSE spectrometers first estimates lead to a beam height that can be as small as 1.5 cm, with a beam width reaching 6 cm. In the following we investigate the repercussion these smaller beam cross sections might have on the NSE instrument design. For this purpose, we considered a simple model case, which however catches the main characteristics of a NSE spectrometer. It turns out that irrespective of the choice of magnetic field layout, the use of a rectangular beam cross-section with a moderate aspect ratio of 1:4 (or larger), which mimics the dimensions of the ESS “pancake” moderator beams, reduces the field integral inhomogeneity in comparison to the square cross-sections. However, it will not be possible to preserve a high resolution and at the same time reduce the length of the instrument. Consequently, NSE spectrometers will perform better at the ESS but they will not be substantially compacter than at other neutron sources e.g. ILL or FRM2.
2.Separation of contributions due to magnetic layout and due to beam averages
We start by defining a general layout of a precession region generated by solenoids as shown in Fig. 1. In this case, for a not too large neutron beam (i.e. when
Fig. 1.
Schematic representation of a neutron trajectory, in the
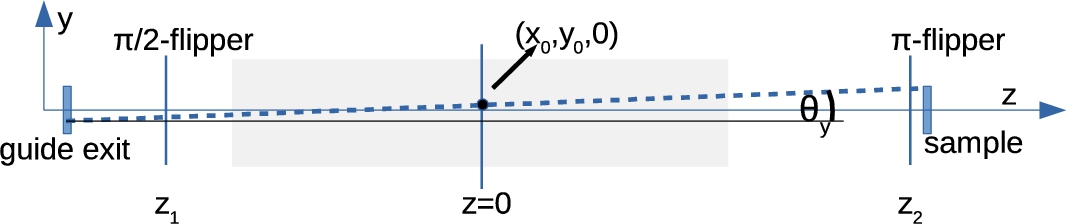
We use the same notations as Pasini et al. [11] and define the mean field integral:
Using Eq. (8), Eq. (11) and Eqs (12)–(15), the deviation from the field line integral,
Equation (17) shows that it is possible to partially decouple effects of magnetic layout – which manifest themselves in the magnitude of H, G, U and effects of beam properties – which manifest themselves in several beam averages
Equation (16) and Eq. (17) are qualitatively similar to the Eq. (12), and Eq. (26), respectively, provided in the paper of Pasini et al. [11], with the difference that they are valid for any shape of a neutron beam. The contribution of one arm to the reduction of spin-echo amplitude is then given by:
From Eq. (18), it is apparent that in order to reach longer Fourier times, one needs to minimize the intrinsic field integral inhomogeneity. For this purpose one must consider which terms contribute the most in Eq. (17), and how these can be minimised.
In the special case, where
In Eq. (19), the prefactors
3.Calculation details
The calculation of the field integral inhomogeneity,
Fig. 2.
Schematic drawing of the first arm of a NSE spectrometer. The magnetic layout is characterized by the lengths L,
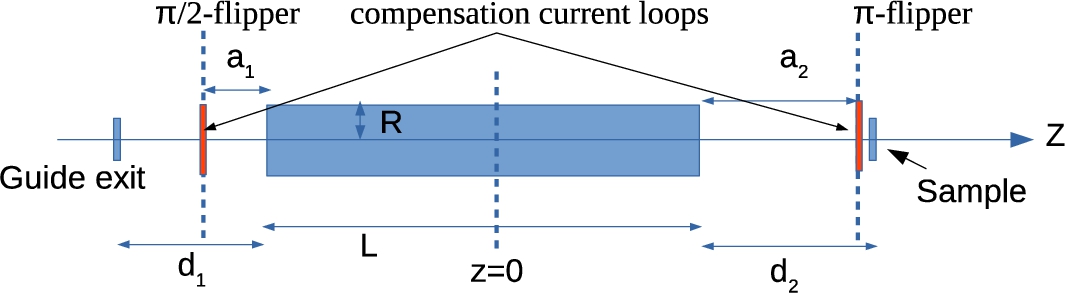
3.1.Magnetic field integrals
In order to evaluate the magnetic field integrals, one needs to calculate
The lower and upper integral boundaries,
The integrals of Eqs (13)–(15) were calculated using Mathematica®, based on Eq. (21), Eq. (25) and
3.2.Beam averages
As it can be seen from the definition of θ in Section 2, the
4.Results
4.1.Symmetric magnetic layout
We first consider the special case where
We also consider rectangular and circular cross-sections both for the guide exit and the sample. As can be seen from the general results provided in the Appendix A, the beam averages depend on the distance from the guide exit to the sample, and on the position of the main coil with respect to the start and end of neutron trajectories. For this reason, in the following we will first consider the symmetric setup, where
4.1.1.Minimization of beam averages for a symmetric beam setup
The general expressions for the beam averages,
Similar results are obtained in the case where the sample size is much smaller than that of the guide exit, as shown in the lower part of Table 1. Also in this case, a change of the aspect ratio from 1:1 to 1:4 leads to a decrease in the beam averages by at least a factor of 3. The trend persists also in the case, where the sample size is much larger than the size of the guide exit. These results are not shown in Table 1 because they are exactly the same as for the previous case, provided
Table 1
Beam averages calculated for the symmetric beam setup (
| Averages & conditions | Guide shape | ||||
| Rectangle | “pancake” ( | Square ( | Circle | ||
| Sample size is the same as of the guide exit | |||||
| 0.067 | 0.070 | 0.189 | 0.1042 | ||
| 0.044 | 0.058 | 0.311 | 0.1667 | ||
| 1.07 | 1.13 | 3.02 | 1.67 | ||
| Sample is much smaller than the guide exit | |||||
| 0.0125 | 0.0134 | 0.0389 | 0.0208 | ||
| 0.05 | 0.054 | 0.156 | 0.0833 | ||
| 0.2 | 0.215 | 0.622 | 0.3333 | ||
4.1.2.Minimization of beam averages for an asymmetric beam setup
If the sample size is the same as that of the guide exit, the minima in
Fig. 3.
Optimal s-parameter obtained by minimising the beam averages,
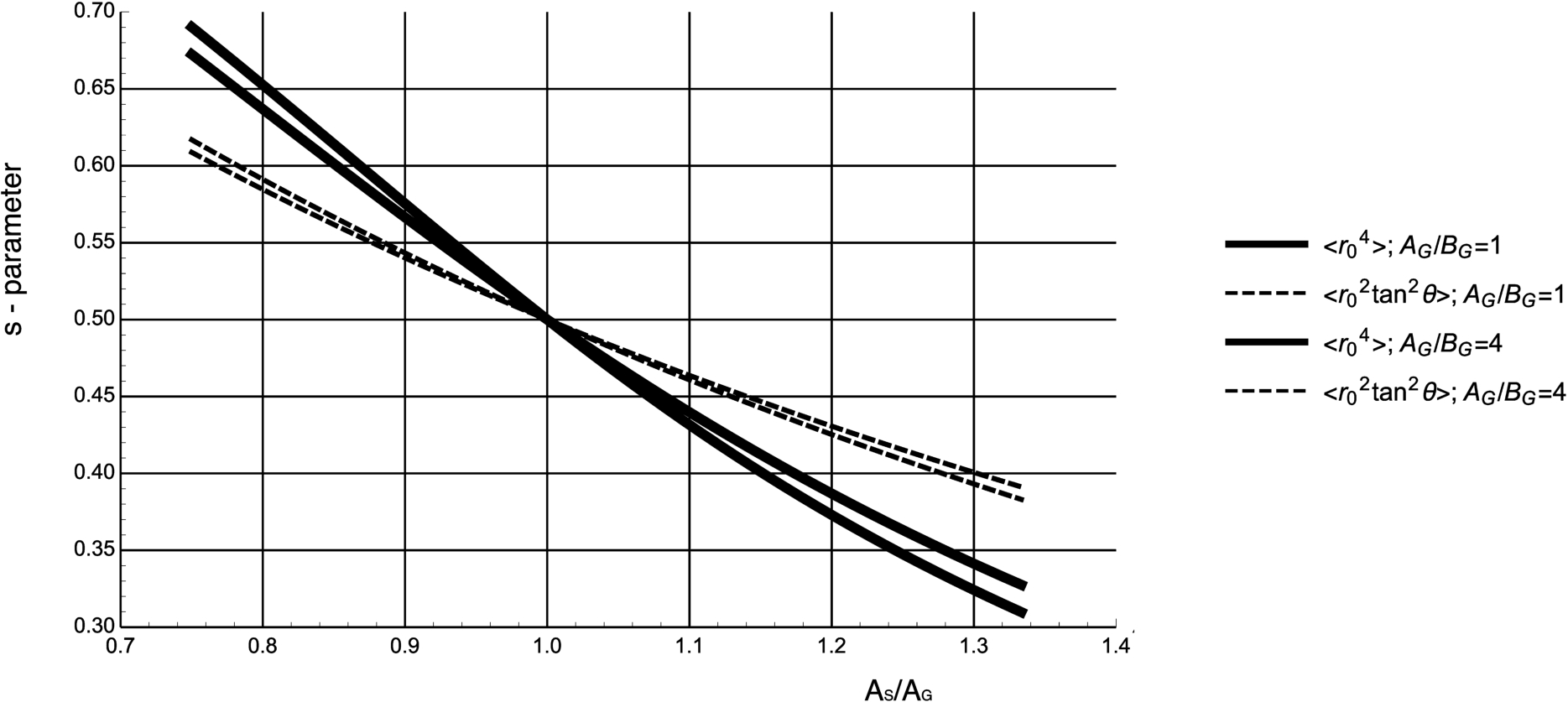
In practice, the geometry of the NSE spectrometers is fixed. Nonetheless, it may be possible to increase s by increasing
For a specific instrument geometry, the good compromise for the value of the s-parameter may result from the minimum of
In the next section, we consider the contributions from the intrinsic magnetic field inhomogeneity and show that for a solenoid, it is more important to minimize
4.1.3.Minimization of intrinsic magnetic field inhomogeneity
In principle, the length of the magnetic layout, which is
The beam averages were discussed in the previous section and in the following we will look at their pre-factors in Eq. (20). We evaluated
Fig. 4.
Calculated magnetic layout-dependent contributions to
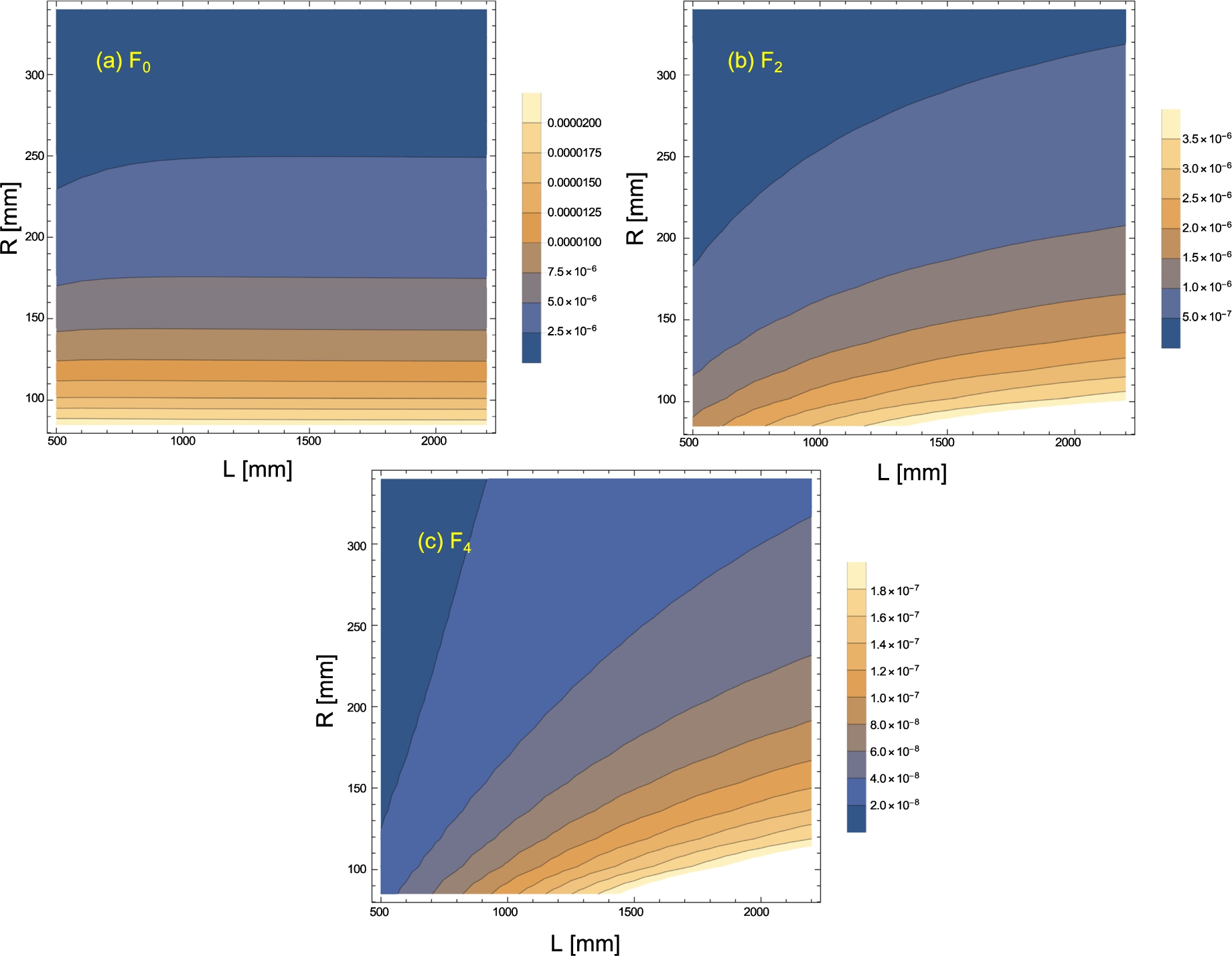
Thus, for a solenoid, the major contribution to
The other terms reduce slightly the absolute field inhomogeneities for shorter coils. However, as the mean field integral is proportional to the coil length, the relative field integral inhomogeneity will be lower (i.e. better) for longer coils.
4.2.Asymmetric magnetic layout
In general, the magnetic layouts of the NSE instruments are not necessarily symmetric. For example, the distance between the first
We note that beam averages of
Fig. 5.
Calculated magnetic layout-dependent contributions for an asymmetric magnetic layout (
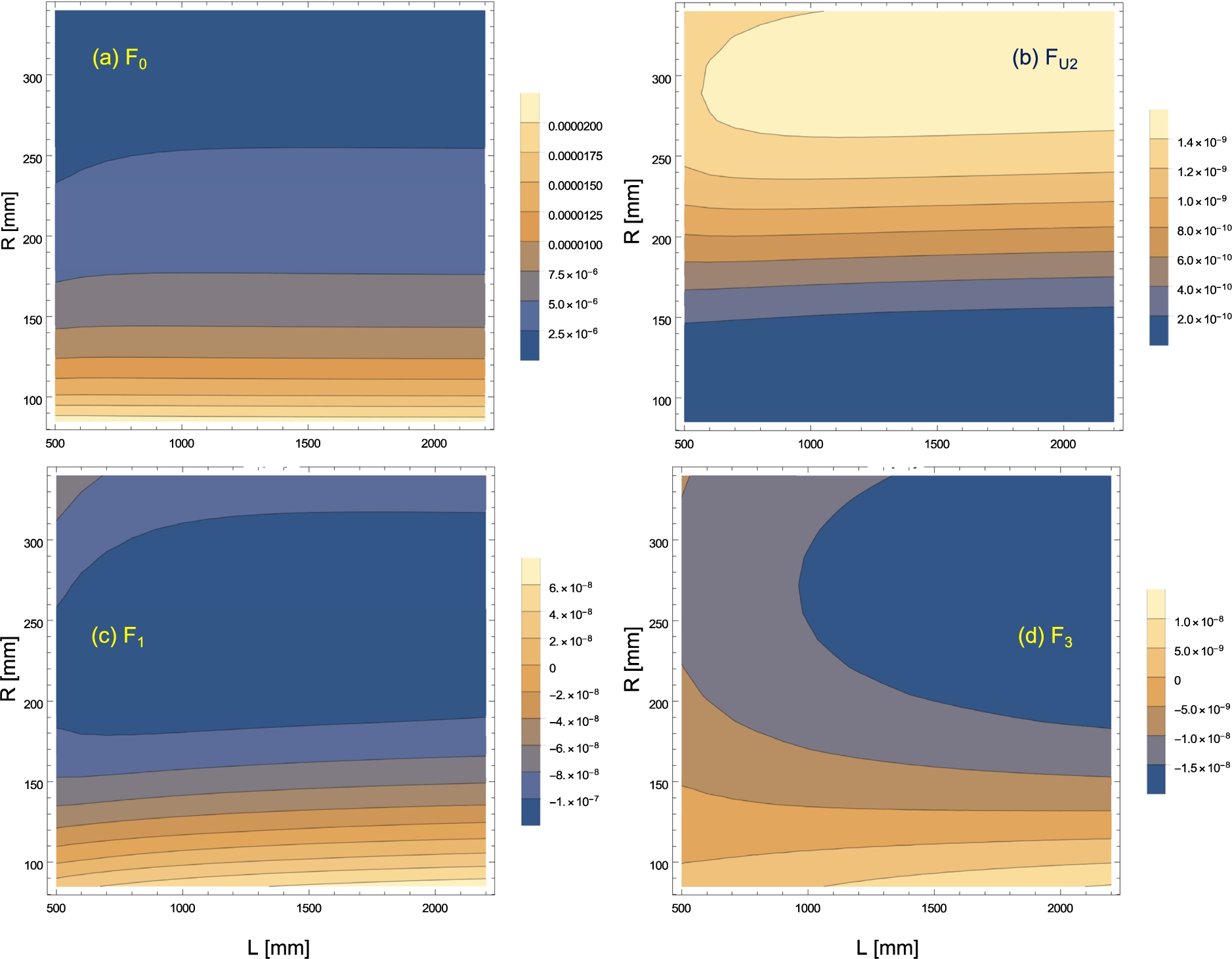
5.Conclusion
Before moving to the conclusions, it is important to note that our calculations involve only the first arm of an NSE spectrometer. Nonetheless, all considerations can also be applied for the second arm and the magnetic fields after the sample. An important difference, however, is that detector size is much larger than that of the sample. This is analogous to the case of a guide exit much smaller than the size of the sample and the results obtained in this case can be applied. In this respect we note that all existing instruments have adopted a symmetric configuration with the same coil geometry before and after the sample. However, if the difference between the guide and detector dimensions exceeds the present “standard”, as it might be the case at a future NSE instrument at the ESS, one might consider adopting a non-symmetric setup with a different magnetic field optimisation before and after the sample. On the other hand, as the layout of the instrument will not be fundamentally affected by the reduced incoming beam dimensions, one may consider “expanding” the neutron beam cross-section in the vertical direction, by inserting a “polarising-all-neutrons” device in the beam delivery system [14], and thus partly restore the symmetry between the two arms of the spectrometer while benefiting from a higher neutron flux.
The semi-analytical magnetic field calculations discussed above show that a circular shape for the sample and the guide exit leads to lower field integral inhomogeneity in comparison to a square one. However, in practice, guides usually have square or rectangular cross-sections and so do the detectors. Using circular beam masks would lead to a loss of flux. By choosing rectangular cross-sections with a moderate aspect ratio, e.g. 1:4, one can reach even smaller beam averages than for circular shape.
Consequently, there is a clear gain with the “pancake” moderator beams. Indeed, rectangular beam cross-sections with a height over width ratio, e.g. 1:4, that mimic the ESS “pancake” moderator beams lead to the best results, and improve the homogeneity of the magnetic field integrals. On the other hand, because relative inhomogeneities become worse for shorter coils, in order to reach high resolution, i.e. long Fourier times, the length of the instruments cannot be reduced. NSE spectrometers should perform better at the ESS, but they will not be more compact than e.g. at the ILL or FRM2.
Notes
1 The neutron beam trajectories before and after the sample are one-to-one correlated in the case of the direct beam (the part of the beam that has not been scattered by the sample) and the Bragg peaks. This feature is very important for the design and operation of SESANS [5,13] and Larmor diffraction [12] instruments.
Acknowledgements
 This work was performed within the World class Science and Innovation with Neutrons in Europe 2020 (“SINE2020”) project, funded by the European Commission, Grant Agreement no. 654000.
This work was performed within the World class Science and Innovation with Neutrons in Europe 2020 (“SINE2020”) project, funded by the European Commission, Grant Agreement no. 654000.
Appendices
Appendix A.
Appendix A.Beam averages
For the calculations of beam averages we use the definition of
A.1.A rectangular cross-section
An average is a multiple integral
The s-values corresponding to the respective minima can be obtained by imposing the conditions
We do not provide the expressions for the optimum s as a function of
A.2.A circular cross-section
For an average over a circular guide exit with a radius
The results are
For
Appendix B.
Appendix B.Beam averages for calculation of the contributions that involve U
For the calculations of
Table 2
Beam averages calculated from Eqs. (B.1)–(B.3) for a rectangular guide exit and sample shapes and for different values of the s-parameter and the aspect ratio
| Sample and guide exit of the same size, | ||||||
| 0 | 0 | −0.067 | −0.021 | 0.067 | 0.021 | |
| 0 | 0 | −0.377 | −0.141 | 0.377 | 0.141 | |
| 0.089 | 0.045 | 0.136 | 0.062 | 0.136 | 0.062 | |
| Sample smaller than the guide exit, | ||||||
| −0.053 | −0.018 | −0.112 | −0.037 | −0.014 | −0.006 | |
| −0.213 | −0.073 | −0.440 | −0.158 | 0.015 | 0.011 | |
| 0.080 | 0.035 | 0.161 | 0.064 | 0.055 | 0.028 | |
| Sample larger than the guide exit, | ||||||
| 0.112 | 0.039 | 0.010 | 0.007 | 0.257 | 0.085 | |
| 0.448 | 0.154 | −0.166 | −0.073 | 1.06 | 0.38 | |
| 0.188 | 0.087 | 0.153 | 0.077 | 0.377 | 0.154 | |
References
[1] | K.H. Andersen, M. Bertelsen, L. Zanini, E.B. Klinkby, T. Schonfeldt, P.M. Bentley and J. Šaroun, Optimization of moderators and beam extraction at the ESSThis article will form part of a virtual special issue on advanced neutron scattering instrumentation, marking the 50th anniversary of the journal, J. Appl. Cryst 51: ((2018) ), 264–281. doi:10.1107/S1600576718002406. |
[2] | O. Chubar, P. Elleaume and J. Chavanne, A three-dimensional magnetostatics computer code for insertion devices, J. Synchrotron. Rad. 5: ((1998) ), 481–484. doi:10.1107/S0909049597013502. |
[3] | B. Farago, P. Falus, I. Hoffmann, M. Gradzielski, F. Thomas and C. Gomez, The IN15 upgrade, Neutron News 26: (3) ((2015) ), 15–17. doi:10.1080/10448632.2015.1057052. |
[4] | O. Holderer, M. Monkenbusch, R. Schätzler, H. Kleines, W. Westerhausen and D. Richter, The JCNS neutron spin-echo spectrometer J-NSE at the FRM II, Measurement Science and Technology 19: (3) ((2008) ), 034022. doi:10.1088/0957-0233/19/3/034022. |
[5] | T. Keller, R. Gaehler, H. Kunze and R. Golub, Features and performance of an NRSE spectrometer at BENSC, Neutron News 6: (3) ((1995) ), 16–17. doi:10.1080/10448639508217694. |
[6] | F. Mezei, The Neutron Spin Echo method, in: Neutron Spin Echo, F. Mezei, ed., Springer-Verlag, (1980) , pp. 3–26. doi:10.1007/3-540-10004-0. |
[7] | F. Mezei, Coherent approach to neutron beam polarization, Imaging Processes and Coherence in Physics 112: ((1980) ), 279. |
[8] | F. Mezei, Conclusion: Critical points and future progress, in: Neutron Spin Echo, F. Mezei, ed., Springer-Verlag, (1980) , pp. 178–192. doi:10.1007/3-540-10004-0. |
[9] | M. Ohl, M. Monkenbusch, D. Richter, C. Pappas, K. Lieutenant, T. Krist, G. Zsigmond and F. Mezei, The high-resolution neutron spin-echo spectrometer for the SNS with |
[10] | C. Pappas, G. Kali, T. Krist, P. Böni and F. Mezei, Wide angle NSE: The multidetector spectrometer SPAN at BENSC, Physica B: Physics of Condensed Matter 283: (4) ((2000) ), 365–371. doi:10.1016/S0921-4526(00)00341-0. |
[11] | S. Pasini and M. Monkenbusch, Optimized superconducting coils for a high-resolution neutron spin-echo spectrometer at the European Spallation Source, ESS, Meas. Sci. Technol. 26: (3) ((2015) ). |
[12] | M. Rekveldt, T. Keller and R. Golub, Larmor precession, a technique for high-sensitivity neutron diffraction, Europhysics Letters (EPL) (2001). |
[13] | M.T. Rekveldt, Neutron reflectometry and SANS by neutron spin echo, Physica B 234: ((1997) ), 1135–1137. doi:10.1016/S0921-4526(97)00138-5. |
[14] | D.M. Rodriguez, P.M. Bentley and C. Pappas, How to polarise all neutrons in one beam: A high performance polariser and neutron transport system, Journal of Physics: Conference Series 746: (1) ((2016) ), 012015. |
[15] | P. Schleger, B. Alefeld, J. Barthelemy, G. Ehlers, B. Farago, P. Giraud, C. Hayes, A. Kollmar, C. Lartigue and F. Mezei, The long-wavelength neutron spin-echo spectrometer IN15 at the Institut Laue-Langevin, Physica B-Condensed Matter 241: ((1997) ), 164–165. doi:10.1016/S0921-4526(97)00539-5. |
[16] | L. Zanini, K. Batkov, E. Klinkby, F. Mezei, E. Pitcher and A. Takibayev, Moderator configuration options for ESS, JAEA-Conf 126: ((2015) ). |
[17] | C. Zeyen and P. Rem, Optimal Larmor precession magnetic field shapes: Application to neutron spin echo three-axis spectrometry, Meas. Sci. Technol. 7: (5) ((1996) ), 782–791. doi:10.1088/0957-0233/7/5/010. |




