Study on population behavior under home quarantine policies of COVID-19 in China based on double-layer network evolutionary games
Abstract
In the practice of COVID-19 prevention and control in China, the home quarantine policy directly connects and manages the residents, which plays a significant role in preventing the spread of the epi-demic in the community. We evaluate the effectiveness of current home quarantine policy in the actual execution process based on the evolutionary game relationship between the community and res-idents. This paper establishes a double-layer coupled complex network game model, and uses the multi-agent modeling method to study the game relationship between the community and residents in the context of home quarantine policies. The results show that initial strategy of the community with strict supervision and reasonable government reward allocation will increase the proportion of the residents complying with the quarantine rule. When 80% of the communities chose to supervise strictly at the beginning, people are more likely to follow the rules. While when the residents can only get 20% of the government’s reward, the proportion of choosing to violate the quarantine rules is much higher than that when they can get 80% of the reward. Besides, the structure of small-world network and environmental noise will also affect the residents’ strategy. As the probability of reconnection of the small-world network rises from 0.2 to 0.8, the proportion of residents who choose to comply with the strategy becomes much higher. When the environmental noise reaches 0.5, the ratio of residents who choose to violate the strategy is higher than the ratio of complianc. The study is helpful to provide the basis for the government to formulate the quarantine policy and propose an optimization for making effective quarantine measures. In this way, the government can adjust the parameters to make residents achieve the possible level of compliance with quarantine policies as high as possible to contain the spread of the epidemic.
1Introduction
With the gradual and effective control of the COVID-19, China has entered the regular stage of epidemic prevention and control. The domestic epidemic situation is generally stable, while clusters of epidemics caused by sporadic cases have appeared in some areas. The effective identification and control of sporadic cases has become an important link in preventing the further spread of the epidemic. In this stage, instead of nationwide strict prevention and control policies, more refined non-therapeutic and targeted measures have efficiently contained several COVID-19 clusters [1].
China has mainly established seven protection and prevention networks in different layers, as shown in Fig. 1, including hospital treatment, Fangcang hospitals, vaccination, centralized isolation, nucleic acid test, home quarantine and mask wearing, while hospital treatment, medical isolation and vaccination are hospital-level measures, the first two layers correspond to different types of infected people: for patients with severe syndrome, they are sent into hospitals for admission and treatment; as for mild and asymptomatic patients, Fangcang hospitals have been set up to ensure their recovery. Centralized isolation and nucleic acid test are measures taken by the government, nucleic acid test is used to screen all vulnerable people, while suspected patients, patients with fever who cannot rule out the possibility of infection and close contacts need to be isolated collectively under medical observation. Home quarantine belongs to the community layer, which can effectively prevent the spread of the disease among communities. Mask wearing is the most common and extensive protection measure in the resident layer. The protection and prevention system takes measures to different groups of people from top to bottom in the aspects of hospitals, governments, communities and residents, which has largely controlled the spread of the epidemic.
Fig. 1
Epidemic prevention and control network system in China.

According to the Guidelines on the Novel Coronavirus-Infected Pneumonia Diagnosis and Treatment (version 8), there are four categories of people for home quarantine and medical observation: close contacts and special groups of people in close contacts; people entering China under the “7 + 7” policy; patients discharged from hospital and asymptomatic infected people released from quarantine; others who are assessed as unable to be placed under centralized isolation for medical observation by professionals. Due to the large scale of residents and high management costs, the home quarantine rule is often actually supervised and executed by the local communities. Marston, C et al. emphasized the necessity of the participation of communities in a pandemic as they are well placed to work with others to design collective response [2]. In China, the community played an important role in controlling the transmission of COVID-19. The National Health and Construction Commission of China issued the “Notice on Strengthening Community Prevention and Control of Pneumonia Epidemics Caused by Novel Coronavirus Infection”[3], claiming that comprehensive prevention and control measures based on communities should be put forward in a scientific and orderly manner, detect cases as early as possible and contain the spread of the epidemic effectively. However, at present, quarantine policies implemented in each area are different, and there is no unified definition, which brings confusion in practice. Currently, due to a lack of personnel and awareness of epidemic prevention, it is difficult to enforce home quarantine, which is one of problems that the grassroots epidemic prevention and control faces.
In recent years, with the reform of community governance, the interests of administrative forces and social forces in community governance are intertwined and complicated, so there is a long-term game relationship. In managing public health emergencies, there exist conflicts of interest among governments, communities, and residents, so it is important to analyze the interaction of each party’s behavior strategy [4]. In the process of the epidemic quarantine policies, the community replaces the government to supervise and manage residents who need to be quarantined; moreover, due to the system of community-level self-governance, there exists initiatives in the actual execution of the work. Therefore, there will be an interactive game between the community and residents, and the decisions of each subject will affect the effect of the quarantine policies.
Since the outbreak of COVID-19 epidemic, scholars from various countries have carried out researches from different aspects based on the classical epidemiological transmission model (Susceptible Infected Recovered Model, SIR) proposed by Kermack and McKendrick [5]. Some scholars have improved the model according to the characteristics of COVID-19, and the effect of epidemic prevention and control measures on controlling the spread of the epidemic was studied. Tang et al. explored the impact of quarantine and isolation measures on the final stage of the development of the epidemic in China based on the SEIR model [6]. Zhang et al. utilized the SICRD model to find that the time and intensity of intervention play an important role in controlling the scale of the epidemic [7]. The study by Hellewell et al. proved that in most cases, highly effective contact tracing and case isolation are sufficient to control a new outbreak of COVID-19 within 3 months [8].
These studies mainly analyzed and predicted the transmission dynamics of the COVID-19 based on a homogeneous network, that is, they assumed that the contact probabilities of different individuals in the network were the same, without considering the impact of the topology of the social network on the spread of the epidemic. However, the actual network is often not homogeneous, with the characteristics of small world and scale-free [9]. Considering that, other scholars supplemented relevant studies based on the complex network structure.
Newman proved that the SIR model could be accurately solved on a variety of networks [10]. Subsequently, Pastor-Satorras and Vespignani simulated the spread of infectious diseases on scale-free networks and discovered infectious diseases were ubiquitous in scale-free networks, and the topology of the network had a great influence on the spread of infectious diseases [11]. In recent years, with the popularity of complex network research, more scholars have considered the impact of network topology when studying the spread of COVID-19 epidemic. Wang et al. considered the heterogeneity of the number of contacts on the basis of asymptomatic infections in the SLIAR model [12] and studied the spreading dynamics of influenza-like diseases in the two non-uniform networks which are quenching network and annealing network [13]. In addition, other scholars have considered other realistic factors on the basis of complex networks and infectious disease models. For example, Zhang and Li constructed a random SEIR epidemic dynamic model that considers migration and human consciousness [14].
Compared with the study of transmission dynamics in a single-layer network, the real disease transmission process can be described more accurately in a double-layer or a multi-layer network. Zheng et al. constructed a two-layer network UAU-SIR model to characterize the coupling between the spread of infectious diseases and disease-related information or consciousness, and used the Markov chain method to work out the epidemic threshold [15]. This is an advanced method focusing on epidemic dynamics on multiple-layer coupling complex networks, and can describe the real transmission process than single-layer and homogeneous networks network transmission dynamics more accurately.
In addition, there are some scholars also used evolutionary game methods to study on major emergency public health events. Liu et al. combined the evolutionary game between the government and the public with the SI model, taking the large-scale spread of the epidemic, the control of the epidemic, and the active governance and control into account and fitted the stage of epidemic spread in these three situations of management and control [16]. Fan et al. used evolutionary game and system dynamics methods to study the evolutionary strategic stability points of the government, the community and the residents under dynamic and static reward and punishment mechanisms in public health emergency management [4].
The traditional evolutionary game describes the relationship between individual and group behavior from the perspective of system, and introduces the factors that affect individual behavior in the evolutionary model, thus affecting the group’s decision-making behavior. Based on complex network theory, network evolutionary game describes the relationship between individual and group behavior more accurately, and provides a new perspective of group evolution, which can be used to analyze the evolution process of complex multi-agent system. Existing researches on infectious diseases mainly focus on combining complex networks with infectious disease models, or using evolutionary games for analysis. Few combine evolutionary games with multi-layer complex networks to study how different subjects interact with each other in the study on COVID-19. Considering this, in addition to the advanced method mentioned above [15], this study adopts the method combining evolutionary game theory and double-layer coupling network to model public health event policy, hoping to carry out research from micro and macro perspectives and draw novel conclusions.
Therefore, based on the perspective of the game relationships between the community and the quarantined residents on a double-layer complex network, this paper analyses the impact of the implementation of the quarantine rules under the different strategic choices of the two parties, explores the evolutionary behavior and learning mechanism of the two game subjects of the community and the residents, and simulates evolution mechanism in the conditions of different parameters using Agent-Based Modeling(ABM) method. This paper aims to evaluate the home quarantine policy of COVID-19 prevention in China, and to figure out whether and to what extent residents will comply with the quarantine policy under different situations. According to the results of analysis, this paper is committed to shedding light on optimization suggestions during the process of developing and implementing policies and provide effective decision-making basis for the formulation of effective epidemic prevention measures.
The novelty of this paper can be divided into practical contributions and theoretical contributions. As for practical contributions, this research is of great significance to clarify the interest relationship among communities and residents for the improvement of the emergency prevention and control system and the implementation of prevention and control policies. In major public health emergencies, the community allocates resources, contacts the masses and mediates conflicts from the micro level to ensure the effective implementation of policies. While residents are the most basic nodes in the social network, and their extensive participation and positive response have an important impact on the effectiveness of the prevention and control. The strategies of two subjects complement and influence each other, and neither is indispensable. Based on realistic scenarios, this paper analyzes the roles and functions of communities and residents respectively in public health emergencies. It contributes to studying the influence of interest game and strategy learning on the implementation of prevention and control policies among them, which can better promote the construction of emergency prevention and control system.
In terms of theoretical contributions, firstly, this paper concludes the epidemic prevention and control network system in China, where the community layer and the resident layer play important roles in the protection and prevention networks. It shows the construction of the collaborative management system of public health emergencies is a social system project that requires the cooperation of multiple subjects. Therefore, the mechanism and platform of multi-subjects’ collaborative participation in the emergency management is of great significance for the improvement of the emergency prevention and control system. Secondly, a two-layer complex coupling network is established to simulate the evolutionary behavior and learning mechanism of the two game players, community and residents, from a micro perspective, and the effectiveness of epidemic prevention policies was fitted from multiple perspectives. This paper gives contributions to combining the evolutionary game theory and two-layer complex coupling network in the field of public health emergencies, which may provide a new methodological perspective for follow-up relative research.
The rest of the paper is organized as follows: Section 2 establishes the evolutionary game model and double-layer complex network. Section 3 simulates the results of evolutionary game under different conditions of related parameters, and the analysis of the effect of rules and implications for optimization are given in Section 4.
2Materials and Methods
2.1Evolutionary game model
2.1.1Two-party game strategies
When implementing the quarantine policy, the community needs to implement certain supervision measures for the quarantined group, including registering the information of quarantined people, conducting health tests regularly etc. According to the Protocol for Prevention and Control of COVID-19 (Edition 7), during the home medical observation period, community staff should register the home-quarantined observers in their jurisdiction. If the home-quarantined observers develop fever, dry cough, fatigue, diarrhea and other symptoms, community health services staff should promptly report to the local health administrative department and the centers for disease control and prevention in the district, and transfer them to designated medical institutions for investigation, diagnosis and treatment according to regulations [17].
In the process, relevant staff in the community can choose to strictly supervise people who are quarantined at home, such as daily visits, registration temperature measurement, daily patrols, etc.; they can also choose inaction, which means no specific supervision measures are taken for quarantined people, so the strategic space of the community is Scommunity = (Y1: active supervision, Y2: inaction), the probabilities of the two strategies are y and 1 –y, respectively. Residents who need to be quarantined can choose to follow the 14-day home quarantine policies, or they can choose to violate the rules and go out for free activities. Their strategic space is Sresidents = (X1: compliance, X2: violation), the probabilities of the two strategies are x and 1 - x, respectively.
2.1.2The establishment of game model
For the community, actively monitoring includes taking regular temperature measurement, timely reporting, real-time supervision, etc., which costs labor, material, financial, and time. These costs are recorded as C. The residents will also afford a certain amount of time and money due to the inability to go out, work, or associate with others under the requirements of home quarantine, which is recorded as a. At this time, because the epidemic is effectively controlled, the community and the residents will jointly receive a government reward of E. Assume that the reward distribution ratio obtained by the community is w, while the proportion of people’ is 1-w.
When the residents violate the rules, they shall be imposed a fine or other punishments according to the law in China, and this penalty amount is recorded as b. Only when the community chooses active supervision, people who violate the rules will be punished at the cost of b with a certain probability q (qb > a), q denotes the possibility that their misbehavior is discovered by the local community. At the same time, a violation of the quarantine rules will cause the expansion of the spread of the epidemic with the probability of p, which will have a negative impact on the society. We let V denote the loss of social benefits, which is suffered by the community, then the loss of the community is recognized as pV.
When the community takes inaction, namely there is no cost to governance the residents. In this situation, if people choose to comply with the rules, then their cost is still a; if they choose to violate, it will cause the epidemic to spread widely with the probability p, thus causing loss to the community at the cost of pV, while there is no punishment for them due to the community’s inaction. The parameters of the game model and their definitions are shown in Table 1:
Table 1
Related parameters and definition
| Parameter | Definition |
| x | The probability that the residents comply with the quarantine rules, then the probability that the residents violate the quarantine rules is 1-x, 0≤x≤1 |
| y | The probability that the local community chooses active supervision on the residents, then the probability that the local community chooses inaction is 1-y, 0≤y≤1 |
| b | The punishment when residents are punished by the community when they violate the quarantine rules |
| a | The cost of time and money paid by the residents to comply with the quarantine rules |
| C | Costs incurred by the community when the nearby community actively supervises |
| V | The loss of the local community due to the expansion of the epidemic |
| E | The government’s reward when the community chooses to actively supervise and the residents chooses compliance |
| w | The distribution ratio of government rewards received by the community |
| 1-w | The distribution ratio of government rewards received by residents |
| q | The probability that the residents will be punished by the community for violating the quarantine rules when the community actively supervises |
| p | The probability that residents’ violation of the quarantine rules will cause the spread of the epidemic to expand |
The payment matrix of both parties is shown in Table 2:
The payment matrix of both parties is shown in Table 2:
Table 2
Game payment matrix of community and residents
| Residents | Local community | |
| Active supervision y | Inaction 1-y | |
| Compliance x | -a+(1-w)E | -a |
| -C+wE | 0 | |
| Violation 1-x | -bq | 0 |
| -C-pV | -pV | |
2.2Construction of a double-layer complex network
2.2.1The construction logic of a double-layer network
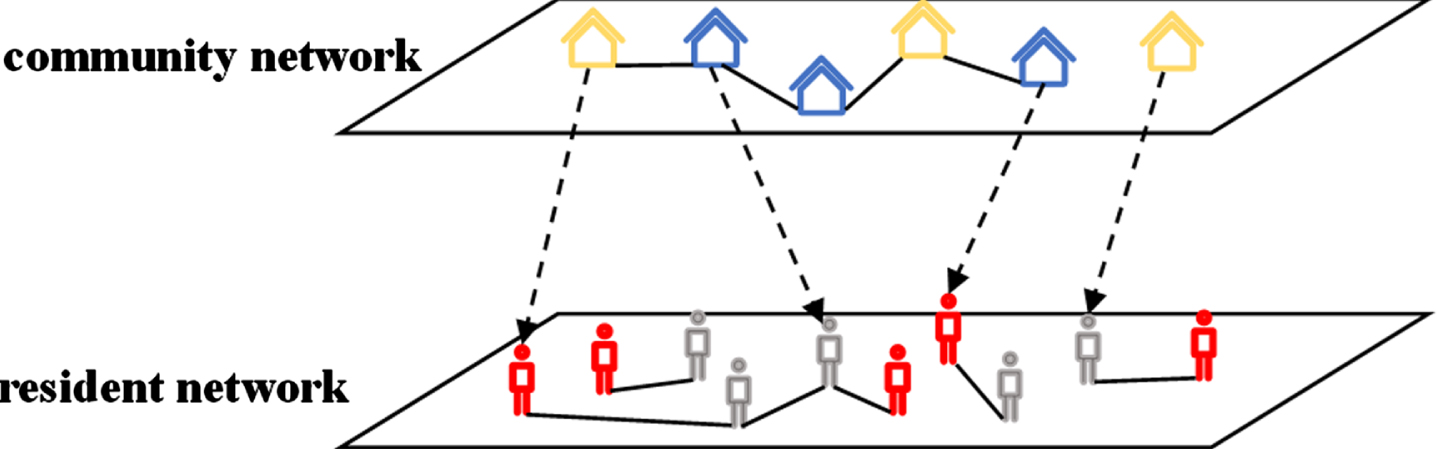
The relationship between two groups of the community and the residents is supervision and supervised, namely the local community supervises residents who need to be quarantined and residents are supervised by the local community. And the relationship within each group is the general homogeneity relationship, which means they can learn from each other’s strategies. This article regards the community network as the upper-level network, in which each node in the network represents each community in the reality and each edge represents a neighbor relationship; while the social network of residents is recognized as the lower-level network, in which each node represents each resident in the society and each edge represents a neighbor relationship.
2.2.2The construction of sub-networks of the community and residents
Related studies have found that real social networks have the characteristics of a small world, that is, the network has a large clustering coefficient and a small average distance [18]. Therefore, this article uses an undirected and unauthorized small-world network to describe the social network of the residents, which means some people who have few social relationships in the network can be connected through a few short acquaintance relationships. A connected and undirected edge in this network means that two nodes have a social relationship, which includes online and offline connections, and the nodes are closely connected.
The number of nodes in the community network is relatively small, and the distribution is relatively independent. To simplify the analysis, it is assumed that the distribution of nodes on the community network has the characteristics of the ER network.
2.2.3The construction of a double-layer network of the community and the residents
The community nodes in the upper network establish a directed connection with the residents nodes in the lower network according to the principle of distance priority, that is, a community node will establish a supervision and supervised directed connection with residents nodes that are close to them. And a community node can establish multiple connections with different residents nodes in the lower-level network, while each residents node can only have one connection with the closest community node in the upper-level network. The double-layer network is shown in Fig. 2:
Fig. 2
double-layer network visualization of communities and residents.
2.3Evolutionary game model on the double-layer network
2.3.1Hypothesis
Hypothesis 1: Both communities and residents are bounded rationality, they choose strategies according to their expected return, and there is a certain probability that the optimal strategy is not selected by two parties;
Hypothesis 2: Communities and residents have game relationships with neighbors in another layer of the network who have established a directed connection with each other;
Hypothesis 3: Two groups can learn from neighbor nodes in the same layer of the network, and their strategic update is based on the comparison with their neighbors on the result of payoffs in the previous game.
2.3.2The establishment of game model
The community network and the residents’ social network are represented as Ga = (V, E), (a = 1,2), V represents the collection of all nodes in the network, E = eij represents the collection of all edges. G1 = (V1,E1)represents the community network (the upper-level network), G2 = (V2,E2) represents the residents’ social network(the lower-level network). i represents a node in the network G1, j represents a node in the network G2, li and lj represents the degree of node i in the network G1 and node j in the network G2 respectively, si represents the strategy of node i selection in network G1, sj indicates the strategy selected by node j in the network G2. The nodes in the community network will play games with their neighbor nodes in the residents’ social network according to the game matrix in Table 2.
The game evolution rules of the double-layer network are as shown in Fig. 3:
Fig. 3
The process of the game model.
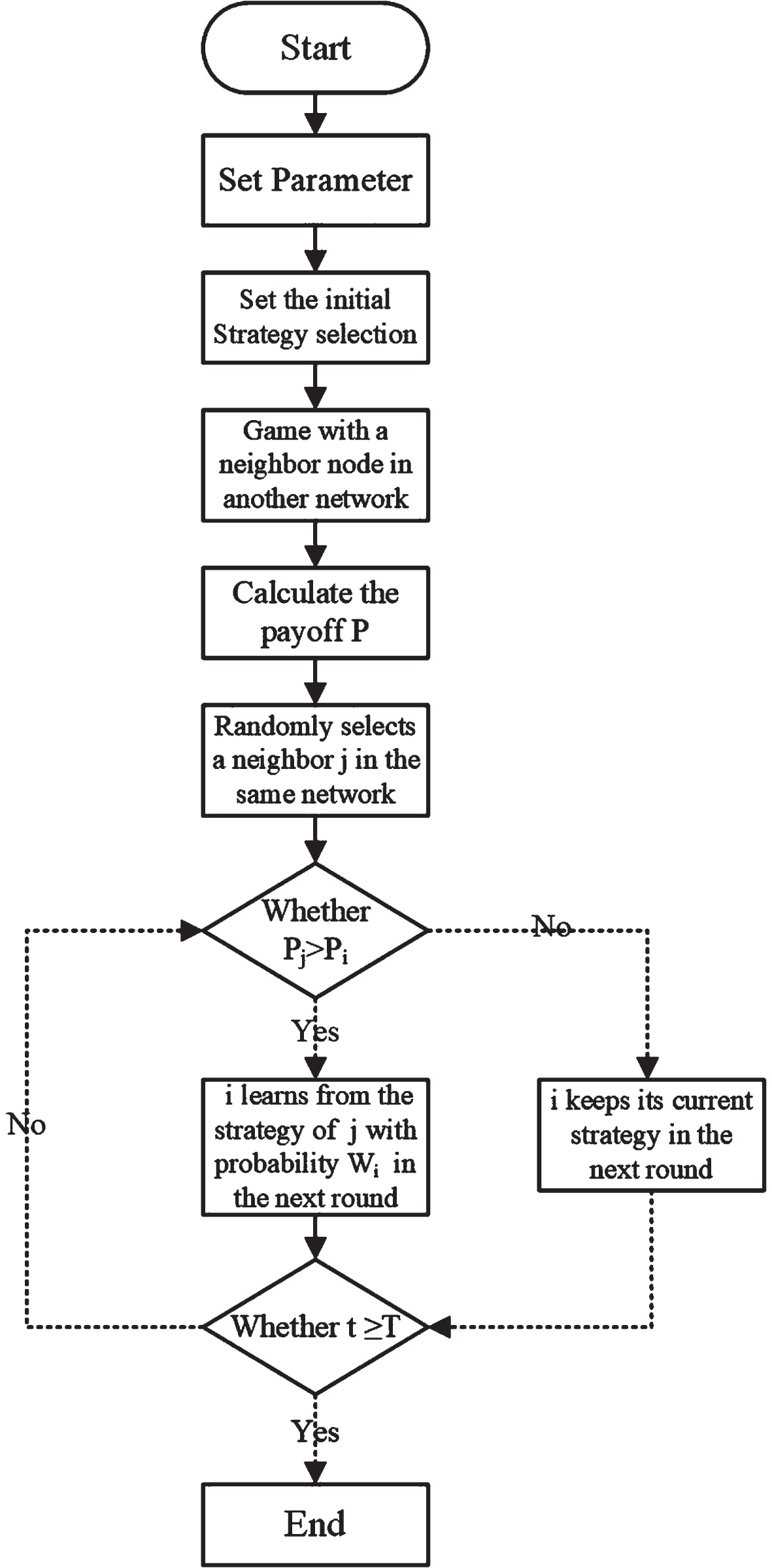
Each node participating in the game may adjust its strategy selection at time t according to the comparison of the payoff of its neighbors and its own at time t-1. This paper solves the stable solution based on the evolutionary game payoff matrix, and introduces an evolutionary rule to explore the influence of individual heterogeneity and network structure on the stability of the game.
(1) Game
Each node in the G1 network plays a game with its neighbor nodes in the G2 network, and counts its own payoff. Therefore, the total payoff of the node after a round of the game is counted as follows:
(1)
The node j2 in the G2 network plays a game with his only neighbor node i in the G1 network, and the total payoff of the node after a round of the game is counted as follows:
(2)
(2) Learning
After a round of the game, community nodes in the upper network will randomly select a neighboring node of the same network to compare their payoffs, so will residents nodes in the lower network. There is a certain probability for each node to decide whether to learn the neighbor’s strategy to change its own strategy in this round. This article adopts Fermi rule [19] as the strategy updating rule:
(3)
(4)
(3) Repeat the above steps, after a certain period of time, when network and the game have become stabilized, and calculate the average stable cooperation level of each network.
3Results
3.1Basic variable settings of NetLogo simulation platform
ABM is an approach simulates the dynamics of complex systems based on describing the continuous interaction of agents who are heterogeneous in terms of information and decision rules, while the agent stands for each component of the system or each individual in the specific situation. It models each agent from a microscopic perspective from the bottom up and allows spontaneous emergence at the macroscopic level [21]. ABMs polymerize interactions at the micro level to macro level, which describe direct interactions among agents in a group accurately and contribute to more comprehensive policy assessments. Therefore, this paper uses the NetLogo6.2.0 simulation platform to conduct evolutionary game simulation research on complex networks through the ABM method.
According to the steps of game simulation on the double-layer network, WS small world network is first generated, and all nodes on the network are divided into two types: the yellow house-shaped nodes represent communities with strict supervision and the blue ones represent communities with inaction, while the gray person-shaped nodes stand for residents choosing compliance and the red ones stand for those with violation. In the initial NetLogo interface, the initial parameters of the network can be determined by adjusting the slider of each parameter, as shown in Fig. 4.
Fig. 4
Initial state of WS small world network.

In Fig. 4, the left side shows the relevant initial parameters of the model. For example, n-residents represents the scale of residents, that is, the total number of people who need to be quarantined at one time, n-communities represents the number of communities, and k represents the value of the environmental noise parameter in the formula (3) and (4). Payoff is the payoff matrix obtained in Table 2. The initial parameters of the variables in the payoff matrix are shown by each slider such as a, b, c, v, E, w, q, p, etc. in the figure. x0 represents the proportion of residents who choose to comply with the quarantine rules in the initial state, and y0 represents the initial proportion of the community’s choice of active supervision. The graph on the bottom left shows the change in the proportion of the number of residents and communities who choose different strategies over time.
In Fig. 4, the right side is the view interface of the model. The human-shaped node represents residents, and the gray ones represent those who comply with the quarantined strategy and are quarantined at home, while the red ones represent people who violate the rules; the house-shaped nodes represent communities, and the yellow nodes represent communities with the choice of active supervision, while the blue nodes represent communities that choose inaction. The rewiring-probability at the bottom of the view interface represents the random reconnection probability p of the WS small-world network; clustering-coefficient and average-path-length reflect the basic characteristics of the social small-world network of residents: there is a relatively small average path length and a relatively high clustering coefficient.
Table 3 shows the corresponding initial parameter settings in the initial state:
Table 3
Simulation parameter values
| Parameters | a | b | c | V | E | w | q | p | x0 | y0 | k | Rewiring-probability |
| Values | 5 | 10 | 10 | 50 | 20 | 0.5 | 0.8 | 0.05 | 0.5 | 0.5 | 0.1 | 0.2 |
3.2The impact of related parameters on evolutionary stability strategies
(1) Simulation results of different initial strategy ratios of communities
When x0 = 0.5, let y0 = 0.2, 0.5, 0.8 respectively, keep other parameters unchanged and take T = 200 iterations, the result of evolutionary stability is shown in Fig. 5:
Fig. 5
two-party strategy evolution results when y0 = 0.2, 0.5, 0.8.

It can be seen from Fig. 5 that the initial strategy ratio of the community has an impact on the strategy choice ratio of the residents. When y0 = 0.5, that is, half of the communities choose active supervision initially, the proportion of residents who choose to comply with the quarantine requirements (“X” in the graph) fluctuates as the increasing of iterations, but it is slightly higher than the proportion of people who choose violation(“1-X” in the graph); when y0 = 0.2, however, the proportion of people who choose to violate is slightly higher than the proportion of those who choose to comply; when y0 = 0.8, after several iterations, the proportion of residents who choose the “X” strategy stabilizes at 1 basically. In addition, the proportion of the community’s strategies always fluctuates, while residents can remain relatively stable after a certain period of time in any condition, indicating that the community’s choice of strategies will affect the residents. The higher the proportion of the community choosing active supervision, the more likely the residents will abide by the quarantine requirements; while 80% of the communities chose to supervise at the beginning, after a moment all the people will choose to follow the rules and nobody chooses to violate them.
(2) Simulation results of different reconnection probabilities in small world networks
When x0 = y0 = 0.5, keep other initial parameters unchanged, and let p = 0.2, p = 0.4 and p = 0.6, p = 0.8, the evolutionary stability results are shown in Fig. 6:
Fig. 6
Evolution result when p = 0.2, 0.4, 0.6, 0.8.
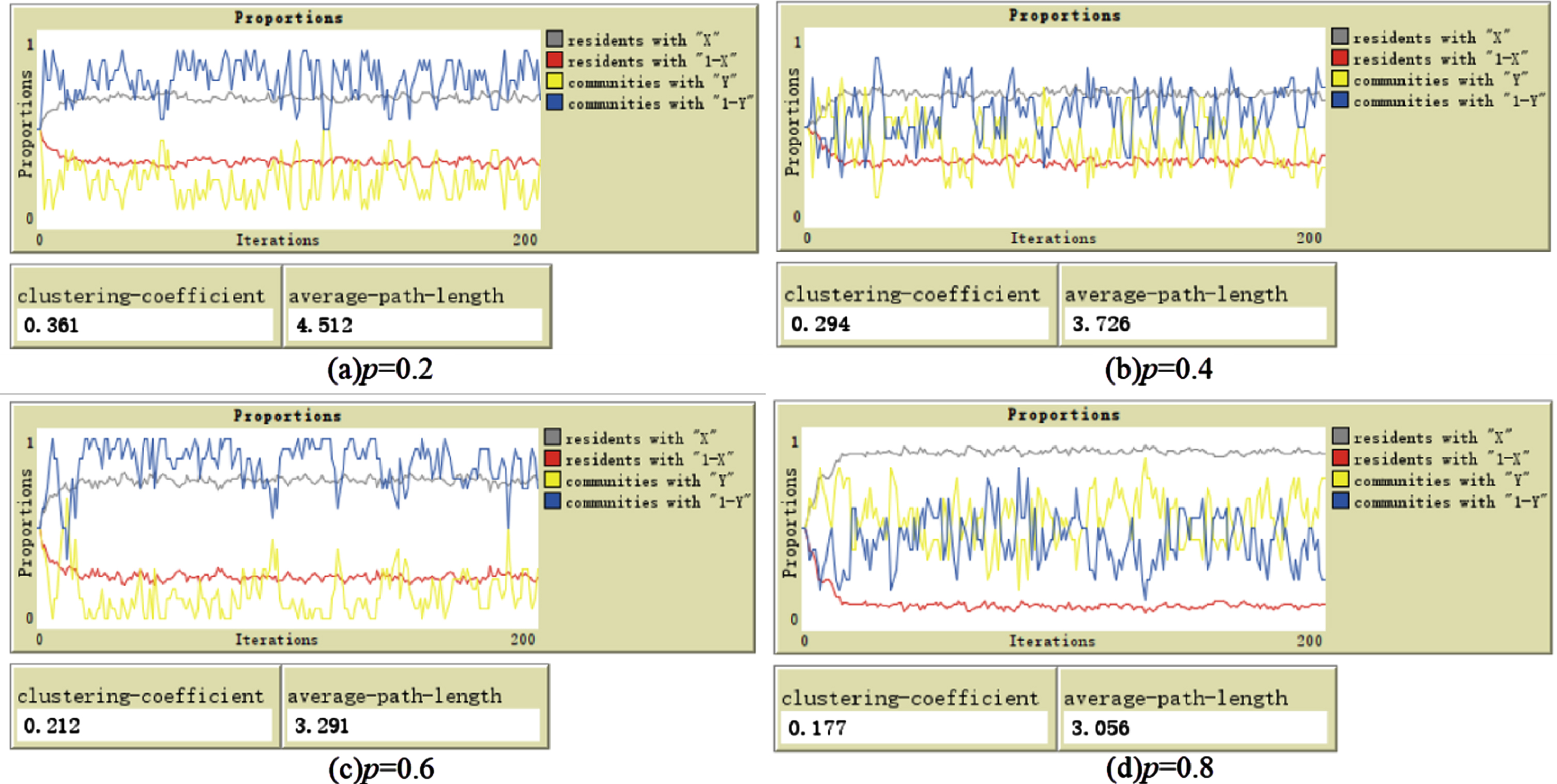
We can see from Fig. 6 that under the initial condition of x0 = y0 = 0.5, as the reconnection probability p increases, the clustering coefficient and average path length of the small world network gradually decrease, and the small world network gradually evolves to a completely random network. When the probability of reconnection is 0.2, the proportion of residents who choose to comply with the strategy is slightly higher than the proportion of those who choose to violate. When the probability of reconnection reaches 0.8, the proportion of residents who choose to comply with the strategy is much higher than the proportion of the other strategy, and the difference in the proportion of different strategic choices is getting larger. In addition, with the increase in the probability of reconnection, the proportion of the residents with different strategies reaches a relatively stable state at a faster rate, which shows that different network structures have an impact not only on the proportion of residents’ strategy selection but also the stabilization speed. This is because in the small-world network, as the probability of network reconnection increases, the average path length and clustering coefficient decrease accordingly. On the other hand, the reduction of the clustering coefficient makes the lower-level residents network tend to present a decentralized state, and the heterogeneity of the network is more obvious. People with larger average degrees have greater influence and are more likely to influence neighboring nodes to learn from their strategies, thereby reducing the time for all nodes to evolve to a relatively equilibrium state.
(3) Simulation results of the government reward distribution parameter w
When x0 = y0 = 0.5 and other initial parameters are kept unchanged, let w = 0.2, w = 0.5, w = 0.8 respectively, the evolutionary stability results are shown in Fig. 7:
Fig. 7
The evolution result of w = 0.2, 0.5, 0.8.

When w = 0.2 and w = 0.5, the proportion of residents who comply with isolation is greater than the proportion of violations, and it is obvious that w = 0.2, that is, when the government’s rewards for residents account for 80 percent of the total reward, the proportion of residents who choose to quarantine is higher than when w = 0.5, that is, the reward from the government when the reward is equally divided; and when w = 0.8, that is, when the residents can only get 20% of the government’s reward, the proportion of choosing to violate the quarantine rules is much higher than that choosing complying with the quarantine requirements. As for the community, when the distribution parameter w takes different values, there is no obvious difference, and the proportion of their choice always fluctuates around 0.5, which shows that people are more sensitive to w than the community group.
(4) Simulation results of environmental noise k
k is the environmental noise variable in Equation (3) and Equation (4). When k is very large, such as close to 1, the probability of node’s learning strategy W is approximately 0.5, which means that the probability of residents imitating their neighbor’s strategy is 0.5 and their selections are more random. On the other hand, when k is very small, for example, close to 0, the value of W will be close to 1, indicating that external factors will not interfere with the learning strategy of the node, and there is a high probability that the node will imitate its neighbors. When x0 = y0 = 0.5 and other initial parameters are kept unchanged, k = 0.1 and k = 0.5 are taken respectively, the evolutionary stability results are shown in Fig. 8:
Fig. 8
The evolution result when k = 0.1, k = 0.5.
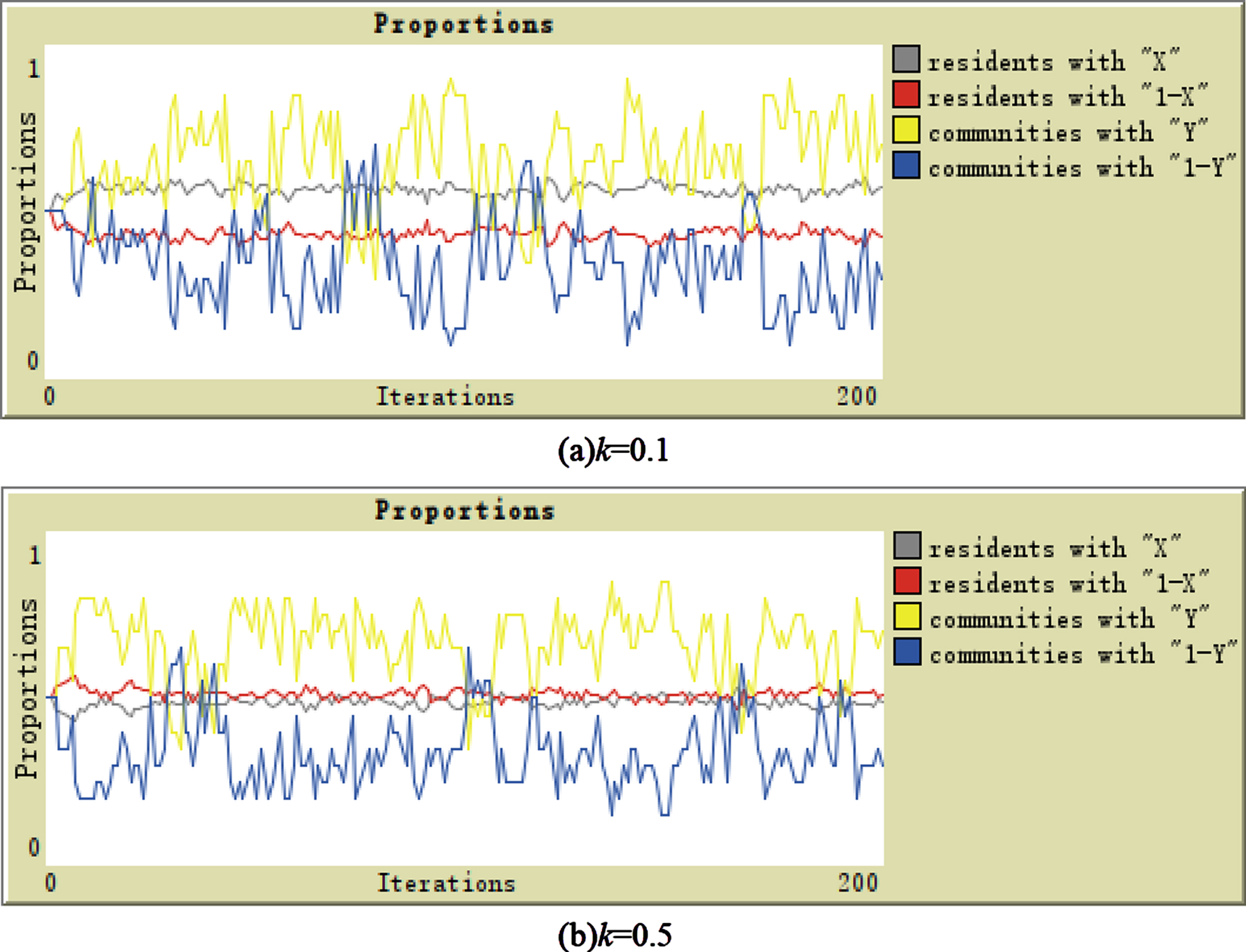
When other conditions remain unchanged, let k = 0.5, the ratio of residents who choose to violate the strategy is higher than the ratio of compliance, which is contrary to the previous default situation when k = 0.1. It shows that when the environmental noise becomes larger, the residents are more likely to be affected by various information in the surrounding environment rather than choose strategies in the next round based on the difference between their payoffs and those of their neighbors, thus changing their original choices of choosing the strategy.
4Discussion
4.1Analysis on the effect
This paper explores the evolutionary equilibrium from a macro perspective through the replication dynamic method, then uses the ABM method, basing on complex networks and individual learning strategies according to the real interaction among agents, and analyze the topology of the small world network and reveal the evolution process of the residents and community strategic selections under the double-layer network from a microscopic perspective of view. The simulation conclusions are mainly drawn from four perspectives:
(1) The initial ratio of the strategy of the community(y0) has a significant impact on the evolutionary strategy choice of the residents’ choice on whether to obey the quarantine rules or not. At the same time, initial ratios of communities’ choices at different levels will make the residents’ strategies reach an equilibrium state at different speeds. A reasonable initial percentage of communities’ choices will guide the group of residents to reach an ideal ratio of their strategies and achieve an equilibrium state as soon as possible. That is, the greater the proportion of communities choosing active regulation in the beginning, the higher the proportion of residents choosing to obey quarantine policies and they will reach a stable state more quickly.
(2) The topological structure of the complex network has an important influence on the evolution of the game and the choice of strategy. In the small-world network, as the probability of reconnection increases, the small-world network gradually evolves to an ER network. The proportion of residents choosing quarantine increases as the residents are more tended to be influenced by neighbor nodes and primary nodes, and the time to evolve to a relatively equilibrium state also decreases.
(3) We found that different parameter settings have a significant impact on the strategy selection and the evolution of the network. In the group game between two parties, the government subsidy distribution parameter w can effectively regulate the behavior of residents, when the community and the residents share the government’s rewards equally, the proportion of people choosing to obey the quarantine rules is slightly higher than that of those violating the rules; while when residents get more percentage of the government’s rewards, the proportion of people choosing to comply with the rules will increase significantly. In other words, a reasonable reward distribution mechanism can effectively increase the proportion of residents who choose quarantine strategies.
(4) Environmental noise also exerts a significant impact on the strategy ratios of residents. The greater the environmental noise, which means they are more likely to be influenced by various information in the environment, and their choice of whether to adhere to the rules is more random, and this kind of randomness is not conducive to the effectiveness of the quarantine policy.
4.2Implications for Optimization
According to the analysis of the above simulation results, we can get enlightenment of optimization from four aspects:
(1) The government should pay close attention to the initial motivation of the community, that is, whether the community positively responds to the government’s policy in the initial state, and actively supervise and manage residents in the community. The initial decision of the community will affect the strategic choice of residents and the evolutionary results as well as the evolutionary tine of both parties. Therefore, the government, as the policymaker of the epidemic prevention and quarantine rules, should not only grasp the promotion and implementation of the quarantine policy macroscopically, but also go deep into the grassroots organizations, evaluate different communities’ initial intentions, supervise and warn some communities that choose inaction in the beginning timely, and try to increase the proportion of the community’s initial strategy for active supervision as much as possible.
(2) In the social network, some people who are main nodes and have more social relationships have a greater impact on their neighbors, and their choice of strategy will become a reference for others. Therefore, for these special and important individuals, communication and supervision should be strengthened to minimize their choices in violation of the quarantine rules as far as possible, thus they can play a correct guiding role for other individuals in the social network. In addition, the government and the community may implement mandatory intervention measures when necessary, to guide other residents to choose to obey the rules, thus having a positive effect on epidemic control.
(3) The government must determine a reasonable reward and punishment mechanism as well as distribution ratio. Although the government does not directly participate in group games, different levels of subsidies it sets will affect the strategic choices of both parties, and thus affecting the effectiveness of epidemic control.
(4) Providing interactive channels will eliminate the communication barriers and promote the connections between the residents and the community. Relevant organizations can take actions to issue the latest notices on a public opinion platform, promptly dispel rumors, etc., and pay attention to the physiological and psychological demands of the quarantined people, to minimize the negative impact of the dissemination of online rumors and negative information in social networks.
Inevitably, this paper has certain limitations. Firstly, we assume that the network structure is fixed, without considering the evolution of the network. Actually, the double-layer network may change dynamically over time. As time goes by, there may be new residents entering the network and some exiting the network after quarantine. Secondly, our research does not consider the heterogeneity of individual residents, such as their perception of the epidemic, the risk level of the epidemic from the places of departure, and so on. Thirdly, because of the dispersion of the individual, other simulation tools like AnyLogic can be combined with the ABM method allowing more accurate simulations. We will incorporate these limitations into future research to provide theoretical foundations and decision-making support for relevant organizations to formulate home quarantine policies under the epidemic.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Funding
This work was supported by the Major Projects of National Social Science Foundation of China (Grant No. 20&ZD155); the Philosophy and Social Sciences Research Project of Chinese Ministry of Education (Grant No. 19JHQ091).
References
[1] | Yang Z. and Li J. , Letter from China: Response after the first wave of COVID-19, Respirology 26: (3) ((2021) ), 273–274. |
[2] | Marston C. , Renedo A. and Miles S. , Community participation is crucial in a pandemic, LANCET 395: (10238) ((2020) ), 1676–1678. |
[3] | The National Health and Construction Commission of China (2020) Notice on Strengthening Community Prevention and Control of Pneumonia Epidemics Caused by New Coronavirus Infection. In: http://www.nhc.gov.cn/jkj/s3577/202001/dd1e502534004a8d88b6a10f329a3369.shtml. |
[4] | Fan R.G. , Wang Y.B. and Lin J.C. , Study on Multi-Agent Evolutionary Game of Emergency Management of Public Health Emergencies Based on Dynamic Rewards and Punishments, International Journal of Environmental Research and Public Health 18: (16) ((2021) ). |
[5] | Kermack W.O. and McKendrick A.G. , A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London (1927), 700–721. |
[6] | Tang B. , Xia F. , Tang S. , Bragazzi N.L. , Li Q. , Sun X. , Liang J. , Xiao Y. and Wu J. , The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China, International Journal of Infectious Diseases 95: ((2020) ), 288–293. |
[7] | Zhang J. , Dong L. , Zhang Y. , Chen X. , Yao G. and Han Z. , Investigating time, strength, and duration of measures in controlling the spread of COVID-19 using a networked meta-population model, Nonlinear Dynamics 101: (3) ((2020) ), 1789–1800. |
[8] | Hellewell J. , Abbott S. , Gimma A. , Bosse N.I. , Jarvis C.I. , Russell T.W. , Munday J.D. , Kucharski A.J. , Edmunds W.J. , Sun F. , Flasche S. , Quilty B.J. , Davies N. , Liu Y. , Clifford S. , Klepac P. , Jit M. , Diamond C. , Gibbs H. , van Zandvoort K. , Funk S. and Eggo R. M. , Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts, The Lancet Global Health 8: (4) ((2020) ), e488–e496. |
[9] | Newman M.E.J. , The Structure and Function of Complex Networks, Siam Review 45: (2) ((2003) ), 167–256. |
[10] | J N.M.E. , Spread of epidemic disease on networks, Physical review. E, Statistical, nonlinear, and soft matter physics 66: (1 Pt 2) ((2002) ). |
[11] | Pastor-Satorras R. and Vespignani A. , Epidemics and immunization in scale-free networks, Wiley-VCH Verlag GmbH & Co. KGaA 2002. |
[12] | Arino J. , Brauer F. , Driessche P.V.D. , Watmough J. and Wu J. , A final size relation for epidemic models, Mathematical Biosciences & Engineering Mbe 4: (2) ((2017) ), 159–175. |
[13] | Wang Y. , Wei Z. and Cao J. , Epidemic dynamics of influenza-like diseases spreading in complex networks, Nonlinear Dynamics 101: (3) ((2020) ), 1801–1820. |
[14] | Zhang Y. , Li Y. and Martínez E. , Evolutionary Dynamics of Stochastic SEIR Models with Migration and Human Awareness in Complex Networks, Complexity 2020: ((2020) ), 3768083. |
[15] | Zheng C. , Wang Z. and Xia C. , A Novel Epidemic Model Coupling the Infectious Disease with Awareness Diffusion on Multiplex Networks. In: Proceedings of the 30th Chinese Control and Decision Conference (2018 CCDC) pp. 1057–1063. |
[16] | Liu D. , Wang W. and Sun K. , Scenario forecasting model and prevention-control measurements of important public health event based evolutionary game, Systems Engineering—Theory & Practice 32: ((2012) ), 937–946. |
[17] | Protocol for Prevention and Control of COVID-19 (Edition 7). Chinese Journal of Infection Control 19: (11) ((2020) ), 1042–1048. |
[18] | Watts D.J. and Strogatz S.H. , Collective dynamics of ‘small-world’ networks, Nature 393: (6684) ((1998) ), 440–442. |
[19] | Szabó G. and Toke C. , Evolutionary prisoner’s dilemma game on a square lattice, Physical Review E - Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics 58: (1) ((1998) ), 69–73. |
[20] | Hauert C. and Szabo G. , Game theory and physics, Am j phys 73: (5) ((2005) ), 405–414. |
[21] | Jiang G. , Ma F. , Shang J. and Chau P.Y.K. , Evolution of knowledge sharing behavior in social commerce: An agent-based computational approach, Information Sciences 278: ((2014) ). |




