A novel interval-valued spherical fuzzy CODAS: Reopening readiness evaluation of academic units in the era of COVID-19
Abstract
Combinative distance-based assessment (CODAS) is a multi-criteria decision-making (MCDM) method that is based on the Euclidean and Hamming distances of alternatives from the average scores of attributes. Spherical fuzzy sets, as the recent extensions of ordinary fuzzy sets, were developed based on Pythagorean and neutrosophic sets and enable decision-makers to express their membership, non-membership, and hesitancy degrees independently and in a larger domain than most other fuzzy extensions. This paper proposes a new interval-valued spherical fuzzy CODAS method and provides extra space for catching the vagueness in the nature of the problem. The feasibility and practicality of the proposed model are illustrated with an application for evaluating the reopening readiness of academic units for campus education in the era of COVID-19. Three decision-makers from a higher education institution evaluate four academic units with respect to five strategic criteria and prioritize them according to their readiness levels for the campus type of education. Sensitivity and comparative analyses, theoretical and practical contributions, limitations, and future research avenues are also presented in the study.
1Introduction
Today, the COVID-19 epidemic has impacted a variety of organizations, including higher education institutions. In a number of countries, many of these institutions have been shuttered entirely or in part as a result of pandemic measures. However, particularly with the commencement of vaccines, it is being considered to reopen universities and return to campus education. On the other hand, these institutions have several academic departments engaged in a variety of complicated tasks, and assessing their readiness for campus education is not an easy process. Certain strategic criteria must be met at these institutions in order for students, academics, and administrative personnel to continue their activities on campuses securely during this pandemic era. It has become a necessity for academic units to deal with the problem of evaluating a number of academic units according to many criteria with a systematic, numerical, and generally accepted method.
MCDM is a mathematical method for selecting the best feasible predetermined alternative from some potential candidates with respect to a set of conflicting criteria [36]. The problem of assessing academic units’ pandemic readiness levels can also be characterized as an MCDM problem. In such a problem, academic units are alternatives, and the measures that will be used to assess these academic units’ reopening readiness levels appear to be the criteria.
On the other hand, many MCDM problems involve qualitative criteria that cannot be quantified directly, and considering the nature of the problem, these criteria are frequently inaccurate and cannot be characterized by crisp or deterministic models. Decision-makers can only evaluate these criteria linguistically, and fuzzy set theory [44], which is predicated on the premise that people think in linguistic terms rather than numerical terms, is well suited to modeling linguistic expressions and has become an integral component of MCDM models in recent years.
Spherical fuzzy sets [23] are a relatively new extension of conventional fuzzy sets and have the following two main characteristics: First, their spherical features allow decision-makers to express their judgements over a greater region. Second, in a spherical fuzzy environment, decision-makers’ hesitancy can be described separately from membership and non-membership degrees. Interval-valued spherical fuzzy sets [18], on the other hand, with their interval-valued domain rather than a single point, enable users greater fuzziness modeling capability.
In this study, the readiness of higher education institution units to return to physical education during the COVID-19 era is assessed. For this purpose, a unique fuzzy MCDM approach is created. The main highlights of this study are as follows: (1) The CODAS approach is integrated with interval-valued spherical fuzzy sets to boost fuzziness modeling capabilities. (2) The applicability of the suggested method is demonstrated by assessing academic units’ re-opening readiness, which is a relevant and significant concern that higher education institutions face during and after a pandemic. (3) Many MCDM models in the literature do not provide sensitivity analyses for both criterion and decision-maker weights. In order to assess the stability of the methodology, sensitivity analyses for criteria and decision-maker weights are conducted. (4) The rationality of the developed model is tested through a comparative study. For this purpose, the proposed methodology is compared with other state-of-the-art fuzzy MCDM methods.
The rest of the study is given as follows: Section 2 sheds light on the literature for spherical fuzzy sets and CODAS based MCDM studies. Section 3 gives the basic mathematical operations of interval-valued spherical fuzzy sets and the steps of the ordinary CODAS method prior to model development. Section 4 presents the detailed explanation of the proposed methodology by presenting a flowchart and a step-by-step description. Section 5 illustrates the model with an application in the following manner: First, the MCDM problem is described and the criteria are presented; later, the numerical solution of the problem is presented through the steps of the model; and finally, sensitivity and comparative analyses are given. Section 6 finalizes the paper by presenting main contributions; limitations, and future research avenues.
2Literature review
In this section, relevant research is offered in order to further illuminate the themes of the study and to clarify the originality of the work. To provide insight on the literature gap, spherical fuzzy set theory and the CODAS approach are discussed independently in this context. First, a summary of decision-making studies based on spherical fuzzy sets is provided, followed by a discussion of various fuzzy CODAS applications.
2.1Spherical fuzzy sets
Various extensions of ordinary fuzzy sets have been reported in the literature; and the most prominent ones are as follows: Intuitionistic fuzzy sets [4] were introduced as an extension of ordinary fuzzy sets and enable modeling of the membership and non-membership degrees of decision-makers. The second form of these fuzzy sets, named intuitionistic fuzzy sets of type two [3] were later presented by the same author as a generalized form of the first sets and provide more space for modeling membership and non-membership degrees. Pythagorean fuzzy sets [41] were developed by another scholar; however, they have the same characteristics with previously developed type two form of intuitionistic fuzzy sets. Interval-valued intuitionistic fuzzy sets were developed by Atanassov [2], and membership and non-membership degrees were presented as intervals rather than exact values.
Neutrosophic sets [34] were introduced to handle incomplete, indeterminate and inconsistent information. Neutrosophic sets have degrees of truthiness, indeterminacy, and falsity instead of membership, non-membership, and hesitancy respectively. Interval-valued neutrosophic sets were propsoed by Wang et al. [38] by generalizing single-valued neutrosophic sets and interval-valued intuitionistic fuzzy sets. Hesitant fuzzy sets [35] deal with the problems in which membership degree can take many possible values. On the other hand, in interval-valued hesitant fuzzy sets [7] the membership degrees of an element are denoted by several possible interval type of values rather than single type of exact ones. Picture fuzzy sets [10] have positive, neutral, negative, and refusal membership degrees, and these can be considered as yes, abstain, no, and refusal types of opinions of voters. Cuong [9] later developed the notion of interval-valued picture fuzzy sets, which are based on the same concept as other interval-valued fuzzy extensions. The q-rung orthopair fuzzy sets are introduced by Yager [42] and provide more space than intuitionistic fuzzy sets for modeling membership and non-membership degrees, and interval-valued q-rung orthopair fuzzy sets [19] enable modeling these expressions in an interval-valued form.
Spherical fuzzy sets were developed by Kutlu Gündoğdu and Kahraman [23], and after that, many researchers have begun to utilise them in the development of various decision-making processes. Oztaysi et al. [27] proposed a spherical fuzzy AHP based dynamic pricing model for location based systems, and Kutlu Gundogdu [22] developed MULTIMOORA with spherical fuzzy sets and presented an illustrative example for a personnel selection problem. Onar et al. [26] developed a spherical regret based MCDM method and evaluated healthcare equipment stocks with the proposed model, and Sharaf [32] evaluated geothermal energy systems by integrating spherical fuzzy sets with the PROMETHEE method. Moreover, Sharaf [33] extended classical VIKOR method in a spherical fuzzy environment and illustrated the applicability of their models via a supplier selection problem, and Ashraf et al. [1] proposed a spherical fuzzy based mathematical model for controlling the transmission and spread of COVID-19 by using TOPSIS and COPRAS methods in their study.
Interval-valued spherical fuzzy sets [18] have begun to be used in many decision making problems. Gul and Ak [17] used interval-valued spherical fuzzy TOPSIS for marble manufacturing facility evaluation, and Demirel [12] and Balin [5] applied it to stabilizer system selection problems for cruise and naval ships. On the other hand, Farrokhizadeh et al. [13] extended the maximizing deviation technique and used an interval-valued spherical fuzzy set for determining criteria weights and showed the applicability of their model via the advertisement strategy selection problem, and Menekse and Camgoz-Akdag [24] suggested an internal audit decision support model based on a novel interval-valued spherical fuzzy ELECTRE.
2.2CODAS applications
CODAS [21] is an MCDM method that determines the relative preferences of alternatives based on their distances from the negative-ideal point. The key advantage of this technique is that it ranks outcomes based on two types of distance measures [16]. To produce more efficient and accurate aggregation solutions, the combinative structure of Euclidean and Hamming distances is taken into account in terms of the intangibility of the decision-maker and the uncertainty of the decision-making scenario [39]. This method uses a primary measure of Euclidean distance and a secondary measure of Hamming distance. If the degree of closeness between Euclidean distances is less than a threshold number, Hamming distance is used as a comparison, and having a larger distance is preferred. Indeed, the CODAS model is controlled by a threshold parameter, and it can be represented by two different kinds of distance techniques depending on the value of this parameter. This allows the model to benefit from the properties of both techniques. Due to its inherent characteristics [30], CODAS has a systematic and clear calculation procedure that is logically valid for describing the fundamental principles of real-world decision-making situations. CODAS is a useful tool for dealing with decision-making problems, and it is widely used in the literature due to its simple and effective mathematics. As a result, this technique may be used to efficiently evaluate and rank units in the context of reopening during a pandemic.
The CODAS technique has spawned a plethora of literature in recent years. Dayyani et al. [11] evaluated stages of rural settlement texture deterioration by applying a CODAS methodolgy. The authors presented their study in a crisp environment and did not allow the CODAS technique to model the problem’s inherent uncertainty. Ghorabaee et al. [16] extended CODAS with trapezoidal fuzzy sets and applied it to a market segment evaluation problem, and Vinodh and Wankhede [37] used triangular fuzzy sets and handled an industrial decision-making problem. In both studies, triangular and trapezoidal fuzzy MCDM models are superior to a crisp based MCDM while dealing with real-world decision-making problems. However, these fuzzy sets cannot fully capture the decision maker’s comprehensive cognition, as the decision maker may hesitate between many triangular or trapozoidal fuzzy sets due to a lack of pertinent knowledge regarding the decision problems.
Bolturk [6] and Pérez-Dominguez et al. [28] presented Pythagorean fuzzy CODAS methods and handled supplier selection and public transport evaluation problems. The authors used membership, non-membership, and indeterminacy degrees while extending the CODAS technique. In Pythagorean fuzzy sets, however, the indeterminacy degree cannot be represented separately and can be derived from membership and non-membership degrees; thus, the contribution of indeterminacy degree to ultimate ranking of alternatives is debatable.
On the other hand, Karagoz et al. [20] developed an intutionistic fuzzy CODAS method for dismantling center location problem to aid waste managers. When creating the CODAS, the authors used membership and non-membership degrees, but did not account for decision makers’ levels of hesitancy. On the other hand, Roy et al. [30] and Yeni and Özçelik [43] proposed interval-valued intuitionistic fuzzy CODAS models with applications to automotive material and personnel selection problems, and Seker and Aydin [31] evaluated the public transportation alternatives by developing an AHP integrated CODAS in an interval-valued intuitionistic fuzzy atmosphere. Although the above-mentioned works model intuitionistic fuzzy sets as intervals and add substantial fuzziness modeling capabilities to the CODAS method, the previously-mentioned remark that there is no degree of hesitancy in intutionistic fuzzy sets pertains similarly to these studies.
3Preliminaries
Since the proposed methodology integrates interval-valued spherical fuzzy sets for modeling information uncertainty, and the CODAS method for ranking the alternatives, this section introduces some basic characteristics of these methods. Section 3.1 presents basic mathematical operations of interval-valued spherical fuzzy sets, and section 3.2 gives the steps of classical CODAS.
3.1Interval-valued spherical fuzzy sets
The definition; addition, multiplication, multiplication by a scalar, power, aggregation and defuzzification operators [18] of interval-valued spherical fuzzy sets are given as follows:
Definition: An interval-valued spherical fuzzy set
(1)
Note that, for the case,
For convenience, an interval-valued spherical fuzzy number,
where [a, b] ⊂ [0, 1] , [c, d] ⊂ [0, 1] , [e, f] ⊂ [0, 1] and (b2 + d2 + f2) <1.
Note also that,
Basic operations:
Addition
(2)
Multiplication
(3)
(4)
Power of
(5)
Aggregation operator. Let
(6)
Defuzzification operator. Defuzzification operator i.e. score function for interval-valued spherical fuzzy sets is defined as below.
(7)
3.2Classical CODAS method
CODAS [21] is an MCDM methodology that ranks the alternatives according to their distances to Euclidean and Hamming distances with respect to negative ideal solutions. the steps of classical CODAS is as follows:
Construct the decision matrix as given in Equation 8.
(8)
Calculate the normalized decision matrix as given in Equation 9.
(9)
Obtain weighted normalized decision matrix as given in Equation 10.
(10)
Calculate the negative ideal solution as given in Equation 11.
(11)
Calculate the Euclidean EDi and Hamming HDi distances from the negative ideal solution as given in Equations 12 and 13, respectively.
(12)
(13)
Obtain the relative assessment matrix as given in Equation 14.
(14)
(15)
Calculate the appraisal score ASi as given in Equation 16 and rank the alternatives.
(16)
4Methodology
In this section, a novel MCDM method is proposed by extending classical CODAS method with interval-valued spherical fuzzy sets. The flowchart (Fig. 1) and the details of the proposed model are presented below.
Fig. 1
The flowchart of the proposed methodology.
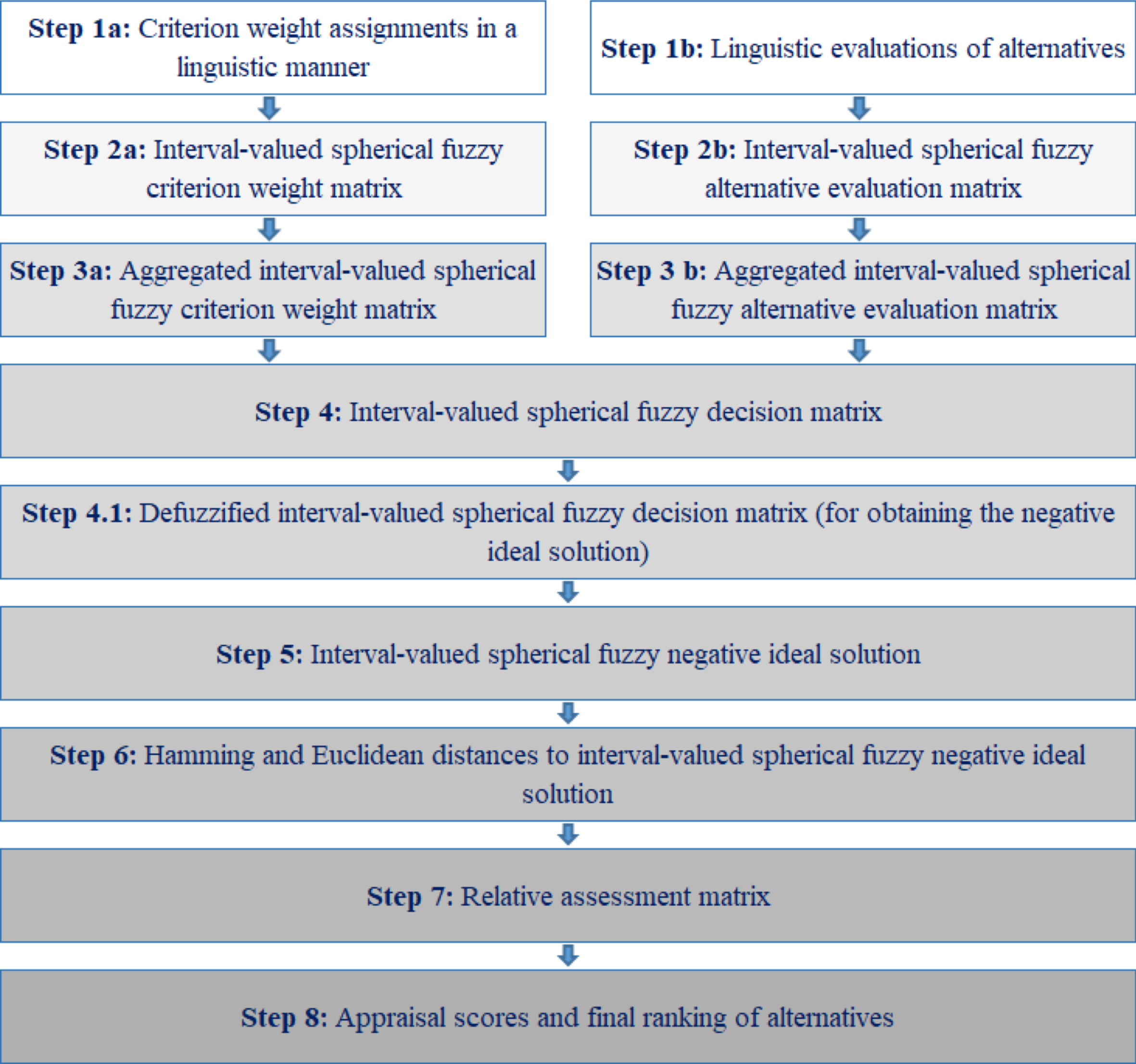
Define an MCDM problem with a set of alternatives and the most related criteria. Use a unified criteria type by converting cost criteria to benefit criteria. Let Xi be the selected alternatives as Xi = {X1, X2, . . . . , Xm}; Cj be the criteria set as Cj = {C1, C2, . . . . , Cn} and let wj be the weight vector of all criteria as wj = {w1, w2, . . . . , wn} where w = (w1, w2, . . . , wn) ; wj ∈ [0, 1] and
Step 1a. Assig the criteria weights:
Criterion weights are assigned by each decision-maker by utilizing the linguistic terms given in Table 1.
Table 1
Linguistic terms and corresponding interval-valued spherical fuzzy numbers [18]
| Linguistic terms | [a, b] , [c, d] , [e, f] |
| Absolutely more Importance (AMI) | ([0.85,0.95], [0.10,0.15], [0.05,0.15]) |
| Very High Importance (VHI) | ([0.75,0.85], [0.15,0.20], [0.15,0.20]) |
| High Importance (HI) | ([0.65,0.75], [0.20,0.25], [0.20,0.25]) |
| Slightly More Importance (SMI) | ([0.55,0.65], [0.25,0.30], [0.25,0.30]) |
| Equally Importance (EI) | ([0.50,0.55], [0.45,0.55], [0.30,0.40]) |
| Slightly Low Importance (SLI) | ([0.25,0.30], [0.55,0.65], [0.25,0.30]) |
| Low Importance (LI) | ([0.20,0.25], [0.65,0.75], [0.20,0.25]) |
| Very Low Importance (VLI) | ([0.15,0.20], [0.75,0.85], [0.15,0.20]) |
| Absolutely Low Importance (ALI) | ([0.10,0.15], [0.85,0.95], [0.05,0.15]) |
Step 2a. Transform linguistic evaluations to an interval-valued spherical fuzzy form:
Convert the linguistic evaluations obtained from each decision-maker to their fuzzy forms and obtain interval-valued spherical fuzzy criterion weight matrices. Use Table 1 for the conversion.
Step 3a. Aggregate criterion weight matrices collected from the decision-makers:
Aggregate all criterion weight matrices and obtain aggregated interval-valued spherical fuzzy criterion weight matrix by utilizing the geometric mean operator that is given in Equation 17. By doing so, we obtain one unique collective criterion weight matrix.
(17)
Step 1b. Evaluate the alternatives:
The performance of alternatives are evaluated by decision-makers with respect to criteria by utilizing the same linguistic terms given in Table 1.
Step 2b. Transform linguistic evaluations to interval-valued spherical fuzzy forms:
Convert the linguistic evaluations obtained from each decision-maker to their fuzzy forms and obtain interval-valued spherical fuzzy alternative evaluation matrices. Use Table 1 for the conversion process.
Step 3b. Aggregate evaluation matrices collected from the decision-makers:
Aggregate all alternative evaluation matrices and obtain aggregated interval-valued spherical fuzzy alternative evaluation matrix. By doing so, we obtain one unique collective alternative evaluation matrix. Utilize the geometric aggregation operator that is given in Equation 17 for the aggregation operation.
Step 4. Obtain the final decision matrix:
Multiply the aggregated criterion weight matrix by aggregated alternative evaluation matrix, and obtain the interval-valued spherical fuzzy decision matrix. Utilize the multiplication operator that is given in Equation 18.
Multiplication
(18)
Step 4.1. Defuzzify interval-valued spherical fuzzy decision matrix:
Obtain the crisp form of interval-valued spherical fuzzy decision matrix by utilizing defuzzification operator that is given in Equation 19. Note that the defuzzification is done to obtain the negative ideal solution. It’s also worth noting that the crisp version of fuzzy numbers is utilized for ranking, which is a very handy technique to obtain the negative ideal solution.
(19)
Step 5. Calculate the negative ideal solution.
Determine the negative ideal solution X- based on crisp form of interval-valued spherical fuzzy decision matrix as in Equation 20.
(20)
Step 6. Evaluate the distance of each alternative from the negative ideal solution:
Calculate the total distance between alternative Xi and the interval-valued spherical fuzzy negative ideal solution X- based on the Euclidean and Hamming distances as they are given in Equations 21 and 22, respectively.
(21)
(22)
Step 7. Define the relative assessment matrix:
Determine the relative assessment matrix as given in Equation 23.
(23)
(24)
Step 8. Calculate the appraisal scores and rank of alternatives accordingly:
Calculate the appraisal scores as given in Equation 25 and rank the alternatives according to descending appraisal scores. The higher the appraisal score, the better the alternative.
(25)
5Application
The proposed interval-valued spherical fuzzy CODAS methodology is applied to a reopening readiness evaluation of academic units for face-to-face education in the COVID-19 period. For this goal, four academic units are evaluated, namely: faculty of A (X1), faculty of B (X2), faculty of C (X3) and faculty of D (X4). After a comprehensive literature review, five criteria are determined as COVID-19 task force (C1), general hygiene measures (C2), ventilation and sanitation practices (C3), process for reporting a suspected case (C4) and guidance for students who missed classes (C5). A brief explanation of these criteria is also given in section 5.1. There are three decision-makers, who are all qualified managers from a higher education institution with the same experience level, and thus each decision-maker has a weight of 1/3. This section is organized as follows: Section 5.1 defines the MCDM problem and summarizes the criteria; section 5.2 presents the numerical solution of the problem by following the steps given in section 4. Section 5.3 presents the sensitivity analysis for both criteria and decision-maker weights, and section 5.4 compares the model with other six MCDM models to illustrate the validity of the proposed interval-valued spherical fuzzy CODAS.
5.1Problem definition and related criteria
Throughout the world, higher education institutions have been deeply affected by the COVID-19 pandemic and subsequent lockdown periods [29]. During the pandemic, many educational institutions closed their campus activities either completely or partially to combat the difficulties of the pandemic [25]. Since limited physical distance activities can cause various mental and psychological problems that may become habitual in humans [14], the issue of reopening higher education institutions, during COVID-19, have become an important agenda all over the world. In the process of reopening, protecting the health of students, academicians, and administrative staff has become an important goal, and educational institutions have to apply best practices in this context [40]. For reopening during the pandemic, higher education institutions should consider the following strategic criteria to ensure that students can return to campus education safely [8]:
COVID-19 task force. Making communications about the pandemic, announcing the new measures taken, coordinating and implementing online education.
General hygiene measures. Hygiene and cleaning materials, personal protective equipment, mask and thermometer stock levels, and the availability of stations controlling the body temperature of academicians and students.
Ventilation and sanitation practices. Availability of guidelines on sanitation, ventilation, and cleaning procedures; cleaning of door handles, computers, keyboards, and all other furniture; cleaning of toilets and floors with bleach with appropriate concentration.
Process for reporting a suspected case. The existence of systems that report to local health institutions in the event of the detection of a confirmed or suspected case, the tracing of academicians and students, and monitoring their health status.
Guidance for students who missed classes. The availability of opportunities for foreign students who cannot attend the campus due to the conditions in their countries, such as delayed registration, application for distance education, and submitting project reports instead of written examinations.
5.2Numerical solution
The structure of the MCDM problem is given in Fig. 2, and the numerical solution is presented as follows:
Step 1a. Five criteria are evaluated by three decision-makers by utilizing the readily given linguistic table and a criterion weight is assigned to each one as given in Table 2.
Fig. 2
The structure of the MCDM problem.
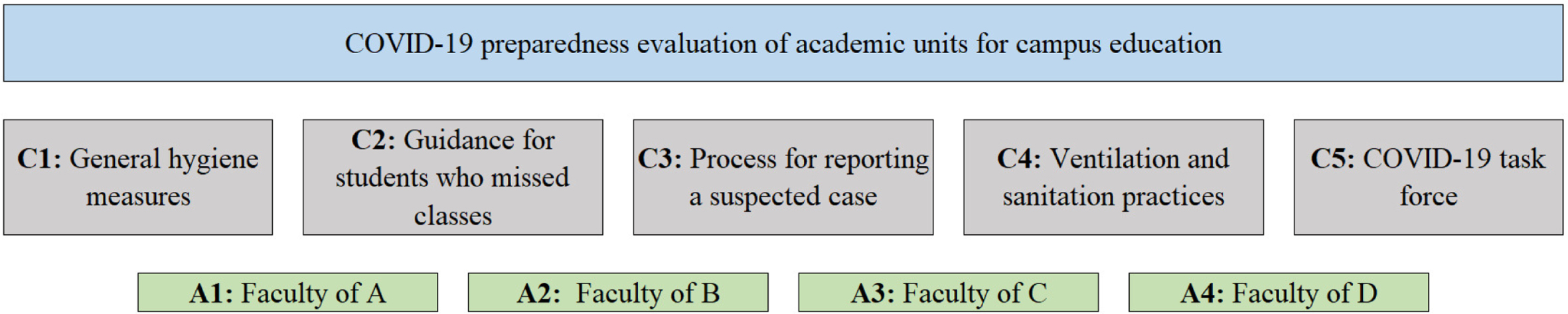
Table 2
Criterion weights
| C1 | C2 | C3 | C4 | C5 | |
| DM1 | VHI | LI | EI | VHI | SMI |
| DM2 | AMI | LI | SLI | HI | VHI |
| DM3 | VHI | VLI | SMI | VHI | AMI |
Step 2a. The linguistic evaluations are converted to their spherical fuzzy forms and an interval-valued spherical fuzzy criterion weight matrix is obtained as given in Table 3.
Table 3
Criterion weight matrix
| DM | C1 | C2 | C3 | C4 | C5 |
| DM1 | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) |
| DM2 | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.25, 0.30], [0.55, 0.65], [0.25, 0.30]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) |
| DM3 | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.15, 0.20], [0.75, 0.85], [0.15, 0.20]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) |
Step 3a. Aggregated interval-valued spherical fuzzy criterion weight matrix is obtained as given in Table 4.
Table 4
Aggregated interval-valued spherical fuzzy
| C1 | C2 | C3 | C4 | C5 |
| ([0.78, 0.88], [0.14, 0.18], [0.13, 0.19]) | ([0.18, 0.23], [0.69, 0.79], [0.18, 0.23]) | ([0.41, 0.48], [0.44, 0.53], [0.27, 0.34]) | ([0.72, 0.82], [0.17, 0.22], [0.17, 0.22]) | ([0.71, 0.81], [0.18, 0.23], [0.17, 0.23]) |
Step 1b. Four alternatives are evaluated by three decision-makers with respect to five criteria as given in Table 5.
Table 5
Linguistic evaluations of alternatives
| C1 | C2 | C3 | C4 | C5 | ||
| DM1 | X1 | AMI | ALI | VLI | HI | VLI |
| X2 | VHI | HI | VHI | SMI | HI | |
| X3 | LI | VHI | EI | HI | EI | |
| X4 | HI | AMI | SMI | VHI | SMI | |
| DM2 | X1 | AMI | VHI | VHI | EI | VHI |
| X2 | VLI | SMI | LI | SMI | AMI | |
| X3 | HI | ALI | AMI | HI | EI | |
| X4 | VHI | HI | HI | HI | HI | |
| DM3 | X1 | VLI | ALI | VHI | SLI | VHI |
| X2 | HI | EI | AMI | HI | LI | |
| X3 | SMI | VHI | LI | SMI | VHI | |
| X4 | VHI | AMI | HI | VHI | HI |
Step 2b. Linguistic evaluations are converted to their spherical fuzzy forms and interval-valued spherical fuzzy alternative evaluation matrix is obtained as given in Table 6.
Table 6
Alternative evaluation matrix
| C1 | C2 | C3 | C4 | C5 | ||
| DM1 | X1 | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.10, 0.15], [0.85, 0.95], [0.05, 0.15]) | ([0.15, 0.20], [0.75, 0.85], [0.15, 0.20]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.15, 0.20], [0.75, 0.85], [0.15, 0.20]) |
| X2 | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | |
| X3 | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | |
| X4 | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | |
| DM2 | X1 | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) |
| X2 | ([0.15, 0.20], [0.75, 0.85], [0.15, 0.20]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | |
| X3 | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.10, 0.15], [0.85, 0.95], [0.05, 0.15]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | |
| X4 | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | |
| DM3 | X1 | ([0.15, 0.20], [0.75, 0.85], [0.15, 0.20]) | ([0.10, 0.15], [0.85, 0.95], [0.05, 0.15]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.25, 0.30], [0.55, 0.65], [0.25, 0.30]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) |
| X2 | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.50, 0.55], [0.45, 0.55], [0.30, 0.40]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | |
| X3 | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.55, 0.65], [0.25, 0.30], [0.25, 0.30]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | |
| X4 | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) |
Step 3b. Aggregated interval-valued spherical fuzzy alternative evaluation matrix is obtained as given in Table 7.
Table 7
Aggregated alternative evaluation
| C1 | C2 | C3 | C4 | C5 | |
| X1 | ([0.48, 0.57], [0.50, 0.60], [0.12, 0.20]) | ([0.20, 0.27], [0.76, 0.89], [0.08, 0.19]) | ([0.44, 0.52], [0.50, 0.60], [0.16, 0.22]) | ([0.43, 0.50], [0.43, 0.53], [0.26, 0.33]) | ([0.44, 0.52], [0.50, 0.60], [0.16, 0.22]) |
| X2 | ([0.42, 0.50], [0.51, 0.61], [0.17, 0.23]) | ([0.56, 0.64], [0.32, 0.40], [0.26, 0.34]) | ([0.50, 0.59], [0.42, 0.51], [0.16, 0.23]) | ([0.58, 0.68], [0.23, 0.28], [0.23, 0.28]) | ([0.48, 0.56], [0.43, 0.51], [0.18, 0.24]) |
| X3 | ([0.42, 0.50], [0.44, 0.53], [0.22, 0.27]) | ([0.38, 0.48], [0.60, 0.74], [0.11, 0.22]) | ([0.44, 0.51], [0.48, 0.58], [0.22, 0.30]) | ([0.61, 0.72], [0.22, 0.27], [0.22, 0.27]) | ([0.57, 0.64], [0.38, 0.47], [0.27, 0.36]) |
| X4 | ([0.72, 0.82], [0.17, 0.22], [0.17, 0.22]) | ([0.78, 0.88], [0.14, 0.19], [0.12, 0.19]) | ([0.61, 0.72], [0.22, 0.27], [0.22, 0.27]) | ([0.72, 0.82], [0.17, 0.22], [0.17, 0.22]) | ([0.61, 0.72], [0.22, 0.27], [0.22, 0.27]) |
Step 4. Interval-valued spherical fuzzy decision matrix is obtained as given in Table 8.
Table 8
Decision matrix
| Alternative | C1 | C2 | C3 | C4 | C5 |
| X1 | ([0.37, 0.50], [0.51, 0.62], [0.16, 0.25]) | ([0.04, 0.06], [0.88, 0.96], [0.13, 0.15]) | ([0.18, 0.25], [0.63, 0.74], [0.27, 0.32]) | ([0.31, 0.41], [0.46, 0.56], [0.29, 0.37]) | ([0.31, 0.42], [0.53, 0.63], [0.21, 0.28]) |
| X2 | ([0.33, 0.44], [0.52, 0.63], [0.20, 0.27]) | ([0.10, 0.15], [0.73, 0.83], [0.25, 0.29]) | ([0.21, 0.28], [0.58, 0.68], [0.28, 0.34]) | ([0.42, 0.56], [0.29, 0.35], [0.28, 0.34]) | ([0.34, 0.45], [0.46, 0.55], [0.23, 0.30]) |
| X3 | ([0.32, 0.44], [0.46, 0.55], [0.24, 0.31]) | ([0.07, 0.11], [0.81, 0.91], [0.17, 0.20]) | ([0.18, 0.24], [0.62, 0.72], [0.30, 0.36]) | ([0.44, 0.58], [0.27, 0.34], [0.27, 0.33]) | ([0.40, 0.51], [0.42, 0.51], [0.30, 0.40]) |
| X4 | ([0.56, 0.72], [0.21, 0.28], [0.21, 0.28]) | ([0.14, 0.20], [0.70, 0.80], [0.20, 0.25]) | ([0.25, 0.34], [0.48, 0.58], [0.32, 0.39]) | ([0.51, 0.66], [0.24, 0.30], [0.23, 0.30]) | ([0.43, 0.58], [0.28, 0.35], [0.27, 0.34]) |
Step 4.1. Defuzzified interval-valued spherical fuzzy decision matrix is obtained as given in Table 9.
Table 9
Defuzzified interval-valued spherical fuzzy decision matrix
| Alternative | C1 | C2 | C3 | C4 | C5 |
| X1 | -0.137 | -0.852 | -0.447 | -0.159 | -0.215 |
| X2 | -0.193 | -0.608 | -0.367 | 0.113 | -0.112 |
| X3 | -0.128 | -0.747 | -0.434 | 0.149 | -0.037 |
| X4 | 0.337 | -0.543 | -0.227 | 0.259 | 0.138 |
Step 5. Interval-valued spherical fuzzy negative ideal solution is obtained as given in Table 10.
Table 10
Interval-valued spherical fuzzy negative ideal solution
| C1 | C2 | C3 | C4 | C5 | |
| -0.193 | -0.852 | -0.447 | -0.159 | -0.215 | |
| ([0.85, 0.95], [0.10, 0.15], [0.05, 0.15]) | ([0.20, 0.25], [0.65, 0.75], [0.20, 0.25]) | ([0.25, 0.30], [0.55, 0.65], [0.25, 0.30]) | ([0.65, 0.75], [0.20, 0.25], [0.20, 0.25]) | ([0.75, 0.85], [0.15, 0.20], [0.15, 0.20]) |
Step 6. The Euclidean and Hamming distances to the ideal negative solution are obtained as given in Table 11.
Table 11
Euclidean and Hamming distances to the ideal worst scenario
| Alternative | Euclidean distance | Hamming distance |
| X1 | 0.027 | 0.009 |
| X2 | 0.147 | 0.091 |
| X3 | 0.151 | 0.101 |
| X4 | 0.306 | 0.226 |
Step 7. Relative assessment matrix is obtained as given in Table 12.
Table 12
Relative assessment matrix
| Alternative | X1 | X2 | X3 | X4 |
| X1 | 0.000 | -0.110 | -0.113 | -0.218 |
| X2 | 0.130 | 0.000 | -0.004 | -0.137 |
| X3 | 0.136 | 0.004 | 0.000 | -0.135 |
| X4 | 0.339 | 0.180 | 0.174 | 0.000 |
Step 8. The appraisal scores of alternatives are obtained as given in Table 13.
Table 13
Appraisal scores of alternatives
| Alternative | Appraisal score | Ranking |
| X1 | -0.441 | 4 |
| X2 | -0.012 | 3 |
| X3 | 0.005 | 2 |
| X4 | 0.693 | 1 |
The ranking of alternatives is obtained as follows:
X4 > X3 > X2 > X1 Since alternative X4 has the highest appraisal score, reopening readiness level of faculty of D (X4) is the best.
5.3Sensitivity analysis
In this study, to certify the developed model, two separate sensitivity analyses are presented with respect to change in criterion and decision-maker weights on the final rankings. In the first study, one-at-a-time sensitivity analysis is conducted based on each criterion. For this purpose, the reference criterion weight values, namely absolutely more importance (AMI), equally importance (EI) and absolutely low importance (ALI), are determined in order to see the effect of the change in the criterion weights on the final rankings. Then, assigning these reference values to each criterion one by one, the model is run and alternatives are ranked. The results obtained according to a total of 15 scenarios obtained in this way are presented in Fig. 3.
Fig. 3
Ranks of the alternatives with respect to the changes in criteria weights.
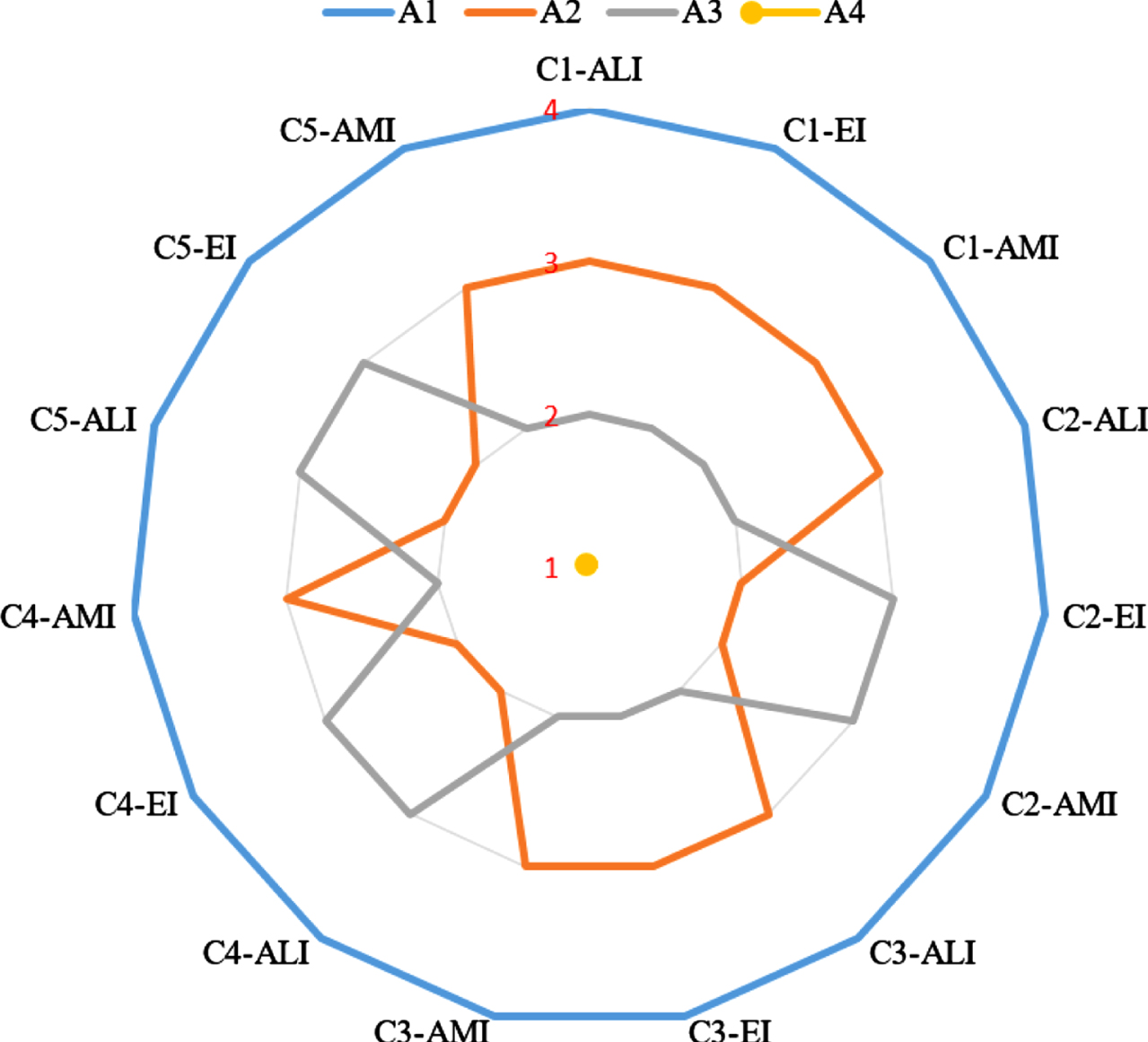
In all scenarios, the alternative X4 has the first and alternative X1 has the last rank. Even with extreme values, it can be seen that alterations in criterion weights have little effect on the model’s conclusion.
In the second analysis, the weights of the decision-makers are changed significantly and on the basis of different values of weights, 10 different scenarios are obtained. Fig. 4 presents the final rankings and the weight distributions of decision-makers.
Fig. 4
Ranks of the alternatives with respect to the changes in decision-maker weights.
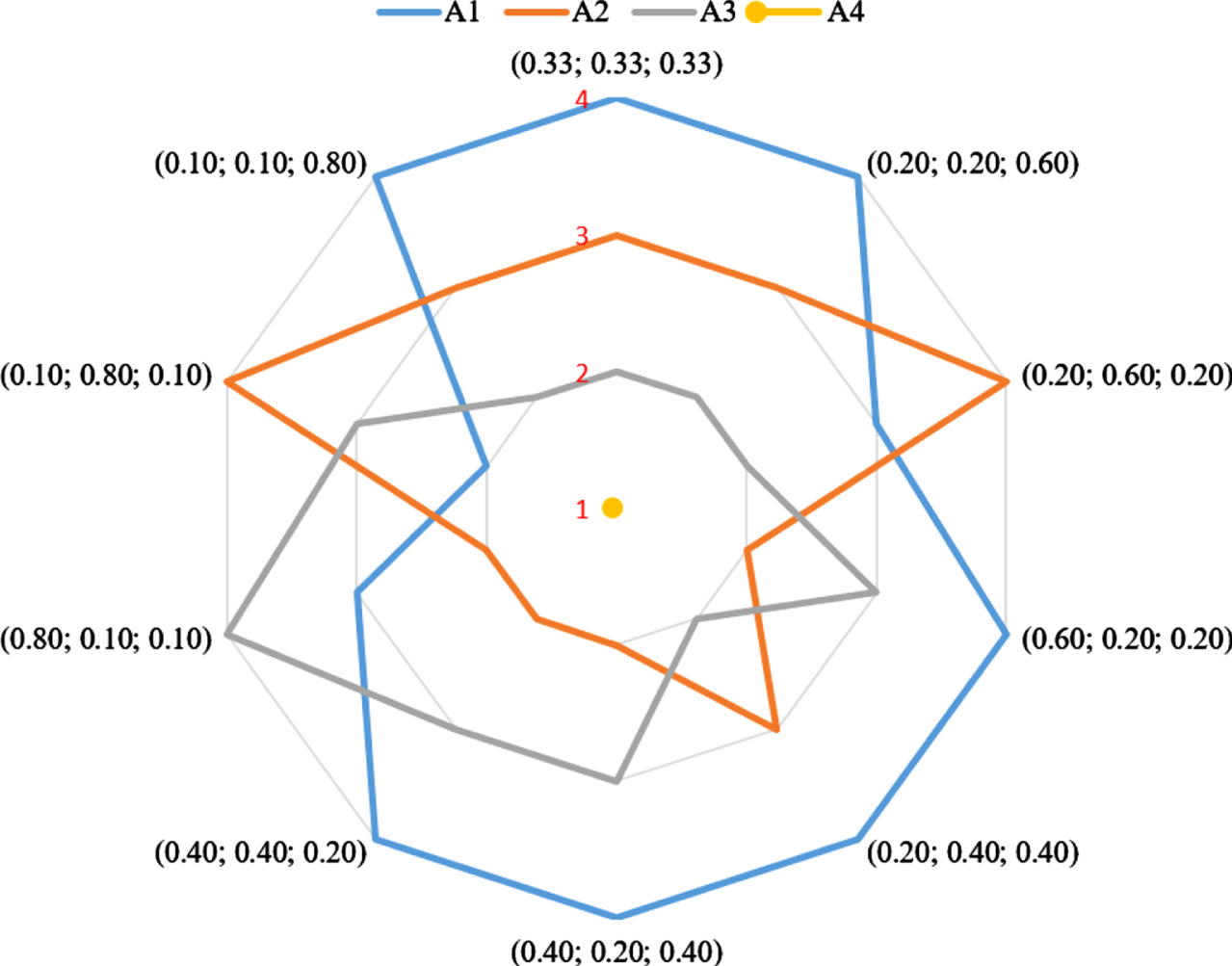
Alternative X4 is the best choice in all scenarios, whereas alternative X1 is the worst choice in seven of them. Although the ranking order of the other two alternatives may vary depending on the weight combinations used, the suggested approach produces reliable results in general and has adequate consistency across various decision-maker weight scenarios.
5.4Comparative analysis
A comparative study with other state-of-the-art MCDM approaches is conducted to illustrate the rationality and effectiveness of this study. For this purpose, the same problem is solved with six different MCDM models developed in spherical fuzzy and intuitionistic fuzzy environments. The selected models for comparative analysis are spherical fuzzy TOPSIS, spherical fuzzy CODAS, spherical fuzzy EDAS, intuitionistic fuzzy TOPSIS, intuitionistic fuzzy CODAS and intuitionistic fuzzy TOPSIS. The appraisal scores obtained from the proposed model and other six MCDM models are given in Table 14.
Table 14
Appraisal scores and rank correlations (ρik) for different approaches
| Proposed methodology | SF TOPSIS | SF CODAS | SF EDAS | IF TOPSIS | IF CODAS | IF EDAS | |
| X1 | –0.441 | 0.190 | –0.219 | 0.298 | 0.044 | –0.251 | 0.000 |
| X2 | –0.012 | 0.336 | –0.103 | 0.682 | 0.315 | –0.055 | 0.356 |
| X3 | 0.005 | 0.427 | 0.010 | 0.445 | 0.343 | –0.035 | 0.416 |
| X4 | 0.693 | 1.000 | 0.327 | 0.995 | 1.000 | 0.386 | 1.000 |
| ρik | 1.000 | 1.000 | 1.000 | 0.964 | 1.000 | 1.000 | 1.000 |
The ranking of appraisal scores are same in all models except one case. In spherical fuzzy EDAS, different from other models, the order of the second and third alternatives has changed; however, in all models the best alternative is X4 and the worst one is X1. Additionally, a statistical approach is used to determine the similarity of the ranking orders derived from this comparison research. Spearman’s rank correlation approach is used to determine if there is substantial rank correlation between two sets of values as given in Equation 26.
(26)
6Conclusion
Many countries have decided to close higher education institutions in order to prevent the spread of the COVID-19 virus, and worldwide, more than a million students have been affected by quarantine, lockdown, and school closure. On the other hand, within the scope of returning to normal life, the reopening of these educational institutions is on the agenda of the whole world, and in order for these institutions to return to face-to-face education, they must meet some strategic criteria such as organizing their infrastructure and human resources, implementing preventive measures and activities, making necessary arrangements for student affairs, and limiting physical contact. At this point, there is a problem with figuring out how ready academic units are to reopen, which is usually based on a set of qualitative criteria. This kind of problem can only be figured out in a linguistic manner, which can be a bit vague and imprecise.
In this study, the classical CODAS method, which has already been accepted in many problems in the literature, is extended with interval-valued spherical fuzzy sets. While the spherical fuzzy sets allow modeling the vagueness in the problem, the increased dimension with interval-valued structure significantly increases the capability of the model in this regard. The proposed model is applied to the problem of evaluating the reopening readiness levels of academic units for the campus type of education in the age of COVID-19. Theoretical and practical contributions, limitations, and future research recommendations of the study are given below, respectively.
6.1Main contributions
The following are the main contributions of this study, which can also be considered its advantages:
(1) Many universities converted to distance education during the pandemic era, and as a result of the pandemic’s waning effect, many of these institutions have begun to return to face-to-face education in the post-pandemic period. However, the question of whether these institutions are prepared for physical education has arisen, and in this context, the necessity to assess these institutions’ readiness has arisen. In contrast to past research, in this study, the reopening readiness levels of academic units within the scope of the pandemic are addressed through a fuzzy MCDM approach. For this purpose, a set of evaluation criteria is established and a novel decision support model is introduced based on an interval-valued spherical fuzzy CODAS.
(2) While the standard CODAS technique is an effective MCDM technique, it cannot describe the uncertainty inherent in a problem. On the other hand, the available CODAS models are mainly either crisp-based studies or they do not have capabilities that can thoroughly model the vagueness in the nature of the problem. To address the uncertainty, this study proposes a new MCDM methodology that extends the standard CODAS technique with interval-valued spherical fuzzy sets. Within the methodology, the classical CODAS steps are carried out in an interval-valued spherical fuzzy environment, including the computation of the Euclidean and Hamming distances.
(3) Spherical fuzzy sets are already known to allow more space for decision-makers to express their evaluations than most other fuzzy extensions, and membership, non-membership, and hesitation degrees can be modeled individually in spherical fuzzy sets. The proposed interval-valued character allows spherical fuzzy sets to model the aforementioned degrees in a larger area. Unlike previous literature, the proposed model not only presents the advantages of spherical fuzzy sets but also extends them to an interval-valued structure to comprehensively address the vagueness and uncertainty.
(4) The presented strategic criteria set, as well as the importance levels of these criteria, may be used as a reference for a better understanding of the reopening readiness assessment problem faced by higher education institutions and, to some extent, other sectors. With its dynamic structure, the proposed model can be used as a decision support tool for higher education institutions, as well as other sectors confronting similar types of difficulties.
6.2Limitations and future research avenues
The following comments can be made as the limitations of this study:
(1) Although, this study provides some meaningful guidance for evaluating the pandemic readiness of academic units, a limited number of criteria are presented.
(2) This is a solely expert-dependent model that ranks alternatives based on the opinions of decision-makers and lacks a feature that directly reflects the institution’s numerical data.
For further research, it is possible to extend the developed model in many ways, as follows:
(1) Other types of spherical fuzzy sets e.g., trapezoidal spherical fuzzy sets can be developed to increase the fuzziness modeling capacity of the model.
(2) Reopening readiness evaluation criteria can be extended and grouped into sub-categories, and with a more comprehensive set of criteria, a pandemic readiness index can be developed.
(3) In this study, the geometric mean operator is used for aggregating the matrices. However, the arithmetic mean operator can also be used alternatively, and the obtained results can be compared.
(4) The proposed methodology can be applied to other decision-making problems such as sustainable building material selection or construction-contractor selection with many other MCDM techniques, e.g., ELECTRE.
(5) Supervised machine learning algorithms can be integrated into the model to make use of available data within the institutions, and by doing so, both the dependency of the model on the expert can be reduced, and the opportunity can be given to the model to update itself with new data entries, which makes the model more intelligent and practical.
(6) On the other hand, in linguistic settings, words may imply non-identical things to different decision-makers, implying the need of representing a personalized individual semantics [15], and there may be some instances when decision makers may employ unbalanced linguistic terms sets that are not consistently and symmetrically distributed to offer linguistic evaluations of alternatives [45]. In the future, other scholars can consider how to deal with consensus-achieving problems in such situations and propose a model for an interval-valued spherical fuzzy linguistic environment.
References
[1] | Ashraf S. , Abdullah S. and Almagrabi A.O. , A new emergency response of spherical intelligent fuzzy decision process to diagnose of covid19, Soft Computing, pages 1–17, (2020) . doi: https://doi.org/10.1007/s00500-020-05570-8 |
[2] | Atanassov K. , Gargov, g265: Interval valued intuitionistic fuzzy sets, Fuzzy Sets Syst 31: ((1989) ), 0165–0114. doi: https://doi.org/10.1016/0165-0114(89)90205-4 |
[3] | Atanassov K. , Geometrical interpretation of the elements of the intuitionistic fuzzy objects, Preprint IM-MFAIS-1-89, Sofia, (1989) . |
[4] | Atanassov K.T. , Intuitionistic fuzzy sets, Fuzzy Sets and Systems 20: (1) ((1986) ), 87–96. doi: https://doi.org/10.1016/s0165-0114(86)80034-3 |
[5] | Balin A. , A novel fuzzy multi-criteria decision-making methodology based upon the spherical fuzzy sets with a real case study, Iranian Journal of Fuzzy Systems 17: (4) ((2020) ), 167–177. doi: https://doi.org/10.22111/IJFS.2020.5413 |
[6] | Bolturk E. , Pythagorean fuzzy codas and its application to supplier selection in a manufacturing firm, Journal of Enterprise Information Management, (2018) . doi: https://doi.org/10.1108/jeim-01-2018-0020 |
[7] | Chen N. , Xu Z. and Xia M. , Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis, Applied Mathematical Modelling 37: (4) ((2013) ), 2197–2211. doi: https://doi.org/10.1016/j.apm.2012.04.031 |
[8] | Cheng S.-Y. , Wang C.J. , Shen A.C.-T. and Chang S.-C. , How to safely reopen colleges and universities during covid-19: experiences from taiwan, Annals of Internal Medicine 173: (8) ((2020) ), 638–641. doi: https://doi.org/10.7326/m20-2927 |
[9] | Cuong B.C. , Picture fuzzy sets, Journal of Computer Science and Cybernetics 30: (4) ((2014) ), 409. doi: https://doi.org/10.15625/1813-9663/30/4/5032 |
[10] | Cuong B.C. and Kreinovich V. , Picture fuzzy sets-a new concept for computational intelligence problems, In 2013 third world congress on information and communication technologies (WICT 2013), pages 1–6. IEEE, (2013) . doi: https://doi.org/10.1109/wict.2013.7113099 |
[11] | Dayyani L. , Pourtaheri M. and Ahmadi H. , Evaluation of texture deterioration stages of rural settlements on the tehran metropolitan fringe using the decision-making method of ow and codas, Journal of Housing and the Built Environment, pages 1–49. (2021) . doi: https://doi.org/10.1007/s10901-021-09835-y |
[12] | Demirel H. , A novel fuzzy multi-criteria decision-making methodology based upon the spherical fuzzy sets for stabilizer selection of cruise ships, Brodogradnja: Teorija i praksa brodogradnje i pomorske tehnike 71: (3) ((2020) ), 1–11. doi: https://doi.org/10.21278/brod71301 |
[13] | Farrokhizadeh E. , Seyfi-Shishavan S.A. , Gundoğdu F.K. , DonyatalabY., KahramanC. and SeifiS.H., A spherical fuzzy methodology integrating maximizing deviation and topsis methods, Engineering Applications of Artificial Intelligence 101: ((2021) ), 104212. doi: https://doi.org/10.1016/j.engappai.2021.104212 |
[14] | Fraser S. , Lagacé M. , Bongué B. , Ndeye N. , Guyot J. , Bechard L. , Garcia L. , Taler V. and Adam S. , et al., Ageism and covid-19: what does our society’s response say about us? Age and Ageing 49: (5) ((2020) ), 692–695. doi: https://doi.org/10.1093/ageing/afaa097 |
[15] | Gao Y. and Zhang Z. , Consensus reaching with noncooperative behavior management for personalized individual semantics-based social network group decision making, Journal of the Operational Research Society, pages 1–18, (2021) . |
[16] | Ghorabaee M.K. , Amiri M. , Zavadskas E.K. , Hooshmand R. and Antuchevičienė J. , Fuzzy extension of the codas method for multi-criteria market segment evaluation, Journal of Business Economics and Management 18: (1) ((2017) ), 1–19. doi: https://doi.org/10.3846/16111699.2016.1278559 |
[17] | Gul M. and Ak M.F. , A modified failure modes and effects analysis using interval-valued spherical fuzzy extension of topsis method: case study in a marble manufacturing facility, Soft Computing 25: (8) ((2021) ), 6157–6178. doi: https://doi.org/10.1007/s00500-021-05605-8 |
[18] | Gundoğdu F.K. and KahramanC., A novel fuzzy topsis method using emerging interval-valued spherical fuzzy sets, Engineering Applications of Artificial Intelligence 85: ((2019) ), 307–323. doi: https://doi.org/10.1016/j.engappai.2019.06.003. |
[19] | Joshi B.P. , Singh A. , Bhatt P.K. and Vaisla K.S. , Interval valued q-rung orthopair fuzzy sets and their properties, Journal of Intelligent & Fuzzy Systems 35: (5) ((2018) ), 5225–5230. doi: https://doi.org/10.3233/JIFS-169806 |
[20] | Karagoz S. , Deveci M. , Simic V. , Aydin N. and Bolukbas U. , A novel intuitionistic fuzzy mcdm-based codas approach for locating an authorized dismantling center: a case study of istanbul, Waste Management & Research 38: (6) ((2020) ), 660–672. doi: https://doi.org/10.1177/0734242X19899729 |
[21] | Keshavarz Ghorabaee M. , ZavadskasE.K., TurskisZ. and AntuchevicieneJ., A new combinative distance-based assessment (codas) method for multi-criteria decision-making, Economic Computation & Economic Cybernetics Studies & Research 50: (3) ((2016) ). |
[22] | Kutlu Gundoğdu F. , A spherical fuzzy extension of multimoora method, Journal of Intelligent & Fuzzy Systems 38: (1) ((2020) ), 963–978. doi: https://doi.org/10.3233/jifs-179462 |
[23] | Kutlu Gundoğdu F. and KahramanC., Spherical fuzzy sets and spherical fuzzy topsis method, Journal of Intelligent & Fuzzy Systems 36: (1) ((2019) ), 337–352. doi: https://doi.org/10.3233/jifs-181401 |
[24] | Menekse A. and Camgoz-Akdag H. , Internal audit planning using spherical fuzzy electre, Applied Soft Computing 114: ((2022) ), 108155. |
[25] | Mukherjee U.K. , Bose S. , Ivanov A. , Souyris S. , Seshadri S. , Sridhar P. , Watkins R. and Xu Y. , Evaluation of reopening strategies for educational institutions during covid-19 through agent based simulation, Scientific Reports 11: (1) ((2021) ), 1–24. doi: https://doi.org/10.1038/s41598-021-84192-y |
[26] | Onar S.C. , Kahraman C. and Oztaysi B. , Multi-criteria spherical fuzzy regret based evaluation of healthcare equipment stocks, Journal of Intelligent & Fuzzy Systems (Preprint) ((2020) ), 1–11. doi: https://doi.org/10.3233/jifs-189073 |
[27] | Oztaysi B. , Onar S.C. and Kahraman C. , A dynamic pricing model for location based systems by using spherical fuzzy ahp scoring, Journal of Intelligent & Fuzzy Systems (Preprint) ((2020) ), 1–10. doi: https://doi.org/10.3233/jifs-189097 |
[28] | Perez-Dominguez L. , Duran S.-N.A. , Lopez R.R. , Perez-Olguin I.J.C. , Luviano-Cruz D. and Gomez J.A.H. , Assessment urban transport service and pythagorean fuzzy sets codas method: A case of study of ciudad juarez, Sustainability 13: (3) ((2021) ), 1281. doi: https://doi.org/10.3390/su13031281 |
[29] | Quattrone F. , Borghini A. , Emdin M. and Nuti S. , Protecting higher education institutions from covid-19: insights from an italian experience, Journal of American College Health, pages 1–2, (2020) . doi: https://doi.org/10.1080/07448481.2020.1791885 |
[30] | Roy J. , Das S. , Kar S. and Pamučar D. , An extension of the codas approach using interval-valued intuitionistic fuzzy set for sustainable material selection in construction projects with incomplete weight information, Symmetry 11: (3) ((2019) ), 393. doi: https://doi.org/10.3390/sym11030393 |
[31] | Seker S. and Aydin N. , Sustainable public transportation system evaluation: A novel two-stage hybrid method based on ivif-ahp and codas, International Journal of Fuzzy Systems 22: (1) ((2020) ), 257–272. doi: https://doi.org/10.1007/s40815-019-00785-w |
[32] | Sharaf I.M. , Evaluating geothermal energy systems using spherical fuzzy promethee, In Decision Making with Spherical Fuzzy Sets, pages 375–397. Springer, (2021) . doi: https://doi.org/10.1007/978-3-030-45461-6_16 |
[33] | Sharaf I.M. , Spherical fuzzy vikor with swam and swgm operators for mcdm, In Decision Making with Spherical Fuzzy Sets, pages 217–240. Springer, (2021) . doi: https://doi.org/10.1007/978-3-030-45461-6_9 |
[34] | Smarandache F. , A unifying field in logics: Neutrosophic logic, In Philosophy, pages 1–141. American Research Press, (1999) . |
[35] | Torra V. , Hesitant fuzzy sets, International Journal of Intelligent Systems 25: (6) ((2010) ), 529–539. doi: https://doi.org/10.1002/int.20418 |
[36] | Triantaphyllou E. , Multi-criteria decision making methods, In Multi-criteria decision making methods: A comparative study, pages 5–21. Springer, (2000) . doi: https://doi.org/10.1007/978-1-4757-3157-6_2 |
[37] | Vinodh S. and Wankhede V.A. , Application of fuzzy dematel and fuzzy codas for analysis of workforce attributes pertaining to industry 4.0: a case study, International Journal of Quality & Reliability Management, (2020) . doi: https://doi.org/10.1108/ijqrm-09-2020-0322 |
[38] | Wang H. , Smarandache F. , Sunderraman R. and Zhang Y.-Q. , interval neutrosophic sets and logic: theory and applications in computing: Theory and applications in computing, volume5: . Infinite Study, (2005) . doi: https://doi.org/10.5281/zenodo.8818 |
[39] | Wang P. , Wang J. , Wei G. , Wu J. , Wei C. and Wei Y. , Codas method for multiple attribute group decision making under 2-tuple linguistic neutrosophic environment, Informatica 31: (1) ((2020) ), 161–184. |
[40] | Wrighton M.S. and Lawrence S.J. , Reopening colleges and universities during the covid-19 pandemic, Annals of Internal Medicine 173: (8) ((2020) ), 664–665. doi: https://doi.org/10.7326/m20-4752 |
[41] | Yager R.R. , Pythagorean fuzzy subsets, In 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS), pages 57–61. IEEE, (2013) . doi: https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375 |
[42] | Yager R.R. , Generalized orthopair fuzzy sets, IEEE Transactions on Fuzzy Systems 25: (5) ((2016) ), 1222–1230. doi: https://doi.org/10.1109/tfuzz.2016.2604005 |
[43] | Yeni F.B. and Özçelik G. , Interval-valued atanassov intuitionistic fuzzy codas method for multi criteria group decision making problems, Group Decision and Negotiation 28: (2) ((2019) ), 433–452. doi: https://doi.org/10.1007/s10726-018-9603-9 |
[44] | Zadeh L. , Fuzzy sets, Information and Control 8: (3) ((1965) ), 338–353. doi: https://10.1016/s0019-9958(65)90241-x |
[45] | Zhang Z. , Li Z. and Gao Y. , Consensus reaching for group decision making with multi-granular unbalanced linguistic information: A bounded confidence and minimum adjustment based approach, Information Fusion 74: ((2021) ), 96–110. |




