Spherical bipolar fuzzy weighted multi-facility location modeling for mobile COVID-19 vaccination clinics
Abstract
A pandemic was declared in 2020 due to COVID-19. The most important way to deal with the virus is mass vaccination which is a complex task in terms of fast transportation and process management. Hospitals and other health centers are appropriate for vaccination process. In addition, in order to protect other patients from COVID-19 and provide rapid access to vaccines, mobile vaccination clinics can also be considered. In this study, the location assignments of mobile vaccination clinics that can serve some regions of three cities in Turkey are examined. The linear formulation of the problem is given, and the multi-facility location problem for COVID-19 vaccination is investigated with Lagrange relaxation and modified saving heuristic algorithm. For the proposed fuzzy MCDM integrated saving heuristic, the importance of candidate locations is calculated with the aid of decision makers who give their views in spherical bipolar fuzzy information. The results of different approaches are compared, and it is intended to guide future studies.
1Introduction
Vaccinations are very important to control and eliminate a variety of diseases which are vaccine preventable such as Measles, Hepatitis B etc., and therefore have a major impact on public health [1, 2]. While vaccination activities are intensified, the locations where vaccination is performed are also diversified. Traditional health care locations such as doctor’s offices and hospitals are mostly preferred for vaccination [3]. Additionally, during an epidemic (e.g., influenza) alternative locations like pharmacies can be also used for the same purpose [4]. These places are easily accessible and provide vaccinations for people who are inconvenient to enter traditional health care locations [5].
Since the beginning of 2020, the whole world has been struggling with the pandemic caused by the COVID-19 virus. Many people died due to the virus, and more people are treated in pandemic hospitals for this reason [6]. Numerous pharmaceutical companies in various countries have produced COVID-19 vaccines that are claimed to be protective against the virus. Accordingly, a large number of vaccination centers are needed for these to be applied to people all over the world. Although vaccination will take place in traditional and non-traditional places such as hospitals and pharmacies, these are not considered sufficient to vaccinate all people.
It is possible to deal with an emerging epidemic or pandemic with mass vaccination studies [7]. For the vaccination of such a high number of people, different vaccination location alternatives can be considered in addition to the fixed locations. One of the alternatives used to increase and facilitate vaccination activities is mobile vaccination clinic. Mobile vaccination clinics can be set up anywhere for short or long periods. This alternative was used for various diseases. In the past, the Marion County Department of Health in West Virginia, USA used a mobile vaccine clinic for the H1N1 vaccine [8]. Hannings et al. [9] examined the perceptions of the patients on the influenza mobile vaccination clinic run by pharmacy students at 27 mobile points. Chen et al. [10] followed a mobile clinic program in Houston, which provided for vaccination for children. It is thought that this alternative can also be used in COVID-19 vaccination.
In the pandemic, it is necessary to quickly determine where the mobile vaccination clinics should be located in a certain region. With a suitable assignment program, authorities can be reached at less cost and more effectively. It also contributes to manage public resources correctly. These assignments can be categorized as a multi-facility location problem (MFLP).
The assignment problems are special cases of transportation problems. Location assignment problems are widely discussed for medical services, hospitals, ambulances in the literature such as assignment problems for emergency medical services [11], ambulances [12], hospital departments [13] etc. These special problems can be solved by Branch and Bound Algorithm [14], Hungarian Algorithm [15], Wimmert [16] etc. In addition, heuristic algorithms are also proposed. Heuristics acquire close to optimum results in a short time for large-scale problems. In the literature, many studies used heuristic methods for location-allocation problems. In one of these, the heuristic algorithm assumes that all facilities are initially open. Subsequently, it is aimed to determine the facility to be closed. This is possible by using approximate routing costs for open facilities [17]. A version of the saving algorithm is introduced by Clark and Wright [18]. They presented a saving concept to the single depot vehicle routing problems and produced a greedy type heuristic to find a vehicle routing structure that is close to the optimum structure. A similar greedy approach for the uncapacitated facility location problem is to start with all facilities open and then, one by one, close a facility whose closing leads to the greatest increase in profit as stated in the study of Kuehn and Hamburger [19]. Another saving heuristic is proposed by Hansen et al. [20] but in a model structure with multiple vehicles, capacitated facilities and capacitated vehicles. Their solution is based on decomposing the problem into three subproblems, and the heuristic stops when no further cost improvements are possible. As multi-facility mobile vaccination assignment problem is a capacitated fixed charge location problem, studies of this problem are useful. To solve this problem, enumerative search scheme [21], Branch and Bound Algorithm [22], Branch and Bound Algorithm and Lagrange relaxation [23], Lagrange relaxation Heuristic Algorithm [24], an adaptive sampling algorithm using Ant Colony Optimization [25], and so on.
The multi-facility location problem has also been investigated in non-deterministic environments [26, 27]. New heuristics have been developed in studies based on stochastic processes [28]. Fuzzy logic studies have also been carried out in uncertain environments. Fuzzy criteria and fuzzy goal programming are used to locate new facilities [29, 30]. Canos et al. [31] categorized quantitative fuzzy models, and they specifically discussed the classical p-median problem as a fuzzy model. In addition, it is possible to find various studies in the literature seeking solutions for facility location problems using fuzzy logic [32–35].
To express uncertainty, chronologically, fuzzy set theory by Zadeh [36] and intuitionistic fuzzy sets by Atanassov [37] originally introduced. Based on their ideas, Smarandache [38] proposed neutrosophic fuzzy set which is generalization of fuzzy set theory and intuitionistic fuzzy sets. As an extension of fuzzy sets, spherical fuzzy numbers are presented [39]. These fuzzy sets differ from others in that they are three-dimensional. “In spherical fuzzy numbers, while the squared sum of membership, non-membership and hesitancy parameters can be between 0 and 1, each of them can be defined between 0 and 1 independently to satisfy that their squared sum is at most equal to 1“ [40]. Bipolar-valued fuzzy sets, which is given to the fuzzy literature by Lee [41, 42] is an extension of fuzzy sets whose membership degree range is extended from the interval [0,1] to [–1,1]. Princy and Mohana [43] are proposed the spherical bipolar fuzzy methodology to handle fuzzy multi-criteria decision making (MCDM) problems.
This study contributes to the literature by combining fuzzy MCDM methods and multi-facility location problem in addition to previous studies. For the multi-facility location problem, existing heuristic algorithms are considered and the linear expression of the problem is expanded using Lagrange relaxation to compare the effectiveness of the methodology. The saving heuristic algorithm is adapted for spherical bipolar fuzzy information. The proposed algorithm is applied for the first time in the assignment of mobile vaccination clinics for the pandemic.
The remain of this paper is organized as follows. Section 2 first gives preliminaries and definitions of spherical bipolar fuzzy sets and multi-facility location problem with Lagrange relaxation. Then, proposed methodology is explained with a heuristic algorithm. Section 3 solves the multi-facility location problem of mobile vaccination clinics to make optimum number of assignments within the candidate locations to serve some regions of three cities in Turkey. The results and comparisons are discussed in Section 4. Conclusions and future directions are mentioned in Section 5.
2Methodology
In this section, preliminaries and definitions of spherical bipolar fuzzy sets are given. To present the case based linear programming formulation, general model of capacitated fixed charge facility location problem is represented. Based on the generalized model, linear expression of mobile vaccination clinics assignment problem is proposed. Then, the Lagrange relaxations formula is given. The modified fuzzy saving heuristic algorithm is introduced step by step.
2.1Spherical bipolar fuzzy sets
This section gives the preliminaries and definitions of the proposed method with spherical bipolar fuzzy information:
Definition 1. [38] A spherical bipolar fuzzy set (SBFS)
(1)
For each u, the numbers
Definition 2. [38] Let
(2)
(3)
(4)
(5)
Definition 3. [38] Spherical Bipolar Weighted Arithmetic Mean (SBWAM) with respect to w = w1, w2, …, wn;
(6)
Definition 4. [38] The score function and accuracy function for ranking SBFS are defined by,
(7)
(8)
2.2Linear formulation of general capacitated fixed charge facility location problem
The capacitated fixed charge facility location problem has a finite set of users with demand of service and a finite set of potential locations for the facilities that offer service to users.
Inputs:
cij = Assignment cost from i to j (i = 1,2, ... ,n) (j = 1,2, ... ,m)
hi = Demand of customer i
fj = Cost of locating facility at location j
kj = capacity of locating facility at location j
Decision variables:
Xij ∈ R amount of demand at node i that is satisfied by a facility at location j
Equations:
(9)
(10)
(11)
(12)
The objective function (9) minimizes the total costs including demand-weighted assignment and locating facilities. Constraint (10) states that each customer’s demand must be assigned to locations. Constraint (11) defines that the total assigned demand to the location j cannot exceed the capacity of location j. Constraint (12) defines that if the location i and location j are conflicted, then the amount of demand at node i that is satisfied by a facility at location j should be zero.
2.3Linear formulation of mobile vaccination clinics assignment problem
Based on the general expression of capacitated fixed charge facility location problem, the revised linear programming formulation of the fuzzy weighted multi-facility location problem to assign mobile vaccination clinics is as follows:
Inputs:
cij = Assignment cost (distance or travel time) from i to j (i = 1,2, ... ,n)(j = 1,2, ... ,m)
di = Demand of customer i
fj = Cost of locating facility at location j
k = Number of facilities to locate
N = Maximum number of customers a location can serve
Decision variables:
xij ∈ R the assignment rate of demand of customer i to location j (consider di = hi and dixij = Xij from general formulation)
Equations:
(13)
(14)
(15)
(16)
(17)
The objective function (13) minimizes the total costs including demand-weighted assignment and locating facilities. Constraint (14) states that each customer’s demand must be assigned to locations. Constraint (15) defines that the total rate of customer demand assigned to these candidate locations cannot exceed the number assigned customers. Constraint (16) means that only k candidate locations must be selected. Constraint (17) defines that if the location i and location j are conflicted, then the assignment rate of demand should be zero. Otherwise, this rate depends only on whether the facility is opened at that point.
2.4Lagrange relaxation of mobile vaccination clinics assignment problem
Lagrange relaxation is a relaxation method which approximates a difficult problem of constrained optimization by a simpler problem. A solution to the relaxed problem is an approximate solution to the original problem and provides useful information. The method penalizes violations of inequality constraints using a Lagrange multiplier, which imposes a cost on violations. These added costs are used instead of the strict inequality constraints in the optimization.
To observe the total cost of ignoring not being able to meet all the demands of a customer, constraint (14) is relaxed. Thus, the linear formulation of the relaxed fuzzy weighted multi-facility location problem is as follows.
Inputs:
cij =Assignment cost (distance or travel time) from i to j (i = 1,2, ... ,n) (j = 1,2, ... ,m)
di =Demand of customer i
fj =Cost of locating facility at location j
k = Number of facilities to locate
N = Maximum number of customers a location can serve
ui = lagrange multiplier
Decision variables:
xij ∈ R the assignment rate of demand of customer i to location j (consider di = hi and dixij = Xij from general formulation)
(18)
Constraints (15)–(16) and (17).
To observe the total cost of ignoring the confliction of locations, the constraint (17) is relaxed. Thus, the linear formulation of the relaxed fuzzy weighted multi-facility location problem is as follows.
Inputs:
cij =Assignment cost (distance or travel time) from i to j (i = 1,2, ... ,n) (j = 1,2, ... ,m)
di =Demand of customer i
fj =Cost of locating facility at location j
k = Number of facilities to locate
N = Maximum number of customers a location can serve
wi = lagrange multiplier
Decision variables:
xij ∈ R the assignment rate of demand of customer i to location j (consider di = hi and dixij = Xij from general formulation)
(19)
Constraints (14)-(15) and (16).
2.5Heuristic Algorithm for mobile vaccination clinics assignment problem
In this section, proposed algorithm is given to multi-facility location problem with spherical bipolar information. based on Clarke & Wright [18] and Kuehn & Hamburger [19].
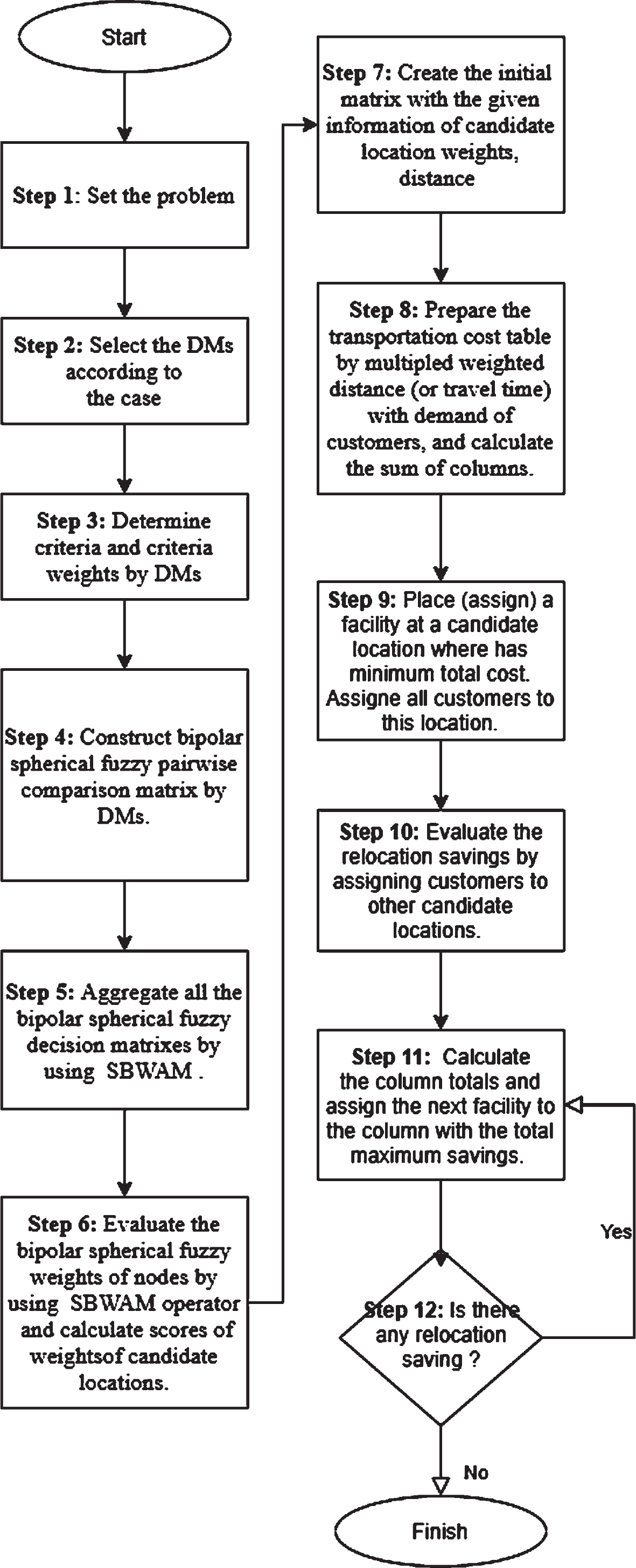
This algorithm consists of two main parts. The first part is to weight the candidate locations by using spherical bipolar MCDM method. In the second part, the calculated weights affect the transportation costs matrix. With the heuristic algorithm, the facilities are assigned to candidate locations with minimum cost. Maximum saving is calculated in each iteration. When the saving is over, optimum assignment number and assignment pairs are found. Figure 1 illustrates the flowchart of the proposed algorithm.
Fig. 1
Flowchart of the proposed algorithm.
The steps of spherical bipolar fuzzy MCDM approach [38] to calculate weights of candidate locations are described as follows:
Step 1: Set the problem.
Step 2: Select the DMs (decision makers) according to the case and let E ={ e1, e2 … , eq } be a collection of DMs.
Step 3: Determine criteria and criteria weights by DMs. Let C ={ c1, c2, …, cn } be the collection of criteria and a ={ a1, a2, …, an } be the collection of weight vector of criteria set with
Step 4: Construct spherical bipolar fuzzy pairwise comparison matrix by DMs according to determined criteria and locations. Let
Step 5: Aggregate all the spherical bipolar fuzzy decision matrixes by using
Step 6: Evaluate the spherical bipolar fuzzy weights of nodes by using SBWAM operator with
After the weights of candidate locations are calculated, the assignments are made. The heuristic algorithm for multi-facility location problem is proposed based on the studies [18] and [19]. In our approach the first facility is placed in a minimum cost location. The new location where each facility is then placed should further improve the solution. The optimum number and location of facilities that give the minimum cost are determined. The steps of heuristic algorithm is as follows:
Step 7: Create the initial matrix with the given information of candidate location weights, distances (or travel times) between customer and candidate location, and demands of customers.
Step 8: Prepare the transportation cost table by multiplied weighted distance (or travel time) with demand of customers, and calculate the sum of columns. (Benefits are positive and costs are negative.)
Step 9: Place (assign) a facility at a candidate location where has minimum total cost. Assign all customers to this location.
Step 10: Evaluate the relocation saving by assigning customers to other candidate locations.
Step 11: Calculate the column totals and assign the next facility to the column with the total maximum saving. Customers who have these saving is assigned to that location.
Step 12: Revize the saving matrix. If there is saving, then go to Step 11. Otherwise, end the algorithm.
This process is finished when the minimum total cost is achieved. This is also the point where a new facility to be established does not provide any additional saving.
3Case study
This section aims to illustrate the proposed spherical bipolar fuzzy MCDM adapted heuristic algorithm for multi-facility location problem on a mobile vaccination center assigment case. According the proposed algorithm mentioned in the previous section, the problem has two main parts. The first part introduces the spherical bipolar fuzzy MCDM method for calculation of weights for candidate locations according to the determined criteria and view’s of DMs. The second part obtains the assignments with the aid of heuristic algorithm for multi-facility location.
Step 1: In 2020, a pandemic was declared all over the world due to COVID-19. Vaccination studies started quickly. In Turkey, it was decided to use the traditional fixed location of health centers for vaccination. In addition, mobile vaccination clinics can be proposed to speed up immunization and to keep COVID-19 processes separate from other diseases. As a case study, the location assignments of mobile vaccination clinics that can serve some regions of three cities (İstanbul, Ankara, İzmir) in Turkey are examined. For İstanbul, 15 candidate locations are determined by DMs and the city is divided into 20 regions. The DMs suggested 8 candidate locations and 10 regions for Ankara, and 5 candidate locations and 6 regions for İzmir. For illustrate the proposed approaches, the data of İzmir region is shown step by step. The problem of which candidate points to establish a mobile vaccination clinic and which areas benefit from these clinics is investigated.
Step 2: Five DMs are selected in health sector as E ={ e1, e2 … , e5 }.
Step 3: The DMs determined criteria as C ={ c1, c2, c3, c4 } with c1: distance, c2: easy transportation, c3: environmental conditions c4: capacity. The criteria weights w ={ a1, a2, a3, a4 } are determined as a1:0.33, a:0.21, a3:0.29, a4:0.17 by DMs.
Step 4-5: According to determined criteria and candidate locations, spherical bipolar fuzzy pairwise comparison matrixes are constructed by DMs, and aggregated by using SBWAM. Collective spherical bipolar fuzzy decision matrix is evaluated as follows.
Step 6: Spherical bipolar fuzzy weights and scores of weights of candidate locations are represented in Tables 1 and 2 by using Equation (7).
Table 1
Spherical bipolar fuzzy weights of five candidate locations
| Candidate location |
|
| 1 | (0.355,0.369,0.413,-0.089,-0.687,-0.378) |
| 2 | (0.507,0.527,0.440,-0.085,-0.574,-0.398) |
| 3 | (0.609,0.472,0.401,-0.225,-0.691,-0.276) |
| 4 | (0.639,0.271,0.355,-0.150,-0.454,-0.411) |
| 5 | (0.324,0.599,0.490,-0.425,-0.510,-0.461) |
Table 2
Scores of weights of candidate locations
| Candidate location |
| Normalised (= wj) |
| 1 | 0.130 | 0.323 |
| 2 | 0.101 | 0.249 |
| 3 | 0.029 | 0.073 |
| 4 | 0.109 | 0.271 |
| 5 | 0.034 | 0.085 |
3.1İzmir data
In İzmir, the DMs select six regions (i={A,B,C,D,E,F}) and five candidate locations (j={1,2,3,4,5}). Each location can serve maximum three regions. The travel times of the regions to the candidate locations are given in Table 3. In tables, the travel times of conflicted locations and regions are marked (C={{B,3},{C,1},{D,2}}) with X.
Table 3
Travel times information (minutes) of Izmir data
| Candidate location | 1 w1: | 2 w2: | 3 w3: | 4 w4: | 5 w5: |
| Region | 0.323 | 0.249 | 0.073 | 0.271 | 0.085 |
| A | 12.4 | 32.09 | 68.71 | 3.7 | 82.64 |
| B | 21.7 | 20.05 | X | 14.78 | 35.42 |
| C | X | 36.10 | 27.48 | 14.78 | 70.83 |
| D | 18.6 | X | 130.55 | 18.48 | 82.64 |
| E | 12.4 | 48.13 | 54.97 | 3.39 | 106.25 |
| F | 30.99 | 71.39 | 82.45 | 33.26 | 35.42 |
The fixed clinic cost (cij), demand (dij) and weighted travel times (
Table 4
Fixed cost, demand and weighted travel times information of Izmir
| Candidate location Region | 1 | 2 | 3 | 4 | 5 | Demand (person) |
| A | 4 | 8 | 5 | 1 | 7 | 3000 |
| B | 7 | 5 | X | 4 | 3 | 4000 |
| C | X | 9 | 2 | 4 | 6 | 2000 |
| D | 6 | X | 9.5 | 5 | 7 | 2400 |
| E | 4 | 12 | 4 | 2 | 9 | 2000 |
| F | 10 | 17.8 | 6 | 9 | 3 | 1500 |
| Fixed clinic cost (£) | 5000 | 3000 | 6000 | 7000 | 2000 |
This problem is solved by GAMS using the linear programming formulation in Section 2.3. The number of locations to be selected at minimum cost is three. Cost values for different numbers of selected locations are shown in the Table 5. Since three selected
Table 5
Cost values for different selected locations for Izmir
| Number of selected locations | 1 | 2 | 3 | 4 | 5 |
| Total Cost | infeasible | 56,500£ | 54,500£ | 62,900£ | 62,500£ |
locations are optimum, the assignments for this statement are given in Table 6. The remainder of this sub-section continues with optimum statement.
Table 6
Results of assignment problem for Izmir
| Selected locations | 3 | 4 | 5 |
| Assigned Region | C | A,D,E | B,F |
| Total Cost | 54,500 £ | ||
As mentioned in Section 2.4, constraint (14) is relaxed, the assignment all demands is ignored. This problem is solved by GAMS, and the total cost decreased to 52.496,083 £ as it allowed not all demands of a region to be assigned. Figure 2 shows that the iterations of Lagrange relaxation with their total cost results.
Fig. 2
Iteration results of Lagrange relaxation for constraint (14) of Izmir data.
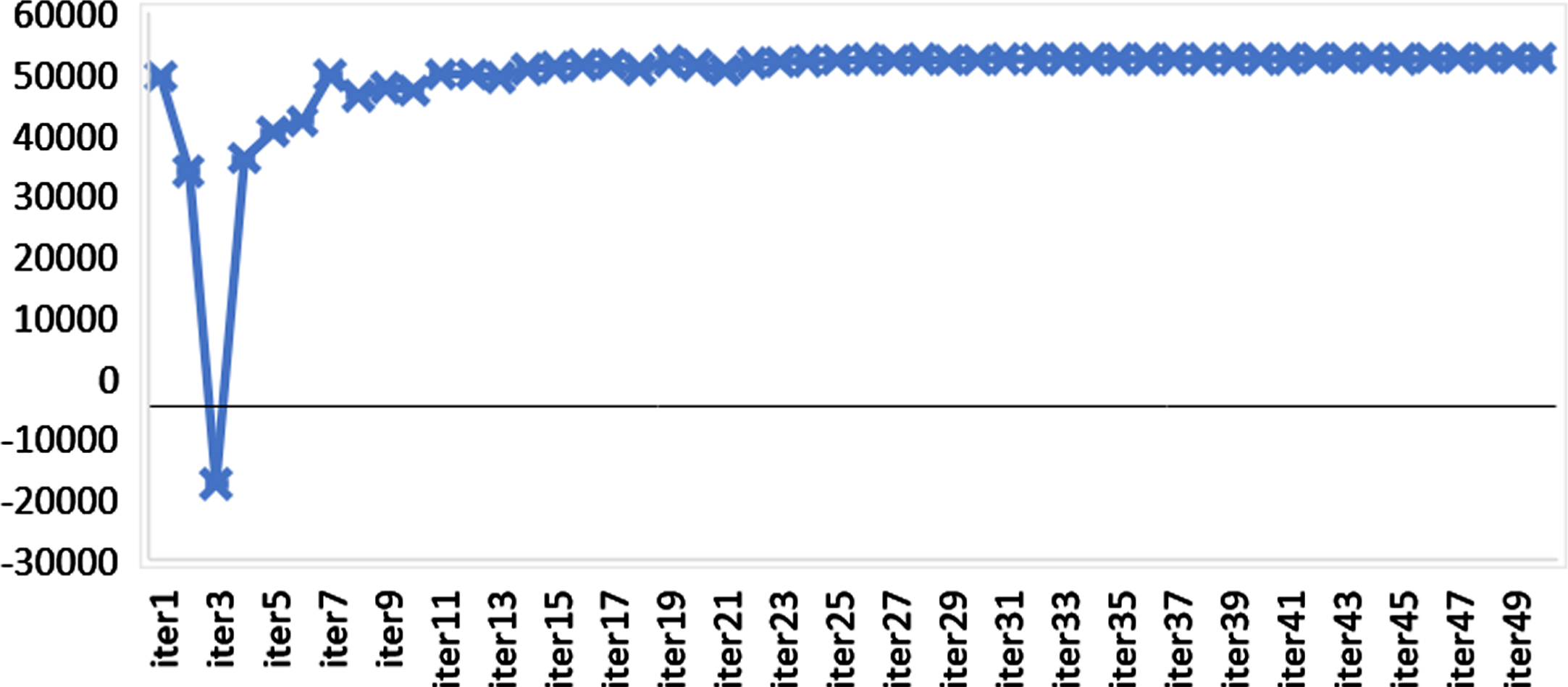
After, constraint (17) is relaxed, and conflictions are ignored. The travel times of conflictions are cB3 = 3, cC1 = 4, cD2 = 3 . This problem is solved by GAMS, and the total cost decreased to 50,700 £ as it allowed less costly assignments in conflicted areas.
The problem is also solved by proposed modified saving heuristic algorithm. Step by step solution for İzmir data is as follows:
Step 7: The initial matrix is given in Table 4 with the given information of weighted travel time between customer region and candidate location, and the population (demand) of people living in region.
Step 8: The transportation cost table is prepared in Table 7 by multiplied weighted travel time with population of the region, and the sum of columns are calculated. All data in this table are cost type.
Table 7
Transportation cost matrix
| Candidate locations Region | 1 | 2 | 3 | 4 | 5 |
| A | 12000 | 24000 | 15000 | 3000 | 21000 |
| B | 28000 | 20000 | X | 16000 | 12000 |
| C | X | 18000 | 4000 | 8000 | 12000 |
| D | 14400 | X | 22800 | 12000 | 16800 |
| E | 8000 | 24000 | 8000 | 4000 | 18000 |
| F | 15000 | 26700 | 9000 | 13500 | 4500 |
| Clinic cost (£) | 5000 | 3000 | 6000 | 7000 | 2000 |
| Total cost (£) | 82400 | 115700 | 64800 | 63500 | 86300 |
Step 9: A mobile vaccination clinic is assigned at candidate location “4” where has minimum total cost with 63.500 £. All regions are assigned to candidate location “4”.
Step 10: The relocation saving (benefit) is evaluated in Table 8 by assigning customers to other candidate locations.
Table 8
Saving matrix
| Candidate locations Region | 1 | 2 | 3 | 4 | 5 |
| A | – | – | – | A* | – |
| B | – | – | X | B | 4000* |
| C | X | – | 4000 | C | – |
| D | – | X | – | D* | – |
| E | – | – | – | E* | – |
| F | – | – | 4500 | F | 9000* |
| Clinic cost (£) | 5000 | 3000 | 6000 | – | 2000 |
| Total saving (£) | –5000 | –3000 | 2500 | – | 11000 |
Step 11: Another mobile vaccination clinic is assigned at candidate location “5” where has maximum saving with 11.000 £. Region B and F are assigned to candidate location “5”.
Step 12: The saving matrix is revised in Table 9. The candidate locations have no saving. But each location can serve maximum three regions, and location “4” serves four region. Thus, algorithm goes to Step 11, and another mobile vaccination clinic is assigned at candidate location “3” where has maximum saving with -2.000 £. Region C is assigned to candidate location “3”.
Table 9
Fixed cost, demand and weighted travel times information of Ankara data
| Candidate locations | 1 w1 : | 2 w2 : | 3 w3 : | 4 w4 : | 5 w5 : | 6 w6 : | 7 w7 : | 8 w8 : | Demand (person) |
| Regions | 0.108 | 0.104 | 0.135 | 0.118 | 0.153 | 0.142 | 0.099 | 0.141 | |
| A | 3 | 5 | 6 | 2 | 1 | 8 | 3 | 6 | 2000 |
| B | 4 | 6 | 7 | 9 | 5 | X(4) | 2 | 5 | 3600 |
| C | 4 | 2 | 3 | 8 | X(8) | 5 | 6 | 2 | 4200 |
| D | 7 | 4 | 7.5 | 3 | 2 | 3 | 8 | 7 | 2800 |
| E | 4 | 10 | 8 | X(2) | 4 | 7 | 7 | 5 | 4100 |
| F | 3 | 11.5 | 5 | 6 | 5 | 5 | 3 | 9 | 5300 |
| G | 6 | 7 | 4 | 8 | 3 | 9 | 5 | 3 | 2900 |
| H | X(3) | 8 | 2 | 7 | 6 | 1 | 8.5 | 1.5 | 3200 |
| I | 5 | 4 | 6.5 | 5 | 9 | 5 | 7 | X(4) | 2400 |
| J | 4 | 13 | 2 | 4 | 3 | 7 | 6 | 5 | 6200 |
| Clinic Cost (£) | 4500 | 3500 | 7000 | 6000 | 3000 | 3500 | 5500 | 8000 |
The saving matrix is revised in Table 10. Candidate locations have no saving and selected locations serve within the limit of maximum capacity (three regions). Thus, a new clinic is not required, and algorithm ends.
Table 10
Cost values for different selected locations for Ankara
| Number of selected locations | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Total Cost | infeasible | infeasible | infeasible | 120,100£ | 118,400£ | 123,600£ | 122,400£ | 130,400£ |
The final version of the assignments and costs are given in Table 11.
Table 11
Revised saving matrix
| Candidate locations Region | 1n | 2 | 3 | 4 | 5 |
| A | – | – | – | A* | – |
| B | – | – | X | – | B* |
| C | X | – | 4000 | C | – |
| D | – | X | – | D* | – |
| E | – | – | – | E* | – |
| F | – | – | – | – | F* |
| Clinic cost (£) | 5000 | 3000 | 6000 | – | – |
| Total cost (£) | –5000 | –3000 | –2000 | – | – |
As a result of the mobile vaccination clinic assignment problem by applying the proposed heuristic algorithm, it would be appropriate for three mobile vaccination clinics to serve. These clinics are assigned to candidate locations “3”, “4”, and “5”. The clinic which is located at candidate location “3” serves one region, region C. The clinic which is located at candidate location “4” serves two regions, region A, D and E. The clinic which is located at candidate location “5” serves three regions, region B and F. After the assignments, the total cost of assigning three mobile vaccination clinics to serve six regions is 54,500 £. The results of the heuristic algorithm are same as the GAMS solution of the problem given in Table 6.
3.2Ankara data
In Ankara, the DMs select ten regions (i={A,B,C,D,E,F,G,H,I,J}) and eight candidate locations (j={1,2,3,4,5,6,7,8}). Each location can serve maximum three regions. The fixed clinic cost (cij), demand (dij) and weighted travel times (
Table 12
Revised saving matrix
| Candidate locations Region | 1 | 2 | 3 | 4 | 5 |
| A | – | – | – | A* | – |
| B | – | – | X | – | B* |
| C | X | – | C | – | |
| D | – | X | – | D* | – |
| E | – | – | – | E* | – |
| F | – | – | – | – | F* |
| Clinic cost (£) | 5000 | – | 6000 | – | – |
| Total saving (£) | –5000 | – | –2000 | – | – |
This problem is solved by GAMS using the linear programming formulation in Section 2.3. The number of locations to be selected at minimum cost is five. Cost values for different numbers of selected locations are shown in the Table 13. Since five selected locations are optimum, the assignments for this statement are given in Table 14. The remainder of this sub-section continues with optimum statement.
Table 13
The final assignment matrix
| Candidate locations Region | 1 | 2 | 3 | 4 | 5 | Cost (£) |
| A | – | – | – | A | – | 3000 |
| B | – | – | X | – | B | 12000 |
| C | X | – | C | – | – | 4000 |
| D | – | X | – | D | – | 12000 |
| E | – | – | – | E | – | 4000 |
| F | – | – | – | – | F | 4500 |
| Clinic cost (£) | – | – | 6000 | 7000 | 2000 | 15000 |
| Total saving (£) | – | – | – | – | – | 54500 |
Table 14
Results of assignment problem for Ankara
| Selected locations | 1 | 2 | 5 | 6 | 7 |
| Assigned Region | E,F | C,I | A,G,J | D,H | B |
| Total Cost | 118,400£ | ||||
As mentioned in Section 2.4, constraint (14) is relaxed, the assignment of all demands is ignored. This problem is solved by GAMS, and the total cost decreased to 40.729,465 £ as it allowed not all demands of a region to be assigned. Figure 3 shows that the iterations of Lagrange relaxation with their total cost results.
Fig. 3
Iteration results of Lagrange relaxation for constraint (14) of Ankara data.
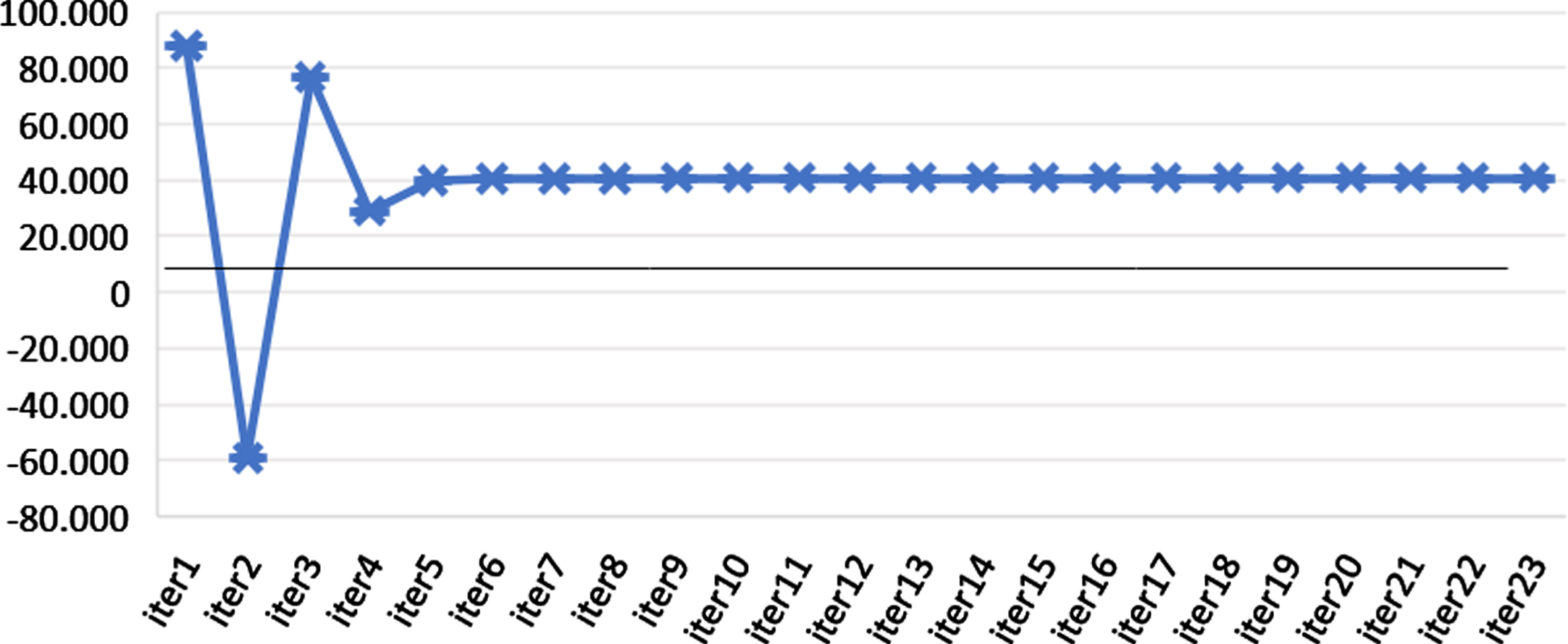
After, constraint (17) is relaxed, and conflictions are ignored. The travel times of conflictions are cB6 = 4, cC5 = 8, cE4 = 2, cH1 = 3, cI8 = 4 . This problem is solved by GAMS, and the total cost decreased to 109,400 £ as it allowed less costly assignments in conflicted areas.
The problem is also solved by proposed modified saving heuristic algorithm. Steps are not shown due to the size of the problem. As a result of the algorithm, the same assignment results as in Table 14 are obtained.
3.3İstanbul data
In Istanbul, the DMs select twenty regions (i= {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,R,S,T,U}) and fifteen candidate locations (j={1,2,3,4,5,6,7,8,9,10, 11,12,13,14,15}). Each location can serve maximum three regions. The clinic cost (cij), demand (dij) and weighted travel times (
Table 15
Fixed cost, demand and weighted travel times information of Istanbul data
| Candidate locations | 1 w1 : | 2 w2 : | 3 w3 : | 4 w4 : | 5 w5 : | 6 w6 : | 7 w7 : | 8 w8 : | 9 w9 : | 10 w10 : | 11 w11 : | 12 w12 : | 13 w13 : | 14 w14 : | 15 w15 : | Demand (person) |
| 0.050 | 0.098 | 0.060 | 0.048 | 0.066 | 0.069 | 0.081 | 0.044 | 0.051 | 0.081 | 0.084 | 0.055 | 0.055 | 0.080 | 0.078 | ||
| Regions | ||||||||||||||||
| A | 1 | 6.5 | (X)8 | 5 | 8 | 4 | 3 | 2 | 9 | 5 | 4 | 10 | 8 | 2 | 13.5 | 1500 |
| B | 6 | 3.5 | 3 | 2 | 5 | 1 | 4 | 7 | 8 | 3 | 1 | 8 | 3 | 4.5 | 5 | 4200 |
| C | 5 | 6 | 4 | 4 | 3 | 8 | 7 | 6 | 6 | 4 | 4 | 7 | 3 | 4 | 5 | 6700 |
| D | 8 | 4 | 2.5 | 7 | 6 | 4 | 4 | 5 | 4 | 4 | (X)8 | 6 | 3 | 4 | 6 | 3600 |
| E | 6 | 9 | 6 | 5 | 7 | 5 | (X)3 | 7 | 10 | 7 | 6 | 6 | 4 | 6 | 8 | 5700 |
| F | 2 | 12 | 5 | 4 | (X)1 | 3 | 4 | 8 | 6 | 7 | 6 | 9 | 7 | 6 | 9 | 3900 |
| G | 9 | 4 | 3 | 6 | 7 | 9 | 7 | (X)4 | 4 | 5 | 8 | 8 | 2 | 3 | 1 | 5700 |
| H | 7 | 5 | 1 | 9 | 1 | 7 | 10.5 | 4.5 | 7 | 2 | 9 | 6 | (X)6 | 9 | 3 | 1900 |
| I | 5 | 8 | 6.5 | 8 | 6 | 6 | 9 | 3 | 1 | 2 | 7 | 7 | 6 | 11 | 1 | 2200 |
| J | 3 | 11 | 3 | 3 | 4 | 2 | 5 | 6 | 3 | 4 | (X)1 | 9 | 7 | 9 | 3 | 4600 |
| K | 4 | 4 | 9 | 4 | 9 | 3 | 2 | 9 | 8 | 1 | 2 | 5 | 12 | 9 | 7 | 7200 |
| L | 6 | 9 | 4 | 5 | 2 | 5 | 6 | 4 | 7 | 9 | 3 | 6 | 3.5 | 4 | 3 | 8100 |
| M | (X) | 1 | 3 | 7 | 3 | 8 | 1 | 2 | 11 | 5 | 9 | 9 | 5 | 7 | 4 | 2900 |
| N | 7 | 3 | 9.5 | 1 | 9 | 4 | 3 | 2 | 4 | 7.5 | 7 | 7 | 5 | 7 | 8 | 3600 |
| O | 9 | 12 | 2 | 3 | 4 | 1 | 8 | 4 | 9 | 6 | 1 | 7 | 7.5 | 6 | 8 | 7100 |
| P | 7 | 10.5 | 3 | 4 | 1 | 7 | 7 | 8 | 9 | (X)12 | 4 | 4 | 2 | 8 | 7.5 | 4500 |
| R | 5 | 2 | 7 | 5 | 6 | 2 | 7 | 6 | 8 | 10 | 6 | 5 | 2 | 6 | 14 | 5600 |
| S | 4 | 7 | 2 | 9 | 5 | 4 | 13.5 | 7.5 | 4 | 5 | 6 | 5 | 7 | 3 | 11 | 6200 |
| T | 3 | 8 | 5.5 | 4 | 8 | 3 | (X)6 | 4 | 3 | 4 | 5 | 6 | 10 | 2 | 9 | 2700 |
| U | 2 | 10 | 7 | 5 | 7 | 5 | 4 | 7 | 1 | 7 | 6.5 | 5 | 8 | 3.5 | 10 | 4900 |
| Clinic Cost (£) | 5000 | 6500 | 4000 | 3700 | 4800 | 6200 | 5700 | 7800 | 8100 | 6500 | 8300 | 7600 | 3900 | 4100 | 5800 |
This problem is solved by GAMS using the linear programming formulation in Section 2.3. The number of locations to be selected at minimum cost is nine. Cost values for different numbers of selected locations are shown in the Table 16. Since nine selected locations are optimum, the assignments for this statement are given in Table 17. The remainder of this sub-section continues with optimum statement.
Table 16
Cost values for different selected locations for Istanbul
| Number of Selected locations | 1–6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Total Cost | infeasible | 229,700£ | 228,400£ | 216,900£ | 223,400£ | 222,700£ | 230,300£ | 238,100£ | 241,300£ | 249,600£ |
Table 17
Results of assignment problem for Istanbul
| Selected locations | 1 | 3 | 4 | 5 | 6 | 7 | 13 | 14 | 15 |
| Assigned Region | A,F,U | D,H,S | N | C,L,P | B,J,O | K,M | E,R | T | G,I |
| Total Cost | 216,900£ | ||||||||
As mentioned in Section 2.4, constraint (14) is relaxed, the assignment of all demands is ignored. This problem is solved by GAMS, and the total cost decreased to 86.650,00 £ as it allowed not all demands of a region to be assigned. Figure 4 shows that the iterations of Lagrange relaxation with their total cost results.
Fig. 4
Iteration results of Lagrange relaxation for constraint (14) of Istanbul data.
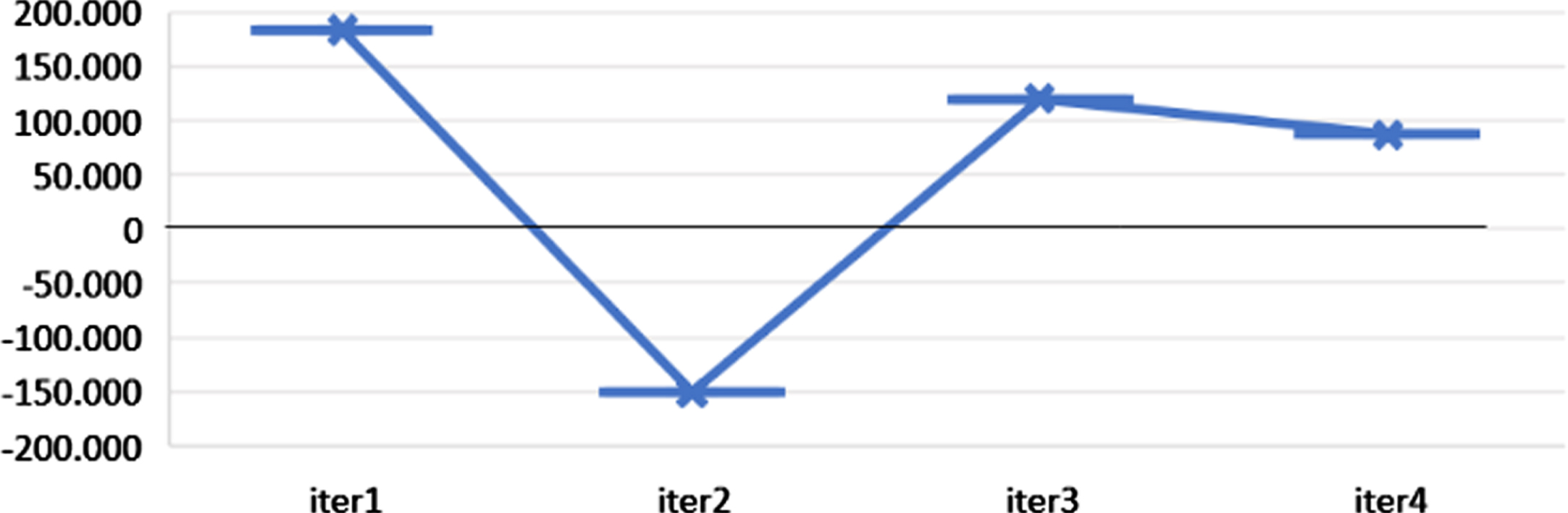
After, constraint (17) is relaxed, and conflictions are ignored. The travel times of conflictions are cA3 = 8, cD11 = 8, cE7 = 3, cF5 = 1, cG8 = 4, cH13 = 6, cJ11 = 1, cM1 = 2, cP10 = 12, cT7 = 6 . This problem is solved by GAMS, and the total cost decreased to 202,700 £ as it allowed less costly assignments in conflicted areas.
The problem is also solved by proposed modified saving heuristic algorithm. Steps are not shown due to the size of the problem. As a result of the algorithm, the same assignment results as in Table 17 are obtained.
4Results and discussion
Table 18 gives the results of applied approaches. As in this table, the results of the original MIP (Mixed Integer Programming) problems are same as proposed heuristic. Since this is a small-scale problem, the results of proposed heuristic give the optimum results. Thus, it is clear that proposed algorithm is robust. For all data, two different Lagrange relaxation are applied. The relaxation of constraint (14) relaxes the problem of having to assign all customers to the facility. Thus, the total costs of three cities are reduced. With this relaxation, the total cost in Istanbul has decreased the most with 130,250£. But the largest rate of cost reduction has been in Ankara with (-% 65,6). The relaxation of constraint (17) relaxes the problem of not assigning conflicting regions. Thus, the total costs of three cities are reduced. With this relaxation, the total cost in Istanbul has decreased the most with 14,200£. But the largest rate of cost reduction has been in Ankara with (-% 7,6).
Table 18
Results comparison of assignment problems for Izmir, Ankara and Istanbul data with different approaches
| Instance | GAMS | Proposed | Lagrange relaxation | |
| (MIP) | Heuristic | Const(6) | Const(9) | |
| İzmir (6Rx5 S) | 54,500£ | 54,500£ | 52,496.083£ (–% 3,67) | 50,700£ (–% 6,97) |
| Ankara (10Rx8 S) | 118,400£ | 118,400£ | 40.729,465£ (–% 65,6) | 109,400£ (–% 7,6) |
| İstanbul (20Rx15 S) | 216,900£ | 216,900£ | 86.650£ (–% 60,05) | 202,700£ (–% 6,54) |
5Conclusions
The vaccines developed against the pandemic caused by the COVID-19 virus hold great hope. However, it poses a major problem to vaccinate large masses. In addition to the fixed located health centers, mobile vaccination clinics have been proposed to speed up vaccination and to keep COVID-19 processes separate from other diseases. In this study, we investigate an assignment problem to locate mobile vaccination clinics in Turkey’s big cities (İstanbul, Ankara, İzmir). Multiple locations are determined as candidate locations, and their weights are calculated with a spherical bipolar fuzzy MCDM method based on determined criteria by DMs. The linear formulation of the problem is given, and the multi-facility location problem for COVID-19 vaccination is solved with GAMS. A hybrid spherical bipolar fuzzy heuristic algorithm is proposed based on saving matrix to handle the multi-facility location problem for optimum mobile vaccination clinics number. In addition, based on the existing algorithms, the linear expression of the problem has been expanded using Lagrange relaxation to show the effectiveness of the methodology. The proposed approach is applied on the data for three cities, and the results are compared.
For future studies, we recommend to use proposed multi-facility location heuristic algorithm with other fuzzy sets extentions such as intuitionistic fuzzy sets, Pythagorean fuzzy sets, spherical fuzzy sets etc. As a step forward, new criteria can be considered in weighting candidate locations. The problem can be enlarged by including other cities data, and new result can be compared with this article. New heuristic algorithms can be proposed, and the procedures can be compared with existing algorithms. The MCDM approaches may be adapted to the algorithm’s steps, and imprecise data can be added to the mobile facility location problem.
Acknowledgment
This work has been supported by the Scientific Research Projects Commission of Galatasaray University under grant number # FBA-2020-1036.
References
[1] | Torun S.D. and Bakırcı N. , Vaccination coverage and reasonsfor non-vaccination in a district of Istanbul, BMC PublicHealth 6: ((2006) ), 125. |
[2] | Orenstein W.A. and Ahmed R. , Simply put: vaccination saves lives, PNAS 114: (16) ((2017) ), 4031–4033. |
[3] | Lee B.Y. , Mehrotra A. , Burns R.M. and Harris K.M. , Alternativevaccination locations: who uses them and can they increase fluvaccination rates? Vaccine 27: (32) ((2009) ), 4252–4256. |
[4] | Bartsch S.M. , Taitel M.S. , DePasse J.V. , Cox S.N. , Smith-Ray R.L. , Wedlock P. , et al., Epidemiologic and economic impact of pharmaciesas vaccination locations during an influenza epidemic, Vaccine 36: (46) ((2018) ), 7054–7063. |
[5] | Kim N. and Mountain T.P. , Role of non-traditional locations forseasonal flu vaccination: empirical evidence and evaluation, Vaccine 35: (22) ((2017) ), 2943–2948. |
[6] | “WHO (World Health Organization),” 2020. Accessed on: Dec. 21, 2020. [Online]. Available: https://COVID19.who.int/ |
[7] | Heymann D.L. and Aylward R.B. , “Mass vaccination: when and why,” in Mass Vaccination: Global Aspects—Progress and Obstacles, Springer, Berlin, Heidelberg, (2006) , pp. 1–16. |
[8] | “Mobile vaccination clinic reaches rural areas,” 2014. Accessed on: Dec. 22, 2020. [Online]. Available: https://www.cidrap.umn.edu/practice/mobile-vaccination-clinic-reaches-rural-areas |
[9] | Hannings A.N. , Duke L.J. , Logan L.D. , Upchurch B.L. , Kearney J.C. , Darley A. , et al., Patient perceptions of studentpharmacist–run mobile influenza vaccination clinics, J.Am. Pharm. Assoc. 59: (2) ((2019) ), 228–231. |
[10] | Chen W. , Misra S.M. , Zhou F. , Sahni L.C. , Boom J.A. and Messonnier M. , Evaluating partial series childhood vaccination servicesin a mobile clinic setting, Clin. Pediatr. 59: (7) ((2020) ), 706–715. |
[11] | Yang S. , Hamedi M. and Haghani A. , Integrated approach for emergencymedical service location and assignment problem, Transp. Res.Rec 1882: (1) ((2004) ), 184–192. |
[12] | Van Barneveld T.C. , Bhulai S. and van der Mei R.D. , The effect ofambulance relocations on the performance of ambulance serviceproviders, Eur. J. Oper. Res 252: (1) ((2016) ), 257–269. |
[13] | Abdel-Basset M. , Manogaran G. , El-Shahat D. and Mirjalili S. , “Integrating the whale algorithm with Tabu search for quadraticassignment problem: A new approach for locating hospitaldepartments,’, Appl. Soft Comput 73: ((2018) ), 530–546. |
[14] | Ross G.T. and Soland R.M. , A branch and bound algorithm for thegeneralized assignment problem, Math. Progr. 8: ((1975) ), 91–103. |
[15] | Mills-Tettey G.A. , Stentz A. and Dias M.B. , “The Dynamic Hungarian Algorithm for the Assignment Problem With Changing Costs,” Carnegie Mellon Univ., Pittsburgh, PA, Tech. Rep. CMU-RI-TR-07-27, 2007. [Online]. Available: https://www.ri.cmu.edu/pub_files/pub4/mills_tettey_g_ayork_or_2007_3/mills_tettey_g_ayorkor_2007_3.pdf |
[16] | Wimmert R.J. , A mathematical method of equipment location, Journal of Industrial Engineering 9: ((1958) ), 498–505. |
[17] | Srivastava R. , Alternate solution procedures for thelocation-routing problem, Omega 21: (4) ((1993) ), 497–506. |
[18] | Clarke G. and Wright J.W. , Scheduling of vehicles from a centraldepot to a number of delivery points, Oper. Res. 12: (1964), 568–581. |
[19] | Kuehn A. and Hamburger M.J. , A heuristic program for locatingwarehouses, Manage. Sci. 9: ((1963) ), 643–666. |
[20] | Hansen P.H. , Hegedahl B. , Hjortkjaer S. and Obel B. , A heuristicsolution to the warehouse location-routing problem, Eur. J.Oper. Res. 76: (1) ((1994) ), 111–127. |
[21] | Ellwein L.B. and Gray P. , Solving fixed charge location-allocationproblems with capacity and configuration constraints, AIIETransactions 3: (4) ((1971) ), 290–298. |
[22] | Akinc U. and Khumawala B.M. , An efficient branch and bound algorithmfor the capacitated warehouse location problem, Manage. Sci 23: (6) ((1977) ), 585–594. |
[23] | Nauss R.M. , An improved algorithm for the capacitated facilitylocation problem, J. Oper. Res. Soc. 29: (12) ((1978) ), 1195–1201. |
[24] | Klincewicz J.G. and Luss H. , A Lagrangian relaxation heuristic forcapacitated facility location with single-source constraints, J. Oper. Res. Soc. 37: (5) ((1986) ), 495–500. |
[25] | Venables H. and Moscardini A. , An adaptive search heuristic for the capacitated fixed charge location problem, International Workshop on Ant Colony Optimization and Swarm Intelligence (2006), 348–355. |
[26] | Jamil M. , Batta R. and Malon D.M. , The travelling repairperson home baselocation problem, Trans. Sci. 28: (2) ((1994) ), 150–161. |
[27] | Laporte G. , Louveaux F.V. and Mercure H. , Models and exact solutionsfor a class of stochastic location-routing problems, Eur. J.Oper. Res 39: (1) ((1989) ), 71–78. |
[28] | Stowers C.L. and Palekar U.S. , Location models with routingconsiderations for a single obnoxious facility, Transp. Sci. 27: (4) ((1993) ), 350–362. |
[29] | Bhattacharya U. , Rao J.R. and Tiwari R.N. , Fuzzy multi-criteriafacility location problem, Fuzzy Sets Syst. 51: (3) ((1992) ), 277–287. |
[30] | Bhattacharya U. , Rao J.R. and Tiwari R.N. , Bi-criteriamulti-facility location problem in fuzzy environment, FuzzySets Syst. 56: ((1993) ), 145–153. |
[31] | Canós M.J. , Ivorra C. and Liern V. , An exact algorithm for thefuzzy pmedian problem, Eur. J. Oper. Res. 116: (1) ((1999) ), 80–86. |
[32] | Chen C.B. and Wei C.C. , An efficient fuzzy MADM method for selectingfacility locations, J. Eng. Valuat. Cost Anal. 2: (1) ((1998) ), 19–32. |
[33] | Darzentas J. , A discrete location model with fuzzy accessibilitymeasures, Fuzzy Sets Syst 23: ((1987) ), 149–154. |
[34] | Rao J.R. and Saraswati K. , Facility location problem on networkunder multiple criteria fuzzy set theoretic approach, Int. J.Syst. Sci. 19: (12) ((1988) ), 2555–2559. |
[35] | Zhou J. and Liu B. , Modeling capacitated location-allocation problemwith fuzzy demands, Comput. Ind. Eng. 53: ((2007) ), 454–468. |
[36] | Zadeh L.A. , Fuzzy sets, Inform. Control 8: ((1965) ), 338–353. |
[37] | Atanassov K. , Intuitionistic fuzzy sets, Fuzzy Sets Syst. 20: ((1986) ), 87–96. |
[38] | Smarandache F. , Neutrosophy: Neutrosophic Probability, Set, and Logic. Ann Arbor, MI, USA: American Research Press, (1998) . |
[39] | Gündoğdu F.K. and Kahraman C. , Spherical fuzzysets and spherical fuzzy TOPSIS method, J. Intell. FuzzySyst 36: (1) ((2019) ), 337–352. |
[40] | Gündoğdu F.K. and Kahraman C. , “Spherical fuzzy analytic hierarchy process (AHP) and its application to industrial robot selection,” International Conference on Intelligent and Fuzzy Systems, İstanbul, Turkey, 23–25 July, 2019. |
[41] | Lee K.M. , “Bipolar-valued fuzzy sets and their operations,” in Proc. Conf. Intell. Technol., Bangkok, Thailand, 2000, pp. 307–312. |
[42] | Lee K.M. , Comparison of Interval-valued fuzzy sets, Intuitionisticfuzzy sets, and bipolar-valued fuzzy sets, J. Korean Inst.Intell. Syst. 14: (2) ((2004) ), 125–129. |
[43] | Princy R. and Mohana K. , Spherical bipolar fuzzy sets and itsapplication in multi criteria decision making problem, J. NewTheory 32: ((2020) ), 58–70. |




