Annotation with adpositional argumentation
Abstract
This paper explains Adpositional Argumentation (AdArg), a new method for annotating arguments expressed in natural language. In describing this method, it provides the guidelines for designing a Gold Standard Corpus (GSC) of argumentative discourse in terms of so-called argumentative adpositional trees (arg-adtrees). The theoretical starting points of AdArg draw on the combination of the linguistic representation framework of Constructive Adpositional Grammars (CxAdGrams) with the argument categorisation framework of the Periodic Table of Arguments (PTA). After an explanation of these two frameworks, it is shown how AdArg can be used for annotating arguments expressed in natural language. This is done by providing the arg-adtrees of four concrete examples of arguments, which substantiate the four basic argument forms distinguished in the PTA. The present exposition of the fundamental tenets of AdArg enables the building of a GSC of argumentative discourse, that means an annotated corpus of texts and discussions of undisputable high-quality according to argumentation theory experts. Such a GSC should be conveniently annotated in terms of arg-adtrees, which is a time-consuming process, as it needs highly skilled annotators and human supervision. However, its role is crucial for developing instruments for computer-assisted argumentation analysis and eventual application based on machine learning natural language processing algorithms.
1Introduction
Over the last decade, Computational Argumentation has emerged as an independent field of research. One of the core challenges within this field is to develop methods for representing argumentative texts and discussions so as to enable their analysis and evaluation. So far, researchers have developed various computational models of argument that are used, for example, in developing tools for argument mapping, argument mining and computer-aided human decision making—for a representative collection of recent work within this field, see Modgil et al. [21].
One would expect researchers within the field of Computational Argumentation to draw on insights from the long-standing fields of Argumentation Theory and Rhetoric, which have produced a great many theories about the way in which people support their points of view with arguments. These linguistic and pragmatic theories pertain to the nature and constituents of various types of arguments, the structure of different genres of argumentative discourse, as well as the stylistic features of such discourse. In combination with normative standards regarding the validity, reasonableness, and effectiveness of argumentation, this knowledge is used for providing theoretically informed analyses and evaluations of argumentative texts and discussions—for a comprehensive survey, see van Eemeren et al. [8].
So far, however, researchers in the fields of Artificial Intelligence in general and Computational Argumentation in particular have used only a small part of the insights generated within Argumentation Theory and Rhetoric. Since these insights are expressed in informal terms, they are not easily transferred in operative models suitable for computation—for a historical overview of argumentation models in AI related settings, see Bench-Capon and Dunne [3].
An important characteristic of current computational models of argument is that most—if not all—of them operate on the abstract level of complete propositions and the interactions between them, without taking into account the detailed linguistic and pragmatic information contained in these propositions. This goes, for example, for approaches inspired on Dung’s abstract argumentation frameworks [6], which study sets of atomic arguments and their interrelations.
It also applies to approaches that take Walton’s argument schemes [32] as a point of departure, in which an argument scheme is taken to consist of a conclusion and a set of premises—see, e.g., Dondio and Longo [7]. However, in reality rarely premises are independent, hence they do not form a set. For example, if n is a natural number (first premise), and it is even (second premise), then the remainder of the division of it by 2 is 0 (conclusion). In this case, to make sense of the conclusion and of the second premise, the first premise is strictly needed.
Another example is given by approaches based on the Toulmin model [26]. They are able to provide a detailed description of the techniques for monological and dialogical structure of arguments and the resolution of the conflicts (via semantics), as described in Longo’s five-layers model [16, 17], with a practical application in Rizzo and Longo [22]. Although the Toulmin model, apart from conclusion and premises, does contain linguistic elements that are relevant for analyzing and evaluating argumentation, it only covers a small part of the linguistic and pragmatic richness of arguments expressed in natural language. As an immediate consequence, the process of reconstruction of arguments should be performed before applying Longo’s five-layers model.
In relation to the approaches just mentioned, we argue that the linguistic and pragmatic analysis should be performed in advance, that is, before treating arguments in a purely non-linguistic, abstract, formal way. As a result, the very notion of what is an argument will be clarified and expressed in terms that satisfy both researchers in Artificial Intelligence and in Argumentation Theory.
In this paper, we explain Adpositional Argumentation (AdArg), a high-precision method for representing arguments expressed in natural language. While partially based on Gobbo and Wagemans [12, 13], the main aim of this paper is to show how the method can be employed for the purpose of building a Gold Standard Corpus (GSC) of argumentative discourse. This means that we shall refine, extend, adapt, and illustrate the theoretical framework of AdArg as it is explained in earlier papers. It is important to underline that AdArg does not contradict the abovementioned approaches. Rather, it enables the formal modeling of argumentative discourse on a different level of abstraction, namely, on the level of the natural language in which arguments are expressed. This means that our work may be used as input for approaches such as the ones mentioned above, which model argumentation on a non-linguistic, more abstract level.
The paper is structured as follows. In Section 2, we give a brief example of argument reconstruction, illustrating four requirements we think are important for reaching a high level of inter-annotator agreement. In Section 3, we explain the theoretical framework of the Periodic Table of Arguments (PTA). We focus on its compliance with the first requirement of enabling a normalization of natural arguments. By including analyses of examples of such arguments that instantiate all four basic argument forms distinguished in the PTA, we also illustrate its compliance with the second requirement of being a comprehensive yet flexible categorisation of argument. Next, in Section 4, we briefly describe the mathematical foundations of Constructive Adpositional Grammars (CxAdGrams) as well as the characteristics of its central notion of ‘adpositional tree’. We then show in Section 5 how to combine CxAdGrams and the PTA into AdArg, demonstrating the compliance of our argument representation method with annotation requirements three and four. In the conclusion of the paper, Section 6, we reflect on remaining issues in relation to the further improvement and implementation of the guidelines for building a GSC of argumentative discourse.
2Argument reconstruction
A recent annotation of a debate between Clinton and Trump [2] gives an example of a natural argument that can be reconstructed as consisting of two propositions, one of which functioning as the conclusion and the other as the premise. This is the original text:
(largest banks in America) are much bigger than they were when we bailed them out for being too big to fail, we have got to break them up.
On the level of complete propositions, this text can be reconstructed as follows:
(conclusion) We should break up the largest banks in America.
(premise) They are much bigger than they were when we bailed them out for being too big to fail.
Now, in order to analyze such arguments in more detail, and also to subsequently evaluate their quality, the human analyst disposes of an extensive set of tools developed in the field of Argumentation Theory and Rhetoric such as those for explicitizing implicit premises, analyzing the quality of warrants, and asking critical questions associated with argument schemes. Unfortunately, a great many of these methods and techniques have not yet been formalized in computational terms because they are based on linguistic and pragmatic information that is more fine-grained than the level of propositions and their interrelations.
Another problem that occurs when a single argument is reconstructed in terms of premise and conclusion, is that there is a risk that different analysts—who can also be annotators of a corpus of argumentative texts—reconstruct the same argument in different ways, or even, worse, in incompatible ways. They might, for instance, interpret the argumentative force in different ways, because of the ambiguity of natural language or differences in their subjective level of knowledge about argumentation theoretical concepts or rhetorical techniques.
In our view, a high level of inter-annotator agreement could be achieved by respecting the following requirements. First of all, the annotation of argumentative discourse should take place by using a controlled language format, that is, a normal form, expressed in terms of a clear step-by-step procedure with explicit constraints for the formulation of both premise(s) and conclusion. Second, this procedure should enable the analyst to classify properly the arguments by the means of a taxonomy that is comprehensive because it covers all possible arguments as identified in the tradition of Argumentation Theory—and at the same time flexible, so to be robust to the incoming data. Third, it should permit the analyst not only to identify the meaningful parts of the natural language material, but also to eventually hide non-necessary linguistic details. Fourth and last, the method for representing arguments should represent the linguistic and pragmatic information that is relevant for the analysis and evaluation of arguments in an adequate way and be formal(izable) to the extent that it can be used for the purpose of building tools that automatize these tasks.
3The periodic table of arguments
The Periodic Table of Arguments (PTA) is a formal linguistic categorisation of argument types developed by Wagemans [31]. The PTA systematizes the traditional multitude of incomplete, informal—and sometimes even inconsistent—taxonomies of argument into a systematic and comprehensive whole, reducting ambiguity in the analysis and therefore highening inter-annotator agreement. Below, we explain assumptions and constituents of the PTA’s theoretical framework for the purposes of designing AdArg.
In the PTA and henceforth in AdArg, an argument is a building block of persuasive discourse. Within such a building block, it is always possible to find one or more premises, indicated by the Greek letter π—standing for the Greek equivalent πρóτασ ι ς (protasis)—and one and one only conclusion, indicated by the Greek letter σ—standing for the Greek equivalent
A minimal argument consists of two statements, a conclusion σ and a premise π. For the purposes of this paper, we will give examples of minimal arguments only. Linguistically, connectors between a conclusion and a premise in a minimal argument present themselves in two complementary types: progressive and retrogressive—for details see van Eemeren and Snoeck Henkemans [9]. The progressive form presents at first the premise π and then the conclusion σ. In English, the connector typically takes the form of ‘so’, but also ‘therefore’, ‘thus’, or other forms, are possible. The analyst should be trained in recognizing all these forms as progressive connectors. Conversely, the retrogressive form presents first the conclusion σ and then the premise π. The typical retrogressive connector in English is ‘because’, but, again, others are possible. For the sake of simplicity, in this paper we will give only examples of concrete arguments with the retrogressive connector ‘because’. For more details on the linguistic representation, see the next section.
Within the theoretical framework of the PTA, an argument is conceptualized as a combination of two statements: a conclusion, which is doubted, and a premise, which is (more) certain. An arguer who supports a conclusion with a premise can be assumed to aim for rendering that conclusion (more) acceptable for the addressee. In order to explain how this leverage of acceptability from the premise to the conclusion works, the PTA assumes the ‘law of the common term’—see Wagemans [28]. This law states that the premise, in order to fulfill the pragmatic aim of rendering the conclusion (more) acceptable, should share exactly one common term with the conclusion. While this common term can be characterised as the ‘fulcrum’ of the leverage of acceptability taking place within the argument, the relationship between the non-common terms, which expresses the underlying mechanism of the argument, functions as its ‘lever’.
The law of the common term yields two basic possibilities of argument forms. If the common term is the subject of the two statements, the argument has the form ‘a is X, because a is Y’. In this case, the subject (a) functions as the fulcrum and the relationship between the predicates (X and Y) as the lever of the argument. For this reason, such arguments are called ‘predicate arguments’ (pre).
If the common term is the predicate, the argument has the form ‘a is X, because b is X’. In this case, the predicate (X) is the fulcrum and the leverage of acceptability can be explained by assuming that there is some kind of relationship between the non-common terms of the premise and the conclusion, namely their subjects (X and Y). Within the framework of the PTA, such arguments are called ‘subject arguments’ (sub).
The theoretical framework of the table is based on three partial characterisations of an argument. We have just explained the first characterisation, which entails the distinction between predicate (pre) and subject (sub) arguments.
The second characterisation is based on there being two possible ways of expressing statements that have an argumentative function: as a proposition or as an assertion—see Wagemans [28]. The difference between the two is that in the latter, the epistemic commitment of the arguer regarding the acceptability of the statement is explicitly present in the discourse. The statement We only use 10% of our brain, for example, is expressed as a proposition, while the statement It is true that we only use 10% of our brain is expressed as an assertion.
Within the framework of the PTA, the distinction between propositions and assertions is used to characterize arguments as ‘first-order’ (1) or ‘second-order’ (2). In normalizing first-order arguments, the analyst can work with statements that are expressed as propositions. But for second-order arguments, the normalization takes place on the level of assertions. This means that if the epistemic commitment to the acceptability of the statement is not present in the actual discourse, the analyst may have to add a conventional expression of this commitment, ‘is true’ (⊤), as the predicate of the premise and/or the conclusion of the argument in order to comply with the law of the common term. In combination with the distinction between predicate and subject arguments, this yields two additional argument forms: ‘q is ⊤, because q is Z’, which is called a second-order predicate argument and has the proposition q functioning as the fulcrum and the relation between ⊤ and Z as its lever, and ‘q is ⊤, because r is ⊤’, which is called a second-order subject argument and has the epistemic commitment marker ⊤ as the fulcrum and the relation between propositions q and r as its lever.
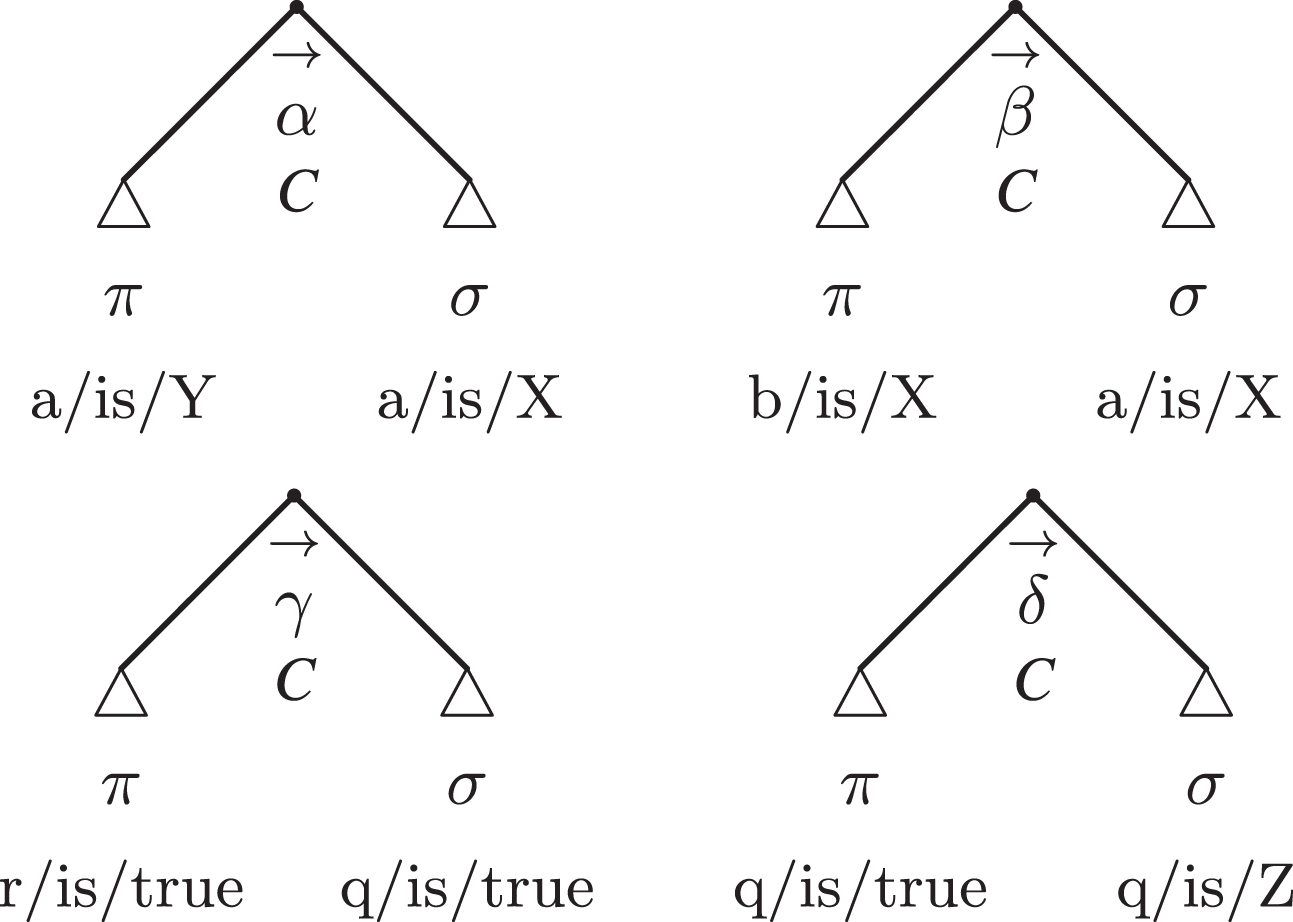
The notions of ‘argument form’, ‘fulcrum’ and ‘lever’ can be illustrated by means of an argument diagram. For the sake of simplicity, we will do this for the first-order predicate and subject arguments, which are situated in the Alpha Quadrant (α) and the Beta Quadrant (β) of the PTA respectively—see Table 1.
Table 1
Overview of first-order argument forms
| Quadrant | Conclusion | Premise | Retrogressive argument (progressive variant) |
| α | a is X | a is Y | a is X, because a is Y (a is Y, so a is X) |
| β | a is X | b is X | a is X, because b is X (b is X, so a is X) |
Figure 1 shows the argument diagram of first-order predicate arguments. In this type of argument, the conclusion ‘a is X’ (σ) is supported by the premise ‘a is Y’ (π). The direction of the arrows towards the fulcrum (in this case, the subject a) means that two different properties (in this case, the predicates X and Y) are ascribed to the same subject. The relation
Fig.1
Argument diagram of a first-order predicate argument.
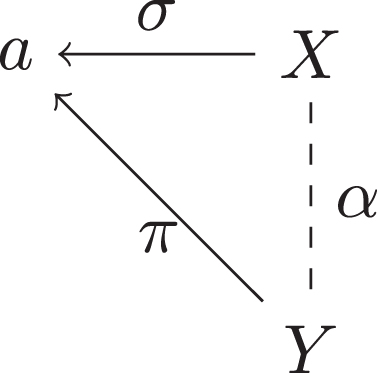
Figure 2 illustrates the situation in the case of first-order subject arguments, where the fulcrum is the predicate (X), which means that the conclusion ‘a is X’ (σ) is supported by the premise ‘b is X’ (π). The lever of this type of argument is the relationship between the different subjects (a and b).
Fig.2
Argument diagram of a first-order subject argument.
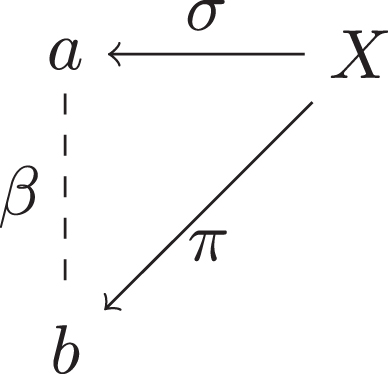
As said above, the theoretical framework of the PTA takes the conclusion and the premise of an argument to be expressed by statements. The third characterisation of arguments that constitues this framework is the argument substance, i.e., the specific combination of types of statements. This is determined on the basis of a tripartite typology that distinguishes between statements of fact (F), statements of value (V), and statements of policy (P)—see [31]. An argument can thus be said to substantiate one of nine possible different combinations of types of statements, conventionally put in the order σπ: PP, PV, PF, VP, VV, VF, FP, FV, FF. The government should invest in jobs, because this will lead to economic growth, for instance, can be characterized as a PF argument, since its combines a statement of policy (P) in its conclusion σ—expressed in the normal form before the retrogressive connector because—with a statement of fact (F) in its premise π. For other examples of these types and statements and instructions on how to distinguish them, please refer to the Argument Type Identification Procedure.1
In order to help the human user of the PTA, conventional colors were added across the four quadrants, indicating the combination of the types of statements instantiated by the argument.2 The color scheme is based on the idea of representing statements of policy, value and fact by means of the primary color triad red, yellow and blue respectively. As a result, combinations of types of statements are represented by these primary colors if they are of the same type, and by the appropriate secondary colors if they are different. An argument that has a statement of policy as its conclusion and a statement of fact as its premise, for instance, is represented by means of the color purple, because that is the secondary color obtained by mixing red (policy) and blue (fact). For typographic reasons, the colors of the PTA will not be represented here. Readers can refer to Table 2 for the correspondences between the combinations of types of statements and their conventional colors.
Table 2
Conventional colors of the argument types
| Values (σπ) | Conventional color |
| PP | Red |
| VV | Yellow |
| FF | Blue |
| PV, VP | Orange |
| PF, FP | Purple |
| VF, FV | Green |
In sum, each argument should be classified as (1) a first-order or second-order argument; (2) a predicate or subject argument; and finally, (3) as one out of nine possible combinations of types of statements. The superposition of these three partial characterisations, taken together, yields a factorial typology of argument that can be used in order to develop tools for analysing, evaluating, and generating arguments in natural language. The theoretical framework of the PTA distinguishes between four different ‘argument forms’, a notion that comprises the first two partial characteristics mentioned above. In the visual representation of the PTA, the argument types instantiating these forms are situated in four different quadrants, which are indicated with letters α, β, γ, and δ respectively. Within each quadrant, arguments are further differentiated depending on the specific combination of types of statements—see Table 3. For each of the types of argument characterised in this way, the reconstruction of the natural language material (even in combination with visual aids) is done in the normal forms that leads to the formulation of a specific element present in the PTA.
Table 3
Overview of argument types (PTA version 2.4)
| Quadrant | Argument form | Existing types |
| α | 1 pre | FF, VF, VV, PV |
| β | 1 sub | FF, VV, PF, PP |
| γ | 2 sub | VF, VV, PF |
| δ | 2 pre | VF, VV, PF, PV, PP |
When taken together, the three partial characterizations of argument constitute a theoretical framework that allows for 2 × 2 ×9 = 36 systematic types of arguments. However, not all possible combinations in theory are found in practice. For instance, in the Alpha Quadrant there is no PP element, while in the Beta Quadrant there is no VF element—see subsections 3.1 and 3.2 for details. On the other hand, there can be more than one element corresponding to an argument type, depending on the linguistic formulation of the lever, i.e., the relation between the non-common terms of the premise and the conclusion. Each element representing the abovementioned systematic types of argument may host a number of ‘isotopes’, which are named in accordance with the existing dialectical and rhetorical traditions of argument classification. In the following, we will present the argument types that are situated within each quadrant of the PTA and describe their main characteristics.3
3.1The alpha quadrant
The Alpha Quadrant of the PTA comprises all the first-order predicate arguments. Let us introduce them via a concrete linguistic instantiation, to which we will refer from now on as example 1: The suspect was driving fast, because he left a long trace of rubber on the road. This argument is to be identified as a first-order predicate argument (1 pre) since it has the form ‘a is X, because a is Y’ with the subject a as the fulcrum. In fact, both linguistic subjects, he and The suspect, point to the same referent. Such anaphora resolution can be performed by the analyst, possibly assisted by tools of computational linguistics, although anaphora resolution is a well-known NLP hard problem [19]. More details about the linguistic analysis are in Section 4.
After determining that the right quadrant for this argument is alpha, we can pass to the analysis of the single statements. In particular, example 1 combines a statement of fact (F) in the conclusion σ, The suspect was driving fast, with another statement of fact (F) in the premise π, he left a long trace of rubber on the road. The systematic name of this argument is therefore 1 pre FF.
Within every quadrant, the horizontal placing of the type of argument is determined by the specific combination of types of statements that it instantiates (FF, VF, PF, etc.), while the various isotopes, which reflect the linguistic variations in the formulation of the lever and relate the PTA to the traditional names of argument types, are placed in a vertical line. Readers are invited to think about the history of Mendeleev’s Periodic Table of Elements, upon which the PTA is inspired: not all elements were found in the same moments, but there were some empty spaces left, as such chemical elements were theoretically possible; analogously, the PTA contains spaces for theoretically possible argumentative elements which have not (yet) been found.
In consulting the PTA (see Figs. 3 to 6), the analyst (eventually with the assistance of an expert system or another type of ad hoc software) quickly realises that there are four isotopes of the systematic name 1 pre FF: Sig, Cau, Ef, Cor.
Fig.3
The Alpha Quadrant of the PTA.
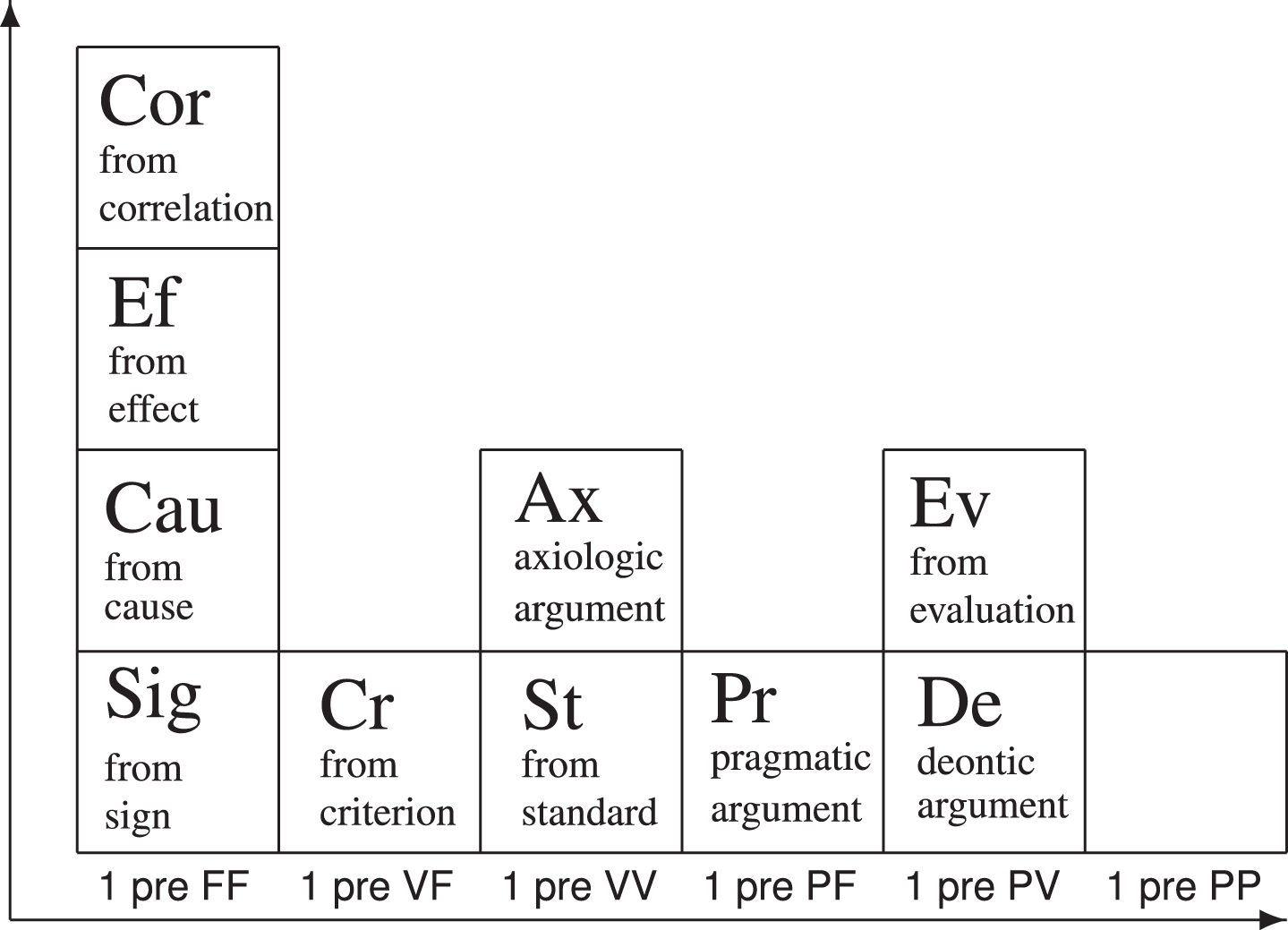
Fig.4
The Beta Quadrant of the PTA.
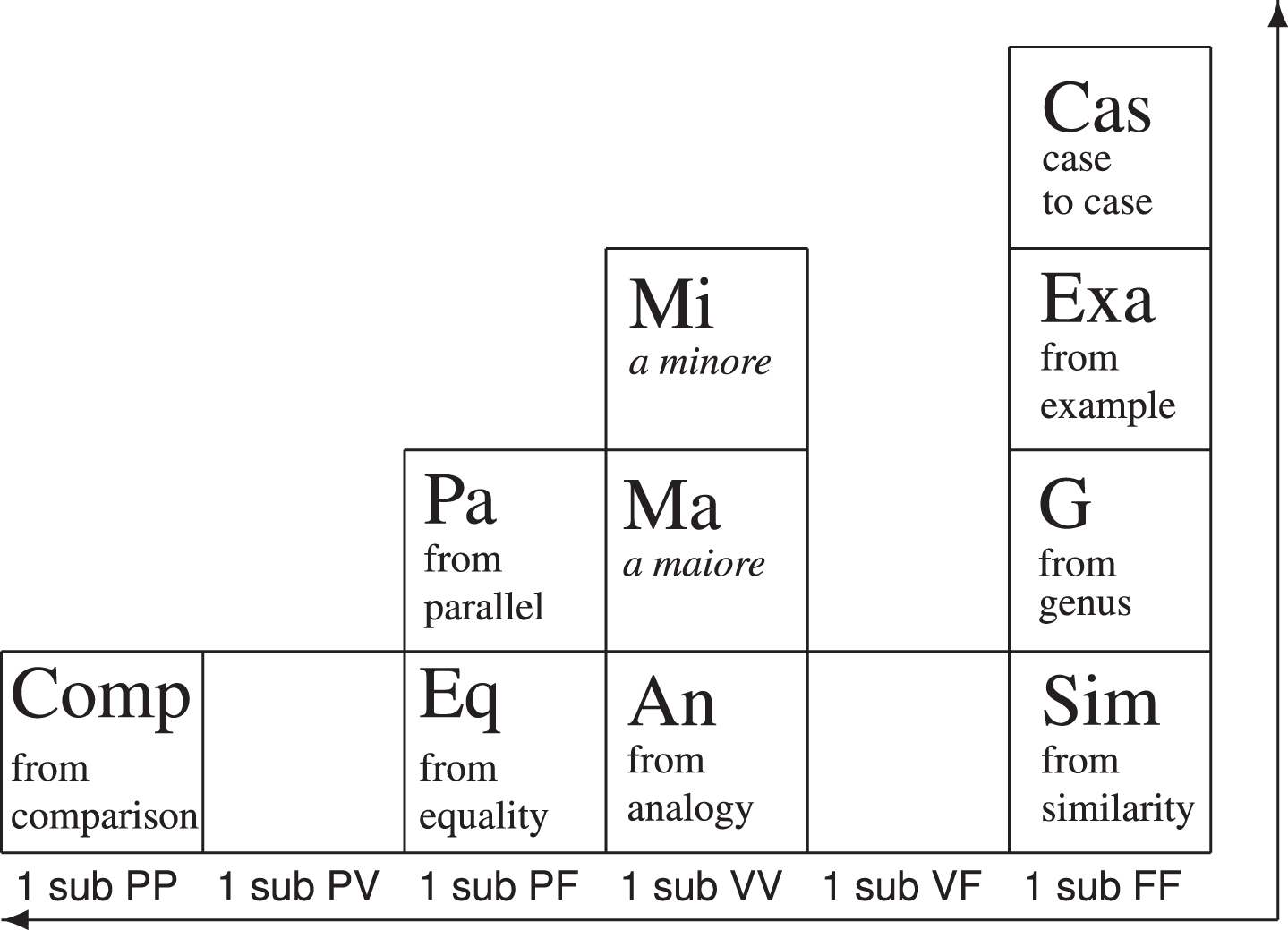
Fig.5
The Gamma Quadrant of the PTA.
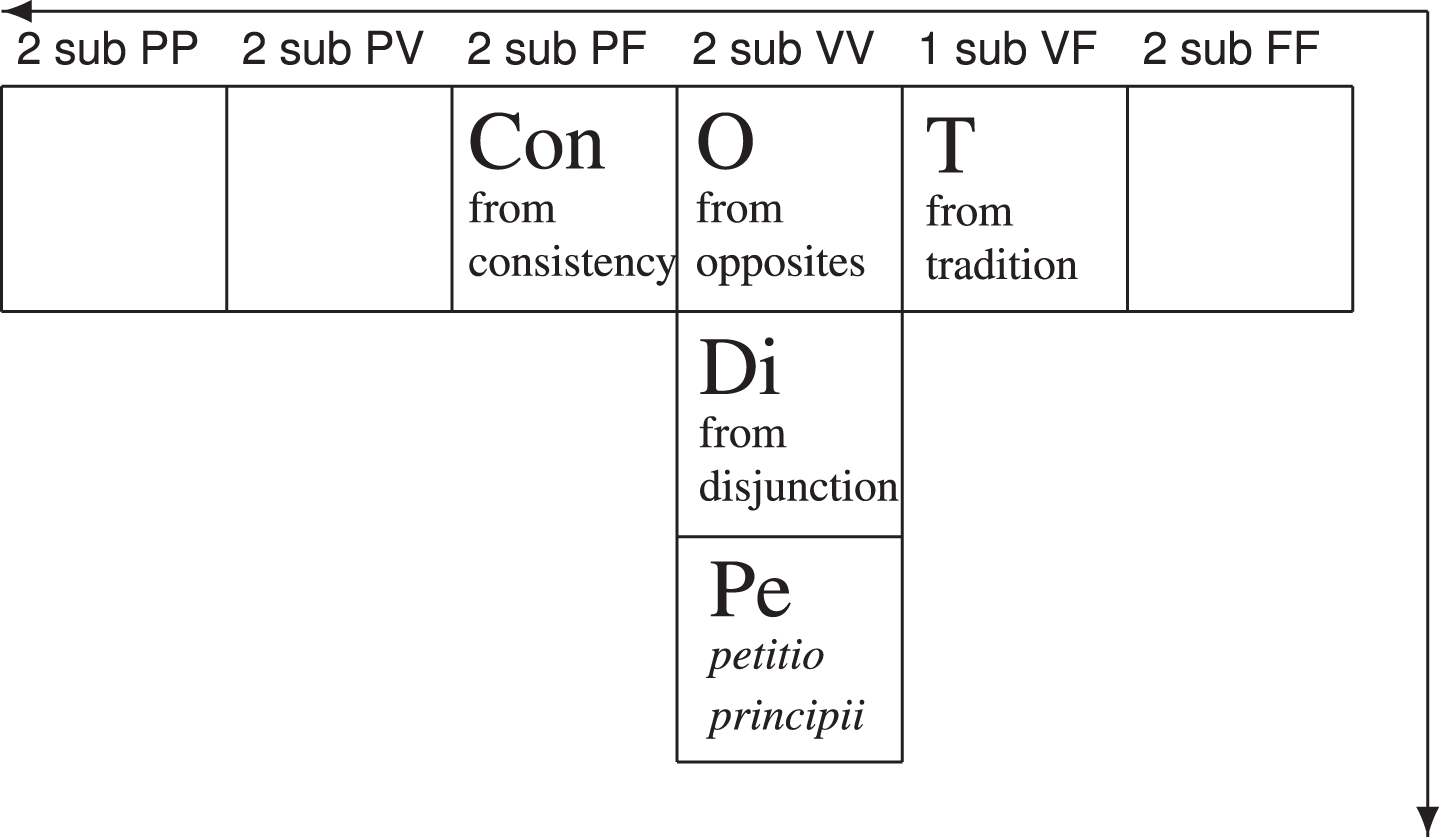
Fig.6
The Delta Quadrant of the PTA.
Given that in our example, the relation between the premise and the conclusion can be captured by saying that the predicate of the statement expressed in the premise, leaving a long trace of rubber on the road, is an ‘effect’ for the predicate of the conclusion, driving fast, the most suitable candidate for providing a traditional name of this specific isotope of 1 pre FF is ‘argument from effect’.
We argue that this crucial step can be semi-automatized thanks to the linguistic analysis in terms of argumentative adpositional trees (arg-adtrees). Section 4 will illustrate in detail the procedure, using example 1.
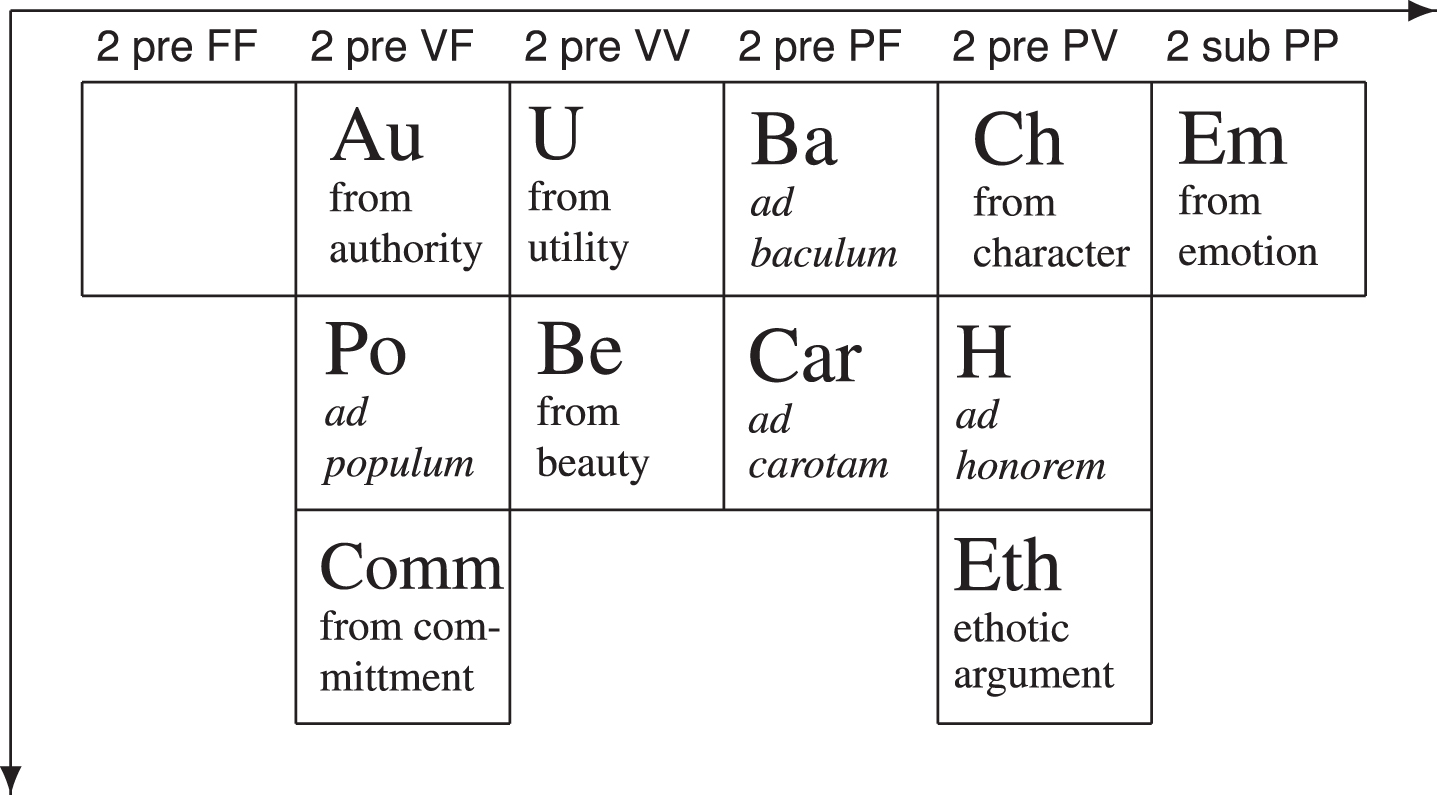
3.2The beta quadrant
The Alpha and Beta Quadrants contain the first-order arguments, which are conventionally situated on the positive side of the vertical axis of the Cartesian space representing the PTA. In particular, the Beta Quadrant is adjacent to the Alpha Quadrant on the left (Figs. 3 and 4). The Beta Quadrant represents all and only first order subject arguments. Figure 4 shows that the empty elements, 1 sub VF and 1 sub PV, are situated in different spots then those of the Alpha Quadrant.
With the exception of the argument type with the systematic name 1 sub PP, in the Beta Quadrant every systematic type has isotopes. In order to illustrate the Beta Quadrant, we will introduce another concrete instantiation, which we call for simplicity example 2. The linguistic formulation of this example is the result of the reconstruction of an explanation of legal reasoning—see Kolb [15]. In particular, it states: Cycling on the grass is forbidden, because walking on the grass is forbidden.
In this case, it is obviously the predicate is forbidden (X) that functions as the fulcrum, while the subjects a and b are different. The argument thus follows the form ‘a is X, because b is X’ and can be identified as a subject argument. Both conclusion σ and premise π are statements of value V, therefore the systematic name of the argument type is 1 sub VV.
Three ‘isotopes’ are possible: from analogy (An), a maiore (Ma) and a minore (Mi). Both a maiore (Ma) and a minore (Mi) argument types entails an asymmetric comparison, that is, the respective values V of conclusion σ and premise π are not on the same level, while the argument from analogy (An) does not show a particular asymmetry. Thus, the analyst will classify example 2 as an instance of the argument from analogy (An)—see Fig. 4. A detailed explanation of the linguistic aspects of example 2 is found in Section 4.
3.3Second-order arguments and the gamma quadrant
After having discussed these examples of first-order arguments, we now turn to the second-order ones. In general, these arguments come in the same two forms as their first-order counterparts, depending on which term is the common term and thus functions as the fulcrum: second-order subject arguments have the predicate as the common term and second-order predicate arguments the subject. The difference with first-order arguments is that the analyst, in order to identify the type of argument, adds the epistemic commitment to the truth or acceptability of the conclusion (or both the conclusion and the premise) to the statements. As we explained earlier, this means that the argument is analysed on the level of the assertion instead of that of the proposition.
The epistemic commitment is added in the form of its conventional expression ‘is true’ (⊤). In particular, while in the Gamma Quadrant this expression functions as the fulcrum, in the case of arguments situated in the Delta Quadrant the addition of ⊤ concerns only the conclusion (σ). In Table 4, we provide an overview of the resulting argument forms.
Table 4
Overview of second-order argument forms
| Quadrant | Conclusion | Premise | Retrogressive argument (progressive variant) |
| γ | q is ⊤ | r is ⊤ | q is ⊤, because r is ⊤ (r is ⊤, so q is ⊤) |
| δ | q is ⊤ | q is Z | q is ⊤, because q is Z (q is Z, so q is ⊤) |
Unlike first-order arguments, the argumentative force of second-order arguments does not particularly rely on the object level, that is, the inner structure of the propositions, but on the meta-level, that means its semantic and pragmatic information. In fact, the fulcrum, which expresses the epistemic commitment of the arguer, cannot be found inside the inner traits of the argument but on the truthiness at the assertion level.
After this general explanation of the nature of second-order arguments, we start our discussion of concrete examples with the Gamma Quadrant, which entails all second-order subject arguments. Let us consider the argument War is bad (σ) because peace is good (π). Both σ and π are statements of value, so the systematic name of this argument, which from now on we will call example 3, is 2 sub VV.
It is worth noting, that, on the object level, neither the subject a of σ (War) and the subject b of π (peace) coincide, nor the predicates X (is bad) and Y (is good). In example 3, there is a clear opposition, that relies on the semantic information: it is pretty straightforward that the pairs ‘war/peace’ and ‘bad/good’ are antonyms. For this reason, within the three ‘isotopes’ (Fig. 5) example 3 is identified by the analyst as an argument from opposites (O).
The peculiarity of the Gamma Quadrant is that on the level of the propositions themselves no fulcrum is found. For this reason, this quadrant can be called the receptaculum ignorantiae, as the argumentative force is found elsewhere. In fact, neither semantic nor structural information (see Section 4 for the latter) suffices to find the fulcrum, which is implicit. Thus, a level of abstraction should be added, in order to find the fulcrum. We call this level of abstraction the layer of epistemic information.
While first-order arguments can bring particular intentional states, such intentional states do not act as the fulcrum. For instance, in example 1 both the conclusion and the premise can be considered committments, in terms of intentional states: ⊤(I am telling you that) The suspect was driving fast, because he left a long trace on the road. However, since this pragmatic information is not crucial for the identification of the type of argument, such epistemic information is taken into consideration only in the case of second-order arguments.
For instance, example 3 is made by two statements of values expressing beliefs, that can be reconstructed like this: ‘you should believe that σ because you already believe π’ (in symbols: ⊤VV). It is such intentional state that represents the fulcrum of example 3, and therefore its argumentative force—for more details, see Chapter 6 in [10]. If specifications are not needed, the umbrella predicate ‘is true’ (symbol: ⊤) is conventionally adopted.
3.4The delta quadrant
Figure 6 shows the types of arguments within the Delta Quadrant of the PTA found until now, up to version 2.4.4 Let us introduce example 4, from the reconstruction of a quite famous meme: We only use 10% of our brain, because it is said by Einstein. The fulcrum here is to be found in the subject, which is a full statement, ‘we only use 10% of our brain’ and ‘it’, represented by q. Clearly, if the statement in full is only the subject, we need to add a second-order predicate, that in first approximation will be ‘is true’ (⊤). The reconstruction will be transformed as follows: We only use 10% of our brain (q) [is true (⊤)], because q is said by Einstein (Z). On a more sophisticated level of analysis of the epistemic information hidden behind the ⊤, we could say that the first statement is one of speaker belief’s, hence it can be reconstructed as ‘I believe that q’.
4Constructive adpositional grammars
In this section, we shall demonstrate how the theoretical framework of CxAdGrams can be applied to the types of argument situated in the four quadrants of the PTA. More in particular, we will provide an analysis of examples 1–4. However, before to to delve into the topic, a legitimate question can be raised: why should we care of a fine-grained analysis of the linguistic material underlying the arguments? In other words, why is an identification of the type of argument in terms of the PTA not enough?
The answer of this question is twofold. The first answer is general. The method of reconstructing arguments we are illustrating should operate on the level of the individual words, in order to help the analyst in the reconstruction itself. Our aim is to go beyond the pure subjectivity in reconstruction, and the identification of a heuristic—if not a step-by-step procedure—cannot avoid linguistic analysis. Our hypothesis is that the application of CxAdGrams to the task of argument reconstruction can be treated as a supervised machine learning problem, as outcomes are predicted on the base of the data provided, analogously to the task of automatic summarization—see at least Nenkova and McKeow [20].
The second answer is more specific. While the argumentative and pragmatic information is language-independent to a large extent, the concrete arguments largely depends on the natural language in use. Figure 7 illustrates the detailed levels of abstraction within a single argument.
Fig.7
Levels of abstraction within arguments.
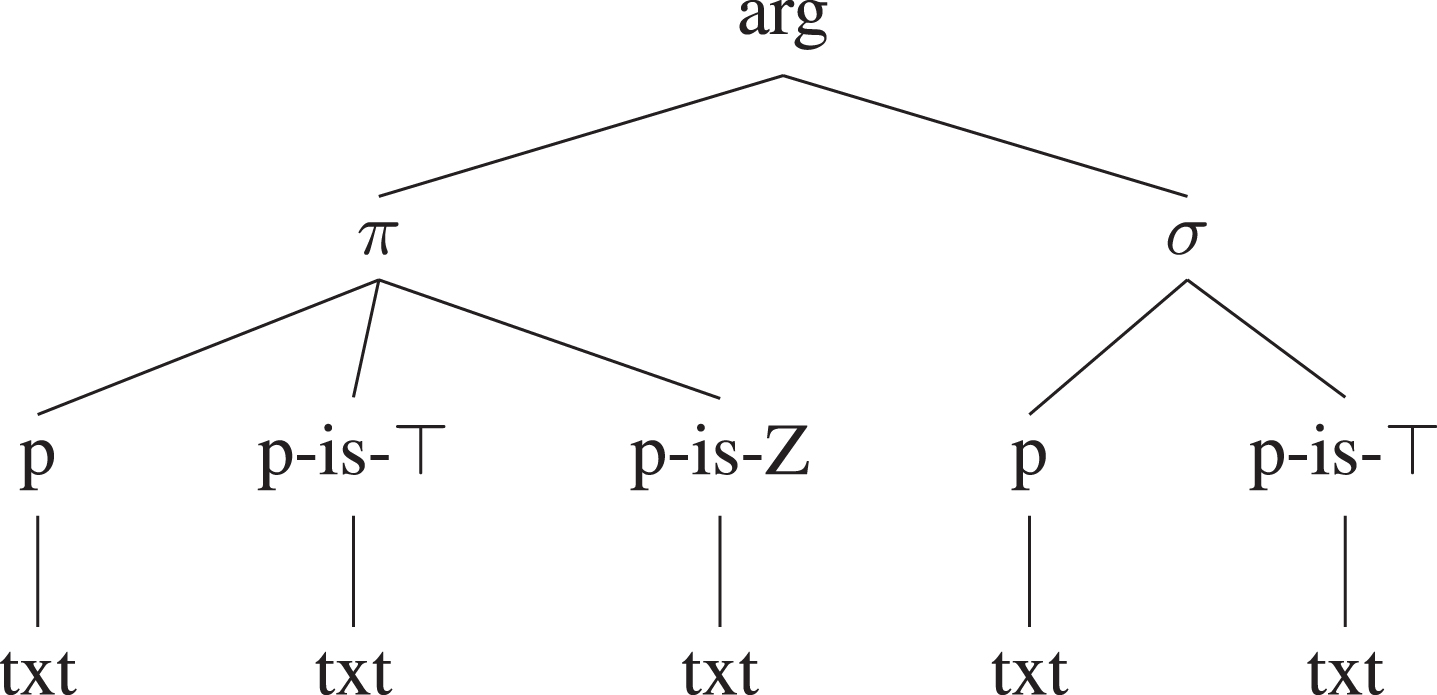
These levels can be identified as points of attack. On the upmost level (arg), the argument itself can be attacked as a whole, through critical questions against the solidity of the whole architecture. This in practice means that the attacker will question the solidity of the ‘because’ (in case of retrogressive arguments: symbol ←) or of the ‘so’ (progressive: →), or other natural language connectors. Other levels of attack are on the propositional level, that is the level of the premise(s) (π), and that of the connection between the premise and the conclusion, that of the ‘argumentative lever’ – see Section 3 above. These two levels could be managed nicely with the only use of the PTA. However, attacks can arrive at the level of the epistemic information (p-is-⊤; e.g. ‘I do not share your belief’), in case of second-order arguments—or, more in general, on the level of the statement—an attack can question the solidity of the statement being a fact (F; e.g. ‘p is fake’), values (V; e.g. ‘I have different values’), and policy (P; e.g. ‘this policy is not feasible’). Quite often, such attacks focus on a particular linguistic element (txt, in Fig. 7) of the argument. This is the the specific reason why we need a linguistic representation of arguments.
We can add a practical reason for a linguistic representation. In an argumentative discourse, the vast majority of statements are arguments; however, it is possible to find expressive statements that are functional for argumentations but are not arguments, such as Shakespeare’s Mark Anthony speech incipit: Friends, Romans, countrymen, lend me your ears. In the Gold Standard Corpus (GSC) to be made, such statements should be represented in terms of pragmatic adtrees—for details, see Chapter 6 of Gobbo and Benini [10].
In the following section, we will present the fundamentals of CxAdGrams for the purposes of the Adpositional Argumentation (AdArg), while in the next sections we will analyse examples 1–4 in terms of argumentative adpositional trees (arg-adtrees).
4.1Mathematical foundations
CxAdGrams in all their variations—so far, morphosyntactic, argumentative, pragmatic, but phonological are also possible—are based on a simple mathematical method, described in the Appendix B of the fundamental book Gobbo and Benini [10]. Interested readers can look there for a comprehensive presentation; here, we will convey only the necessary information for the scope of the present paper.
Constructive mathematics is an approach to mathematics that is premised on the idea that regarding the formulas of a theorem, the information content of any statement should be strictly preserved—see Bridges and Richman [4]. This is established by avoiding the use of the Law of Excluded Middle, unlike classic logic. Mathematical representations of natural language grammars following the constructive approach are well known in mathematical and computational linguistics, the first ones being proposed by Adjukiewicz [1] and Church [5].
In CxAdGrams, a grammar category is a category [18] enriched with grammar characters (gc) and a set of basic constructions, essentially capturing the notions of valency (val), and the adjunctive (A) and circumstantial (E) relations. An adtree is a syntethic and syntactic description of the objects of a grammar category, which takes the graphical form of a tree, apt to be easily presented, analysed and manipulated. However, the notion of adtree is inadequate to represent the real constructions inside languages, apart the most basic and elementary ones. For this reason, CxAdGrams introduce the notion of transformation; mathematically, transformations are in fact maps of a grammar category into itself which preserve the structure of grammar categories—an endofunctor; see Chapter 4 of Gobbo and Benini [10]; this aspect is out of the scope of the present paper.
Using category theory to model AdGrams is justified because it allows to inherit for free a number of mathematical notions and constructions which have a fundamental meaning in the analysis of a language. For example, the formal notions of sieve and co-sieve on an object (expression) E correspond to the collection of the valid subexpressions of E and to the collection of all the expressions containing E, respectively.
While this way of formally identifying the sub- and the super-pieces of an expression is useful in the mathematical analysis of linguistics, it becomes really essential when using AdGrams to model the natural language for other purposes, such as AdArg. In fact, identifying expressions in a coherent way, that is, if an expression is considered to be equivalent to another expression then we can always substitute the first expression with the second one in the fragment of the language under analysis, corresponds to imposing a Grothendieck topology over the considered fragment, which naturally generates a topos of sheaves. This abstract, complex, and very rich mathematical object represents in an explicit way the information the fragment conveys by the structure of the language alone.
However, since a topos of sheaves can be fully described in term of fibrations, it becomes possible to computationally manipulate this abstract entity. In fact, a convenient way to write fibrations is given by Homotopy Type Theory [27], in which a fibration is represented by a dependent product, or, in logical terms, by a bounded universal quantification.
Avoiding the complex mathematical descriptions, the fragment collecting all the expressions of interest, even identifying some of them as soon as the identification makes mathematical sense, can be synthetically described in a formal language, the one of Homotopy Type Theory [27], which is, at the same time, a functional programming language, a logical theory powerful enough to analyse the properties of the fragment, and a topological description of how the expressions in the fragment are related one with the others.
4.2Syntactic adpositional trees
From a linguistic point of view, adtrees represent natural language expressions in terms of recursive trees, in which the relations between linguistic elements can be described as hierarchical in that the one element ‘governs’ the other (which then ‘depends’ on the former). Each adtree represents a minimal pair of linguistic elements and their relation, expressed in terms of adpositions. Figure 8 (left) shows the abstract adtree structure. The governing element (gov) is conventionally put on the right leaf at the bottom of the rightmost branch, while conversely the dependent element (dep) is put on the left leaf at the bottom of the leftmost branch. Immediately thereunder one can find the grammar characters (gc). Finally, the adposition (adp), which represents the relation between the governor and the dependent, is depicted as a hook under the bifurcation of the two branches.
Fig.8
The abstract adtree structure and example 0.
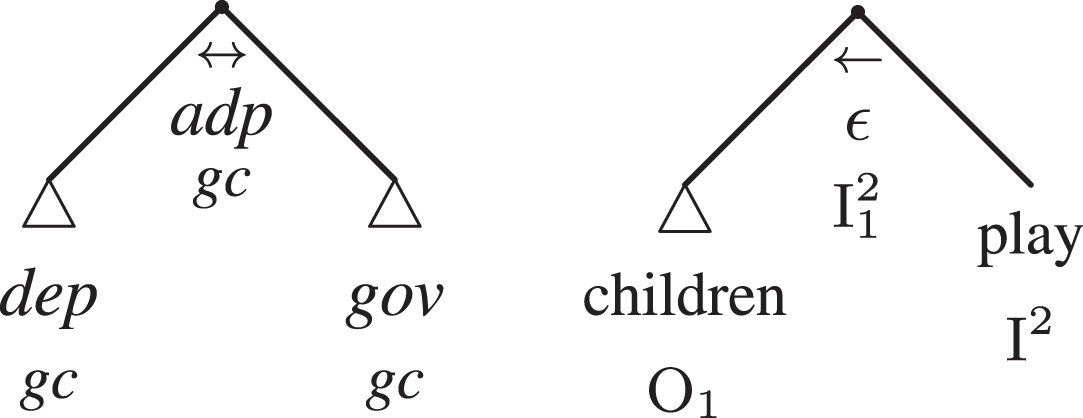
On the right there is the syntactic adtree of example 0 children play: we say ‘syntactic’ as the morphological analysis of children is hidden under the triangle △. In general, the triangles on the leaves indicate the possibility of recursion, the fact that another adtree can be appended to each adtree leaf recursively, if needed. This possibility illustrates the fact that the analyst can hide or show details through the use of triangles, according to her needs. The comparison between the abstract and the concret adtree in Fig. 8 helps the reader to understand the roles of each and every element: the left arrow ← indicates an unmarked information prominence, as the default is that the governor (in example 0, play) is more prominent than the dependent (in this case, children). In arg-adtrees, the unmarked information prominence correspond to the progressive form (see Section 3). The left-right arrow ↔ indicates underspecification. By convention, non-morphological adpositions are indicated by Greek letters: in the case of a syntactic relation, the letter is an epsilon (ɛ); in the case of an argument, it will be one of the letters for the quadrants (α, β, γ, δ), or π and σ for indicating the argumentative function of the statements.
Finally, from a formal point of view, adtrees can be seen as formulas, which means that they are suitable for natural language processing. The tabular presentation of Fig. 9 corresponds to the syntactic adtree example 0 in Fig. 8.
Fig.9
The tabular adtree of example 0.
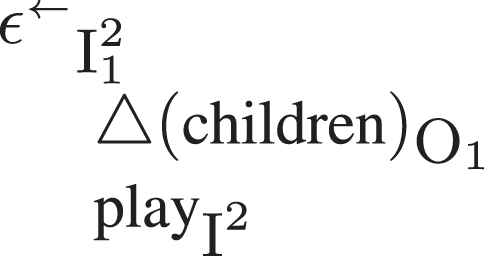
Under the adpositions and the governor and dependent leaves readers can find the grammar characters (gc): in example 0, they are respectively:
Table 5 shows the possible grammar characters (gc). Adjective (A) and circumstantials (E) are both modifiers, and for this reason in general they appear as dependents (dep). It is worth noting that the left and right branches of a linguistic adtrees follow different rules of construction: while governors (gov, right branches) can have more dependents, dependents (dep left branches) can have one and one only governor.5
Table 5
Linguistic grammar characters
| Value | Name | Function | Examples |
| A | Adjunctive | Modifier of O | Adjectives, articles |
| E | Circumstantial | Modifier of I | Adverbs, adverbial expressions |
| I | Verbant | Valency ruler | Verbs, interjections |
| O | Stative | Actants | Nouns, pronouns name-entities |
| U | Underspecified | Transferer | Prepositions, Conjunctions, Derivational Morphemes |
Each proposition is analysed in terms of phrases, which are depicted as subtrees; each phrase presenting a ruling verb is built around that verb, which is posed as the rightmost leaf of the respective subtree. The variable gc will take the value of
Let us provide an analysis of a prototypical example of a trivalent verb. In the case of the English verb to open, we will have a first actant that fulfils the role of the opener (e.g. a concierge), a second actant indicating the opened object (e.g. a door), and a possible third actant for the instrument (e.g. a key). Note that the semantic role of the beneficiary (e.g. the client, in the phrase the concierge opens the door with the key for the lady) is an extra-valent actant, as it cannot be advanced (e.g. the phrase the key opens the door is incomplete but still depicts the same scene, while the lady opens the door changes the picture substantially).
The formal representation of the grammar characters of the morphosyntactic material by Tesnière in its original French version [24] was indicated using four letters (A, E, I, O). This notation method is preserved in CxAdGrams so as to remain consistent with the original model. However, for technical reasons, an additional grammar character was inserted (U) that did not exist in Tesnière’s structural syntax [24].
Direct objects of transitive verbs are often the second actant in English, and so they will be indicated as: O2. In the previous example, door is O2, concierge is O1, and key is O3. True adverbs, such as here, now, or sentence adverbs—which modifies the whole phrase structure—such as obviously or technically will be indicated as: E.
Figures 10 and 11 show the fully expanded syntactic adtree of example 1 without argumentative information. In general, this level of detail is not needed to the analyst of arguments. Here, they were included to show how the presentation of a full sentence appears, especially in the tabular formula of Fig. 11, that would be quite similar to an entry of a knowledge base. The reader is invited to note the presence of every grammar character in Table 5.
Fig.10
The fully expanded syntactic adtree of example 1.
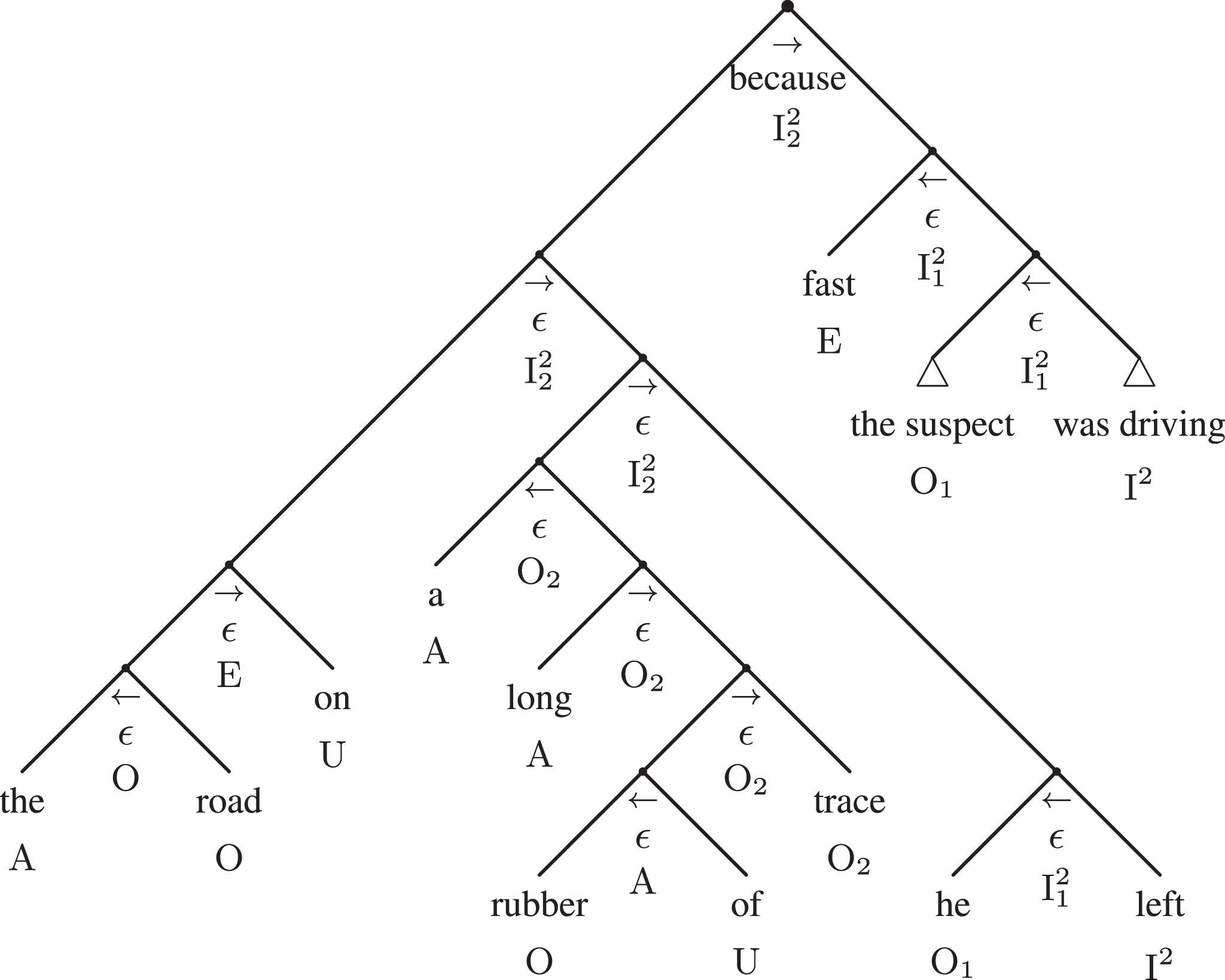
Fig.11
The fully expanded tabular adtree of example 1.
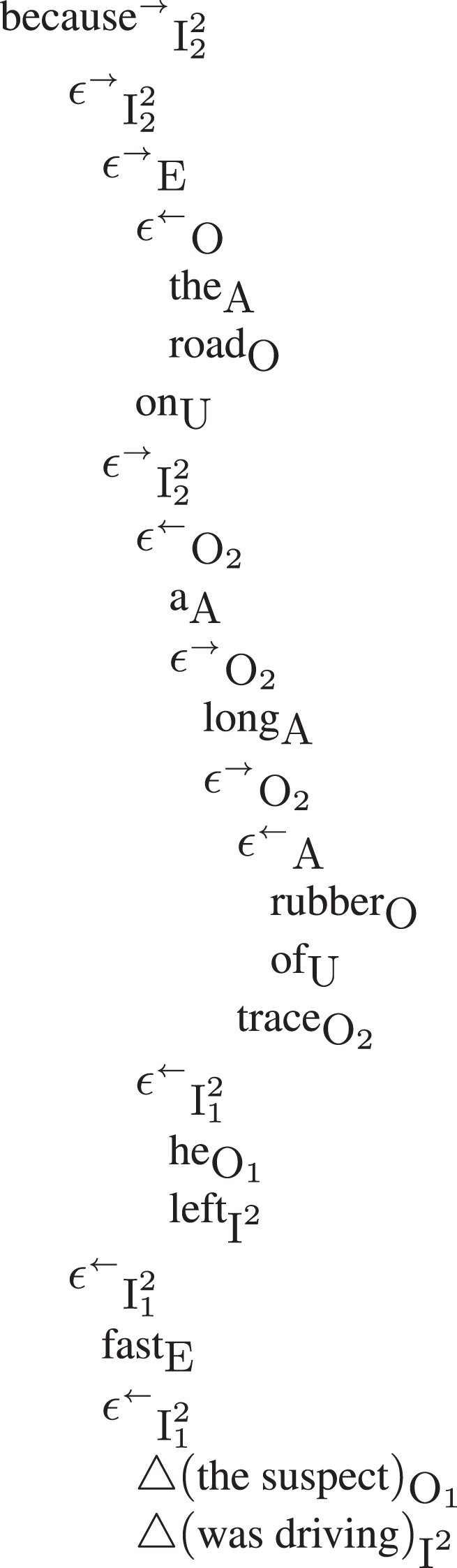
As we mentioned above, although the main application of the constructive adpositional approach is (morpho)syntactic analysis, it can be applied to pragmatic and argumentative analysis as well. This means that an element of the PTA encapsulates an argumentative valency (arg-val) embedded in its own type. For instance, an argument from authority (Au) cannot be conceived without an explicit, specific actant, fulfilling the role of the authority. The corollary is that the argumentative valency is independent from the linguistic valency, although the underlining representation mechanism is exactly the same.
5The design of adpositional argumentation
In this section we combine CxAdGrams and PTA together so to design AdArg. In order to do so, we develop the notion of ‘argumentative adtree’ (arg-adtree). We will explain how such an adtree makes use of all the expressive of linguistic adtrees taken from the framework of CxAdGrams, while at the same time incorporates the pragmatic information resulting from the argument analysis taken from the framework of the PTA.6
In arg-adtrees, a particular emphasis is put on the first actant, which is the subject because its identification permits to classify the argument itself as a subject or predicate argument, as seen in Section 3. Therefore, in arg-adtrees, we consider the argumentative valency (arg-val): as we are constructing for the purposes of the argument analysis, we put the first actant O1 in evidence as the leftmost subtree of the given phrase. After individuating the subject, the analyst considers the argumentative in-valent actants, that is the actants that are embedded in the type of argument in the appropriate quadrant of the PTA. This procedure of explicitation of the in-valent actant structure permits to clarify the inner functioning of the conclusion of the argument, and eventually it deepens the analysis of the argument itself in terms of robustness.
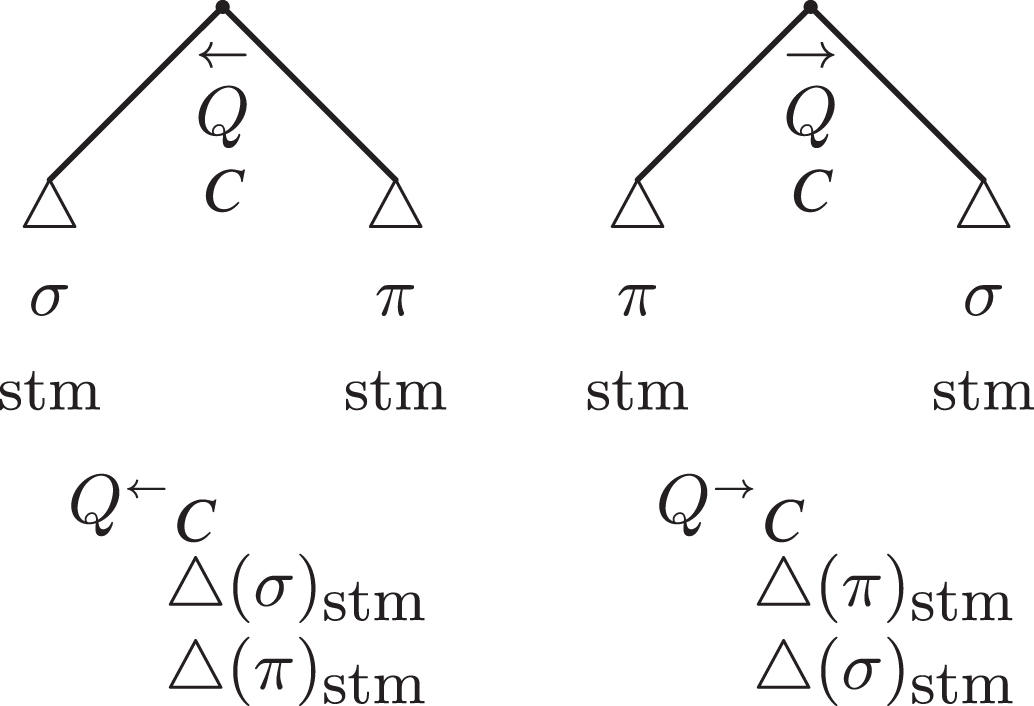
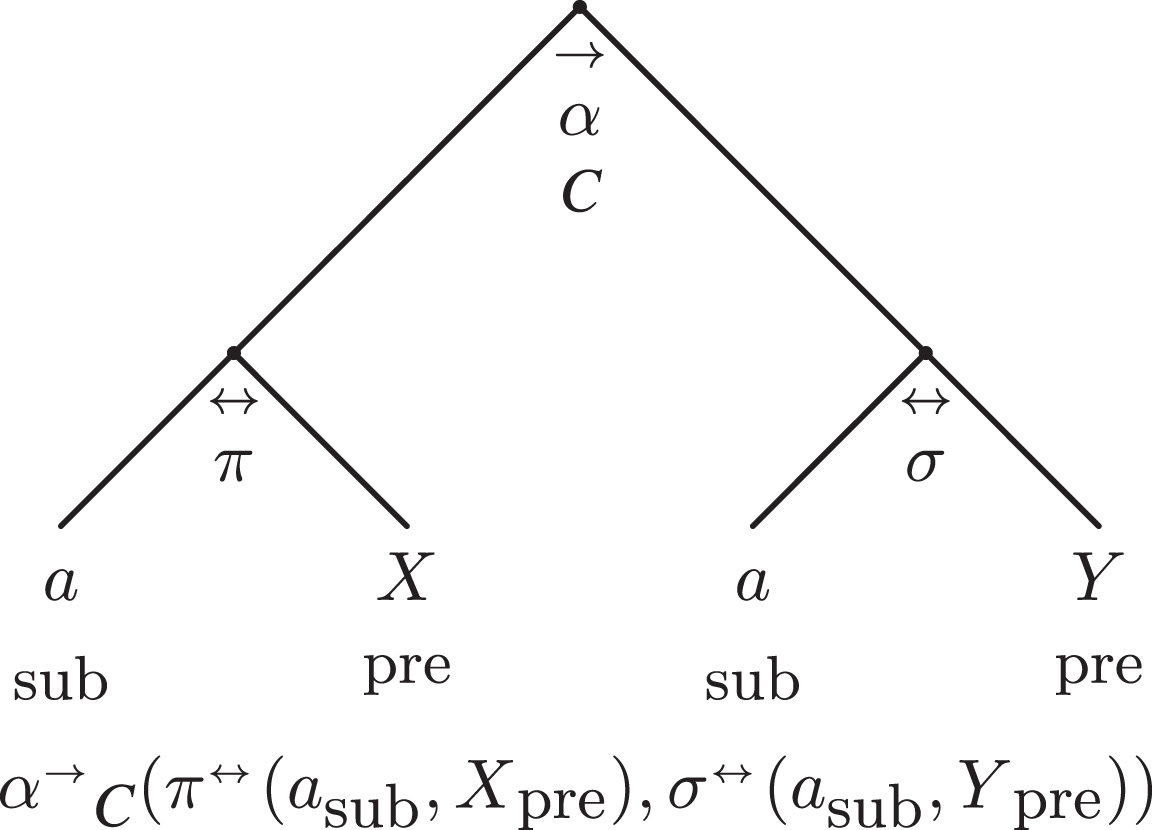
Figure 12 shows the abstract arg-adtrees, in their progressive forms (on the left; indicated by the information prominence arrow: ←) as well as in the retrogressive one (on the right; symbol: →), both as trees and as tabulars.7 The letter Q as the adposition is a placemark for a generic PTA quadrant, while the letter C as the grammar character of the adposition is a placemark of the combination of the types of statements—see Table 2.
Fig.12
The standard and tabular abstract arg-adtrees.
For the sake of simplicity, we consider only retrogressive arguments, as in the concrete examples 1–4 we are going to analyse in the following sections.
Figure 13 shows the abstract arg-adtrees of first- and second-order retrogressive arguments, and they correspond to the information already seen in Tables 1 and 4. In order to illustrate how the representation works, we turn now to reconstruct examples 1–4 in terms of the framework explained above. The examples cover all the quadrants of the PTA, and therefore they instantiate different combinations of types of statements.
Fig.13
The abstract arg-adtrees of arguments in the four quadrants.
A caveat is needed here: in designing the Gold Standard Corpus (GSC), the decision of including linguistic adtrees too or not is a matter of balancing time and effort, which depends on practical considerations that are out of the scope of the present paper. The purpose of the next sections is to clarify how to transform a syntactic adtree into an argumentative one, in order to guarantee the possibility of having a choice between starting from linguistic adtrees, and representing argumentative ones as tree transformations, or encoding argumentative adtrees directly.
5.1First-order argumentative adtrees
Figure 14 shows the abstract arg-adtree for the Alpha Quadrant. The grammar characters (gc) shows that the subject (sub) is the same (a), therefore it is the fulcrum—see section 2.1. For reasons of space, we omit the analogous abstract arg-adtrees of the other quadrants.
Fig.14
Abstract argumentative tree of alpha-arguments.
In particular, the adtree of the premise (π) of the argument, he left a long trace of rubber on the road is depicted as the leftmost subtree, while the linguistic adtree of the conclusion (σ), the suspect was driving fast is the rightmost subtree, as the conjunction is retrogressive, in this case because. For the sake of simplicity, let us concentrate on the statement that constitutes the premise (π) of example 1 only.
A human readable representation of the syntactic adtree of this statement 1 is the compact adtree in Fig. 15, where linguistic details have been conveniently compacted through triangles: △.8
Fig.15
The compact syntactic adtree of example 1.
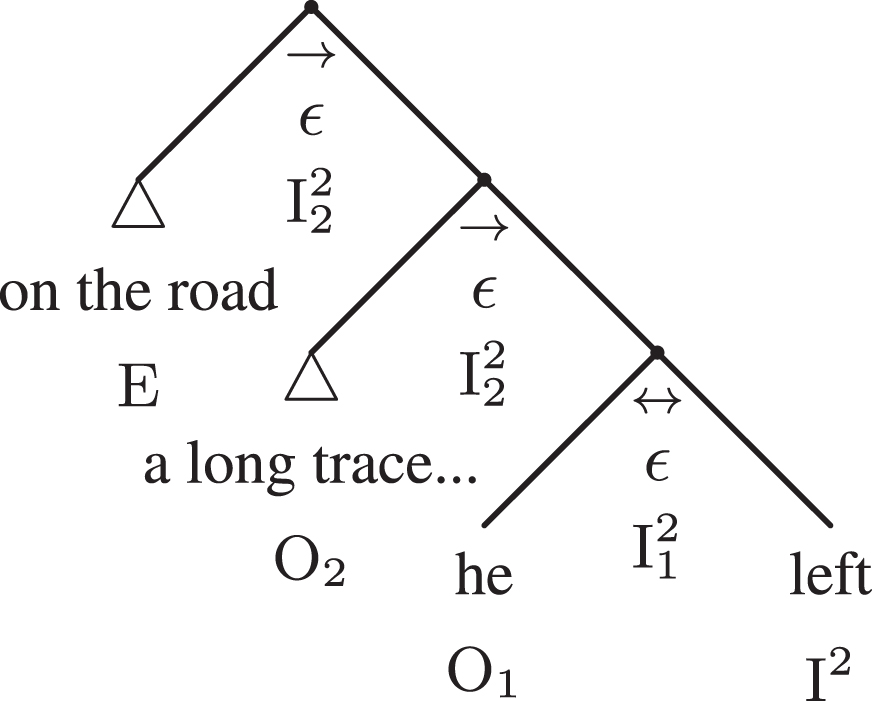
The in-valent arguments O1 and O2 are close to the main governor I2 and they saturate its linguistic valence one branch after the other (
Figure 16 shows the correspondent argumentative adtree, and it should be put in contrast with the syntactic adtree of Fig. 15. The arg-adtree of the argument can be derived from its linguistic counterpart by adding information that is relevant for identifying the type of argument and possibly condensing information that is too detailed for the purposes of the analysis.
Fig.16
The compact argumentative adtree of example 1.
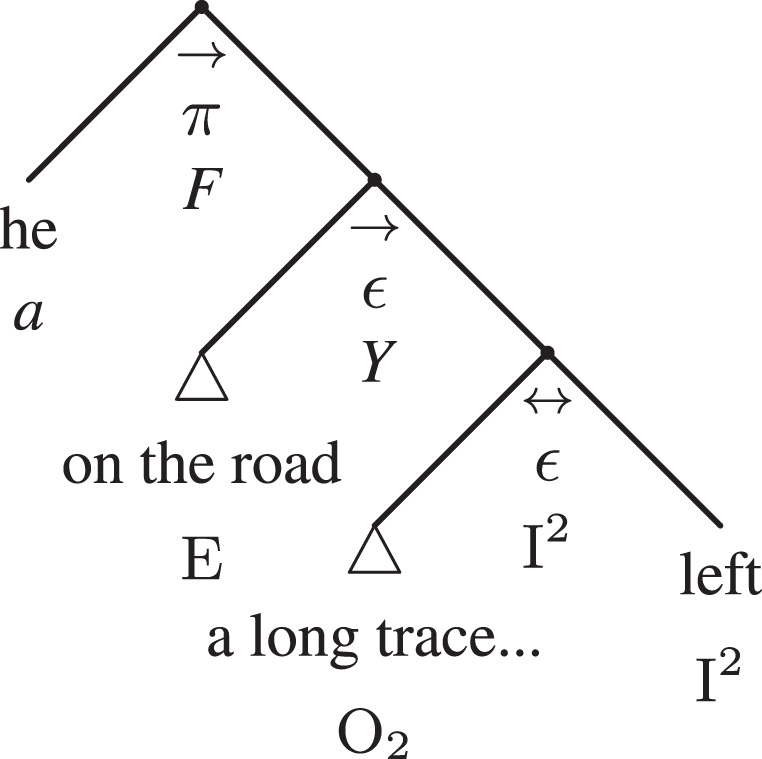
First, the upmost hook does not indicate linguistic information only (ɛ) but it marks the whole adtree as the premise (π) and as a statement of fact (F).
Second, the subject put in evidence is not only an actant of the verb (O1) but a crucial part of the argument itself (a, which subsumes the linguistic information). For this reason, it is found as the leftmost sub-branch. All the rest is part of the predicate, identified by the hook Y. In particular, it is worth noting that the information of the circumstantial (E) on the road, while it is peripherical from a linguistic point of view, it is central in argumentative terms, being a possible point of attack: for example, if the trace were left not ‘on the road’ but ‘on a rough road’, the whole argument could possibly collapse by doubting the statement of fact (F).
Figure 17 shows the complete compact arg-adtree of example 1. The Adpositional Argumentation (AdArg) endevour helps the analyst both by providing an argumentative valency carved into the element of the PTA, and through the analysis of the in-valent structure. Let see an example of analysis of the latter. In example 1, the analyst has seen that the verb ruling the conclusion (σ), ‘to drive’, has two actants: the driver (O1) and the vehicle (O2). In the example, the information carried by the second actant is unexpressed; however, that does not imply that it does not exist, rather that it is hidden. In other words, adtrees permit to show this information under the form of a barred subtree. Let us suppose that we have to analyse not a single argument but a whole argumentative text. In such a case, unexpressed actants can be helpful to show what is present in the argument structure and what is—on purpose or not—omitted.
Fig.17
The argumentative adtree of Example 1
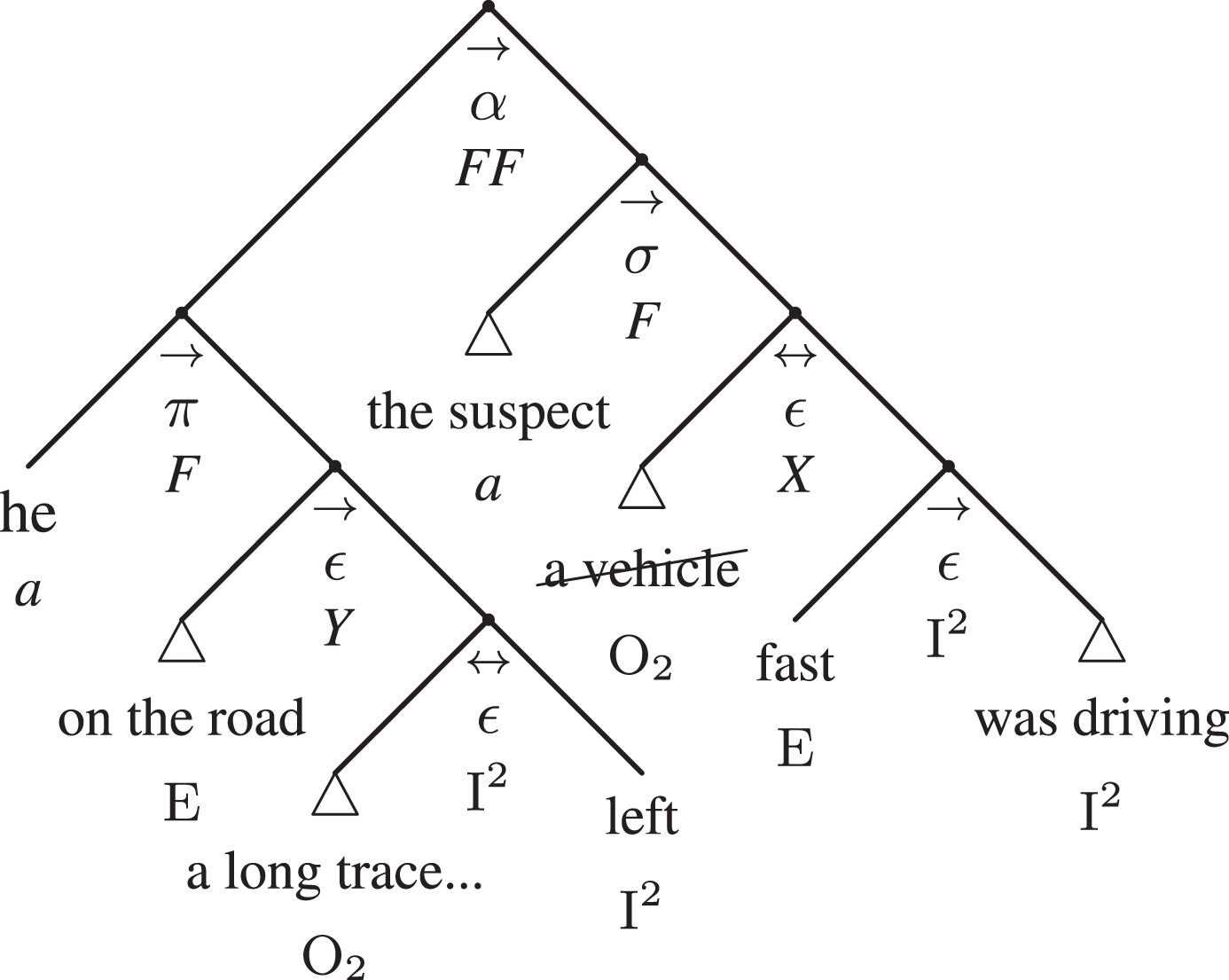
In particular, what is interesting here is that the categorial grammar subject ‘the suspect’, is metonymically identical with the driver O1, even if, strictly speaking, it is the motor vehicle O2 that left the long trace on the road. Interestingly, the effect in the argument is expressed by apparently peripherical elements in the linguistic structure of the propositions, in particular: fast, which is the circumstantial (E) of the conclusion (σ); the second actant O2, a long trace; finally, its circumstantial (E), on the road. In other words, even if circumstantials (E) represent inessential information from the point of view of linguistic soundness, they are central for the sake of the argument: if the suspect weren’t driving fast long traces on the road possibly couldn’t be left; in other words, the argumentative correlation is sustained by both circumstantials (E) and the explicit second actant O2, a long trace.
If we forget to represent the second actant O2 (a vehicle) of the conclusion σ, we lose an important piece of information, and that’s why it is important to represent it in the argumentative adtree.
Let us turn our attention to example 2. As in the previous example, we first present the linguistic analysis of the statements in the premise and the conclusion without including any information about the type of argument and then explain how the transformation from the linguistic adtree (Fig. 18) to the arg-adtree (Fig. 19) takes place.
Fig.18
The linguistic adtree of Example 2
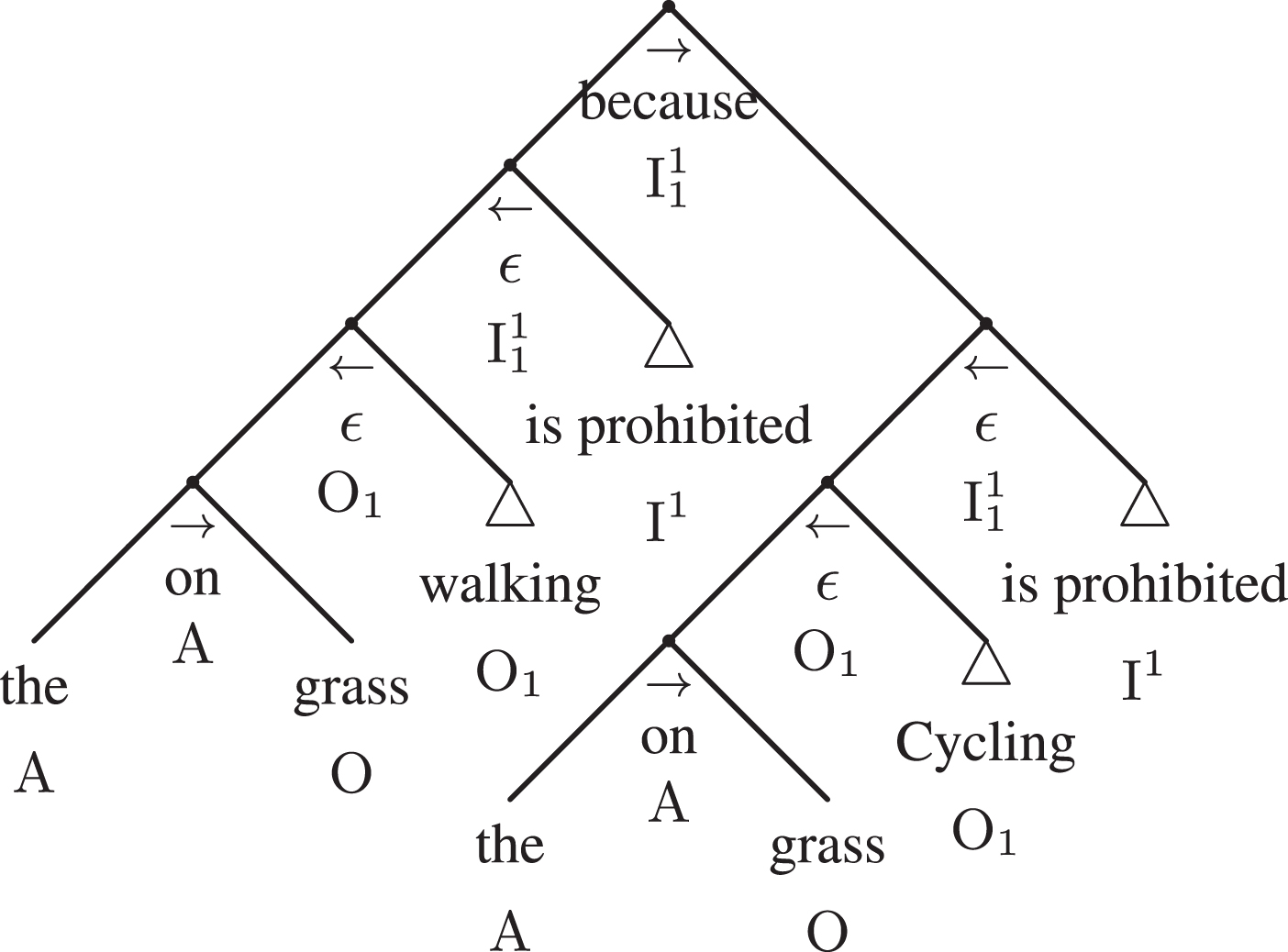
Fig.19
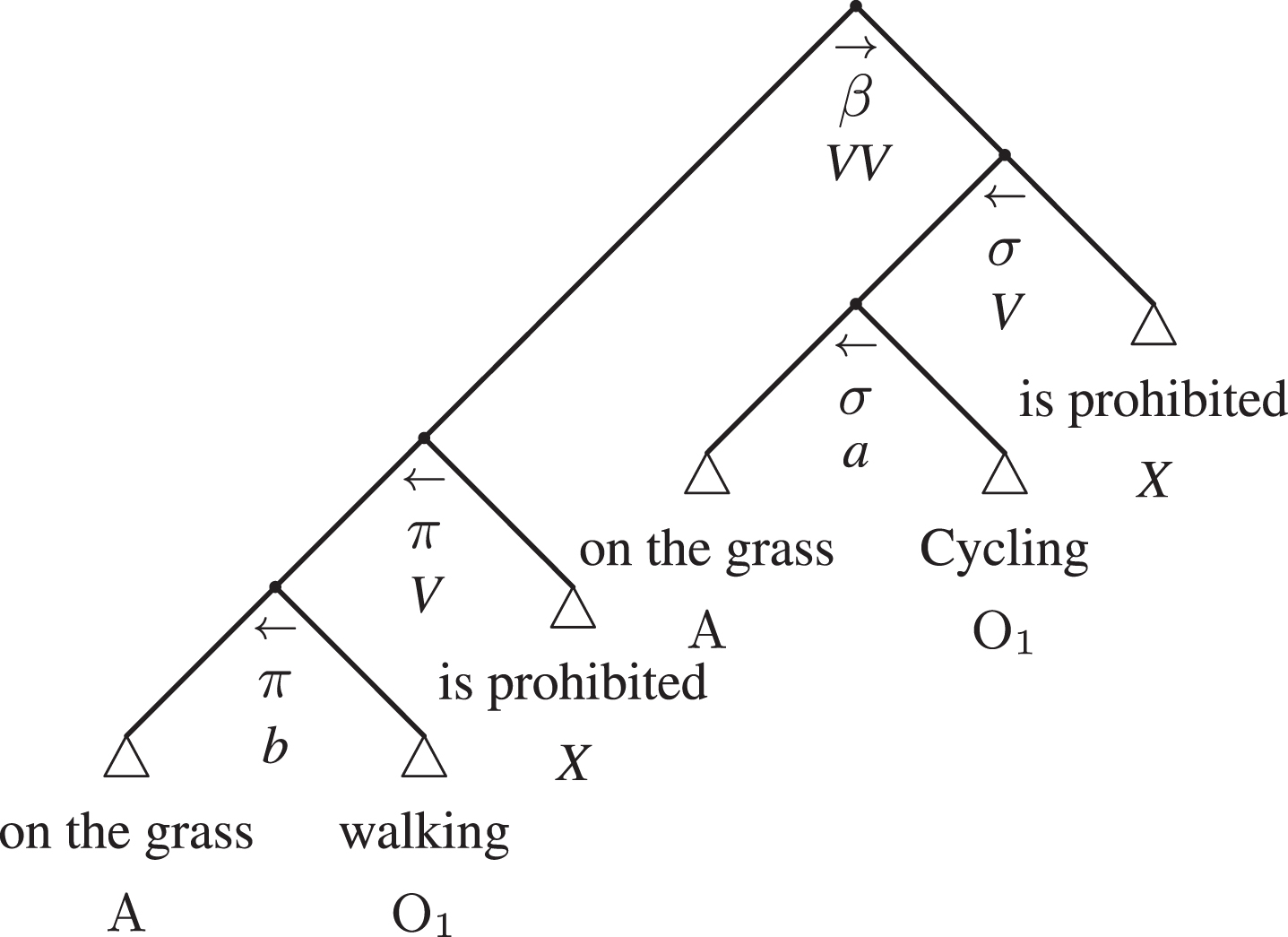
The argumentative adtree of Example 2
The linguistic adtree is rather symmetric, as the premise and the conclusion share the same structure. The prepositional groups on the grass modify respectively the subjects Cycling and walking (O1), and therefore it is an adjunct (grammar character: A; see Fig. 18).
Figure 19 shows the complete argumentative adtree of the example. On the top hook, there is information regarding the quadrant (in this case, α) and the combination of types of statement (indicated with a generic C in Fig. 4) under the hook that connects premise and conclusion. In this case, it is a combination of two factual statements (FF), which correspond to ‘Ef’ in the PTA (see Fig. 3).
In this case, the arg-adtree appears very similar to the syntactic adtree. The subtrees of the subjects a and b, respectively of the conclusion (σ) and the premise (π), put in evidence the similar parts (on the grass), which are essential parts of the argument. In fact, if we cut them, the resulting phrase becomes: Cycling is prohibited because walking is prohibited, which loses all its pragmatic force.
We argue that these two examples show that arg-adtrees are powerful tools in order to show where the pragmatic force is placed within the linguistic material.
5.2Second-order argumentative adtrees
Figure 13 already depicted the abstract argumentative adtrees at the second-order. Figure 20 shows the compact arg-adtree of example 3 of the Gamma Quadrant, War is bad because peace is good.
Fig.20
The compact argumentative adtree of example 3
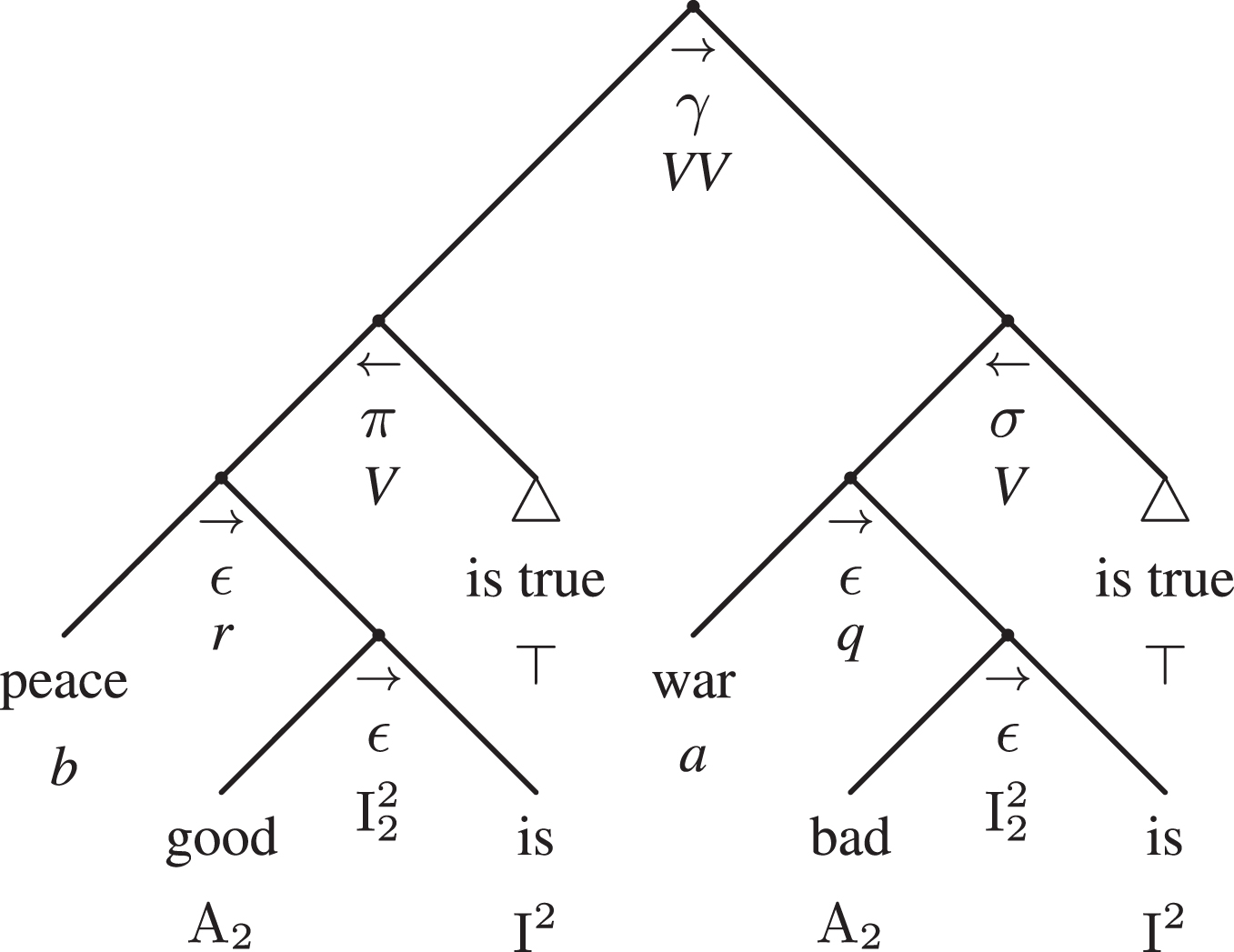
Like in the case of example 2, this adtree is rather symmetric. Both the conclusion (σ) and the premise (π) are statements of values (V) epistemically supported by the speaker’s belief, represented by the umbrella term ‘true’ (⊤). As it happens in all elements of the PTA in the Gamma Quadrant, their epistemic information is the fulcrum—as explained in Section 3.3.
In Fig. 21, finally, we pictured the arg-adtree of the example We only use 10% of our brain, because it is said by Einstein, which can be characterized as a second-order predicate argument combining a value with a fact (2 pre VF). While the statement types are indicated under the hooks of the adtrees representing the conclusion and the premise respectively, the information under the hook that joins them into an argument contains pragmatic information about the argument type 2 pre being abbreviated as δ since that is the corresponding quadrant, and C is instantiated as VF since that is the combination of types of statements. Differently from the second-order arguments in the Gamma Quadrant, those in the Delta Quadrant have one statement expressed (or normalised) as an assertion, namely the conclusion. From comparing the arg-adtree with the original text, the analyst will find the fulcrum in terms of epistemic information (symbol: ⊤) as the main predicate of the conclusion. In this way, the analysis reveals that the argument is based on a relation between the fact that Einstein said something and the truth of that something.
Fig.21
The compact argumentative adtree of example 4
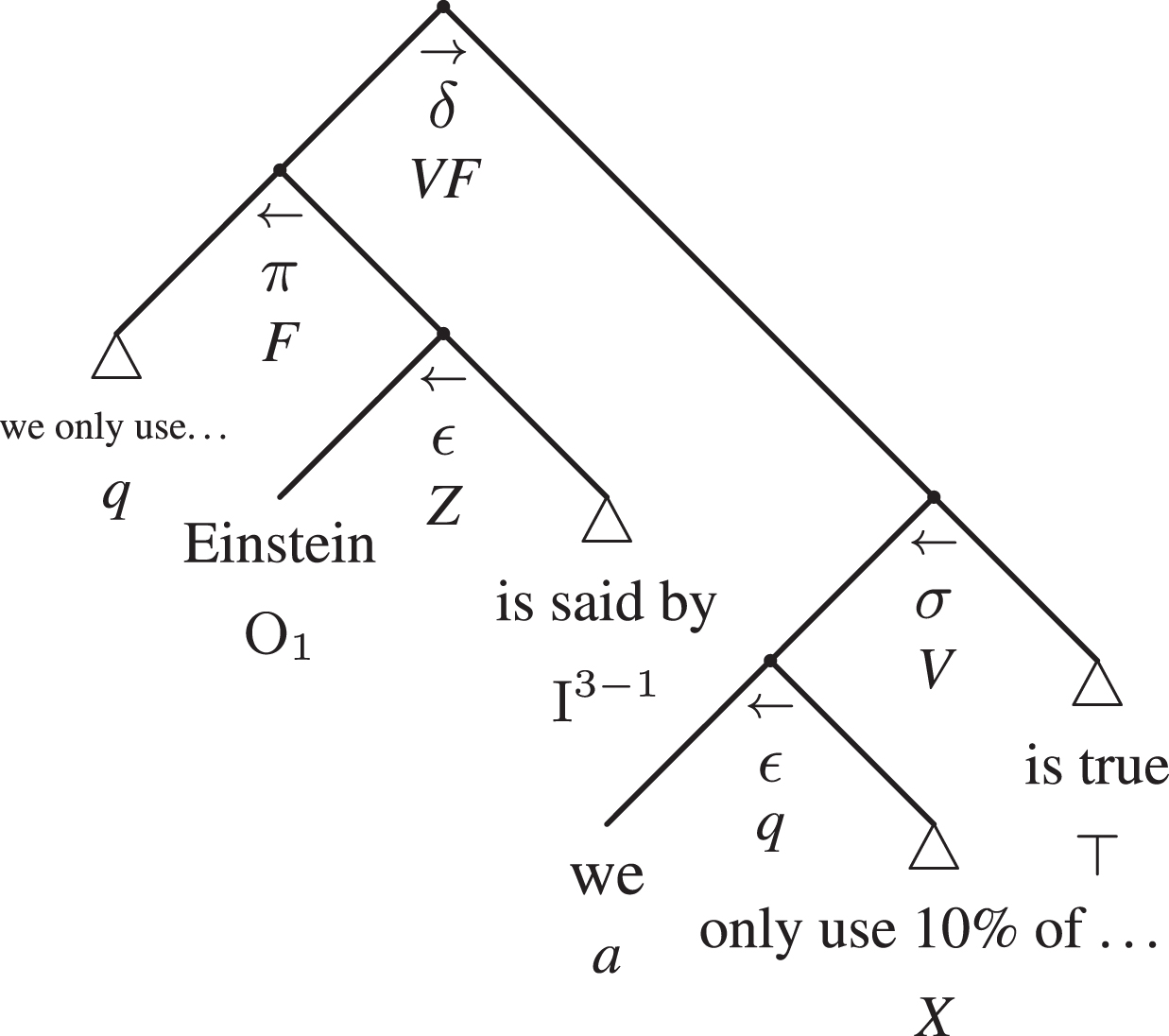
As we remarked earlier, the advantage of working with adtrees is that while there is no loss of information, the analyst may show or hide information according to her needs and depending on the aim of the analysis. In the case of arguments from authority such as the one in the last example, for their evaluation it is important to know which authority is referred to. This has been made clear in the adtree by putting ‘Einstein’ into evidence.
6Conclusion
In this paper we presented the theoretical framework of Adpositional Argumentation (AdArg). We have shown how the existing frameworks of Constructive Adpositional Grammars (CxAdGrams) and the Periodic Table of Arguments (PTA) can be combined to develop a high precision tool for reconstructing and representing arguments expressed in natural language. In particular, the guidelines presented in this paper are the necessary steps in developing a complete procedure for implementing a Gold Standard Corpus (GSC)—for a definition and known issues, see Wissler et al.. In fact, whereas the state-of-the-art in Computational Argumentation has automatized the extraction of complete propositions and their relations, our method prepares the ground for a more fine-grained computer-assisted analysis and evaluation of argumentative texts.
The central notion in this endeavour is that of the so-called ‘argumentative adpositional tree’ (arg-adtree). Apart from representing the linguistic features of the statements that function as the conclusion and the premise of the argument under scrutiny, such an arg-adtree contains pragmatic information regarding the order of presentation of the statements, the type of argument they substantiate, and the argumentative function of their constituents.
By providing a fully-fledged reconstruction of four concrete examples of argument types, we showed for each of the four basic argument forms in the PTA how to transform the linguistic adtrees of the statements that are involved in the argument into argumentative adtrees. Such a transformation permits to represent the linguistic and pragmatic information that is relevant for the evaluation of the argument under scrutiny.
By indicating how to apply CxAdGrams to the reconstruction of various argument types, we have further extended its analytical potential to pragmatic aspects of discourse. In doing so, we have shown that CxAdGrams is not only suitable for the purpose of analysing and representing aspects of language itself, but also of the way in which language is used in communication (i.c., the persuasive efforts that are characteristic of argumentative discourse).
While the analytical tools developed in argumentation theory mostly produce selective representations of premises and conclusions, our reconstruction procedure reveals linguistic and pragmatic information in greater detail. It therefore helps in providing a more fine-grained analysis of the linguistic aspects of statements that are used in arguments. The latter is important for the subsequent evaluation of the quality of the argumentation, because the ‘point of attack’ of a particular argument may be found in a single word instead of in a complete proposition.
Current research in argumentation theory usually separates the analysis of the external organisation of an argument—the so-called ‘argumentation structure’—from its internal organisation—the so-called ‘argument scheme’. By developing the notion of argumentative adtree, we have provided an instrument that enables an integrated analysis of these two aspects of argumentative discourse. The whole endevour is represented in Table 6. In particular, the argumentative discourse can be analyzed on different levels of aggregation: the micro-level of a single argument (argument scheme), the meso-level of a complex configuration of arguments (argumentation pattern or structure), and the macro-level of complete argumentative texts or discussions—or even argumentative corpora—within specific domains of discourse (rhetorical genres). In this paper, we have explained a method for representing arguments on the micro-level. However, given the features of CxAdGrams, in particular the recursive nature of adtrees, this method can be extended for both the meso- and the macro-levels. More in general, CxAdGrams provide a way to represent punctuation as conjunctions between sentences, thus they permit to represent a whole text in the terms of a single, comprehensive adtree. The implementation of annotated corpora—starting from the GSC—represents the macro-level. Such an annotated corpus could be a huge adtree representing the concatenations of all arguments and relevant linguistic material, such as expressives or declarations, supporting the arguments themselves—for an example, see again Shakespeare’s example mentioned at the end of Section 4.
Table 6
Different levels of aggregation of Adpositional Argumentation
| Level | Unit |
| Micro | Single argument (scheme) |
| Meso | Complex argumentation structures and patterns |
| Macro | Argumentative genres and corpora |
AdArg is research in progress and therefore it should pass experimental validation when it reaches a sufficient mature form. In the current stage of development, we are annotating a whole real-world argumentative speech to test the robustness of the approach and to get feedback on what could be the next steps. In the long run annotated corpora will be at disposal. In order to reach such a goal, the building of corpora should be supported by a tool that implements the formal linguistic model in computational terms. In our view, such a tool would assist the analyst in making decisions regarding what linguistic and pragmatic pieces of information to include in specific reconstructions of argumentative discourse. Thanks to the combination of the linguistic and pragmatic information included in our framework with example-based data extracted from past analyses, the aim is to partially automatize the whole procedure using Artificial Intelligence techniques, verified through robust empirical data.
Notes
1 J.H.M. Wagemans, Argument Type Identification Procedure (ATIP), Published online January 28, 2019, http://periodic-table-of-arguments.org/argument-type-identification-procedure.
2 See the official web site: J.H.M. Wagemans, Periodic Table of Arguments: The building blocks of persuasive discourse. Published online December 9, 2017, http://periodic-table-of-arguments.org.
3 For a figure of the PTA version 2.4 as a whole and other examples analysed in detail, see the official web site of the PTA: J.H.M. Wagemans, Periodic Table of Arguments: The building blocks of persuasive discourse. Published online December 9, 2017, http://periodic-table-of-arguments.org.
4 See also the official web site: J.H.M. Wagemans, Periodic Table of Arguments: The building blocks of persuasive discourse, http://periodic-table-of-arguments.org.
5 The number of dependents of each governor gives the structure of the adtree, which is defined by the Tesnerian concept of valency. Readers unfamiliar with the original concept of valency are referred to Tesnière’s fundamental book, either in French [24] or in its English translation [25]. The relation between Tesnerian structural syntax and CxAdGrams is clarified in Gobbo and Benini [11].
6 Such a transformation is formally justified by the so-called conjugate construction in the formal model of CxAdGrams—see Definition B.1.4, p. 211 in Gobbo and Benini [10].
7 The LaTeX package adtrees is part of the standard CTAN repository: M. Benini and F. Gobbo, adtrees—Macros for drawing adpositional trees.
8 In adtrees, some branches are longer than others just for human readability. Their symbolic representation does not consider these typographical details. See the bottom of Fig. 14.
Acknowledgments
This paper is the result of a research collaboration between the founders of CxAdGrams, Federico Gobbo and Marco Benini, and the initiator of the Periodic Table of Arguments, Jean H.M. Wagemans. Gobbo and Benini are mostly responsible for Section 4, Wagemans for Section 3, whereas all other sections are the result of a collaborative effort.
References
[1] | Adjukiewicz. K. , Die syntaxische Konnexität, Studia Philosophica 1: ((1935) ), 1–27. |
[2] | Visser J. , Duthie R. , Lawrence J. , Reed. C. , Intertextual correspondence for integrating corpora, In: CalzolariN. ChoukriK. CieriC. DeclerckT. GoggiS. HasidaK. HitoshiIsahara H. MaegaardB. MarianiJ. MazoH. MorenoA. OdijkJ. PiperidisS. TokunagaT.. (eds.) LREC 2018 Workshops Online Proceedings ((2018) ), 3511–3517 . |
[3] | Bench-Capon T.J.M. , Dunne. P.E. , Argumentation in Artificial Intelligence, Artificial Intelligence 171: ((2007) ), 619–641. DOI: 10.1016/j.artint.2007.05.001 |
[4] | Bridges D. , Richman. F. , Varieties of Constructive Mathematics, Cambridge University Press (1987) . |
[5] | Church A. , A formulation of the simple theory of types, Journal of Symbolic Logic 5: ((1940) ), 56–58. |
[6] | Dung. P. , On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and nperson games, Artificial Intelligence 77: ((1995) ), 321–357. |
[7] | Dondio P. , Longo. L. , Computing trust as a form of presumptive reasoning, Warsaw ((2014) ), 274–281. DOI: 10.1109/WI-IAT.2014.108 |
[8] | van Eemeren F.H. , GarssenB.J., KrabbeE.C.W., SnoeckHenkemans A.F., VerheijH.B. and WagemansJ.H.M.. Handbook of argumentation theory, Springer (2014) . |
[9] | van Eemeren F.H. and Snoeck HenkemansA.F., Argumentation Analysis and Evaluation, Routledge (2016) . |
[10] | Gobbo F. , Benini. M. , Constructive Adpositional Grammars. Foundations of Constructive Linguistics, Cambridge Scholars Publishing, (2011) . |
[11] | Gobbo F. , Benini. M. , Dependency and valency. From Structural Syntax to Constructive Adpositional Grammars, Computational Dependency Theory ((2013) ), 113–135. DOI: 10.3233/978-1-61499-352-0-113 |
[12] | Gobbo F. , Wagemans. J.H.M. , Adpositional Argumentation (AdArg): A new method for representing linguistic and pragmatic information about argumentative discourse, Actes JIAF 2019, Toulouse ((2019) ), 101–107. |
[13] | Gobbo F. , Wagemans. J.H.M. , A method for reconstructing first-order arguments in natural language, University of Trento, Proceedings of AIXIA 2018 ((2019) ), 27–33. |
[14] | Gobbo F. , Wagemans. J.H.M. , Building argumentative adpositional trees: Towards a high precision method for reconstructing arguments in natural language, Proceedings of the 9th Conference of ISSA, University of Amsterdam ((2019) ), 408–420. |
[15] | Kolb. R. , The law of treaties: An introduction. Edward Elgar Publishing (2016) . |
[16] | Longo. L. , Argumentation for knowledge representation, conflict resolution, defeasible inference and its integration with machine learning, Machine Learning for Health Informatics, Springer ((2016) ), 183–208. |
[17] | Longo L. , Dondio. P. , Defeasible reasoning and argumentbased systems in medical fields: An informal overview, 2014 IEEE 27th International Symposium on Computer-Based Medical Systems, IEEE ((2014) ), 376–381. |
[18] | MacLane S. , Categories for the Working Mathematician, 2nd edition, Graduate Texts in Mathematics 5, Springer (1998) . |
[19] | Mitkov R. (ed.), The oxford Handbook of computational Linguistics, Oxford University Press, ((2012) ). DOI: 10.1093/oxfordhb/9780199276349.013.0014 |
[20] | Nenkova A. , McKeow. K. , Automatic Summarization, Foundations and Trends in Information Retrieval 2-3: ((2011) ), 103–233. |
[21] | Modgil S. , Budzynska K. , Lawrence. J. , Computational Models of Argument, Proceedings of COMMA 2018, ((2019) ). |
[22] | Rizzo L.M. and LongoL.. Representing and inferring mental workload via defeasible reasoning: A comparison with the NASA Task Load Index and the Workload Profile, Proceedings of the 1st Workshop on Advances In Argumentation In Artificial Intelligence AI3@AI*IA, CEURS ((2017) ), 126–140. |
[23] | Searle. J. , Making the social world. The structure of human civilization, Oxford University Press, (2010) . |
[24] | Tesnière. L. , Éléments de Syntaxe Structurale, Paris, Klincksieck, (1959) . |
[25] | Tesnière. L. , Elements of Structural Syntax, (OsborneT. and KahaneS., Trans.), Amsterdam, John Benjamins, (2015) . |
[26] | Toulmin. S. , The uses of argument, Cambridge University Press, (1958) . |
[27] | The Univalent Foundations Program, Homotopy Type Theory: Univalent Foundations of Mathematics, Princeton, Institute of Advanced Studies, (2013) . |
[28] | Wagemans. J.H.M. , Four basic argument forms, Research in Language 17: ((2019) ), 57–69. DOI: 10.2478/rela-2019-0005 |
[29] | Wagemans. J.H.M. , Assertoric syllogistic and the Periodic Table of Arguments, Argumentation and Inference: Proceedings of the 2nd ECA, ((2018) ), 1–14. |
[30] | Wagemans. J.H.M. , Analogy, similarity, and the Periodic Table of Arguments, Studies in Logic, Grammar and Rhetoric 55: ((2018) ), 63–75. DOI: 10.2478/slgr-2018-0028 |
[31] | Wagemans J.H.M. , Constructing a Periodic Table of Arguments, Argumentation, Objectivity, and Bias:, Proceedings of the 11th International Conference of OSSA ((2016) ), 1–12. |
[32] | Walton D.N. , Reed C. , Macagno. F. , Argumentation Schemes, Cambridge University Press, (2008) . |
[33] | Wissler L. , Almashraee M. , Monett D. , Paschke. A. , The Gold Standard in Corpus Annotation, 5th IEEE Germany Student Conference ((2014) ). DOI: 10.13140/2.1.4316.3523 |




