Research on community evolution based on node influence and multi-attribute fusion

1.Introduction

The community evolution refers to changes such as the merging, splitting and forming of virtual communities in social networks. The events that may occur over time in virtual communities in the network will lead to dynamic evolution of the structure of virtual communities [1]. Therefore, how to effectively improve the accuracy of identifying community evolution events and evolution paths is of great value to the application of implied group structure analysis and public opinion early warning in social networks. For example, in a disease transmission network, by identifying and tracking multiple affected communities and analyzing the characteristics of communities with high prevalence, trends in disease transmission can be effectively predicted and epidemic prevention and control preparations can be made in advance. In the E-commerce platform network, through the evolution trend of community structure between online buyers and commodities to predict the buyers of different commodities to purchase degree, to achieve the purpose of formulating the corresponding supply strategy. In the rumor information transmission network, the social influence brought by rumor transmission can be reduced by analyzing the propagation rules of topics, predicting the spreading trend of topics and taking effective measures in time.

As an important problem in dynamic social network analysis, the relevant methods of community evolution can be divided into three categories: community evolution analysis algorithm based on point coincidence degree, edge coincidence degree and core node. Among them, the idea based on point coincidence degree is to cut the dynamic network into a series of static time slice networks, use the community detection algorithm to identify the community structure in the time slice network, and distinguish the evolutionary events between communities in the adjacent time slice [2, 3]. The idea of edge coincidence degree is that the influence of edges on the internal topology of communities is considered. Firstly, the network community structure of different time slices is found by using relevant methods, and then the evolutionary relationship is determined by searching the maximum edge coincidence degree between communities at different time points on the time axis [4, 5]. The idea of the core node is to discover the core node of the community by detecting the continuous and stable connection between nodes, and at the same time track the evolution path of the community structure with the incremental calculation method [6, 7, 8].

Although the above research has achieved a good application effect, there are still the following problems that make the low accuracy of similar community identification results:

In order to solve the above problems, the similarity between communities from the perspective of the internal topology is evaluated, the obtained community topology with the calculation process of node influence is combined, and the similarity between communities from the two aspects of community stability and community difference is judged. Therefore, an evolution model EMNI based on node influence is proposed in this paper. The model can effectively improve the accuracy of identifying community evolution events and provide a basis for the subsequent research on community structure evolution prediction. The contributions of this paper are as follows:

2.Related works

In recent years, with the in-depth research on community evolution, similarity determination, as the main method of community evolution identification, has obtained different research results. Yu et al. [9] based on community similarity, introduced community activity parameters and discriminated evolutionary events by combining similarity and activity. Yang et al. [10] analyzed the similarity between communities by Jaccard coefficient, and studied the evolutionary characteristics of users in social networks by analyzing the characteristics of individuals newly added to communities. Chen et al. [11] proposed a community detection algorithm based on dynamic mechanism, which defined the similarity between nodes and clustered them into different evolutionary communities according to the evolution of node states over time. Nie et al. [12] studied the relationship between the stability of network structure and dimension during the evolution of emergencies, obtained the implied time features in the network according to the Jaccard correlation dimension, and verified the relationship between phase changes of emergencies and Jaccard distance matrix. Kaveh et al. [13] proposed a new mapping based community evolution identification method ICEM and tracking the different transformation characteristics of communities over time. This method maps each node to a (T,C) pair and sets observation time window T and community C. The performance advantage of the algorithm is verified on 17 public datasets.

In the evolution of community structure, the characteristics of key nodes can influence the evolution events. Therefore, many scholars have combined the characteristics of core nodes with similarity determination to study community evolution. Dhouiou et al. [14] determined the category of evolutionary events by defining and analyzing the changes of core nodes. Karan et al. [15] described the evolution process of community topological structure based on the intensity and frequency of interaction between nodes and the degree of overlap between different communities. Wang et al. [16] proposed a dynamic overlapping community evolution recognition algorithm based on topological potential field, and tracked community evolution events based on changes of core nodes in the topological potential field. Yang et al. [17] judged the differences between communities according to the core vertex set, and studied the types of community evolution from two aspects of similarity and difference. Feng et al. [18] proposed a community similarity discrimination method combining deep learning with core nodes to study community evolution and prediction.

In order to improve the accuracy of identifying community evolution events, many scholars proposed the method of constructing community evolution framework or evolution model for different applications. Zhang et al. [19] proposed an improved event framework, defined various evolutionary events based on the framework, studied the community structure and community evolutionary events on prediction models of different evolutionary events, and achieved good results in advertising recommendation and public opinion guidance. Narimene et al. [20] divided the dynamic network into a series of time frames and discussed how to select an appropriate network segmentation scale to improve the accuracy of evolutionary prediction. Experiments with the proposed framework on Facebook and Higgs Twitter datasets verify the role of network fragmentation events in predicting community evolution. Yu et al. [21] converted the three tasks of sequential community detection, evolution analysis and link prediction into a unified framework and extracted the evolution pattern, and an evolution model framework based on orthogonal nonnegative matrix factorization was proposed to analyze and predict the time-varying structure of dynamic networks from local and global perspectives. Experiments on real and artificial networks verify the advantages of the proposed framework in dynamic network analysis tasks. Ye et al. [22] introduced the balanced label propagation algorithm (BLPA) to solve the problems of fragmented topic evolution and insufficient network evolution in specific DBLP data sets, and extracted mobile author nodes and corresponding community topics, as well as mobile author node topics based on community discovery. Using the research method of vertical theme distribution and horizontal theme evolution, the interactive mechanism and law of theme evolution and structure evolution were analyzed. Qiao et al. [23] proposed an evolutionary analysis framework based on strong and weak events for the lack of consideration of “weak events” occurring in small communities in community evolution events. The framework proposed the constraints of “weak contraction”, “weak expansion”, “weak merge” and “weak split”, and verified the feasibility of the framework. Yu et al. [24] proposed an evolutionary Bayesian non-negative matrix decomposition model (EvoBNMF) to analyze the community structure with evolutionary characteristics. By introducing evolutionary behavior, the model quantified the transition intensity of the community between adjacent snapshots and verified the performance advantages of the method in sequential community detection. Etienne et al. [25] analyzed the shortcomings of modeling and forecasting methods for critical events, designed a sliding window analysis method based on the historical information of community changes, and proposed a model to simulate the evolution of community structure by using autoregressive mode. In addition, by analyzing the structural characteristics, network scale and temporal characteristics of social networks, and combining with the historical information of community evolution events, a framework based on supervised learning was proposed to identify and track evolution events, which can effectively improve the accuracy of community evolution prediction [26, 27].

In conclusion, the existing research method based on similarity or evolutionary framework which ignored the study of community evolution from the micro level, therefore, “structural characteristics combined with node properties”, that is, mining global characteristics and local characteristics of community structure, and integrating the core node attributes to study the community evolution is proposed in this paper, to improve recognition accuracy of evolutionary events.

3.Community similarity discrimination method based on multi-attribute fusion

To analyze the evolution of the community of the dynamic network, an appropriate time window according to the data interval and the collection duration is selected, and the time slice processing for the dynamic network is cut. Then, for each time slice, Louvain [28]community discovery algorithm and the similarity comparison strategy to compare the similarity of adjacent time slice communities are adopted. Finally, the evolutionary events are identified by event detection algorithm.

A dynamic network is considered as a collection of a series of static networks, which is divided into static networks according to time slices, so the dynamic network is expressed as G={G1,G2,…,Gi,…,Gn}, where Gi=(Vi,Ei) represents the static network at the i-th moment, Vi and Ei represents the nodes set and edges set in the network Gi respectively. The community set divided by time slice network Gt at time t is described as Ct={Ct1,Ct1,…,Ctk}, k represents the number of communities on the network at this time slice.

4.Community evolution model EMNI

5.Experimental results and analysis

The three experimental data sets are selected, and the social network graph formed by the experimental data sets is used to conduct experiments on the EMNI model. The effects of EMNI model on identifying various evolutionary events in different data sets are discussed. In order to verify the validity of the EMNI model, which is compared with three representative community evolution algorithms. The open source real dynamic network datasets are as follows:

In order to reduce the influence of noise and ensure the validity of identification results of community evolution. The community with less than 3 nodes was deleted.

5.1Community division results

The time window division of dynamic network data requires community discovery of each time slice network. The community division results of Hepth, Enron and Bitcon datasets are as Fig. 1.

Figure 1.

Community division results.

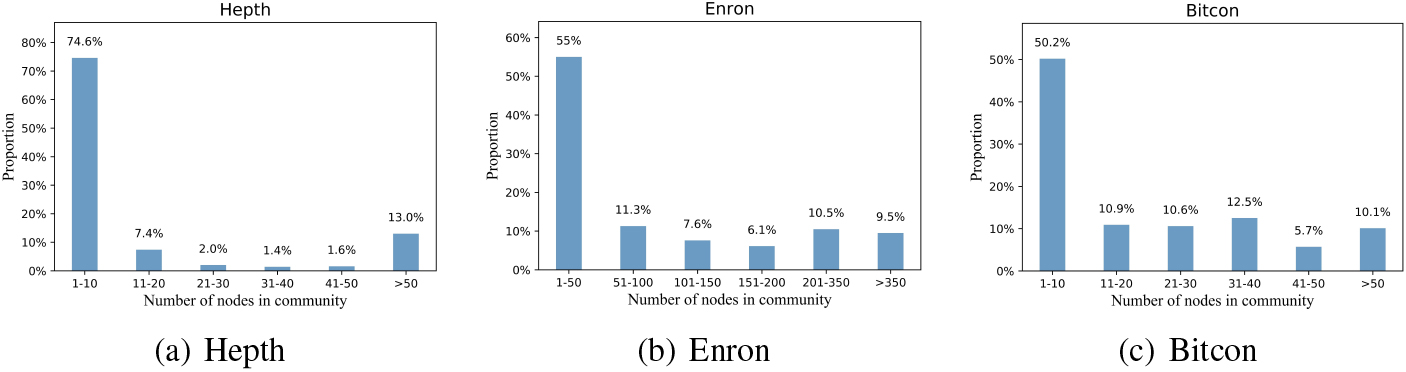
As can be seen from the results of community division, most communities in Hepth data set are small communities with less than 10 nodes, accounting for 74.6%, while communities with more than 50 nodes account for 13%, which is a representative small community data set. In Enron’s data set, 55% of communities have 1–50 nodes, 33.5% have 51–350 nodes, and 9.5% have more than 350 nodes, which represent large community datasets. The number of community scale of the Bitcoin data set is between the Hepth data set and the Enron data set. It can be seen from Figure 1, the data sets selected have different scales and different node distribution characteristics, which can better verify the evolution characteristics in different data sets.

5.2Classification results of community evolution

In EMNI evolution model, the parameter α is the threshold of the degree of difference, β is the threshold of the degree of stability, and γ is the threshold of the allowable community fluctuation range. As the value of γ, 90% of fixed nodes and 10% of floating nodes are more in line with the real network evolution, so the value of experiment γ is 0.1. Take different values for α and β, and compare the experimental results.

5.2.1Hepth data set

Set the value range of parameter α to 0.1–0.5, with 0.1 as the incremental value, and the value range of parameter β to 0.2–0.4, with 0.05 as the incremental value. Take different values for α and β, and the influence of parameters on the number of evolutionary events are shown in Fig. 2. The Stack diagram of event effects of different parameters is shown in Fig. 3.

Figure 2.

The influence of parameters α and β on the number of evolutionary events.

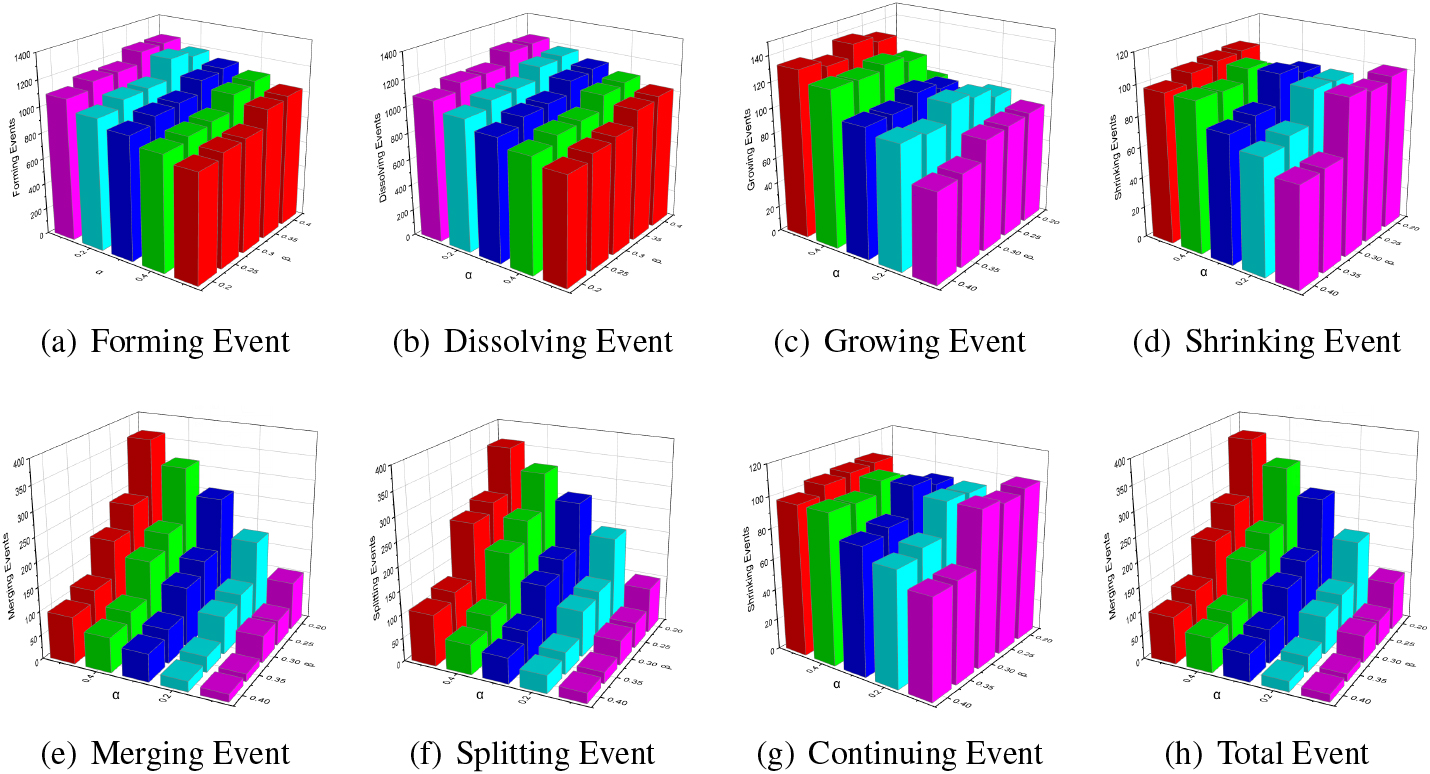
Figure 3.

Stack diagram of event effects of different parameters.

The number of evolutionary events in different parameter values is shown in Table 2. As the increases of parameter α value, the number of Growing and Dissolving evolutionary events gradually decreases, while the number of other evolutionary events gradually increases. With the increase of parameter β value, he number of Growing and Dissolving evolutionary events gradually increase, Merging and Splitting gradually decrease, while the number of Growing, Shrinking and Continuing evolution events will reach the maximum when the value is 0.3. Finally, as the variation range of the total number of evolution events recognized with the change of parameters is not large, the value of 0.5 and 0.3 are taken as the best parameter values, and the distribution of each evolution event is relatively balanced at this time.

Table 2

Number of evolution events under different parameter values

α	β	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
0.1	0.2	1096	1081	90	101	101	97	13	2579
0.2	0.2	1012	1009	97	82	176	194	15	2585
0.3	0.2	951	941	89	83	256	260	17	2597
0.4	0.2	886	875	98	89	312	314	15	2589
0.5	0.2	832	820	108	86	363	360	16	2585
0.1	0.25	1152	1138	89	98	53	54	13	2597
0.2	0.25	1070	1064	105	100	93	108	18	2558
0.3	0.25	1006	1000	106	101	150	163	18	2544
0.4	0.25	920	931	122	96	196	235	15	2515
0.5	0.25	870	867	133	107	245	263	16	2501
0.1	0.3	1153	1136	88	101	56	52	13	2599
0.2	0.3	1079	1073	109	101	79	98	18	2557
0.3	0.3	1022	1015	111	106	124	137	17	2532
0.4	0.3	942	947	127	105	165	192	17	2495
0.5	0.3	880	894	138	106	195	243	16	2472
0.1	0.35	1244	1234	73	66	16	24	10	2667
0.2	0.35	1171	1165	95	80	33	47	16	2607
0.3	0.35	1118	1109	103	87	71	74	15	2577
0.4	0.35	1064	1056	123	97	91	90	14	2535
0.5	0.35	1008	1002	128	104	120	125	14	2501
0.1	0.4	1250	1239	71	65	16	22	9	2672
0.2	0.4	1189	1184	98	75	22	38	14	2620
0.3	0.4	1140	1130	103	83	58	55	15	2584
0.4	0.4	1090	1076	124	98	73	64	15	2540
0.5	0.4	1029	1024	133	98	98	109	15	2506

In order to verify the effect of identifying evolutionary events, the evolutionary event classification results obtained by EMNI model are compared with GED [29], PCET [30] and SGCI [31] models, and the parameters used in the comparison model are determined according to the optimal parameters given in the original experiment. The balanced of event distribution and the number of identified communities are used to compare and analyze different models. The experimental results are shown in Table 3.

Table 3

Comparison of evolution results of Hepth data set

Model	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
EMNI	880	894	138	106	195	243	16	2472
GED	854	848	93	21	10	4	1	1831
PCET	–	1126	129	75	52	36	38	1456
SGCI	–	90	64	33	119	110	6	422

In terms of the number of communities identified, compared with the other three models, EMNI can identify more evolutionary events, 26%, 41% and 83% more than GED, PECT and SGCI models, respectively. In particular, it is superior to other models in the identification of Growing, Shrinking, Merging, Splitting and Continuing events. The reason is that ENMI model, when discriminating the similarity between communities, combines the internal structure characteristics of communities with the attribute characteristics of nodes from the micro level, and obtains more node structure information through DeepWalk.

In terms of the balanced of event distribution, different combinations of evolutionary events are randomly selected to verify their distribution equilibrium, and the optimal distribution equilibrium of various combinations of evolutionary events is discussed for comparison by many experiments. As can be seen from Table 3, the PECT model and SGCI model do not define Forming events, and the proportion of Continuing events identified in the continuous time slice is small in the four models. In additional, the SGSI model only identifies stable communities, that is, only the communities that appear continuously in more than three time slices are analyzed, the Dissolving events identified are far smaller than other models. Taking four combinations of Growing, Shrinking, Merging and Splitting for example, the proportion distribution among the identified evolutionary events is shown in Fig. 4.

Table 4

Number of evolution events under different parameter values

α	β	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
0.5	0.2	319	237	75	58	156	154	29	1028
0.5	0.25	343	253	78	65	121	105	34	999
0.5	0.3	365	276	73	68	100	84	34	1000
0.5	0.35	409	319	77	67	61	41	33	1007
0.5	0.4	432	345	79	62	43	26	29	1016

Figure 4.

The result of the event distribution.

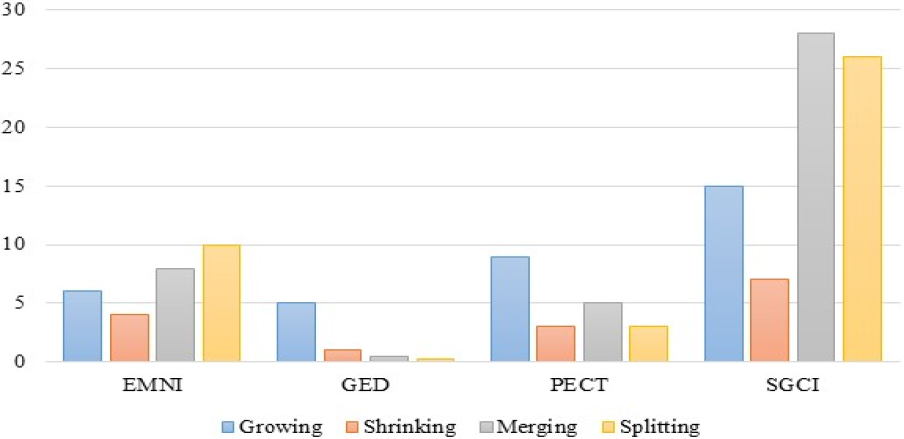
As can be seen from Fig. 4, GED model has poor performance in the identification effect of evolutionary events and the balanced of event distribution in networks with many small communities. PCET model has a good effect on the identification of Continuing events, but identify fewer Merging and Splitting events. The reason is that PCET model considers the community variability in the identification of Continuing events, but considers the number of the same nodes in the two communities in the identification of community similarity. The SGCI model is poor in identifying Dissolving events in communities with more instabilities in the data set. Compared with other models, EMNI model has obvious advantages in identifying the balanced distribution and the number of evolutionary events.

5.2.2Enron data set

In the Enron data set, the settings of parameters α and β are the same as those of the data set Hepth, the influence of parameters on the number of evolutionary events are shown in Fig. 5, and the stack diagram of event effects of different parameters is shown in Fig. 6. The partial data of the number of evolutionary events under different parameters are shown in Table 4, when the value of is α 0.5 and β the value of is 0.3 as the optimal parameter value, the distribution of each evolution event is relatively balanced.

Figure 5.

The influence of parameters α and β on the number of evolutionary events.

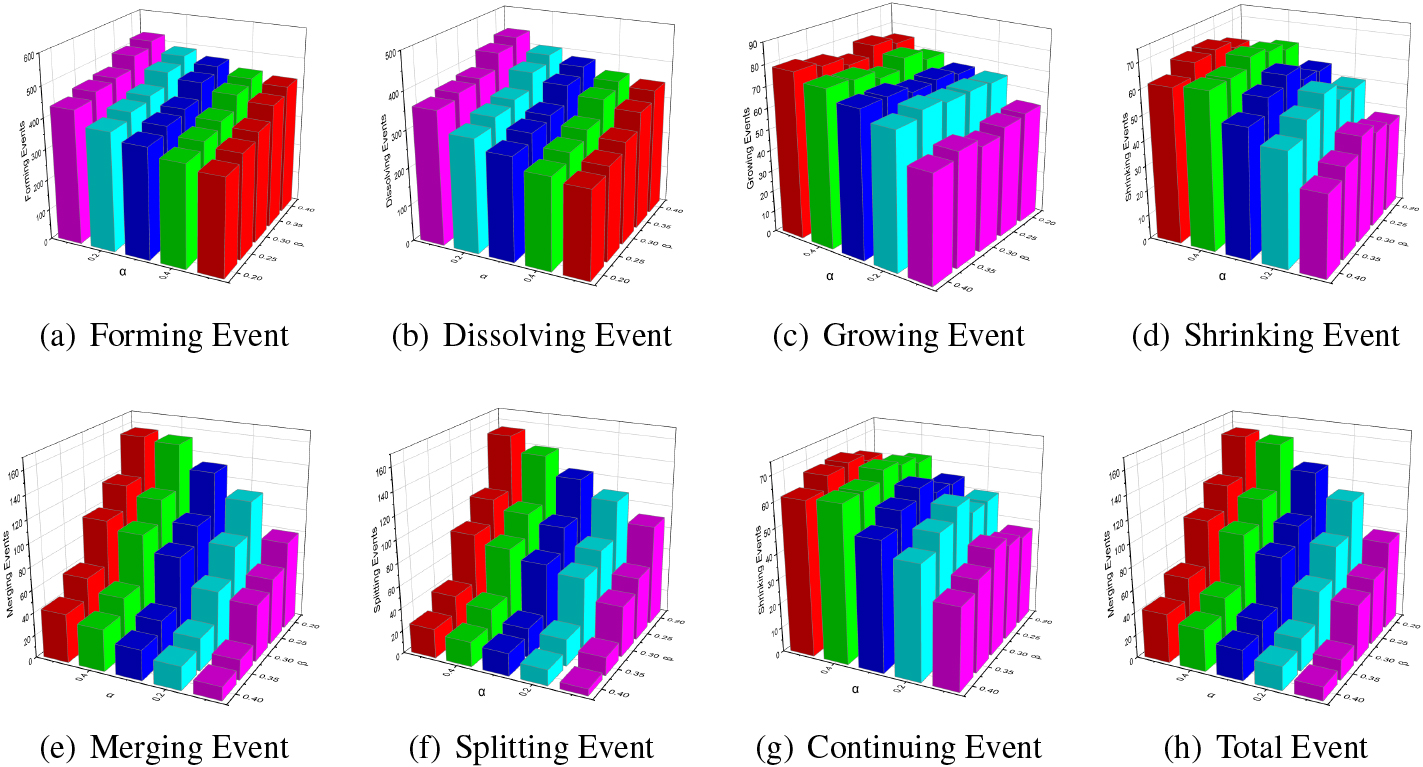
Figure 6.

Stack diagram of event effects of different parameters.

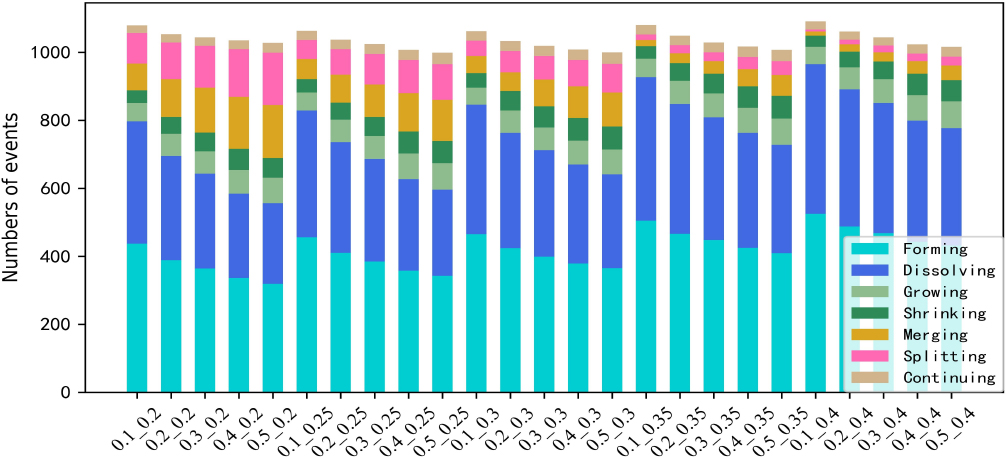
It can be seen from Table 5, the community evolution model EMNI recognizes more evolutionary events, and the distribution of the recognized events is relatively balanced. GED model has poor identification effect on Merging, Splitting and Continuing events. The performance of the PECT model on the Enron data set is similar to the Hepth data set. It can better identify other evolutionary events, but it is less effective in the recognition of Merging and Splitting events. The SGCI model is used to identify the stable communities lasting more than three time slices. It can be seen that the communities in the data set change rapidly, and more communities do not continue to exist in the dynamic network. There, SGCI model has the poor performance in identifying the balanced distribution and the number of evolutionary events.

Table 5

Comparison of evolution results of Enron data set

Model	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
EMNI	365	276	73	68	100	84	34	1000
GED	345	259	51	42	4	2	15	718
PCET	–	325	97	65	22	24	50	583
SGCI	–	61	51	42	23	16	11	227

5.2.3Bitcon data set

In Bitcon data set, the value range of parameter α to 0.1–0.5, with 0.1 as the incremental value, and the value range of parameter β to 0.2–0.4, with 0.05 as the incremental value. The influence of parameters on the number of evolutionary events are shown in Fig. 6, and the stack diagram of event effects of different parameters is shown in Fig. 7. The partial data of the number of evolutionary events under different parameters are shown in Table 6, when the value of α is 0.5 and the value of β is 0.25 as the optimal parameter value, the distribution of each evolution event is relatively balanced.

Table 6

Number of evolution events under different parameter values

α	β	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
0.5	0.2	94	94	9	38	30	63	98	426
0.5	0.25	133	134	9	45	32	29	44	426
0.5	0.3	165	165	8	38	28	12	26	442
0.5	0.35	197	189	7	30	23	8	11	465
0.5	0.4	216	216	4	24	20	4	6	490

Figure 7.

The influence of parameters α and β on the number of evolutionary events.

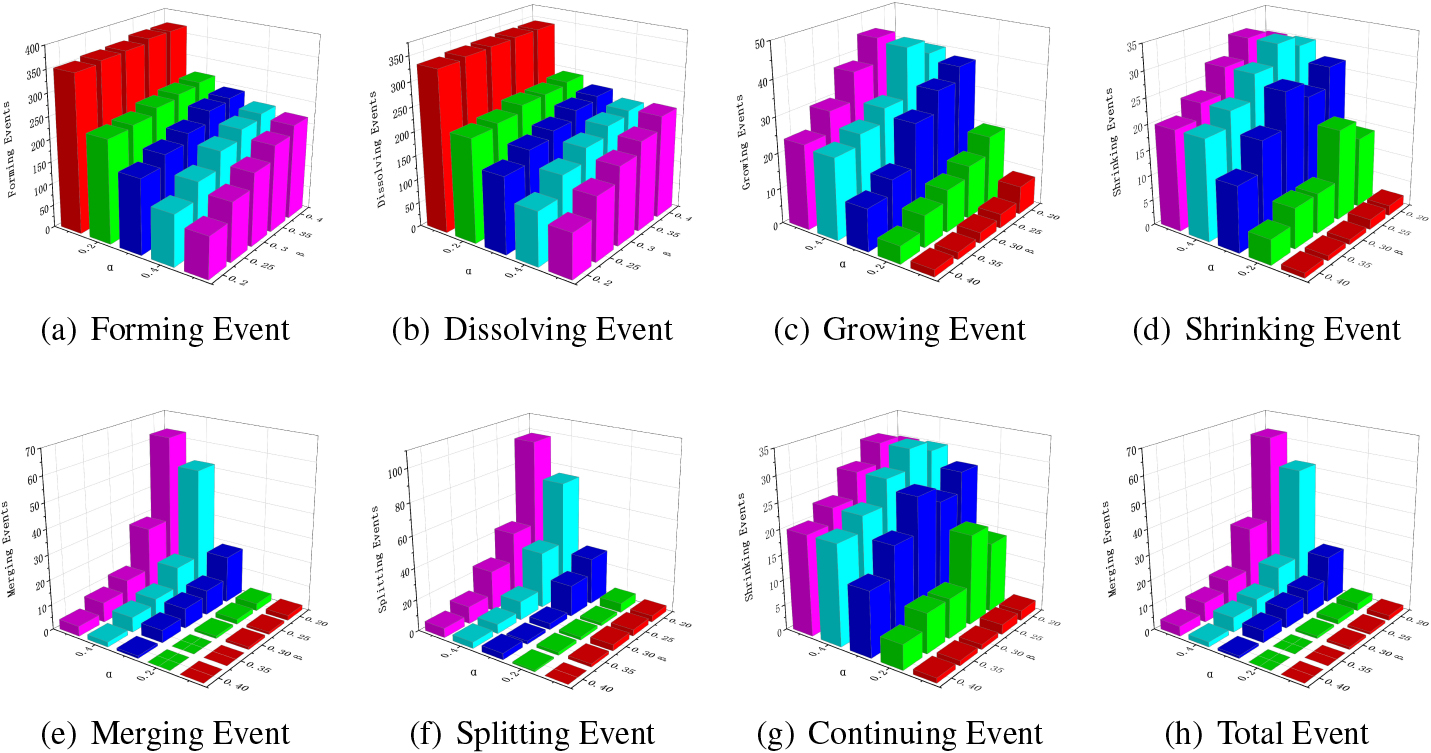
Table 7

Comparison of evolution results of Bitcon data set

Model	Forming	Dissolving	Growing	Shrinking	Merging	Splitting	Continuing	Total
EMNI	133	134	9	45	32	29	44	426
GED	190	192	21	15	0	2	5	425
PCET	–	223	49	31	16	23	30	372
SGCI	–	192	15	15	0	0	5	227

Figure 8.

Stack diagram of event effects of different parameters.

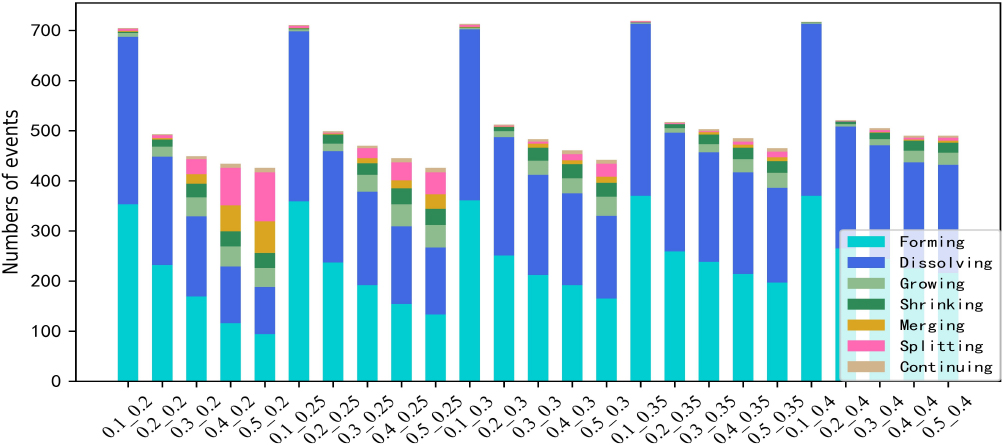
In summary, EMNI model has achieved good results in data sets with different data distributions and scale. The similarity discrimination method, which combines the internal structure of community with node attributes, improves the identification accuracy and the balance of event distribution of community evolution events.

6.Conclusion

In order to improve the identification accuracy of community evolutionary events, an evolutionary event detection model EMNI that combines node attribute information with community internal structure features is proposed in this paper. Firstly, the influence of nodes is evaluated based on topological structure of nodes, and the relationship between local clustering coefficient of nodes and influence of nodes is discussed. Secondly, the similarity between communities is calculated by multi-attribute fusion of community stability and difference, and the relationship between the threshold of stability and difference is analyzed, as well as the influence on the evolution process of communities. Finally, seven types of evolutionary events in the EMNI model are redefined and described based on the similarity discrimination formula between communities. Verification on real data sets shows that: (1) Compared with other models, ENMI model can improve the identification accuracy of community evolution events and the distribution balance of community evolution events, which accords with the results of real community evolution events; (2) The community evolution events identified by the threshold parameters of community stability and difference are different.

By setting the optimal threshold parameters reflecting the community structure and node attribute characteristics, the combination of multi-attribute fusion community internal structure and node characteristics can improve the accuracy of similarity determination between communities is verified from the micro level, and a basis for accurately identifying the evolution events between communities provided in this paper. Since community evolution events may occur in different dimensions and non-adjacent event slices, it is the future work to identify the evolution events occurring in communities between non-adjacent time slices, extract and analyze the characteristics of different dimensions in the process of community evolution, and predict the evolution trends.