3D reconstruction based on hierarchical reinforcement learning with transferability
Abstract
3D reconstruction is extremely important in CAD (computer-aided design)/CAE (computer-aided Engineering)/CAM (computer-aided manufacturing). For interpretability, reinforcement learning (RL) is used to reconstruct 3D shapes from images by a series of editing actions. However, typical applications of RL for 3D reconstruction face problems. The search space will increase exponentially with the action space due to the curse of dimensionality, which leads to low performance, especially for complex action spaces in 3D reconstruction. Additionally, most works involve training a specific agent for each shape class without learning related experiences from others. Therefore, we present a hierarchical RL approach with transferability to reconstruct 3D shapes (HRLT3D). First, actions are grouped into macro actions that can be chosen by the top-agent. Second, the task is accordingly decomposed into hierarchically simplified sub-tasks solved by sub-agents. Different from classical hierarchical RL (HRL), we propose a sub-agent based on augmented state space (ASS-Sub-Agent) to replace a set of sub-agents, which can speed up the training process due to shared learning and having fewer parameters. Furthermore, the ASS-Sub-Agent is more easily transferred to data of other classes due to the augmented diverse states and the simplified tasks. The experimental results on typical public dataset show that the proposed HRLT3D performs overwhelmingly better than recent baselines. More impressingly, the experiments also demonstrate the extreme transferability of our approach among data of different classes.
1.Introduction
3D reconstruction is important in field of engineering, such as CAD/CAE/CAM, 3D printing, virtual reality/augmented reality, and so on. The classic methods are to learn a deep neural network that outputs 3D models directly from images or predicts implicit functions. However, they are not interpretable or cannot obtain a detailed reconstruction process.
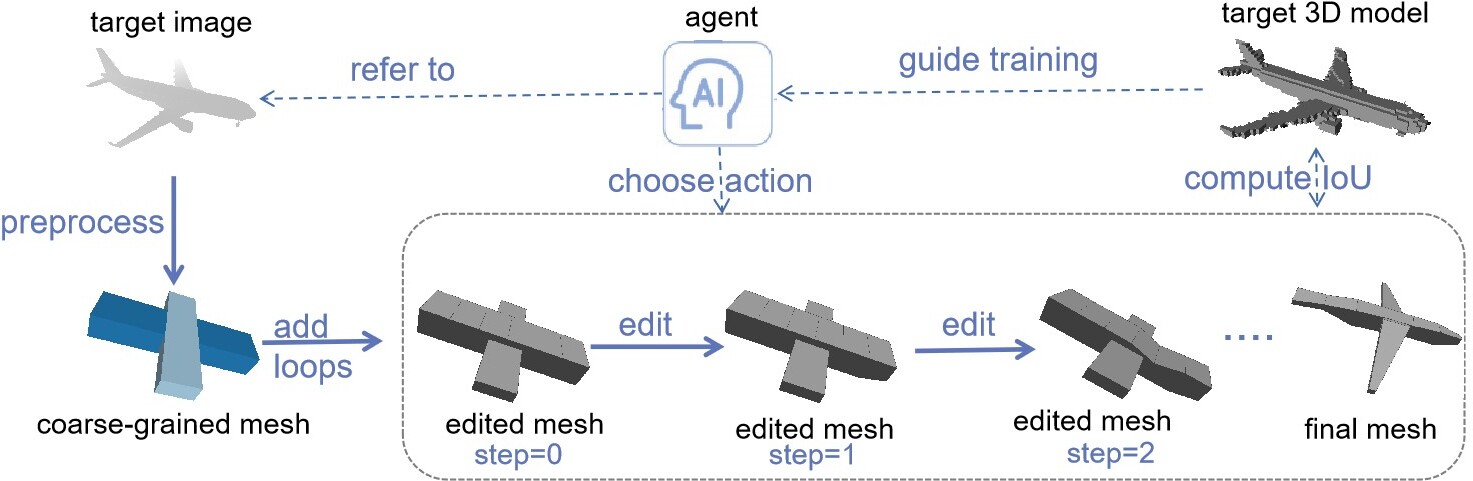
Figure 1.
The process of reconstructing the target image into final mesh step by step. First, the coarse-grained mesh is obtained and loops are added. Then the agent chooses action to edit mesh by referring to the target image. The IoU between target 3D model and the edited mesh guides the training of the agent so that it can choose more appropriate actions.
To make the reconstruction process interpretable, Lin et al. [1] proposed an reinforcement learning (RL) method that mimics human modelers. The agent is trained to reconstruct a mesh model by selecting a series of actions, which are defined as the movement of vertices in the original coarse-grained mesh. However, problems still exist in there. It is a complex issue to simultaneously decide which vertex to edit and how to edit it, especially when there are many vertices to be edited. The complex action space leads to low reconstruction accuracy since it will increase the search space exponentially. The agent cannot determine a reasonable action until enough of the environment has been explored. In addition, agents for data of different classes are trained without learning knowledge from other related experiences. In reality, people usually make decisions with the aid of previous experiences. Similarly, the learning agent will usually require less exploration if it is guided by transferred knowledge.
To solve the abovementioned problems, we present a hierarchical RL approach with transferability to reconstruct 3D shapes (HRLT3D). The HRL is adapted into 3D reconstruction for the first time, aiming to simplify the reconstruction action space and establish more general sub-agents. Generally, modelers first perceive which part of the shape needs to be edited, and then decide how to edit it. Therefore, primitive actions are grouped into macro actions, each of which affects a part of the shape. The top-agent chooses a macro action, and then the related sub-agent selects a primitive action that is grouped in the macro action. It is the cooperation between a higher-level decision-maker (top-agent) and a lower-level executor (sub-agent), where the former controls the direction from a global perspective, and the latter considers the local optimum. In addition, the sub-agent based on augmented state space (ASS-Sub-Agent) is proposed to replace a group of sub-agents, where the distinctive features of each sub-task are taken as the augmentation of the state. It promotes training efficiency benefiting from fewer parameters and the shared learning process. Furthermore, the augmentation enriches the features of states, thus increasing the diversity of the state distribution. Consequently, the ASS-Sub-Agent is easier to generalize to data of other classes. It transfers knowledge from the source tasks, thus benefiting the performance of the target tasks [2].
Our main contributions can be summarized as follows:
• To the best of our knowledge, this is the first work to adapt HRL to 3D reconstruction. Agents can achieve better reconstruction accuracy due to action simplification.
• We propose a novel ASS-Sub-Agent to accelerate the agent training. In addition, it increases the diversity of state distribution and improves transferability.
The rest of this paper is organized as follows. In Section 2, some related works of 3D reconstruction, hierarchical reinforcement learning and transfer learning are provided. Then, the proposed method is introduced in Section 3. In Section 4, the results of reconstruction and transferability are demonstrated on different datasets. Finally, the conclusion and future works are provided in Section 5.
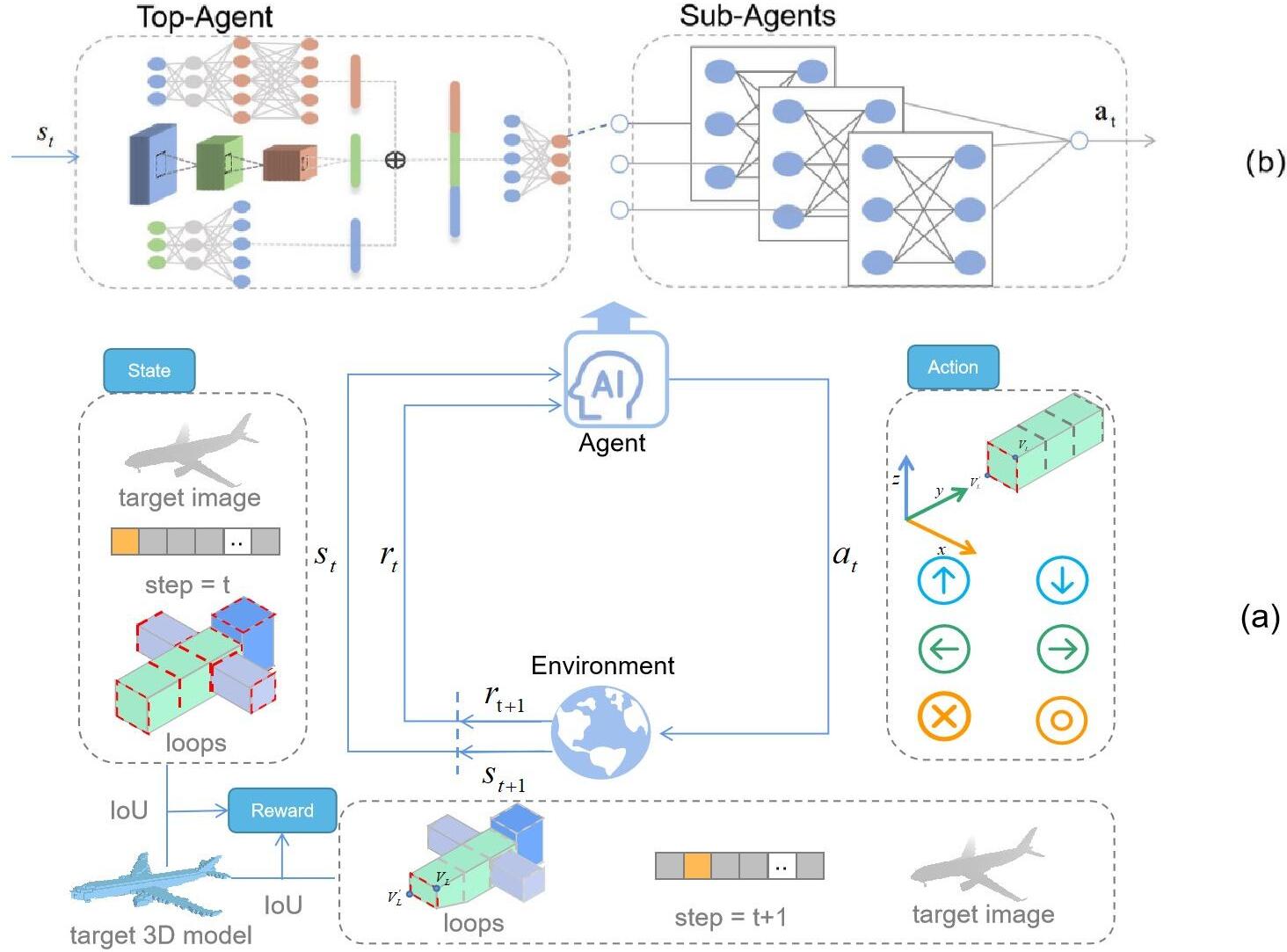
Figure 2.
Framework Overview. (a) is the process of RL, the agent maps the observed state to action. The state
2.Related work
Many methods have been proposed to reconstruct 3D models from images. The development of CAD software promotes 3D reconstruction [3, 4, 5, 6]. However, it is usually suitable for professional modelers only. In recent years, with the development of deep learning [7, 8, 9, 10], the 3D reconstruction method combined with deep learning has gained attention. A typical method is to directly output 3D models from images by training a neural network [11, 12, 13, 14, 15]. Another popular method recently is to learn a neural network which approximates the implicit function [16, 17, 18, 19, 20, 21]. Besides, methods based on generative adversarial network (GAN) have been applied to 3D shape reconstruction or style reconstruction after making significant progress in 2D generation [22, 23, 24, 25, 26]. These methods have accomplished remarkable results, but they lack interpretability or cannot provide a detailed step-by-step reconstruction process. This makes it difficult to apply the reconstructed models to the field of engineering. In engineering ,using existing knowledge or models can greatly shorten the development cycle [27, 28, 29], and interpretability makes them more reliable and usable [30, 31, 32].
Researchers have attempted to recognize the modeling process by deep neural networks, which can increase the flexibility of model reuse [33, 34]. However, it usually requires synthetic data for the network training. Others generate mesh models according to the given points [35, 36]. First, they generate the coarse-grained mesh model and the error for each vertex contained in the mesh model is calculated. The vertices are then edited according to the error. However, these methods require the given points for the error calculation. RL has been widely used in traffic [37, 38, 39, 40, 41, 42, 43, 44], engineering [45, 46, 47], and health care [48]. For 3D reconstruction, it can provide interpretable reconstruction process step-by-step by simulating human modelers. The human-simulated method can help solve many problems in engineering [49], and may in turn help human modelers become better [50]. In addition, it can train the network according to the reward given by the environment without supervision. Lin et al. [1] proposed a two-step method for 3D shape reconstruction using reinforcement learning (RL): (1) approximate a rough mesh shape and (2) edit the mesh to create a detailed shape. Seiya et al. [51] introduced an encoder-decoder network for the problem of fixed viewpoint in [1]. Although these methods are promising in terms of interpretability, the complex action space of editing the vertices of meshes has become an obstacle to achieving high accuracy since optimization essentially refers to finding an appropriate action sequence in the search space [52]. Moreover, learning without considering previous related experiences may lead to higher sample complexity [53]. HRL has the potential to accomplish a complex task by decomposing it into simpler sub-tasks through a hierarchy of agents. The most popular HRL methods include feudal learning [54], hierarchical abstract machines [55], MAXQ [56], and options framework [57, 58, 59]. Sutton et al. [57] first proposed the options framework, where a set of actions is considered as an option. In the options framework, an option
The combination of transfer learning (TL) and RL has attracted considerable attention from researchers in order to improve the efficiency of RL, such as policy distillation [63, 64], and learning from demonstrations [65, 66], and so on. The combination of various methods can compensate for each other’s shortcomings [67, 68]. However, the knowledge of complex agents can easily fail to be transferred since the inconsistent state distribution among data of different classes, worse still may result in negative impact. Researchers have tried to improve the transferability by decomposing the agent into more reuseable sub-agents [69, 70, 71]. Tessler et al. [69] learned reusable skills for solving tasks in Minecraft through a hierarchical approach.
Frans et al. [70] developed a meta learning approach based on hierarchically structure, where sub-agents were learned and switched between different tasks. These methods indicate the potential of hierarchical ideas in promoting transferability. However, none of these techniques have been applied to 3D reconstruction.
3.The proposed approach
3.1Framework overview
As shown in Fig. 1, the goal is to reconstruct a 3D shape as similar to the target 3D model as possible from the provided target image. First, obtain the coarse-grained mesh through heuristic [36] or deep learning methods [1], and then add loops on it. Second, the agent is trained to choose an editing action at each step to edit the mesh. This paper focuses on better training of the agent. The intersection over union (IoU) between the edited mesh and the target 3D model is calculated at each step. If the IoU increases after editing, the agent’s decision is encouraged; otherwise, it will be punished. The agent is constantly trained through trial and error.
As shown in Fig. 2a, the agent observes the current state
Figure 2b describes the option hierarchical framework. The agent can be decomposed into the top-agent and a set of sub-agents. The top-agent chooses an option, and then the option-related sub-agent will decide to execute which action. To simplify the training of sub-agents, we proposed ASS-Sub-Agent to replace the set of sub-agents. The details of the option hierarchical framework and ASS-Sub-Agent are described separately in Sections 3.3 and 3.4. Finally, Section 3.5 will show how to transfer knowledge to other classes.
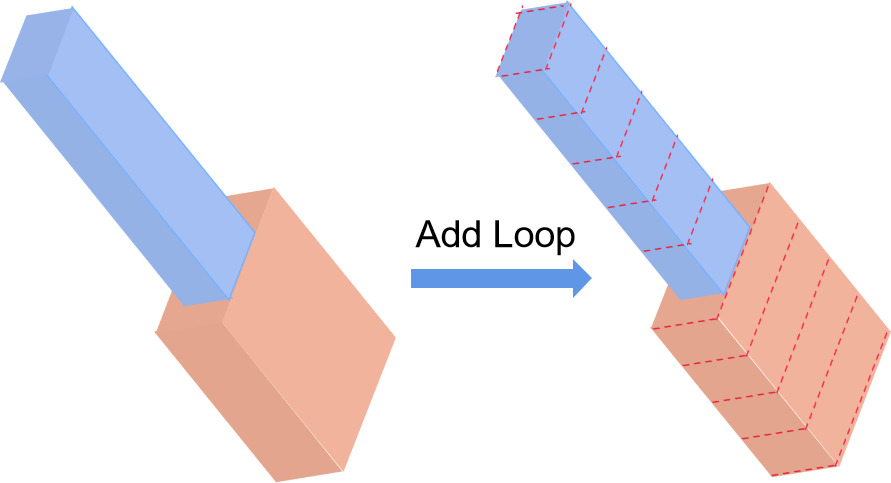
Figure 3.
We assign
3.2Reinforcement learning modeling
In this subsection, the details of state, action and reward are described.
The proposed approach focuses on adjusting a coarse-grained mesh to have more details according to the provided target image. The coarse-grained mesh is composed of several cuboids, which do not have any loops at first. For further editing, the coarse-grained mesh is subdivided by adding loops [72]. The loop is a rectangle on the cuboid surface, in which the plane is vertical to the longest cuboid side. Here, we assign n loops
Finally, the IoU can be used as a metric of the similarity between the edited mesh and the target 3D model. Accordingly, the reward is the increment of IoU after an action is executed. The use of the metric that is highly relevant to human perception can intrinsically optimize the training of the model [73].
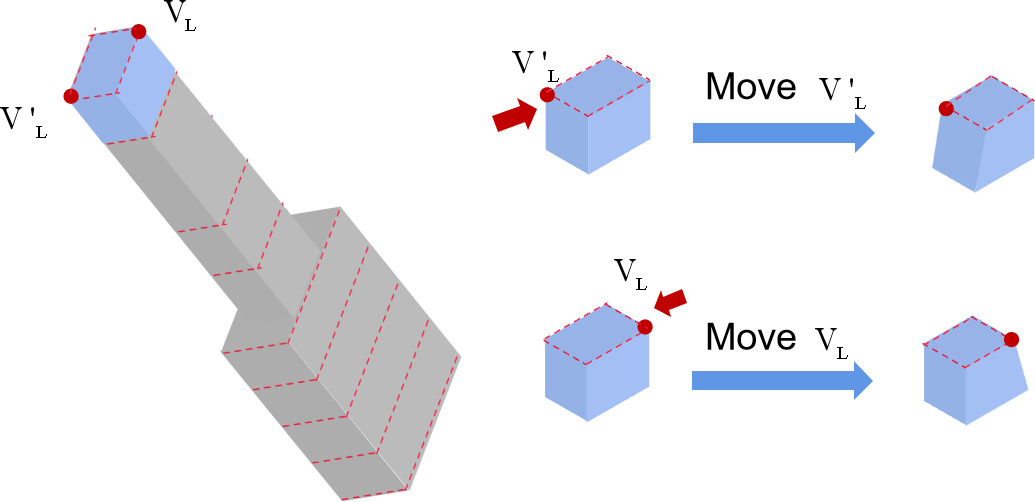
Figure 4.
For one loop, the movements of two corner vertices
3.3Hierarchical options framework
To define our problem as one that can be handled hierarchically, we are inspired by the options framework [57, 58], which first chooses an option, and then selects an action based on the current option. For a coarse-grained mesh, the HRLT3D first observes which part is the most different from the target shape, and then decides how to adjust it. In this stage, each loop can represent one part of the original mesh. Therefore, we group the actions operating on one loop into a macro action, equivalently referred to as an option. Therefore, 36
The agents are trained by updating the value function
(1)
where
(2)
To simplify training, we set
The sub-agents are trained using double deep Q-network (DDQN) [77]. The DDQN using double agents to learn value function, current agent and target agent. For option
(3)
where
(4)
(5)
Figure 5.
The triple can be the input of top-agent, which will output an option related with loop index. The features of the loop as the augmentation of state are inputted into ASS-Sub-Agent, which decides how to operate on this loop.
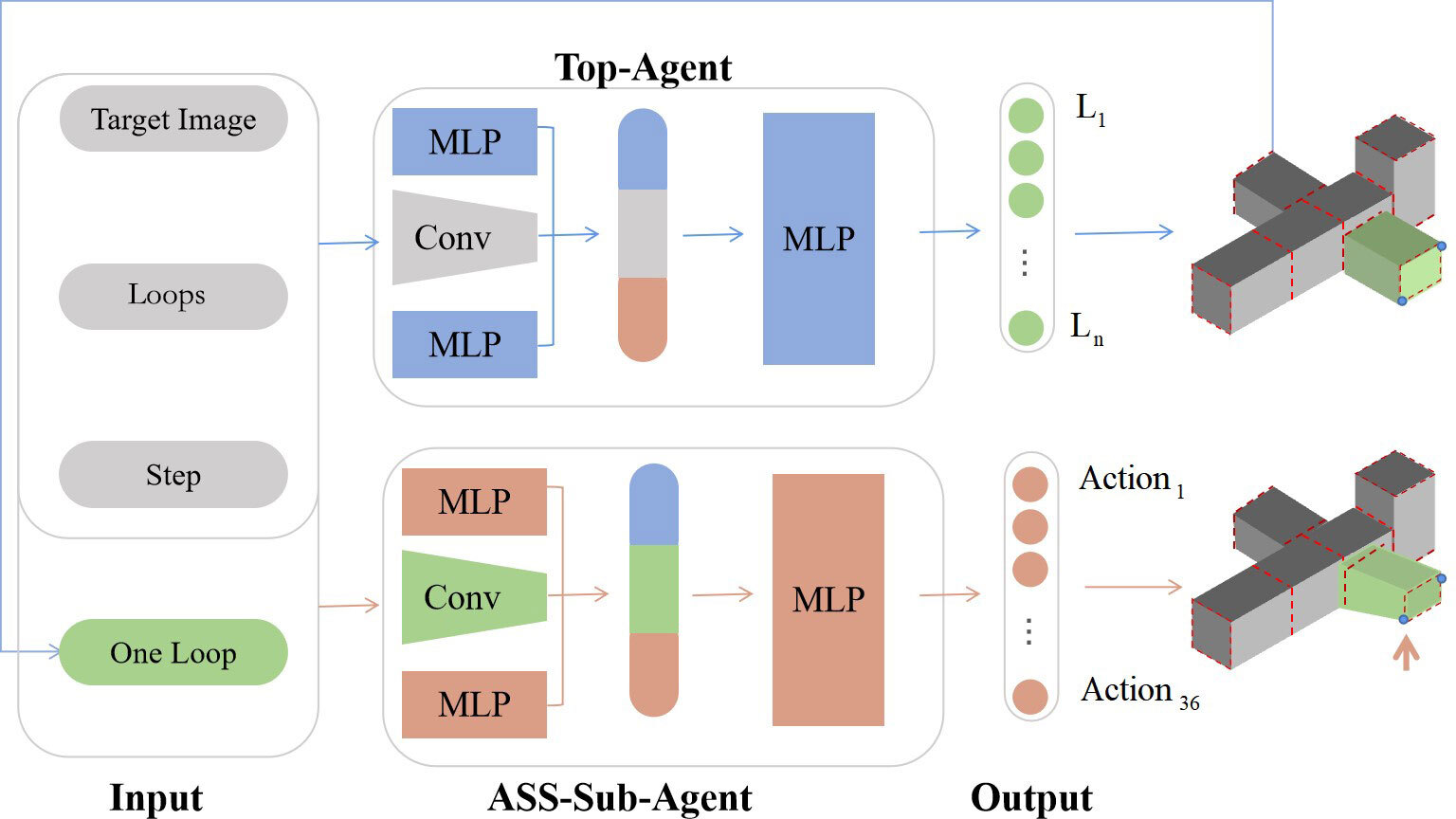
3.4ASS-Sub-Agent
Although the options framework can simplify the action space for each agent, the training parameters are increased since we need to learn the sub-agent for each option. Note that the sub-agents for different options are dealing with the same kind of problem except different loops are to be operated. It is feasible to use an agent to implement the functions of a set of sub-agents. In order to identify which option is being operated on, we propose to train a sub-agent based on an augmented state space (ASS-Sub-Agent) by incorporating the distinctive features of options as part of the state. In this stage,
Bacon et al. [58] posed that an augmented state may lead to a larger state space, resulting in a poor learning effect. In contrast, an augmented state can promote our learning and transfer for the following two reasons. First, the training process can be shared by ASS-Sub-Agent, which speeds up learning. Second, the diversity of states makes the agent more general to data of other classes.
3.5Transfer learning based on the hierarchical framework
Transfer learning can promote learning efficiency by using existing knowledge [78, 23]. Most transfer learning based on the hierarchical framework trains a set of sub-agents on source data and then reuse them on target data. The top-agent is retrained for each different data point when to execute which sub-agent. We follow a similar architecture, and the details are shown in the pseudocode of Algorithm 3.5.
Transfer learning based on hierarchical framework[1] Initialize the top-agent
To transfer the trained agent from the source data to the target data, the key step is to initialize the parameters of the top-agent and ASS-Sub-Agent. Consistent with the classic method, the proposed transfer procedure retrains the top-agent through random initialization parameters, and reuses the parameters of ASS-Sub-Agent. The experience
4.Experiments and analysis
Table 1
Quantitative results comparison with recently related methods. We report the average accumulated rewards R and the final similarity evaluated by IoU on each class
| Airplane | Car | Guitar | |||||
|---|---|---|---|---|---|---|---|
| Method | IoU | R | IoU | R | IoU | R | |
| GAN-based | 3D-GAN (NIPS, 2016) [22] | 0.302 | – | 0.614 | – | 0.375 | – |
| ASTA3D (WACV, 2022) [26] | 0.319 | – | 0.589 | – | 0.463 | – | |
| RL-based | DDQN (AAAI, 2016) [77] | 0.166 | 0.484 | 0.002 | 0.284 | ||
| Lin et al. (ECCV,2020) [1] | 0.314 | 0.135 | 0.605 | 0.123 | 0.493 | 0.184 | |
| Seiya et al. (VISIGRAPP,2022) [51] | 0.252 | 0.073 | 0.579 | 0.096 | 0.409 | 0.099 | |
| Ours (DDQN) | 0.353 | 0.174 | 0.644 | 0.162 | 0.508 | 0.199 | |
| Ours | 0.378 | 0.199 | 0.649 | 0.167 | 0.527 | 0.218 | |
Figure 6.
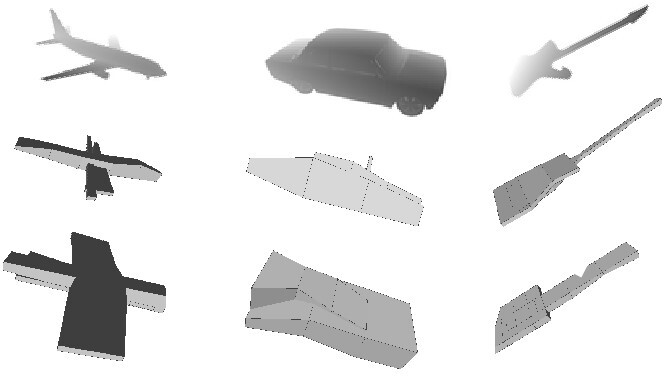
Qualitative results of our method, RL-based baseline [1] and GAN-based baseline [22]. The first row shows the target images. The second row and the third row show the mesh results of RL-based baseline and the voxel results of GAN-based baseline separately. The last row is our mesh results.
![Qualitative results of our method, RL-based baseline [1] and GAN-based baseline [22]. The first row shows the target images. The second row and the third row show the mesh results of RL-based baseline and the voxel results of GAN-based baseline separately. The last row is our mesh results.](https://content.iospress.com:443/media/ica/2023/30-4/ica-30-4-ica230710/ica-30-ica230710-g006.jpg)
4.1Experimental settings
The proposed method is based on RL, so we compare it with two recent RL-based baselines [1, 51], which are published in 2020 and 2022 in this filed. The work [1] is an important first stepping stone towards 3D reconstruction by RL. All the RL-based methods use the framework of DDQN [77]. In addition, the GAN-based methods [22, 26] that are promising in the field of 3D reconstruction are compared. The proposed method is unsupervised, where the target 3D models are used only for calculating the IoU. For fair comparisons, 3D-GAN [22] uses the target 3D models only as real objects for the training of the discriminator. ASTA3D [26] directly reconstructs 3D models from 2D images through a differentiable renderer without requiring 3D target models.
This paper follows the dataset from [1, 51], which is the first public dataset since 2020 for this topic. It has three classes: airplanes, cars, and guitars. Each of class contains 650 shapes, where 600 are used for training and 50 are used for testing. In addition, the Fusion 360 Gallery dataset [80] is also used to verify the effectiveness of the proposed method. The Fusion 360 Gallery dataset has rich 2D and 3D geometric data coming from CAD models. We extract 1000 sets of data, which are the pairs of 2D target images and the target 3D models. Among them, 900 are used for training and 100 are used for testing.
For the parameter settings, we set the discounted factor
All of the experiments are trained and tested under the same hardware and software. The model is trained on a single NVIDIA RTX 3090 GPU , the main memory is 64 GB, and the CPU clock frequency is 2.5–4.4 GHz. The network model is implemented on Python 3.6 and PyTorch 1.9.1. The training of our model takes 15 minutes per epoch for the class airplane, car and guitar and 25 minutes for the Fusion 360 Gallery datasets. We trained 200 epochs for each class.
4.2Reconstruction experiments and analysis
In this subsection, we compare the reconstruction results, which use the cumulative reward
Table 2
The accumulated reward improvement of our method over the state-of-art method
| Lin et al. | Ours | Improvement | Rate | |
|---|---|---|---|---|
| Airplane | 0.135 | 0.199 | 0.064 | 47.4% |
| Car | 0.123 | 0.167 | 0.044 | 35.7% |
| Guitar | 0.184 | 0.218 | 0.028 | 15.2% |
Table 3
The standard deviation of the accumulated reward over the state-of-art method
| Method | Airplane | Car | Guitar |
|---|---|---|---|
| Lin et al. | 0.052 | 0.034 | 0.046 |
| Ours | 0.051 | 0.023 | 0.024 |
Table 4
Quantitative results comparison with recently related methods on Fusion 360 Gallery dataset
| Method | IoU | |
|---|---|---|
| GAN-based | 3D-GAN (NIPS, 2016) [22] | 0.155 |
| ASTA3D (WACV, 2022) [26] | 0.141 | |
| RL-based | DDQN (AAAI, 2016) [77] | 0.098 |
| Lin et al. (ECCV,2020) [1] | 0.143 | |
| Ours | 0.208 |
To intuitively compare the improvement, we list the cumulative reward improvement of our method over Lin et al. [1], which is the state-of-art method recently in this field. As shown in Table 2, our method improved by 47.4%, 35.7% and 15.2% on airplanes, cars and guitars respectively.
Table 3 shows the standard deviation of the accumulated reward, which can reflect the stability of the training. We can see that our method achieves a smaller standard deviation among the three classes.
Figure 6 displays the qualitative results, where the mesh model reconstructed by our method is visually closer to the target image. As shown in Table 4 and Fig. 7, the quantitative and qualitative results of the Fusion 360 Gallery dataset are still better than those of the baselines. Although the objects in the Fusion 360 Gallery dataset do not belong to the same class, which makes the learning of the neural network more difficult, our method has achieved relatively good results in terms of quantity and quality.
Figure 7.
Qualitative results of our method, RL-based baseline [1] and GAN-based baseline [22] on Fusion 360 Gallery dataset. The first row shows the target images. The second row and the third row show the mesh results of RL-based baseline and the voxel results of GAN-based baseline separately. The last row is our mesh results.
![Qualitative results of our method, RL-based baseline [1] and GAN-based baseline [22] on Fusion 360 Gallery dataset. The first row shows the target images. The second row and the third row show the mesh results of RL-based baseline and the voxel results of GAN-based baseline separately. The last row is our mesh results.](https://content.iospress.com:443/media/ica/2023/30-4/ica-30-4-ica230710/ica-30-ica230710-g007.jpg)
Table 5
Quantitative performance between our method and the baseline under different greedy probabilities. Three groups of experiments are conducted and the source class data for each are listed in brackets
| Airplane (Car) | Car (Airplane) | Guitar (Airplane) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | Type of | JP | PE | AP | JP | PE | AP | JP | PE | AP |
| Lin et al. [1] | Fixed | 0.011 | 0.042 | 0.042 | 0.037 | 0.101 | 0.102 | 0.021 | 0.112 | 0.131 |
| Incremental | 0.007 | 0.081 | 0.081 | 0.001 | 0.143 | 0.148 | 0.148 | 0.152 | ||
| Ours | Fixed | 0.062 | 0.156 | 0.198 | 0.118 | 0.185 | 0.185 | 0.041 | 0.179 | 0.219 |
| Incremental | 0.047 | 0.192 | 0.198 | 0.067 | 0.179 | 0.182 | 0.043 | 0.207 | 0.222 | |
Figure 8.
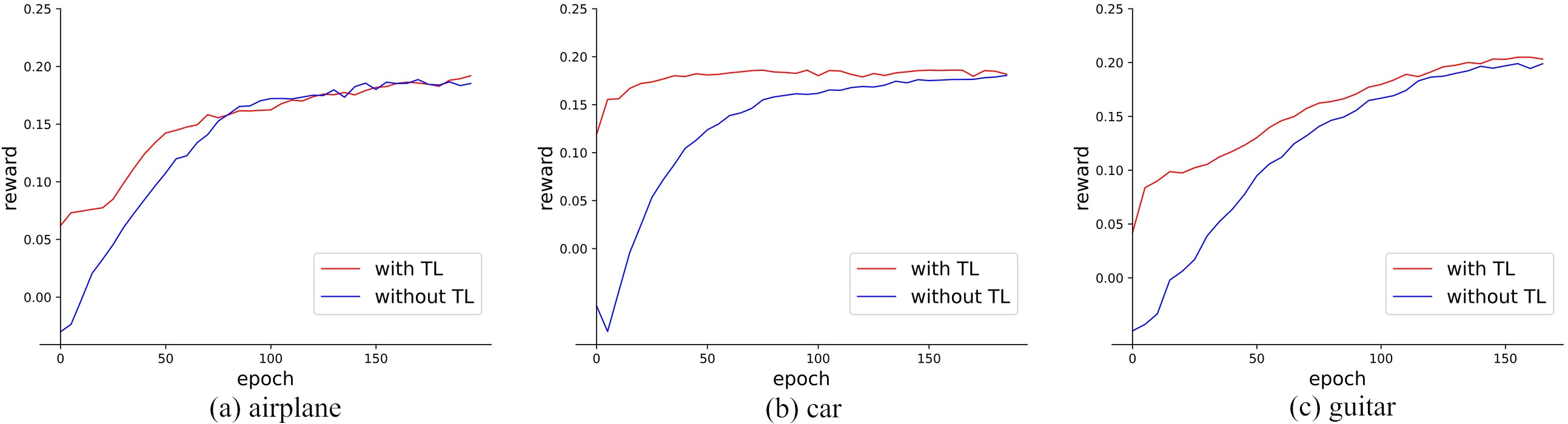
Comparison of our method with and without transfer on three classes. The charts show the change of cumulative reward with the training epoch. The orange line represents the change of our method with transfer, and blue one is else.
4.3Transferability experiments and analysis
In addition to the performance improvement, in this subsection, we confirm the transferability of HRLT3D. That is, we train the top-agent and the ASS-Sub-Agent on source class data first. Then, we re-train the top-agent and fine-tune the ASS-Sub-Agent on the target class data. Finally, we test the performance on target class data. Specifically, we conduct three groups of experiments compared with the state-of-art RL-based method [1]. We use the following representative metrics [81, 82] to evaluate transfer performances:
• Jumpstart Performance (JP): the initial performance (reward).
• Asymptotic Performance (AP): the ultimate performance (reward).
• Performance after specific training Epoch (PE): We get the performance (reward) after 100 epochs.
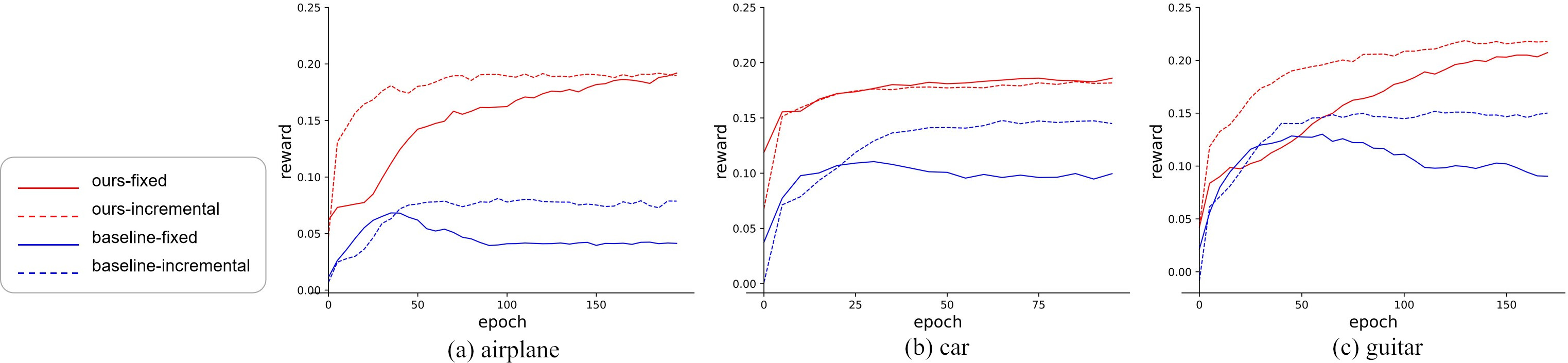
At first, we show the impact of training with transfer in Fig. 8. The orange line represents the test result changing with the training epoch, while the blue line is that without transfer. As we can see, agent with transfer can explore better JP, and it can converge to a fairly or even better AP. To demonstrate that our method improves the transferability, we also compared the effects of our method and baseline with transferred knowledge obtained from source class data. Besides, different greedy probabilities will affect the exploration of the environment, and correspondingly affect the transfer results. Therefore, two kinds of greedy probabilities are explored, which are the fixed probability of 0.98 and the incremental probability increasing linearly from 0.5 to 0.98. Table 5 quantifies the transfer learning performances of our method and the baseline under different probabilities. We carried out three groups of experiments, and the source class data for each are listed in brackets. It can be seen from the Table 5 that our method under fixed or incremental greedy probability can achieve better results. We use Mann-Whitney
Figure 9.
Comparison of the transferability between our method and baseline on three classes. The charts show the change of cumulative reward with the training epoch. The orange lines represent the change of our method with transfer learning, and blue lines represent the change of baseline with transfer learning. The solid lines represents the use of fixed greedy probability, and the dotted lines represent the use of incremental greedy probability
4.4Ablation study
Ablation study of ASS-Sub-Agent. To demonstrate the impact of ASS-Sub-Agent, we compare the qualitative results of our method with and without ASS-Sub-Agent in Fig. 10. The second row shows our results with ASS-Sub-agent. Apparently, under the same number of training epochs, the training results with ASS-Sub-Agent are better than those without it. Because the sub-agents cannot share the training process without ASS-Sub-Agent and each sub-agent is trained for only
Table 6
Ablation study of hyperparameters. The test values are smaller and greater than the selected value, and the result is relative to us
| Hyper-parameter | Value | Result | Value | Result |
|---|---|---|---|---|
| Discounted factor | 0.5 | 1.0 | ||
| Greedy probability | 0.5 | 1.0 | ||
| Loop number | 5 | 20 |
Figure 10.
Qualitative results of the ablation study of ASS-Sub-Agent. The first row shows the target images, the second row and the third row show the mesh results of ours with and without ASS-Sub-Agent separately.
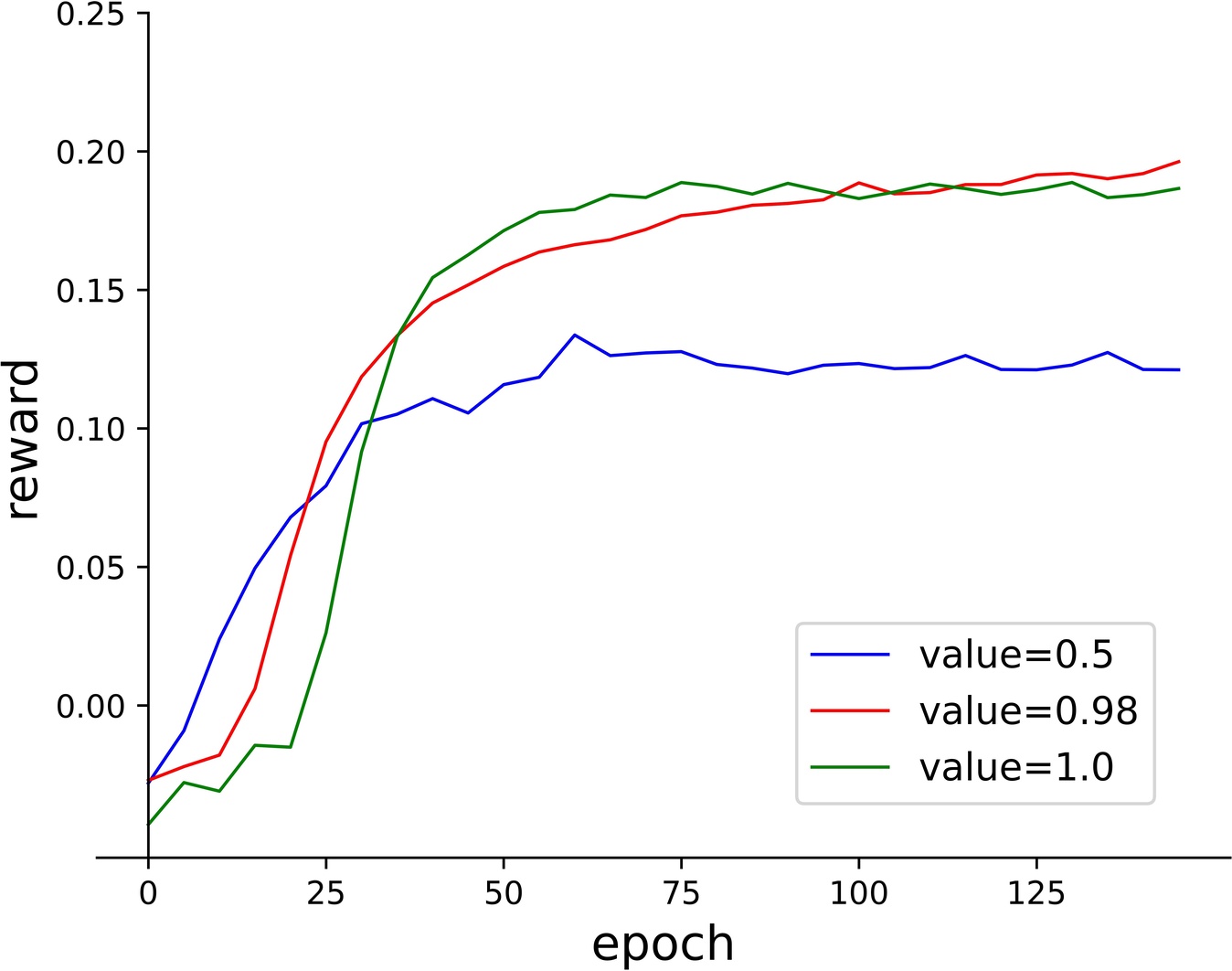
Ablation study of hyperparameters. We refer to the baseline to set the hyperparameters, which can also ensure fairness. To verify the appropriateness of the selected hyperparameters, we performed an ablation study. As shown in the Table 6, we test the values that are smaller and greater than the selected value respectively and obtain relative results. It can be seen that the results with other values are worse than the results with selected values, indicating that the selected values of hyperparameters are reasonable. Specifically, for the discounted factor
Figure 11.
The influence of the greedy probability. The charts show the change of cumulative reward with the training epoch using different probabilities.
5.Conclusion and future works
This paper aims to simplify the complex action space in the RL-based 3D reconstruction method and improve the transferability of the agent. The proposed HRLT3D firstly adapted HRL into 3D reconstruction. Specifically, the action space is hierarchically divided into which loop can be edited and how to edit the loop, and they are determined by the top-agent and the related sub-agent respectively. To promote the training efficiency and transferability of sub-agent, we trained it based on an augmented state space. The experimental results showed that the proposed HRLT3D significantly improved the reconstruction performance and transferability.
However, the proposed method still has limitations and needs more future works. The reconstruction resolution is limited to the number of loops. For the future works, we hope to reconstruct 3D shapes with higher resolution (more loops). Considering the transferability of the proposed method, it is possible and efficient to transfer the agent trained in lower resolution data to the reconstruction of higher resolution. In addition, we will extend our work with other advanced learning methods for fast learning, such as parallel computing [83], neural dynamic classification algorithm [84], dynamic ensemble learning algorithm [85], finite element machine [86], and contrastive learning [87, 88]. Moreover, since the actions defined in this paper can be executed by CAD software, the CAD software can be used as an environment to interact with agents. However, the type of action is defined only as the movement of vertices, which cannot satisfy the real needs of CAD software. In the future, more action types could be added to allow richer operations. Finally, for the datasets, other classic 3D datasets [89, 90] that contain 2D images and corresponding 3D shapes can be utilized. We anticipate that our work could be extended to a wider range of datasets in the future.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant No. 62072348 and 62102268, the Stable Supporting Program for Universities of Shenzhen under Grant 20220812102547001, China Yunnan province major science and technology special plan project (No. 202202AF080004), the Research Foundation of Shenzhen Polytechnic under Grants 6022312044K and 6023310030K. The numerical calculations in this paper have been done on the supercomputing system in the Supercomputing Center of Wuhan University.
References
[1] | Lin C, Fan T, Wang W, Nießner M. Modeling 3d shapes by reinforcement learning. In: European Conference on Computer Vision. Springer; (2020) . pp. 545-61. |
[2] | Liu H, Gu F, Lin Z. Auto-sharing parameters for transfer learning based on multi-objective optimization. Integrated Computer-Aided Engineering. (2021) ; 28: (3): 295-307. |
[3] | Adeli H, Fiedorek J. A MICROCAD system for design of steel connections – II. Applications. Computers & Structures. (1986) ; 24: (3): 361-74. |
[4] | Adeli H, Fiedorek J. A MICROCAD system for design of steel connections – I. Program structure and graphic algorithms. Computers & Structures. (1986) ; 24: (2): 281-94. |
[5] | Chuang LC, Adeli H. Design-independent CAD Window system using the object-oriented paradigm and HP X widget environment. Computers & Structures. (1993) ; 48: (3): 433-40. |
[6] | Adeli H, Yu G. An integrated computing environment for solution of complex engineering problems using the object-oriented programming paradigm and a blackboard architecture. Computers & Structures. (1995) ; 54: (2): 255-65. |
[7] | Rafiei MH, Khushefati WH, Demirboga R, Adeli H. Supervised Deep Restricted Boltzmann Machine for Estimation of Concrete. Aci Materials Journal. (2017) ; 114: (2): 237-44. |
[8] | Hassanpour A, Moradikia M, Adeli H, Khayami R, Babaki PS. A novel end-to-end deep learning scheme for classifying multi-class motor imagery electroencephalography signals. Expert Systems. (2019) ; 36: (6). |
[9] | Martins GB, Papa JP, Adeli H. Deep learning techniques for recommender systems based on collaborative filtering. Expert Systems. (2020) ; 37: . |
[10] | Nogay HS, Adeli H. Machine learning (ML) for the diagnosis of autism spectrum disorder (ASD) using brain imaging. Reviews in the Neurosciences. (2020) ; 31: . |
[11] | Choy CB, Xu D, Gwak JY, Chen K, Savarese S. 3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction. In: European Conference on Computer Vision. (2016) . |
[12] | Fan H, Hao S, Guibas L. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). (2017) . |
[13] | Girdhar R, Fouhey DF, Rodriguez M, Gupta A. Learning a Predictable and Generative Vector Representation for Objects. In: European Conference on Computer Vision. (2016) . |
[14] | Hne C, Tulsiani S, Malik J. Hierarchical Surface Prediction for 3D Object Reconstruction. In: 2017 International Conference on 3D Vision (3DV). (2017) . |
[15] | Song Y, He F, Duan Y, Liang Y, Yan X. A kernel correlation-based approach to adaptively acquire local features for learning 3D point clouds. Computer-Aided Design. (2022) ; 146: : 103196. |
[16] | Mescheder L, Oechsle M, Niemeyer M, Nowozin S, Geiger A. Occupancy Networks: Learning 3D Reconstruction in Function Space. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). (2019) . |
[17] | Mildenhall B, Srinivasan PP, Tancik M, Barron JT, Ramamoorthi R, Ng R. Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM. (2021) ; 65: (1): 99-106. |
[18] | Park JJ, Florence P, Straub J, Newcombe R, Lovegrove S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. In: 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). (2019) . |
[19] | Chibane J, Alldieck T, Pons-Moll G. Implicit Functions in Feature Space for 3D Shape Reconstruction and Completion. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). (2020) . |
[20] | Jiang C, Sud A, Makadia A, Huang J, Funkhouser T. Local Implicit Grid Representations for 3D Scenes. In: 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). (2020) . |
[21] | Ibing M, Lim I, Kobbelt L. 3d shape generation with grid-based implicit functions. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. (2021) . pp. 13559-68. |
[22] | Wu J, Zhang C, Xue T, Freeman B, Tenenbaum J. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. Advances in neural information processing systems. (2016) ; 29: . |
[23] | Bostanabad R. Reconstruction of 3D Microstructures from 2D Images via Transfer Learning. Computer-Aided Design. (2020) ; 128: : 102906. |
[24] | Shi Y, Aggarwal D, Jain AK. Lifting 2d stylegan for 3d-aware face generation. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. (2021) . pp. 6258-66. |
[25] | Liu F, Liu X. 2D GANs Meet Unsupervised Single-View 3D Reconstruction. In: Computer Vision – ECCV 2022: 17th European Conference, Proceedings, Part I. Tel Aviv, Israel: Springer; 2022 October 23-27. pp. 497-514. |
[26] | Petersen F, Goldluecke B, Deussen O, Kuehne H. Style Agnostic 3D Reconstruction via Adversarial Style Transfer. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. (2022) . pp. 3664-73. |
[27] | Qin F, Qiu S, Gao S, Bai J. 3D CAD model retrieval based on sketch and unsupervised variational autoencoder. Advanced Engineering Informatics. (2022) ; 51: : 101427. Available from: https://www.sciencedirect.com/science/article/pii/S1474034621001798. |
[28] | Wang GG, Tan Y. Improving Metaheuristic Algorithms With Information Feedback Models. IEEE Transactions on Cybernetics. (2019) ; 49: (2): 542-55. |
[29] | Wang Y. Controlled kinetic Monte Carlo simulation for computer-aided nanomanufacturing. Journal of Micro and Nano-Manufacturing. (2016) ; 4: (1). |
[30] | Leal F, Veloso B, Malheiro B, Burguillo JC, Chis AE, González-Vélez H. Stream-based explainable recommendations via blockchain profiling. Integrated Computer-Aided Engineering. (2022) ; 29: (1): 105-21. |
[31] | Schwan C, Schenck W. A three-step model for the detection of stable grasp points with machine learning. Integrated Computer-Aided Engineering. (2021) ; 28: (4): 349-67. |
[32] | Demertzis K, Iliadis L, Kikiras P, Pimenidis E. An explainable semi-personalized federated learning model. Integrated Computer-Aided Engineering. (2022) ; 29: (4): 335-50. |
[33] | Lee J, Lee H, Mun D. 3D convolutional neural network for machining feature recognition with gradient-based visual explanations from 3D CAD models. Scientific Reports. (2022) ; 12: : 14864. |
[34] | Yeo C, Kim B, Cheon S. Machining feature recognition based on deep neural networks to support tight integration with 3D CAD systems. Scientific Reports. (2021) ; 11: : 22147. |
[35] | Kwon K, Mun D. Iterative offset-based method for reconstructing a mesh model from the point cloud of a pig. Computers and Electronics in Agriculture. (2022) ; 198: : 106996. |
[36] | Repnik B, Žalik B. A fast algorithm for approximate surface reconstruction from sampled points. Advances in Engineering Software. (2012) ; 53: : 72-8. |
[37] | Sørensen RA, Nielsen M, Karstoft H. Routing in congested baggage handling systems using deep reinforcement learning. Integrated Computer-Aided Engineering. (2020) ; 27: (2): 139-52. |
[38] | Wang Y, Hou S, Wang X. Reinforcement Learning-based Bird-view Automated Vehicle Control to Avoid Crossing traffic. Computer-Aided Civil and Infrastructure Engineering. (2021) ; 37: (7). |
[39] | Chen S, Dong J, Ha PYJ, Li Y, Labi S. Graph Neural Network and Reinforcement Learning for Multiagent Cooperative Control of Connected Autonomous Vehicles. Computer-Aided Civil and Infrastructure Engineering. (2021) ; 36: (7). |
[40] | Gao T, Li Z, Gao Y, Schonfeld P, Feng X, Wang Q, et al. A deep reinforcement learning approach to mountain railway alignment optimization. Computer-Aided Civil and Infrastructure Engineering. (2022) ; 37: (1). |
[41] | Shi H, Nie Q, Fu S, Wang X, Zhou Y, Ran B. A Distributed Deep Reinforcement Learning Based Integrated Dynamic Bus Control System in a Connected Environment. Computer-Aided Civil and Infrastructure Engineering. (2022) ; 37: (15). |
[42] | Shi H, Zhou Y, Wang X, Fu S, Gong S, Ran B. A Deep Reinforcement Learning based Distributed Connected Automated Vehicle Control under Communication Failure. Computer-Aided Civil and Infrastructure Engineering. (2022) ; 37: (15). |
[43] | Chen BW, Yang SH, Kuo CH, Chen JW, Lo YC, Kuo YT, et al. Neuro-Inspired Reinforcement Learning to Improve Trajectory Prediction in Reward-Guided Behavior. International Journal of Neural Systems. (2022) ; 32: (9). |
[44] | Daranda A, Dzemyda G. Reinforcement learning strategies for vessel navigation. Integrated Computer-Aided Engineering. (2023) ; 1-14. |
[45] | Li S, Snaiki R, Wu T. A Knowledge-Enhanced Deep Reinforcement Learning-Based Shape Optimizer for Aerodynamic Mitigation of Wind-Sensitive Structures. Computer-Aided Civil and Infrastructure Engineering. (2021) ; 36: (6). |
[46] | Jeong JH, Jo H. Deep reinforcement learning for automated design of reinforced concrete structures. Computer-Aided Civil and Infrastructure Engineering. (2021) ; 36: (12). |
[47] | Fan X, Zhang X, Yu X. A Graph Convolution Network-Deep Reinforcement Learning Model for Resilient Water Distribution Network Repair Decisions. Computer-Aided Civil and Infrastructure Engineering. (2022) ; 37: (12). |
[48] | Kucukoglu B, Rueckauer B, Ahmad N, de Ruyter van Steveninck J, Guclu U, van Gerven M. Optimization of Neuroprosthetic Vision via End-to-end Deep Reinforcement Learning. International Journal of Neural Systems. (2022) ; 33: (11). |
[49] | Liu X, Zhang G, Mastoi MS, Neri F, Pu Y. A human-simulated fuzzy membrane approach for the joint controller of walking biped robots. Integrated Computer-Aided Engineering. (2023) ; 1-16. |
[50] | Regli W. Design and Intelligent Machines. Ai Magazine. (2017) ; 38: (3). |
[51] | Ito S, Ju B, Kaneko N, Sumi K. Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning. In: VISIGRAPP. (2022) . |
[52] | Wang GG, Guo L, Gandomi AH, Hao GS, Wang H. Chaotic Krill Herd algorithm. Information Sciences. (2014) ; 274: : 17-34. Available from: https://www.sciencedirect.com/science/article/pii/S0020025514002291. |
[53] | Wan M, Gangwani T, Peng J. Mutual information based knowledge transfer under state-action dimension mismatch. JMLR: Workshop and Conference Proceedings. (2020) ; 124: . |
[54] | Dayan P, Hinton GE. Feudal Reinforcement Learning. In: Hanson S, Cowan J, Giles C, editors. Advances in Neural Information Processing Systems(NIPS). vol. 5. Morgan-Kaufmann; (1992) . |
[55] | Parr R, Russell S. Reinforcement Learning with Hierarchies of Machines. In: Jordan M, Kearns M, Solla S, editors. Advances in Neural Information Processing Systems(NIPS). vol. 10. MIT Press; (1997) . |
[56] | Dietterich TG. Hierarchical reinforcement learning with the MAXQ value function decomposition. Journal of artificial intelligence research. (2000) ; 13: : 227-303. |
[57] | Sutton RS, Precup D, Singh S. Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artificial Intelligence. (1999) ; 112: (1–2): 181-211. |
[58] | Bacon PL, Harb J, Precup D. The option-critic architecture. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 31; (2017) . |
[59] | Kulkarni TD, Narasimhan K, Saeedi A, Tenenbaum J. Hierarchical Deep Reinforcement Learning: Integrating Temporal Abstraction and Intrinsic Motivation. In: Lee D, Sugiyama M, Luxburg U, Guyon I, Garnett R, editors. Advances in Neural Information Processing Systems(NIPS). vol. 29. Curran Associates, Inc.; (2016) . |
[60] | Xue Y, Zhu H, Neri F. A self-adaptive multi-objective feature selection approach for classification problems. Integrated Computer-Aided Engineering. (2022) ; 29: (1): 3-21. |
[61] | Zhu H. Avoiding Critical Members in a Team by Redundant Assignment. IEEE Transactions on Systems, Man, and Cybernetics: Systems. (2020) ; 50: (7): 2729-40. |
[62] | Yang H, Li WD, Hu KX, Liang YC, Lv YQ. Deep ensemble learning with non-equivalent costs of fault severities for rolling bearing diagnostics. Journal of Manufacturing Systems. (2021) ; 61: : 249-64. Available from: https://www.sciencedirect.com/science/article/pii/S0278612521001953. |
[63] | Hinton G, Vinyals O, Dean J, et al. Distilling the knowledge in a neural network. In: 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). (2015) . |
[64] | Polino A, Pascanu R, Alistarh D. Model compression via distillation and quantization. In: International Conference on Learning Representations(ICLR). (2018) . |
[65] | Hester T, Vecerik M, Pietquin O, Lanctot M, Schaul T, Piot B, et al. Deep q-learning from demonstrations. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 32; (2018) . |
[66] | Yang M, Nachum O. Representation matters: offline pretraining for sequential decision making. In: International Conference on Machine Learning. PMLR; (2021) . pp. 11784-94. |
[67] | Garg H, Majumder P, Nath M. A hybrid trapezoidal fuzzy FUCOM-AHP approach and their application to identification of monkeypox risk factors. Computational and Applied Mathematics. (2022) ; 41: (8): 1-24. |
[68] | Iannino V, Colla V, Maddaloni A, Brandenburger J, Rajabi A, Wolff A, et al. A hybrid approach for improving the flexibility of production scheduling in flat steel industry. Integrated Computer-Aided Engineering. (2022) ; 29: (4): 367-87. |
[69] | Tessler C, Givony S, Zahavy T, Mankowitz D, Mannor S. A deep hierarchical approach to lifelong learning in minecraft. In: Proceedings of the AAAI Conference on Artificial Intelligence. vol. 31; 2017. |
[70] | Frans K, Ho J, Chen X, Abbeel P, Schulman J. Meta learning shared hierarchies. In: International Conference on Learning Representations(ICLR). (2017) . |
[71] | Yang T, Hao J, Meng Z, Zhang Z, Hu Y, Cheng Y, et al. Efficient deep reinforcement learning via adaptive policy transfer. In: International Joint Conference on Artificial Intelligence (IJCAI). (2020) . |
[72] | Liang Y, He F, Zeng X, Luo J. An improved loop subdivision to coordinate the smoothness and the number of faces via multi-objective optimization. Integrated Computer-Aided Engineering. (2022) ; 29: (1): 23-41. |
[73] | Wu H, He F, Duan Y, Yan X. Perceptual metric-guided human image generation. Integrated Computer-Aided Engineering. (2022) ; 29: (2): 141-51. |
[74] | Yuan L, Liu Y, Lin Y, Zhao J. An automated functional decomposition method based on morphological changes of material flows. Journal of Engineering Design. (2017) ; 28: (1): 47-75. doi: 10.1080/09544828.2016.1258459. |
[75] | Luo J, He F, Gao X. An enhanced grey wolf optimizer with fusion strategies for identifying the parameters of photovoltaic models. Integrated Computer-Aided Engineering. (2022) ; 30: (1): 89-104. |
[76] | Luo J, He F, Li H, Zeng XT, Liang Y. A novel whale optimisation algorithm with filtering disturbance and nonlinear step. International Journal of Bio-Inspired Computation. (2022) ; 20: (2): 71-81. |
[77] | Van Hasselt H, Guez A, Silver D. Deep reinforcement learning with double q-learning. In: Proceedings of the AAAI conference on artificial intelligence. vol. 30; (2016) . |
[78] | Nogay HS, Adeli H. Detection of Epileptic Seizure Using Pre-trained Deep Convolutional Neural Network and Transfer Learning. European Neurology. (2020) ; 83: (6). |
[79] | Bordel B, Alcarria R, Robles T. Recognizing human activities in Industry 4.0 scenarios through an analysis-modeling-recognition algorithm and context labels. Integrated Computer-Aided Engineering. (2022) ; 29: (1): 83-103. |
[80] | Willis KD, Pu Y, Luo J, Chu H, Du T, Lambourne JG, et al. Fusion 360 gallery: A dataset and environment for programmatic cad construction from human design sequences. ACM Transactions on Graphics (TOG). (2021) ; 40: (4): 1-24. |
[81] | Taylor ME, Stone P. Transfer learning for reinforcement learning domains: A survey. Journal of Machine Learning Research. (2009) ; 10: (7). |
[82] | Zhu Z, Lin K, Zhou J. Transfer learning in deep reinforcement learning: A survey. arXiv preprint arXiv:200907888. (2020) . |
[83] | Pérez-Hurtado I, Martínez-del Amor MÁ, Zhang G, Neri F, Pérez-Jiménez MJ. A membrane parallel rapidly-exploring random tree algorithm for robotic motion planning. Integrated Computer-Aided Engineering. (2020) ; 27: (2): 121-38. |
[84] | Rafiei MH, Adeli H. A New Neural Dynamic Classification Algorithm. IEEE Transactions on Neural Networks and Learning Systems. (2017) ; 288: (12). |
[85] | Alam KMR, Siddique N, Adeli H. A Dynamic Ensemble Learning Algorithm for Neural Networks. Neural Computing with Applications. (2020) ; 32: (10). |
[86] | Pereira DR, Piteri MA, Souza AN, Papa J, Adeli H. FEMa: A Finite Element Machine for Fast Learning. IEEE Transactions on Neural Networks and Learning Systems. (2020) ; 32: (10). |
[87] | Zhang J, He F, Duan Y, Yang S. AIDEDNet: Anti-interference and detail enhancement dehazing network for real-world scenes. Frontiers of Computer Science. (2023) ; 17: (2): 172703. |
[88] | Si T, He F, Zhang Z, Duan Y. Hybrid contrastive learning for unsupervised person re-identification. IEEE Transactions on Multimedia. (2022) . |
[89] | Chang AX, Funkhouser T, Guibas L, Hanrahan P, Huang Q, Li Z, et al. Shapenet: An information-rich 3d model repository. arXiv preprint arXiv:151203012. (2015) . |
[90] | Wu Z, Song S, Khosla A, Yu F, Zhang L, Tang X, et al. 3d shapenets: A deep representation for volumetric shapes. In: Proceedings of the IEEE conference on computer vision and pattern recognition. (2015) . pp. 1912-20. |




