Beyond Quasi-Adjoint Graphs: On Polynomial-Time Solvable Cases of the Hamiltonian Cycle and Path Problems

Kasprzak, Marta

doi:10.15388/24-INFOR568

Beyond Quasi-Adjoint Graphs: On Polynomial-Time Solvable Cases of the Hamiltonian Cycle and Path Problems

Article type: Research Article

Authors: Kasprzak, Marta

Affiliations: Institute of Computing Science, Poznan University of Technology, Piotrowo 2, 60-965 Poznan, Poland

Keywords: directed line graph, quasi-adjoint graph, Hamiltonian cycle, Hamiltonian path

DOI: 10.15388/24-INFOR568

Journal: Informatica, vol. 35, no. 4, pp. 807-816, 2024

Received September 2023

Accepted September 2024

Published: 2024

Get PDF

Abstract

The Hamiltonian cycle and path problems are fundamental in graph theory and useful in modelling real-life problems. Research in this area is directed toward designing better and better algorithms for general problems, but also toward defining new special cases for which exact polynomial-time algorithms exist. In the paper, such new classes of digraphs are proposed. The classes include, among others, quasi-adjoint graphs, which are a superclass of adjoints, directed line graphs, and graphs modelling a DNA sequencing problem.

1Introduction

The problem of searching for a Hamiltonian cycle or path is fundamental in graph theory and useful in modelling real-life problems. Electronic circuit design, job scheduling, and sequencing of DNA chains are just a few examples of such an application. In its decision version, the problem for directed or undirected graphs belongs to the NP-complete class of computationally hard problems. As the problem is regularly used, a lot of effort was put into designing more and more efficient algorithms (see, e.g., Jäger and Zhang, 2010; Björklund, 2014). On a more theoretical ground, research was directed toward proving polynomial-time solvability of Hamiltonicity for subsequent classes of graphs. There are many works related to the problem in undirected graphs (see surveys of Gould, 1991; Gross et al., 2013), its directed version was not so extensively studied (e.g., Favaron and Ordaz, 1986; Bang-Jensen and Gutin, 1999).

In the paper, superclasses of (directed) quasi-adjoint graphs are defined and proven to have a polynomial-time solution of the Hamiltonian cycle problem and, partially, the Hamiltonian path problem. Section 2 introduces necessary definitions and summarizes previous work, Section 3 contains theoretical results including algorithms, and a conclusion is given in Section 4.

2Theoretical Background

The following statements refer to directed graphs with, in general, loops and multiple arcs accepted. Throughout the paper, standard terminology from graph theory is used, see, e.g. Berge (1973). Let V stand for the set of vertices of a graph G=(V,A), and A for its set of arcs. The Hamiltonian cycle (path) in G is a directed cycle (path) including every vertex v∈V exactly once; the Eulerian cycle (path) is a directed cycle (path) including every arc a∈A exactly once. Transpose graph GT=(V,A′) of a digraph G=(V,A) has (u,v)∈A′ if and only if (v,u)∈A.

The problem of searching for a Hamiltonian cycle or a Hamiltonian path is NP-hard even if all vertices in a digraph have their indegree and outdegree not exceeding 2 (Garey and Johnson, 1979). It is solvable in polynomial time when restricted to special subclasses of digraphs, for example, acyclic digraphs (Lawler, 1976), directed line graphs (Kasteleyn, 1963), or specific variations of dense digraphs (Bang-Jensen and Gutin, 2002).

A directed line graph is a 1-graph (a graph with no multiple arcs) where the following holds for all pairs u,v of its vertices:

N+(u)∩N+(v)≠∅⇒N+(u)=N+(v)∧N−(u)∩N−(v)=∅,

where N+(u) is the set of (direct) successors of vertex u and N−(u) is the set of its (direct) predecessors (Blazewicz et al., 1999). As defined in Berge (1973) in the context of directed graphs, adjoint G=(V,A) of a graph H=(U,V) is a 1-graph whose vertices represent arcs of H and in which (u,v)∈A if and only if the head of arc u is the tail of arc v in H. H is not necessarily a 1-graph. If H is a 1-graph, its adjoint G is a directed line graph (Blazewicz et al., 1999). 1-graph G is an adjoint if and only if the following property is satisfied for all u,v∈V (Berge, 1973):

N+(u)∩N+(v)≠∅⇒N+(u)=N+(v).

The relation between vertices of adjoint G and arcs of the corresponding graph H leads to the polynomial-time solvability of the Hamiltonian cycle and path problems in adjoints. There is a Hamiltonian cycle (path) in graph G if and only if graph H contains an Eulerian cycle (path) (Blazewicz et al., 1999), this property follows from the definitions. Such a conversion of problems is not possible for analogous situation of an undirected line graph and its corresponding graph (Bertossi, 1981).

Adjoints have this useful property because of the vertex-arc relation with their graphs H, and a question arose whether this class could be widened. In 2008, its superclass of quasi-adjoint graphs was defined and a polynomial-time exact algorithm solving the Hamiltonian cycle problem was provided (Blazewicz et al., 2008). Digraph G is a quasi-adjoint graph if and only if, for all u,v∈V, the following property holds:

N+(u)∩N+(v)≠∅⇒N+(u)=N+(v)∨N+(u)⊂N+(v)∨N+(v)⊂N+(u).

Quasi-adjoint graphs, unlike adjoints, can be multigraphs. They are a superclass of, among others, digraphs modelling a bioinformatical problem of isothermic DNA sequencing by hybridization, which are 1-graphs intersecting the class of adjoints (Blazewicz et al., 2004; Blazewicz and Kasprzak, 2006). (For more relations of quasi-adjoint graphs and adjoints with other classes of digraphs, see the systematization made in Blazewicz and Kasprzak (2012) and Kasprzak (2018).) The recognition whether a graph is a quasi-adjoint graph can be done in O(n3) time, and the exact algorithm solving the Hamiltonian cycle problem within it works in O(n2+m2) time, where n is the number of its vertices and m the number of arcs (Blazewicz et al., 2008). The algorithm also uses a transformation of a graph G into the corresponding graph H, but this time it is more complicated and includes insertion of extra structures. There, the numbers of vertices before the transformation and arcs after the transformation differ, nevertheless, the correspondence between the Hamiltonian and Eulerian cycles is preserved. This algorithm can be easily adjusted to solve the Hamiltonian path problem (Kasprzak, 2018).

3Superclasses of Quasi-Adjoint Graphs

Fig. 1

Graph G∉Gq and its transpose graph GT∈Gq. G is not a quasi-adjoint graph because of any of these pairs of vertices: {a,b}, {a,e}, {b,d}, {d,e}. In GT all pairs of vertices satisfy the condition for quasi-adjoint graphs.

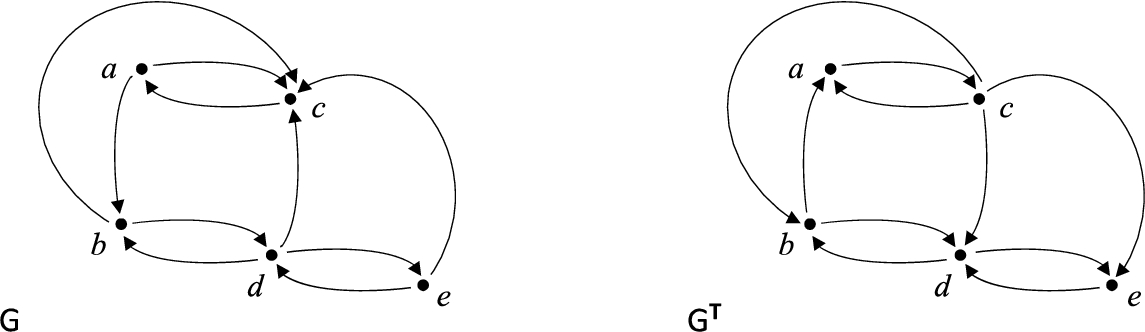
The considered class of polynomially solvable instances of the Hamiltonian cycle/path problem can be further extended. The simplest extension is to add to quasi-adjoint graphs their counterparts with the adjacency matrix transposed. Obviously, digraph G has a Hamiltonian cycle/path if and only if its transposed counterpart GT has (see an example in Fig. 1). Adjoints are digraphs whose membership in this class does not change after the transposition, however, it is not the case of quasi-adjoint graphs. Let Ga be the class of adjoints, and Gq the class of quasi-adjoint graphs.

Proposition 1.

G∈Ga⇔GT∈Ga.

Proof.

According to the definition, every two vertices of an adjoint have their sets of successors either identical or disjoint. Consequently, if two vertices have a common predecessor, they must have the same sets of predecessors, because all the predecessors point to the same subset of vertices. □

Lemma 1.

Gq≠{G:GT∈Gq}.

Proof.

Figure 1 presents an example of a graph, which becomes the quasi-adjoint graph after the transposition of its adjacency matrix. □

The following extension of the quasi-adjoint graphs takes into account the above property. Let G′ be the class of digraphs where the following holds for all u,v∈V:

(3.1)

N+(u)∩N+(v)≠∅⇒|⋃z∈ZN−(z)|⩽|Z|,

where Z=N+(u)∖N+(v) or Z=N+(v)∖N+(u) (a choice made independently for each pair u,v toward satisfying the clause). Analogously, let G″ be the class of digraphs with the property

(3.2)

N−(u)∩N−(v)≠∅⇒|⋃z∈ZN+(z)|⩽|Z|

satisfied for all u,v∈V, where Z=N−(u)∖N−(v) or Z=N−(v)∖N−(u).

Theorem 1.

(i) Gq⊂G′. (ii) Gq∪{G:GT∈Gq}⊂G′∪G″.

Proof.

From the definition, for each pair of vertices of a quasi-adjoint graph, their sets of successors are either disjoint or one of them is a subset of the other. If they are disjoint, the left part of the clause defining elements of G′ (clause (3.1)) is fulfilled. Otherwise, at least one of the equations for Z gives Z=∅ and the inequality from the clause is fulfilled. Thus, Gq is a subset of G′. The subset is proper, an example graph belonging to G′∖Gq is shown in Fig. 2(A). This completes the proof for (i).

Fig. 2

(A) An example graph G∈G′∖Gq. Pair a,c does not satisfy the condition for quasi-adjoint graphs but satisfies the one for G′. (B) An example graph G∉G′∪G″. An obstacle to belonging to this class follows from pairs of vertices b,c (when the membership in G′ is considered) or a,d (for G″). After the reduction according to the procedure from the proof of Theorem 2 made for pair a,b, when the membership in G′ is considered, arc (a,d) is removed and G∈G′. Or, in the variant of the reduction for G″ made for the same pair of vertices, arc (c,b) is removed and G∈G″.

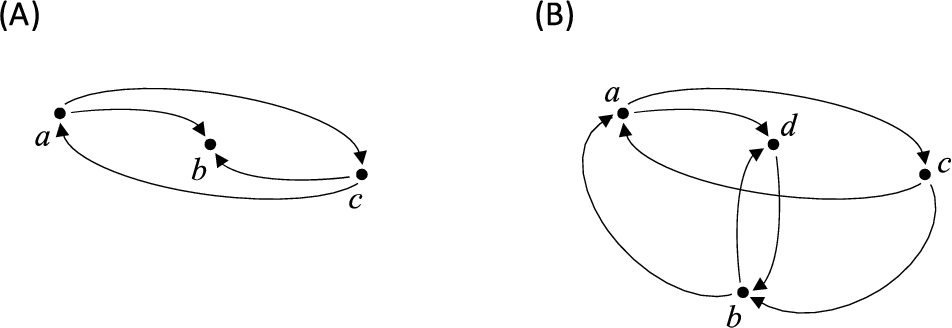
The same we have for the clause for G″ (clause (3.2)) and a graph G such that GT∈Gq, because the transposition is realized in the clause by replacing successors with predecessors and vice versa. Therefore, the property from (ii) is also satisfied. According to Lemma 1, classes Gq and {G:GT∈Gq} are different, this justifies the presence of sum of these sets in (ii). □

The joint class G′∪G″ is interesting in such a sense that its elements are polynomially solvable instances of the Hamiltonian cycle problem. It should be noticed that these graphs can bring the positive, as well as the negative answer to the problem. The recognition whether a graph belongs to this class can be done in O(n4) time (clause (3.1) or (3.2) checked in O(n2) time for all pairs of vertices).

Theorem 2.

The Hamiltonian cycle problem in graphs belonging to G′∪G″ can be polynomially solved in O(n4+m2) time.

Proof.

The algorithm solving the problem consists of two stages. Firstly, graph G∈G′∪G″ is reduced to a quasi-adjoint graph or its transposed version. Secondly, the algorithm for the Hamiltonian cycle problem from Blazewicz et al. (2008) is applied to the reduced G, if G∈G′, or to GT otherwise.

The reduction is made by removal of arcs where no arc having the possibility of composing any Hamiltonian cycle is removed. For G∈G′, all pairs u,v∈V sharing a successor are analysed, and if the inequality from clause (3.1) is fulfilled for Z=N+(u)∖N+(v) and |Z|>0, where N+(v)∖N+(u)≠∅, all arcs from u to N+(u)∩N+(v) are marked to be removed; if the inequality is fulfilled for Z=N+(v)∖N+(u) and |Z|>0, where N+(u)∖N+(v)≠∅, all arcs from v to N+(u)∩N+(v) are marked to be removed. It is enough to mark (and, further, to remove) arcs in one of these cases to get N+(u) and N+(v) disjoint, thus satisfying the condition for quasi-adjoint graphs. (However, as we see later in Algorithm 1, we may remove arcs in both of these cases, and it does not affect Hamiltonicity.) Such an operation is legitimized by the fact that, in any Hamiltonian cycle in G (if it exists), vertices from Z need exactly |Z| direct predecessors. Because the number of their predecessors in G is not greater than |Z|, a Hamiltonian cycle entering any of the predecessors must leave it toward one of the elements of |Z|. We may say that vertices from Z ‘bind’ all their predecessors in a cycle, u (v) among them. As a consequence, none of the arcs from u (v) to N+(u)∩N+(v) will be used in a solution.

If N+(u)∖N+(v)=∅ or N+(v)∖N+(u)=∅, pair u,v fulfills the condition from the definition of quasi-adjoint graphs and, typically, no arc is removed. However, arcs marked to be removed for other pairs, characterized as in the above paragraph, can have an influence on u,v. If some arcs leaving u have been marked and N+(u)⊆N+(v), N+(u) after the removal stays encapsulated in N+(v) and the condition is fulfilled. But the encapsulation will be not preserved if N+(v)⊂N+(u) and arcs leaving u and entering only a part of N+(v) are to be removed. In that situation, arcs leaving v that break the encapsulation are also marked for removal according to the following rule. Each time a pair u,w is solved as described in the previous paragraph, where arcs from u to elements of U=N+(u)∩N+(w) are marked for removal (so Z=N+(u)∖N+(w)), all arcs going from v to U are also marked for removal for all v having N+(v)⊂N+(u) and N+(v)∖U≠∅. Such v is one of predecessors of some elements of Z, thus is bound by one of such elements in any Hamiltonian cycle in G. As a consequence, all arcs going from v to U can be safely removed as they will never be used. See Fig. 3 for an example.

Finally, all the marked arcs are removed from G. Analogous operations are performed for G∈G″∖G′ with predecessors instead of successors. This procedure takes O(n4) time. If, at any moment, we get |⋃z∈ZN−(z)|<|Z| (resp. |⋃z∈ZN+(z)|<|Z|), there is no Hamiltonian cycle in the graph and the algorithm can be stopped. The algorithm from Blazewicz et al. (2008) solving the Hamiltonian cycle problem in quasi-adjoint graphs works in O(n2+m2) time in a general case (O(n4) for 1-graphs). Hence, the overall time complexity of the current algorithm is O(n4) under the assumption that m is bounded by O(n2), O(m2) otherwise. □

If graph G has m significantly greater than n2, we can simply reduce the overall time complexity by analysing its underlying 1-graph.

Fig. 3

An illustration for the operations described in the proof of Theorem 2. Let u,w be the analysed pair of vertices. They share a successor, and the inequality from clause (3.1) is fulfilled for both Z=N+(w)∖N+(u) and Z=N+(u)∖N+(w). Therefore, either arc (w,b) may be marked for removal (with U=N+(u)∩N+(w)={b} and Z=N+(w)∖N+(u)={a}) or arc (u,b) (with U={b} and Z=N+(u)∖N+(w)={c,d,e,f}). The former case is simpler: after the removal all the pairs from the set {w,u,v,v′,v″} fulfill the condition for quasi-adjoint graphs, and arcs do not need to be removed anymore. In the latter case, after the removal of (u,b) only, these pairs would not fulfill the condition: {w,v}, {w,v′}, {u,v}, {u,v′}. But here we have the situation that there are some vertices v (v and v′ in the example) such that N+(v)⊂N+(u) and arcs leaving u and entering only a part of N+(v) are marked for removal. According to the rule from the proof, all arcs going from v to U and from v′ to U are also marked for removal. After the removal, all the pairs from the set {w,u,v,v′,v″} fulfill the condition for quasi-adjoint graphs.

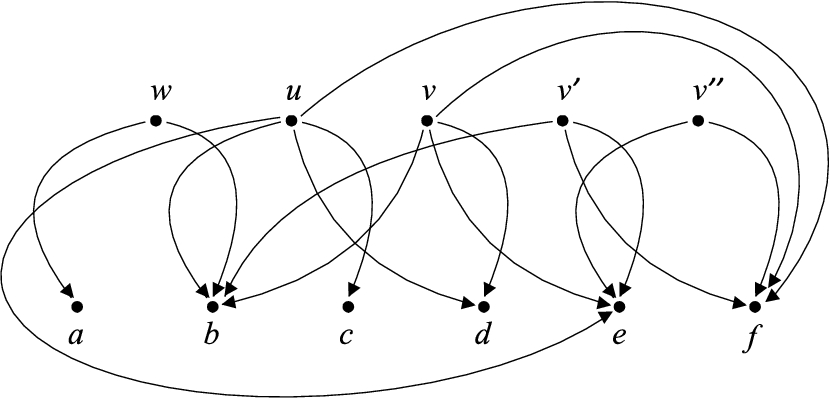
As we see, the algorithms for recognizing graphs from G′∪G″ and for solving the Hamiltonian cycle problem in these graphs are of the same computational complexity as the algorithm solving the problem in quasi-adjoint graphs. Keeping the same complexity function, we can further extend the class of polynomially solvable instances of the problem. The reduction made by the procedure from the proof of Theorem 2 for a pair of vertices can make another pair consistent with the condition for G′ or G″. Therefore, some graphs outside G′∪G″ may, after the reduction, become members of this class. An example of such a situation is shown in Fig. 2(B).

Precisely, the reduction from the proof of Theorem 2 in the case of a graph outside G′∪G″ can be applied to these pairs of its vertices that fulfill the appropriate condition (either for G′ or G″, see the caption of Fig. 2(B)). However, the reduction can be naturally extended as in Algorithm 1.

Algorithm 1

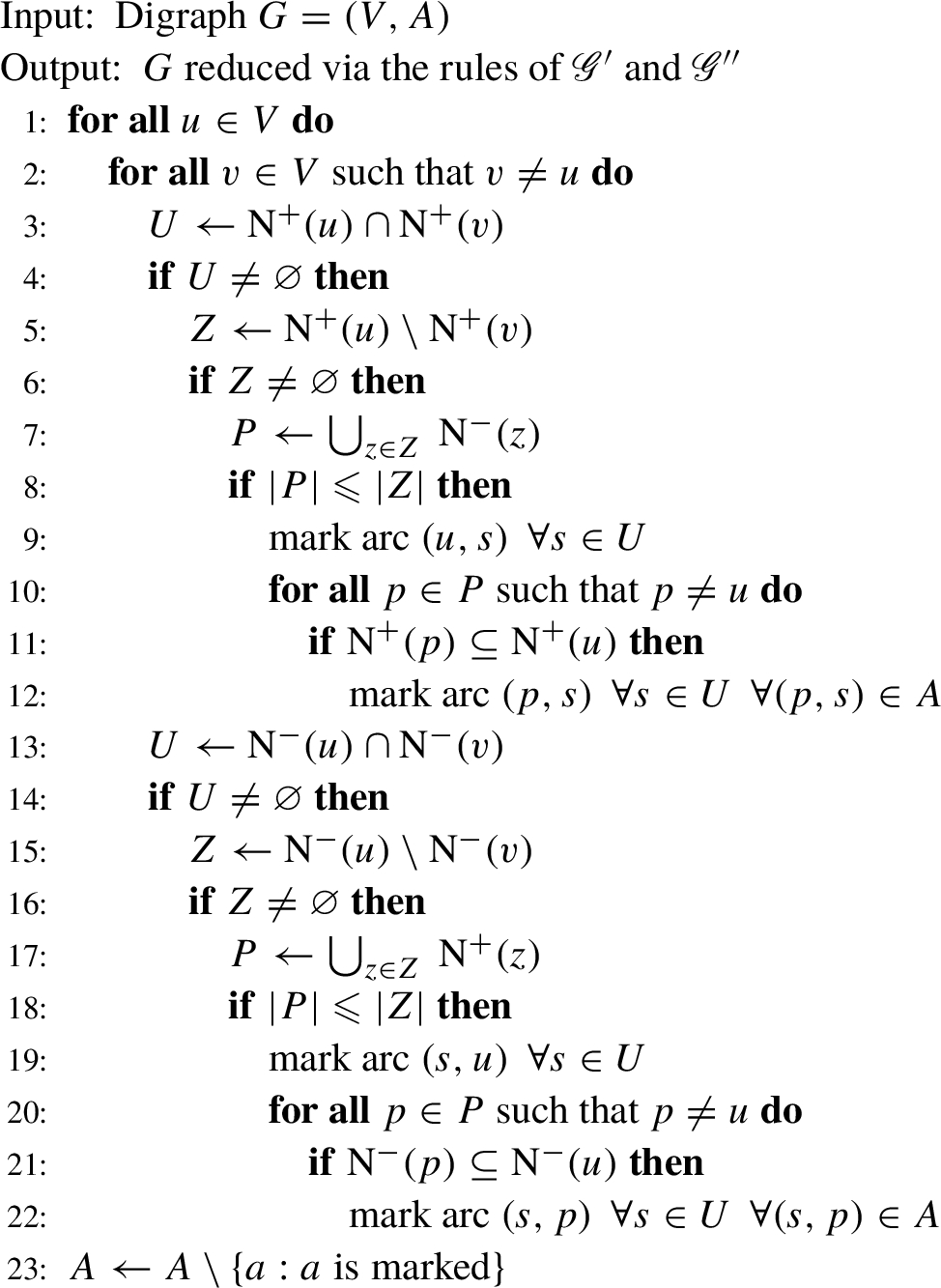
Theorem 3.

Algorithm 1 works in O(n4) time and keeps all Hamiltonian cycles in G.

Proof.

The time complexity immediately follows from the pseudocode. The correctness, i.e. whether all Hamiltonian cycles are preserved after the reduction, has been partially analysed in the proof of Theorem 2, here it remains to prove that: (i) the algorithm can be applied to a graph outside G′∪G″ without losing any solution to the Hamiltonian cycle problem; (ii) the operations assuming the opposite direction of arcs, i.e. the reduction toward G′ or G″, can be alternated; (iii) the removal can be safely done for a pair u,v where N+(v)⊂N+(u); (iv) the removal can be safely done for p such that N+(p)=N+(u).

(i) As the reduction is made only for pairs that satisfy the appropriate condition, only these arcs are removed which for sure will not compose any solution of the problem. (ii) The arcs marked to be reduced stay in the graph until the end of the algorithm, thus they do not influence other connections. Every next operation of marking an arc is independent of the previous ones. At any moment we can treat the graph as having the opposite direction of all its arcs, as it does not change the answer to the problem. (iii) Although such a pair already fulfills the condition for quasi-adjoint graphs, a reduction made for it can help to positively classify another pair. Only arcs that do not compose any solution are marked for the reduction. (iv) Vertex p with the same set of successors as u has the same connections that will never be used, thus safe to be removed. □

By re-running the algorithm, one increases its efficiency as new pairs of vertices can meet the required criteria. If the number of runs is constant, the complexity function does not grow. If one decides to re-run the algorithm as long as there are some reductions made, the number of runs is upper bounded by O(m).

Another observation led to a further extension of the considered classes. If, among all successors (resp. predecessors) of a pair of vertices, there is one with a unique predecessor (resp. successor), it binds in any Hamiltonian cycle its predecessor (resp. successor). Such a case can be added to the clauses defining Gq, {G:GT∈Gq}, G′, and G″ without changing their property of polynomial-time solvability of the Hamiltonian cycle problem. Let G′∗ be a class of digraphs having the following property satisfied for all u,v∈V:

(3.3)

N+(u)∩N+(v)≠∅⇒|⋃z∈ZN−(z)|⩽|Z|∨miny∈Y{N−(y)}=1,

where Z=N+(u)∖N+(v) or Z=N+(v)∖N+(u) (a choice made independently for each pair u,v toward satisfying the clause) and Y=N+(u)∪N+(v). Let G″∗ be a class of digraphs with the following property satisfied for all u,v∈V:

(3.4)

N−(u)∩N−(v)≠∅⇒|⋃z∈ZN+(z)|⩽|Z|∨miny∈Y{N+(y)}=1,

where Z=N−(u)∖N−(v) or Z=N−(v)∖N−(u) and Y=N−(u)∪N−(v).

Theorem 4.

The Hamiltonian cycle problem in graphs belonging to G′∗∪G″∗ can be polynomially solved in O(n4+m2) time.

Proof.

The reduction is done similarly as for the graphs in G′∪G″ except for these pairs u,v∈V for which the last expression in clauses (3.3) or (3.4) is fulfilled. If G∈G′∗ and u,v share a successor, and there exists a vertex y∈N+(u)∪N+(v) that has only one predecessor, then all arcs leaving N−(y), except the one from N−(y) to y, are marked for removal. This way we get N+(u) and N+(v) disjoint, thus satisfying the condition for quasi-adjoint graphs. Here no conflict between vertices having encapsulated successor sets is present. If G∈G″∗∖G′∗ and u,v share a predecessor, and there exists a vertex y∈N−(u)∪N−(v) that has only one successor, then all arcs entering N+(y), except the one from y to N+(y), are marked for removal. See Fig. 4 for an example.

After the removal of the marked arcs from G, the algorithm solving the Hamiltonian cycle problem in quasi-adjoint graphs is executed with, optionally, the reversed orientation of arcs if G∈G″∗∖G′∗. The reduction procedure still takes O(n4) time, thus the overall time complexity is O(n4) under the assumption that m is bounded by O(n2), O(m2) otherwise. □

Fig. 4

An example graph, which does not belong to G′, but belongs to G′∗. The condition for G′ (clause (3.1)) is not fulfilled by the pair u,v. The condition for G′∗ (clause (3.3)) is fulfilled by all the pairs from the graph. After the reduction from the proof of Theorem 4 made for u,v, the graph becomes a quasi-adjoint graph.

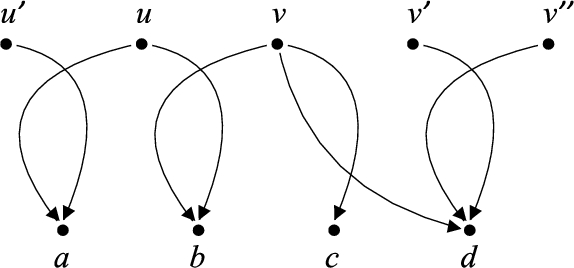
It should be noticed that the example graph from Fig. 2(B) does not belong to any of the classes G′, G″, G′∗, G″∗, but can be reduced to be a member of any of them by Algorithm 1 run once or the procedure from the proof of Theorem 2. It shows potential wide applicability of the approach proposed here.

When solving the Hamiltonian path problem in graphs from class G′∪G″, one encounters a complication. A natural approach consisting in running O(n2) times an algorithm for the Hamiltonian cycle problem, with successive pairs of vertices assumed as the ends of the path and their connection fixed in the cycle, cannot be easily applied here. It works for quasi-adjoint graphs, where, after the appropriate modification, a graph still belongs to this class (Kasprzak, 2018). Here, the addition of the arc from the last to the first vertex, accompanied by the removal of some arcs or not, can make the graph no longer an element of G′∪G″.

Let a be the assumed beginning of the path, b its end, and the added arc be (b,a) (not present in the initial graph). The complication is for the cases where, for a pair u,v, clause (3.1) or (3.2) was fulfilled with |⋃z∈ZN−(z)|=|Z| or |⋃z∈ZN+(z)|=|Z|, respectively, and a or b supplied one of the sides of these equations. Whether the arcs initially entering a/leaving b (or both) will be removed or not, the pair u,v can lose the required property. Therefore, the case of the Hamiltonian path in the considered classes (also G′∗ and G″∗) needs a special treatment, including such exceptions. The algorithm from the proof of Theorem 2 could be used directly to these elements of the classes, supplemented by arc (b,a), that are not such problematic instances.

4Conclusion

Until now, the quasi-adjoint graphs were the widest class of digraphs proven to have a polynomial-time solution of the Hamiltonian cycle and path problems based on the transformation of graphs G into H. The extended classes of digraphs defined in the paper add new cases to this class. In addition, the reduction of arcs being a part of the proposed algorithms can function standalone and can be applied to digraphs outside the classes, possibly resulting in polynomial-time solutions for them.

The case of the Hamiltonian path has a more complicated solution because of the underlying assumptions in the definitions of the classes. Research on the algorithm for this problem could especially benefit, as the Hamiltonian path model is willingly used for real-life problems. As one of the current applications, the computational part of the process of genome assembly can be given, modelled, among others, as searching for variants of such a path (Swat et al., 2021).

References

1	Bang-Jensen, J., Gutin, G. ((1999) ). On the complexity of Hamiltonian path and cycle problems in certain classes of digraphs. Discrete Applied Mathematics, 95: , 41–60.
2	Bang-Jensen, J., Gutin, G. ((2002) ). Digraphs. Theory, Algorithms and Applications. Springer-Verlag, London.
3	Berge, C. ((1973) ). Graphs and Hypergraphs. North-Holland Publishing Company, London.
4	Bertossi, A.A. ((1981) ). The edge Hamiltonian path problem is NP-complete. Information Processing Letters, 13: (4–5), 157–159.
5	Björklund, A. ((2014) ). Determinant sums for undirected hamiltonicity. SIAM Journal on Computing, 43: (1), 280–299.
6	Blazewicz, J., Kasprzak, M. ((2006) ). Computational complexity of isothermic DNA sequencing by hybridization. Discrete Applied Mathematics, 154: (5), 718–729.
7	Blazewicz, J., Kasprzak, M. ((2012) ). Reduced-by-matching graphs: toward simplifying Hamiltonian circuit problem. Fundamenta Informaticae, 118: (3), 225–244.
8	Blazewicz, J., Hertz, A., Kobler, D., de Werra, D. ((1999) ). On some properties of DNA graphs. Discrete Applied Mathematics, 98: (1–2), 1–19.
9	Blazewicz, J., Formanowicz, P., Kasprzak, M., Markiewicz, W.T. ((2004) ). Sequencing by hybridization with isothermic oligonucleotide libraries. Discrete Applied Mathematics, 145: (1), 40–51.
10	Blazewicz, J., Kasprzak, M., Leroy-Beaulieu, B., de Werra, D. ((2008) ). Finding Hamiltonian circuits in quasi-adjoint graphs. Discrete Applied Mathematics, 156: (13), 2573–2580.
11	Favaron, O., Ordaz, O. ((1986) ). A sufficient condition for oriented graphs to be Hamiltonian. Discrete Mathematics, 58: (3), 243–252.
12	Garey, M.R., Johnson, D.S. ((1979) ). Computers and Intractability. A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, San Francisco.
13	Gould, R.J. ((1991) ). Updating the Hamiltonian problem – a survey. Journal of Graph Theory, 15: (2), 121–157.
14	Gross, J.L., Yellen, J., Zhang, P. (Eds.) ((2013) ). Handbook of Graph Theory, second edition. Chapman and Hall/CRC, Boca Raton.
15	Jäger, G., Zhang, W. ((2010) ). An effective algorithm for and phase transitions of the directed Hamiltonian cycle problem. Journal of Artificial Intelligence Research, 39: , 663–687.
16	Kasprzak, M. ((2018) ). Classification of de Bruijn-based labeled digraphs. Discrete Applied Mathematics, 234: , 86–92.
17	Kasteleyn, P.W. ((1963) ). A soluble self-avoiding walk problem. Physica, 29: (12), 1329–1337.
18	Lawler, E.L. ((1976) ). Combinatorial Optimization: Networks and Matroids. Holt, Rinehart and Winston, New York.
19	Swat, S., Laskowski, A., Badura, J., Frohmberg, W., Wojciechowski, P., Swiercz, A., Kasprzak, M., Blazewicz, J. ((2021) ). Genome-scale de novo assembly using ALGA. Bioinformatics, 37: (12), 1644–1651.