Interval-Valued Spherical Fuzzy Analytic Hierarchy Process Method to Evaluate Public Transportation Development
Abstract
Consensus creation is a complex challenge in decision making for conflicting or quasi-conflicting evaluator groups. The problem is even more difficult to solve, if one or more respondents are non-expert and provide uncertain or hesitant responses in a survey. This paper presents a methodological approach, the Interval-valued Spherical Fuzzy Analytic Hierarchy Process, with the objective to handle both types of problems simultaneously; considering hesitant scoring and synthesizing different stakeholder group opinions by a mathematical procedure. Interval-valued spherical fuzzy sets are superior to the other extensions with a more flexible characterization of membership function. Interval-valued spherical fuzzy sets are employed for incorporating decision makers’ judgements about the membership functions of a fuzzy set into the model with an interval instead of a single point. In the paper, Interval-valued spherical fuzzy AHP method has been applied to public transportation problem. Public transport development is an appropriate case study to introduce the new model and analyse the results due to the involvement of three classically conflicting stakeholder groups: passengers, non-passenger citizens and the representatives of the local municipality. Data from a real-world survey conducted recently in the Turkish big city, Mersin, help in understanding the new concept. As comparison, all likenesses and differences of the outputs have been pointed out in the reflection with the picture fuzzy AHP computation of the same data. The results are demonstrated and analysed in detail and the step-by-step description of the procedure might foment other applications of the model.
1Introduction
Public transport development often requires participatory decision-making procedure involving not only heterogeneous and probably conflicting participant groups, but also survey respondents in every group with different personal characteristics. An evident way for clustering the respondents in the survey pattern is to create preliminary stakeholder groups based on their motivation and interest in transport development (Macharis and Bernardini, 2015). Following this idea, a possible division of survey participants can be e.g. forming the three groups of passengers, non-passengers and municipality (Ghorbanzadeh et al., 2019) or passengers, transport company managers and local government representatives (Duleba et al., 2012). Apart from this clustering, however, the homogeneity of these groups cannot be guaranteed and the vagueness and impreciseness of evaluations are still with a high risk, mainly in the non-expert groups in the pattern.
Measuring the consistency of the responses is an available tool in many different multi-criteria decision-making (MCDM) techniques. In Analytic Hierarchy Process (AHP), the creator himself proposed a consistency check (Saaty, 1977) for filtering out the non-consistent responses and evaluators. In this original approach, for the created Consistency Ratio (CR), Saaty determined a threshold value, 0.1, and all evaluations above this CR were rejected and all below were accepted. Although throughout the decades many authors criticized and improved the consistency measure by CR (Karapetrovic and Rosenbloom, 1999; Lane and Verdini, 1989; Rallabandi et al., 2016), it fundamentally has not changed and is still widely applied in recent AHP applications (Lin et al., 2020; Wu et al., 2020). Cho and Cho (2008) even proposed that the weights of different stakeholder groups in the final decision should be determined by their evaluation consistency measured by CR.
Even if consistency is fulfilled, many MCDM models consider pure evaluation scores as untrustworthy or not completely trustworthy values in survey analysis. Several methodological solutions exist for this problem in the area of AHP, the two major approach for dealing with insecure scoring is fuzzy models and interval-type models. Recently, fuzzy AHP is combined with other techniques e.g. VIKOR (Awasthi and Chauhan, 2011; Wang et al., 2019) or TOPSIS (Chou et al., 2019; Zyoud et al., 2016), but the objective of fuzzification is the same: to mitigate the uncertainty of scoring by examining the environmental values of each score. The same motivation refers to interval AHP type models (Pamučar et al., 2018; Wang et al., 2018), which consider the neighbour values of each score in reaching the final decision priorities.
Both the fuzzy and interval type models, however, have the common characteristics that they do not allow the respondents themselves to express their insecurity about scoring specific parts of the pairwise comparisons and they do not make distinctions between the certain and uncertain judgements, they treat all judgements automatically uncertain. Some lately emerged techniques called hesitant models in AHP (Tüysüz and Şimşek, 2017; Zhu and Xu, 2014) consider the uncertain judgements by their expression from the decision makers themselves and calculate the final priorities by these uncertainties.
In case of multiple evaluator groups, gaining a consensual final priority of the alternatives or criteria is another dominant field in MCDM and this problem has made a severe impact on many AHP models (Bozóki et al., 2016; Ossadnik et al., 2016; Triantaphyllou et al., 2020). The hesitant approach is capable of dealing also with this problem by applying the hesitancy not only for individuals but also for stakeholder groups, consequently the consensus could be gained.
Our paper aims to introduce a model which creates consensus first within each defined evaluator group, then among the participating evaluator groups, reaching a final agreement in weight criteria of a decision. For consensus creation, three types of score values are considered: membership, non-membership and hesitant, which are derived from the original scale of AHP, the Saaty-scale. The model also considers vague or imprecise evaluations and the calculation procedure of using fuzzy and interval values makes the results more trustworthy. We indicate the method by a real-world case study on public transport development decision, with the involvement of three different stakeholder groups: passengers, non-passenger citizens and the representatives of transportation department in the municipality. The real data have been gathered using a survey in Turkey. First, the useful methodology is applied to the problem of public transportation evaluation with the real data. One of the most attractive features of our proposed model is also that it makes group consensus in a logical and objective way even in case of conflicting groups.
The remainder of the paper is structured as follows: first we overview the relevant models of group decision-making in public transportation, then we present the methodology of the new Interval-valued Spherical Fuzzy Set (IV-SFS) model and the extension of AHP by I-SFS. Afterwards, the case study is introduced and the detailed calculation process for criteria prioritization and consensus creation is demonstrated. Finally, we draw some conclusions and remark some further research.
2Fuzzy Extensions of Analytic Hierarchy Process (AHP): A Literature Review
The ordinary fuzzy sets, proposed by Zadeh (1965), have an important impact on the development of decision-making problems in an uncertain environment. In recent years, various researchers have introduced many extensions of ordinary fuzzy sets. Type-2 fuzzy sets (Zadeh, 1975); intuitionistic fuzzy sets (Atanassov, 1986); neutrosophic sets (Smarandache, 2000); hesitant fuzzy sets (Torra, 2010); Pythagorean fuzzy sets (Yager, 2013); picture fuzzy sets (Cu’ò’ng, 2014) and spherical fuzzy sets (Gündoğdu and Kahraman, 2019) are most famous and popular extensions of ordinary fuzzy sets.
Analytic Hierarchy Process (AHP) and its fuzzy extensions are popular and widely used multi criteria decision-making (MCDM) methodologies. In the following, we will focus on a state-of-the-art review on existing fuzzy AHP extensions. The convectional AHP approach proposed by Saaty (1977) is a simple and practical approach to solve complex problems targeting to prioritize the most important criteria and alternatives. In the face of this reality, there are some weak points of AHP such as structuring the problem in a hierarchical way, rating derivation, consistency issue and pairwise comparison numbers (Abastante et al., 2019; Duleba and Moslem, 2019; Ghorbanzadeh et al., 2019; Ishizaka, 2019). Moreover, there is a risk of gaining vague scoring in pairwise comparisons, and even if the scoring is trustworthy, the aggregation might also include a risk of misunderstanding the real intention of the decision makers. To overcome these concerns, some scholars have extended the AHP method for solving MCDM complex problems under a variety of different fuzzy environments over the last 40 years. For instance, using AHP with triangular fuzzy numbers (Van Laarhoven and Pedrycz, 1983), Buckley’s fuzzy AHP (Buckley, 1985), fuzzy AHP with interval type-2 fuzzy sets (Kahraman et al., 2014), AHP-hesitant group decision making (Zhu and Xu, 2014), Z-number extension of an integrated AHP (Sahrom, 2014), type-2 fuzzy set of linguistic AHP (Abdullah and Najib, 2014), hesitant fuzzy analytical hierarchy process (Öztaysi et al., 2015), group intuitionistic fuzzy AHP (Liao and Xu, 2015a), intuitionistic fuzzy AHP (Sadiq and Tesfamariam, 2009), interval-valued intuitionistic fuzzy AHP (Abdullah and Najib, 2016), interval-valued fuzzy Delphi AHP (Minatour et al., 2016), Pythagorean fuzzy analytic hierarchy process (Mohd and Abdullah, 2017), neutrosophic analytic hierarchy process (Abdel-Basset et al., 2017), interval-valued neutrosophic AHP (Bolturk and Kahraman, 2018), hesitant fuzzy linguistic AHP (Zheng et al., 2018).
In this paper, we propose a novel extension of AHP by interval-valued spherical fuzzy set (IV-SFS) model in the evaluation of public transportation. In many real situations, the evaluators’ judgements could be imprecise, or the evaluators cannot select the exact numbers for evaluation process. For solving these significant problems, Lee and Li (2011) used fuzzy AHP to support user involvement in house layout design. Kahraman et al. (2014) integrated a new model, which is a combination of the fuzzy AHP and the interval type-2 fuzzy sets. The authors extended Buckley’s fuzzy AHP method utilizing the interval type-2 fuzzy sets, which is a generalized standard of interval type-1 fuzzy sets, along with a new ranking method for type-2 fuzzy sets for supplier selection problem. Abdullah and Najib (2014) developed a new model for fuzzy AHP characterized by the interval type-2, which can handle with the uncertainty and vagueness problems. In the paper they employed trapezoidal fuzzy numbers with simple arithmetical formula to enhance the judgement in the decision process. Kilic and Kaya (2015) proposed a hybrid approach by integrating type-2 fuzzy AHP and type-2 fuzzy TOPSIS methods to assess investment projects. To overcome both qualitative and quantitative criteria under vagueness, type-2 fuzzy AHP was employed by Erdoğan and Kaya (2016) for choosing the best alternative fuel bus for public transportation in Istanbul. Sahrom (2014) extended Z-number of AHP approach to avoid the uncertainty and vagueness problems in the classical AHP. Zhu and Xu (2014) developed the hesitant group decision-making analytical hierarchy process to overcome evaluators’ hesitant judgements that each of them could apply several possible values to refer to the original judgements. The AHP-HGDM approach considers an extension of the analytical hierarchy process-group decision making. In order to express the evaluator’s uncertain judgements, Liao and Xu (2015a) provided a theoretical support for the group decision making with the intuitionistic fuzzy analytic hierarchy process. The authors proposed a novel aggregation technique to fuse the individual intuitionistic fuzzy preference relations and they proved that if all individual intuitionistic fuzzy preference relations are of a multiplicative consistency, then their aggregated intuitionistic fuzzy preference relation is always perfectly multiplicative consistent. Öztaysi et al. (2015) developed a hesitant fuzzy AHP method involving multi-experts’ linguistic evaluations aggregated by ordered weighted averaging operator. There are other applications in this domain such as Boltürk et al. (2016), where the authors presented a new hesitant fuzzy AHP method in order to solve a warehouse location selection problem for a Turkish humanitarian relief organization by using hesitant fuzzy preference information. To overcome the various AHP problems like uncertainty and vagueness, linguistic judgements of evaluators were used. Abdullah and Najib (2016) developed a new approach for preference scale in the framework of the interval-valued intuitionistic fuzzy analytic hierarchy process. In their research, the pairwise comparison matrix is represented by interval-valued intuitionistic fuzzy numbers with the hesitant degree. Due to the limited knowledge of the evaluators, they might be unable to express their point of view exactly through evaluating the pairwise comparison judgements in the group decision making. To handle this kind of problem, Abdel-Basset et al. (2017) employed the neutrosophic set theory, which is basically represented by a triangular neutrosophic number, where it defines uncertain, inconsistent, and incomplete information about real world problems. Many researchers believe that the classical AHP approach is predominantly not suitable to evaluate properly real problems because it involves the uncertainty in linguistic judgement. For this reason, Mohd and Abdullah (2017) extended the classical AHP by incorporating the Pythagorean fuzzy sets. Bolturk and Kahraman (2018) proposed the interval-valued neuromorphic AHP model and applied it to select modes of alternative energy to illustrate the integrated model. The decision information could be vague and uncertain, and to address this problem, fuzzy set consideration is an appropriate solution. In order to derive comprehensive criteria scores Zheng et al. (2018) developed a super decision matrix by involving objective and subjective criteria together. Their model was based on developing hesitant fuzzy linguistic analytic network process and the authors illustrated the new model by a real-life problem. In order to handle the uncertain information, Yildiz and Kahraman (2019) developed an integrated AHP methodology based on Buckley’s Fuzzy set with Z-numbers for estimating the improvement factors of social Sustainability, where Z-number is an ordered pair of fuzzy numbers,
One of the most attractive features of our proposed model is that it makes group consensus in a logical and objective way even in case of conflicting groups. Recently, the consensus issue has become a hot significant matter in group decision making utilizing preference relations. In several complex problems and because of modern-life decision problems, many sectors utilize multiple evaluators in different groups to evaluate the pairwise comparisons in the conventional AHP method to take a decision for these complex problems, and the model called group AHP (GAHP). Evaluating pairwise comparison matrices in AHP is crucial for the evaluators, due to the difficulty in conceiving all criteria of the related problem. All the evaluators may estimate their judgements by employing preference representation formats, such as interval preference relation (Saaty and Vargas, 1987), linguistic frame work (Saaty, 2008) and fuzzy preference relations (Chiclana et al., 2001). It was realized that a precise numerical value cannot covey the ambiguous knowledge of evaluator’s preference level. To rationalize uncertainty associated with vagueness, fuzzy set theory has been created (Zadeh, 1965), It handles vague data in terms of set memberships (e.g. triangular fuzzy numbers, trapezoidal fuzzy numbers, interval numbers). Atanassov (1986) integrated the fuzzy set to present intuitionistic fuzzy set to treat the uncertainty and vagueness in the pairwise comparisons. To overcome any vagueness and minimize the uncertainty in decision making process, Efe (2016) focused on integrating AHP method with type 1 fuzzy numbers. The author preferred using type 1 fuzzy numbers because it is easier and more practical than other types. The rule structure of type 1 fuzzy numbers and type 2 fuzzy numbers are the same, except that the antecedent and consequent are of the respective types, moreover, type 2 fuzzy sets generalize type 1 fuzzy sets, whereas type 2 fuzzy set lets us incorporate uncertainty about the membership function into fuzzy set theory. However, type 1 and type 2 fuzzy numbers do not consider the indeterminacy degree in the pairwise comparisons. Kar (2015) proposed fuzzy AHP for group decision making under consensus achievement to evaluate group preferences for supplier selection.
The AHP approach in fuzzy environments does not take into consideration the evaluators’ hesitancy. However, AHP approach in hesitant fuzzy environment handles this significant issue through assigning more than one membership degree to avoid evaluators’ hesitancy. Also, AHP in Pythagorean and intuitionistic environment take the hesitancy of evaluator in consideration, on the other hand, evaluators do not have the ability to decide the hesitancy. The AHP approach in almost all fuzzy environments suffers from the comprehensive perspective paucity, due to the violent progress in the fuzzy set theory which occurs over time. Spherical fuzzy Sets (SFS) have been recently presented by Gündoğdu and Kahraman (2019), where the hesitancy, membership and non-membership degrees of a decision maker can be assigned by satisfying unit sphere condition.
Our proposed method combines the ultimate flanks of all AHP extensions in fuzzy environment by exposing the assignment of indeterminacy and proposing a large preference domain for evaluator’s judgements. The objective of our paper is to present the interval-valued spherical fuzzy AHP method and its first application on examining the quality of public bus transportation in Mersin Municipality, Turkey, by a questionnaire survey with three conflicting participant groups.
3Interval-Valued Spherical Fuzzy Sets: Preliminaries
Spherical fuzzy sets (SFS) have recently been introduced to the literature with some advantages. In this type of fuzzy sets, a larger preference domain is defined for evaluators to assign membership functions. The only constraint is that the squared sum of the spherical parameters is allowed to be at most 1.0. The spherical fuzzy sets are represented by three functions expressing the degree of membership, the degree of indeterminacy and the degree of non-membership. Spherical fuzzy set based models can be employed in situations requiring human opinions concerning more responses of types: true, hesitant, false, and refusal degrees. Basically, SFS are a generalization of Pythagorean Fuzzy Sets, and picture fuzzy sets (Gündoğdu and Kahraman, 2019, 2020; Ashraf et al., 2019). In the following, definition of single-valued spherical fuzzy sets is presented:
Definition 3.1.
Single-valued Spherical Fuzzy Sets (SFS)
(1)
(2)
(3)
For each x, the numbers
Interval-valued fuzzy sets are used for incorporating a larger uncertainty on the parameters of a fuzzy set into the model with an interval instead of a single point. Hence, interval-valued SFS should be preferred when you are not sure about the values of membership, non-membership and hesitancy degrees of a spherical fuzzy set. In this section, definition of Interval-valued spherical fuzzy sets (IV-SFS) is summarized and arithmetic operators, aggregation operations and score functions are given.
Definition 3.2.
An Interval-valued Spherical Fuzzy Set
(4)
The pair
Definition 3.3.
Let
(5)
(6)
(7)
(8)
Multiplication by a scalar:
(9)
kth Power of
(10)
Definition 3.4.
Interval-Valued Spherical Weighted Arithmetic Mean (IVSWAM) with respect to,
(11)
Definition 3.5.
Interval-Valued Spherical Geometric Mean (IVSWGM) is presented in Eq. (12) under the same conditions that are defined in Definition 3.4.
(12)
Definition 3.6.
The score function is used for the comparison of two IV-SFS number. The score function of IV-SFS number
(13)
Definition 3.7.
The accuracy function of IV-SFS number
(14)
4Extension of AHP with Interval-Valued Spherical Fuzzy Sets
The proposed interval-valued spherical fuzzy AHP (ISF-AHP) method consists of several steps as given in this section.
Step 1. Form the hierarchical structure based on four levels
In this step, a hierarchical structure consisting of at least three levels is developed. Level 1 shows an objective that means selecting the best alternative based on score index. The score index is estimated based on a finite set of criteria
Step 2. Construct pairwise comparison matrices
Pairwise comparisons using interval-valued spherical fuzzy evaluation matrices are constructed based on the linguistic terms of importance given in Table 1. The consistency ratio of each pairwise comparison matrix is calculated. For this purpose, switch the linguistic terms in the pairwise comparison matrix to their corresponding score indices given in Table 1. Then, apply the classical consistency check ratio formula (Zeshui and Cuiping, 1999). It can be said that pairwise comparison matrices are consistent, when the consistency ratio is less than 10%. Otherwise, decision-makers must consider their judgements once again.
Step 3. Aggregate the individual evaluator groups’ interval-valued spherical fuzzy weights
Table 1
Linguistic terms used for pairwise comparisons (Gündoğdu and Kahraman, 2020).
| Linguistic terms | Score index | |
| Absolutely More Importance (AMI) | 9 | |
| Very High Importance (VHI) | 7 | |
| High Importance (HI) | 5 | |
| Slightly More Importance (SMI) | 3 | |
| Equal Importance (El) | 1 | |
| Slightly Low Importance (SLI) | 1/3 | |
| Low Importance (LI) | 1/5 | |
| Very Low Importance (VLI) | 1/7 | |
| Absolutely Low Importance (ALI) | 1/9 |
In the real-life problems, there can be many different types of evaluators. Firstly, to get individual evaluator groups’ weights
Step 4. Constitute the interval-valued spherical fuzzy local weights of each criterion
Then, to obtain the interval-valued spherical fuzzy local weights
Step 5. Construct the hierarchical form to obtain global weights
Eq. (15) defuzzified the criteria weights by using a modified score function. 1.0 is added to the previous definition of score function since a positive score value may be more useful for spherical calculations.
(15)
Step 6. The local weights at each level are multiplied by each related sub-criterion local weight to estimate the final global weights
(16)
After this calculation, normalized global weights of each criterion and sub-criterion are obtained. If alternatives exist in the problem, algorithm must continue with Step 7.
Step 7. Compute the weighted decision matrix and find the global preference weights
The normalized global criteria weights
(17)
The final spherical fuzzy AHP score
(18)
Step 8. Defuzzify the final score of each alternative and normalize the defuzzified values using the Eq. (15) and Eq. (16), respectively.
Step 9. Determine the rank among alternatives with respect to the normalized and defuzzified final scores. The best alternative has the largest final score value.
5A Case Study: Assessment of Public Transportation
To demonstrate our proposed novel interval-valued spherical fuzzy AHP methodology, we utilize a case study given by Duleba and Moslem (2019). The presented study is implemented to evaluate citizen demands for public bus transportation in Mersin city, Turkey. The survey was performed between July and September 2017. In this real-life case study, there are 97 evaluators (17 government representatives in the transportation field, 40 public passengers, and 40 non-passengers who participated in the survey for evaluating public transportation. In addition, the composed data has been examined using an interval-valued spherical fuzzy analytic hierarchy process (ISF-AHP) to accomplish the overall weights from three different evaluator’s groups, viz. passengers, non-passenger citizens and the representatives of transportation department in the municipality.
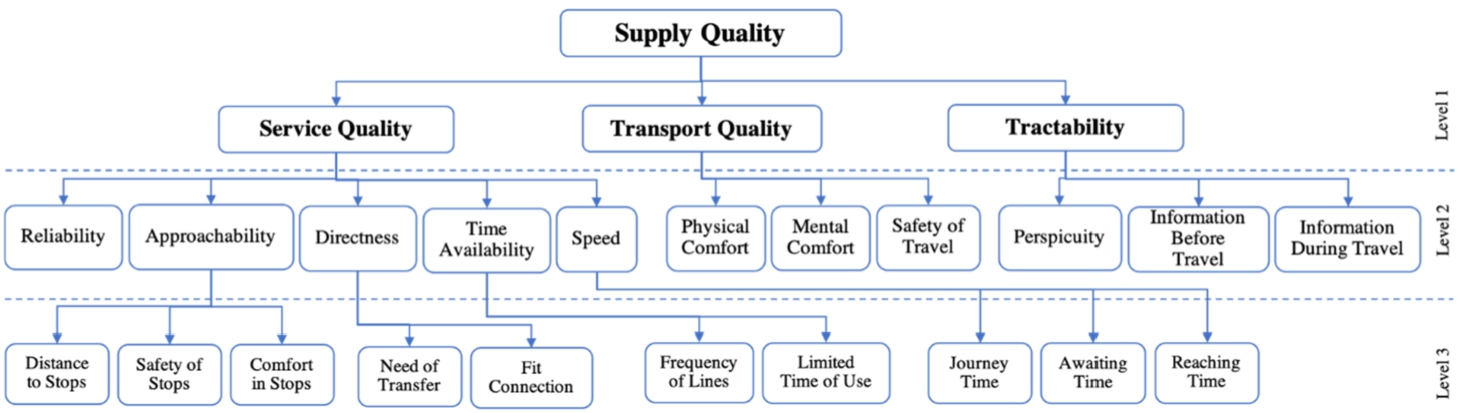
In this case study, no alternatives were used, only the weight score of each criterion was analysed. Hence, first five steps of the proposed method were performed. In Fig. 1, there are three levels and the 1st level consists of three main criteria which are service quality, transport quality and tractability. In Level 2, there are many sub-criteria which are related to the main criteria. Then, Level 2 items have been specified in more detail on the third level.
As an initial step, pairwise comparisons using interval-valued spherical fuzzy evaluation matrices are constructed based on the linguistic terms in Table 1 in terms of three different types of evaluators. The consistency ratio of each pairwise comparison matrix is calculated based on the corresponding score indices in Table 1 by applying the classical consistency measurement. The consistency ratio of each pairwise comparison matrix is less than 10%, that means all matrices are tolerably consistent.
Figure 1 demonstrates how the attributes of public transport supply quality are structured into a three-level hierarchy. Level 1 is the most general and contains three big items of satisfaction measure. Service quality can be defined by those service elements which are dominantly pre-transport (e.g. reaching the nearest bus stop, waiting for the certain line in the stops) or post-transport (e.g. connecting vehicles, transfer) and the total speed of travel is also allocated to this general attribute. Transport quality covers all criteria that can be associated with the presence of the passengers on the vehicle, thus the physical comfort (available seats or air-conditioning), the mental comfort (politeness of the driver, disturbances by other passengers) and the safety of travel (feeling safe during the journey) belong here. Tractability contains all attributes connected to the information about the trips; perspicuity means the understandability of timetables, while information before and during the travel reflects the provided information to the potential or real passengers.
Perhaps some more items need to be explained in more detail. Directness reflects the necessity of changing lines and vehicles for reaching the final destination. The limited time of use is the attribute that expresses the first line in the early hours and the last line in the late hours on a certain day. In the hierarchy, each attribute is explained by the lower level elements connected to the certain attribute.
Table 2
Interval-valued spherical fuzzy weights and defuzzified local weights with respect to main criteria.
| Passengers’ assessments | |||
| Service quality | ([0.57, 0.66], [0.33, 0.42], [0.23, 0.30]) | ||
| Transport Quality | ([0.69, 0.81], [0.22, 0.29], [0.20, 0.26]) | ||
| Tractability | ([0.32, 0.36], [0.66, 0.76], [0.21, 0.30]) | ||
| Non-passengers’ assessments | |||
| Service Quality | ([0.33, 0.38], [0.60, 0.71], [0.24, 0.32]) | ([0.39, 0.45], [0.56, 0.66], [0.23, 0.31]) | 0.761 |
| Transport quality | ([0.51, 0.59], [0.37, 0.45], [0.25, 0.32]) | ([0.58, 0.68], [0.32, 0.40], [0.23, 0.30]) | 1.235 |
| Tractability | ([0.71, 0.83], [0.21, 0.27], [0.18, 0.25]) | ([0.52, 0.60], [0.45, 0.55], [0.21, 0.30]) | 1.032 |
| Decision-makers’ Assessments | |||
| Service quality | ([0.32, 0.36], [0.66, 0.76], [0.21, 0.30]) | ||
| Transport quality | ([0.57, 0.66], [0.35, 0.44], [0.22, 0.29]) | ||
| Tractability | ([0.71, 0.83], [0.21, 0.27], [0.18, 0.25]) | ||
Based on Table 2, passenger evaluator group of the analysed public transportation system specified the development of “Transport quality” as the most important issue; but the decision maker and non-passenger groups specified the development of “Tractability” as the most important attribute. After aggregation and normalization steps “Tractability” development is the essential issue for passenger, decision maker and non-passenger participants.
Table 3
Interval-valued spherical fuzzy weights and defuzzified local weights with respect to sub-criteria of “Transport Quality”.
| Passengers’ assessments | |||
| Physical comfort | ([0.45, 0.52], [0.44, 0.52], [0.25, 0.33]) | ||
| Mental comfort | ([0.34, 0.38], [0.59, 0.70], [0.24, 0.32]) | ||
| Safety of travel | ([0.74, 0.86], [0.19, 0.25], [0.17, 0.23]) | ||
| Non-passengers’ assessments | |||
| Physical comfort | ([0.33, 0.38], [0.60, 0.71], [0.24, 0.32]) | ([0.48, 0.55], [0.46, 0.55], [0.23, 0.31]) | 0.977 |
| Mental comfort | ([0.51, 0.59], [0.37, 0.45], [0.25, 0.32]) | ([0.43, 0.49], [0.48, 0.58], [0.25, 0.33]) | 0.887 |
| Safety of travel | ([0.62, 0.72], [0.26, 0.32], [0.23, 0.29]) | ([0.54, 0.62], [0.41, 0.49], [0.22, 0.30]) | 1.096 |
| Decision-makers’ assessments | |||
| Physical comfort | ([0.74, 0.86], [0.19, 0.25], [0.17, 0.23]) | ||
| Mental comfort | ([0.45, 0.52], [0.44, 0.52], [0.25, 0.33]) | ||
| Safety of travel | ([0.34, 0.38], [0.59, 0.70], [0.24, 0.32]) | ||
Table 3 indicates that the most important attribute is “Safety of travel” for passenger and non-passenger evaluator groups in the development of “Transport quality”; but the decision maker group specified the development of “Physical comfort” as the most important issue. After aggregation and normalization steps, development of “Safety of travel” is the essential attribute for passenger, decision maker and non-passenger participants.
Table 4
Interval-valued spherical fuzzy weights and defuzzified local weights with respect to sub-criteria of “Tractability”.
| Passengers’ assessments | |||
| Perspicuity | ([0.34, 0.38], [0.59, 0.70], [0.24, 0.32]) | ||
| Information before travel | ([0.46, 0.53], [0.40, 0.48], [0.27, 0.34]) | ||
| Information during travel | ([0.69, 0.81], [0.22, 0.29], [0.20, 0.26]) | ||
| Non-passengers’ assessments | |||
| Perspicuity | ([0.32, 0.36], [0.66, 0.76], [0.21,0.30]) | ([0.39, 0.45], [0.56, 0.66], [0.23, 0.31]) | 0.763 |
| Information before travel | ([0.69, 0.81], [0.22, 0.29], [0.20,0.26]) | ([0.61, 0.71], [0.29, 0.36], [0.22, 0.29]) | 1.296 |
| Information during travel | ([0.57, 0.66], [0.33, 0.42], [0.23,0.30]) | ([0.50, 0.58], [0.47, 0.56], [0.22, 0.30]) | 0.990 |
| Decision-makers’ assessments | |||
| Perspicuity | ([0.57, 0.66], [0.35, 0.44], [0.22, 0.29]) | ||
| Information before travel | ([0.71, 0.83], [0.21, 0.27], [0.18, 0.25]) | ||
| Information during travel | ([0.32, 0.36], [0.66, 0.76], [0.21, 0.30]) | ||
Table 4 shows that the most important sub-criterion is “Information during travel” for passenger evaluator group in the development of “Tractability”; however, the decision-maker and non-passenger evaluators’ group specified the development of “Information before travel” as the most important issue and also this sub-criterion must be considered after all steps have been performed.
Table 5
Interval-valued spherical fuzzy weights and defuzzified local weights with respect to sub-criteria of “Service Quality”.
| Passengers’ assessments | |||
| Approachability | ([0.70, 0.81], [0.20, 0.26], [0.19, 0.25]) | ||
| Directness | ([0.38, 0.45], [0.50, 0.58], [0.24, 0.31]) | ||
| Time availability | ([0.63, 0.75], [0.26, 0.33], [0.21, 0.27]) | ||
| Speed | ([0.28, 0.32], [0.67, 0.77], [0.20,0.28]) | ||
| Reliability | ([0.52, 0.61], [0.36, 0.44], [0.23,0.30]) | ||
| Non-passengers’ assessments | |||
| Approachability | ([0.29, 0.33], [0.63, 0.74], [0.22, 0.29]) | ([0.50, 0.59], [0.43, 0.53], [0.21, 0.29]) | 1.033 |
| Directness | ([0.58, 0.68], [0.28, 0.35], [0.23, 0.29]) | ([0.49, 0.57], [0.39, 0.47], [0.24, 0.30]) | 1.055 |
| Time availability | ([0.38, 0.44], [0.51, 0.60], [0.24, 0.31]) | ([0.46, 0.55], [0.43, 0.52], [0.23, 0.30]) | 0.993 |
| Speed | ([0.48, 0.56], [0.38, 0.46], [0.25, 0.31]) | ([0.45, 0.53], [0.48, 0.58], [0.22, 0.29]) | 0.925 |
| Reliability | ([0.73, 0.85], [0.19, 0.25], [0.17, 0.24]) | ([0.47, 0.55], [0.49, 0.59], [0.20, 0.28]) | 0.934 |
| Decision-makers’ assessments | |||
| Approachability | ([0.63, 0.75], [0.26, 0.33], [0.21, 0.28]) | ||
| Directness | ([0.52, 0.61], [0.36, 0.44], [0.23, 0.30]) | ||
| Time availability | ([0.42, 0.49], [0.47, 0.56], [0.23, 0.30]) | ||
| Speed | ([0.70, 0.81], [0.20, 0.26], [0.19, 0.25]) | ||
Table 5 indicates that for the development of “Service Quality”, the most important sub-criterion is “Speed” for decision-makers, “Reliability” for non-passengers and “Approachability” for passengers. When the individual weights are aggregated, the important sub-criterion is “Directness”.
Table 6
Interval-valued spherical fuzzy weights and defuzzified local weights for 3rd Level with respect to sub-criteria of “Approachability”.
| Passengers’ assessments | |||
| Distance to stop | ([0.65, 0.75], [0.24, 0.30], [0.22, 0.28]) | ||
| Safety of stops | ([0.45, 0.53], [0.42, 0.50], [0.26, 0.33]) | ||
| Comfort in stops | ([0.34, 0.39], [0.57, 0.67], [0.25, 0.33]) | ||
| Non-passengers’ assessments | |||
| Distance to stop | ([0.35, 0.40], [0.54, 0.64], [0.26, 0.34]) | ([0.42, 0.48], [0.53, 0.63], [0.23, 0.32]) | 0.826 |
| Safety of stops | ([0.57, 0.66], [0.28, 0.35], [0.25, 0.32]) | ([0.53, 0.61], [0.36, 0.43], [0.24, 0.31]) | 1.130 |
| Comfort in stops | ([0.46, 0.53], [0.40, 0.48], [0.27, 0.34]) | ([0.48, 0.56], [0.43, 0.52], [0.24, 0.32]) | 1.006 |
| Decision-makers’ assessments | |||
| Distance to stop | ([0.32, 0.36], [0.66, 0.76], [0.21, 0.30]) | ||
| Safety of stops | ([0.57, 0.66], [0.35, 0.44], [0.22, 0.29]) | ||
| Comfort in stops | ([0.71, 0.83], [0.21, 0.27], [0.18, 0.25]) | ||
In view of Level 3, Table 6 shows that the most important sub-criterion is “Distance to stop” for passenger evaluator group, “Safety of Stops” for non-passenger group and “Comfort in Stops” for government representatives in the development of “Approachability”. After aggregation step, “Safety of stops” is the most important sub-criterion based on local weights.
Table 7
Interval-valued spherical fuzzy weights and defuzzified local weights for 3rd Level with respect to sub-criteria of “Speed”.
| Passengers’ assessments | |||
| Journey time | ([0.45, 0.52], [0.44, 0.52], [0.25, 0.33]) | ||
| Awaiting time | ([0.34, 0.38], [0.59, 0.70], [0.24, 0.32]) | ||
| Time to reach stops | ([0.74, 0.86], [0.19, 0.25], [0.17, 0.23]) | ||
| Non-passengers’ assessments | |||
| Journey time | ([0.46, 0.53], [0.40, 0.48], [0.27, 0.34]) | ([0.50, 0.58], [0.37, 0.45], [0.25, 0.32]) | 1.085 |
| Awaiting time | ([0.44, 0.49], [0.48, 0.58], [0.29, 0.38]) | ([0.37, 0.41], [0.56, 0.67], [0.25, 0.34]) | 0.726 |
| Time to reach stops | ([0.52, 0.59], [0.37, 0.45], [0.28, 0.37]) | ([0.58, 0.67], [0.32, 0.40], [0.24, 0.32]) | 1.220 |
| Decision-makers’ assessments | |||
| Journey time | |||
| Awaiting time | |||
| Time to reach stops | |||
In view of Level 3, Table 7 indicates that the most important concern is “Time to reach stops” for passenger and non-passenger evaluator groups, whereas “Journey time” is the essential criterion for government representatives in the development of sub-criterion of “Speed”. According to the local weights, “Time to reach stops” is assumed as important concern.
Table 8
Interval-valued spherical fuzzy weights and defuzzified local weights for 3rd Level with respect to sub-criteria of “Directness”
| Passengers’ assessments | |||
| Need of transfer | ([0.53, 0.60], [0.34, 0.41], [0.27, 0.35]) | ||
| Fit connection | ([0.40, 0.45], [0.50, 0.60], [0.28, 0.36]) | ||
| Non-passengers’ assessments | |||
| Need of transfer | ([0.37, 0.42], [0.62, 0.72], [0.23, 0.33]) | ([0.42, 0.48], [0.54, 0.64], [0.25, 0.34]) | 0.811 |
| Fit connection | ([0.74, 0.86], [0.21, 0.29], [0.17, 0.24]) | ([0.58, 0.66], [0.35, 0.44], [0.24, 0.32]) | 1.188 |
| Decision-makers’ assessments | |||
| Need of transfer | ([0.38, 0.43], [0.58, 0.68], [0.25, 0.34]) | ||
| Fit connection | ([0.65, 0.75], [0.26, 0.33], [0.22, 0.29]) | ||
“Fit connection” is a more important sub-criterion than “Need of transfer” in the improvement of “Directness” as shown in Table 8.
Table 9
Interval-valued spherical fuzzy weights and defuzzified local weights for 3rd Level with respect to sub-criteria of “Time availability”.
| Passengers’ assessments | |||
| Frequency of lines | ([0.65, 0.75], [0.26, 0.33], [0.22, 0.29]) | ||
| Limited time of use | ([0.38, 0.43], [0.58, 0.68], [0.25, 0.34]) | ||
| Non-passengers’ assessments | |||
| Frequency of lines | ([0.53, 0.60], [0.34, 0.41], [0.27, 0.35]) | ([0.50, 0.57], [0.45, 0.54], [0.25, 0.34]) | 1.002 |
| Limited time of use | ([0.40, 0.45], [0.50, 0.60], [0.28, 0.36]) | ([0.48, 0.55], [0.47, 0.57], [0.25, 0.34]) | 0.954 |
| Decision-makers’ assessments | |||
| Frequency of lines | ([0.37, 0.42], [0.62, 0.72], [0.23, 0.33]) | ||
| Limited time of use | ([0.74, 0.86], [0.21, 0.29], [0.17, 0.25]) | ||
“Frequency of lines” is slightly more significant sub-criterion than “Limited time of use” in the improvement of “Time availability” as given in Table 9.
To obtain global weights of each criterion and sub-criterion, the local weights at each level are multiplied by each related sub-criterion local weight. After this multiplication, Eq. (16) can be used to normalize the global criteria weights to estimate final weights as given in Table 10.
Table 10
Final weights for all hierarchical levels.
| Level 1 | Level 2 | Level 3 | |||
| Criteria | Final weight | Sub-criteria | Final weight | Sub-criteria | Final weight |
| Service quality | 0.251 | Approachability | 0.0745 | Distance to stop | 0.0861 |
| Safety of stops | 0.1178 | ||||
| Comfort in stops | 0.1048 | ||||
| Directness | 0.0760 | Need of transfer | 0.0863 | ||
| Fit connection | 0.1264 | ||||
| Time availability | 0.0716 | Frequency of lines | 0.1004 | ||
| Limited time of use | 0.0955 | ||||
| Speed | 0.0667 | Journey time | 0.1012 | ||
| Awaiting time | 0.0677 | ||||
| Time to reach stops | 0.1138 | ||||
| Reliability | 0.0673 | – | – | ||
| Tractability | 0.341 | Perspicuity | 0.0745 | – | – |
| Information before travel | 0.1266 | – | – | ||
| Information during travel | 0.0967 | – | – | ||
| Transport quality | 0.408 | Physical comfort | 0.1143 | – | – |
| Mental comfort | 0.1037 | – | – | ||
| Safety of travel | 0.1282 | – | – | ||
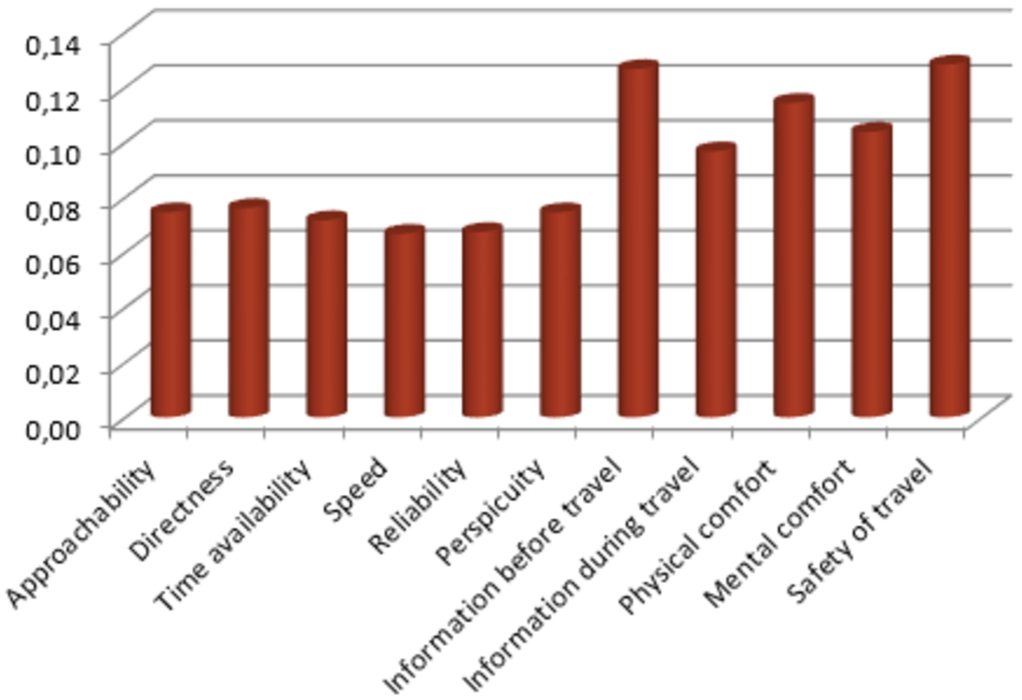
The comparison of Level 2 sub-criteria is given in Fig. 2. Based on the comparison, the improvement of “Safety of travel”, “Information before travel” and “Physical comfort” are the most important issues while that of “Speed”, “Reliability”, and “Time availability” ranked lower than the eleven other criteria compared at this level.
Fig. 2
Final scores for aggregating different evaluator groups on Level 2.
In terms of “Service Quality”, each sub-criterion is detailed with the third level items. For instance, the “Directness” is associated with two items which are “Need of transfer” and “Fit connection” (Fig. 3).
Fig. 3
Final scores for aggregating different evaluator groups on Level 3.
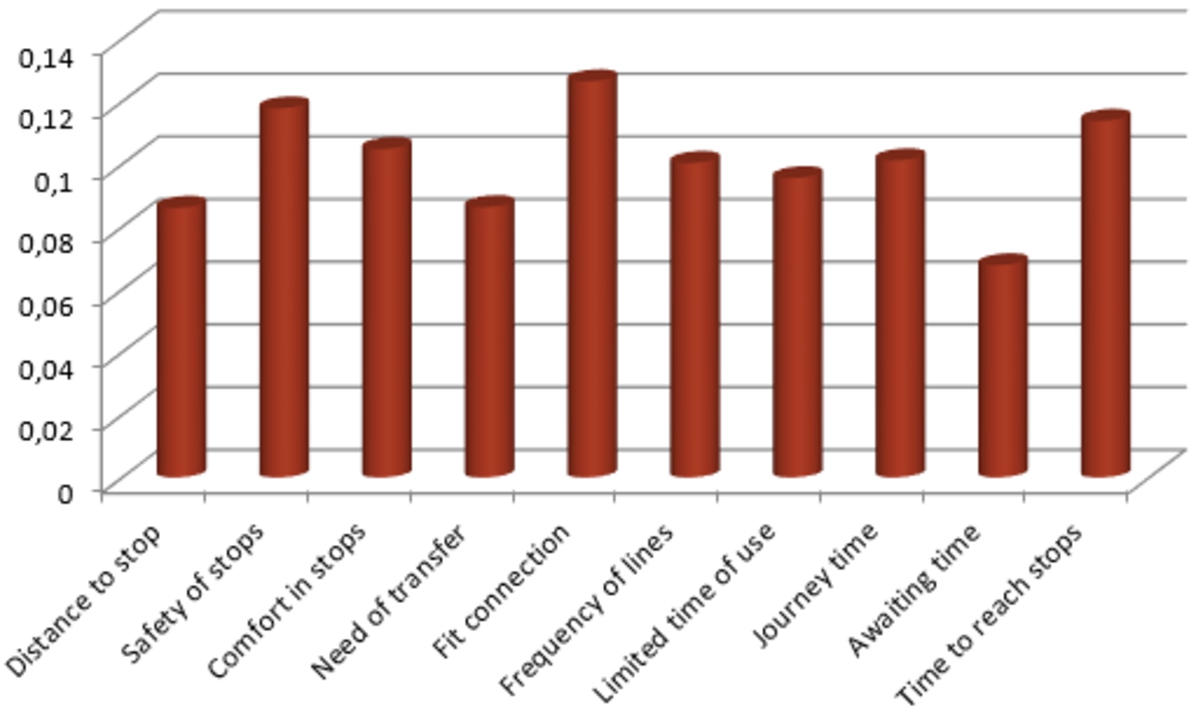
At the third level, “Fit connection” is the most essential issue to be developed for the evaluators, followed by “Safety of stops”, “Time to reach stops” and “Comfort in stops”. However, the results of this level indicated that “Awaiting time” is not as important as the other criteria and ranked lowest with a weight of less than 0.07.
The applied model has provided useful information in terms of of public transport development for transport planners. The best possible development scheme, which considers all aspects of passengers, non-passenger citizens and the local municipality, in our case, is the focus on transport quality issues, especially increasing the safety of travel and the physical comfort of the passengers. This could be reached by better maintenance of the vehicles and training of the drivers to achieve a safer driving style and increased physical comfort during the journey. Another important issue could be a better presentation of information to the passengers before the travel by e.g. an online information platform or more informative timetables. Furthermore, all stakeholder groups agree on the need for more fit connections between lines in order to reduce the time gap when changing vehicles. The planners should pay increased attention to the non-direct trips of the citizens and synchronize the timetables of different bus lines and tram or train connections. Also, the safety of the bus stops is recommended to be increased by the more proper creation of stop sites integrated to the traffic. As it can be seen, the application of our model can be a direct help for setting up transport amelioration agenda in the examined city.
6Comparative Analysis
To investigate the influence of the methodology on the results, in this section, we have performed a comparative analysis using a different AHP approach. To do this, Picture fuzzy AHP methodology that was developed by Gündoğdu et al. (2021) will be utilized. The steps of the picture fuzzy AHP are given as follows:
Step 1. Construct the linguistic judgements’ matrices. The same linguistic terms given in Section 5 have been used for the Picture fuzzy AHP method. These linguistic terms are converted into picture fuzzy numbers which contain membership, non-membership and hesitancy degrees. Based on Table 11.
Step 2. Aggregate the stakeholders’ judgements to get local weights by using picture fuzzy geometric mean operator given in Eq. (19).
(19)
Table 11
Picture fuzzy linguistic terms and equivalent numbers.
| Linguistic terms | Picture fuzzy numbers | Intensity of importance |
| Absolutely High Importance (AHI) | 9 | |
| Very High Importance (VHI) | 7 | |
| High Importance (HI) | 5 | |
| Slightly High Importance (SMI) | 3 | |
| Equal Importance (El) | 1 | |
| Slightly Low Importance (SLI) | 1/3 | |
| Low Importance (LI) | 1/5 | |
| Very Low Importance (VLI) | 1/7 | |
| Absolutely Low Importance (ALI) | 1/9 |
Step 3. Obtain global weights of each criterion by aggregating the s decision-maker’s judgements
(20)
Step 4. Obtain the final picture fuzzy weights for each criterion and sub-criterion by utilizing Eq. (21)
(21)
Step 5. Defuzzify and normalize final picture fuzzy weights by using Eq. (22) and Eq. (23), respectively.
(22)
(23)
Table 12
Final weights for all hierarchical levels.
| Levels | Criteria | Final weights | Rank |
| Level 1 | Service quality | 0.221 | 3 |
| Transport quality | 0.445 | 1 | |
| Tractability | 0.334 | 2 | |
| Level 2 | Approachability | 0.070 | 7 |
| Directness | 0.071 | 6 | |
| Time availability | 0.061 | 9 | |
| Speed | 0.059 | 11 | |
| Reliability | 0.059 | 10 | |
| Physical comfort | 0.126 | 3 | |
| Mental comfort | 0.105 | 4 | |
| Safety of travel | 0.151 | 1 | |
| Perspicuity | 0.062 | 8 | |
| Information before travel | 0.144 | 2 | |
| Information during travel | 0.090 | 5 | |
| Level 3 | Directness to stop | 0.084 | 8 |
| Safety of stops | 0.128 | 2 | |
| Comfort in stops | 0.109 | 4 | |
| Need for transfer | 0.073 | 9 | |
| Fit connection | 0.141 | 1 | |
| Frequency of lines | 0.087 | 7 | |
| Limited time of use | 0.101 | 5 | |
| Journey time | 0.095 | 6 | |
| Awaiting time | 0.061 | 10 | |
| Time to reach stops | 0.121 | 3 |
As seen from Table 12, “Transport Quality” is also the most important criterion in Level 1. Based on the comparison of Level 2, the improvement of “Safety of travel”, “Information before travel”, and “Physical Comfort” are the most critical issues like our case study. In Level 3, the “Fit connection” criterion is the critical quality aspect as well. The comparative results indicate that the final weights are not the same with the proposed approach but the ranking of the criteria is almost the same in both methods. In terms of membership degrees, both methodologies have the same assumptions. However, the interval-valued spherical fuzzy AHP method presents the decision maker a more comprehensive range of membership function definitions.
7Discussion
Based on the demonstrated results, the merit of interval-valued spherical fuzzy set model is palpable in creating consensus among different stakeholder groups. The practical implications of the paper are as follows. In the proposed ISF-AHP model, decision-makers can assign linguistic terms given in Table 1. However, they may assign intermediate linguistic terms when they are indifferent between two successive terms. Their corresponding numerical values have been readily taken from the linguistic scales given in the paper. Decision-makers’ judgements could be easily aggregated by using interval-valued spherical fuzzy geometric and arithmetic aggregation operators. Vagueness and impreciseness in public transportation design are considered by interval-valued spherical fuzzy sets. A larger domain is used for assigning membership, non-membership and hesitancy degrees.
As presented, the conflicting evaluator groups had significantly different priority ranking in all levels and without the application of the model, the consensus could have been merely reached by another voting round, negotiations or assigning subjective weights to group opinions.
Note that creating the final weights is fair and democratic from many aspects in ISF-AHP methodology. First, the evaluators themselves determine their confidence in scoring not only within the specific group but also globally, in the consideration of all groups.
In addition, the defuzzification process in the calculation of the criteria weights has an important role. Nevertheless, in the literature, defuzzification has not yet been extensively studied as interval-valued spherical fuzzy sets have recently been introduced. Novel definitions for defuzzification formula may lead to slight differences on criteria weights. However, until the last step, we do not need to use the defuzzification formula.
Further, in the analysis, the case of agreed prioritization of two groups (dominancy over the third group) determines the final result, which means that the extreme opinion of a specific stakeholder cannot abuse the majority of responses and other opinions are still considered and dominancy is kept. See the example of the first level (Table 2) in which Tractability gained the majority by two stakeholders, while the priority of the passenger evaluator group (Transport quality as the most important attribute) got minority, thus Tractability became the overall first positioned criterion. Level 2 also demonstrates this logic, e.g. Table 3 presents that since two groups voted for Safety of travel, the overall result considered this dominancy.
Another essential characteristic of the new ISF-AHP methodology is that in case of very conflicting group priorities, the final priority can be such ranking that is different from all stakeholder groups’ ranking. See the example of the second level. For Service quality elements (Table 5), passengers voted for Approachability as the most crucial criterion, Non-passengers for Reliability and Government for Speed. Since the attribute Directness gained high scores even if it was not ranked first from any of the stakeholders, in the final consensus it could gain the first position. In our esteem, this is a very democratic consensus creation, because none of the groups should convince the others for accepting its opinion, in case of non-approximating priorities, a new ranking can be created which is acceptable for all groups.
8Conclusion
This paper aimed to introduce a new interval-valued spherical fuzzy set model for the consideration of vague and less confident responses and the creation of consensus in the case of participating evaluator groups with different motivation, interest or information related to the decision problem. For this purpose, the selected case study on the public transport development of Mersin with applying passenger, non-passenger and government stakeholders has been proven convenient.
The model characteristics of IV-SFS made possible not only the consideration of imprecise or hesitant scoring by the fuzzification and interval approach, but also the synthesis of the different opinions by treating the groups themselves as individuals in the overall calculation, following the spherical fuzzy logic intra and extra groups.
Results show that the model is suitable for survey analysis, especially when involving non-expert evaluators and heterogeneous respondent pattern in complex decision making. Besides, a comparative analysis is performed to show the validity of the proposed methodology. The results demonstrate that both approaches have proposed the same ranking. We can conclude that our methodology is robust. The main advantage of the interval-valued spherical fuzzy AHP method is that it is presenting a more comprehensive domain of membership function definitions to the decision-makers. As all methodologies, the introduced model also has some limitations. The model in its current form is not capable of a priori differentiation among fixed group weights in the decision. In reality, it is possible that a certain participatory stakeholder (e.g. government) by its position claim higher weight in the final decision than the others.
We did not include this possibility, because in the case study, this requirement did not emerge. We note, however, that it is possible to integrate a priori stakeholder weights in the ISFS methodology, merely an extra calculation step should be added.
Also, the defuzzification step of the methodology could be considered as subjective and might be further sophisticated. For the first introduction of the method, this step could be regarded as suitable in the current case but we accept other approaches for this defuzzification phase of the ISF-AHP procedure.
As a remark for further research, the comparison of the introduced model’s outcomes with the results of other possible group consensus creation methods including Multi-actor, Multi-criteria Analysis, MAMCA (Macharis and Bernardini, 2015), Bayesian approach (Gargallo et al., 2007) or preference maps (Triantaphyllou et al., 2020) can be suggested. It would also be interesting to apply rank correlation methods e.g. Spearman or Kendall concordance calculations to reveal the strength of concordance for each consensus creation method in the group-wise and the gained consensual priority rankings. We assume that the technique with the highest concordance score for the stakeholder and global rankings reflects the real intentions of the participants in opinion synthesis the best.
Acknowledgements
The first author would like to thank the support of MTA Bolyai research scholarship, No. BO/8/20.
References
1 | Abastante, F., Corrente, S., Greco, S., Ishizaka, A., Lami, I.M. ((2019) ). A new parsimonious AHP methodology: assigning priorities to many objects by comparing pairwise few reference objects. Expert Systems with Applications, 127: , 109–120. https://doi.org/10.1016/j.eswa.2019.02.036. |
2 | Abdel-Basset, M., Mohamed, M., Zhou, Y., Hezam, I. ((2017) ). Multi-criteria group decision making based on neutrosophic analytic hierarchy process. Journal of Intelligent and Fuzzy Systems, 33: (6), 4055–4066. https://doi.org/10.3233/JIFS-17981. |
3 | Abdullah, L., Najib, L. ((2014) ). A new type-2 fuzzy set of linguistic variables for the fuzzy analytic hierarchy process. Expert Systems with Applications, 41: (7), 3297–3305. https://doi.org/10.1016/j.eswa.2013.11.028. |
4 | Abdullah, L., Najib, L. ((2016) ). A new preference scale mcdm method based on interval-valued intuitionistic fuzzy sets and the analytic hierarchy process. Soft Computing, 20: (2), 511–523. https://doi.org/10.1007/s00500-014-1519-y. |
5 | Ashraf, S., Abdullah, S., Aslam, M., Qiyas, M., Kutbi, M.A. ((2019) ). Spherical fuzzy sets and its representation of spherical fuzzy t-norms and t-conorms. Journal of Intelligent and Fuzzy Systems, 36: (6), 6089–6102. |
6 | Atanassov, K.T. ((1986) ). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20: (1), 87–96. https://doi.org/10.1016/S0165-0114(86)80034-3. |
7 | Awasthi, A., Chauhan, S.S. ((2011) ). Using AHP and Dempster–Shafer theory for evaluating sustainable transport solutions. Environmental Modelling and Software, 26: (6), 787–796. https://doi.org/10.1016/j.envsoft.2010.11.010. |
8 | Bolturk, E., Kahraman, C. ((2018) ). A novel interval-valued neutrosophic AHP with cosine similarity measure. Soft Computing, 22: (15), 4941–4958. https://doi.org/10.1007/s00500-018-3140-y. |
9 | Boltürk, E., Çevik Onar, S., Öztayşi, B., Kahraman, C., Goztepe, K. ((2016) ). Multi-attribute warehouse location selection in humanitarian logistics using hesitant fuzzy AHP. International Journal of the Analytic Hierarchy Process, 8: (2), 271–298. https://doi.org/10.13033/ijahp.v8i2.387. |
10 | Bozóki, S., Csató, L., Temesi, J. ((2016) ). An application of incomplete pairwise comparison matrices for ranking top tennis players. European Journal of Operational Research, 248: (1), 211–218. https://doi.org/10.1016/j.ejor.2015.06.069. |
11 | Buckley, J.J. ((1985) ). Fuzzy hierarchical analysis. Fuzzy Sets and Systems, 17: (3), 233–247. https://doi.org/10.1016/0165-0114(85)90090-9. |
12 | Chiclana, F., Herrera, F., Herrera-Viedma, E. ((2001) ). Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets and Systems, 122: (2), 277–291. https://doi.org/10.1016/S0165-0114(00)00004-X. |
13 | Cho, Y.-G., Cho, K.-T. ((2008) ). A loss function approach to group preference aggregation in the AHP. Computers and Operations Research, 35: (3), 884–892. https://doi.org/10.1016/j.cor.2006.04.008. |
14 | Chou, Y.-C., Yen, H.-Y., Dang, V.T., Sun, C.-C. ((2019) ). Assessing the human resource in science and technology for Asian countries: application of fuzzy AHP and fuzzy TOPSIS. Symmetry, 11: (2), 251. https://doi.org/10.3390/sym11020251. |
15 | Cu’ò’ng, B.C. ((2015) ). Picture fuzzy sets. Journal of Computer Science and Cybernetics, 30: (4), 409–420. https://doi.org/10.15625/1813-9663/30/4/5032. |
16 | Duleba, S., Moslem, S. ((2019) ). Examining Pareto optimality in analytic hierarchy process on real data: an application in public transport service development. Expert Systems with Applications, 116: , 21–30. https://doi.org/10.1016/j.eswa.2018.08.049. |
17 | Duleba, S., Mishina, T., Shimazaki, Y. ((2012) ). A dynamic analysis on public bus transport’s supply quality by using AHP. Transport, 27: (3), 268–275. https://doi.org/10.3846/16484142.2012.719838. |
18 | Efe, B. ((2016) ). An integrated fuzzy multi criteria group decision making approach for ERP system selection. Applied Soft Computing, 38: , 106–117. https://doi.org/10.1016/j.asoc.2015.09.037. |
19 | Erdoğan, M., Kaya, I. ((2016) ). Evaluating alternative-fuel busses for public transportation in Istanbul using interval type-2 fuzzy AHP and TOPSIS. Journal of Multiple-Valued Logic and Soft Computing, 26: (6), 625–642. |
20 | Gargallo, P., Moreno-Jiménez, J.M., Salvador, M. ((2007) ). AHP-group decision making: a Bayesian approach based on mixtures for group pattern identification. Group Decision and Negotiation, 16: (6), 485–506. https://doi.org/10.1007/s10726-006-9068-0. |
21 | Ghorbanzadeh, O., Moslem, S., Blaschke, T., Duleba, S. ((2019) ). Sustainable urban transport planning considering different stakeholder groups by an interval-AHP decision support model. Sustainability, 11: (1), 9. https://doi.org/10.3390/su11010009. |
22 | Gündoğdu, F.K., Kahraman, C. ((2019) ). Spherical fuzzy sets and spherical fuzzy TOPSIS method. Journal of Intelligent and Fuzzy Systems, 36: (1), 337–352. https://doi.org/10.3233/JIFS-181401. |
23 | Gündoğdu, F.K., Kahraman, C. ((2020) ). A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Computing, 24: (6), 4607–4621. https://doi.org/10.1007/s00500-019-04222-w. |
24 | Gündoğdu, F.K., Duleba, S., Moslem, S., Aydın, S. ((2021) ). Evaluating public transport service quality using picture fuzzy analytic hierarchy process and linear assignment model. Applied Soft Computing, 100: , 106920. |
25 | Ishizaka, A. ((2019) ). Analytic hierarchy process and its extensions. In: New Perspectives in Multiple Criteria Decision Making. Springer, pp. 81–93. https://doi.org/10.1007/978-3-030-11482-4_2. |
26 | Kahraman, C., Öztayşi, B., Uçal Sari, I., Turanoğlu, E. ((2014) ). Fuzzy analytic hierarchy process with interval type-2 fuzzy sets. Knowledge-Based Systems, 59: , 48–57. https://doi.org/10.1016/j.knosys.2014.02.001. |
27 | Kar, A.K. ((2015) ). A hybrid group decision support system for supplier selection using analytic hierarchy process, fuzzy set theory and neural network. Journal of Computational Science, 6: , 23–33. https://doi.org/10.1016/j.jocs.2014.11.002. |
28 | Karapetrovic, S., Rosenbloom, E.S. ((1999) ). A quality control approach to consistency paradoxes in AHP. European Journal of Operational Research, 119: (3), 704–718. https://doi.org/10.1016/S0377-2217(98)00334-8. |
29 | Kilic, M., Kaya, İ. ((2015) ). Investment project evaluation by a decision making methodology based on type-2 fuzzy sets. Applied Soft Computing, 27: , 399–410. https://doi.org/10.1016/j.asoc.2014.11.028. |
30 | Lane, E.F., Verdini, W.A. ((1989) ). A consistency test for AHP decision makers. Decision Sciences, 20: (3), 575–590. https://doi.org/10.1111/j.1540-5915.1989.tb01568.x. |
31 | Lee, J.-H., Li, T.-C. ((2011) ). Supporting user participation design using a fuzzy analytic hierarchy process approach. Engineering Applications of Artificial Intelligence, 24: (5), 850–865. https://doi.org/10.1016/j.engappai.2011.01.008. |
32 | Liao, H., Xu, Z. ((2015) ). Consistency of the fused intuitionistic fuzzy preference relation in group intuitionistic fuzzy analytic hierarchy process. Applied Soft Computing, 35: , 812–826. https://doi.org/10.1016/j.asoc.2015.04.015. |
33 | Lin, C., Kou, G., Peng, Y., Alsaadi, F.E. (2020). Aggregation of the nearest consistency matrices with the acceptable consensus in AHP-GDM. Annals of Operations Research, 1(17). https://doi.org/10.1007/s10479-020-03572-1. |
34 | Macharis, C., Bernardini, A. ((2015) ). Reviewing the use of multi-criteria decision analysis for the evaluation of transport projects: time for a multi-actor approach. Transport Policy, 37: , 177–186. https://doi.org/10.1016/j.tranpol.2014.11.002. |
35 | Minatour, Y., Bonakdari, H., Aliakbarkhani, Z.S. ((2016) ). Extension of fuzzy Delphi AHP based on interval-valued fuzzy sets and its application in water resource rating problems. Water Resources Management, 30: (9), 3123–3141. https://doi.org/10.1007/s11269-016-1335-5. |
36 | Mohd, W.R.W., Abdullah, L. (2017). Pythagorean fuzzy analytic hierarchy process to multi-criteria decision making. AIP Conference Proceedings, 1905. https://doi.org/10.1063/1.5012208. |
37 | Moslem, S., Ghorbanzadeh, O., Blaschke, T., Duleba, S. ((2019) ). Analysing stakeholder consensus for a sustainable transport development decision by the fuzzy AHP and interval AHP. Sustainability, 11: (12), 3271. https://doi.org/10.3390/su11123271. |
38 | Ossadnik, W., Schinke, S., Kaspar, R.H. ((2016) ). Group aggregation techniques for analytic hierarchy process and analytic network process: a comparative analysis. Group Decision and Negotiation, 25: (2), 421–457. https://doi.org/10.1007/s10726-015-9448-4. |
39 | Öztaysi, B., Onar, S.Ç., Boltürk, E., Kahraman, C. ((2015) ). Hesitant fuzzy analytic hierarchy process. In: 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp. 1–7, IEEE. https://doi.org/10.1109/FUZZ-IEEE.2015.7337948. |
40 | Pamučar, D., Stević, Ž., Zavadskas, E.K. ((2018) ). Integration of interval rough AHP and interval rough MABAC methods for evaluating university web pages. Applied Soft Computing, 67: , 141–163. https://doi.org/10.1016/j.asoc.2018.02.057. |
41 | Rallabandi, L.N.P.K., Vandrangi, R., Rachakonda, S.R. ((2016) ). Improved consistency ratio for pairwise comparison matrix in analytic hierarchy processes. Asia-Pacific Journal of Operational Research, 33: (03), 1650020. https://doi.org/10.1142/S0217595916500202. |
42 | Saaty, T.L. ((1977) ). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15: (3), 234–281. https://doi.org/10.1016/0022-2496(77)90033-5. |
43 | Saaty, T.L., Vargas, L.G. ((1987) ). Uncertainty and rank order in the analytic hierarchy process. European Journal of Operational Research, 32: (1), 107–117. |
44 | Saaty, T.L. ((2008) ). Decision making with the analytic hierarchy process. International Journal of Services Sciences, 1: (1), 83–98. https://doi.org/10.1504/IJSSci.2008.01759. |
45 | Sadiq, R., Tesfamariam, S. ((2009) ). Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stochastic Environmental Research and Risk Assessment, 23: (1), 75–91. https://doi.org/10.1007/s00477-007-0197-z. |
46 | Sahrom, N.A. (2014). A z-number extension of an integrated analytic hierarchy process-fuzzy data envelopment analysis for risk assessment. Masters thesis, Universiti Teknologi MARA. http://ir.uitm.edu.my/id/eprint/16365. |
47 | Smarandache, F. (2000). A Unifying Field In Logics: Neutrosophic Logic. Neutrosophy, Neutrosophic Set, Neutrosophic Probability. ISBN 1-879585-76-6. Contents: Preface by Charles T. Le: 3. |
48 | Torra, V. ((2010) ). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25: (6), 529–539. https://doi.org/10.1002/int.20418. |
49 | Triantaphyllou, E., Hou, F., Yanase, J. ((2020) ). Analysis of the final ranking decisions made by experts after a consensus has been reached in group decision making. Group Decision and Negotiation, 29: , 271–291. https://doi.org/10.1007/s10726-020-09655-5. |
50 | Tüysüz, F., Şimşek, B. ((2017) ). A hesitant fuzzy linguistic term sets-based AHP approach for analyzing the performance evaluation factors: an application to cargo sector. Complex and Intelligent Systems, 3: (3), 167–175. https://doi.org/10.1007/s40747-017-0044-x. |
51 | Van Laarhoven, P.J.M., Pedrycz, W. ((1983) ). A fuzzy extension of Saaty’s priority theory. Fuzzy Sets and Systems, 11: (1–3), 229–241. https://doi.org/10.1016/S0165-0114(83)80082-7. |
52 | Wang, C.-N., Huang, Y.-F., Cheng, I., Nguyen, V. ((2018) ). A multi-criteria decision-making (MCDM) approach using hybrid SCOR metrics, AHP, and TOPSIS for supplier evaluation and selection in the gas and oil industry. Processes, 6: (12), 252. https://doi.org/10.3390/pr6120252. |
53 | Wang, B., Song, J., Ren, J., Li, K., Duan, H. ((2019) ). Selecting sustainable energy conversion technologies for agricultural residues: a fuzzy AHP-VIKOR based prioritization from life cycle perspective. Resources, Conservation and Recycling, 142: , 78–87. https://doi.org/10.1016/j.resconrec.2018.11.011. |
54 | Wu, Z., Jin, B., Fujita, H., Xu, J. ((2020) ). Consensus analysis for AHP multiplicative preference relations based on consistency control: a heuristic approach. Knowledge-Based Systems, 191: , 105317. https://doi.org/10.1016/j.knosys.2019.105317. |
55 | Yager, R.R. ((2013) ). Pythagorean fuzzy subsets. In: 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 57–61. https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375. |
56 | Yildiz, N., Kahraman, C. ((2019) ). Evaluation of social sustainable development factors using Buckley’s fuzzy AHP based on Z-numbers. In: International Conference on Intelligent and Fuzzy Systems. Springer, pp. 770–778. |
57 | Zadeh, L.A. ((1965) ). Fuzzy sets. Information and Control, 8: (3), 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X. |
58 | Zadeh, L.A. ((1975) ). The concept of a linguistic variable and its application to approximate reasoning—I. Information Sciences, 8: (3), 199–249. https://doi.org/10.1016/0020-0255(75)90036-5. |
59 | Zeshui, X., Cuiping, W. ((1999) ). A consistency improving method in the analytic hierarchy process. European Journal of Operational Research, 116: (2), 443–449. https://doi.org/10.1016/S0377-2217(98)00109-X. |
60 | Zheng, Y., He, Y., Xu, Z., Pedrycz, W. ((2018) ). Assessment for hierarchical medical policy proposals using hesitant fuzzy linguistic analytic network process. Knowledge-Based Systems, 161: , 254–267. https://doi.org/10.1016/j.knosys.2018.07.005. |
61 | Zhu, B., Xu, Z. ((2014) ). Analytic hierarchy process-hesitant group decision making. European Journal of Operational Research, 239: (3), 794–801. https://doi.org/10.1016/j.ejor.2014.06.019. |
62 | Zyoud, S.H., Kaufmann, L.G., Shaheen, H., Samhan, S., Fuchs-Hanusch, D. ((2016) ). A framework for water loss management in developing countries under fuzzy environment: integration of fuzzy AHP with fuzzy TOPSIS. Expert Systems with Applications, 61: , 86–105. https://doi.org/10.1016/j.eswa.2016.05.016. |