Mohex Wins 2015 Hex 11×11 and Hex 13×13 Tournaments

1THE TOURNAMENTS

At the 2015 Olympiad there were two Hex tournaments: 11×11 and 13×13. Three programs competed in each tournament: EZO by Kei Takada, supervised by Masahito Yamamoto, from Japan; MOHEX 2.0 (Huang et al., 2013), by Broderick Arneson, Ryan Hayward, Philip Henderson, Aja Huang, and Jakub Pawlewicz, from Canada; and DEEPHEX by Jakub Pawlewicz, from Poland.

EZO is a stronger version of the program that competed in the 2013 Olympiad. EZO uses alpha-beta search with an evaluation function based on a weighted combination of two different network connectivity measures. EZO ran on an i7 laptop.

DEEPHEX is a new program based on Sibling Conspiracy Number Search (Pawlewicz and Hayward, 2015a,b). DEEPHEX , like MOHEX, is based on the Benzene framework, developed by Broderick Arneson, Philip Henderson, Ryan Hayward, Aja Huang, and Jakub Pawlewicz. DEEPHEX ran on a 16 core shared-memory machine. As an opening book, DEEPHEX cached its evaluation scores in a database, running for 24 hours on each possible opening.

MOHEX , the winner of the previous four Olympiad Hex competitions (Hayward et al., 2013), is an MCTS program that uses the Benzene Hex framework built on the code base of FUEGO (Enzenberger et al., 2007), the Go program developed by Martin Müller, Markus Enzenberger and others at the University of Alberta. Benzene allows virtual connection and inferior cell computations. MOHEX performs these computations in UCT tree nodes visited at least 256 times. MOHEX ran on a 24 core shared-memory machine, with 4 cores reserved for the Depth-First Proof Number Search solver, which produces perfect play if it solves the position within the time allotted for a move. MOHEX uses a book — built by Broderick Arneson using Thomas Lincke’s method (Lincke, 2000) — with two 11×11 openings and one 13×13 opening.

Each tournament was a three-player double round robin, so 12 games in total with 8 games per player. Post-game win-detection is by our solver.

1.1The 11×11 Tournament

Fig.1

Participants and observers at the Hex competitions.

Table 1

11×11 cross-table

Here are some selected games.

Game 1. E-M O-I. 1.B[a7] 2.W[swap] 3.W[c9] …    MOHEX sees the win by move 30.B[e4].

Game 2. D-E I-O. 1.B[a3] 2.W[c9] …    EZO opens well, but blunders: 28.W[h2] wins.

Game 5. E-D O-I. 1.B[k5] 2.W[swap] 3.W[i3] …    EZO plays 27.W[i4] instead of j8 or other options that look safer. DEEPHEX sees that 28.B[k2] wins.

Game 9. M-D I-O. 1.B[a6] 2.W[swap] 3.W[g5] …    At move 22, DEEPHEX hesitates between j5, which loses, and i8, which leads to complicated positions where MOHEX cannot find correct moves. But DEEPHEX plays 22.B[j5]. Move 30 wins.

1.2The 13×13 Tournament

Table 2

13×13 cross-table

Above, playoff results are inside parentheses. Here are some selected games.

Fig.2

(a) Game 1: EZO-MOHEX 0-1, and (b) Game 2: DEEPHEX-EZO 1-0.

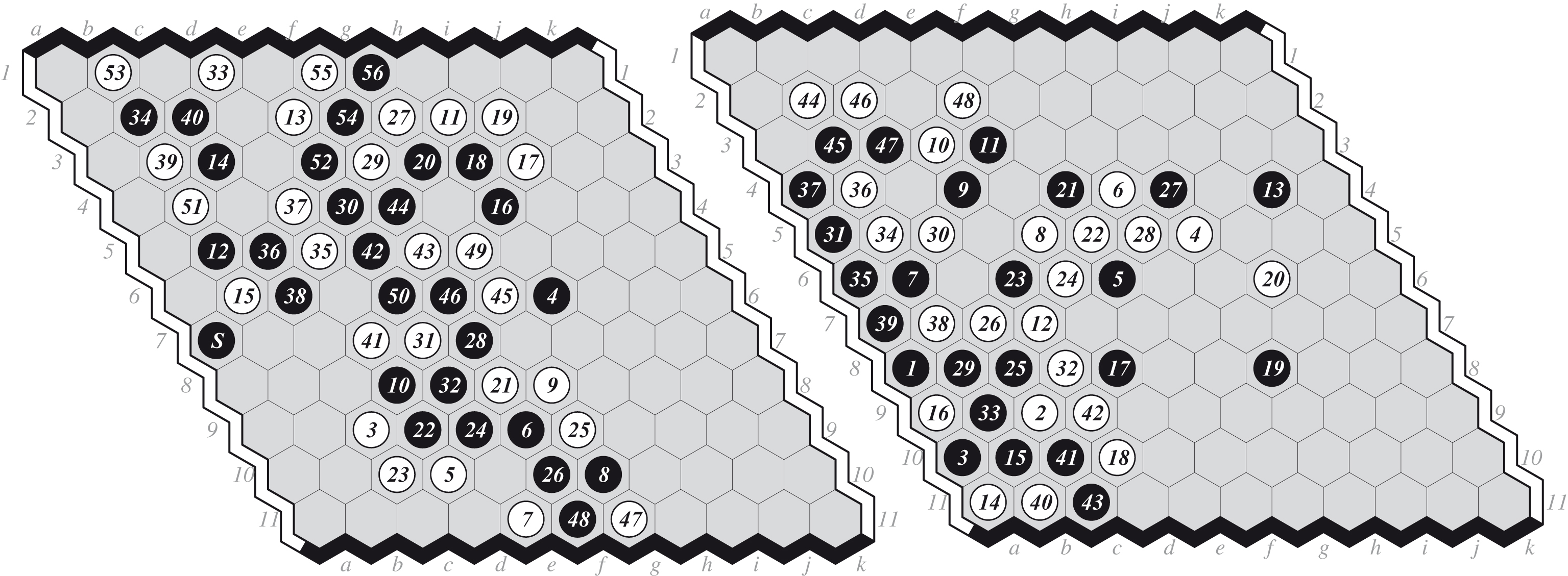
Fig.3

(a) Game 5: EZO-DEEPHEX 0-1, and (b) Game 9: MOHEX-DEEPHEX 1-0.

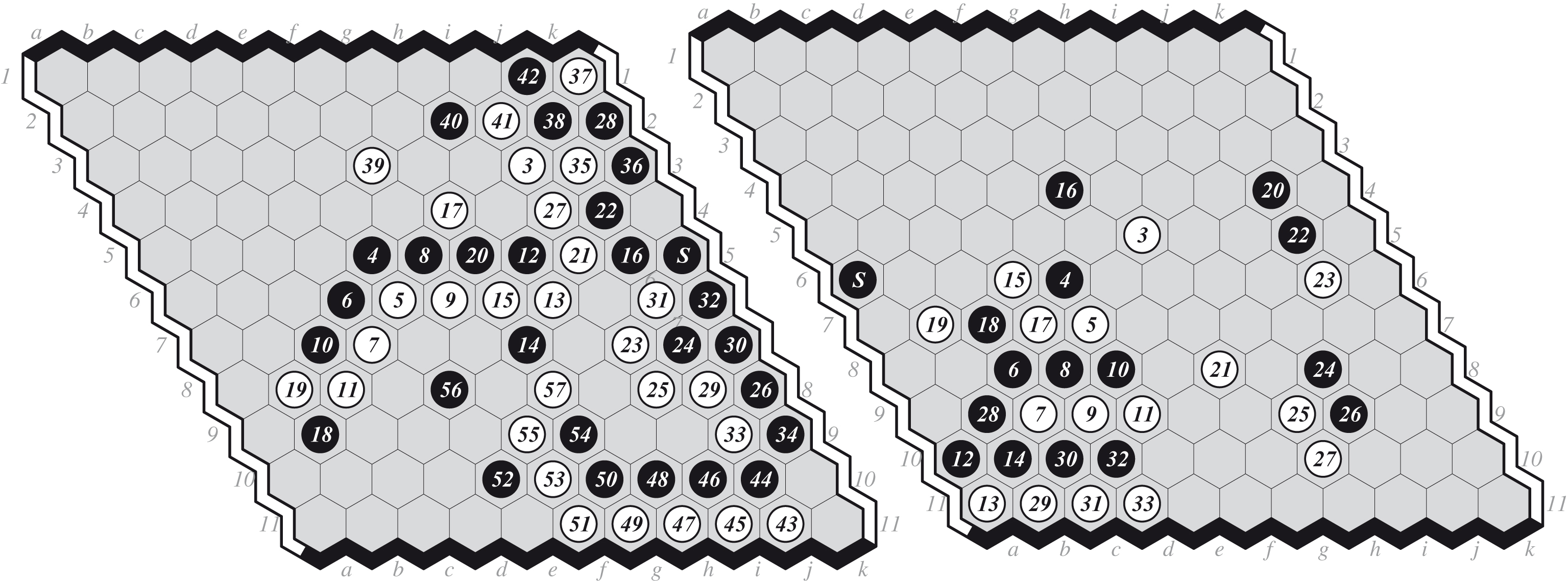
Game 3. M-D I-O. 1.B[a7] 2.W[swap] 3.W[i5] …    For many moves, both programs see this game as even. MOHEX turns the corner with move 29, not seeing how to use i5 to connect to the right side. 45.W[g4] is unexpected, but wins. This game shows the importance of virtual connections and an endgame solver.

Game 6. D-M I-O. 1.B[j2] 2.W[g8] 3.W[d10] …    A close game. MOHEX blunders with 54.W[f9]; 54.W[l11] wins. DEEPHEX sees the win soon after.

Game 11. E-D O-I. 1.B[a4] 2.W[swap] 3.W[k3] …    A close game. From move 20, DEEPHEX behaves unexpectedly, perhaps because its move selection does not consider inferior cells: move 28 considers neither a3 nor f2 (which captures a3). Here MOHEX likes f2, but DEEPHEX plays k4. EZO then takes a3, and gets into a winning position: 47.W[k11] wins, although this takes the solver a long time to check. But EZO plays 47.W[j10] and DEEPHEX grinds out a win.

Fig.4

(a) Game 3: MOHEX-DEEPHEX 1-0, and (b) Game 6: DEEPHEX-MOHEX 1-0.

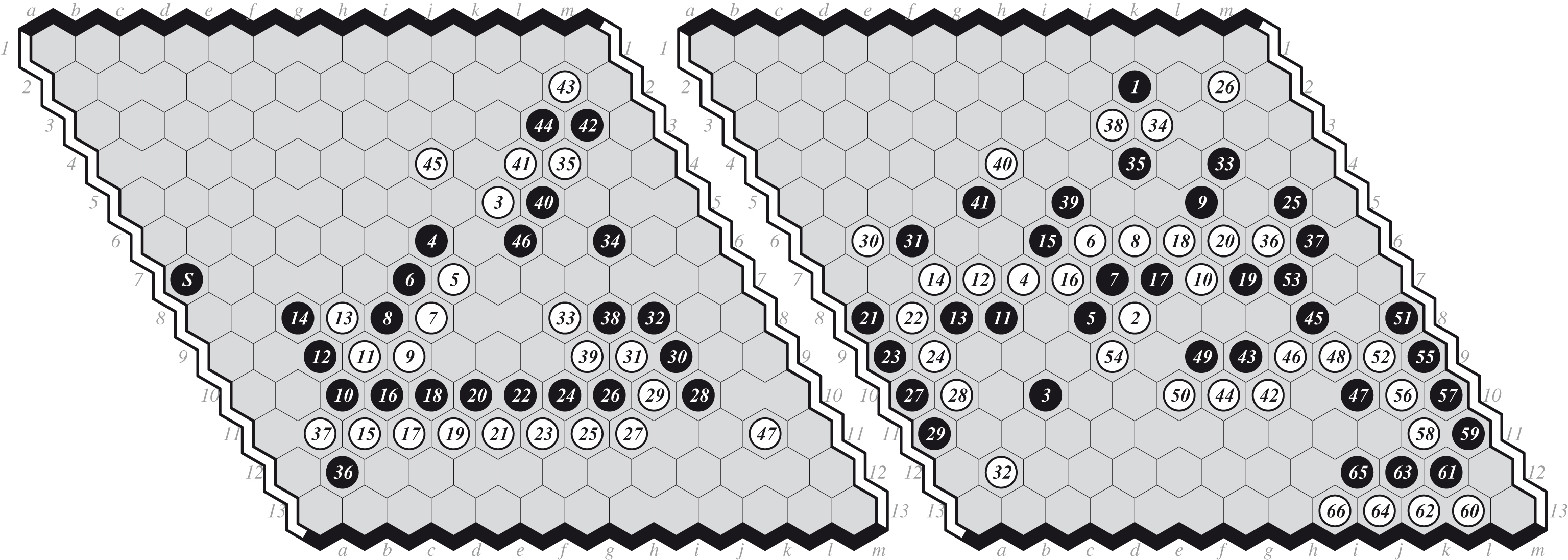
Fig.5

(a) Game 11: EZO-DEEPHEX 0-1, and (b) Playoff Game 1: MOHEX-DEEPHEX 1-0.

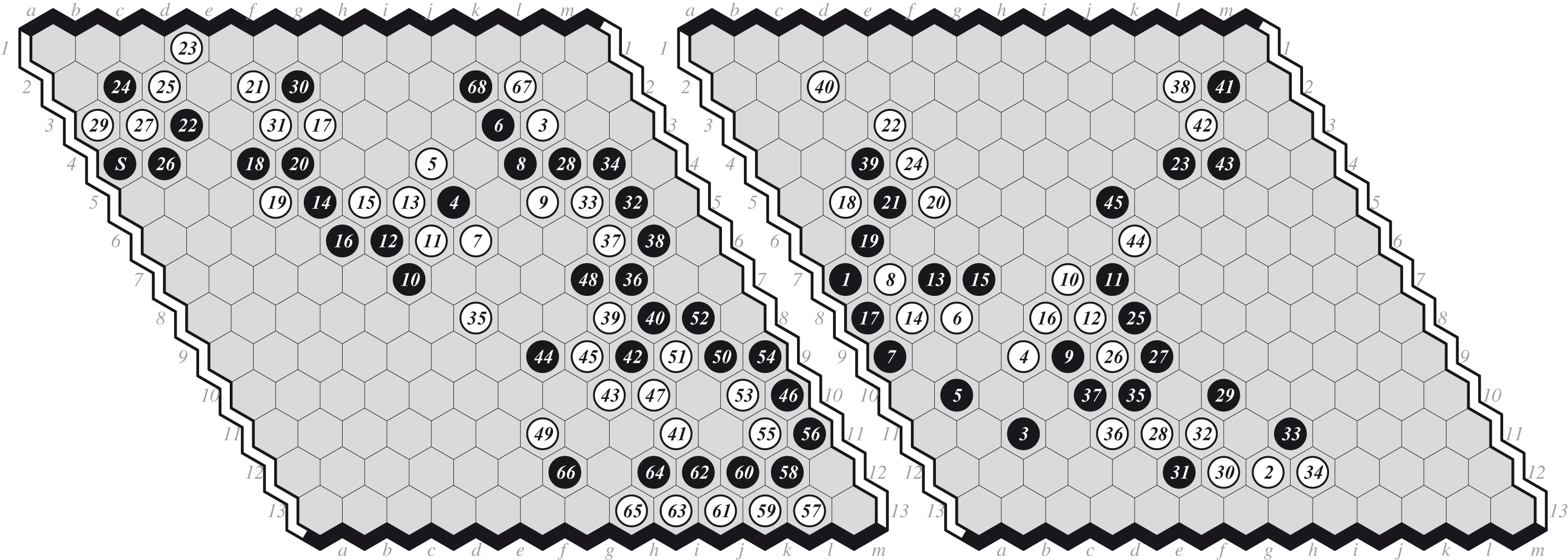
Fig.6

(a) MOHEX-TV 1-0, and (b) TV-DEEPHEX 0-1.

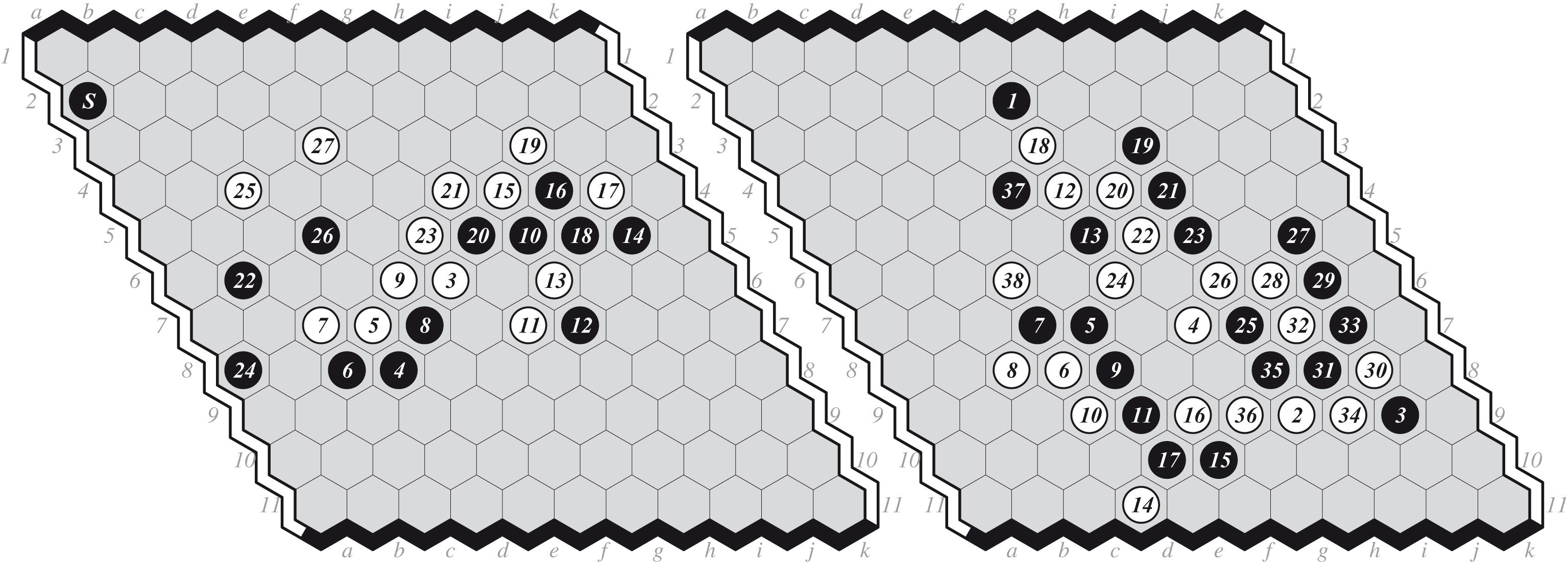
Playoff Game 1. M-D I-O. 1.B[a7] 2.W[h12] 3.B[c11] … Earlier DEEPHEX swapped and lost, so here not-swaps. MOHEX scores increase gradually. Move 46 wins.

2CONCLUSIONS

EZO ’s performance was stronger than its record indicates. It played some strong openings and had winning moves deep into games against DEEPHEX. It was unlucky not to win a game.

DEEPHEX and MOHEX were evenly matched, but play different styles. MOHEX seems stronger in opening and early middle play, but its Monte Carlo simulations cannot handle tactical positions. DEEPHEX thrives on tactical positions, and is especially strong in the late middle game in complicated positions.