Maintaining intellectual diversity in data science

1.1.Collective wisdom, collective madness

The ability of a group to exhibit intelligence superior to any of its constituent members is well established. One of the first to study how collective intelligence emerges was Condorcet, who considered the case of an idealized jury [10]. Consider n jurors, tasked with deciding whether a defendant is guilty or innocent. Each juror is individually only accurate in making this determination with a relatively low probability, say 60%. That is little better than guessing at random. However, assuming that the jurors make up their minds independently, Condorcet showed that collective group decision (determined by a simple vote) is far more likely to be accurate than a single individual, growing quickly with the number of jurors, n. Francis Galton made similar observations regarding the accuracy of collective estimation [13], which is ultimately predicated on the Law of Large Numbers: independent errors made by many individuals tend to cancel out in aggregate, making the group much “smarter” than a single individual. As noted above, these early observations have been replicated since within data science, in ensembles of models and research teams.

However, collective wisdom is contingent on diversity and independence between members of a group [40]. The counterpoint to the collective wisdom of Condorcet’s idealized jury is the collective madness we see when individuals are too strongly influenced by the collective mood. This is exhibited in famous examples of damaging group think, such as Tulip Fever, the South Sea Bubble and other stock market booms and busts [14]. We may also observe on a daily level in our own lives instances where social conformity and peer pressure lead individuals and groups to behave sub-optimally. The community of researchers in data science, statistics, machine learning and artificial intelligence is also subject to individual, social and insitutional forces that discourage a diversity of approaches [12,23,26,39,48]. Certain statistical models become fashionable, are accepted as the new big thing and are soon ubiquitous. Senior researchers train their students in the methods that they know. At any one time, certain types of model are, generally, more accurate and/or efficient than others, and researchers tend to gravitate towards these. The culture of benchmarking one’s new method against the state of the art in terms of accuracy necessitates that researchers utilize the best currently available methodologies if they wish to get their work published. Previous research has shown that when individuals are rewarded solely on the basis of the accuracy of their individual predictions, this tends to lead to a severe lack of diversity and a subsequent catastrophic reduction in collective wisdom, putting the whole collective on a par with a single individual [17,24].

The examples of successful ensemble approaches above demonstrate that diversity has not been extinguished in data science (e.g. [5]). However, in the light of incentives and mechanisms that discourage diversity, and in the knowledge that diversity is critical to the collective wisdom of any community, it behooves us to consider carefully how ideas spread in the research community, and how the incentives and structures inherent to the scientific community can be used to encourage a wider variety of research approaches.

2.1.Networks of scientific interaction

Analyzing the networks of scientific interaction can reveal important information about the current divisions between different methods and the groups of researchers that use them. Furthermore, these network structures also yield a better understanding of the potential for these methods to be better integrated through new interactions. There are many rich sources of data that have recently become available that can be used to characterize the interaction of scientists in different contexts. For example, the Web of Science11 or other bibliometric sources can be used to construct citation networks. Although this is only an imperfect measure of scientific ideas and how they spread, there is quantitative evidence that scientific ideas “spread” through citations [21] and that these networks can be used to predict their spread [36]. Using bibliometric data we can also extract the structure of scientific collaborations and co-authorship networks. Similarly we can reveal collaborations and knowledge transfer in other dimensions, for example through the network of user-repository interactions on Github22 [18]. These networks can be used to understand the potential for spread of ideas and methods between researchers. There are of course other, less formal forms of scientific interaction which are becoming easier to measure. For example, measurements of face-to-face interactions at conferences [38] and exchange and “friendship” on online social platforms such as Twitter and ResearchGate can also be used to map the structure of interactions between scientists.

All of these quantifications of scientific interaction contain different information at different temporal resolutions. However, two pervasive characteristics are community structure and a high inequality, or broad distribution of the centrality (most basically measured through connectedness) of different network components, whether they be researchers or methods.

2.2.Community structure, individual centrality and integrating diverse methods

Modules or communities are, intuitively speaking, the sub units of a network made up of individuals (e.g. researchers or methods) that interact more strongly with each other than with the rest of the network. One interesting approach to integrating diverse perspectives would be to combine methods from distant communities through ensemble methods.

Taking a more decentralized long-term approach, communication channels between researchers operating in these distant communities also need to be established. However, there are many reasons to be wary of a naive approach which simply encourages more unstructured interaction. To retain useful diversity, interaction across communities must not compromise a basic degree of isolation and independence between communities.

The importance of community structure is better understood if we consider the mechanisms that seem to govern the spreading of ideas and innovations. The best studied model is fractional threshold contagion [43], where the probability that an individual becomes “infected” through an infective contact is dependent on the fraction of other infected individuals that it interacts with (in network terms, its neighbors). This rule captures the idea that adoption is a social process: there is pressure to conform, or there are added synergistic benefits to adopting if others whom we interact with adopt. Given such a process, communities serve as incubators for new ideas, through local reinforcement. But communities also have the opposite effect, slowing the adoption ideas that originate outside of them. Increasing connectivity randomly throughout a network could decrease the diversity of ideas, allowing only the most contagious, or those that start in the most well connected places, to persist.

Theoretical work indicates that networks that have modular structure but sustain intermediate levels of connectivity between modules provide optimal conditions for the global uptake of ideas [27]. However, such results do not take into account the hierarchical structure of networks, and how the centrality of nodes (for instance most simply according to degree) determines how effectively inter-modular connectivity can enable global spread.

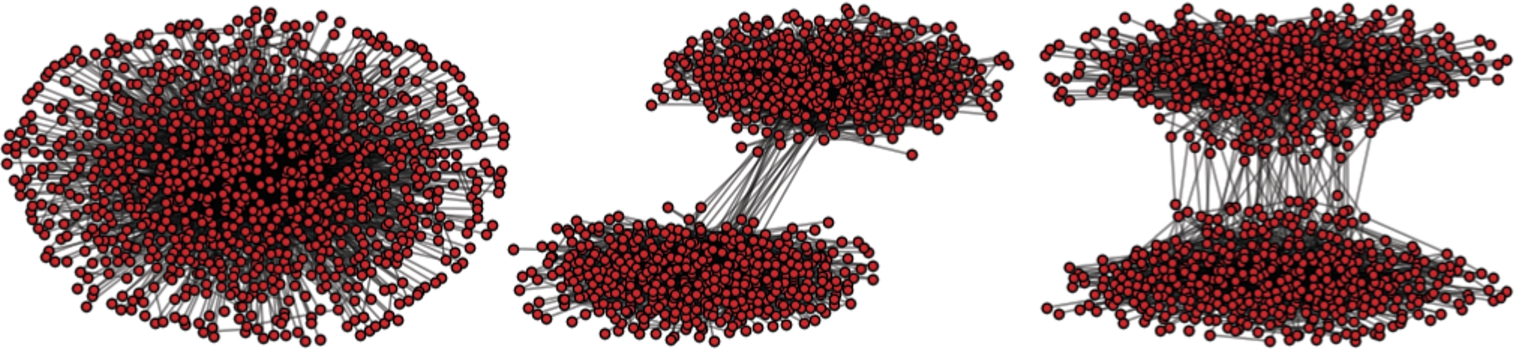
The dynamics of contagion through a fractional threshold mechanisms are driven by the inverse relationship between the connectedness of an individual and its susceptibility to ideas. Thus, more peripheral individuals are more receptive to new ideas and play a key role in sustaining a rich and diverse set of scientific ideas. Therefore, in theory ideas can be more effectively transferred from one community to another through connections between more peripheral individuals rather than highly connected individuals (see Fig. 2 for a schematic of the different network topologies we discuss).

To determine how strongly these theoretical conclusions apply to the spreading of scientific ideas and methods a more extensive empirical validation of the prevalence of fractional threshold contagion is needed. Unfortunately, there is a lack of empirical work selecting between plausible information spreading mechanisms in a statistically principled way, in any context. One of the rare examples [34] does in fact offer evidence for the prevalence of fractional threshold contagion – it provides the best fit (from a pool of standard contagion mechanisms) to observed behavioral changes in schooling fish. However, based on studies of information spread on Twitter microblogging [33,45], we would expect that multiple contagion mechanisms operate in the spread of scientific ideas, for instance depending on characteristics of the idea. Interestingly, despite the uncertainty regarding contagion mechanisms, the key role that peripheral researchers can play in the spreading of ideas due to their sensitivity becomes more generally applicable if we look beyond models that only consider one idea spreading in isolation. Ideas are part of an ecosystem, and they interact with each other through their scientific “hosts”, akin to the dynamics of co-infection and super-infection studied in evolutionary epidemiology [1]. Competition for limited human time and attention is the most studied interaction [15,16,44]. However, there are also synergistic effects between ideas. Most obviously, ideas that are similar and consistent with each other are more likely to be adopted by the same scientist. These interaction effects accentuate rich-get-richer feedbacks in the system and thus reduce diversity. Furthermore, since the most established scientists tend to be the most connected, they experience more information overload and therefore the competition for their attention is greater, and at the same time, they are less likely to adopt novel ideas that contradict the establishment that has secured their privileged position.

Fig. 2.

Three different network topologies that can sustain different diversity of ideas: All networks exhibit stratification, that is, most individuals have a low degree but there is a small number of highly connected individuals. The network on the left has no community structure. This network cannot sustain much diversity. The network in the middle has a strong community structure with inter-community connections through central individuals. In this network the diverse ideas that spark in the different communities cannot spread globally. The network on the right has strong community structure, but with inter-community connections through peripheral individuals. This topology offers a promising approach to sustain the global penetration of diverse ideas that are fostered locally.

2.3.The role of incentives

The type of research that individuals pursue and the methods they use are influenced by their peers and networks, as we have seen above. However, the decisions scientists make in this regard should not be viewed simply as a passive result of community pressure. Instead, these decisions are active choices that are made both to satisfy the researcher’s curiosity, but also to achieve their professional objectives such as promotion, funding and recognition. How scientists are rewarded for their research will affect, in positive or negative ways, the diversity of ideas and therefore the collective wisdom of the scientific community. Scientific ideas and publications exist in a quasi-market, where some are accorded a high value and attract high rewards. A typical researcher is unlikely to pursue highly novel but unpopular ideas if there is no potential for them to be recognized through the awarding of prizes, promotion or further research funding if those ideas later turn out to be fruitful. Likewise, if rewards are systematically allocated to incremental and low-risk research, this will tend to attract more researchers to these areas. Furthermore, researchers are aware of the high premium placed on clear, statistically unambiguous results, and may self-censor weaker findings either by not publishing or by not making data freely available [46]. This is in addition to the external restrictions imposed by journals unwillingness to publish work that does not report a statistically significant positive finding [48].

When individual rewards are oriented solely towards simple criteria of success this tends to suppress diversity and risk-taking [17,24]. Conversely, there is recent evidence that useful diversity can be encouraged by rewarding accurate minority predictions [24]. These are occasions on which an individual or a model predicts correctly, while the majority of others predict incorrectly. This creates an incentive to focus on less exploited sources of information, or more niche features of a data set, since the individual cannot win any reward by simply imitating what the majority of others are already doing. For the individual, this may make their model less accurate overall. But it makes their model far more useful to the community, as it contributes additional information not already presented by others.

Similar ideas are already applied in established methods of ensemble creation. For example, the technique of boosting [35] is a meta-algorithm for assembling ensembles of weak classifiers that act as a strong classifier in aggregate. A common way to achieve this is to iteratively add weak classifiers to an ensemble, re-weighting the data set under consideration after each new classifier is added. Examples within the data that are currently poorly classified are given higher weights, while those which are already well classified are given lower weights. In this way, additional weak classifiers are ‘incentivized’ to focus on accurately classifying the examples that are currently poorly modeled.