Eccentric-wing flutter stabilizer for long-span bridges
Abstract
An aerodynamic device for preventing bridge flutter is presented. It consists of wings positioned along the sides of, and fixed relative to, the bridge deck. Flutter suppression efficiency is high provided the lateral eccentricity of the wings is large. It is a passive device without moving parts. This is an advantage over active or passive devices with moving parts, which meet resistance due to reliability concerns. Results of a numerical study are presented in which the critical wind speed for flutter onset of a bridge without wings and with wings mounted in various configurations was determined. Furthermore, first results of wind tunnel tests are reported and a cost estimate is given.
1Introduction
The design of long-span bridges is often governed by dynamic wind phenomena such as buffeting, vortex shedding, and flutter. Various measures have been proposed and applied to raise the flutter resistance of bridges, that is, their critical wind speed for flutter onset (flutter speed). The concept of the twin suspension bridge was described by Richardson [1] in 1981 and since implemented in a few bridges. It is a passive aerodynamic measure that takes advantage of the gap between the two (or more) bridge decks. The decks need to be connected by cross beams, which are substantial structural elements that cause significant additional costs.
An active aerodynamic device for raising the flutter speed was proposed by Ostenfeld et al. [2] in 1992. It consists of movable wings, installed along the sides of the bridge deck, whose pitch is controlled by actuators. A closed-loop control is envisaged in which, based on accelerometer measurements, an algorithm produces the control signals for the actuators such that the movement of the wings generates stabilizing aerodynamic forces. With such a device, the safety of the bridge depends on energy supply and the proper functioning of control software and hardware – a condition that meets resistance with bridge owners and authorities. The concept has not yet been applied.
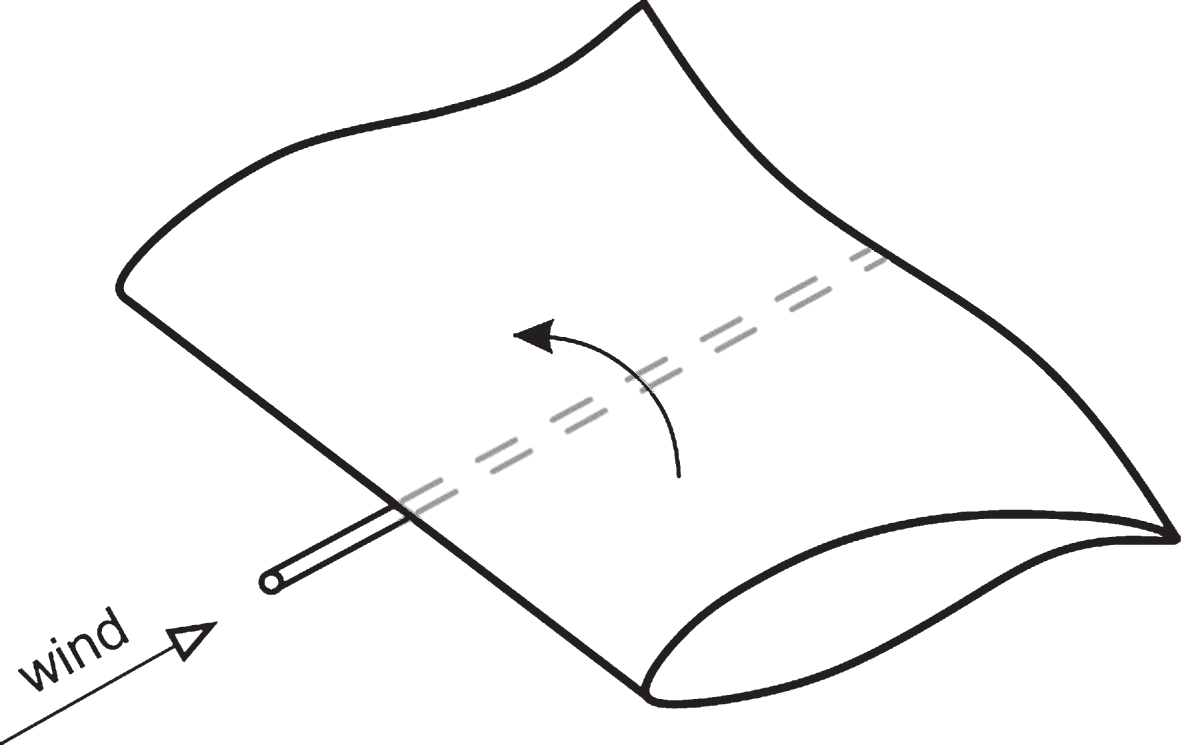
A passive aerodynamic-mechanical device was described by Starossek et al. [3] in 2008, which also includes variable-pitch wings along the sides of the bridge deck (Fig. 1). Instead of being controlled by an actuator, the pitch of a wing follows the movements of a tuned mass damper inside the bridge deck to which the wing is coupled by means of a linkage or gear. With proper tuning, the flutter suppression efficiency can be similar to that of actively controlled wings. Being a passive device, the structural safety of the bridge would not depend on energy supply and a control system. It still includes moving parts though, which raises the threshold of acceptance. The concept has not yet been applied.
Purely aerodynamic devices without moving parts have been proposed by various authors. Dianaet al. [4] examined the effect of various aerodynamic devices rigidly attached to the deck of the envisaged Messina Strait Bridge, including winglets positioned along the edges of the deck. The devices are positioned close to the deck without a distinct vertical or horizontal offset. Hence they form part of the aerodynamic contour of the deck and influence the flow field around it. Only qualitative indications are given in [4] concerning the impact of such devices on the flutter behavior of the bridge and it does not become clear whether and by how much the flutter speed is raised by the examined winglets.
In 1987, Raggett [5] suggested wings rigidly mounted above, or slightly outboard of, the edges of the bridge deck to stabilize the bridge against flutter. The wings are arranged with a distinct vertical offset from the deck so that they are aerodynamically independent of the deck. Liu et al. [6] considered a similar configuration and studied its influence on bridge flutter both analytically and by sectional model wind tunnel tests.
When the wings are considered aerodynamically independent of the deck, their impact on the flutter speed of the bridge can easily be assessed analytically as will be outlined below. The author’s own parametric studies show that this impact is small for the configurations described in [5, 6], that is, for wings arranged with a vertical offset above, or slightly outboard of, the edges of the deck. Closely installed winglets could still be effective because they change the aerodynamic properties of a given deck section. In case of wings positioned with a distinct vertical offset, however, a significant rise of flutter speed only ensues when the wings are also arranged with a pronounced lateral eccentricity.
2Eccentric-wing flutter stabilizer
In view of the development described above, it seems promising, for raising the flutter speed of a bridge, to pursue passive aerodynamic measures that do not include moving parts but, at the same time, are sufficiently efficient to eliminate the need for structural strengthening or substantial additional structural elements. The eccentric-wing flutter stabilizer presented in the following meets these requirements.
The device consists of wings positioned along the sides of the bridge deck. A configuration with wings equally positioned on both sides of the deck is shown in Figs. 2–4. In certain cases, further discussed below, it is advantageous to provide wings on only one side of the deck or to provide wings on both sides, but to design them differently, that is, with different widths and lateral eccentricities (dimensions 2bc and ac in Fig. 2). The wings are mounted on transversely orientated support structures that are laterally attached to the bridge deck. Hence they do not move relative to the bridge deck. It can be shown that the flutter suppression efficiency of the device is high provided the lateral eccentricity of the wings is large.
Wings and support structures are envisioned as light-weight components. The wings are aerodynamically shaped such that the lift under inclined wind is large and the resistance is small. Their profile can be symmetric about a horizontal plane or doubly symmetric approaching an elliptical shape.
The lateral eccentricity of the wings is of the order of the bridge deck width (ac / b ≈ 1.5 to 2.5; see Fig. 2). The width of one wing in the direction transverse to the bridge axis is of the order of one tenth of the bridge deck width (bc/b ≈ 0.05 to 0.20). The wings are preferably positioned above or below the bridge deck with sufficient vertical offset to avoid aerodynamic interference between the wings and the bridge deck including traffic.
For optimum cost efficiency, the wings are not placed over the entire length of the bridge but only at regions where large vibration amplitudes occur (Lc < L; see Figs. 3 and 4). In case flutter is governed by the first symmetric modes of vibration, these regions lie around the center of the main span (Fig. 3). In case flutter is governed by the first antisymmetric modes of vibration, these regions lie around the quarter points of the main span (Fig. 4).
In an alternative configuration, a single wing is replaced by a certain number of wings positioned above each other (Fig. 5). The flutter-suppression efficiency of such a group of wings is approximately the same as for a single wing provided the sum of the widths of the wings is the same as the widthof the single wing and the vertical distance between the individual wings, hc, is not too small. Advantages of such alternative configuration can be easier assembly and lower costs. It also offers less area of attack to the vertical velocity component of turbulent wind by taking advantage of the wind shielding effect provided by the uppermost and lowermost wings.
3Reasons of effectiveness
Because the width of a wing is comparatively small, the lift force on a wing as a function of the vertical and angular motion of the bridge deck can be thought of as quasi-stationary. An angular velocity of the deck,
Another important effect that can be explained by quasi-stationary theory is the aerodynamic stiffness produced by the wings. An angular displacement of the deck, α, is accompanied by the same angular displacement, or pitch, of the wings. The horizontal wind flow acting on a pitched wing produces a lift force on the wing that is proportional to α. This force times the eccentricity, ac, results in a moment on the deck that is proportional to ac α and in phase with +α or -α, depending on whether the wing is positioned on the windward side or the lee side of the deck. In other words, a wing produces aerodynamic stiffness related to the angular displacement of the deck that is proportional to the eccentricity of the wing. This stiffness is negative for a windward wing and positive for a leeward wing. A positive aerodynamic stiffness raises the overall stiffness and hence the natural frequency of torsional vibrations and, therefore, the flutter speed – a negative aerodynamic stiffness vice-versa. In a symmetrical wing layout with wings on both sides of the bridge deck, the aerodynamic stiffness contributions of the wings of both sides cancel and do not affect the flutter speed.
Experimental studies with sectional models in a wind tunnel are in progress. Initial results fit well with the explanations given above and confirm the effectiveness of the device [7]. In particular, a leeward wing always raises the flutter speed. A windward wing with small eccentricity lowers the flutter speed and with large eccentricity raises it. The latter experimental result can be explained by the quadratic versus linear dependency of aerodynamic damping and stiffness on the eccentricity of a wing.
4Determination of flutter speed
The effect of the eccentric-wing flutter stabilizer on the flutter speed has been studied analytically. It is assumed in this study that there is no aerodynamic interference between the bridge deck and the wings. This assumption hinges on the lateral and vertical offsets of the wings being sufficiently great. Wind tunnel tests are required to determine minimum values of these parameters for the no-interference assumption to be valid. Theodorsen’s flutter derivatives [8] are used for modelling the wind forces on the bridge deck. This is deemed sufficiently accurate for determining the relative effectiveness of various wing configurations provided the aerodynamic contour of the deck is a streamlined closed box. The overall system and the wind forces on the wings are modelled in two different ways.
In a first approach, the bridge system is generalized to two degrees of freedom, that is, heave and pitch, and it is assumed that the wind forces on the wings can be calculated by quasi-stationary theory. The rotational damping and stiffness of the two-degrees-of-freedom system is modified by adding theaerodynamic damping and stiffness contributions of the wings as described in the previous section. Theodorsen’s solution procedure [8] for determining the flutter speed is applicable, but has to be supplemented by a further level of iteration, given that the damping and stiffness contributions of the wings depend on the wind speed.
In a second, more sophisticated approach, the bridge deck and the wings are modelled by finite aeroelastic beam elements [9]. This allows for the study of discontinuous configurations where the wings are not placed over the entire length of the bridge. Moreover, the quasi-steady flow assumption for including the wind forces on the wings is no longer required. The wind forces on both the bridge deck and the wings are modelled by using Theodorsen’s flutter derivatives. The details of the flutter analyses will be reported in subsequent publications.
5Parametric study
Parametric computations have been performed for a long-span suspension bridge with a main span length of L = 3,000 m and a single box girder deck with a width of 2b = 38.0 m. The flutter speed of the bridge without wings was computed as 46.3 m/s. Fig. 6 shows the flutter speeds for various wing configurations relative to the flutter speed without wings, all flutter speeds being computed by the second, more sophisticated approach described in the preceding section. The wings are assumed to be placed on the lee side only and along the entire length of the bridge deck. The relative wing width, bc / b, is varied between 0.025 and 0.170. The relative eccentricity, ac / b, is varied between 1.00 and 2.00. For a relative wing width of 0.100 and a relative eccentricity of 2.00, for instance, the flutter speed is raised by 64% corresponding to a value of 75.8 m/s. It can be concluded from Fig. 6 that the flutter-suppression efficiency of the device increases nonlinearly with, and mainly results from, the lateral eccentricity of the wings.
Placing wings on only one side of the bridge deck – or placing wings on both sides but designing them with different widths and lateral eccentricities – is advantageous when the expected maximum wind speeds strongly differ for both transverse directions. The wings on only one side – or, when placing wings on both sides, the wings with the larger widths and lateral eccentricities – are then placed on the lee side of the stronger wind.
When the expected maximum wind speeds are about the same for both transverse directions, identical wings should be placed on both sides of the bridge deck. This can reduce the overall flutter-suppression efficiency of the eccentric-wing flutter stabilizer, as follows from the above discussion of the reasons of effectiveness. The aerodynamic stiffness contributions of the wings of both sides cancel and only their aerodynamic damping is available for raising the flutter speed. However, assuming the same parameters as above (bc/b = 0.100; ac/b = 2.00), the flutter speed would still be raised by 28% over the value without wings. Placing the wings right above the edges of the bridge deck (bc/b = 0.100; ac/b = 1.00), as suggested in [5, 6], would produce a rise of flutter speed of only 4%.
6Cost estimate
A first cost estimate based on a preliminary design has been performed for the cost of support structures and wings [10]. For the configuration considered in the preceding paragraph with wings placed on both sides of the deck, leading to a flutter speed increase of 28%, this additional cost is estimated to be about 4% of the cost of the bridge. Wind loads induced by buffeting and vortex shedding have only roughly been considered in the underlying design. A more accurate analysis might lead to a higher additional cost. The cost of the eccentric-wing flutter stabilizer should be compared to the additional cost when the same 28% increase of flutter speed is achieved by other means. For instance, the flutter speed can be increased by using a twin or multiple instead of a single box girder deck. This entails cross beams for connecting the individual box girders. Such cross beams are substantial additional structural elements and the corresponding cost increase might be larger than the cost increase resulting from the eccentric-wing flutter stabilizer. More accurate cost estimates of the eccentric-wing flutter stabilizer and of competing measures for increasing the flutter speed are required and underway.
7Alternative designs
As outlined above, the windward wings can reduce the overall flutter-suppression efficiency of the device. This disadvantage can be overcome at the cost of introducing moving parts. The wings in such alternative designs would be movably supported or provided with movable elements so that they can take one of two states. The transition from one state to the other takes place when the wind direction changes from one transverse direction to the other transverse direction. The transition is accomplished by a mechanical drive, requiring power supply and a control system, or it is driven by wind action alone. In each respective state, positions are taken that make the leeward wings aerodynamically effective and the windward wings aerodynamically ineffective. Implementing this idea can be achieved, for instance, by providing many short wings and supporting them on rotating bearings, mounted to the support structure, so that each wing can rotate about an axis transverse to the bridge axis (Fig. 7).
Depending on the transverse wind direction, each wing takes one of two positions. A leeward wing aligns horizontally and is aerodynamically effective. A windward wing aligns vertically and is aerodynamically ineffective. The transition can be accomplished by wind action if the outer edge of each wing is shaped in an S-line so that the wind forces create an aerodynamic moment about the bearing axis and the range of rotation is appropriately limited by stops. Such a variant of the eccentric-wing flutter stabilizer has movable parts but the respective motions do not occur, and the wings are fixed, as long as the wind direction does not change. The movable parts are presumably less intricate and costly than those of the devices described in [2] and [3].
8Conclusions
The eccentric-wing flutter stabilizer is a promising device for raising the critical wind speed for flutter onset of bridges. A substantial increase of flutter speed is reached at a small additional cost. Further study is required and underway for confirming the computed flutter speeds by wind tunnel tests with sectional bridge deck models, for more accurately determining the response of the modified bridge system to other dynamic wind loads (buffeting, vortex shedding), for improving the preliminary design of support structures and wings, and for refining the cost estimate.
References
[1] | Richardson JR . The development of the concept of the twin suspension bridge. National Maritime Institute, NMI R 125, Feltham, UK, (1981) . |
[2] | Ostenfeld KH , Larsen A . Bridge engineering and aerodynamics, In: Larsen A. (Ed.), Aerodynamics of Large Bridges. Proceedings of the First International Symposium on Aerodynamics of Large Bridges, Copenhagen, Denmark, February 19-21, 1992, Balkema, Rotterdam, (1992) , pp. 3–22. |
[3] | Starossek U , Aslan H . Passive control of bridge deck flutter using tuned mass dampers and control surfaces. Proceedings, 7th European Conference on Structural Dynamics – EURODYN 2008, Southampton, UK, July 7-9, (2008) . |
[4] | Diana G , Fiammenghi G , Belloli M , Rocchi D , Resta F , Zasso A . Sensitivity analysis on the effects of different aerodynamic devices on the behaviour of a bridge deck. 12th International Conference on Wind Engineering (ICWE 12), Cairns, Australia, July 1-6, (2007) , pp. 2191–98. |
[5] | Raggett JD . Stabilizing winglet pair for slender bridge decks. Proc. Bridges and Transmission Line Structures. ASCE Structures Congress, Orlando, Florida, August 17-20, (1987) , pp. 292–302. |
[6] | Liu Gao , Meng Fanchao , Wang Xiuwei . Mechanism of flutter control of suspension bridge by winglets. 4th International Symposium on Computational Wind Engineering (CWE 2006), Yokohama, Japan, July 16-19, (2006) . |
[7] | Ziems H . Experimental verification of flutter stabilization of long-span bridges by eccentric wings (in German). M.Sc. thesis, Structural Analysis and Steel Structures Institute, Hamburg University of Technology, November 30, (2015) . |
[8] | Theodorsen T . General theory of aerodynamic instability and the mechanism of flutter. NACA, Technical Report No. 496, Washington, D.C., (1934) , pp. 413–33. |
[9] | Starossek U . Prediction of bridge flutter through use of finite elements. Structural Engineering Review (1993) ;5: (4):301–7. |
[10] | Schade R . Flutter stabilization of bridges by means of rigid wings (in German). M.Sc. thesis, Structural Analysis and Steel Structures Institute, Hamburg University of Technology, December 18, (2014) . |
Figures and Tables
Fig.2
Bridge with eccentric-wing flutter stabilizer – cross section.
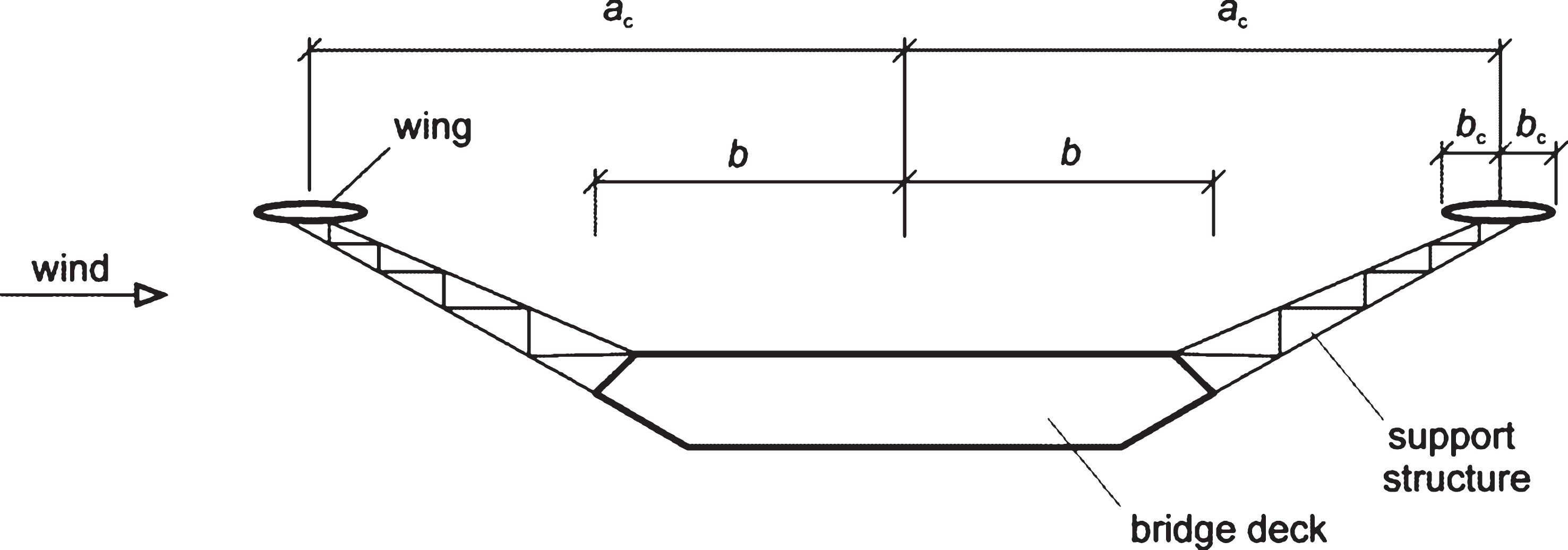
Fig.3
Bridge with eccentric-wing flutter stabilizer around center of main span – plan view (not to scale).
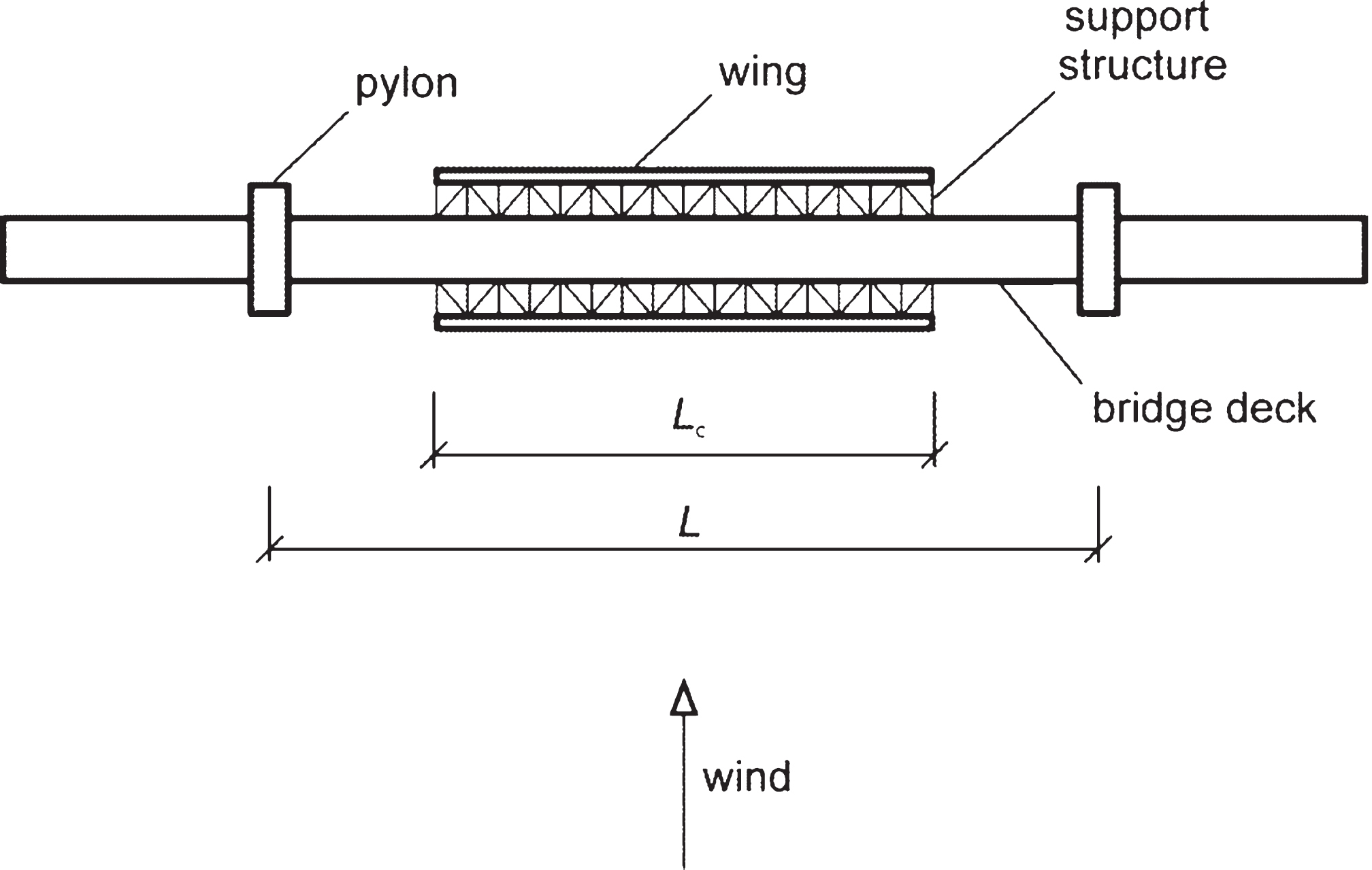
Fig.4
Bridge with eccentric-wing flutter stabilizer around quarter points of main span – plan view (not to scale).
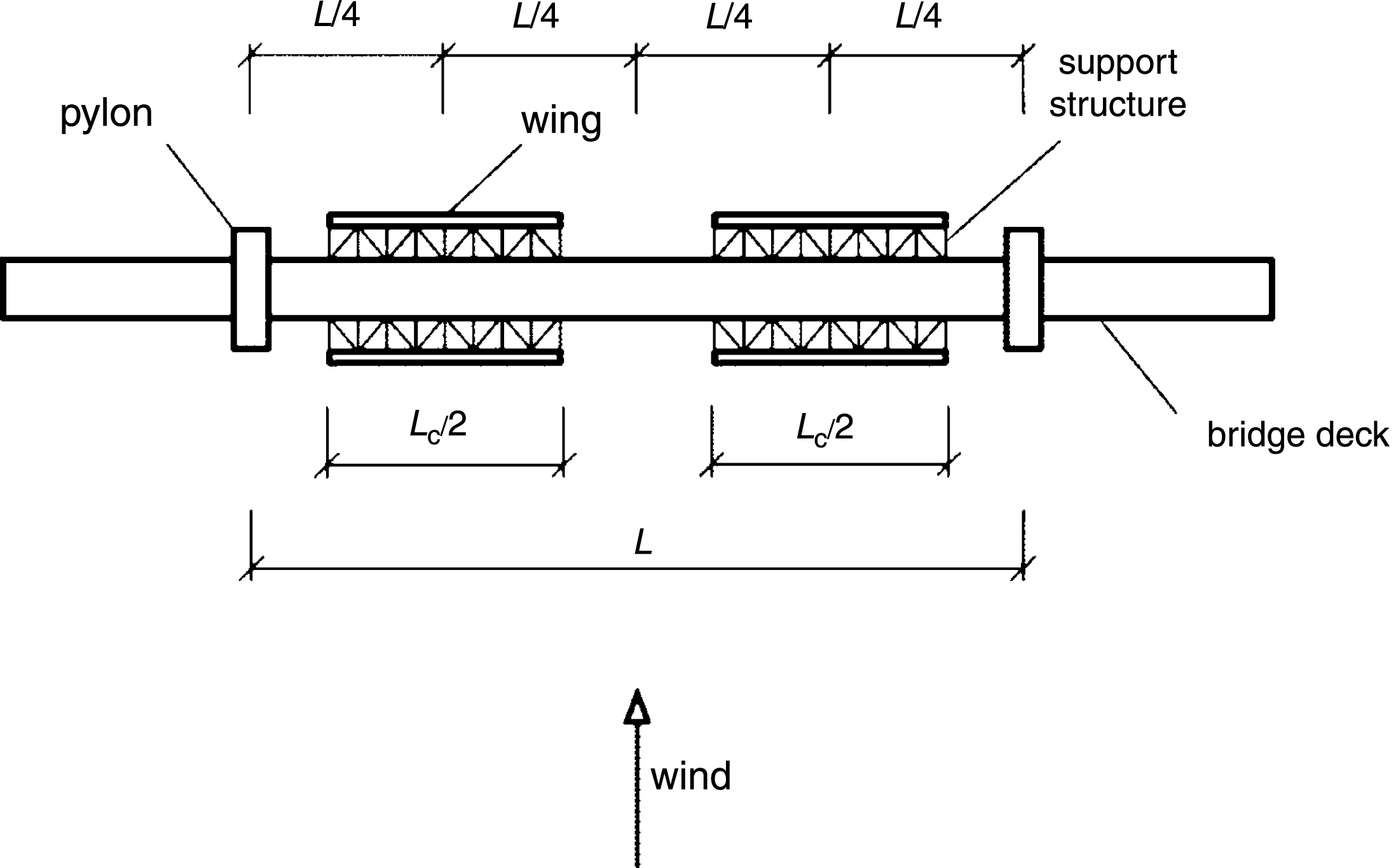
Fig.5
Group of wings replacing a single wing – cross section.
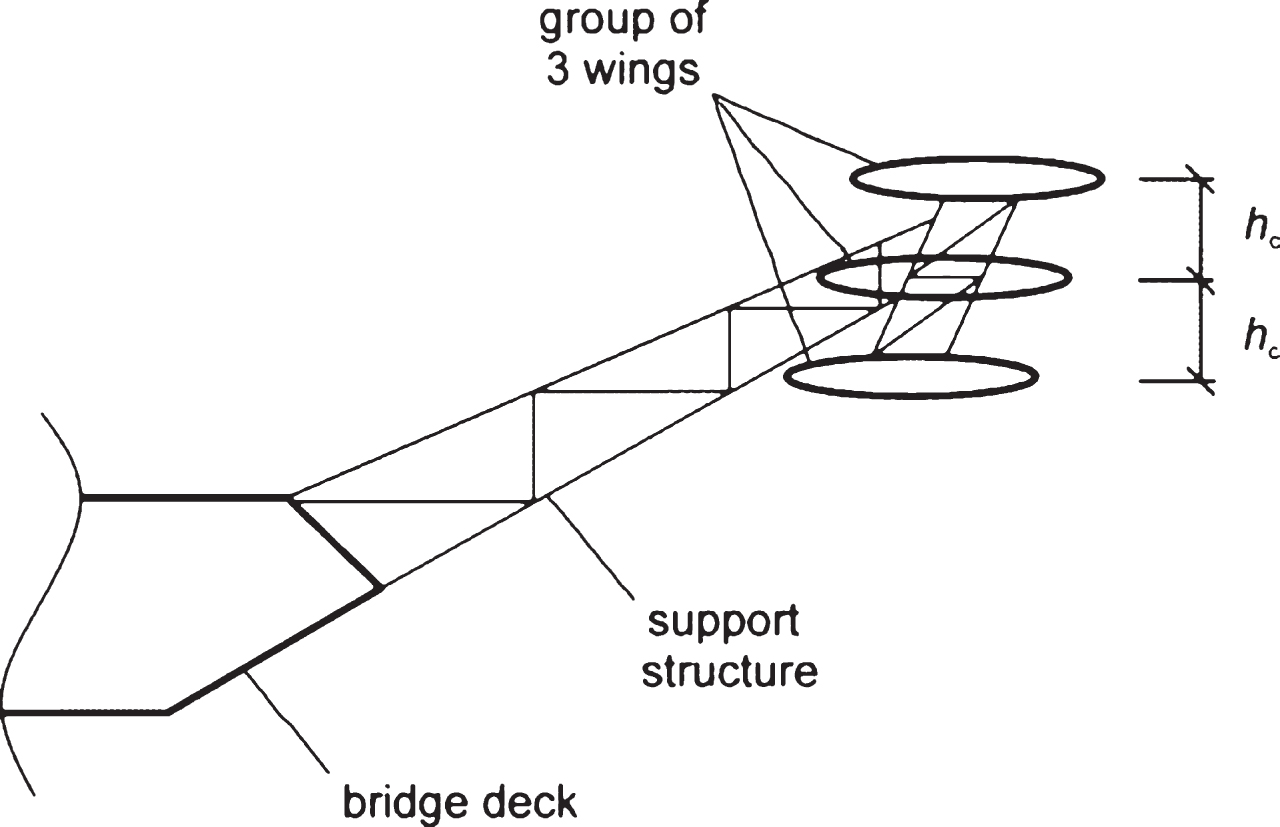
Fig.6
Critical wind speed for flutter onset as function of width and eccentricity of wings of eccentric-wing flutter stabilizer (wings on lee side only).
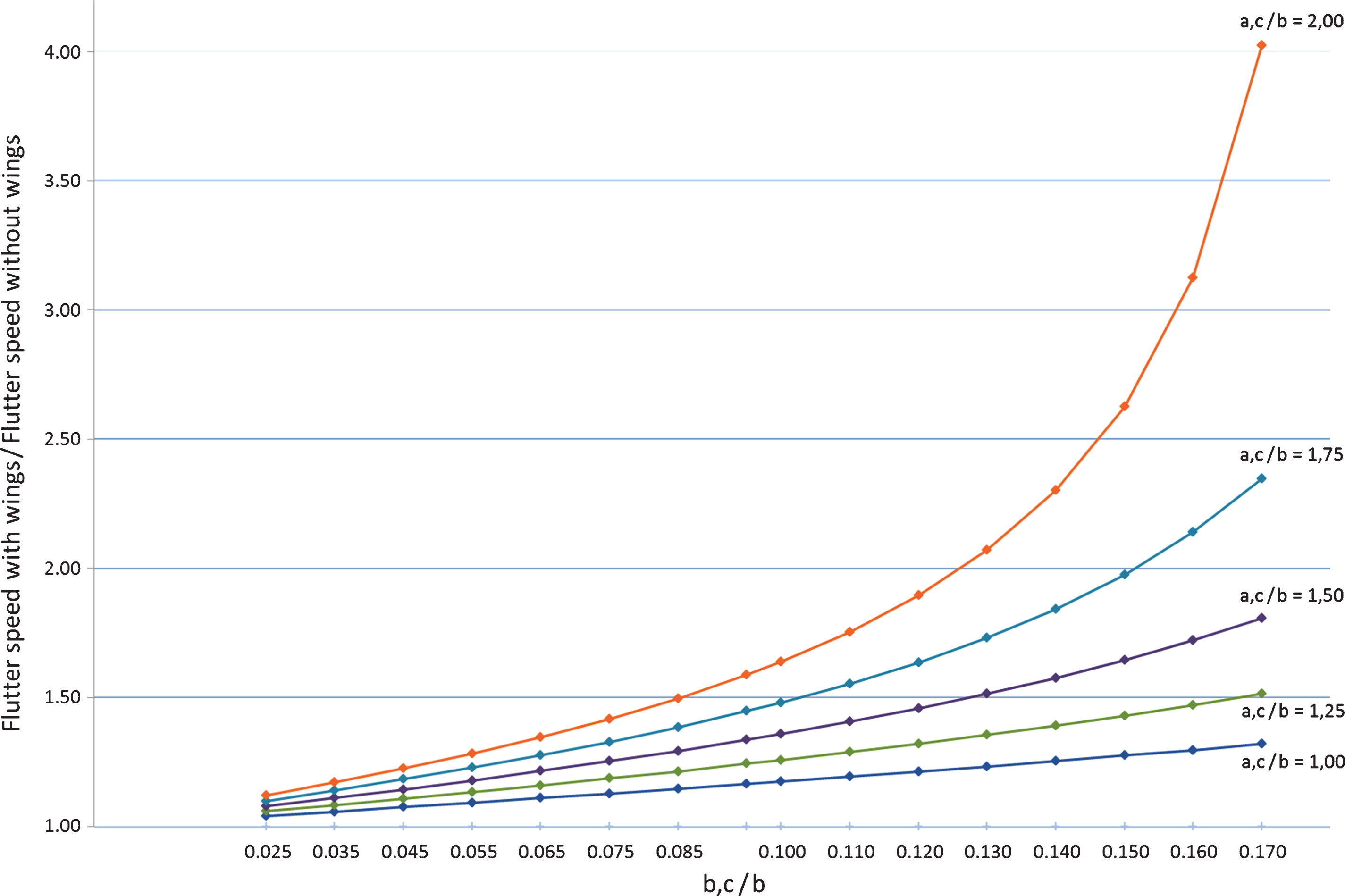
Fig.7
Wing in leeward position aligned horizontally.

![Passive aerodynamic-mechanical device for flutter suppression [3].](https://content.iospress.com:443/media/brs/2016/12-1-2/brs-12-1-2-brs098/brs-12-brs098-g001.jpg)


