Rational argument, rational inference

Introduction

For a good part of the last 50 years, ‘reasoning’ and ‘inference’ within cognitive psychology were almost synonymous with ‘logical reasoning’. Much of the early work within the psychology of reasoning focused on the extent to which the ‘laws of logic’ might be construed as the ‘laws of thought’ (Henle 1962; Fodor 1975; Braine and O'Brien 1991; Oaksford and Chater 2007). The verdict emerging from that body of research was soon a rather negative one, suggesting that people may be rather poor in their ability to distinguish logically valid from invalid inferences and that they are prone to systematic error in their thought (Wason and Johnson-Laird 1972).

Largely unconnected with this body of work, two other strands of research under the header of ‘reasoning’ emerged over that period. One focused on category-based induction (Rips 1975; Osherson, Smith, Wilkie, Lopez, and Shafir 1990), that is, inferences from our knowledge of members of one category (‘robins’) to those of another (‘sparrows’ or ‘birds’). The other was focused on analogical reasoning (Gentner 1983, 1989). This latter area sought to provide an understanding of the way in which knowledge about a base system (e.g. the ‘solar system’) might be transferred to a novel, target system (e.g. ‘the atom’) in a way that was computationally explicit enough to allow implementation of such inference via an actual algorithm (Falkenhainer, Forbus, and Gentner 1989; Holyoak and Thagard 1989; Keane, Ledgeway, and Duff 1994; French; 1995; Hofstadter 1995; Hummel and Holyoak 1997).

Not only did these different ‘reasoning’ literatures remain largely independent of each other (see also, Heit 2007; for some exceptions see, Rips 2001a, 2001b; Oaksford and Hahn 2007; Heit and Rotello 2010), they also remained entirely independent of a fourth strand of research interested in ‘argumentation’, and in particular developmental and applied contexts, such as science education and science communication (e.g. Kuhn 1989, 1991, 1993; Means and Voss 1996; Anderson, Chinn, Chang, Waggoner, and Yi 1997; Klaczynski 2000; Kuhn, Cheney, and Weinstock 2000; Kuhn and Udell 2003; Sadler 2004; Glassner, Weinstock, and Neuman 2005).

However, there are prima facie reasons why these literatures should not be separate. For one, the first three, as noted above, all draw on the terms ‘reasoning’ and ‘inference’. However, at least two of these reasoning literatures (logical reasoning and inductive reasoning) share with the fourth, the use of the term ‘argument’. While it could be that the common use of these terms across these areas is entirely superficial, masking fundamental differences in what the terms mean in each of these areas, the reasonable default assumption would seem to be that these areas share common ground and should be viewed together.

In fact, there has been a more recent development which arguably provides a currency that allows theoretical integration of these hitherto largely separate strands, and this is the rise of Bayesian probability as a normative framework for modelling reasoning and argumentation.11

The rise of Bayes

The idea of applying Bayesian probability to the domain of logical reasoning may seem counter-intuitive, but following the work of Oaksford and Chater (1994), it has become a widespread view (albeit far from uncontested, see e.g. Rips 2001a, 2001b; Oberauer 2006; Klauer, Stahl, and Erdfelder 2007) within the psychology of reasoning that people interpret natural language conditionals in probabilistic terms (Evans and Over 2004), in line with more contemporary philosophical treatments of the conditional (e.g. Edgington 1995; Adams 1998). Oaksford and Chater's work, in particular, has sought to establish that much of the perceived mismatch between the prescriptions of logic and people's performance on logical reasoning tasks stems quite simply from the fact that people do not treat such tasks as logical reasoning tasks, but rather as inductive, probabilistic ones (see e.g. Oaksford and Chater 2007). This behaviour in the laboratory is taken to reflect the fact that deduction, in contrast to induction, necessarily plays only a very limited role in the kinds of day-to-day informal reasoning we must perform (Oaksford and Chater 1991).

At the same time, the category-based induction literature which had been centred around a number of key heuristics that were thought to govern inference (such as the similarity between the category members, their typicality, premise diversity, and numerosity, see Osherson et al. 1990) has been put on a probabilistic footing because these heuristics have been reformulated within a Bayesian framework (Heit 1998; Tenenbaum, Kemp, and Shafto 2007; Kemp and Tenenbaum 2009).

Finally, the scope of reasoning research has recently been broadened considerably beyond the range of arguments traditionally studied in the context of either logical reasoning or category-based induction. Specifically, recent work has sought to demonstrate how Bayesian probability theory can be applied to a wide variety of so-called fallacies of argumentation, that is, the many argument pitfalls that form the focus of text books on critical thinking (e.g. Oaksford and Hahn 2004; Hahn and Oaksford 2006a, 2007a). Probability theory provides a normative framework which captures argument forms as diverse as arguments from ignorance (‘ghosts exist, because no-one has prove that they don't’, see Oaksford and Hahn 2004), slippery slope arguments (‘if we legalize gay marriage, next thing people will want to marry their pets’, see Corner, Hahn, and Oaksford 2011), and circular arguments (‘God exists, because the Bible says so, and the Bible is the word of God’, see Hahn and Oaksford 2007a; Hahn 2011). In each case, it is shown how Bayesian probability distinguishes between textbook examples of these fallacies that intuitively seem weak, and other examples with the same formal structure that seem much more compelling (e.g. ‘this book is in the library, because the catalogue does not say it is on loan’ in the case of the argument from ignorance; or ‘decriminalizing cannabis will eventually make hard drugs acceptable’, in the case of slippery slope arguments). That for most of the fallacies there exists such seeming ‘exceptions’, was a longstanding problem for theoretical treatments of the fallacies (e.g. Hamblin 1970), and it is the ability of Bayesian probability to deal with such content-specific variation that enables it to provide the long-missing formal treatment of the fallacies. The presence of clear predictions about the probabilistic factors that make individual examples weak or strong has also opened up a new programme of experimental research on people's ability to distinguish weak and strong versions of these informal arguments, of which we will provide a more detailed example below.

The Bayesian treatment of the fallacies, in turn, links reasoning research to the wider argumentation literature. The fallacies are considered to be not just fallacies of reasoning, but also of argumentation. In the context of the reasoning literature, the term ‘argument’ refers to a minimal inferential unit comprising premises and a single conclusion. However, the term ‘argument’ also refers to dialogical exchanges between two or more proponents (on these different uses of the term ‘argument’ see O'Keefe 1977; Hornikx and Hahn 2012), and such exchanges may involve a series of individual claims, counter-claims, and supporting statements (Toulmin 1958; Rips 1998). Argumentation researchers have tended to focus on ‘argument’ in this latter sense, including in the context of the fallacies (e.g. Walton 1995; Rips 2002; van Eemeren and Grootendorst 2004; Neuman, Weinstock, and Glasner 2006; van Eemeren, Garssen, and Meuffels 2009, 2012). One central concern for argumentation researchers has been the identification of the procedural norms and conventions that govern different types of such dialogues, including, in particular, ‘rational debate’; though much of that work has been purely theoretical, there is an increasing interest in empirical, psychological investigation of the extent to which people endorse these norms and are aware of their violation in everyday exchanges (Christmann, Mischo, and Groeben 2000; van Eemeren et al. 2009, 2012; Hoeken et al. 2012).

The Bayesian approach with its focus on content, and procedurally oriented theories, do occasionally form rival perspectives. This is true of the fallacies (e.g. van Eemeren and Grootendorst 2004; van Eemeren et al. 2009, 2012); also, differing views obtained about the meaning and status of concepts such as the burden of proof (see e.g. Bailenson and Rips 1996; 2001; van Eemeren and Grootendorst 2004; Hahn and Oaksford 2007b, 2012).

On a more general level, however, it is clear that procedural norms and norms for content evaluation ultimately target very different, and hence complementary, aspects of argument quality: an argument may go wrong, because the evidence presented is weak; an argument, viewed as a dialogue may also go wrong because one party refuses to let the other speak. Content norms do not obviate the need for procedural rules, nor do procedural norms mean that rules for the evaluation of argument content are unnecessary (Hahn and Oaksford 2006b; 2007a; 2012). For this reason also, the two different senses of ‘argument’ are inextricably linked.

The fallacies illustrate also the different reasons why logic alone provides an insufficient standard for argument evaluation. It is not just the focus of logic on structure and the accompanying lack of sensitivity to content that is the problem. Most of the fallacies are not deductively valid, so that logic simply has nothing to say about them. At the same time, lack of deductive validity is not in itself a sufficient measure of fallaciousness, because lack of deductive validity also characterises most of our everyday informal argument, and, at the same time, some fallacies, such as circular arguments are deductively valid. In other words, fallaciousness and logical validity clearly dissociate (see also Oaksford and Hahn 2007). That logically valid arguments may nevertheless be poor arguments may, at first glance, seem surprising. However, this dissociation can arise because argumentation as an activity is concerned fundamentally with belief change: arguments typically seek to convince someone of a position they do not yet hold (see Hahn and Oaksford 2007a; Hahn 2011). Bayesian conditionalisation with its diachronic emphasis on belief change contrasts here with logic which typically reflects a synchronic perspective. A circular argument such as ‘God exists, because God exists’, is synchronically sound, but maximally deficient from a diachronic perspective: premise and conclusion are identical, hence the one can never raise our degree of belief in the other (Hahn 2011). Hence logic and probability, while not themselves at odds (logic constrains what probability assignments are possible), can readily be at odds in their evaluation of arguments.

One area where the absence of sufficient norms for argument evaluation has been felt is the above-mentioned literature on science communication and science education. Here, the Bayesian approach allows one to evaluate content-level factors such as evidential strength, source reliability, and outcome utility. By contrast, previous attempts at analysing science arguments have only been able to focus on the presence or absence of broad structural aspects of arguments such as whether claims are backed by supporting evidence or not, and whether such supporting evidence in turn has been challenged. Researchers have not, however, been able to evaluate the extent to which that evidence or counter-evidence is normatively compelling (see also, Driver, Newton, and Osborne 2000).

Corner and Hahn (2009) conducted an experiment using the Bayesian approach to compare the evaluation of three different types of science and non-science arguments that demonstrate the utility of Bayesian probability as a heuristic framework for psychological research in this area. Specifically, they examined whether there was evidence of systematic differences in the way participants evaluated arguments with scientific content (e.g. about GM foods, or climate change) and arguments about mundane, everyday topics (e.g. the availability of tickets for a concert). These arguments differed radically in content, but they can all be compared to Bayesian prescriptions. Hence it becomes possible to ask whether people's evaluations more closely resemble normative prescriptions in one of these contexts than in the other, and if yes, where systematic deviations and discrepancies lie. This provides but one example of the way in which the probabilistic framework may be of use to those researchers who consider themselves to be interested specifically in argumentation.

In summary, the preceding sections have sought to provide an indication of the way that the normative framework of Bayesian probability provides a conceptual ‘glue’ that links, on a theoretical level, what have been very separate research traditions. In the final section of this article, we seek to provide some illustration of the kind of empirical research this theoretical framework supports.

Refining predictions

In the remainder, we review some specific examples of the way the Bayesian framework has changed the ways of reasoning and argumentation of research. Specifically we discuss examples first from the literature on logical reasoning and then examples relevant to argumentation. In each case, we detail both qualitative and quantitative predictions.

Logic

Prior to the emergence of the Bayesian approach there was a profound mismatch between logical expectations and the observed behaviour in hypothesis testing tasks. Where logic suggested that people should seek evidence to falsify their hypotheses, experimental participants in the reasoning laboratory steadfastly chose evidence that could only confirm their hypotheses. However, Oaksford and Chater (1994) argued that a Bayesian analysis demonstrated that a confirmatory response was in fact optimal, in the sense of selecting the data that was the most informative about the truth or falsity of the hypothesis. This analysis relied on the environmental assumption that the domain sizes of the predicates that featured in our hypotheses were small. For example, take the hypothesis, ‘all ravens are black’: most things are neither black nor ravens. Consequently, a Bayesian approach made the right qualitative predictions in hypothesis testing tasks like Wason's selection task that for years had been taken to indicate human irrationality. Moreover, work by McKenzie, Ferreira, Mikkelsen, McDermott, and Skrable (2001) established that people naturally express hypotheses only in terms of predicates describing rare events or predicates with small domain sizes.

However, the Bayesian perspective not only led to a re-evaluation of people's rationality, it also changed the character of research within the field. Before Oaksford and Chater's Bayesian treatment of the selection task (Oaksford and Chater 1994) data in the psychology of logical reasoning were a (in many ways somewhat haphazard) collection of qualitative phenomena (‘context effects’, ‘suppression effects’, etc.). Correspondingly, researchers made behavioural predictions that differed across experimental conditions in broad, qualitative ways (e.g. ‘higher acceptance rates for this logical argument in condition A than in condition B’). The shift to Bayesian probability as a normative framework altered fundamentally the degree of explanatory specificity within the psychology of reasoning by putting it on a quantitative footing (for a discussion of this point, see also Hahn 2009).

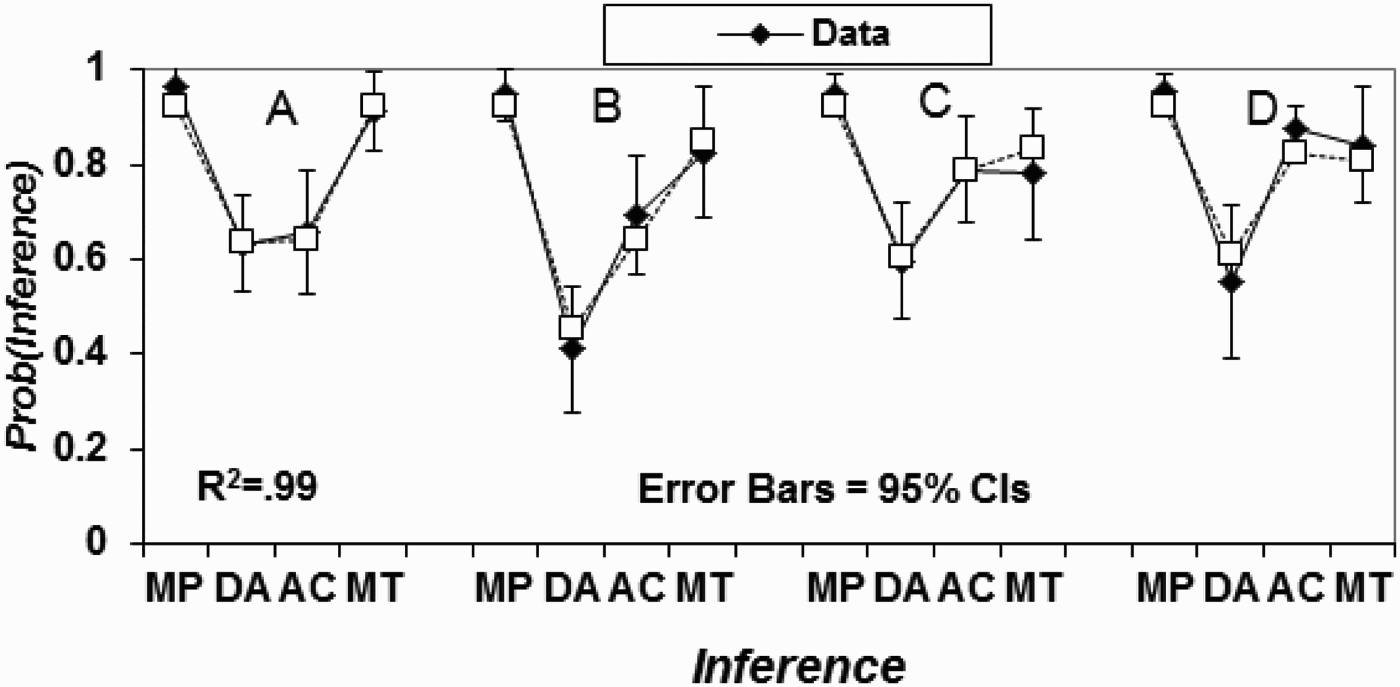
For example, Oaksford, Chater, and Larkin (2000) developed a model of conditional inference as belief revision by Bayesian conditionalisation (Bennett 2003). So consider the conditional:

• (1) If a bird is a swan (swan(x)), then it is white (white(x)).

Two logically valid inferences and two fallacies have traditionally been investigated. All combine (1) with a further premise and participants are asked if a particular conclusion follows. Modus ponens (MP) combines (1) with swan(a) and the conclusion white(a); modus tollens (MT) combines (1) with ¬ white(a) and the conclusion ¬ swan(a), where ‘¬’=not. MP and MT are logically valid. Denying the antecedent (DA) combines (1) with ¬ swan(a) and a conclusion ¬ white(a); affirming the consequent (AC) combines (1) with white(a) and the conclusion swan(a). DA and AC are (logical) fallacies. By Bayesian conditionalisation, on learning that Tweety is a swan (Pr1(swan(a))=1), it can be inferred that the posterior probability of Tweety being white (Pr1(white(a))) is the same as the prior conditional probability, Pr0(white(x)|swan(x)) (the 0 subscript=prior probability; the 1 subscript=posterior probability. Moreover, given this conditional probability and knowledge of the priors, Pr0(white(x)) and Pr0(swan(x), appropriate conditional probabilities can be calculated for MT and the two fallacies (see Appendix 2 for worked examples). This model was fitted quantitatively to data on conditional reasoning performance showing the probability with which each inference is drawn. Figure 1 shows the quantitative fits to Oaksford et al.’s (2000) data when the probabilities of Pr0(white(x)) and Pr0(swan(x)) were systematically varied. The model accounted for 99% of the variance in the data.

Figure 1.

Quantitative fits of Bayesian model to Oaksford et al.’s (2000) data. A to D represent conditions with different assignments of probabilities for Pr₀(white(x)) and Pr₀(swan(x), specifically A: Lo Pr₀ (swan(x)), Lo Pr₀(white(x)); B: Lo Pr₀(swan(x)), Hi Pr₀(white(x)); C: Hi Pr₀(swan(x)), Lo Pr₀(white(x)); D: Hi Pr₀(swan(x)), Hi Pr₀(white(x)).

This also forced the hand of rival approaches which have since taken on board quantitative model evaluation (Schroyens and Schaeken 2003; Oberauer 2006; Klauer et al., 2007) with the consequence that the psychology of reasoning has generally been transformed into an arena where detailed quantitative predictions are not only possible but also increasingly prevalent.

Argumentation: the fallacies and beyond

Research within the Bayesian approach to informal argumentation has also seen both qualitative and quantitative applications of Bayesian probability. A qualitative approach seems appropriate for initial investigation. It is also appropriate where the key question of interest is whether general intuitions about argument strength in lay people correspond to Bayesian prescriptions. For this reason, it seems important not to think of qualitative predictions derived from the Bayesian framework as simply the poor cousins of quantitative modelling, and only second best. This may be illustrated by the application of the Bayesian framework within the philosophy of science and within epistemology, where it has arguably become the dominant formal framework. Here, its application centres around qualitative predictions, and the explanatory and justificatory function of probability theory as a normative framework lies in the fact that fundamental philosophical and scientific intuitions, for example, that more surprising, more diverse, or more coherent evidence should give rise to greater confidence in the truth of a hypothesis may (or may not) be shown to be grounded in Bayesian prescriptions (see e.g. Earman 1992; Howson and Urbach 1996; Bovens and Hartmann 2003; Olsson 2005).

As an example of corresponding fundamental intuitions in the context of argumentation, one may consider some of the very first experimental works within the Bayesian framework (Oaksford and Hahn 2004; Hahn, Oaksford, and Bayindir 2005). This work sought to examine basic intuitions around the argument from ignorance. Formal analysis had shown that positive arguments (‘this drug has side effects, because evidence to that effect has emerged in clinical trials’) are typically normatively stronger than negative arguments (‘this drug does not have side effects, because no evidence to that effect has been observed in clinical trials’), all other things being equal.22 Experimental evidence showed that this qualitative pattern was indeed found in participants’ judgements of argument strength across a range of scenarios. The results of one such study are shown in Figure 2, where the visible differences in ratings for positive and negative arguments correspond to a statistically significant difference in perceived strength. That same study also examined whether people were sensitive to two other fundamental intuitions that have a normative basis in probability theory, namely that evidence from a more reliable source should have greater strength (on this issue see also, Hahn, Harris, and Corner 2009; Hahn, Oaksford, and Harris 2012; Oaksford and Hahn; Lagnado, Fenton and Neil, this volume), and that the degree of prior belief someone has in a claim should influence how convinced they become in light of a given piece of evidence. Figure 2 also shows corresponding effects of reliability and prior belief in participants’ judgements.

Figure 2.

The mean acceptance ratings for Hahn et al. (2005) by source reliability (high vs. low), prior belief (strong vs. weak), and argument type (positive vs. negative) (N=73). Figure reproduced from Hahn and Oaksford (2007).

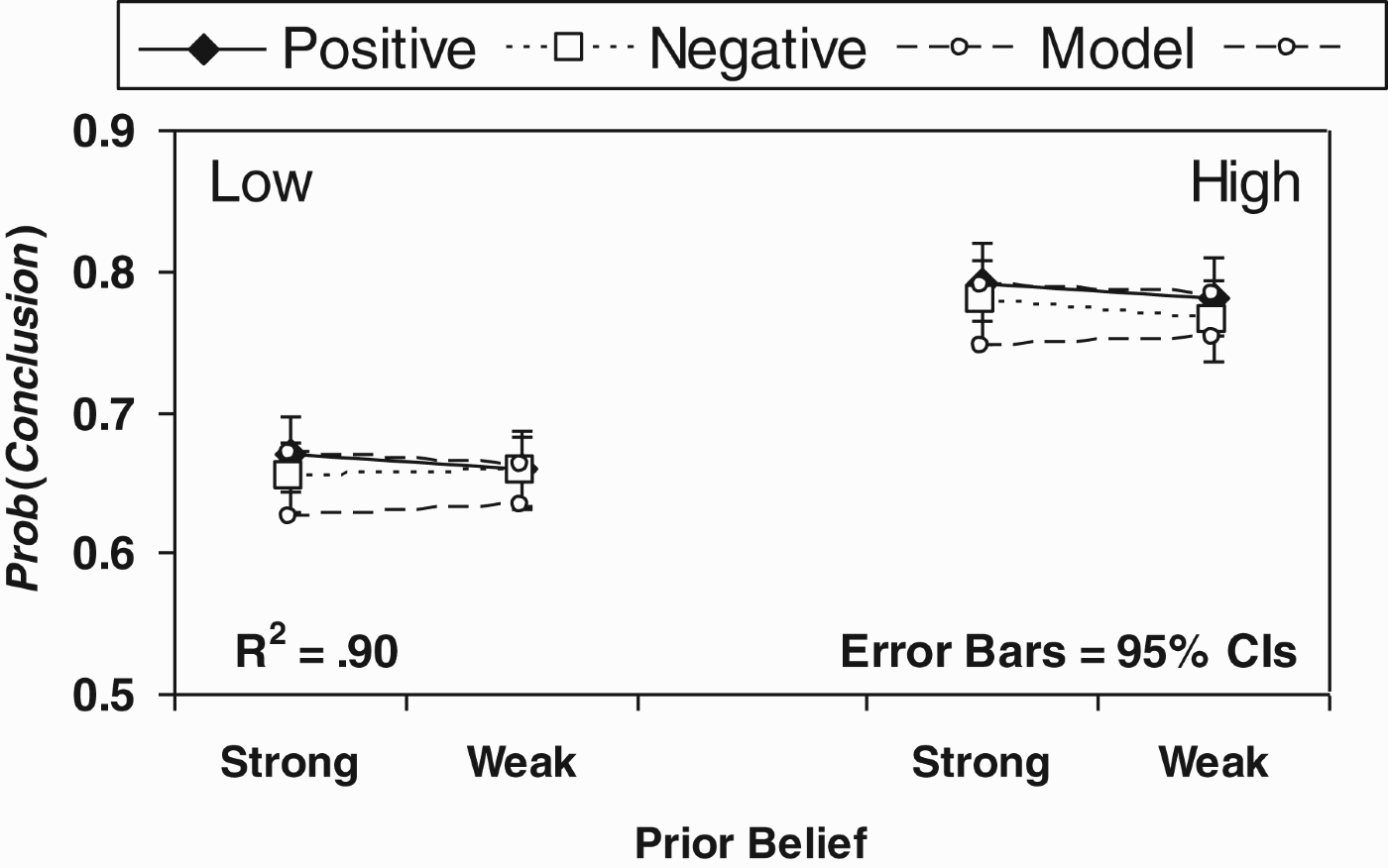
At the same time, quantitative evaluation is possible. The most straightforward way to do this is, again, via model-fitting, and Figure 2 displays also the resultant fits to the data of a (constrained) Bayesian model (for details see Hahn and Oaksford 2007a). For one, such model-fitting is useful as a way of demonstrating visually that a pattern of responses is indeed compatible with Bayesian predictions.

However, whether or not key normative factors of argument strength are reflected in people's basic intuitions is not the only interesting question in this context. One may care also, more specifically, about exactly how closely participants’ intuitions match Bayesian prescriptions, and hence the extent to which they may be considered to be ‘Bayesian’. This question determines how fine-grained an account of human behaviour the normative theory provides, and the extent to which it may be considered to provide a computational level explanation of people's actual behaviour (Anderson 1990), and therefore, whether this behaviour can subsequently be understood as arising from a set of underlying processes that seek to approximate that normative theory.

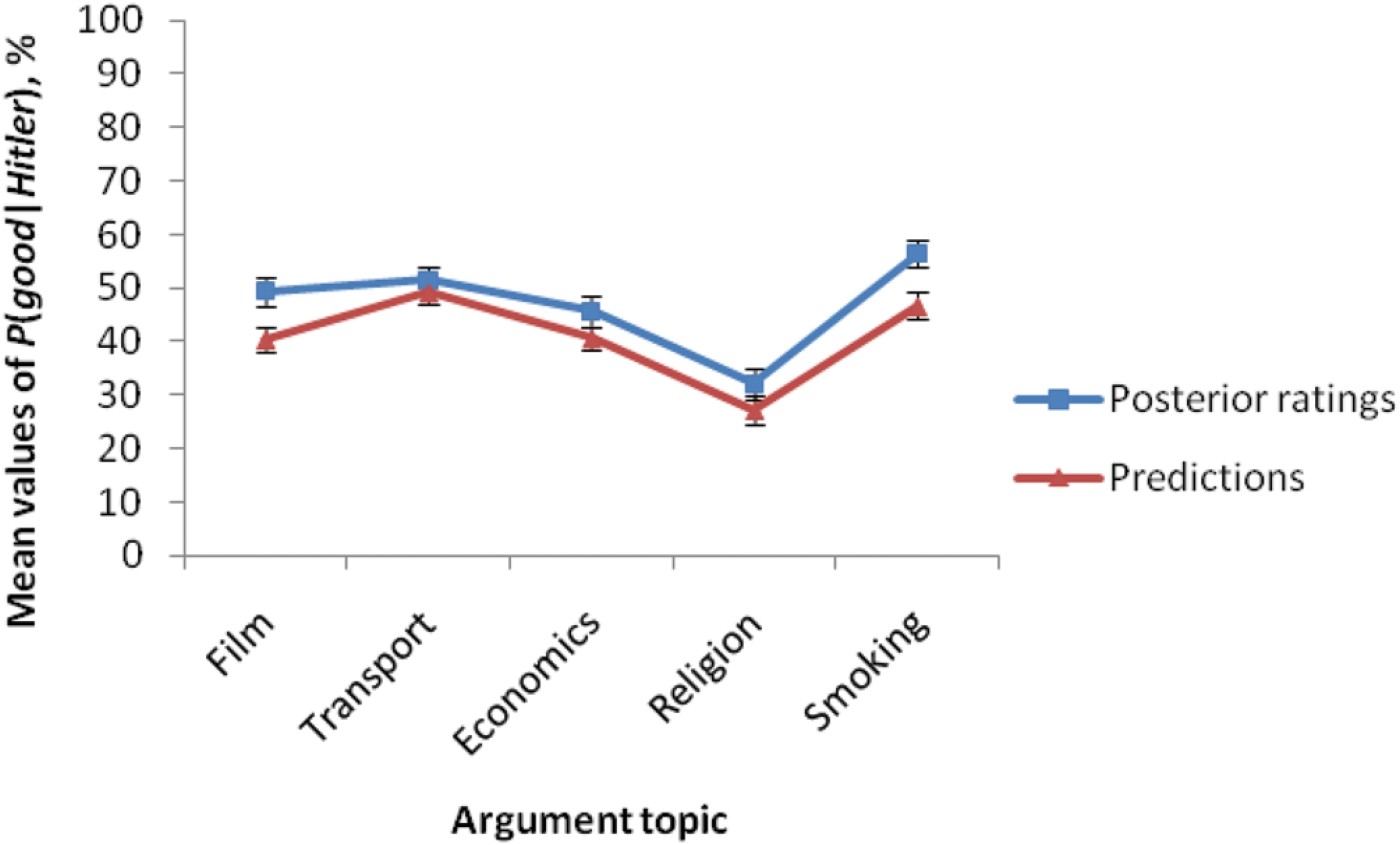
Again, model-fitting provides one route here. However, the most stringent test of the degree to which participants’ treatment of arguments matches the Bayesian account is one in which quantitative predictions are specified a priori. There are two ways in which this can be done: First, participants can provide the relevant conditional probabilities required for such an analysis themselves. For each participant a predicted posterior can be derived from these conditional probabilities – against which a directly rated posterior can be compared. Harris, Hsu, and Madsen (2012) adopted this approach. In Experiment 1, participants read five argument dialogues, which included an ad Hitlerum argument about five different topics (transportation, economics, a religion, a smoking ban in parks, and a film). The structure for the first four topics was that B informed A that a policy on the particular topic was a bad idea because Hitler had implemented the same policy. For the film topic, B argued that a film was not suitable for children because it was one of Hitler's favourites. After each argument, participants reported how convinced A should be that a policy was a good idea/the film was suitable for children. After all five arguments, participants were shown each argument again, and parameter estimates were obtained by asking them for the proportion of bad policies, P(e|¬h), and good policies, P(e| h), that they believed Hitler had been responsible for. Resulting group level model fits demonstrated that the significant difference between argument topics in convincingness ratings was quantitatively predicted by Bayesian predictions derived from these conditional probabilities, which predicted 92% of the variance across topics – with no free parameters. The results are displayed in Figure 3.

Figure 3.

The fit between participants’ original posterior ratings and ratings predicted from their conditional probabilities in Harris et al. (in press).

A further way of specifying a priori the quantitative predictions of the Bayesian approach is to devise an experimental paradigm in which it is possible to objectively determine the appropriate quantitative parameters. Harris et al. (2012) provided one example of this using frequency information (Experiment 3), but a more sophisticated demonstration was provided in Harris and Hahn (2009). Harris and Hahn's study was concerned with ‘coherence’, that is, the way arguments or evidence ‘hang together’, and the impact this has on posterior degrees of belief (see also Bovens and Hartmann 2003; Olsson 2005). Harris and Hahn therefore tested participants’ intuitions against the version of Bayes’ theorem derived by Bovens and Hartmann (2003) for situations in which one is provided with multiple independent reports about a hypothesis (see Appendix 3).

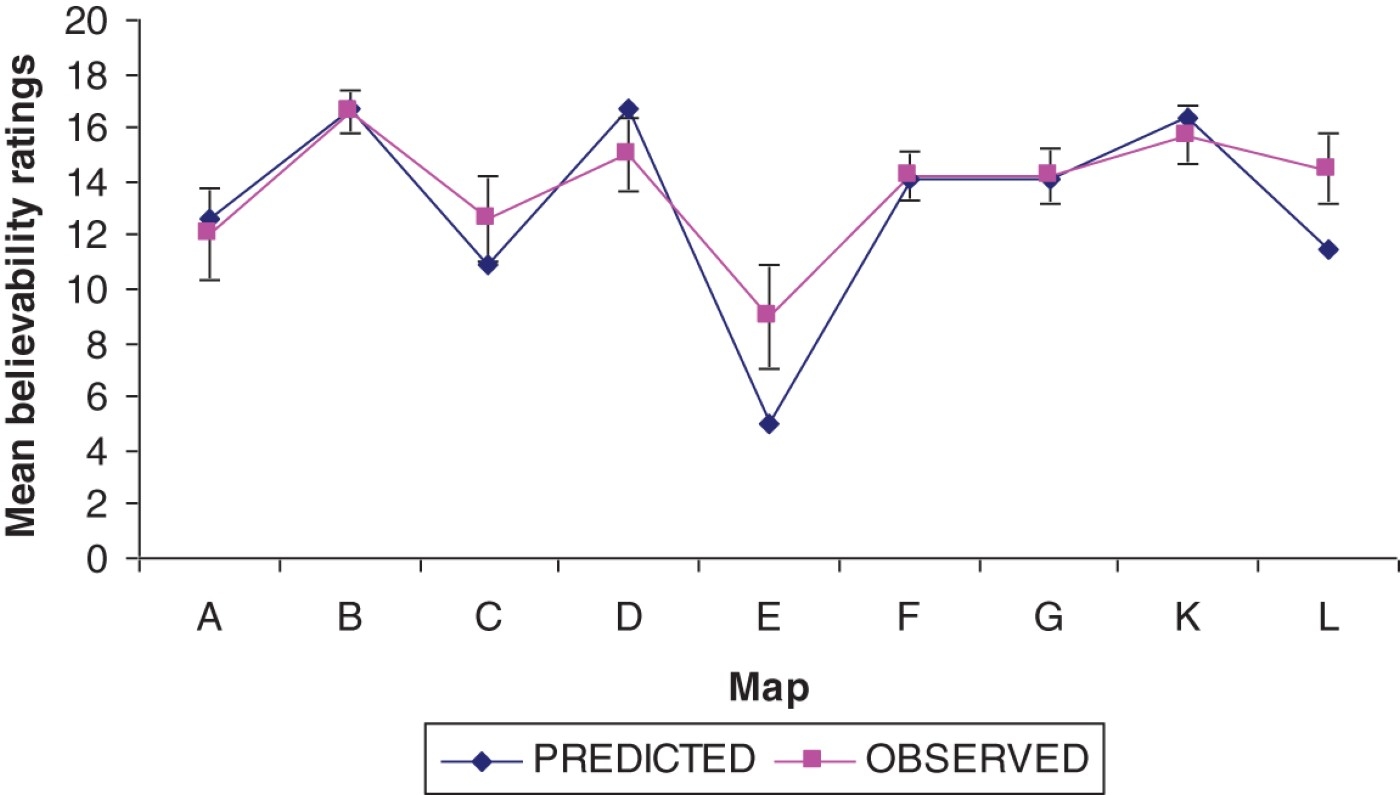
Participants were informed that police were searching for a body in a city. The police received reports from two (or three) independent witnesses whose reliability was less than perfect, but known by the police. The witness reports were displayed on a map of the city, which had been divided into 100 squares, with shading of each of the squares that the witnesses reported as a possible location of the body (for an example, see Figure 4). For each map, participants first saw a case in which the witnesses agreed completely on the body's location, and were informed what the police's posterior was in light of this information. The known reliability of the witnesses was thus provided implicitly. Participants were then required to judge the likelihood of the body being in a specific area of the map for a second distribution of reports in which there were some areas about which the witnesses disagreed as a possible location of the body. Hence, the relevant joint probability distributions were provided in this experiment by the proportions of squares of different shading.

Figure 4.

Example of the kinds of maps seen by participants in Harris and Hahn's (2009) study. Shaded areas labelled ‘1’ indicate areas identified by the first of the two witnesses as a putative location of the missing body. Areas labelled ‘2’ are parts of the city identified as a possible location only by the second witness. Areas labelled ‘1&2’ represent regions of overlap between the two testimonies.

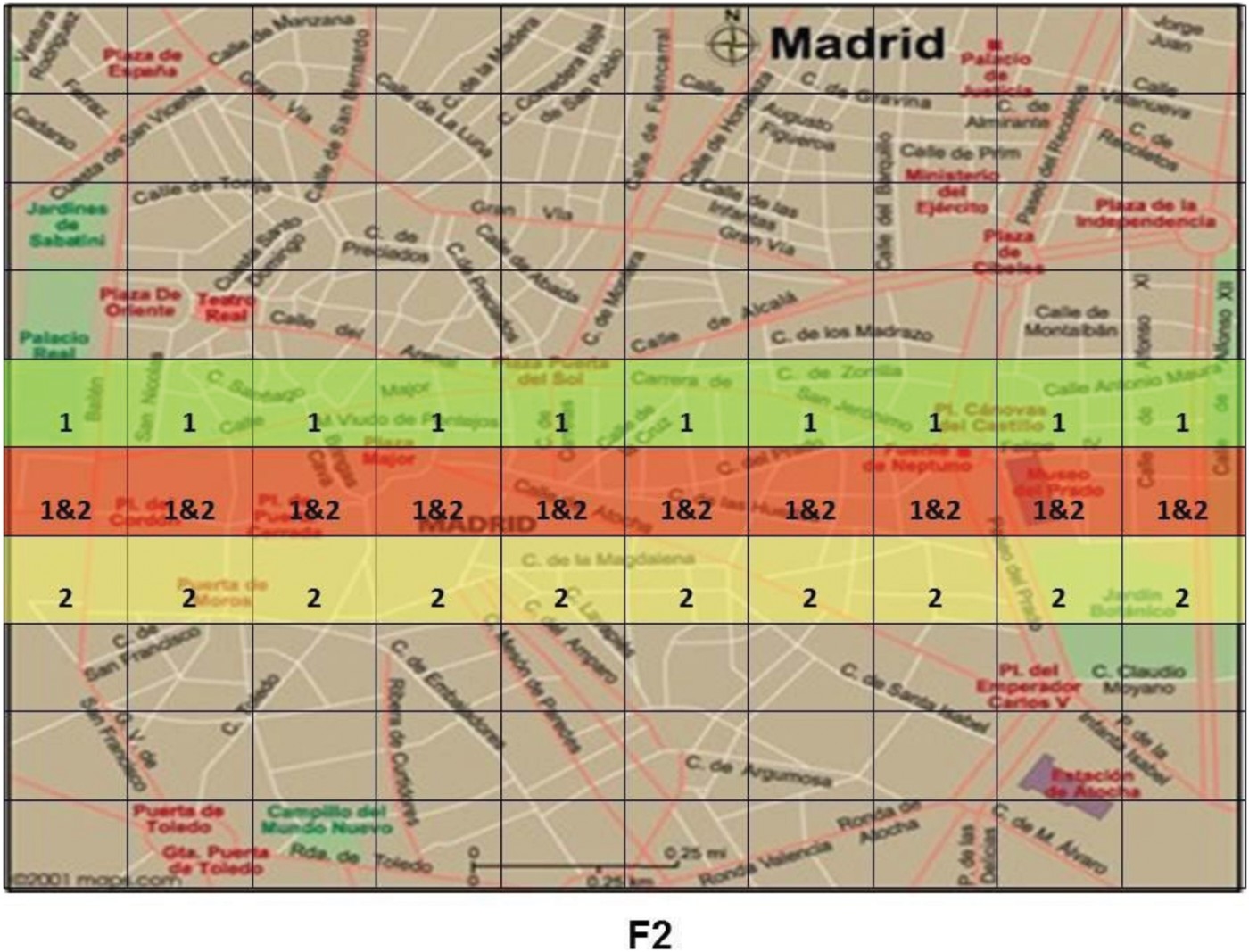
Participants were able to use this information, together with the implicit information about witness reliability, to provide quantitative judgements, 91% of whose variance was predicted by the Bayesian model. The results are shown in Figure 5.

Figure 5.

The quantitative fits between the observed and predicted data from Harris and Hahn (2009).

At the same time, an alternative model based on averaging was shown to provide much poorer fits (see Harris and Hahn 2009, for details, as well as to the averaging models in the context of judgement tasks more generally).

Conclusions and future directions

It has been argued in this paper that the formal framework of Bayesian probability has been instrumental in bringing together previously separate bodies of research, linking both different ‘kinds’ of reasoning and connecting reasoning and argumentation research. In turn, these links, to our mind considerably deepen the theoretical and explanatory depth found previously in any of these areas individually. At the same time, having a formal framework that supports both qualitative and quantitative predictions has profoundly affected the kinds of empirical predictions and hence the kind of empirical research that is possible within these areas.

Needless to say, this integration is not yet complete, and the new empirical possibilities, and with them new questions, are only starting to be explored. Of the many things that remain to be done, one glaring omission should, however stand out from the overview provided. This concerns the topic of analogy. It is the one major strand of reasoning research that has not been linked up in the same way. Yet much about analogy recommends such an integration. First and foremost is the fact that analogy has always been seen as both a form of inference and a type of argument. In the words of Mill (1959), for example,