Towards the simulation of bone-implant systems with a stratified material model
Abstract
BACKGROUND:
The clinical performance of medical devices is becoming increasingly important for the requirements of modern development processes and the associated regulations. However, the evidence for this performance can often only be obtained very late in the development process via clinical trials or studies.
OBJECTIVE:
The purpose of the presented work is to show that the simulation of bone-implant systems has advanced in various aspects, including cloud-based execution, Virtual Clinical Trials, and material modeling towards a point where and widespread utilization in healthcare for procedure planning and enhancing practices seems feasible. But this will only hold true if the virtual cohort data build from clinical Computer Tomography data are collected and analysed with care.
METHODS:
An overview of the principal steps necessary to perform Finite Element Method based structural mechanical simulations of bone-implant systems based on clinical imaging data is presented. Since these data form the baseline for virtual cohort construction, we present an enhancement method to make them more accurate and reliable.
RESULTS:
The findings of our work comprise the initial step towards a virtual cohort for the evaluation of proximal femur implants. In addition, results of our proposed enhancement methodology for clinical Computer Tomography data that demonstrate the necessity for the usage of multiple image reconstructions are presented.
CONCLUSION:
Simulation methodologies and pipelines nowadays are mature and have turnaround times that allow for a day-to-day use. However, small changes in the imaging and the preprocessing of data can have a significant impact on the obtaind results. Consequently, first steps towards virtual clinical trials, like collecting bone samples, are done, but the reliability of the input data remains subject to further research and development.
1.Introduction
The clinical performance of medical devices is becoming increasingly important for the requirements of modern development processes and the associated regulations. However, the evidence for this performance can often only be obtained very late in the development process via clinical trials or studies.
Even nowadays, endoprostheses or implants to stabilize fractures are still selected and applied based on empirically gained knowledge, the individual experience of the attending surgeon and elementary biomechanical estimations. During the use of these implants complications can occur [1, 2]. With fracture stabilizing implants, e.g., a delayed healing process can be observed. Locked implants can cut through intact bone as well as, in the worst case, through the articular cartilage. When using endoprostheses as joint replacements there can be unforeseeable effects like intra operative femur fractures or mechanically induced loosening of the implant, despite of long-term empirically established implants [3, 4]. A patient specific estimation of the probability of complications is currently not possible for the attending surgeon.
Based on these scenarios, the global aim of biomechanical simulations of bone-implant systems, as they are referred to in this work, is twofold. (1) The results obtained by pre-operative analyses of the virtually implanted device can support diagnostic decisions with respect to type and positioning of implants used to treat certain pathologies and will allow to predict the healing process. Furthermore, a risk analysis for mechanical complications is possible. (2) The simulation of devices in virtual patient cohorts will support the optimization and development of new implant systems in Virtual Clinical Trials (VCT). These trials are supposed to speed up development cycles, allow deeper insights into the mechanical functionality of devices within the human tissue and by that are expected to minimize complication rates. In this paper, we will give an overview about the current state of development of our work on a simulation process chain for bone-implant systems with a special focus on material modeling and the contribution of High-Performance Computing (HPC) to this topic.
1.1Background
The whole process of the simulation of bone-implant systems has been subject to many studies in the literature over the past years [5, 6] and has even been demonstrated to be efficiently executable on cloud based computing resources [7, 8]. Furthermore, the approach of VCT is promoted by the European Commission in the final report of the Avicenna Alliance [9] and by the Food and Drug Administration (FDA) in various guidance documents [10]. With this, the baseline has been set to develop the methodology of the simulation of bone-implant systems from the stage of pure academic analyses and considerations towards productive application in clinical environments as well as in implant design and development.
Also for the three prerequisites of structural mechanics simulations, (1) the bone geometry, (2) forces acting on the bone structures and (3) a detailed modeling of the heterogeneous, anisotropic material distribution of the bony structures, significant developments were achieved. The extraction of the bone geometry from clinical Computer Tomography (CT) data is already a standard procedure implemented in various software tools and libraries [11, 12, 13, 14]. Also the determination of representative sets of muscle forces is subject to recent research on the software development and simulation side [15, 16] as well as the experimental side [17].
In the field of material modeling on the basis of CT data, the literature of the past decades shows a path leading from analytical approaches [18] and experimental methods [19] over material data determination via data-processing-based approaches directly applied to clinical CT data [20], to simulation-based approaches that use homogenisation and averaging methods to raise bone micromechanics to the level of continuum mechanics [21, 22].
Like in the case of geometry extraction, the actual continuum mechanical simulations of bone-implant systems can also be based on standard tools as was demonstrated by various studies in the recent past [23, 24]. Even for the communication of engineering type results towards medical and clinical staff approaches are developed [25].
A recent study conducted in 2023 provides compelling evidence of the surging acceptance of computer modeling and simulation within hospital settings [26]. Notably, a substantial 55.0% of respondents reported actively utilizing computational modeling and simulation for procedure planning. The degree of adoption, however, exhibited variation across different medical settings. Among those who employed modeling and simulation for procedure planning, the cardiovascular domain emerged as the most prevalent, closely followed by musculoskeletal applications. In terms of numerical tools employed, Artificial Intelligence (AI) stood out as the most frequently utilized, followed by multiscale modeling, Finite Element Analysis (FEA), and Computational Fluid Dynamics (CFD). These findings collectively underscore the increasing significance and widespread utilization of computer modeling and simulation in enhancing healthcare practices.
1.2Objective
The first objective of this paper is to present an overview of the principle approach towards the analysis of bone-implant systems by means of engineering type Finite Element Method (FEM) simulations. The second objective is to demonstrate how the nondeterministic character of biomechanical models can be captured for the part of human bone material modeling and how HPC can be used to efficiently construct nondeterministic modeling approaches suitable for VCT as well as for the uncertainty quantification of patient specific models with large parameter spaces.
Figure 1.
Anticipated workflow in simulation supported surgery.
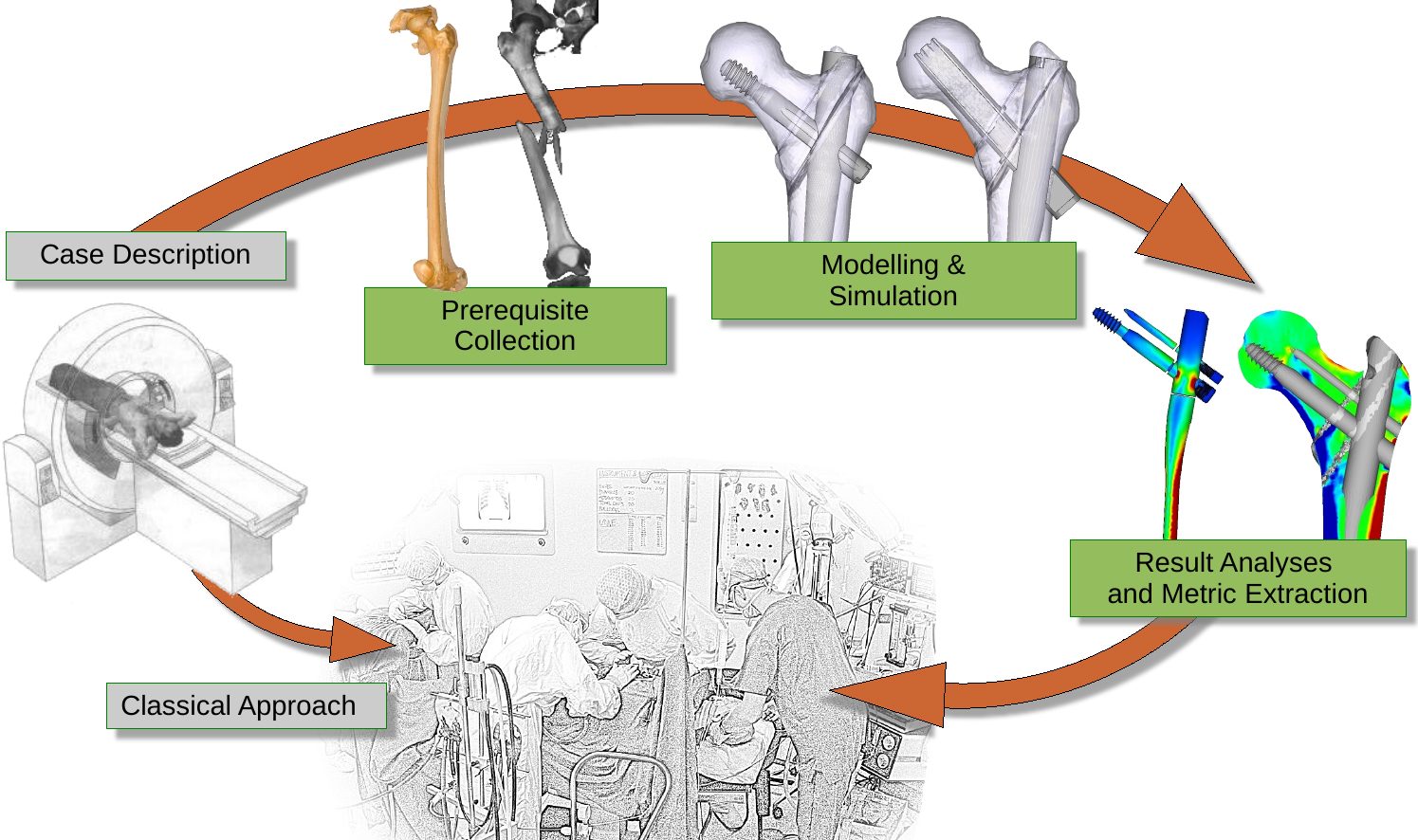
As can be seen in Fig. 1 the principle modeling approach of bone-implant systems is not that different from the classical engineering simulation workflow comprised out of the four steps (1) model generation (i.e. preprocessing), (2) simulation (3) result evaluation (i.e post-processing) and (4) result feedback, even though considerable differences to classical deterministic modeling exist, especially in the first and last step.
Since most of the considered steps are existing pieces, put together from already developed approaches, we present their principles briefly in the Methods section. For the steps “data processing of clinical CT data” and “material modeling” a deeper dive is done. The processing of the clinical CT data is considered in more detail due to its significant difference to clinical routines and the material modeling part due to its impact on the variability of models. This leads to the results section where first findings with respect to the development of a virtual cohort as a baseline for a non deterministic modeling approach for bone-implant systems by means of HPC and its link to clinical CT data are presented.
2.Materials and methods
This section is structured along the steps which have to be taken to execute FEM simulations of bone- implant systems as depicted in Fig. 1 i.e. (1) prerequisite collection, (2) modeling and simulation and (3) result analyses and metric extraction.
2.1Prerequisite collection
Clinical imaging data, as recorded by CT or Magnetic Resonance Imaging (MRI), are the only data which are available from living bones and muscles which have to be represented in discretised form in order to comprise a FEM model of a bone-implant systems with all relevant load- and boundary conditions. One problem that always arises when deriving discrete simulation models from CT data is the discrepancy between clinical data collection schemes and the requirements that are posed to data once they should be used as a baseline for model extraction. In everyday clinical routine especially in the cases of CT data, x-ray exposure and other burdens to the patient have to be kept at the absolute minimum. Additionally, imaging data are collected for visual inspection by trained medical professionals which means that the in-plane resolution of the images in almost every case differs significantly from the one in normal direction of the image plane since the focus lies on the single 2D image. This means the fundamental point is to improve image resolution. This leads to clean geometry extraction and a reproducible baseline for material data generation.
2.1.1Geometry
To achieve increased image resolution we have chosen the approach to combine multiple image reconstructions in different imaging planes. In discussions with the medical staff it was found that the least disturbance of the clinical routine would result from the application of standard protocols, i.e the reconstruction of the image data normal to the three coordinate axes. To combine the three resulting data sets into one 3D data volume with isotropic resolution, the DICOM data were converted with the application 3D-Slicer into VTK-Image data and then combined by means of a VTK-pipeline realized in ParaView [27] as shown in Fig. 2. The image combination process in the ParaView Calculator Filter currently employs a simple mean calculation.
Figure 2.
Image reconstruction planes and recombination pipeline.
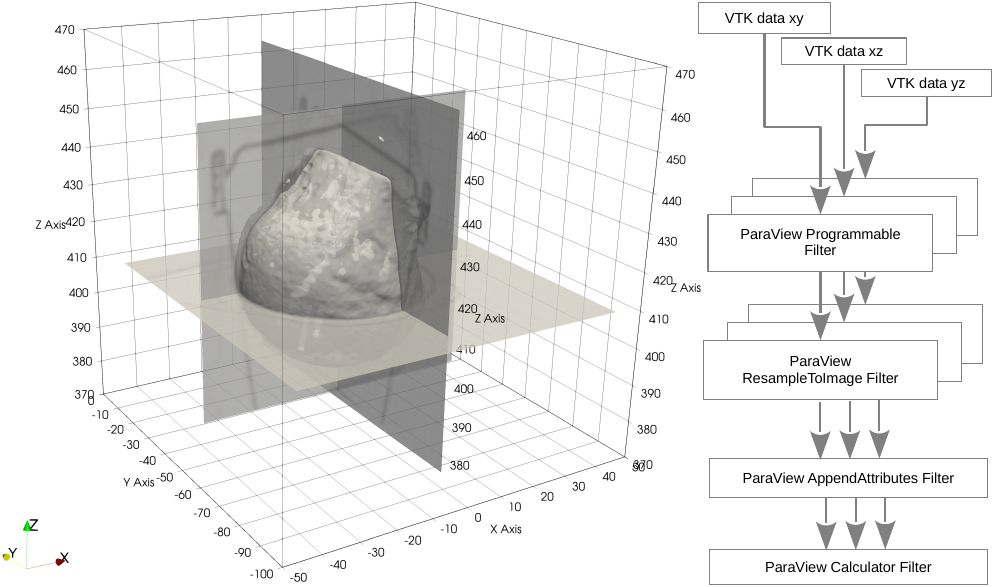
The geometry extraction itself is also done with ParaView by means of the ParaView Contour Filter which is based on isosurface calculation via the marching cubes algorithm. The extracted geometry is then exported as a triangulated surface mesh in a format which can afterwards be imported by the FEM preprocessor ANSA [28].
2.1.2Forces
In the realm of hip arthroplasty and intramedullary femoral implants, the examination of bone-implant structures involves analyzing the interplay of various forces. These forces can be categorized as hip force and a condensed set of muscle forces. In the traditional approach, the forces were taken from the literature. A new approach to determine these forces is based on multi-body simulations combined with an inverse dynamics approach [29, 16, 30]. Inverse dynamics is the numerical approach to determine the internal forces and torques acting on a mechanical system based on measured motions and external forces. It is particularly useful in the analysis of complex mechanical systems, such as human movement or biomechanical structures. Even though it is computationally expensive, we consider this approach necessary to produce realistic transient load patterns usable in virtual clinical trials.
2.1.3Material data
Since an essential factor for bone remodeling is the local micromechanical strain the bone tissue is exposed to, the material modeling is a crucial factor and it is absolutely necessary to apply a sophisticated and calibrated model throughout the complete bone structures. From available studies it is known that bone material shows orthotropic behaviour [19, 31] which in turn shows a complete inhomogeneous distribution across bone structures. Even though phenomenological models exist that can create completely inhomogeneous and orthotropic material data based on clinical CT data [20], the parameter calibration of theses models to certain patient groups or even single patients remains a problematic task especially since experimental data in almost every case are not derived on the correct resolution scale. To overcome these problems we rely on the approach of the effective stiffness matrix which was shown to be applicable to bone by Rietbergen et al. [32]. With the availability of HLRS’s extended HPC resources, the method is applied to harvested bone samples to generate material data suitable for the simulation of bone-implant systems according to [33]. What remains subject to further investigations is the derivation of stratified material models for virtual cohorts which can be used in VCT. The initial steps towards this goal are presented in the results section.
2.2Modeling and simulation
In this section the current modeling and simulation techniques and tools utilized to evaluate bone-implant-structures are described. As explained above, the geometry extracted from clinical CT data is exported as a triangulated mesh. Since a surface mesh derived by a marching cubes algorithm is not suitable for FEM simulations, the mesh has to be restructured to regular triangulation. This is currently done with the FEM preprocessor ANSA. With this tool the necessary mesh improvements, the reassembling of fractured bones and the volume meshing of the bone structures are done. Furthermore the implant structures which in most case are provided as Computer-Aided Design (CAD) data are meshed and integrated into the bone structures. Additionally, loads and boundary conditions are applied with ANSA. To automate the application of boundary conditions a method based on template morphing is currently under development.
Figure 3.
Modelled bone and implant structures.

In Fig. 3 the typical set of bone structures modelled for the analysis of proximal femur implants is shown along with the material distribution in the model which was directly mapped from the clinical CT data with the algorithm described in [20]. Blue areas represent low material stiffness whereas red areas mark regions of high material stiffness. 432 different orthotropic material cards were used in this model combined with 48 orthotropic coordinate systems. Also shown in Fig. 3 are models of the distal humerus. They where used to analyze different external fixation methods of a distal humerus fracture. The question raised by the surgeons was, which fixation option generates the least relative movement within the fracture zone.
The FEM simulation of bone-implant systems is currently done with standard FEM software packages like Abaqus/Standard [34], code_aster [35] or in dynamic situations with LS-DYNA [36].
2.3Result analyses and metric extraction
The result analyses and metric extraction can be done with commercial software packages like the FEM post-processor META [37]. Of particular interest are the locations of plastic strains within the implant structures that can lead to locking of dynamic components inside the implant. Within the bone structures, the major principal strains are evaluated. In the case of implants for fracture stabilization, normal strains within the fracture planes are evaluated. Based on these structural mechanics results metrics are derived and evaluated my means of a scoring system that is discussed in detail in [25]. Based on this scoring system different implants can be evaluated within a single bone structure to find the best implant for a given patient or vice versa, an implant can be evaluated within a virtual cohort to evaluate its average performance score.
3.Results and discussion
Since we present in this work the principle methodological description, how we approach VCT for bone-implant systems based on the combination of already developed steps, we focus on the description of the essential baseline for VCT, i.e. the generation of reliable virtual cohort data from clinical CT data. In addition we present initial results of the resample combine approach which from our point of view is a key methodology to make clinical CT data usable for geometry extraction and material data generation with as less uncertainty due to the data recording and extraction processes as possible.
3.1Data sets for virtual trial testing
A total of 28 clinical CT data sets were harvested, encompassing patients aged between 49 and 90 years. The data set consists of femoral heads from 16 females and 12 males. For the scanning process, femoral heads numbered 1 to 20 were captured using the Siemens
Table 1
Overview of the 28 bone samples with information on the gender, age and weight of the donors as well as the weight of the femoral heads. For samples number 37 and 38, the donor did not want to provide any information on his weight
| Femoral head no. | Gender | Donor age (years) | Donor weight (kg) | Femoral head weight (g) |
|---|---|---|---|---|
| 1 | Male | 74 | 128 | 82 |
| 2 | Female | 90 | 79 | 73 |
| 3 | Female | 84 | 73 | 80 |
| 4 | Female | 65 | 67 | 65 |
| 5 | Male | 68 | 74 | 97 |
| 6 | Female | 49 | 70 | 77 |
| 7 | Female | 53 | 95 | 69 |
| 8 | Female | 69 | 57 | 69 |
| 9 | Male | 80 | 62 | 106 |
| 10 | Male | 61 | 115 | 110 |
| 11 | Male | 77 | 74 | 93 |
| 12 | Male | 72 | 108 | 119 |
| 14 | Female | 76 | 58 | 74 |
| 15 | Female | 83 | 54 | 47 |
| 16 | Female | 88 | 75 | 39 |
| 17 | Female | 74 | 73 | 88 |
| 18 | Female | 85 | 77 | 44 |
| 20 | Male | 71 | 69 | 84 |
| 22 | Male | 57 | 87 | 85 |
| 25 | Male | 69 | 80 | 112 |
| 30 | Female | 55 | 95 | 66 |
| 34 | Female | 65 | 82 | 91 |
| 35 | Female | 60 | 110 | 69 |
| 37 | Male | 62 | – | 78 |
| 38 | Male | 62 | – | 106 |
| 42 | Female | 84 | 68 | 72 |
| 43 | Female | 70 | 86 | 64 |
| 44 | Male | 80 | 75 | 103 |
The process of explantation and imaging of the femoral heads was conducted with the approval of the Ethics Committee of the State Medical Chamber of Baden-Württemberg, under the application F-2020-118. To ensure the authenticity and accuracy of the data while safeguarding the interests and dignity of the tissue donors, the data sets were pseudonymized prior to publication. These data sets, comprising clinical CT data from all 28 cases, were collected and reconstructed in three orientations to align with the described resample combine methodology in the method section. To make these data accessible to the open public, they are published in the data repository of the University of Stuttgart called DaRUS [38, 39, 40].22
The femoral heads are presently securely stored in a locked room at the Institute of Biomaterials and Biomolecular Systems at the University of Stuttgart. Specifically, they are maintained in a freezer at a temperature of
3.2Data evaluation
In this section we present the initial findings of the proposed resample combine method. In Fig. 4 one can see in the upper left the outline of the data volume encompassing the three data sets along with a volume rendering of the contained femoral head no.1 and the line along which the line charts in the upper right and lower part of the figure are plotted. The line chart in the upper right presents the plot of the resampled data sets across the total volume. As can be seen, global differences are non-existent even though, taking a closer look at the data as shown in the lower, zoomed in part of the figure makes it evident that non negligible differences exist if data are reconstructed in different image planes. This is especially true for areas of local maxima and minima which are apparently equally affected.
Table 2
Statistical evaluation of data sets reconstructed in different image planes
| Femoral head no. | Compared data sets | 25% quartile | Mean | 25% quartile |
|---|---|---|---|---|
| 1 | xz–xy | 0.027 | ||
| 1 | yz–xy | 0.0275 | ||
| 1 | yz-xz | 0.0 | 0.017 | |
| 5 | xz–xy | 0.114 | ||
| 5 | yz–xy | 0.057 | ||
| 5 | yz–xz | 0.006 | 0.141 |
Figure 4.
Example of the resample combine method of multiple reconstructions by simple mean calculation.
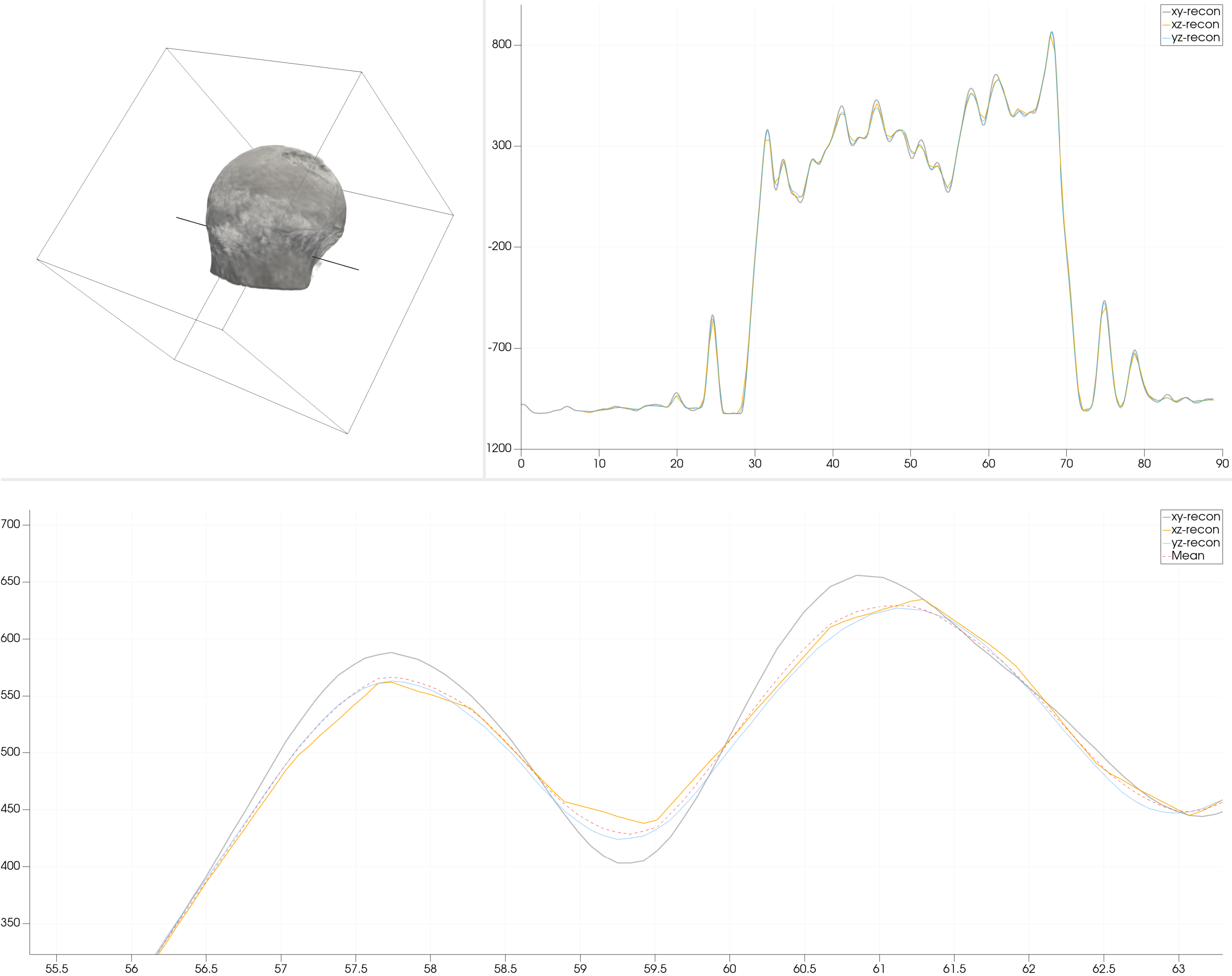
As can be read from Table 2 in which the mean, the 25% quartile and 75% quartile for the comparison of two data sets each in different imaging planes are shown, the result from the line sample presented in Fig. 4 hold true also for complete data fields. Additionally, it can be seen from Table 2 that differences also vary significantly between data sets of different femoral heads even though the same scanning and reconstructions procedures were used to record and reconstruct the different data fields. As can be seen, the maximum deviation of two different data fields reaches 3.6% within femoral head no. 1 while it shows a maximum of 14.1% within femoral head no. 5.
Another interesting results that can be observed from Table 2 is the fact that deviations between data sets are symmetric around the mean value. This leads to the conclusion that the application of the proposed resample combine methodology is not necessary for simulations in which only global strain and displacement results are of interest since local deviations between different reconstructions will be averaged out. Vice versa, however, multiple reconstruction and the application of the resample combine method are absolutely necessary once local strain patterns should be evaluated since these discrepancies subsequently will impact material modeling in which material data are directly mapped from clinical CT data.
4.Conclusion
The conclusions one can draw from the presented methodological paper are twofold. On the one hand, one can state that the maturity of all pieces necessary for the simulation of bone-implant systems has reached a degree from which it is possible to develop a simulation pipeline that drags the model preparation and evaluation turnaround time from weeks per model down to the level of a regular engineering simulation process and with that brings VCT into feasible reach.
On the other hand, one can show with relatively simple evaluations that the foundation for VCT, the virtual cohorts can not simply be taken out of the everyday clinical routine since apparently simple things, like the image reconstruction plane in the presented case, can have significant impact on the simulation process’s baseline data that would render results of simulations extremely hard if not impossible to analyse.
To overcome these problems an initial step was made with the physical as well as digital preservation of the harvested femoral heads that will be used in future studies with respect to bone screw reliability and via micro-focus CT scans for the setup of stratified transfer functions to produce reliable inhomogeneous, anisotropic material data from clinical CT data.
Funding
This research was supported by CASE4Med (Computed Aided Solution Engineering for Medical) with the support of a grant from the Baden-Württemberg Ministry for Science, Research and the Arts (MWK), HLRS – in cooperation with the Innovation and Research Center Tuttlingen of Furtwangen University and SICOS BW GmbH.
Ethics statement
The study was approved by the Ethics Committee of the State Medical Chamber of Baden-Württemberg under application F-2020-118.
Notes
Acknowledgments
The authors acknowledge the support by the Stuttgart Center for Simulation Science (SimTech). They also acknowledge the support from Prof. Dr. Ingrid Weiss (University of Stuttgart, Institute of Biomaterials and Biomolecular Systems) for the storage of the bone samples and Prof. Dr.-Ing. Holger Steeb (University of Stuttgart, Institute of Applied Mechanics (MIB)) for the generation of the micro-focus CT scan.
Conflict of interest
The authors declare that they have no conflict of interest.
References
[1] | Holzwarth U, Cotogno G. Total hip arthroplasty: State of the art, prospects and challenges. Publications Office of the European Union. (2012) . doi: 10.2788/31286. |
[2] | American Joint Replacement Registry (AJRR). Annual Report 2021. Online. American Academy of Orthopaedic Surgeons (AAOS). (2021) . Available from: https://www.aaos.org/registries/publications/ajrr-annual-report/. |
[3] | Parker MJ, Stedtfeld HW. Internal fixation of intracapsular hip fractures with a dynamic locking plate: Initial experience and results for 83 patients treated with a new implant. Injury. (2010) ; 41: : 348–51. doi: 10.1016/j.injury.2009.09.004. |
[4] | Gjertsen JE, Vinje T, Engesæter LB, Lie SA, Havelin LI, Furnes O, Fevang JM. Internal screw fixation compared with bipolar hemiarthroplasty for treatment of displaced femoral neck fractures in elderly patients. The Journal of Bone and Joint Surgery-American Volume. (2010) ; 92: : 619–28. doi: 10.2106/jbjs.h.01750. |
[5] | Houshmand B, Ardakani MT, Moscowchi A, Oskoui IZ. Effect of implant design on stress distribution: A finite element study. Journal of Long-Term Effects of Medical Implants. (2022) ; 32: : 39–45. doi: 10.1615/jlongtermeffmedimplants.2022042799. |
[6] | Scannell PT, Prendergast PJ. Cortical and interfacial bone changes around a non-cemented hip implant: Simulations using a combined strain/damage remodelling algorithm. Medical Engineering & Physics. (2009) ; 31: : 477–88. doi: 10.1016/j.medengphy.2008.11.007. |
[7] | Kumara I, Kayes ASM, Mundt P, Schneider R. Data Governance. Data Science for Entrepreneurship. Ed. by Liebregts W, Heuvel WJ van den, and Born A van den. Springer International Publishing. (2023) : 37–62. doi: 10.1007/978-3-031-19554-9_3. |
[8] | Schneider R, Tokmakov K, Liparas D, Hoppe D, Meth K, Mundt EDP, González RS, Gómez AG, Requena MM, Gorroñogoitia Y, Radolović D, Fraternali P, Torres RN, Meditskos G, Vrochidis S, Sivalingam K, Kumara I. Initial implementation and evaluation of the SODALITE platform and use cases. (2020) . Available from: https://www.sodalite.eu/reports/d62-initial-implementation-and-evaluation-sodalite-platform-and-use-cases-0 (visited on 06/01/2023). |
[9] | Viceconti M Henney A MFE. in silico Clinical Trials: How Computer Simulation will Transform the Biomedical Industry. Research and Technological Development Roadmap. (2016) . doi: 10.13140/RG.2.1.2756.6164. |
[10] | Food and Drug Administration. Conduct of Clinical Trials ofMedical Products During the COVID-19 Public Health Emergency. Online. (2020) . Available from: https://www.fda.gov/media/136238/download (visited on 06/01/2023). |
[11] | Kitware Inc. Visualization Toolkit (VTK). (2023) . Available from: https://vtk.org/ (visited on 06/01/2023). |
[12] | Schroeder W, Martin K, Lorensen B. Visualization Toolkit. An Object-Oriented Approach to 3D Graphics. 4th ed. Kitware, (2006) . |
[13] | The Slicer Community. 3D Slicer. (2023) . Available from: https://www.slicer.org/ (visited on 06/01/2023). |
[14] | Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward S, Miller JV, Pieper S, Kikinis R. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magnetic Resonance Imaging. (2012) ; 30: : 1323–41. doi: 10.1016/j.mri.2012.05.001. |
[15] | AnyBody Technology A/S. The AnyBody Modeling System. Available from: http://www.anybodytech.com/ (visited on 06/01/2023). |
[16] | Schmitt S. demoa-base: a biophysics simulator for muscle-driven motion. (2022) . doi: 10.18419/DARUS-2550. |
[17] | Julius Wolff Institute. OrthoLoad – Loading of Orthopaedic Implants. Online. (2023) . Available from: https://orthoload.com/ (visited on 06/01/2023). |
[18] | Hill R. Elastic properties of reinforced solids: Some theoretical principles. Journal of the Mechanics and Physics of Solids. (1963) ; 11: : 357–72. doi: 10.1016/0022-5096(63)90036-x. |
[19] | Ciarelli MJ, Goldstein SA, Kuhn JL, Cody DD, Brown MB. Evaluation of orthogonal mechanical properties and density of human trabecular bone from the major metaphyseal regions with materials testing and computed tomography. Journal of Orthopaedic Research. (1991) ; 9: : 674–82. doi: 10.1002/jor.1100090507. |
[20] | Schneider R, Faust G, Hindenlang U, Helwig P. Inhomogeneous, orthotropic material model for the cortical structure of long bones modelled on the basis of clinical CT or density data. Computer Methods in Applied Mechanics and Engineering. (2009) ; 198: : 2167–74. doi: 10.1016/j.cma.2009.02.010. |
[21] | Hollister SJ, Kikuchi N. A comparison of homogenization and standard mechanics analyses for periodic porous composites. Computational Mechanics. (1992) ; 10: : 73–95. doi: 10.1007/bf00369853. |
[22] | Suquet PM. Elements of homogenization theory for inelastic solid mechanics. Homogenization Techniques for Composite Media. Ed. by Sanchez-Palencia E and Zaoui A. Springer Berlin Heidelberg. (1987) ; 193–278. doi: 10.1007/3-540-17616-0. |
[23] | Eremina GM, Smolin AY. Risk assessment of resurfacing implant loosening and femur fracture under low-energy impacts taking into account degenerative changes in bone tissues. Computer simulation. Computer Methods and Programs in Biomedicine. (2021) ; 200. doi: 10.1016/j.cmpb.2021.105929. |
[24] | Levadnyi I, Awrejcewicz J, Gubaua JE, Pereira JT. Numerical evaluation of bone remodelling and adaptation considering different hip prosthesis designs. Clinical Biomechanics. (2017) ; 50: : 122–9. doi: 10.1016/j.clinbiomech.2017.10.015. |
[25] | Helwig P, Faust G, Hindenlang U, Hirschmüller A, Konstantinidis L, Bahrs C, Südkamp N, Schneider R. Finite element analysis of four different implants inserted in different positions to stabilize an idealized trochanteric femoral fracture. Injury. (2009) ; 40: : 288–95. doi: 10.1016/j.injury.2008.08.016. |
[26] | Lesage R, Oudheusden MV, Schievano S, Hoyweghen IV, Geris L, Capelli C. Mapping the use of computational modelling and simulation in clinics: A survey. Frontiers in Medical Technology. (2023) ; 5. doi: 10.3389/fmedt.2023.1125524. |
[27] | Kitware Inc. ParaView. (2023) . Available from: https://www.paraview.org/ (visited on 06/03/2023). |
[28] | BETA CAE Systems. ANSA. (2023) . Available from: https://www.beta-cae.com/ansa.htm (visited on 06/03/2023). |
[29] | Layton R, Messenger N, Stewart T. Characteristics of hip joint reaction forces during a range of activities. Medical Engineering & Physics. (2022) ; 108: : 103894. doi: 10.1016/j.medengphy.2022.103894. |
[30] | Seth A, Hicks JL, Uchida TK, Habib A, Dembia CL, Dunne JJ, Ong CF, DeMers MS, Rajagopal A, Millard M, Hamner SR, Arnold EM, Yong JR, Lakshmikanth SK, Sherman MA, Ku JP, Delp SL. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLOS Computational Biology. (2018) ; 14. Ed. by Schneidman D. doi: 10.1371/journal.pcbi.1006223. |
[31] | Pithioux M, Lasaygues P, Chabrand P. An alternative ultrasonic method for measuring the elastic properties of cortical bone. Journal of Biomechanics. (2002) ; 35: : 961–8. doi: 10.1016/s0021-9290(02)00027-1. |
[32] | van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. Journal of Biomechanics. (1995) ; 28: : 69–81. doi: 10.1016/0021-9290(95)80008-5. |
[33] | Schneider R. Analyse kontinuumsmechanischer, anisotroper Materialparameter mikrostrukturierter Volumina mit Hilfe direkter mechanischer Simulation. PhD thesis. Universität Stuttgart. (2016) . doi: 10.18419/opus-8752. |
[34] | Dassault Systems. Abaqus/Standard. (2023) . Available from: https://www.3ds.com/de/produkte-und-services/simulia/produkte/abaqus/abaqusstandard/ (visited on 06/03/2023). |
[35] | Électricité de France. Code_Aster. (2023) . Available from: https://code-aster.org (visited on 06/03/2023). |
[36] | ANSYS. LS-DYNA. (2023) . Available from: https://lsdyna.ansys.com/ (visited on 06/03/2023). |
[37] | BETA CAE Systems. META. (2023) . Available from: https://www.beta-cae.com/meta.htm (visited on 06/03/2023). |
[38] | Hermann S, Schneider M, Flemisch B, Frey S, Iglezakis D, Ruf M, Schembera B, Seeland A, Steeb H. Datenmanagement im SFB 1313. (2020) . doi: 10.17192/BFDM.2020.1.8085. |
[39] | Gebert J, Schneider R, Schnabel B, Pelzer F, Helwig P, Schenkengel JP. Scanning Spongiosa: A set of Clinical Computed Tomography Scans of Human Femoral Heads. Online. (2023) . doi: 10.18419/darus-3065. |
[40] | Gebert J, Schneider R, Helwig P, Schenkengel JP. A clinical Computed Tomography Scan of a Human Femoral Head. Online. (2021) . doi: 10.18419/DARUS-1182. |
[41] | Mazurkiewicz AJ. The effect of trabecular bone storage method on its elastic properties. Acta of Bioengineering and Biomechanics. (2018) . doi: 10.5277/ABB-00967-2017-03. |




