A three-dimensional finite element analysis of the effect of archwire characteristics on the self-ligating orthodontic tooth movement of the canine
Abstract
BACKGROUND:
In orthodontics, the tooth movement is a biologic reaction to applied force systems, brackets, archwires, and periodontium tissue.
OBJECTIVE:
To investigate the effects of the various archwire characteristics like the friction coebetween bracket and archwire, the cross-section shape, and the cross-section dimension, on the displacement and the periodontal ligament (PDL) stresses of canine’s movement in a self-ligating treatment using the finite element (FE) analysis method.
METHODS:
Models of teeth and their supporting tissues, brackets and archwires were constructed. Ten kinds of archwires were used for the simulation.
RESULTS:
Considering the translation movement, the maximum displacement, highest stress, and
CONCLUSION:
The archwire characteristics (round archwire, rectangular archwire, cross-section area, and friction coefficient) exhibited different effects on the tooth translation, rotation, and inclination. Our results can assist in the improvement of the self-ligating orthodontic treatment.
1.Introduction
When sliding mechanics are used in the orthodontic treatment, the frictional force between the bracket and the archwire can influence the force transmitted to the teeth, and thus reduce the accuracy and efficiency of the orthodontic tooth movement [1]. Many studies have investigated this friction in vitro. For example, Seo et al. [2] evaluated the effects of the tooth displacement and vibration on the frictional force. Cacciafesta et al. [3] reported that the frictional forces between the ceramic brackets and the stainless-steel brackets increased with an increase in the wire size. Park et al. [4] proposed a new measuring method for measuring the frictional force the between lingual brackets and the archwires. Cacciafesta et al. [5] found that the beta-titanium archwires exhibited a high friction, while stainless steel and nickel-titanium archwires showed a similar friction.
The result of the biological response in the periodontium causes an orthodontic movement of the tooth [6]. However, there are very few investigations on the mechanical stress, particularly those that consider the connection between the frictional forces of the sliding mechanics and orthodontic tooth movement. Evaluation of the stress distributions and the three-dimensional (3D) displacement with an irregular geometry and physical properties is possible using the finite element method (FEM) [7].
Therefore, the current work aims to determine the influence of the friction in the mandibular canine tooth movement and stress distribution during the mandibular canine translation, tipping, and rotation tooth movements using the 3D FE modeling.
2.Materials and methods
The geometry of the 3D FE models of the mandible consisting of teeth with its PDL and alveolar bone was constructed based on CT scanning (Siemens sensation 16, Siemens, German) images (Fig. 1C). PDL was assumed to be 0.25 mm layers around the root of the teeth, as described by previous studies [8, 9]. The passive self-ligating brackets with 0.022
Table 1
Cross section and dimensions of the archwire (inch)
| Archwire number | Circular (diameter) | Archwire number | Rectangular |
|---|---|---|---|
| 1 | 0.012 | 6 | 0.016 |
| 2 | 0.014 | 7 | 0.016 |
| 3 | 0.016 | 8 | 0.016 |
| 4 | 0.019 | 9 | 0.019 |
| 5 | 0.020 | 10 | 0.020 |
Figure 1.
FE model of bracket and archwire (a), FE model of periodontium tissue (b), and the assembly model and boundary condition (c).
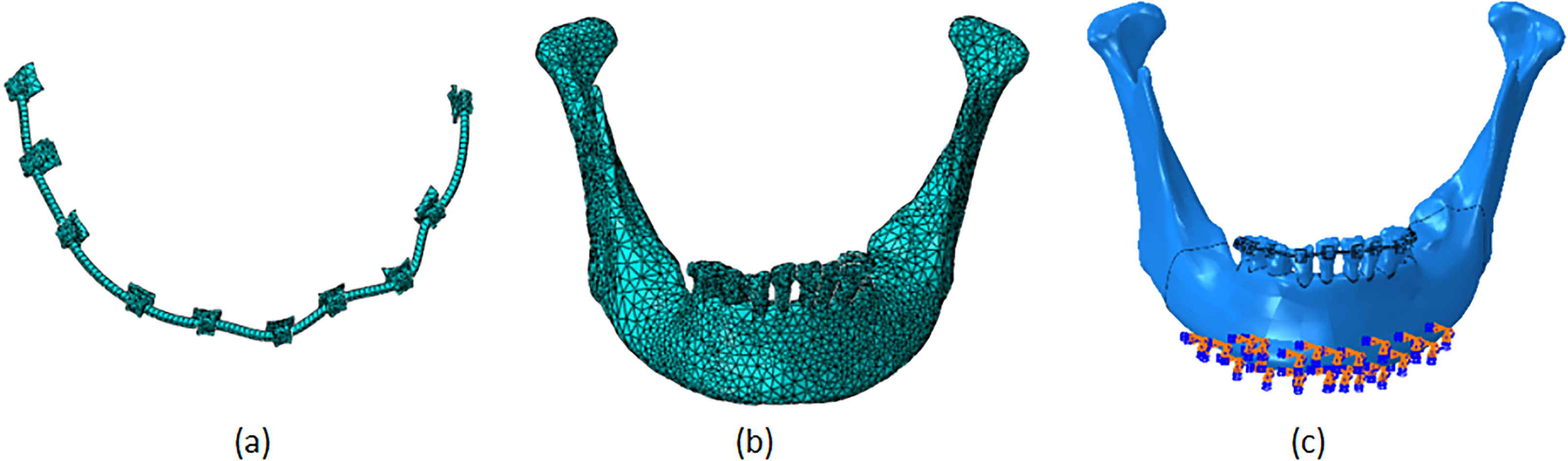
All the constructed solidified models were subjected to FEA in Abaqus. Tetrahedral elements were adopted in the finite element models. The number of nodes and elements for each model are shown in Table 2. FE models with brackets and archwires are shown in Fig. 1. All materials were considered to be isotropic homogeneous elastic materials, and the material parameters were applied to each component, based on previous studies (Table 2) [8, 9, 10].
Table 2
Material properties, element, and node numbers of FE models
| Material | Modulus of elasticity/MPa | Poisson’s ratio | Number of elements | Number of nodes |
|---|---|---|---|---|
| Teeth | 18600 | 0.31 | 15457 | 26371 |
| Alveolar bone | 13700 | 0.3 | 51502 | 80282 |
| PDL | 0.68 | 0.49 | 12891 | 26396 |
| Bracket | 200000 | 0.3 | 6260 | 2260 |
| Archwire | 200000 | 0.3 | 142 | 572 |
A tied condition was established in the ligament-bone, tooth-ligament, and tooth-bracket interfaces. A Coulomb friction condition was established in the contact interfaces between the archwire and bracket surface. The friction coefficient ranged from 0 to 0.5 with an interval of 0.05. The fixed boundary condition was maintained at the base of the mandible and the two ends of the archwire (Fig. 1).
The translation (from labial to lingual side from 0.05 mm to 0.30 mm at 0.05 interval), inclination (the crown incline from labial side to lingual side from 0.5
3.Results
The change in trends of the maximum displacement of the canine, the highest stress of the PDL, and the
3.1Translation
The maximum displacement of the canine, the highest stress of the PDL, and the
Figure 2.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); Rcr (c); in translation cases with five round (A) and rectangular archwires (B) and 0.1 friction coefficient.
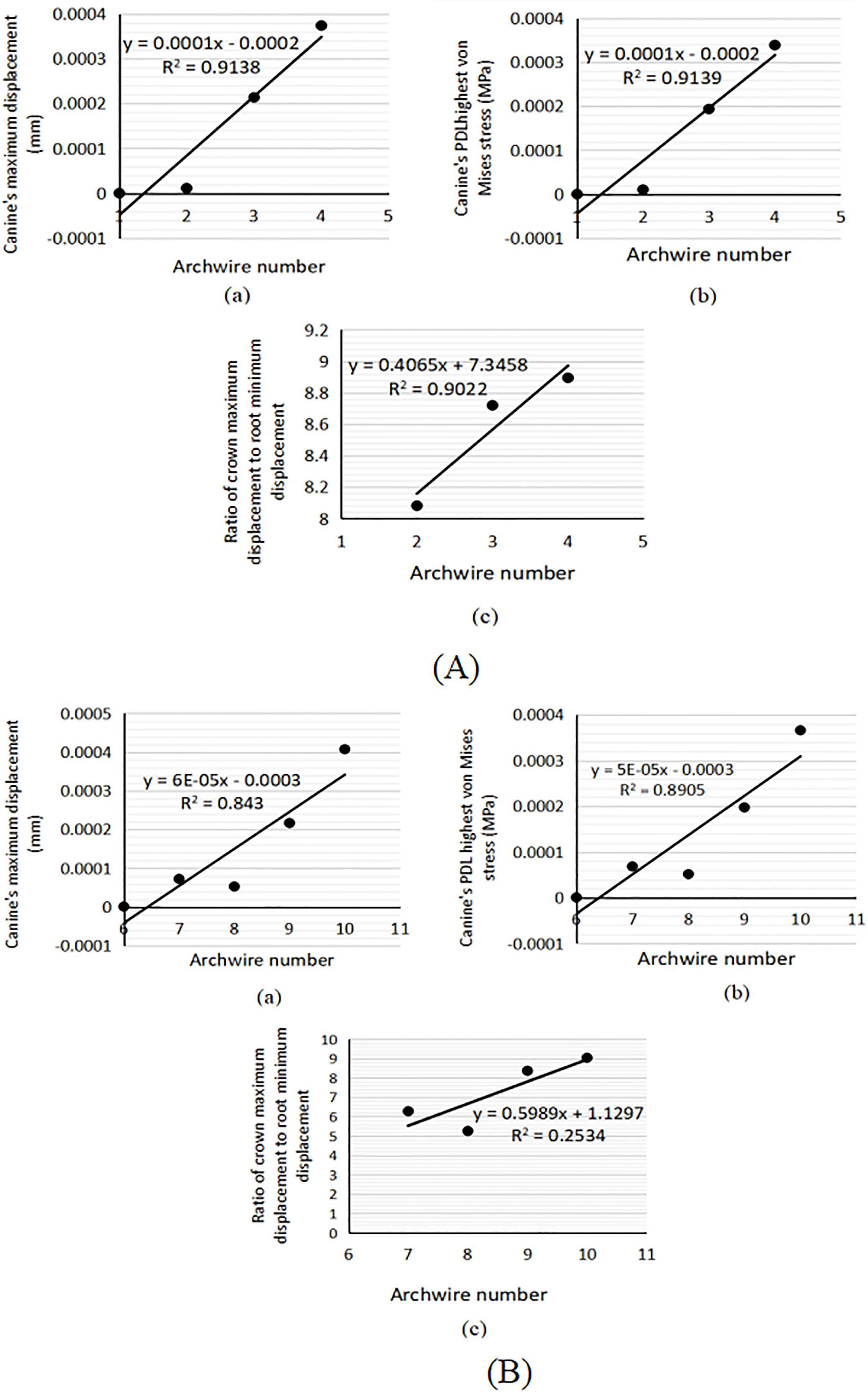
Figure 3.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); Rcr (c); in translation cases with No.4 round (A) and No.9 rectangular (B) archwires.
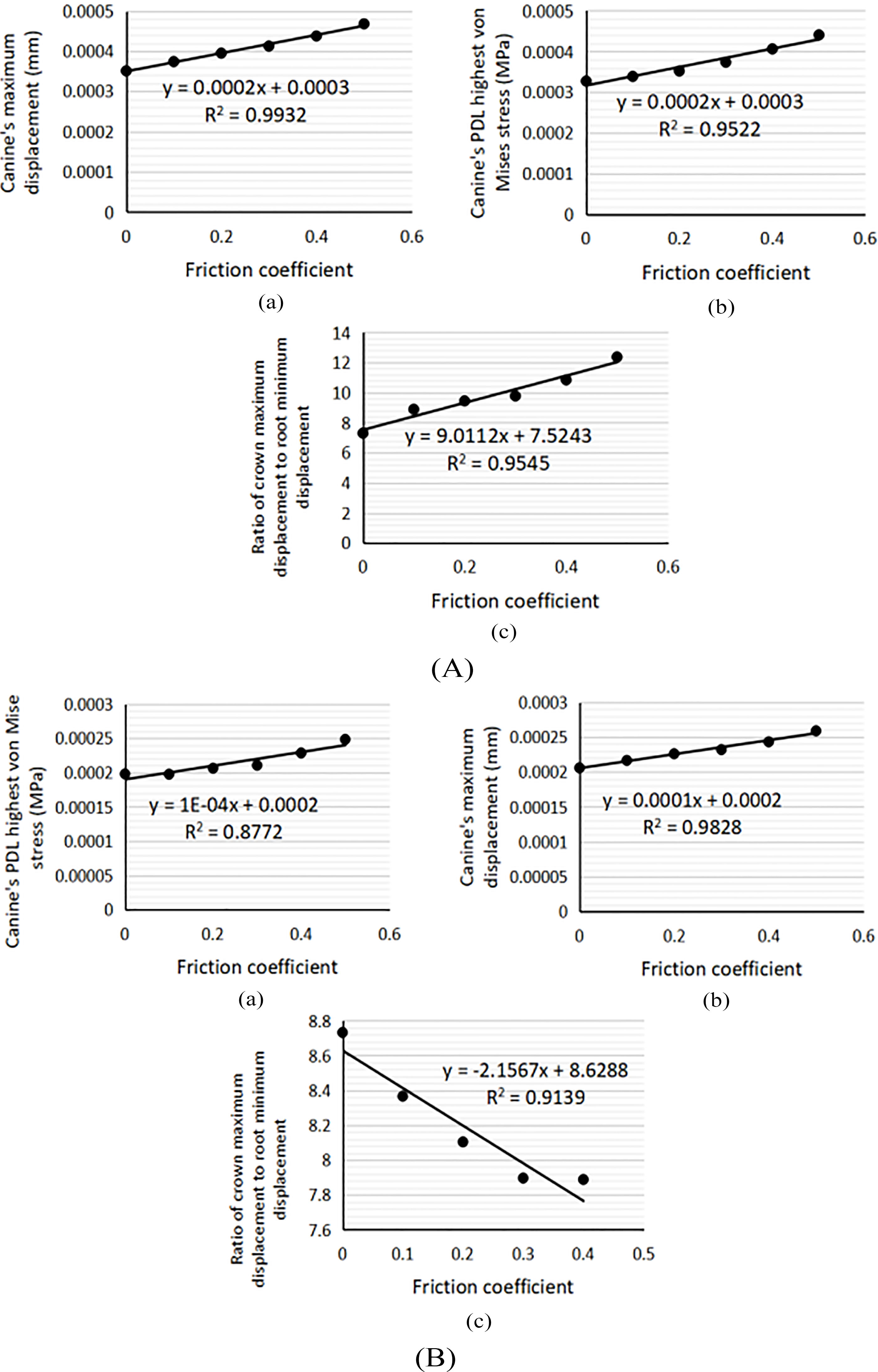
Figure 4.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); Rcr (c); in rotation cases with the five round (A) and rectangular archwires (B) and 0.1 friction coefficient.
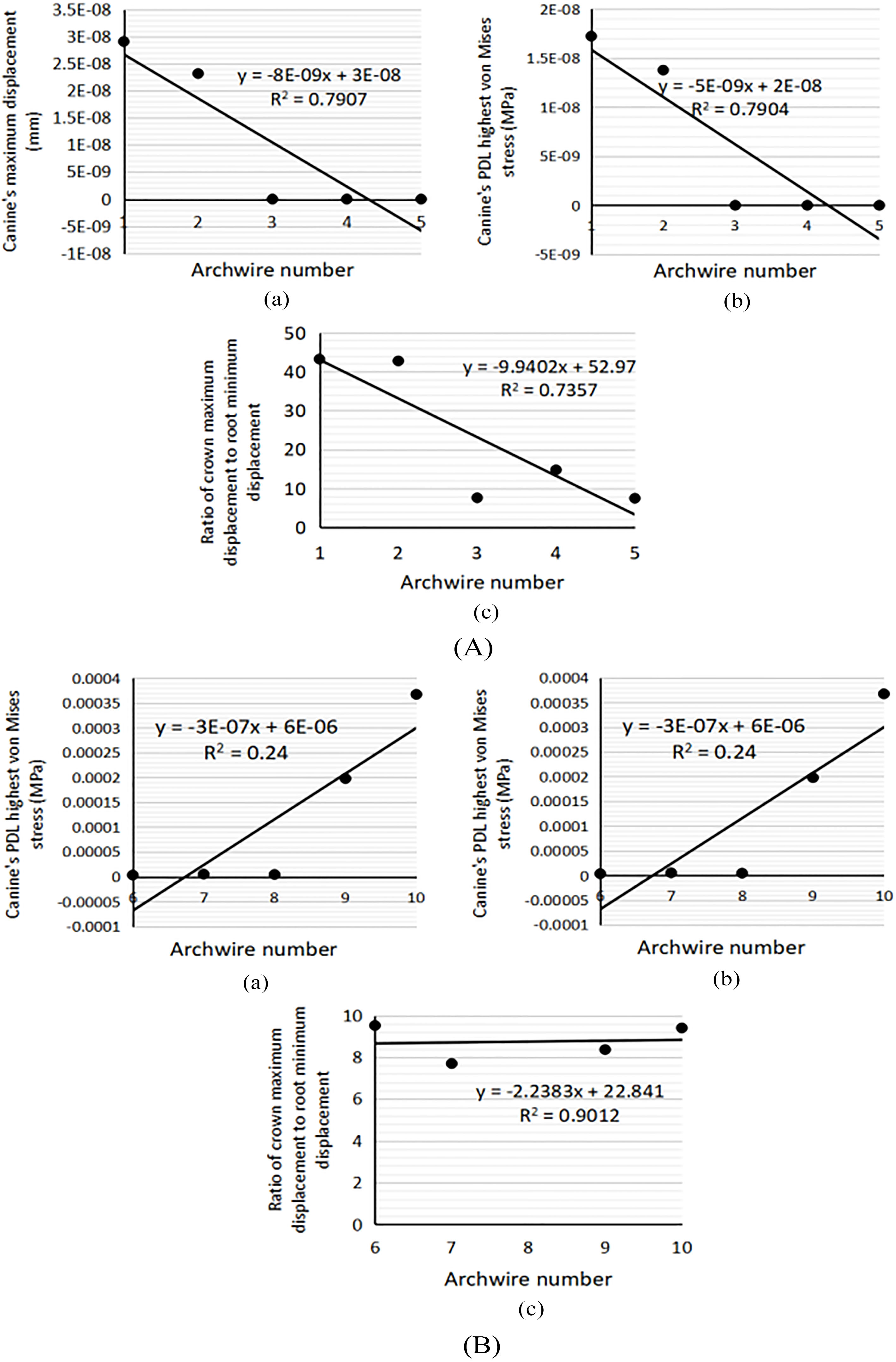
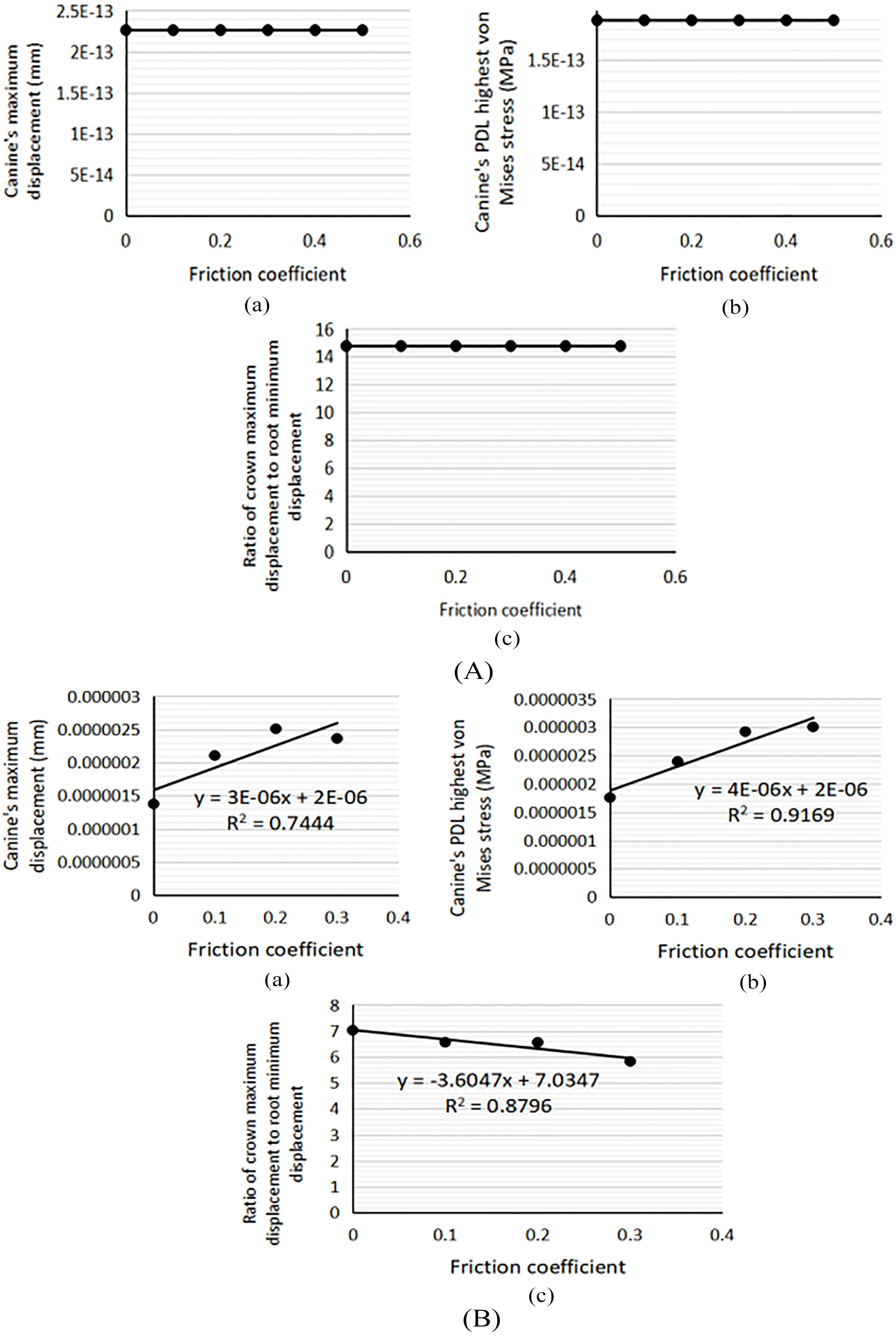
Figure 5.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); Rcr (c); in rotate 2.5
3.2Rotation
All the assesed parameters decreased with an increase in the cross-section area in the round archwire cases (Fig. 4A). In the rectangular archwire cases, the maximum displacement of the canine and the highest stress of the PDL increased with an increase in the cross-section area (Fig. 4B(a) and (b)). However,
Figure 6.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); in inclination cases with five round (A) and rectangular archwires (B) and 0.1 friction coefficient.
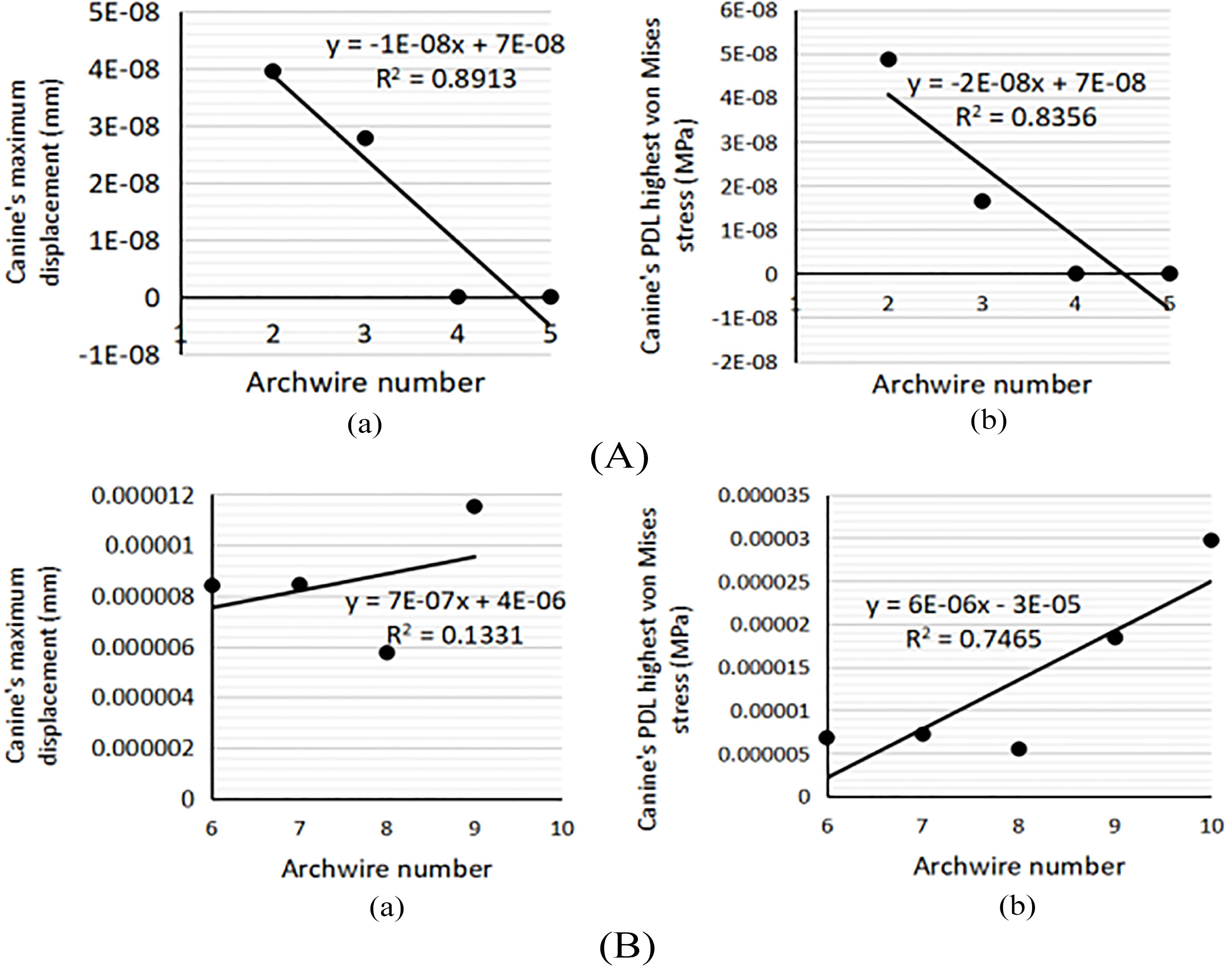
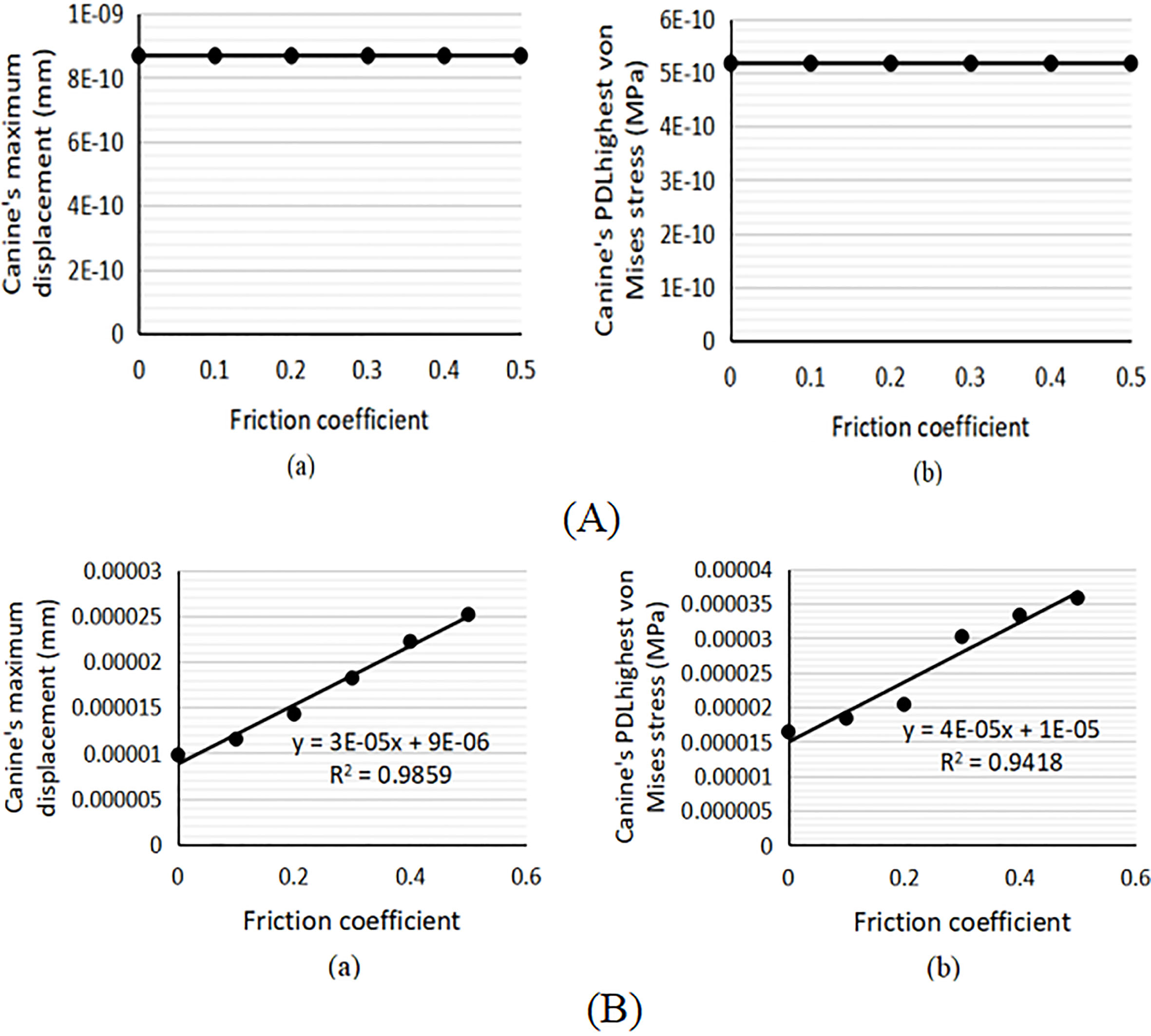
Figure 7.
Maximum canine displacement (a); highest PDL von Mises stress of the canine (b); in incline 3
3.3Inclination
In the round archwire cases, the maximum displacement of the canine and the highest stress of the PDL decreased with an increase in the archwire diameter (Fig. 6A). These parameters increased with an increase in the cross-section area in the rectangular archwire (Fig. 6B). In the round archwire cases, the assesed parameters remained nearly invariant during the different friction coefficients (Fig. 7A). In the rectangular archwire cases, the assesed parameters increased with an increase in the friction coefficient. However, the extent of the increase was minimum (Fig. 7B).
4.Discussion
Self-ligating orthodontic have presented an increased diffusion in the orthodontic practice in the past decades. It is urgent to understand its biomechanical characteristic clearly. Gómez et al. [12] found that the passive self-ligating brackets presented a less frictional resistance and greater contact area between the slot and the archwire, while the spring clip increased the frictional resistance than the conventional ligating treatment. Hence, we conducted this study to evaluate the canine displacement, the PDL stress, and the rotation center related changes in the canine on three types of tooth movement under various friction coefficients, wires with different cross-section shapes and sizes, and different archwire displacements.
Papageorgiou et al. [13] concluded that the archwire had the largest influence on the orthodontic tooth movement and stress in PDL. The results of this study were consistent with their conclusion. Furthermore, this study illustrated the specific influence trends in various movement styles.
Considering the translation movement, the larger the archwire cross-section area is, the quicker the canine translates. The friction between an archwire and bracket can improve the 3D control of the translation in the round archwire cases. However, an increase in the friction coefficient may cause PDL necrosis in the rectangular archwire cases.
Considering the rotation movement, a larger cross-section round archwire decreases rotation control of the canine. The friction coefficient has a minimal influence on the rotation movement of the canine in both the rectangular and round archwire cases.
Considering the inclination movement, a large cross-section area in a round archwire may limit the inclination movement of the canine. However, a large cross-section area rectangular archwire may improve the inclination of the canine. Low friction coefficient has no influence on the inclination of the canine in the round archwire cases, whereas a high friction coefficient may cause PDL necrosis in the rectangular archwire cases.
5.Conclusion
The results of the present investigation demonstrated that the archwire characteristics had the direct influence on the self-ligating orthodontic tooth movement of the canine. Our findings can provide a reference guide to the orthodontists for choosing the proper archwires for special tooth movement needs.
Acknowledgments
This work was supported by the project of Hainan province and Hainan University Natural Science Foundation (118QN184 and KYQD(ZR)1835).
Conflict of interest
None to report.
References
[1] | Prashant PS, Hemant N, Meera G. Friction in orthodontics. Journal of Pharmacy & Bioallied Sciences. (2015) ; 7: (Suppl 2): S334-S338. |
[2] | Seo YJ, Lim BS, Park YG, Yang IH, Ahn SJ, et al. Effect of tooth displacement and vibration on frictional force and stick-slip phenomenon in conventional brackets: a preliminary in vitro mechanical analysis. Eur J Orthod. (2015) ; 37: (2): 158-163. |
[3] | Cacciafesta V, Sfondrini MF, Scribante A, Klersy C, Auricchio F. Evaluation of friction of conventional and metal-insert ceramic brackets in various bracket-archwire combinations. Am J Orthod Dentofacial Orthop. (2003) ; 124: (4): 403-409. |
[4] | Park JH, Lee YK, Lim BS, Kim CW. Frictional forces between lingual brackets and archwires measured by a friction tester. Angle Orthod. (2004) ; 74: (6): 816-824. |
[5] | Cacciafesta V, Sfondrini MF, Ricciardi A, Scribante A, Klersy C, et al. Evaluation of friction of stainless steel and esthetic self-ligating brackets in various bracket-archwire combinations. Am J Orthod Dentofacial Orthop. (2003) ; 124: (4): 395-402. |
[6] | An VS, Geris L, Sloten JV. Analytical determination of stress patterns in the periodontal ligament during orthodontic tooth movement. Medical Engineering & Physics. (2013) ; 35: (3): 403-410. |
[7] | Joo JW, Hoe KH, Cha KS. Finite element modeling and the mechanical analysis of orthodontics. Transaction of Korean Society of Mechanical Engineers (A). (2000) ; 24: (4): 907-915. |
[8] | Cai YQ, Yang XX, He BW, Yao J. Numerical analysis of tooth movement in different plans of transparent tooth correction therapies. Technol Health Care. (2015) ; 23: (3): 299-305. |
[9] | Cai YQ, Yang XX, He BW, Yao J. Finite element method analysis of the periodontal ligament in mandibular canine movement with transparent tooth correction treatment. BMC Oral Health. (2015) ; 15: (1): 106. |
[10] | Bouton A, Simon Y, Goussard F, Teresi L, Sansalone V. New finite element study protocol: Clinical simulation of orthodontic tooth movement. Int Orthod. (2017) ; 15: (2): 165-179. |
[11] | Cai YQ, Yang XX, He BW. Influence of friction in transparent tooth correction treatment: finite element method. J Mech Med Biol. (2015) ; 15: (4): 1550052. |
[12] | Gómez SL, Montoya Y, Garcia NL, Virgen AL, Botero JE. Comparison of frictional resistance among conventional, active and passive selfligating brackets with different combinations of arch wires: a finite elements study. Acta Odontol Latinoam. (2016) ; 29: (2): 130-136. |
[13] | Papageorgiou SN, Keilig L, Hasan I, Jäger A, Bourauel C. Effect of material variation on the biomechanical behaviour of orthodontic fixed appliances: a finite element analysis. Eur J Orthod. (2016) ; 38: (3): 300-307. |




