Biomechanical investigation of orthodontic treatment planning based on orthodontic force measurement and finite element method before implementation: A case study
Abstract
BACKGROUND:
Orthodontic treatment planning (OTP) is primarily depended on clinical experiences of orthodontists at present, while equivocal OTP would increase the possibility of treatment failure.
OBJECTIVE:
The objective was to investigate a methodology for quantitatively evaluating OTP, using theoretical analyses, orthodontic forces measurement (OFM) and finite element method (FEM).
METHODS:
An OTP was theoretically designed based on a clinical case and forces on incisors in OTP were measured on a specialized platform. Further, FEM simulations were performed on the designed OTP and control group. At last, an 18-month tracking was carried out to observe treatment effects of the designed OTP.
RESULTS:
The moving tendencies of incisors were in keeping with ideal treatment from the designed OTP through FEM; the maximal hydrostatic stress and logarithmic strain in periodontal ligament (PDL) decreased by 26.81% and 32.60% compared to the control group. Clinical feedback indicated that a controllable correction of incisors was realized after 18 months, which was in accord with the FEM result and root/bone resorption by reason of stress/strain reduction on PDL did not occur.
CONCLUSIONS:
Biomechanical responses of periodontium can be quantitatively estimated using OTM and FEM. This study provided an alternative technological mean for the predictability and optimization of clinical OTP.
1.Introduction
Central incisor with lingual or labial obliquity can frequently be found in the clinic, and it was usually accompanied with root deviation [1]. Malposed root often brought unsubstantial bone plate on one side of the alveolar bone. Impertinent treatment has a high risk of root absorption, bone rupture or even tooth exfoliation in the worst case scenario [2, 3]. On the other hand, orthodontic treatment is almost irreversible, so it is hard to repair failed cases. Therefore, the OTP for vulnerable cases should be conscientiously designed based on their clinical symptoms and multi-evaluation are necessary before treatment implementation.
Currently, OTP is primarily depended on the clinical experiences and subjective judgments of orthodontists, numerous orthodontic plans had not been specially investigated [4]. While equivocal treatment would increase the possibility of failure. On the other hand, orthodontic treatment is a lengthy process, the immediate effect is hard to be observed in a short time [5]. As a result, the judgments of OTP are challenging to implement in clinic. Hence, a regular return visit was extensively adopted in clinic to ensure treatment effects [6, 7], but this will extend treatment period, and the willingness and enthusiasms of patients would likely to reduce at the same time, which will complicate the efforts to realize an ideal orthodontic treatment.
In order to evaluate the biomechanical responses of OTP quantitatively, forces measurement on teeth is required, as well as stress/strain distributions in the periodontium. OFM is tough to apply in mouth directly, so dental models such as plaster models, wax models or resin models were used firstly at present. Moreover, this method was widely used by many international academics [8, 9, 10]. In order to investigate orthodontic forces aroused by the fixed orthodontic appliances, a customized measuring platform was designed by Margherita using a 3-dimensional (3D) printed mouth model [11], the platform could be used to train clinicians to exert lower loads and thus avoided irreversible damages. Similarly, Liu constructed a forces measurement system on a 3D light-cured resin model to measure the forces delivered by invisaligners [12].
FEM had been introduced to the field of orthodontics as a powerful research tool for solving various structural and biomechanical problems for a long time [13, 14]. It is a noninvasive technique that measures the actual amount of stresses experienced at any point on the periodontium, and the displacements of the tooth can be visualized graphically. Besides, the study could repeat as many times as the operator wishes [15]. Barone analyzed the rotational movements of a maxillary incisor and canine through the finite element, and the simulated results helped a dental technician to predict how an orthodontic appliance affected tooth movements [16]. Cai investigated the displacements of canine and stresses on the canine PDL during translation, inclination and rotation with transparent tooth corrective treatment by FEM [17].
Obviously, Both OFM and FEM are effective methods to evaluate the treatment effects of OTP. Employing the biomechanical research techniques of OFM and FEM, a clinical case was studied. Based on the clinical symptoms, an OTP was firstly designed using theoretical analysis with the assistance of an orthodontist. Then OFM was performed on simulated dental models through a specialized platform. Contrastive simulations were performed on maxilla FEM models with the measured forces and moments. At last, in order to observe treatment effects of the designed OTP, long-term clinical feedback of 18 months was collected in clinic.
2.Materials and methods
2.1Case reports
The clinical case is a 35-year-old woman, as shown in Fig. 1, the primary symptoms are central incisors obliquity-crowns incline to the lingual side and roots trend to labial side, but a weak bone plate on labial side complicates the conditions to achieve a routine treatment. For more messages about alveolar bone and roots, a group of CT images was obtained by a spiral CT machine (Toshiba/Aquilion ONE, Florida, US) with parameters as follow: 120 KV, 150 mA.s, pixel size 0.342 mm, 0.5 mm slice thickness, 0.5 mm slice interval and entirely 505 images were acquired. Visibly, malposed roots aroused weak alveolar bone, and the thickness of bone plate on labial side is about 0.45 mm. Brittle alveolar bone entangles the treatment and OTP should be rigorously designed and evaluated before clinical treatment.
Figure 1.
Clinical symptoms of patient.
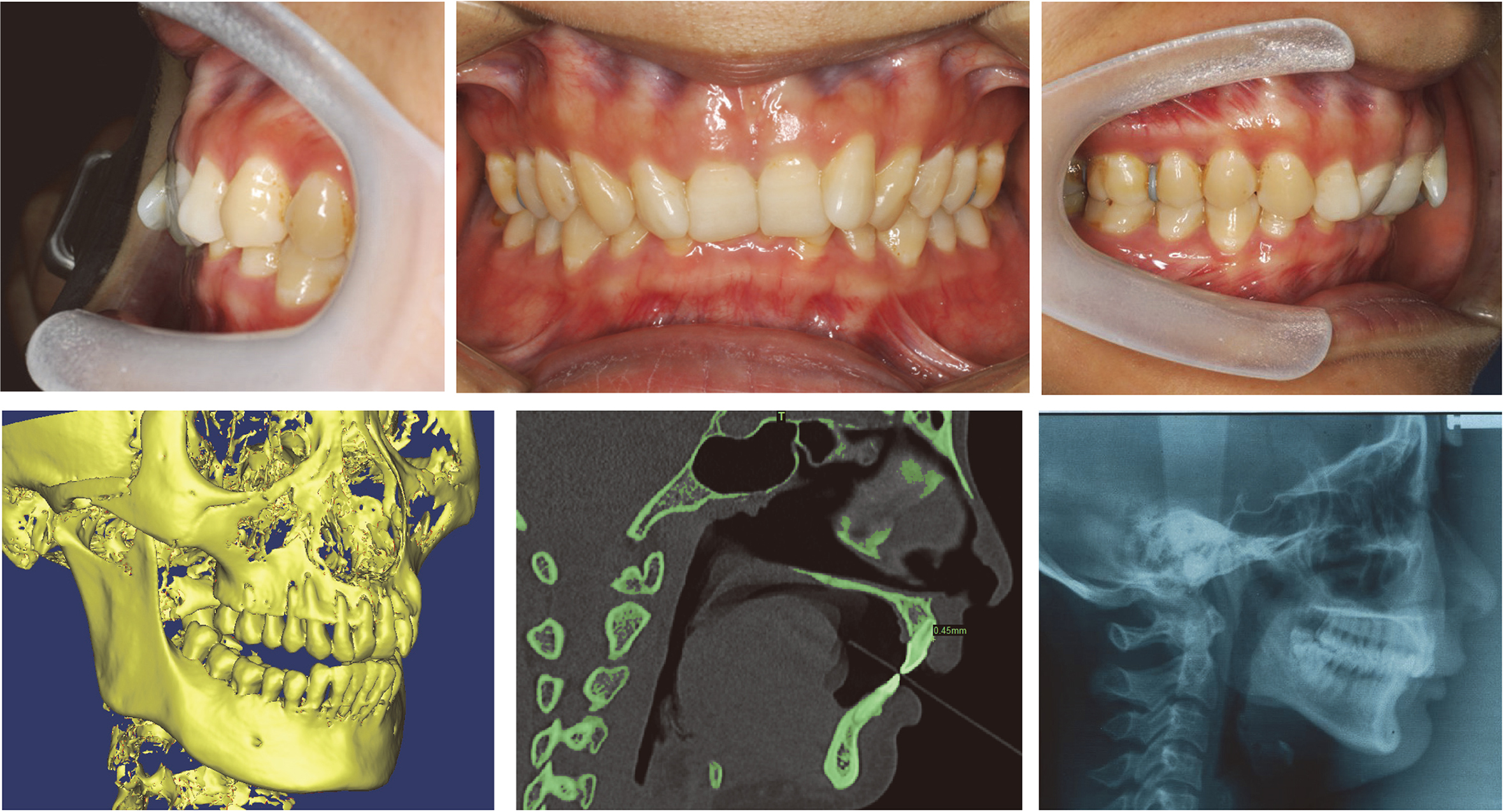
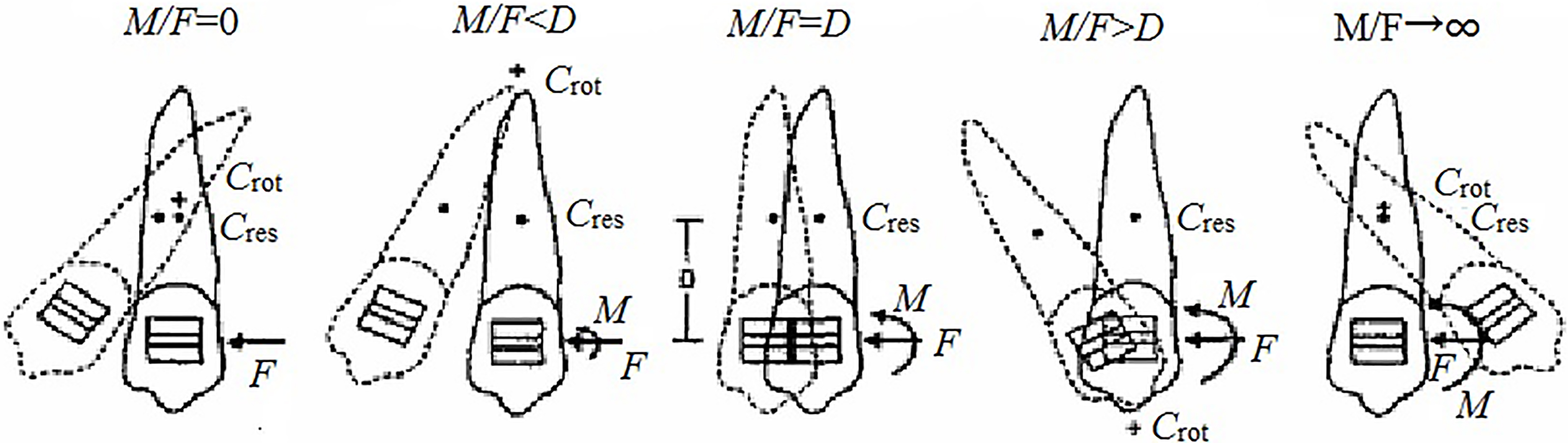
Figure 2.
Relationships between tooth movements and orthodontic force systems.
2.2OTP design
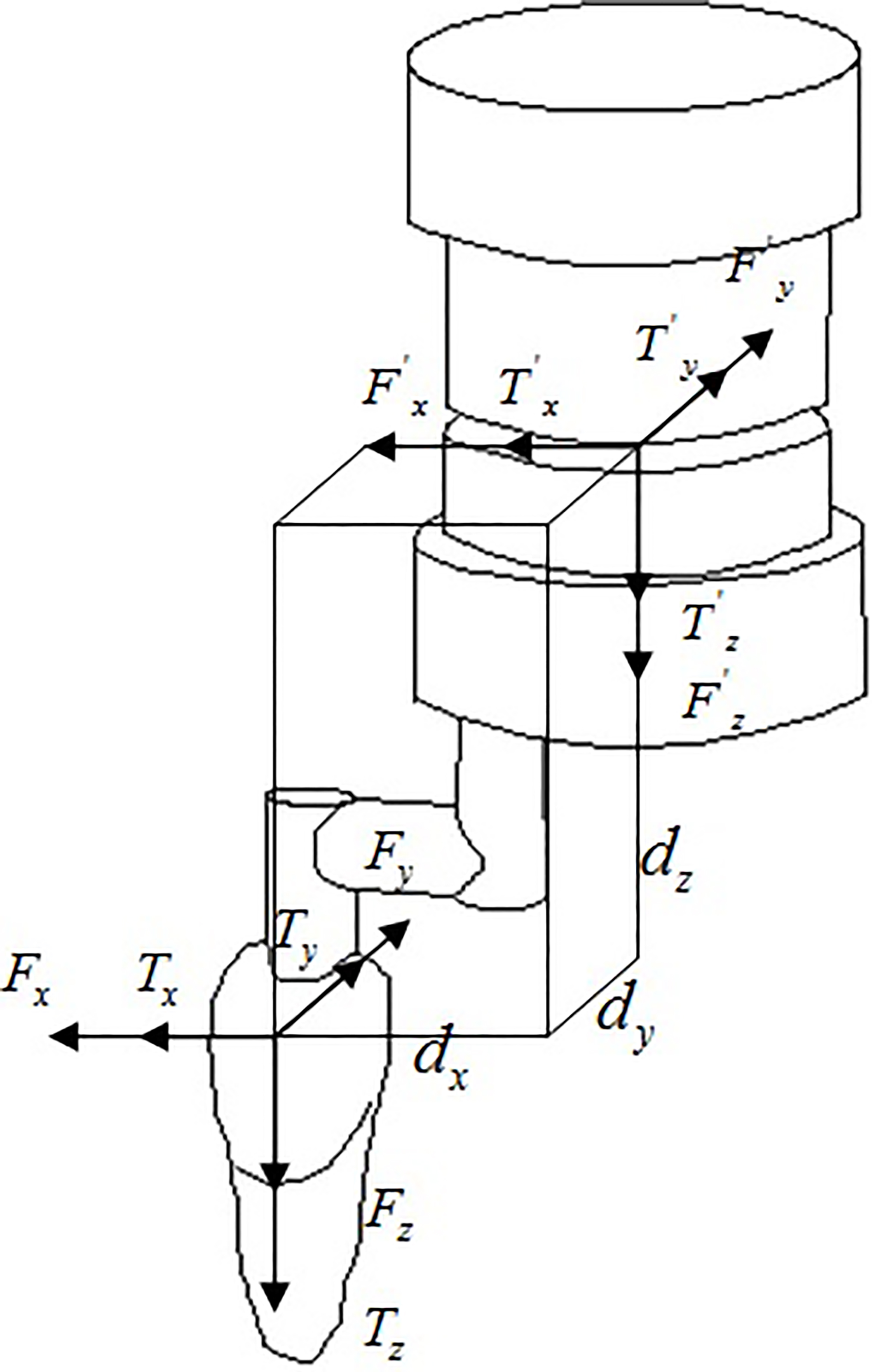
The relationships between tooth movements and orthodontic forces are shown in Fig. 2 [18], where
Figure 3.
Designed OTP.

Figure 4.
3D OFM platform.

2.3OFM platform
A 3D OFM platform was constructed to measure the forces and moments on incisors, as shown in Fig. 4. Measurements were performed on the dental resin model, which was manufactured by the 3D printer (Connex350 Object, Rehovot, Israel) according to patient oral cavity [19], as shown in Fig. 5, the incisors are separated from other parts on the dental model, and their initial positions are maintained by six dowels from top to bottom. In addition, attached poles were designed on the top of crowns used to connect transducers. A standard sequence archwire (SE-D-14-U, Smart technology co. Ltd, Beijing, China) with a diameter of 0.014 feet was assembled on the dental model assisted by self-ligating brackets (31027, Zhejiang Protect Medical Equipment Co., Ltd, Hangzhou, China), as well as the assistant device. The archwire was made from a conventional nickel-titanium alloy, the form is in keeping with ideal arches, and it is typically used in the first phase of orthodontic treatment. The transducers used in the platform are six-dimensional Nano17 F/T (ATI Industrial Automation, North Carolina, USA), which can record forces and moments on incisors in three directions.
Figure 5.
Simulated dental model, (a) digital model; (b) physical model assembled with brackets and archwire.
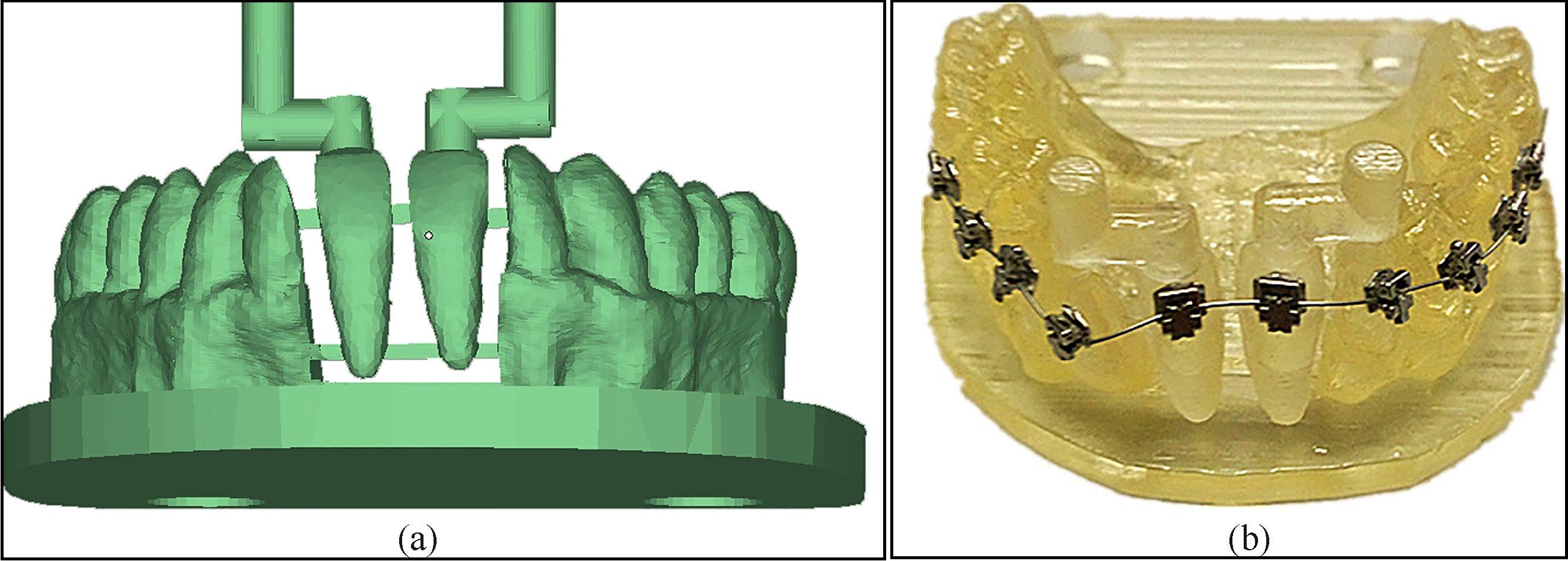
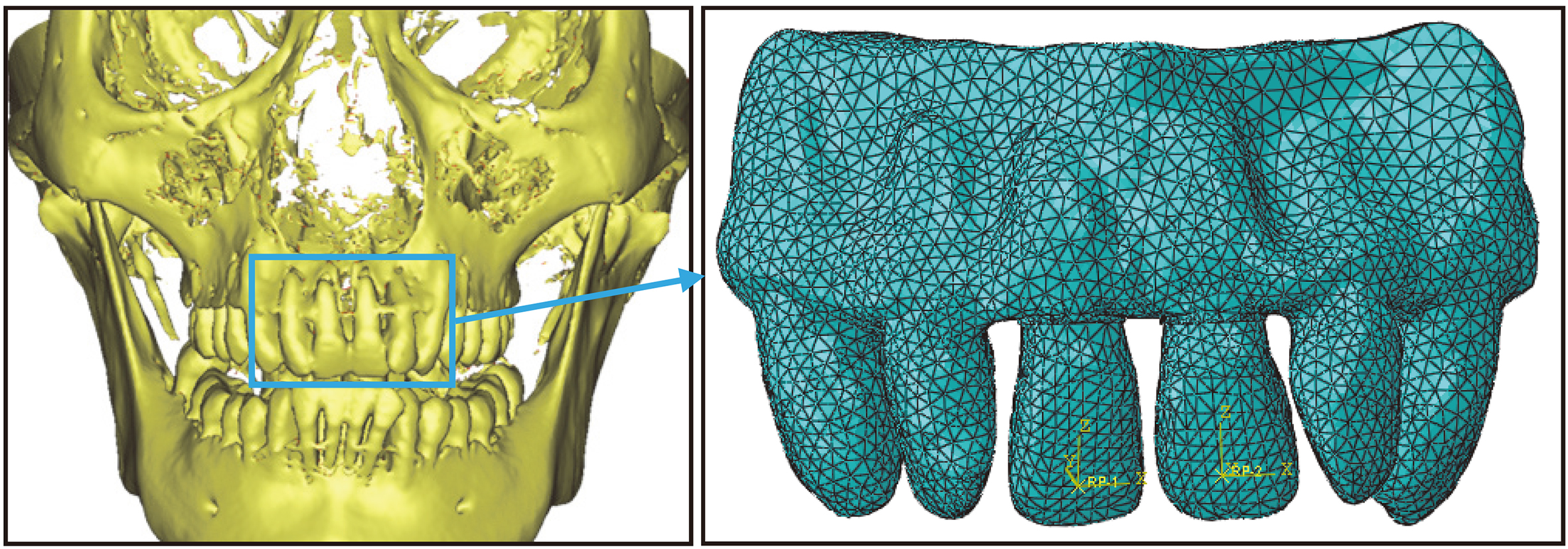
Figure 6.
FEM models in simulation.
The measure steps including: (1) fix dental model on the platform after assembled with orthodontic appliances; (2) adjust transducers location so that the terminal of transducers are connected with incisors, then maintain transducers with magnetic bases; (3) open OFM software and start to record data after resetting, the sampling frequency is 1000 Hz; (4) cut off the dowels to make sure the incisors are not contacted with other objects except for appliances and transducers; (5) after all dowels were cut off, stop recording after 20 s. When all dowels on incisors were removed, the forces and moments produced by appliance deformation will pass to transducers through the poles on incisors top, and then the forces and moments on incisors can be measured.
2.4FEM models
Based on the CT images, 3D triangle mesh models which include teeth, PDL, cortical bone and cancellous bone were first constructed using Mimics 10.0 (Materialise NV, Leuven, Belgium). Then the models were edited using Geomagic Studio 12.0 (3D System, Rock Hill, USA) to obtain FEM models. At last, FEM simulations were performed on Abaqus 6.12 (Dassault Simulia, Boston, USA). In order to reduce calculation amount, FEM models were appropriately simplified, and only incisors and four adjacent teeth were taken into account, as displayed in Fig. 6. In addition, PDL was considered to have a uniform thickness of 0.25 mm [20]. Models were divided into multiple 10-node tetrahedral elements, and each element was assumed to be homogeneous, isotropic and composed of a linearly elastic material with a uniform young’s modulus. The material parameters are listed in Table 1 [21]. The forces and moments are exerted on the bracket centers (the brackets are omitted in the models), and the top of alveolar bone is fixed completely.
Table 1
Material parameters
| Parts | Elasticity modulus (Mpa) | Poisson’s ratio |
|---|---|---|
| Incisors | 20000 | 0.3 |
| PDL | 0.68 | 0.49 |
| Cancellous bone | 1370 | 0.38 |
| Cortical bone | 13700 | 0.26 |
Figure 7.
Schematic of measurement unit.
2.5Clinical verification
In order to verify FEM results and observe the validity of the designed OTP, a long-term of case tracking was carried out. The clinical case is from Zhejiang Provincial People’s Hospital, and data collection is implementing by orthodontist Zhang. Besides, a traditional return visit is still adopted in this study to ensure the security of patient. The clinical recording wiil last 18 months, and CT scan will perform after 18 months.
3.Results
3.1OFM results
Local coordinate systems were constructed on incisors for the conveniences of subsequent analysis and calculations. The center of the bracket was considered as the origin and the mesiodistal, faciolingual and inciso-occluso/apical axes of incisor corresponded to
Table 2
Forces and moments on incisors
| Orthodontic force (N) |
|
|
|
|
|
|
|---|---|---|---|---|---|---|
| 0.0000 | 0.0021 | 0.6024 | ||||
| Orthodontic moment (N.mm) |
|
|
|
|
|
|
| 0.0519 | 0.0016 | 30.8711 | 4.8586 |
In OFM, the total time was 140 s and sample points were 140000, of which 120 s–140 s recorded the forces and moments after the dowels were removed completely. However, the measured data were not the forces on incisors, they were the forces of transducers center. In order to obtain the forces and moments on incisors, requisite transformations were performed. The relationships between forces on transducers center and forces on crowns were displayed in Fig. 7 and Eq. (3.1), where
(1)
Figure 8.
Moving tendency of incisors, the red translucent model was incisor before loading and the nephogram model was incisor after loading. (a) under designed OTP; (b) under common treatment.

3.2FEM results
FEM simulations were performed in two groups with the loading from the measured forces and moments. One was to simulate the designed OTP; another was control group without the assistant device to simulate clinical conventional treatment (only with standard archwire). In order to investigate incisors moving tendencies, the displacements of incisors were separately displayed after amplified, as shown in Fig. 8. In addition, PDL as a crucial role in regulating orthodontic treatment was also emphatically investigated, as shown in Fig. 9. And in order to explore the possibility of bone rupture/absorption, the Von Mises stress and displacement distributions of cortical bone were considered, as shown in Fig. 10.
Figure 9.
Hydrostatic stress/logarithmic strain distributions of PDL, (a) stress under designed OTP, (b) strain under designed OTP, (c) stress under common treatment, (d) strain under common treatment.
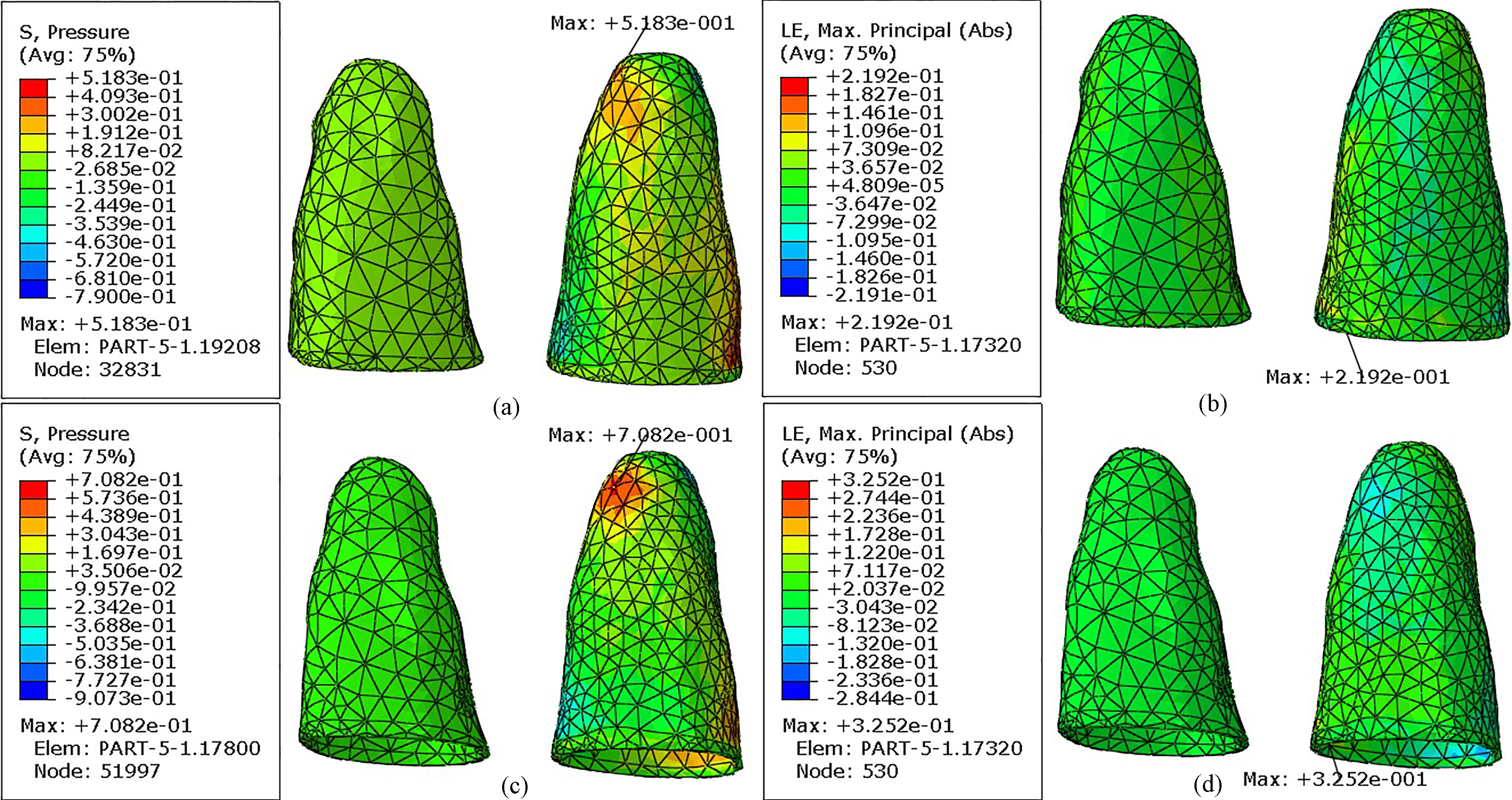
Figure 10.
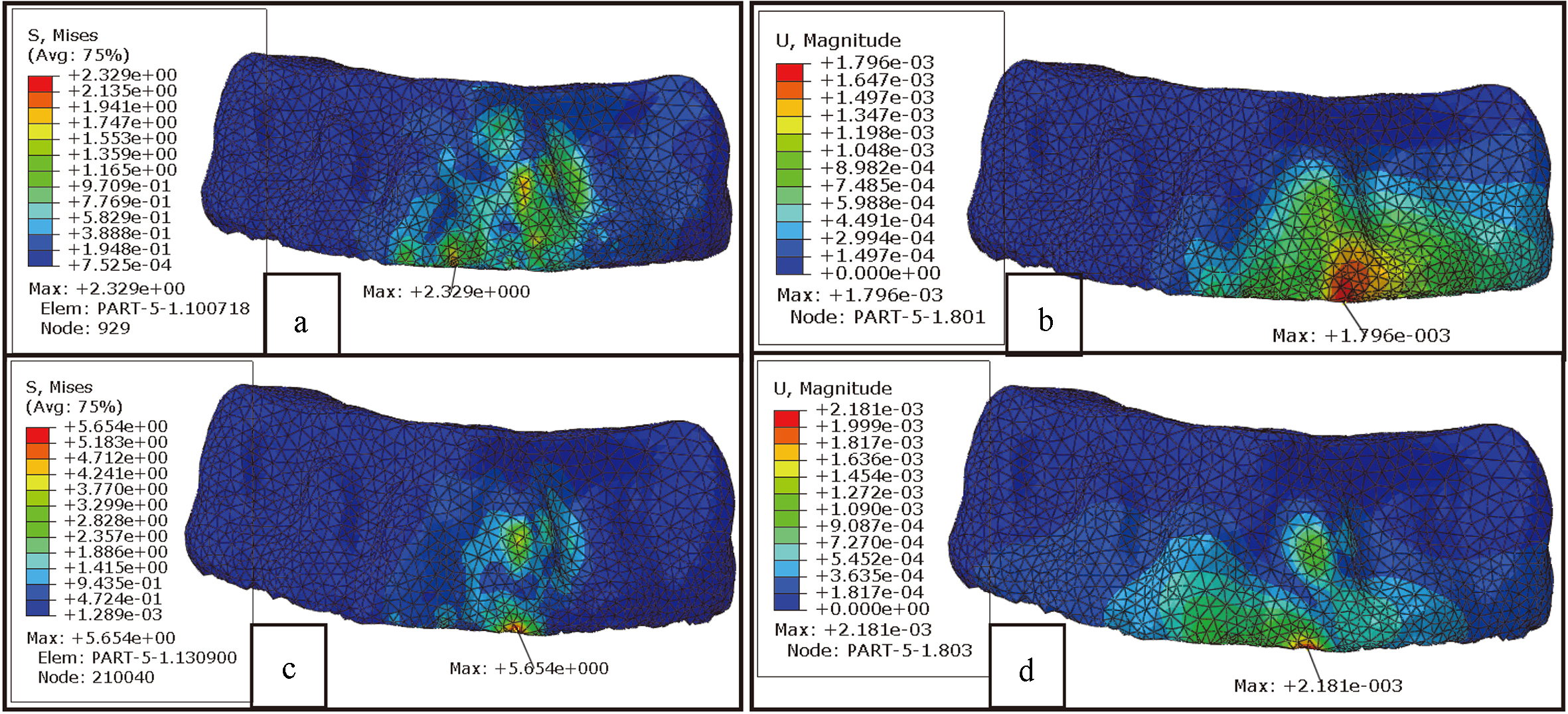
Von Mises Stress and displacement distributions of cortical bone, (a) stress under designed OTP, (b) displacement under designed OTP, (c) stress under common treatment, (d) displacement under common treatment.
3.3Clinical feedback
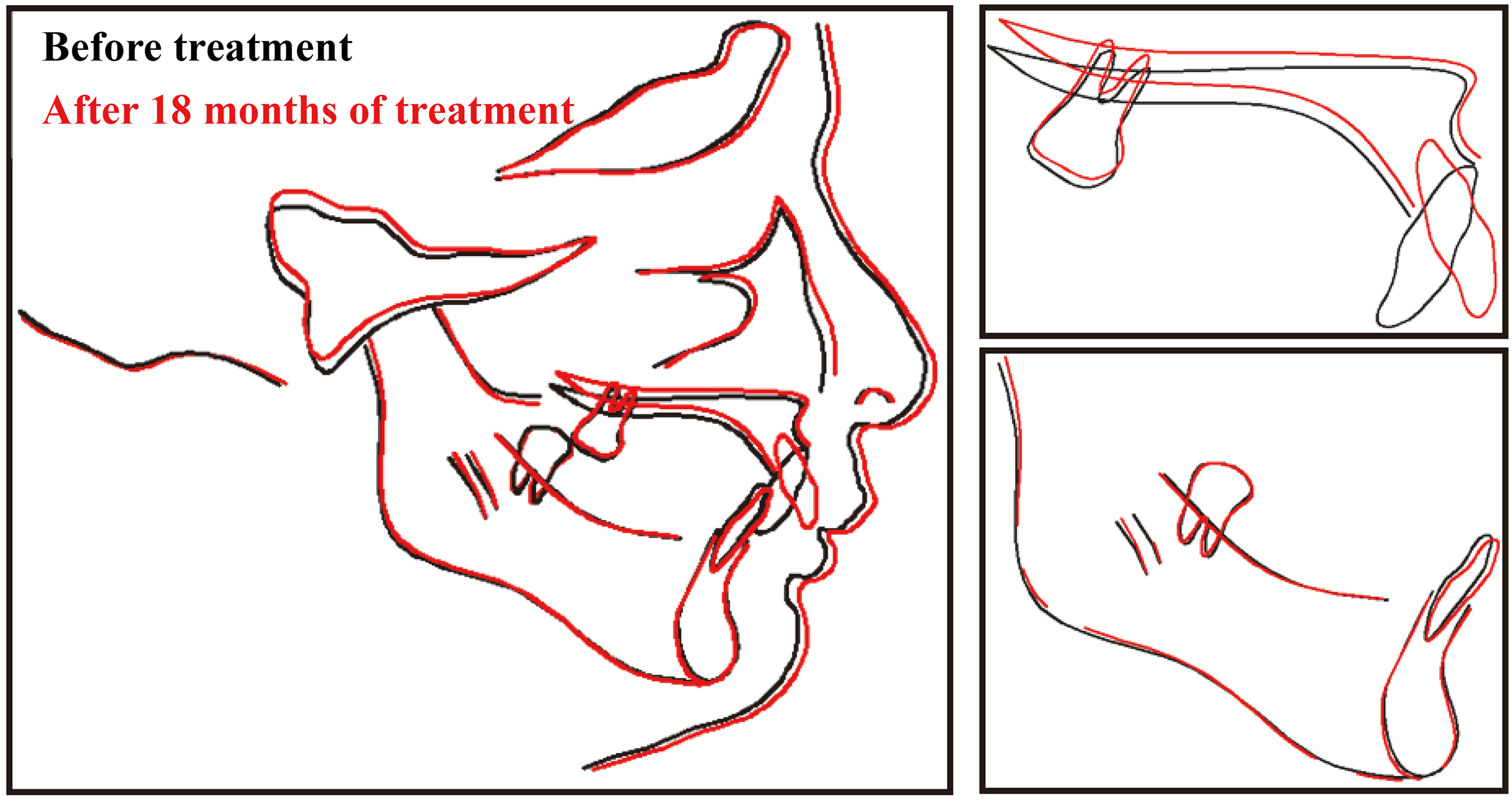
The designed OTP was applied in clinic to investigate the effects of treatment, and relevant data was carefully collected with the help of orthodontist zhang. As displayed in Fig. 11, the process of treatment was recorded by clinical photos to observe the variation of patient in appearance; at the same time, CT images were also acquired to investigate the situation of root and alveolar bone after 18 months of treatment. Based on the CT images, another triangle mesh model was constructed to observe the distributions of incisors visually. Besides, a contrastive graphics before and after 18 months of treatment was also plotted, as shown in Fig. 12.
Figure 11.
Clinical feedback, (a) before treatment, (b) after 9 months, (c) after 18 months, (d) CT image and (e) digital model after 18 months of treatment.
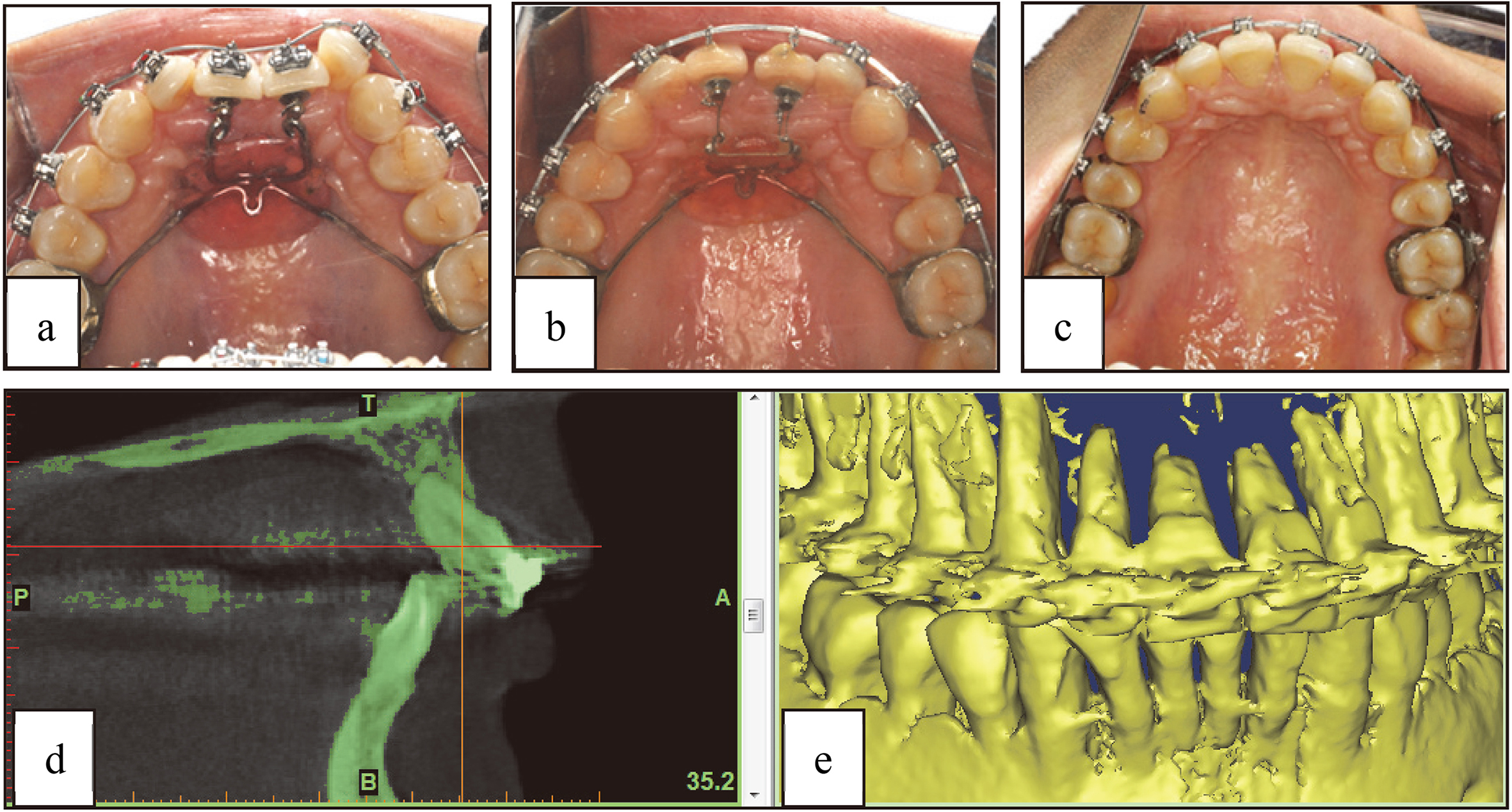
Figure 12.
Contrastive graphics before and after 18 months of treatment.
4.Discussion
Based on the designed OTP, orthodontic forces and moments on incisors were accurately measured. Further, FEM simulations were carried out in order to investigate the biomechanical responses of OTP. In the simulations, the loadings were measured from experiments on the designed OTP, rather than a constant force in lingual or labial direction. As a result, the simulation results had higher reliability compared to other studies [22, 23].
Some studies indicated that ceramic brackets usually presented higher friction values than conven- tional brackets [24], and self-ligating brackets presented lower friction than conventional ones [25], also ligature method can influence the friction [26]. While in our OFM, orthodontic forces were only measured with nickel titanium archwire and metallic self-ligating brackets, other types of archwire or brackets were not taken into account, this is mainly because the pr-designed OTP was designed with nickel titanium archwire and metallic self-ligating brackets, and the aim of OFM was to quantize orthodontic forces on incisors in this situation, and further to estimate its possible treatment effects, the different friction values caused by different types of brackets or ligation method were not our major concerns.
The OFM was performed on the dental model, which was made from resin by 3D printing. On the other hand, while, the material properties of teeth, PDL and alveolar bone were considerably different, and multi-material dental model will get a more accurate data. However, in this study, the measured forces were initial orthodontic forces, which would produce when standard archwire was assembled on disordered teeth and the variations of orthodontic forces along with teeth movements were not taken into account. Hence, the simplified model was still applicative in the measurements. In future works, we will try to investigate the design of multi-material dental model and dynamic measurement of orthodontic forces.
In addition, OFM was only carried out on central incisors and forces on other teeth were not studied. Actually, orthodontic forces should work on every tooth. But limited by the existing experimental facilities, only two teeth can be measured. From the measured values, the forces and moments on incisor 21 were larger than those of on incisor 11, which implies severer dislocation on incisor 21. The magnitude of forces and moments were in good agreement with previous studies [27], and also closed to frequently-used clinical orthodontic forces of 100 g and 150 g [28].
Because the objects of the investigation were incisors and only forces on incisors were measured, FEM models were appropriately simplified in this study; only six teeth were taken into account. Orthodontic forces on other teeth were not measured and considered in FEM models, which may had an impact on simulation results. However, the spaces between each tooth were big, and the magnitude of forces was small in general, the impact can be ignored. Also, the hypothesis was verified by subsequent FEM results, the stress/strain on lateral incisors aroused by central incisor forces was very small. Besides, FEM simulations were only performed on oral tissues, other models (such as brackets and archwire) were not involved. Hence, the slides between brackets and archwire were not considered.
Moreover, the properties of teeth, bone and PDL involved in models were considered as linear materials in FEM. But bone and PDL were characterized as nonlinear, viscoelastic materials [29, 30], and material properties for each of the structures were essential parameters that may influence results [31]. However, Vollmer indicated that the types of tooth movements and the distributions of strains in the oral tissues were not influenced by the assumed non-linearity of the material [32]. In addition, according to our previous study, the nonlinear material can be approximately replaced by linear material if the deformation was small. Hence, even the assumption may had a certain impact on specific values, but it did not prevent to predict incisors moving tendencies.
As shown in Fig. 8, incisors moving tendencies were simulated through FEM in the designed OTP and conventional treatment, respectively. The simulations were only static analysis, and the dynamic procedure of incisors moving with orthodontic forces was not involved, but this did not affect the forecasts of incisors movements in a short period. Simulation results indicated that the movements of incisors root to labial-direction were effectively limited by the assistant device. The moving tendencies of incisors were in good agreement with the ideal treatment under designed OTP, but not in the control group. In the control group, crowns displacements toward labial-direction were so large that risk of bone rupture was increased.
In the physiological process of teeth movements, PDL plays a crucial role in regulating orthodontic tooth movement [33]. A series of studies revealed that stress/strain of PDL was related to tissue necrosis and hyalinization, PDL stress/strain must be in a suitable range, excessive pressure will start to induce PDL occlusion and dysfunction [34, 35], as well as bone resorption. Hence, the hydrostatic stress and logarithmic strain of PDL were taken into account. As shown in Fig. 9, the maximal hydrostatic stress of PDL occurred on the bottom of PDL 21, while the maximal strain of PDL was observed in the cervical region of PDL 21. Compared to conventional treatment of 0.7082 MPa, the maximal stress of PDL was decreased to 0.5183 MPa under designed OTP; the value was down by 26.81% although on the same model. On the other hand, the maximal strain of PDL reduced from 32.52% (conventional treatment) to 21.92% (designed OTP) and the proportional reduction was 32.60%. Lower PDL stress/strain reduced the probabilities of necrosis and hyalinization, as well as root resorption.
The Von Mises stress and displacement of cortical bone were shown in Fig. 10, the maximal Von Mises stress of cortical bone decreased from 5.654 MPa (conventional treatment) to 2.329 MPa (designed OTP), simultaneously the maximal displacement of cortical bone reduced from 2.181E-03 mm (conventional treatment) to 1.796E-03 mm (designed OTP). Besides, the stress/displacement distributions of cortical bone was more uniform in the designed OTP, oversized stress concentration may cause bone rupture/absorption during treatment and finally lead to the failure of treatment.
From the clinical feedback, as shown in Figs 11 and 12, incisor crowns inclined to lingual side step-by-step and roots trended to labial side at the same time, the incisors were gradually rotated with the development of treatment and the occlusal relationships between upper and lower jaws were considerably improved after 18 months. The movements of incisors were in good agreement with FEM results; the risk of bone rupture on the labial side was eliminated. In addition, because of the reduction of PDL stress/strain in the designed OTP through FEM, a mass of root resorption did not occur, as well as alveolar bone resorption caused by overlarge Mises stress or displacement in cortical bone. FEM results predicted treatment effects of OTP before it was adopted in clinic and then increased the dependability of OTP. On the other hand, the feedbacks in clinic verified the validity of OTP and proved the value of FEM.
5.Conclusions
A clinical patient with incisors obliquity was chosen as the object, and an OTP was theoretically designed with the assistance of an orthodontist. Furthermore, orthodontic forces and moments on the incisors were measured, and biomechanical responses of periodontium were investigated through FEM. Finally, treatment effects were acquired after 18 months, the occlusal relationships between upper and lower jaws were tremendously improved, just as FEM predicted.
The biomechanical investigation, based on OFM and FEM, predicted treatment effects of OTP and clinical feedbacks varied the validity of FEM at the same time. A valuable method of orthodontic predicting and evaluating was mentioned, in future works, we will try to investigate the manufacture of more accurate dental model and dynamic measurement of orthodontic forces to further promote the development of biomechanics, this method will be more broadly applied in orthodontic treatment.
Acknowledgments
This work was supported by the grants from the National Natural Science Foundation of China (Grant No. 51375453 and 51775506), and the National Natural Science Foundation of Zhejiang Province (Grant No. LY18E050022).
Conflict of interest
None to report.
References
[1] | Kannabiran P, Thirukonda GJ, Mahendra LP. The crown angulations and inclinations in Dravidian population with normal occlusion. Indian Journal of Dental Research. (2012) : 23: , 53-58. |
[2] | Poleti ML, Freire F, Thais M, Paiz CC, Fischer R, Izabel R, Alvares C, Ana L. Pixel value analysis for detection of simulated early external root resorption. Brazilian Oral Research. (2014) : 28: , 485-490. |
[3] | Badawi H, Major P. Three-dimensional orthodontic force measurements. American Journal of Orthodontics and Dentofacial Orthopedics. (2009) : 136: , 518-528. |
[4] | Ammar HH, Ngan P, Crout RJ, Mucino VH, Mukdadi OM. Three-dimensional modeling and finite element analysis in treatment planning for orthodontic tooth movement. American Journal of Orthodontics and Dentofacial Orthopedics. (2011) : 139: , e59-e71. |
[5] | Aliki T, Siew YC, Nikolaos P, Padhraig SF. How long does treatment with fixed orthodontic appliances last? A systematic review. American Journal of Orthodontics and Dentofacial Orthopedics. (2016) : 149: , 308-318. |
[6] | Iwasaki LR, Freytag LE, Schumacher CA, Walker MP, Williams KB. Validation of a modified McGill Pain Questionnaire for orthodontic patients. Angle Orthodontist. (2013) : 83: , 906-912. |
[7] | Macey R, Glenny AM, Brocklehurst P. Assessing the efficacy and social acceptability of using hygienist-therapists as front-line clinicians. BDJ Team. (2017) : 4: , 19-23. |
[8] | Chen J, Bulucea I, Katona TR, Ofner S. Complete orthodontic load systems on teeth in a continuous full arch wire: The role of triangular loop position. American Journal of Orthodontics and Dentofacial Orthopedics. (2007) : 132: , e1-e8. |
[9] | Chen J, Isikbay SC, Brizendine EJ. Quantification of three-dimensional orthodontic force systems of T-loop arch wires. Angle orthodontist. (2010) : 80: , 566-561. |
[10] | Mittal N, Xia ZY, Chen J, Stewart KT, Liu SS. Three-dimensional quantification of pretorqued nickel-titanium wires in edgewise and prescription brackets. Angle orthodontist. (2013) : 83: , 484-490. |
[11] | Margherita M, Elisa D, Massimo C, Cesare S. Novel universal system for 3-dimensional orthodontic force-moment measurements and its clinical use. American Journal of Orhodontics and Dentofacial Orthopedics. (2015) : 148: , 174-183. |
[12] | Liu LP, He BW, Zhuang JH, Zhang LW, Lv A. Force measurement system for invisalign based on thin film single force sensor. Measurement. (2017) : 97: , 1-7. |
[13] | Anshul C, Maninder SS, Girish C, Seema G, Nimisha C, Ashutosh K. Evaluation of stress changes in the mandible with a fixed functional appliance: A finite element study. American Journal of Orthodontics and Dentofacial Orthopedics. (2015) : 147: , 226-234. |
[14] | Niu WX, Feng TN, Jiang CH. Research Progress of Finite Element Analysis in Traumatic Skull and Brain Injuries. Space Medicine & Medical Engineering. (2014) : 27: , 217-222. |
[15] | Boumaiza D, Aour B. On the efficiency of the iterative coupling FEM-BEM for solving the elasto-plastic problems. Engineering Structures. (2014) : 72: , 12-25. |
[16] | Barone S, Paoli A, Razionale AV, Savignano R. Computer aided modelling to simulate the biomechanical behaviour of customised orthodontic removable appliances. International Journal on Interactive Design and Manufacturing. (2016) : 10: , 387-400. |
[17] | Cai YQ, Yang XX, He BW, Yao J. Finite element method analysis of the periodontal ligament in mandibular canine movement with transparent tooth correction treatment. BMC Oral Health. (2015) : 15: , 106-117. |
[18] | Lars MF, Dieter D. Force systems in the initial phase of orthodontic treatment-a comparison of different leveling archwires. Journal of Orofacial Orthopedics. (2006) : 67: , 6-18. |
[19] | Lim SH, Kim MK, Kang SH. Genioplasty using a simple CAD/CAM (computer-aided design and computer-aided manufacturing) surgical guide. Maxillofacial Plastic and Reconstructive Surgery. (2015) : 37: , 1-6. |
[20] | Toms SR, Eberhardt AW. A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. American Journal of Orthodontics and Dentofacial Orthopedics. (2003) : 123: , 657-665. |
[21] | Qian YL, Fan Y, Liu Z, Zhang M. Numerical simulation of tooth movement in a therapy period. Clinical Biomechanics. (2008) : 23: , s48-s52. |
[22] | Pai SS, Panda S, Pai V, Anandu M, Vishwanath E, Suhas AS. Effects of labial and lingual retraction and intrusion force on maxillary central incisor with varying collum angles: A three-dimensional finite elemental analysis. Journal of Indian Orthodontic Society. (2017) : 51: , 28-37. |
[23] | Ashish H, Balamohan S, Vinay PR, Nikhilanand H, Harish SRK, Jasleen KH. Effect of root proximity of orthodontic mini-implant on bone stress: A dimensional finite element analysis. Journal of Indian Orthodontic Society. (2016) : 50: , 14-18. |
[24] | Reimann S, Bourauel C, Weber A, Dirk C, Lietz T. Friction behavior of ceramic injection-molded (CIM) brackets. Journal of Orofacial Orthopedics. (2016) : 77: , 262-271. |
[25] | Cacciafesta V, Sfondrini MF, Ricciardi A, Scribante A, Klersy C, Auricchio F. Evaluation of friction of stainless steel and esthetic self-ligating brackets in various bracket-archwire combinations. American Journal of Orthodontics and Dentofacial Orthopedics. (2003) : 124: , 395-402. |
[26] | Kahlon S, Rinchuse D, Robison JM, Close JM. In-vitro evaluation of frictional resistance with 5 ligation methods and Gianelly-type working wires. American Journal of Orthodontics and Dentofacial Orthopedics. (2010) : 138: , 67-71. |
[27] | Ahmad A, Cornelius D, Susanne R, Tarek EB, Andreas J, Christoph B. Mechanical properties of different esthetic and conventional orthodontic wires in bending tests. Journal of Orofacial Orthopedics. (2017) : 78: , 241-252. |
[28] | Wahab RMA, Dasor MM, Senafi S, Abdullah AAA, Jemain AA, Abu KN, Yamamoto Z, Ariffin SHZ. Crevicular tartrate resistant acid phosphatase activity and rate of tooth movement under different continuous force applications. African Journal of Pharmacy and Pharmacology. (2011) : 5: , 2213-2219. |
[29] | Mengoni M, Ponthot JP, Boman R. Mesh management methods in finite element simulations of orthodontic tooth movement. Medical Engineering and Physics. (2016) : 38: , 140-147. |
[30] | Hemanth M, Deoli S, Raghuveer HP, Rani MS, Hegde C, Vedavathi B. Stress Induced in the Periodontal Ligament under Orthodontic Loading (Part I): A Finite Element Method Study Using Linear Analysis. Journal Of International Oral Health. (2015) : 7: , 129-133. |
[31] | Javad HM, Farzan G, Behnam M. Numerical simulation of orthodontic bone remodeling. Orthodontic Waves. (2009) : 68: , 64-71. |
[32] | Vollmer D, Bourauel C, Maier K, Jager A. Determination of the centre of resistance in an upper human canine and idealized tooth model. European Journal of Orthodontics. (1999) : 21: , 633-648. |
[33] | Liao ZP, Chen JN, Li W, Darendeliler MA, Swain M, Li Q. Biomechanical investigation into the role of the periodontal ligament in optimizing orthodontic force: a finite element case study. Archives of Oral Biology. (2016) : 66: , 98-107. |
[34] | Hohmann A, Wolfram U, Geiger M, Boryor A, Kober C, Sander C, Sander FG. Correspondences of hydrostatic pressure in periodontal ligament with regions of root resorption: a clinical and a finite element study of the same human teeth. Computer Methods and Programs in Biomedicine. (2009) : 93: , 155-161. |
[35] | Choy K, Pae EK, Park Y, Kim KH, Burstone CJ. Effect of root and bone morphology on the stress distribution in the periodontal ligament. American Journal of Orthodontics and Dentofacial Orthopedics. (2000) : 117: , 98-105. |




