Sparse feature learning for multi-class Parkinson’s disease classification
Abstract
This paper solves the multi-class classification problem for Parkinson’s disease (PD) analysis by a sparse discriminative feature selection framework. Specifically, we propose a framework to construct a least square regression model based on the Fisher’s linear discriminant analysis (LDA) and locality preserving projection (LPP). This framework utilizes the global and local information to select the most relevant and discriminative features to boost classification performance. Differing in previous methods for binary classification, we perform a multi-class classification for PD diagnosis. Our proposed method is evaluated on the public available Parkinson’s progression markers initiative (PPMI) datasets. Extensive experimental results indicate that our proposed method identifies highly suitable regions for further PD analysis and diagnosis and outperforms state-of-the-art methods.
1.Introduction
Parkinson’s disease (a.k.a., Parkinsonism, PD, tremor paralysis) is the most common central nervous system degeneration disease in the elderly [1]. PD is categorized by clinicians as a movement disorder. Possible symptoms include tremor, muscle rigidity, drivel, postural instability, and bradykinesia (slow in movement) [2]. Apart from motor symptoms, non-motor symptoms including depression, anxiety, fatigue, sleep disorders and cognitive disorders can also affect patients from all walks of life [3].
In recent years, it has been observed that PD is also affecting younger people, and this has become one of the popular research. There are approximately 1 million PD patients in USA and 120,000 in UK. Among them, 5 percent are under the age of 40 years [4]. Due to the lack of comprehensive knowledge of PD, most patients fail to seek proper medical treatment in time and are unaware of the disease. PD symptoms are often mistaken as an aging problem. Lacking early intervention treatment, the delayed treatment rate of PD is up to 60% [5, 6]. Current diagnosis of PD mainly depends on clinical symptoms, which is heavily relied on the clinicians’ experience [7]. Therefore, effective ways for early PD diagnosis would be desirable.
Neuroimaging techniques proved to be promising tools for disease diagnosis. Single-photon emission computed tomography (SPECT), magnetic resonance imaging (MRI), diffusion-weighted tensor imaging (DTI) techniques are widely chosen to serve this purpose. With the development of machine learning and data-driven analysis, a great number of recent studies have been proposed to predict and assess the stage of pathology using the brain images. For instance, Fung and Stoeckel performed feature selection via spatial information for classification with SPECT images [8]. Rana et al. proposed a machine learning approach for PD classification using T1-weighted MRI images [9]. Salvatore et al. suggested a principal component analysis (PCA) based method using morphological T1-weighted MRI. In [10], support vector machine (SVM) was adopted for PD diagnosis and progressive supranuclear palsy (PSP) patients. Deep convolutional neural networks (CNN) has also been implemented by Shin et al. for computer-aided detection problems [11].
Nevertheless, most existing research only focus on binary classification to differentiate PD and normal control (NC). A third category called scan without evidence of dopaminergic deficit (SWEDD) lacks sufficient attention. An accurate recognition of SWEDD contributes to offer appropriate therapeutic options to patients [12]. Accordingly, we simultaneously classify three different clinical statuses for practical clinical application instead of binary classification of NC vs. SWEDD or PD vs. SWEDD. Also, the common issue in neuroimaging research is high dimensionality and limited sample size. Feature selection is one of the effective ways to solve this issue. In view of this, we propose a novel feature selection method to select the most representative subset of features to construct a reliable classification model. The obtained informative and discriminative features with relatively small amount can enhance classification performance as well.
2.Data acquisition and preprocessing
2.1Dataset
The data used in this paper is acquired from the Parkinson’s progression markers initiative (PPMI) database.11 PPMI is the first world-wide collaboration of researchers, sponsors, and research participants committing to identify progressive biomarkers to improve PD treatment [13]. They are dedicated to build standardized protocols for acquisition, analysis of the data and to promote the overall comprehension of PD.
Since MRI and DTI images can reveal the detailed structure of the brain, we choose them to provide rich and complementary information in our experiment. MRI image is obtained in the form of a T1-weighted, 3D sequence (i.e., MPRAGE) via Siemens MAGNETOM Trio 3.0T MRI scanners. Then we collect 56 NC, 123 PD, and 29 SWEDD scans. DTI images were selected with the following parameters: slice thickness
Apart from the baseline MRI, DTI data from 208 subjects, we also collect three cerebrospinal fluid (CSF) biomarkers and clinical scores including sleep scores, olfaction scores, depression scores, and MoCA (Montreal Cognitive Assessment) scores to boost performance. The three CSF biomarkers are amyloid beta (1-42) (A
Table 1
Clinical details of all subjects (mean
| NC | PD | SWEDD | |
|---|---|---|---|
| Number | 56 | 123 | 29 |
| Female/male | 22/34 | 47/76 | 12/17 |
| Age | 60.7 | 61.3 | 60.3 |
| Sleep scores | 6.4 | 5.9 | 8.8 |
| Olfaction scores | 33.5 | 22.5 | 30.7 |
| Depression scores | 5.1 | 5.3 | 5.8 |
| MoCA scores | 28.1 | 27.6 | 27.0 |
Since smell dysfunction occurs 90% of cases with PD, the olfaction scores are essential for diagnosis. Scores are obtained from the University of Pennsylvania smell identification test (UPSIT), which is commercially accessible for determining certain individual’s olfactory ability. Lower olfaction score means weaker olfactory function. The MoCA scores are generated in a brief 30-question test by a group at McGill University that assesses different types of cognitive abilities. The clinical details of experimental subjects are listed in Table 1.
2.2Preprocessing
All the MRI and DTI images are initially preprocessed by discarding the noise in the images. We select the nonlinear spatial filtering for denoising to improve the performance. In addition, feature extraction, registration and image fusion is also applied. We perform the anterior commissure-posterior commissure (ACPC) correction using COM algorithm to get a better angle. We use the statistical parametric mapping (SPM)22 to correct geometrical distortion and head motion. Finally, the images are processed by skull-stripping for later operation.
For MRI data, we segment the image and group the tissue into gray matter (GM), white matter (WM) and CSF by the SPM default tissue probability maps. These tissues are the main elements of the central nervous system and can help us to analyze neuronal cell changes. To obtain a higher resolution, all images are then re-sampled until isotropic resolution reaches 1.5 mm after normalization and segmentation. Following the automated anatomical labeling (AAL) atlas, we get 116 region-of-interests (ROIs) in the brain. Then we compute the mean tissue density value of these three tissues in each region and use them as features. For DTI data, we further achieve alignment between structural MRI and DTI, and incorporate affine image registrations based on a cost function weighting using FLIRT.33 Specifically, the DTI data is registered to the T1-weighted structural MRI by an affine transformation [14].
DTI images are based on the movement of water molecule. The fractional anisotropy (FA) coefficient of water molecule movement can reflect structural and functional information. The detailed procedures for calculating FA values are illustrated in DTI preprocessing manual.44 For MRI images, we collect 116 GM and 116 WM and 116 CSF tissue volumes for each subject. For DTI images, we obtain 16 mean FA intensity values for each subject. Additional CSF biomarkers and clinical scores are added as complementary features for later use.
Figure 1.
Flowchart of our method, where T1G is GM of MRI images, T1C stands for CSF of MRI images, DTI-FA stands for FA values of DTI images.
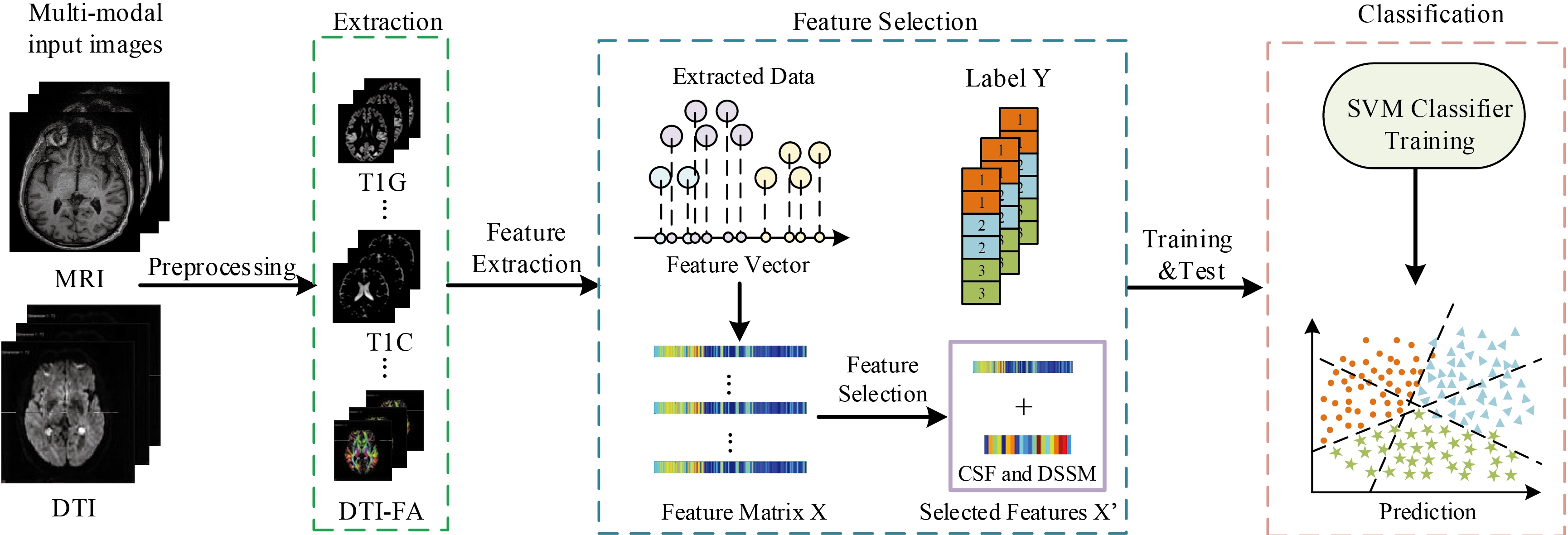
3.Methodology
3.1Overview of the method
The overview of our multi-class classification method is presented in Fig. 1. First, we preprocess the original data and extract the tissue volume in the segmented regions to construct GM, CSF, DTI. Then we perform feature selection to get most important features. Specifically, we add CSF biomarkers and clinical scores to the selected features to build our final feature matrix for training the classifiers. We train the classifiers in a supervised manner. Finally, we use support vector classification (SVC) to classify the samples into 3 different groups.
3.2Sparse discriminative feature selection
High dimensionality and small sample size have always been a bottleneck in brain image analysis. Traditionally, the problem of high dimensionality in original data is always settled by a series of dimension reduction methods, e.g., Principal Component Analysis (PCA), Locally Linear Embedding (LLE) [15], LDA [16], Isometric Feature Mapping (ISOMAP) [17]. All these methods can be split into two categories: feature selection and subspace learning [18]. In our method, we jointly perform a feature selection to put them together for further processing. Specifically, we construct a regularized least square regression model based on the idea of Fisher’s LDA combined with LPP, which takes both global and local information into account [19, 20]. Subspace learning methods such as LDA and LPP can convert the initial feature matrix to a feature matrix with reduced dimensionality [21]. By the sparse regularized linear regression model, the most discriminative and relevant features are collected to enhance the classification performance.
In this paper, we denote
(1)
where
(2)
where
(3)
where
(4)
where
(5)
where
Inspired by [24], we solve Eq. (5) by the accelerated proximal gradient method to iteratively update the value of
3.3SVM classification
Differing from the preceding methods that merely perform a binary classification, a multi-class classification is adopted for PD diagnosis in our method. In machine learning, SVM is a supervised learning model used for pattern recognition, classification and regression analysis. The main idea of SVM is finding the best hyperplane that can separate different class samples with the maximum margin. Hence, we choose the SVM to construct a multi-class classification model. The free and available software libsvm55 toolbox (version: libsvm-2.91) is used to perform the classification task.
In binary SVM classification, we directly make use of the outputs of the prediction function. In multi-class classification, the output of SVM prediction will change, for example, the dimension of decision values is equal to the number of all possible binary classification combinations. For samples belonging to
4.Experiments
A 208
4.1Experimental settings
In our experiments, we perform the multi-class classification NC vs. PD vs. SWEDD via SVM. In the 10-fold cross-validation method, for each subset of experiment, we train feature selection model by different feature combination sets, i.e., GM of MRI (T1G for short), WM of MRI (T1W for short), CSF of MRI (T1C for short), FA of DTI (DTI for short), T1G
Table 2
Classification performance (mean
| Features | NC vs. PD vs. SWEDD | ||||
|---|---|---|---|---|---|
| ACC (%) | SEN (%) | PREC (%) | FSCORE (%) | AUC (%) | |
| T1G | 64.37 | 64.92 | 42.25 | 39.28 | 81.23 |
| T1W | 61.22 | 57.95 | 27.48 | 30.72 | 71.97 |
| DTI | 65.52 | 56.00 | 59.77 | 42.68 | 83.32 |
| T1C | 62.09 | 65.30 | 31.90 | 33.74 | 75.75 |
| GCD | 67.58 | 58.48 | 54.83 | 45.78 | 81.62 |
| WCD | 66.35 | 58.05 | 55.80 | 44.67 | 80.24 |
| GWCD | 67.37 | 61.22 | 54.90 | 47.16 | 82.34 |
| GCD | 65.34 | 41.94 | 60.48 | 78.21 | 86.63 |
| GCD | 78.21 | 84.39 | 56.23 | 65.97 | 91.22 |
| GCD |
78.37 |
84.70 |
66.73 |
70.21 |
94.20 |
Boldface denotes best performance.
Figure 2.
Classification accuracy of various hyperparameters (
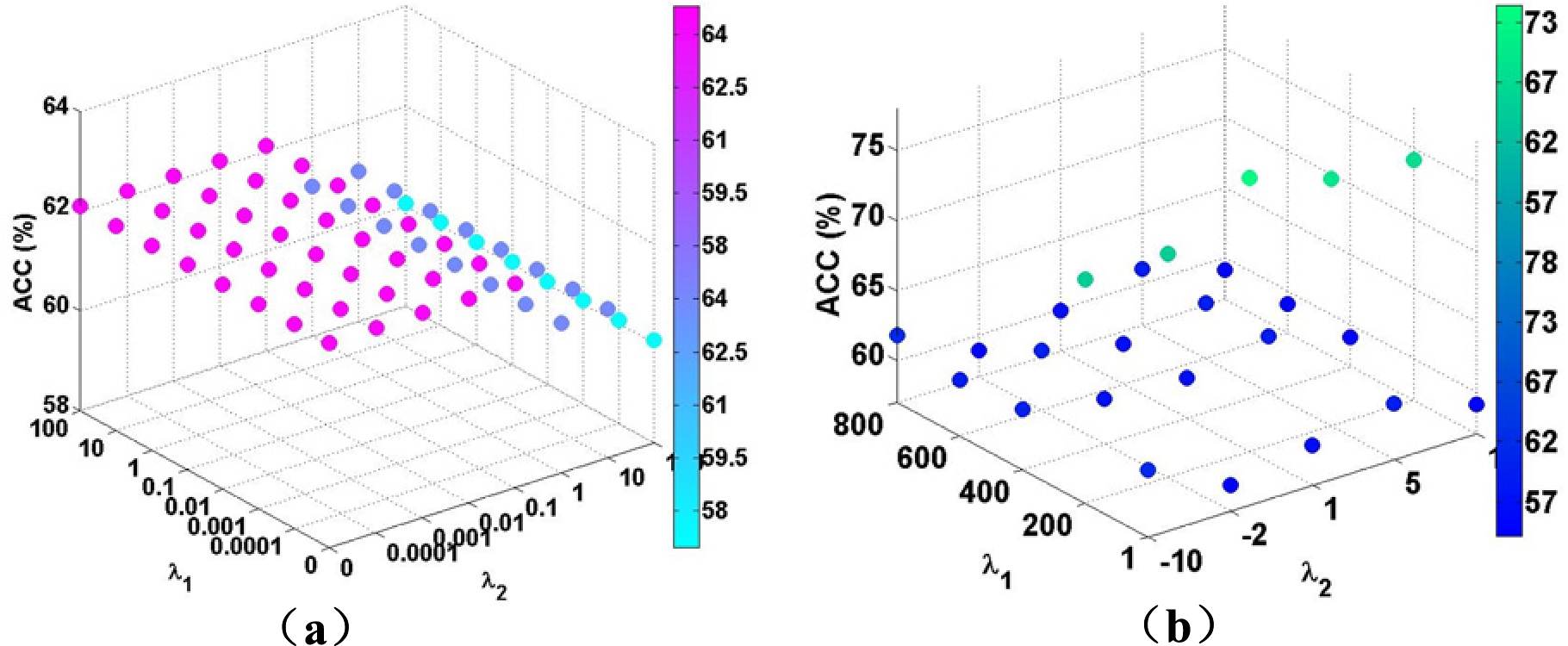
4.2Parameters
The main parameters used in our method is the feature selection tuning parameters in Eq. (4),
4.3Classification results
In the experiments, we use quantitative measurements to evaluate the performance of our method. These measurements include accuracy (ACC), sensitivity (SEN), precision (PREC), F-scores (F1), area under the receiver operating characteristic curve (AUC). Table 2 shows the multi-class classification results of NC vs. PD vs. SWEDD from single modality to multimodal data. Before deciding what features combine together can produce the best results, we perform different sets of feature groups and compare the outputs. We can clearly see that the single modality using only one type of features (T1G, T1W, T1C, DTI) is slightly worse than other combination groups. We noticed that T1W has the least effectiveness as well as the combination including T1W. Among all these combination modes, we select the one with the highest accuracy. Accordingly, we use the GCD combination as the feature matrix before feature selection process. Apart from these features, we add three CSF biomarkers and four clinical scores to the feature matrix before training SVM classifiers. Since these features only take a small proportion in the original data, they have no need for feature selection process. The achieved performance proves that our strategy of adding CSF biomarker and clinical scores boost the classification results. The classification performance with multi-modality features (GCD) combined with CSF and DSSM is always better than those without additional features. Therefore, the combination GCD
Table 3
Classification performance comparison of different types of features among all competing methods and proposed method
| Feature | Method | NC vs. PD vs. SWEDD | ||||
|---|---|---|---|---|---|---|
| ACC (%) | SEN (%) | PREC (%) | FSCORE (%) | AUC (%) | ||
| GCD | Elastic net | 70.33 | 62.92 | 54.03 | 54.36 | 87.15 |
| Lasso | 70.20 | 62.68 | 58.07 | 52.27 | 86.94 | |
| M3T | 70.07 | 62.60 | 54.94 | 49.88 | 86.95 | |
| Lei’s | 72.57 | 68.01 | 53.93 | 54.03 | 89.29 | |
| Proposed |
78.37 |
84.70 |
66.73 |
70.21 |
94.20 | |
Figure 3.
ROC results for comparison between other competing methods.
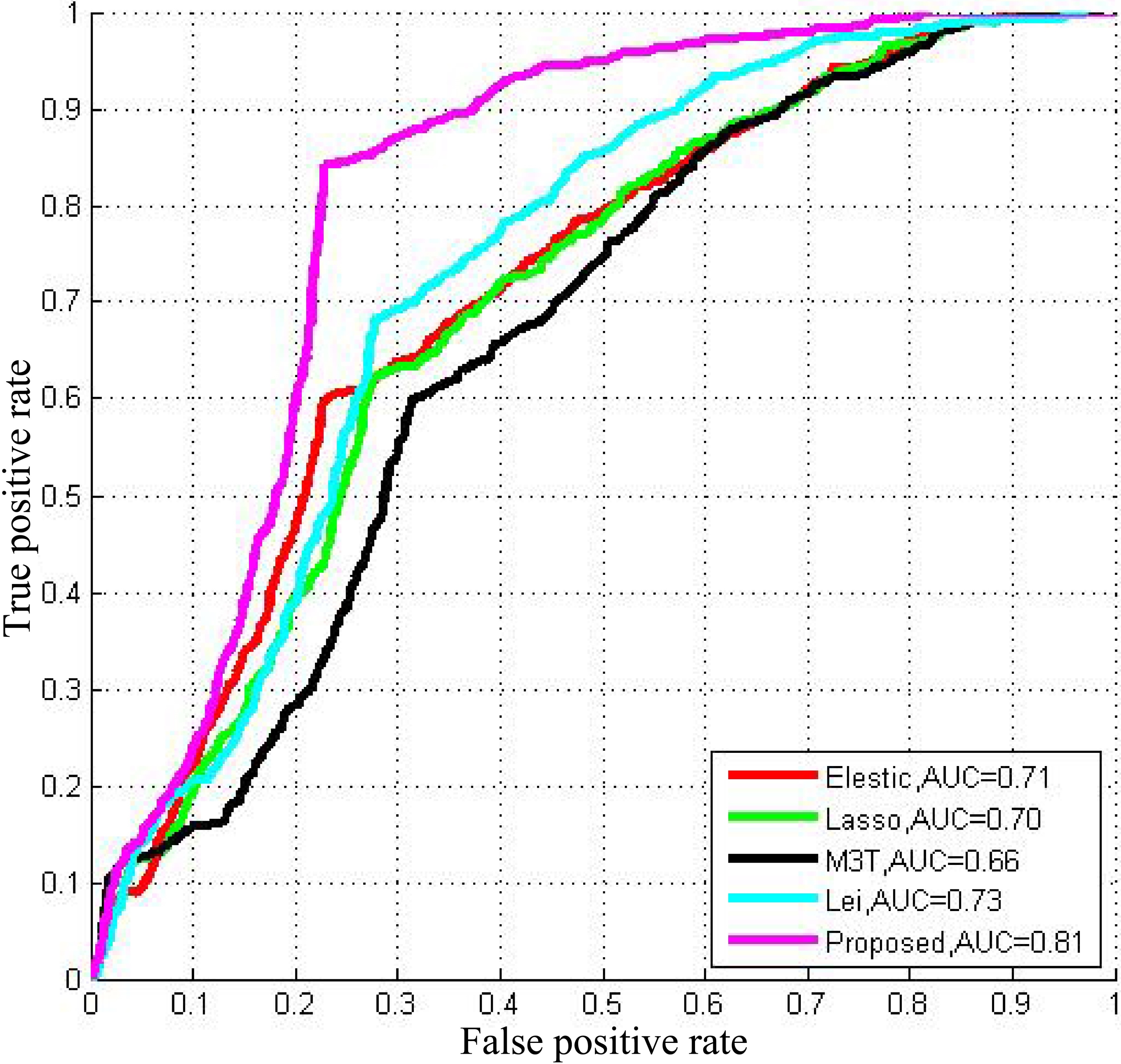
We compare our proposed method with other widely used methods such as elastic net, least absolute shrinkage and selection operator (Lasso) [26], Multi-modal multi-task (M3T) [1], Lei et al.’s [27]. Receiver operating characteristic (ROC) curves based on 100 times cross-validation of comparison among these competing methods and our proposed method are demonstrated in Fig. 3. We observe that the proposed method is superior to competing methods using the organized features. Overall, the proposed method achieves an accuracy of 78.4%, a sensitivity of 84.7%, a precision of 66.7%, an F1 score of 70.2% and an AUC of 94.2% with multi-modality data. Details are illustrated in Table 3. The proposed method with GCD
In our experiment, we combined different features before and after the feature selection. As shown in Table 3, the experimental results demonstrate that our feature selection method enhances the classification performance. We also find that the proposed sparse feature selection method based on multi-modal data outperforms competing methods. Furthermore, our multi-class classification can classify the samples into three categories and shows the efficacy of our proposed method.
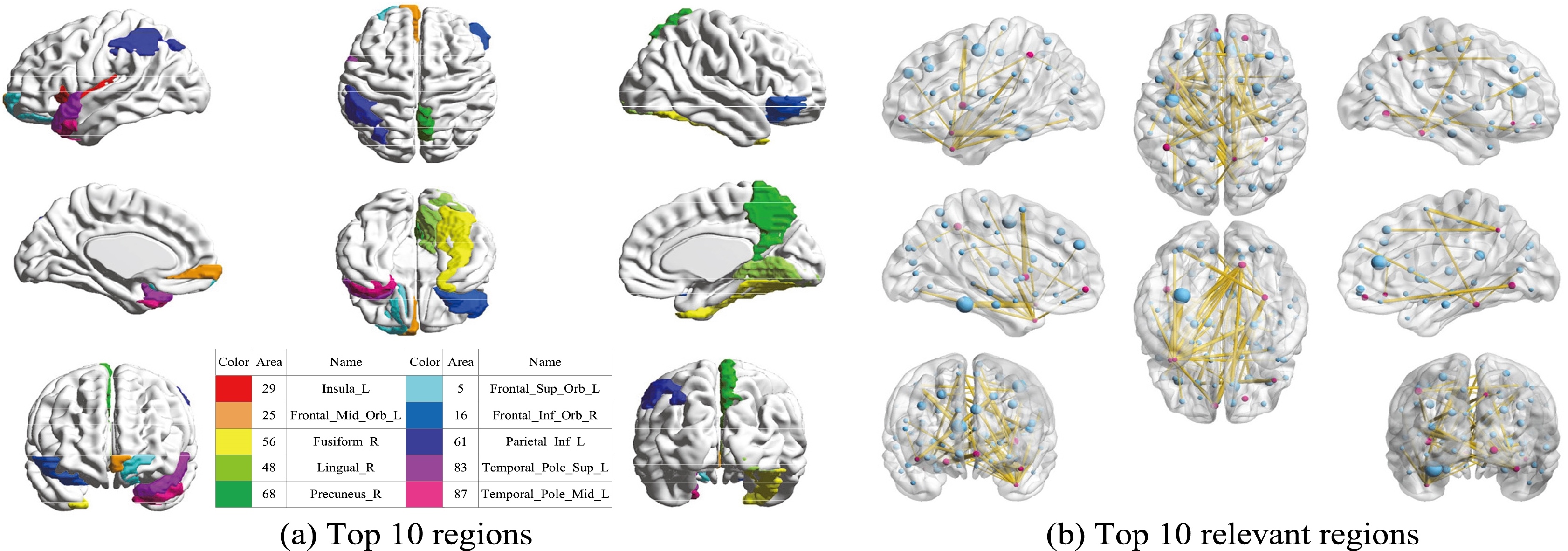
Figure 4.
(a) Top 10 discriminative brain regions obtained from proposed method via for NC vs. PD vs. SWEDD. Brain regions were color-coded. (b) Top 10 relevant brain regions (in blue points) for each top 10 discriminative brain region (in red points).
4.4Related brains regions
Our experiments are based on the assumption that GM or WM or other brain biomarkers are changed. To better facilitate early diagnosis and monitoring the progression of PD for the corresponding treatments, we also studied the relevant and discriminative brain regions about PD. To find the top 10 regions, we utilize the weight coefficient matrix produced in feature selection process through a 10-fold cross validation method. The weight matrices present the significance of all the 116 brain regions. We choose the top 10 regions with the highest weight value in a descending order and delete the repeat regions. The top 10 relevant brain regions selected from multi-class classification are visualized in Fig. 4. Moreover, suffix ‘_L’ indicates the left brain, suffix ‘_R’ indicates the right brain, and different colors indicate different brain regions. The top 10 brain regions recognized with GCD multi-modal features using our proposed method are insula left, middle frontal gyrus (orbital part), fusiform gyrus right, lingual gyrus right, precuneus right, superior frontal gyrus (orbital part), inferior frontal gyrus (orbital part), inferior parietal (but supramarginal and angular gyri), temporal pole (superior temporal gyrus), middle temporal gyrus. To further study the relationship between brain regions and PD, we continue with in-depth study on the top 10 regions by seeking the other top 10 brain regions which have the most correlation with the selected top 10 regions. We use the same weighting matrix as selecting top 10 regions to calculate the Pearson correlation coefficient to represent the correlation among different regions. The weighting coefficient is used to select the 10 other relevant regions of each top 10 brain regions. The results are also visualized in Fig. 4, and the red points in each image represents the top 10 ROIs, and each red point spreads 10 yellow lines to connect 10 other points in blue which indicates the 10 relevant ROIs.
5.Conclusion
In this paper, we introduced a sparse feature selection framework along with a multi-class classification model in PD early diagnosis. To further identify the type of disease (NC or PD or SWEED) for clinical application, we performed a multi-class classification. Using multi-modality data from PPMI neuroimaging dataset, we verified that our method classifies the three categories simultaneously with promising results. Furthermore, we generated 10 relevant ROIs to demonstrate the important regions for PD diagnosis.
Notes
Acknowledgments
This work was supported by National Natural Science Foundation of China (No. 61402296), The Integration Project of Production Teaching and Research by Guangdong Province and Ministry of Education (No. 2012B091100495), Shenzhen Key Basic Research Project (No. JCYJ20150525092940986/ JCYJ20170302153920897/JCYJ20150930105133185/JCYJ20170302153337765), National Natural Science Foundation of Shenzhen University (No. 827000197).
Conflict of interest
None to report.
References
[1] | Zhang D, Shen D. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer’s disease. Neuroimage (2012) ; 59: (2): 895-907. |
[2] | Postuma RB, Berg D, Stern M, Poewe W, Olanow CW, Oertel W, et al. MDS clinical diagnostic criteria for Parkinson’s disease. Movement Disorders (2015) ; 30: (12): 1591-1599. |
[3] | Braak H, Del TK, Rüb U, de Vos RA, Jansen Steur EN, Braak E. Staging of brain pathology related to sporadic Parkinson’s disease. Neurobiology of Aging (2003) ; 24: (2): 197-211. |
[4] | Willis AW, Schootman M, Kung N, Racette BA. Epidemiology and neuropsychiatric manifestations of young onset Parkinson’s disease in the United States. Parkinsonism and Related Disorders (2013) ; 19: (2): 202-206. |
[5] | Prashanth R, Dutta Roy S, Mandal PK, Ghosh S. Automatic classification and prediction models for early Parkinson’s disease diagnosis from SPECT imaging. Expert Systems with Applications (2014) ; 41: (7): 3333-3342. |
[6] | Lei B, Jiang F, Chen S, Ni D, Wang T. Longitudinal analysis for disease progression via simultaneous multi-relational temporal-fused learning. Frontiers in Aging Neuroscience (2017) ; 9: (6). |
[7] | Adeli E, Shi F, An L, Wee C-Y, Wu G, Wang T, et al. Joint feature-sample selection and robust diagnosis of Parkinson’s disease from MRI data. NeuroImage (2016) ; 141: : 206-219. |
[8] | Fung G, Stoeckel J. SVM feature selection for classification of SPECT images of Alzheimer’s disease using spatial information. Knowledge and Information Systems (2007) ; 11: (2): 243-258. |
[9] | Rana B, Juneja A, Saxena M, Gudwani S, Kumaran S, Behari M, et al. A machine learning approach for classification of Parkinson’s disease and controls using T1-weighted MRI. Movement Disorders (2014) ; 29: : S88-S89. |
[10] | Salvatore C, Cerasa A, Castiglioni I, Gallivanone F, Augimeri A, Lopez M, et al. Machine learning on brain MRI data for differential diagnosis of Parkinson’s disease and progressive supranuclear palsy. Journal of Neuroscience Methods (2014) ; 222: : 230-237. |
[11] | Shin HC, Roth HR, Gao M, Lu L, Xu Z, Nogues I, et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Transactions on Medical Imaging (2016) ; 35: (5): 1285-1298. |
[12] | Aerts MB, Esselink RA, Post B, Bp VDW, Bloem BR. Improving the diagnostic accuracy in parkinsonism: A three-pronged approach. Practical Neurology (2012) ; 12: (2): 77-87. |
[13] | Marek K, Jennings D, Lasch S, Siderowf A, Tanner C, Simuni T, et al. The Parkinson progression marker initiative (PPMI). Progress in Neurobiology (2011) ; 95: (4): 629-635. |
[14] | Tao R, Fletcher PT, Gerber S, Whitaker RT. A variational image-based approach to the correction of susceptibility artifacts in the alignment of diffusion weighted and structural MRI. Information Processing in Medical Imaging (2009) ; 21: : 664-675. |
[15] | Ridder DD, Kouropteva O, Okun O, Pietikäinen M, Duin RPW. Supervised locally linear embedding. Springer Berlin Heidelberg; (2003) . |
[16] | Yang S, Zhao C. A fusing algorithm of Bag-Of-Features model and Fisher linear discriminative analysis in image classification. (2012) ; 380-383. |
[17] | Maaten LJPVD, Postma EO, Herik HJVD. Dimensionality reduction: A comparative review. Journal of Machine Learning Research (2009) ; 10: (1): 66-71. |
[18] | Ghodsi A. Dimensionality reduction a short tutorial. General Information (2006) ; 22: (2): 183-207. |
[19] | Zhang L, Qiao L, Chen S. Graph-optimized locality preserving projections. Pattern Recognition (2010) ; 43: (6): 1993-2002. |
[20] | Balakrishnama S, Ganapathiraju A. Linear discriminant analysis – a brief tutorial. Proc of the Int Joint Conf on Neural Networks (1998) ; 3: (94): 387-391. |
[21] | Lei B, Yang P, Wang T, Chen S, Ni D. Relational-regularized discriminative sparse learning for Alzheimer’s disease diagnosis. IEEE Transactions on Cybernetics (2017) ; 47: (4): 1102-1113. |
[22] | Kotsia I, Zafeiriou S, Pitas I. Novel multiclass classifiers based on the minimization of the within-class variance. IEEE Transactions on Neural Networks (2009) ; 20: (1): 14-34. |
[23] | Dai G, Yeung DY. Tensor embedding methods. National Conference on Artificial Intelligence and the Eighteenth Innovative Applications of Artificial Intelligence Conference 16-20 July 2006, Boston, Massachusetts, USA, (2006) . |
[24] | Nesterov Y. Introductory lectures on convex optimization. Applied Optimization (2004) ; 87: (5): xviii, 236. |
[25] | Chui KT, Tsang KF, Chi HR, Ling BWK, Wu CK. An accurate ECG-based transportation safety drowsiness detection scheme. IEEE Transactions on Industrial Informatics (2016) ; 12: (4): 1438-1452. |
[26] | Tibshirani RJ. Regression shrinkage and selection via the LASSO. Journal of the Royal Statistical Society (1996) ; 58: (1): 267-288. |
[27] | Lei H, Huang Z, Zhang J, Yang Z, Tan EL, Zhou F, et al. Joint detection and clinical score prediction in Parkinson’s disease via multi-modal sparse learning. Expert Systems with Applications (2017) ; 80: (1): 284-296. |




