RF ablation thermal simulation model: Parameter sensitivity analysis
Abstract
OBJECTIVE:
The aim of the research is to obtain the relative influences of some critical electro-thermal parameters on the ablation temperature and lesion volume during temperature-controlled radiofrequency ablation (RFA) of liver tumor by parameter sensitivity analysis.
METHODS:
The finite element method (FEM) has been used to establish the simulation model of RFA temperature field, and the sensitivity of the tissue parameters has been analyzed. The effects of six parameters have been taken into account, including the thermal specific capacity (Cp), the thermal conductivity (
RESULTS:
It was found that the ablation temperature and lesion volume increased with increasing the values of
CONCLUSIONS:
It is concluded that these parameter sensitivity results can provide scientific and reliable reference for the specificity analysis of the RF ablation models.
1.Introduction
RFA technology is to apply the AC electric field to the tumor tissue, thus achieving tumor coagulation necrosis by the resistance heating. This technique has been widely used in the treatment of liver tumors due to its minimal invasiveness. However, the ablation quality still depends on the experiences of clinicians. Some studies [1, 2, 3] have shown that RFA outcomes mainly rely on the lesion volume size, shape of the ablation zone and its internal temperature distribution. Thence, the precise characterization of the RFA temperature field is particularly important.
Computer modeling and simulation technology can not only obtain the temperature changes in the ablation zone, but also help doctors to make a reasonable surgical plan before surgery. Zhang [4] established the temperature field models based on the Pennes and Hyperbolic heat transfer equations and discussed the effects of different heat transfer models on the temperature distributions. Nie [5] studied the temperature field of RFA in the spinal tumor conformal therapy. Jin et al. [6] found a RFA model of thyroid treatment based on MRI. Huang et al. [7] attempted to adjust the electrode needle voltage based on the proportional integral feedback control method, to build temperature-controlled RFA simulation model, but did not consider the parameter changes over time. In these literatures, however, the electro-thermal parameters were regarded as fixed values, and the specificity of the biological tissue parameters was not considered. Actually, these parameters will vary with temperature. Rossmann and Haemmerich [8] presented a review of temperature dependence of tissue electro-thermal properties. The study also suggested that all these parameters were necessary for determining absorption of electromagnetic energy (e.g. microwaves or RF current), and estimating the temperature profile. Trujillo and Berjano [9] also investigated the mathematical functions used to describe temperature dependence of electrical and thermal conductivities in RFA models. Thus, using a single reference value in RFA simulation model is not sufficiently accurate. In order to improve the accuracy of the simulation model of liver tumor temperature field, it is necessary to research the influence of changes of tissue parameters on the lesion volume in RFA.
In view of the above, a sensitivity analysis method is required to precisely characterize how the temperature dependence of parameters will influence the simulation temperature and lesion volume. Sensitivity analysis is a quantitative description of the input parameters on the output response [10], and its quantitative index is the variance contribution rate of error. The greater the SS% is, the higher the effects of the parameter on the model responses will be [11]. The purpose of this paper is to achieve the sensitivity of each characteristic parameter by sensitivity analysis method. In the feedback application, the less sensitive parameters can be removed, so as to effectively reduce the complexity of the model, simplify data operations, and further improve the accuracy of the simulation model. This paper mainly analyzes the characteristic parameters of the temperature distribution model by variance analysis method, and obtains the sensitivity parameters which have significant influences on the ablation temperature and lesion volume.
In clinical RF thermal ablation surgery, the temperature-controlled ablation instrument is commonly used. The working principle is to adjust the output power in real time according to the set parameters (center temperature, temperature-raising rate, etc.), acquire a constant central temperature by power compensation, and finally achieve the required thermal coagulation effects. Temperature-controlled RFA model was established based on the ablation instrument RFA-I (Blade Co., Ltd., Beijing, China) and the liver tissue phantom. The temperature field modeling was performed using COMSOL Multiphysics software version 5.1 (COMSOL Inc., Palo Alto, CA, USA). The sensitivity of each characteristic parameter was studied by factor analysis (DOE) in Minitab (State College, PA, USA).
2.Materials and methods
2.1Geometric modeling of RFA
The RFA simulation model was established and solved by the finite element method (FEM) in Comsol software. FEM was used to solve the diffusion equation numerically [12, 13], which offered advantages in speed and flexibility.
Due to the symmetry of the electrode, only half of the model needed to be considered to save computation time. The symmetrical model was constructed into a semi-cylinder of homogenized tissue (50 mm
Figure 1.
Geometry model of the tissue and multi-polar electrode.
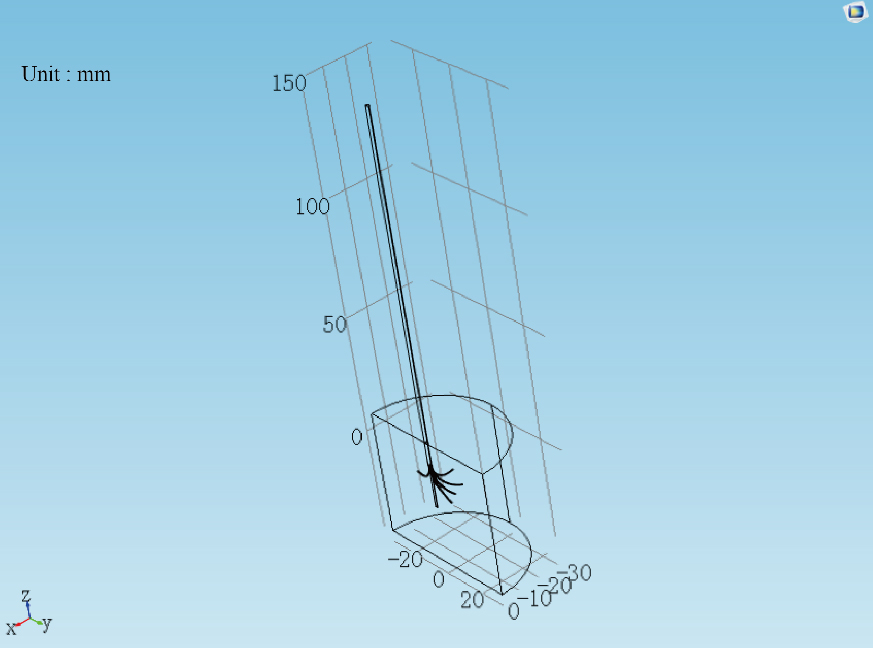
Figure 2.
The shape and distributing range of the electrode.
To obtain the solution of FEM model, the boundary conditions and initial conditions of the simulation model were set. For the current field, the boundary of the multi-polar RF electrode was set as the voltage source, and the boundary of the liver tissue was set as the ground; for the bio-heat transfer physical field, the initial temperature of the model was 28
2.2Mathematical modeling of RFA
The construction of RFA mathematical model was based on electromagnetic governing equation and bio-heat transfer equation. The heat source of each point was created by electromagnetic energy, and the temperature distribution was formed by bio-heat transfer mechanism.
In the process of RFA simulation, the current field is regarded as a heat source, and the control equation is Laplace equation:
(1)
(2)
(3)
where
(4)
where
(5)
The bio-heat transfer equation employed is the classical Pennes bio-heat transfer equation, which is described as follows:
(6)
where
2.3Sensitivity analysis method
Thermal and electric parameters were selected as the influence variables in this study. Response surface methodology (RSM) is a sensitivity analysis technique, which can present the correlations between several input variables and response variables. RSM include 3
Table 1
Input variables and their levels
| Parameter | Unit | Symbol | 0 | 1 | |
|---|---|---|---|---|---|
| Resistance, |
| A | 16 | 16.8 | 17.6 |
| Specific heat capacity, Cp | (J/(Kg | B | 3400 | 3570 | 3740 |
| Thermal conductivity, | (W/(m | C | 0.48 | 0.504 | 0.528 |
| Electrical conductivity, Sigma | (S/m) | D | 0.2 | 0.21 | 0.22 |
| Density, rho | (kg/m | E | 1000 | 1050 | 1100 |
| Dielectric constant, Epsilon | 1 | F | 40 | 42 | 44 |
Table 2
Design of experiments
| Run order | Code value | |||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |
| 1 | 1 | 1 | ||||
| 2 | 1 | 1 | 1 | 1 | ||
| 3 | 1 | 1 | ||||
| 4 | 1 | 1 | ||||
| 5 | 1 | 1 | 1 | 1 | ||
| 6 | 1 | 1 | ||||
| 7 | 1 | 1 | 1 | 1 | ||
| 8 | 1 | 1 | 1 | 1 | ||
| 9 | 1 | 1 | 1 | 1 | ||
| 10 | 1 | 1 | ||||
| 11 | 1 | 1 | 1 | 1 | ||
| 12 | 1 | 1 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 | ||
| 14 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 1 | 1 | ||||
| 16 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 1 | 1 | 1 | 1 | ||
| 19 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 1 | 1 | ||||
| 21 | 1 | 1 | 1 | 1 | ||
| 22 | 1 | 1 | ||||
| 23 | 1 | 1 | ||||
| 24 | 1 | 1 | ||||
| 25 | 1 | 1 | ||||
| 26 | 0 | 0 | 0 | 0 | 0 | 0 |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0 |
| 29 | 1 | 1 | 1 | 1 | ||
| 30 | ||||||
| 31 | 1 | 1 | 1 | 1 | ||
| 32 | 1 | 1 | 1 | 1 | ||
| 33 | 1 | 1 | 1 | 1 | ||
| 34 | 1 | 1 | ||||
| 35 | 1 | 1 | ||||
| 36 | 1 | 1 | 1 | 1 | ||
| 37 | 1 | 1 | 1 | 1 | ||
| 38 | 0 | 0 | 0 | 0 | 0 | 0 |
| 39 | 1 | 1 | ||||
| 40 | 1 | 1 | ||||
| 41 | 0 | 0 | 0 | 0 | 0 | 1 |
| 42 | 0 | 0 | 0 | 0 | 0 | 0 |
| 43 | 1 | 0 | 0 | 0 | 0 | 0 |
| 44 | 0 | 0 | 0 | 0 | 0 | |
| 45 | 0 | 0 | 0 | 0 | 0 | |
| 46 | 0 | 1 | 0 | 0 | 0 | 0 |
| 47 | 0 | 0 | 0 | 0 | 0 | 0 |
| 48 | 0 | 0 | 0 | 0 | 0 | |
| 49 | 0 | 0 | 1 | 0 | 0 | 0 |
| 50 | 0 | 0 | 0 | 0 | 1 | 0 |
| 51 | 0 | 0 | 0 | 0 | 0 | |
| 52 | 0 | 0 | 0 | 0 | 0 | |
| 53 | 0 | 0 | 0 | 0 | 0 | |
| 54 | 0 | 0 | 0 | 1 | 0 | 0 |
Taking into account the non-linearity of the parametric effects during RFA, in the present study, CCD experimental design was used to analyze the influences of thermal and electric parameters on the ablation volume. Six parameters were selected at three levels to analyze parameters sensitivity and the statistical model table (with 54 runs) was listed in Table 2. Parameters and their levels were summarized in Table 1, where (
3.Results
Some representative points including the far field point (0 mm, 15 mm,
According to the 54 runs in Table 2, the temperature field simulation was implemented in Comsol software, and the simulation time was 360 s. Figures 4 and 5 showed the main effects of the parameters
Table 3
Analysis of variance for the far field temperature
| Source | DOF | Adj_SS | Adj_MS | F-value | P-value | SS% |
| Model | 27 | 0.138602 | 0.005133 | 119.47 | 0.0 | 99.23% |
| Linear | 6 | 0.136185 | 0.022698 | 528.25 | 0.0 | 97.50% |
| A | 1 | 0.032656 | 0.032656 | 760.01 | 0.0 | 23.38% |
| B | 1 | 0.033395 | 0.033395 | 777.22 | 0.0 | 23.91% |
| C | 1 | 0.001724 | 0.001724 | 40.12 | 0.0 | 1.23% |
| D | 1 | 0.034916 | 0.034916 | 812.62 | 0.0 | 25.00% |
| E | 1 | 0.033395 | 0.033395 | 777.22 | 0.0 | 23.91% |
| F | 1 | 0.000099 | 0.000099 | 2.29 | 0.142 | 0.07% |
| Square | 6 | 0.00026 | 0.000043 | 1.01 | 0.443 | 0.19% |
| Interaction | 15 | 0.001595 | 0.000106 | 2.47 | 0.022 | 1.14% |
| Error | 25 | 0.001074 | 0.000043 | – | – | – |
| Lack-of-fit | 16 | 0.001074 | 0.000067 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 0.139676 | – | – | – | – |
| Model | 27 | 11.1469 | 0.41285 | 1420.17 | 0.0 | 99.94% |
| Linear | 6 | 11.0018 | 1.83364 | 6307.62 | 0.0 | 98.63% |
| A | 1 | 4.728 | 4.72796 | 16263.93 | 0.0 | 42.39% |
| B | 1 | 0.539 | 0.53898 | 1854.05 | 0.0 | 4.83% |
| C | 1 | 0.1752 | 0.17517 | 602.58 | 0.0 | 1.57% |
| D | 1 | 5.0201 | 5.02006 | 17268.73 | 0.0 | 45.01% |
| E | 1 | 0.539 | 0.53898 | 1854.05 | 0.0 | 4.83% |
| F | 1 | 0.0007 | 0.00069 | 2.38 | 0.136 | 0.01% |
| Square | 6 | 0.0 | 0.0 | 0.01 | 1 | 0.0% |
| Interaction | 15 | 0.0272 | 0.00181 | 6.23 | 0 | 0.24% |
| Error | 25 | 0.0073 | 0.00029 | – | – | – |
| Lack-of-fit | 16 | 0.0073 | 0.00045 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 11.1541 | – | – | – | – |
Figure 3.
The position of representative points in RFA model.
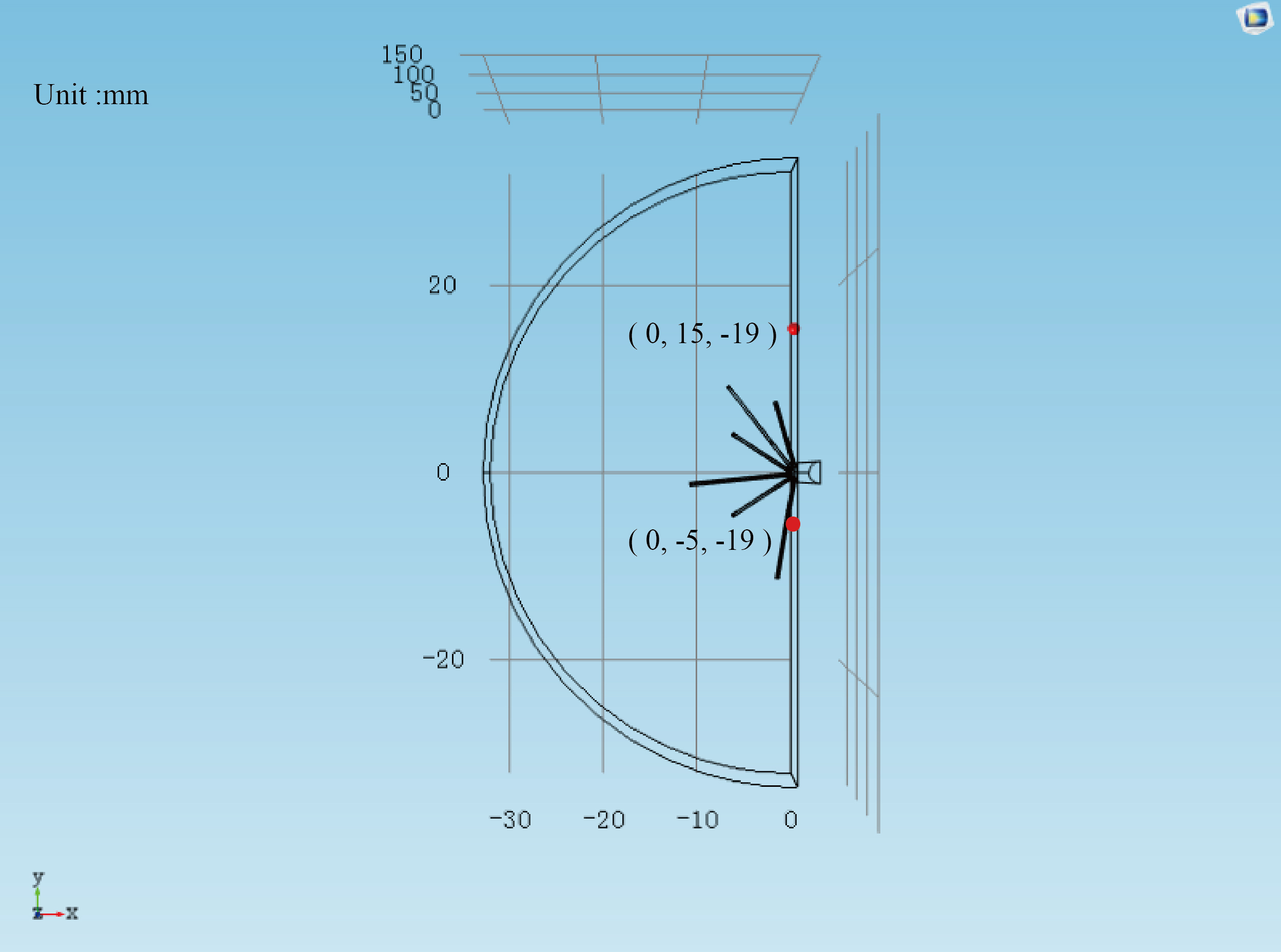
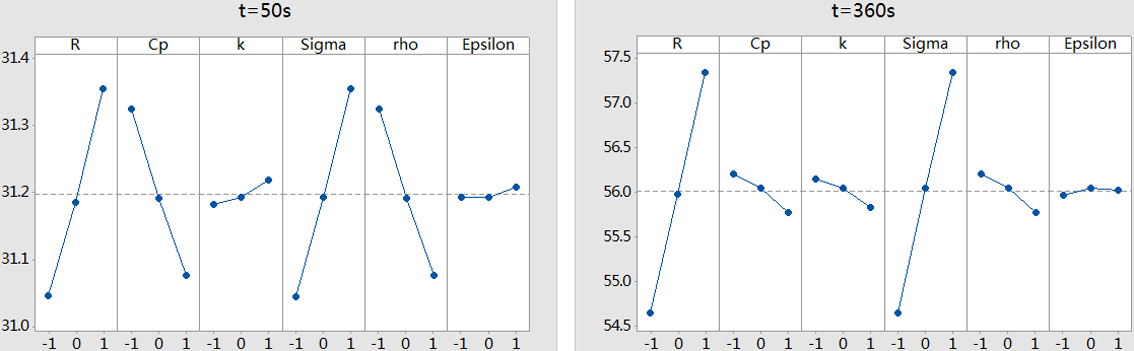
Figure 4.
The main effect of each parameter at
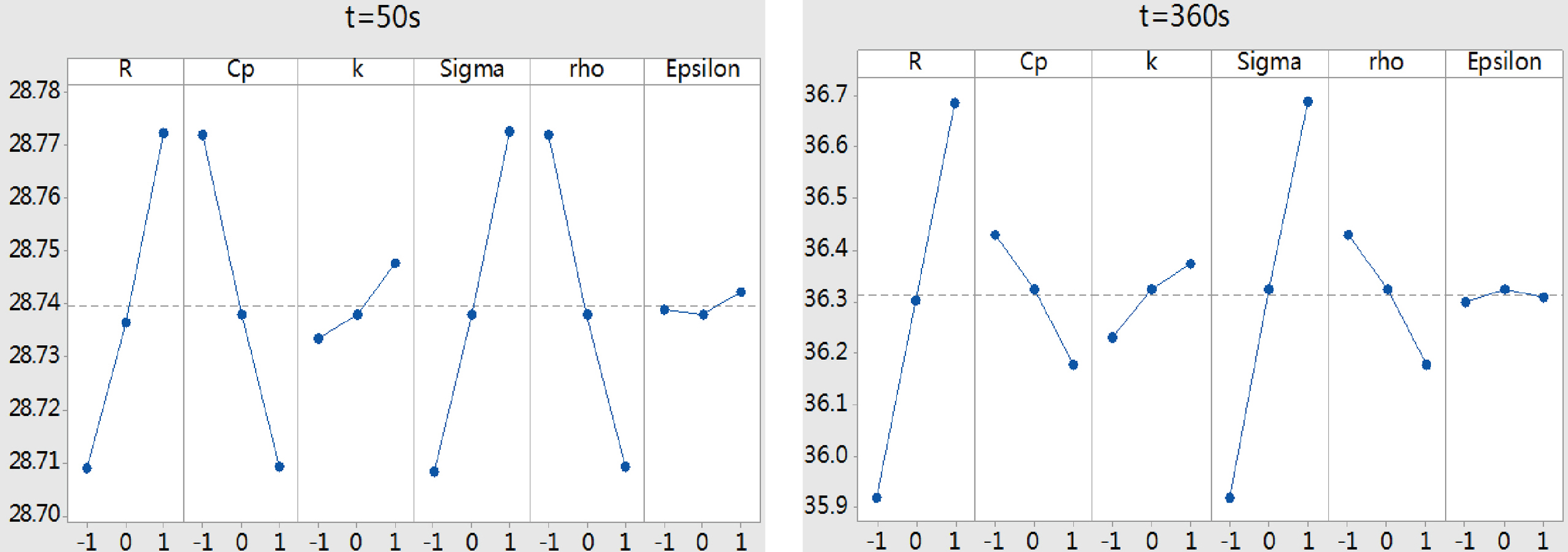
Figure 5.
The main effect of each parameter at
In order to acquire the quantitative analysis of the influences of the parameters on the ablation temperature, the variance analysis was carried out. As shown in Table 3, the F-value is the variance of the mean of the test data. The larger the value is, the more significant the parameter is. The P-value is used to determine the result of the hypothesis test [10]. If the P-value
(7)
where
Table 4
Analysis of variance for the near field temperature
| Source | DOF | Adj_SS | Adj_MS | F-value | P-value | SS% |
|---|---|---|---|---|---|---|
| Model | 27 | 2.67669 | 0.099137 | 118.29 | 0.0 | 99.22% |
| Linear | 6 | 2.62753 | 0.437921 | 522.51 | 0.0 | 97.40% |
| A | 1 | 0.7665 | 0.766497 | 914.56 | 0.0 | 28.41% |
| B | 1 | 0.51714 | 0.517135 | 617.03 | 0.0 | 19.17% |
| C | 1 | 0.0107 | 0.010699 | 12.77 | 0.0 | 0.40% |
| D | 1 | 0.81414 | 0.814139 | 971.4 | 0.0 | 30.18% |
| E | 1 | 0.51714 | 0.517135 | 617.03 | 0.0 | 19.17% |
| F | 1 | 0.00192 | 0.001921 | 2.29 | 0.143 | 0.07% |
| Square | 6 | 0.00374 | 0.000624 | 0.74 | 0.619 | 0.14% |
| Interaction | 15 | 0.03105 | 0.00207 | 2.47 | 0.022 | 1.15% |
| Error | 25 | 0.02095 | 0.000838 | – | – | – |
| Lack-of-fit | 16 | 0.02095 | 0.00131 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 2.69765 | – | – | – | – |
| Model | 27 | 125.645 | 4.6535 | 383.11 | 0.0 | 99.76% |
| Linear | 6 | 123.651 | 20.6085 | 1696.65 | 0.0 | 98.18% |
| A | 1 | 58.098 | 58.0984 | 4783.12 | 0.0 | 46.13% |
| B | 1 | 1.587 | 1.5868 | 130.64 | 0.0 | 1.26% |
| C | 1 | 0.842 | 0.8415 | 69.28 | 0.0 | 0.67% |
| D | 1 | 61.51 | 61.5095 | 5063.95 | 0.0 | 48.84% |
| E | 1 | 1.587 | 1.5868 | 130.64 | 0.0 | 1.26% |
| F | 1 | 0.028 | 0.028 | 2.31 | 0.141 | 0.02% |
| Square | 6 | 0.006 | 0.001 | 0.08 | 0.997 | 0.0% |
| Interaction | 15 | 0.597 | 0.0398 | 3.27 | 0.004 | 0.47% |
| Error | 25 | 0.304 | 0.0121 | – | – | – |
| Lack-of-fit | 16 | 0.304 | 0.019 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 125.949 | – | – | – | – |
Figure 6.
The SS% trendlines for each parameter at far field point.
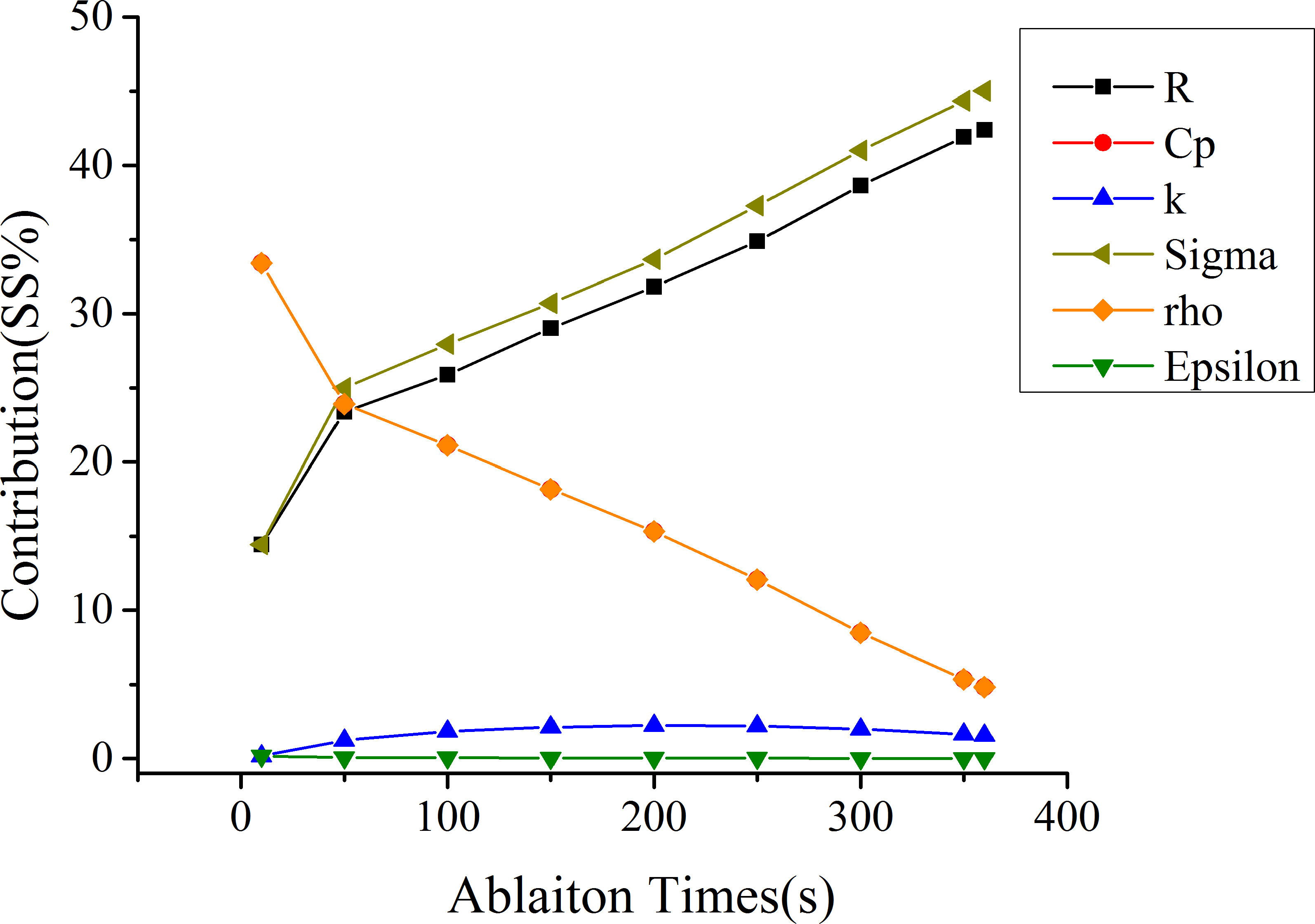
Figure 7.
The SS% trendlines for each parameter at near field point.
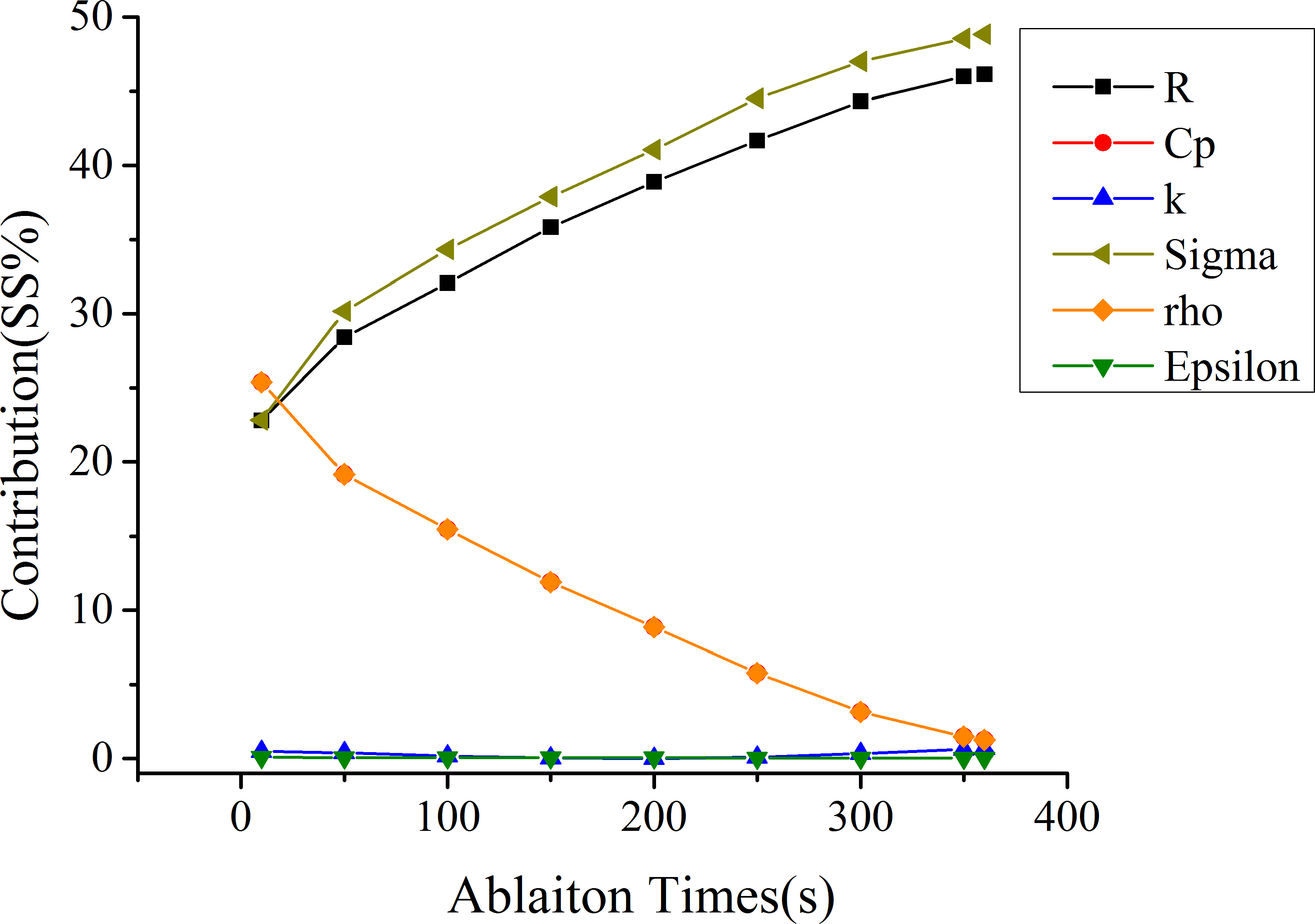
Figure 8.
The main effect of different parameters on the volume of 54

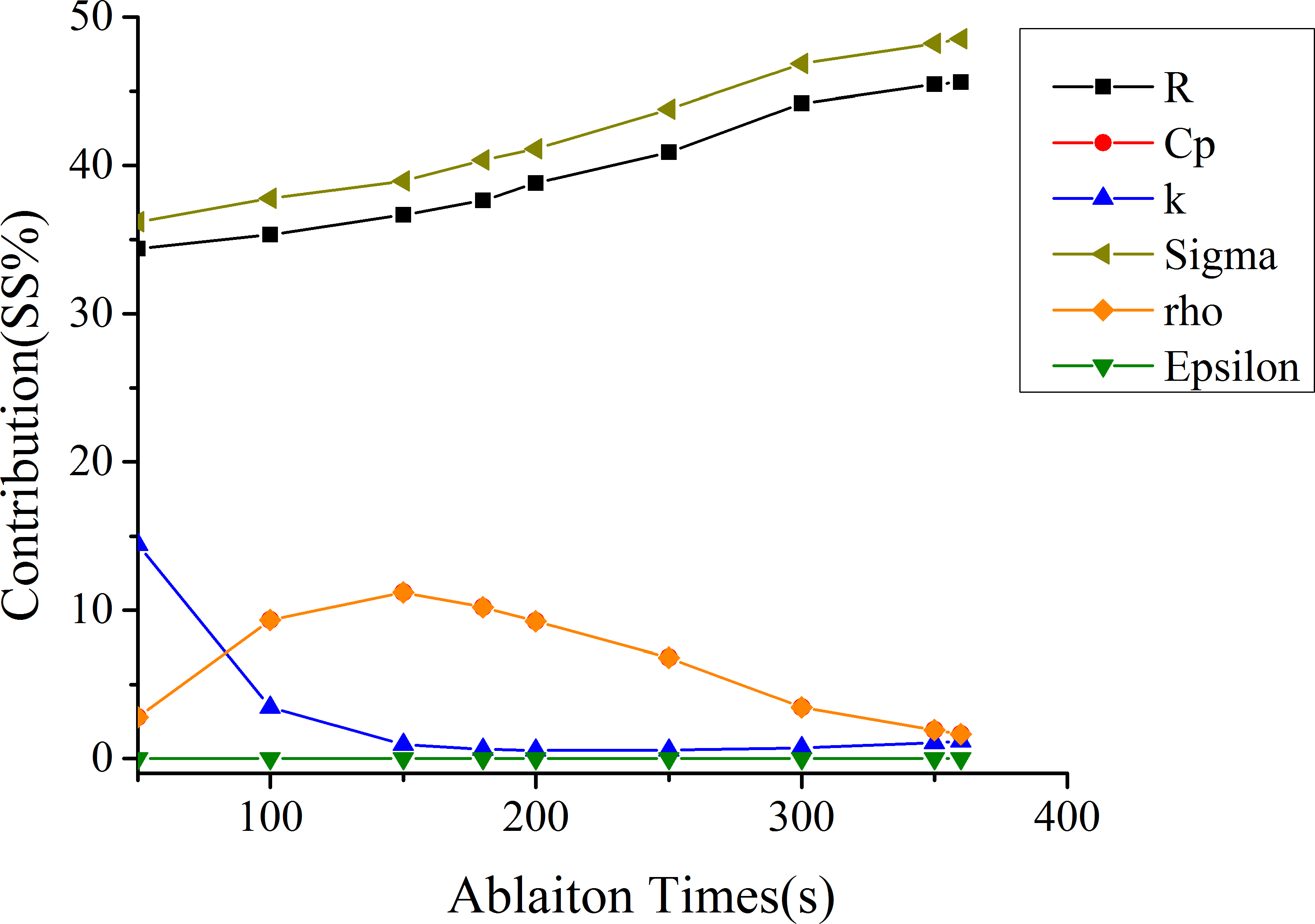
Figure 9.
The contribution rate of each parameter to 54
The SS% values of single parameter in the far field and near field were shown in Tables 3 and 4. The Interaction and Square results between mentioned parameters were also listed. The sensitivity of single parameter, interaction and square item at
This paper also showed the SS% trendlines to more clearly illustrate the changes of the parameter sensitivity during the RFA period. As could be seen in Figs 6 and 7, in the far field, the SS% of Cp and rho ranged from 33.4% to 4.8%; the SS% of Sigma and
However, the sensitivity analysis merely based on individual points had some particularity. This study further discussed the sensitivity of the parameters on thermal coagulation zone, which was the main output of RFA. 50
Table 5
Analysis of variance for 54
| Source | DOF | Adj_SS | Adj_MS | F-value | P-value | SS% |
|---|---|---|---|---|---|---|
| Model | 27 | 398686 | 14766 | 4427.41 | 0.0 | 99.98% |
| Linear | 6 | 379695 | 63282 | 18974.31 | 0.0 | 95.22% |
| A | 1 | 140829 | 140829 | 42225.47 | 0.0 | 35.32% |
| B | 1 | 37234 | 37234 | 11163.93 | 0.0 | 9.34% |
| C | 1 | 13748 | 13748 | 4122.26 | 0.0 | 3.45% |
| D | 1 | 150648 | 150648 | 45169.57 | 0.0 | 37.78% |
| E | 1 | 37234 | 37234 | 11163.93 | 0.0 | 9.34% |
| F | 1 | 2 | 2 | 0.7 | 0.409 | 0.00% |
| Square | 6 | 2358 | 393 | 117.83 | 0.0 | 0.59% |
| Interaction | 15 | 13620 | 908 | 272.24 | 0.0 | 3.42% |
| Error | 25 | 83 | 3 | – | – | – |
| Lack-of-fit | 16 | 83 | 5 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 398769 | – | – | – | – |
| Model | 27 | 3496230 | 129490 | 5531.04 | 0.0 | 99.98% |
| Linear | 6 | 3447637 | 574606 | 24543.72 | 0.0 | 98.59% |
| A | 1 | 1594073 | 1594073 | 68089.24 | 0.0 | 45.59% |
| B | 1 | 57771 | 57771 | 2467.62 | 0.0 | 1.65% |
| C | 1 | 40849 | 40849 | 1744.82 | 0.0 | 1.17% |
| D | 1 | 1697170 | 1697170 | 72492.9 | 0.0 | 48.53% |
| E | 1 | 57771 | 57771 | 2467.62 | 0.0 | 1.65% |
| F | 1 | 3 | 3 | 0.14 | 0.71 | 0.00% |
| Square | 6 | 385 | 64 | 2.74 | 0.035 | 0.0% |
| Interaction | 15 | 2604 | 174 | 7.42 | 0.0 | 0.07% |
| Error | 25 | 585 | 23 | – | – | – |
| Lack-of-fit | 16 | 585 | 37 | – | – | – |
| Pure error | 9 | 0.0 | 0.0 | – | – | – |
| Total | 52 | 3496816 | – | – | – | – |
Figure 8 illustrated the main effects of the parameters on 54
As shown in Fig. 9, the SS% trendlines of 54
4.Discussion
Based on the RFA experiment and FEM model of vitro phantom, the parameters that have a significant influence on ablation zone size of the liver tissue were analyzed. There are two primary contributions: (1) this study has established an accurate RFA model based on the actual power profile and equivalent resistance; (2) because the non-linearity variation of the liver tissue parameters during RFA process, six parameters with three levels each were selected to analyze the sensitivity to ablation temperature and lesion volume. Parameter sensitivity analysis results, presented in this study, could provide a priori information for clinical practitioners and simplify the finite element modeling of liver tumor RFA.
Although many methods can carry out parameter sensitivity analysis, the efficiency of different methods varies widely. In order to estimate the effects of tissue parameters to ablation zone, full factorial experimental design can be used to provide the optimum results by testing all the possible combinations of the parameters. Johansson et al. [19] used a 2
At present, some scholars have conducted sensitivity analysis on the parameters during RFA process. However, there are still some differences between the present sensitivity analysis results. Hall et al. [21] indicated that blood perfusion, electrical conductivity and the cell death model were the most important factors for estimating the ablation zone size in liver RFA models. Similarly, our results obviously demonstrated that electric conductivity was one of the important parameters. Monsalvo et al. [22] analyzed how the variations of the different parameters influenced the temperature in liver tissue through using the complex Taylor series expansion (CTSE) finite element method. The authors have found that the thermal and electrical conductivity of the healthy liver tissue have extremely important influence on the final temperature of RFA simulation models. According to what we has mentioned above, it is clear that electric conductivity is one of the most important parameters, thus confirming the results of our study. Moreover, the insensitivity parameters of the lesion size cannot be focused to simplify the RFA model of liver tumor. However, due to RFA model differences, analysis parameter differences and experimental environment differences (e.g. in vitro experiments or in vivo experiments) during sensitivity analysis, there are a few differences between our results and the previous studies.
Although some important discoveries have been revealed in this paper, there are also limitations. Firstly, the proposed RFA model for predicting the temperature did not consider the cooling effects of large blood vessels. Actually, during RFA of liver tumor, the cooling influence of the large blood vessel (i.e., the blood vessel with the diameter larger than 3 mm) has a remarkable impact on lesion volume [23]. This issue will be taken into account in the future work. Secondly, CCD experimental design needed complex experimental combinations in contrast with the Taguchi’s orthogonal array design. Thirdly, 54
5.Conclusions
In this paper, based on the temperature-controlled RFA simulation model, the influences of the electro-thermal parameters on the temperature distributions and ablation volume were analyzed. According to the main effects and the SS% values, the sensitive parameters were obtained. It can be concluded that the size of the RFA zone was mainly dependent on Sigma and R, and these parameters were positively correlated with ablation zone. The sensitivity of Cp and rho on the ablation zone was reduced over time, and these parameters were negatively correlated with the ablation zone; Epsilon had little effect on the ablation zone during the RFA period. There was no good agreement for the parameter
In conclusion, the most important parameters in predicting the RFA volume are electric conductivity and bioelectric impedance. These results can provide a scientific basis for the feedback regulation of the sensitivity parameters. These extended applications would be the topic of our future study.
Acknowledgments
This work was supported by Beijing Natural Science Foundation [Grant No. 7174279]; National Natural Science Foundation of China [Grant No. 71661167001]; China P-ostdoctoral Science Foundation [Grant No. 2017M620566]; and Postdoctoral Research Fund of Chaoyang District, Beijing [172858].
Conflict of interest
None to report.
References
[1] | Clasen S, Rempp H, Schmidt D, et al. Multipolar radiofrequency ablation using internally cooled electrodes in ex vivo bovine liver: Correlation between volume of coagulation and amount of applied energy. European Journal of Radiology (2012) ; 81: (1): 11113. doi: 10.1016/j.ejrad.2010.10.031 |
[2] | Berjano EJ, Hornero F. Thermal-electrical modeling for epicardial atrial radiofrequencyablation. IEEE Transactions on Biomedical Engineering (2004) ; 51: (8): 1348-1357. |
[3] | Matschek J, Himmel A, Haeseler FV, et al. Mathematical modelling and sensitivity analysis of multipolar radiofrequency ablation in the spine. IFAC Papers Online (2015) ; 48: (20): 243-248. doi: 10.1016/j.mbs.2016.06.008 |
[4] | Zhang M. Study on surgical planning system and key technology of tumor thermal ablation. Beijing University of Technology, (2016) . |
[5] | Nie XH. Study on temperature field of radiofrequency ablation of spinal tumor. Beijing University of Technology, (2016) . |
[6] | Jin C, He Z, Liu J. MRI-based finite element simulationon radiofrequency ablation of thyroid cancer. Computer Methods & Programs in Biomedicine (2014) ; 113: (2): 529-538. |
[7] | Huang W, Luo HY, Pan JH, et al. Construction model of temperature-controlled radiofrequency ablation based on CT images of liver. Journal of Interventional Imaging and Therapeutics (2014) ; 11: (8): 532-536. |
[8] | Rossmann C, Haemmerich D. Review of temperature dependence of thermal properties, dielectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Critical Reviews™ in Biomedical Engineering (2014) ; 42: (6). doi: 10.1615/CritRevBiomedEng.2015012486 |
[9] | Trujillo M, Berjano E. Review of the mathematical functions used to model the temperature dependence of electrical and thermal conductivities of biological tissue in radiofrequency ablation. International Journal of Hyperthermia (2013) ; 29: (6): 590-597. doi: 10.3109/02656736.2013.807438 |
[10] | Akbarzadeh M, Rashidia S, Bovand M, Ellahi R. A sensitivity analysis on thermal and pumping power for the flow of nanofluid inside a wavy channel. Journal of Molecular Liquids (2016) ; 220: : 1-13. |
[11] | Cai Y, Xing Y, Hu D. Study on sensitivity analysis. Journal of Beijing Normal University (Natural Science Edition) (2008) ; 44: (1): 1. |
[12] | Schweiger M, Arridge SR, Hiraoka M, et al. The finite element method for the propagation of light in scattering media: Boundary and source conditions. Medical Physics (1995) ; 22: (11): 1779-1792. doi: 10.1118/1.597634 |
[13] | Li JX, Zhang WJ, Zhang SX. Finite element method and application status. Science and Technology Innovation Guide (2012) ; 31: : 120-121. |
[14] | Cavagnaro M, Pinto R, Lopresto V. Numerical models of microwave thermal ablation procedures. Microwave Conference, IEEE (2014) ; 480-483. doi: 10.1109/eumc.2014.6986475 |
[15] | Haemmerich D. Mathematical modeling of impedance controlled radiofrequency tumor ablation and ex-vivo validation. International Conference of the IEEE Engineering in Medicine and Biology, IEEE (2010) ; 1605-1608. doi: 10.1109/iembs.2010.5626659 |
[16] | Peng T, O’Neill D, Payne S. Mathematical study of the effects of different intrahepatic cooling on thermal ablation zones. International Conference of the IEEE Engineering in Medicine and Biology Society, IEEE (2011) ; 6866-6869. doi: 10.1109/iembs.2011.6091693 |
[17] | Sun DH, Qian F, Sun G, et al. Clinical application of radiofrequency ablation. Jilin Medical Journal (2012) ; 33: (13): 2823-2825. |
[18] | Haase S, Süss P, Schwientek J, et al. Radiofrequency ablation planning: An application of semi-infinite modelling techniques. European Journal of Operational Research (2012) ; 218: (3): 856-864. doi: 10.1016/j.ejor.2011.12.014 |
[19] | Johansson JD, Eriksson O, Wren J, et al. Radio-frequency lesioning in brain tissue with coagulation-dependent thermal conductivity: Modelling, simulation and analysis of parameter influence and interaction. Medical and Biological Engineering and Computing (2006) ; 44: (9): 757-766. doi: 10.1007/s11517-006-0098-1 |
[20] | Jamil M, Ng EYK. Quantification of the effect of electrical and thermal parameters on radiofrequency ablation for concentric tumour model of different sizes. Journal of Thermal Biology (2015) ; 51: : 23-32. doi: 10.1016/j.jtherbio.2015.03.002 |
[21] | Hall SK, Ooi EH, Payne SJ. Cell death, perfusion and electrical parameters are critical in models of hepatic radiofrequency ablation. International Journal of Hyperthermia (2015) ; 31: (5): 538-550. doi: 10.3109/02656736.2015.1032370 |
[22] | Monsalvo JF, García MJ, Millwater H, et al. Sensitivity analysis for radiofrequency induced thermal therapies using the complex finite element method. Finite Elements in Analysis and Design (2017) ; 135: : 11-21. doi: 10.1016/j.finel.2017.07.001 |
[23] | Poch FGM, Rieder C, Ballhausen H, et al. The vascular cooling effect in hepatic multipolar radiofrequency ablation leads to incomplete ablation ex vivo. International Journal of Hyperthermia (2016) ; 32: (7): 749-756. |
[24] | Zhang B, Moser MAJ, Zhang EM, et al. A review of radiofrequency ablation: Large target tissue necrosis and mathematical modelling. Physica Medica (2016) ; 32: (8): 961-971. doi: 10.1016/j.ejmp.2016.07.092 |
[25] | Pearce JA. Comparative analysis of mathematical models of cell death and thermal damage processes. International Journal of Hyperthermia (2013) ; 29: (4): 262-280. doi: 10.3109/02656736.2013.786140 |




