Optimization of a passively suspended injection impeller for Left ventricular assist device

1.Introduction

Various types of implantable Left ventricular assist devices (LVADs) have been applied in the treatment of end-stage heart failure [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Currently, the third-generation blood pumps with noncontact bearings, such as magnetic or hydrodynamic bearings, have been developed to improve the durability of the devices. A blood pump with a magnetic bearing levitates the impeller using magnetic force generated by a controllable electromagnet, which requires displacement sensors and complex control systems [11, 12, 13]. In contrast, a blood pump with a hydrodynamic bearing levitates the impeller using the localized high pressure generated either by the grooves or the tapered blade surfaces based on lubrication theory [14, 15]. As the hydrodynamic bearing is a passive bearing, the blood pump has high reliability since additional displacement sensors or control components are not required. However, present blood pumps with hydrodynamic bearings require very small gaps between the impeller and the housing, resulting in high manufacturing cost and shear stress. We previously developed a rotary blood pump with a passively levitated impeller and a large bearing gap between the housing and the impeller in the range of 0.6 mm [16]. The impeller was levitated by the force generated by the injection flow. The large bearing gap was beneficial to reduce the shear stress and the cost of the device. The axial movement of the impeller was measured quantitatively, while the radial suspension of impeller was evaluated qualitatively in the previous work. In addition, the radial motion of the impeller depends on the radial suspension force, centrifugal force, radial magnetic force, and radial hydraulic force. As the radial suspension force provides the only positive stiffness to suspend the impeller, it is a critical factor to affect the radial stability.

The purpose of the present study is to determine the optimal injection angle of the impeller to improve its radial stability by increasing the radial suspension force. As the radial and axial suspension forces generated by the single injection channel were equal, the axial suspension force was chosen as the evaluation parameter. First, the impellers with different injection angles were numerically calculated with a focus on enlarging the axial suspension force. Second, the radial motion of impeller was experimentally measured with laser displacement sensors to verify the effectiveness of numerical analysis.

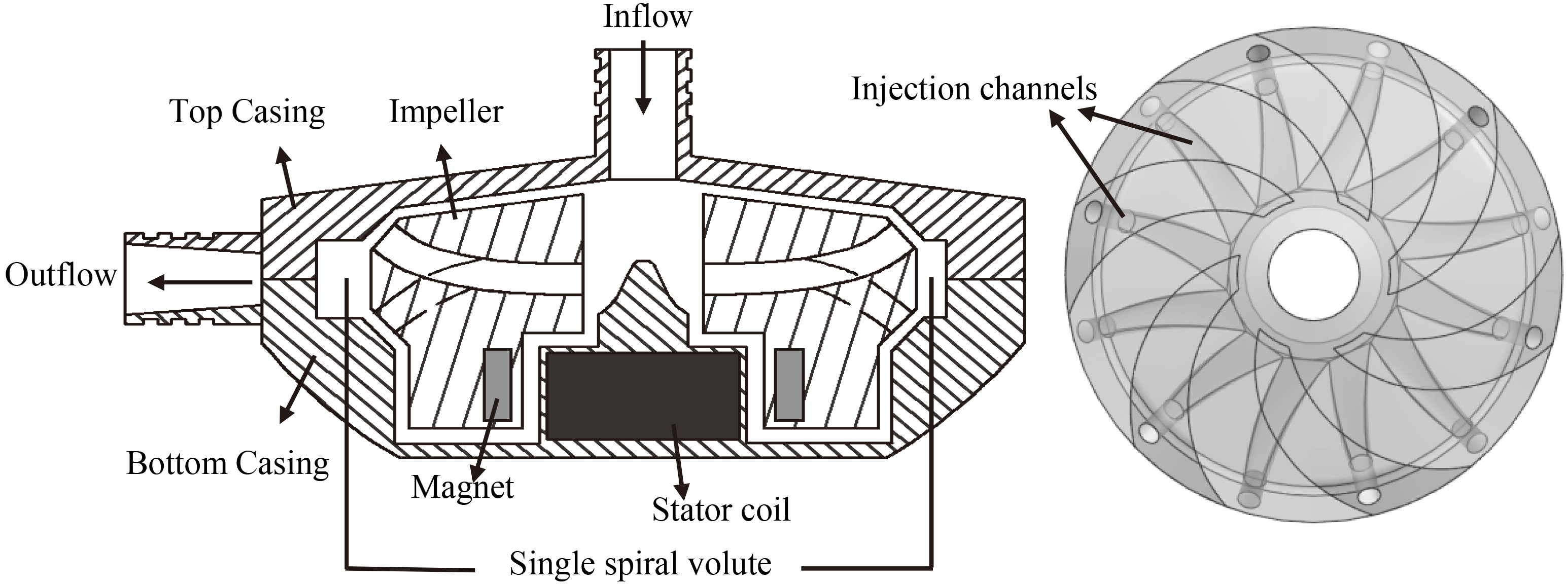
Figure 1.

Structure of the developed centrifugal blood pump and impeller.

2.Materials and methods

2.1LVAD with a passively suspended impeller

Figure 1 illustrates the developed rotary blood pump with a passively suspended impeller. The diameter of the pump casing is 80 mm, and its height is 27 mm. The total axial or radial gap between the impeller and the casing is 0.6 mm. The Neodymium Iron Boron permanent magnets are sealed in the impeller, and the stator coils are placed in the pump casing. The impeller is driven through the electromagnetic interaction between the magnets and the coils. The semi-open impeller has twelve injection channels. The outlets of six injection channels are distributed on the blades while the other six outlets are placed on the lower sloping surface of impeller. When the impeller rotates, the blood is forced to accelerate along the channels and injected into the gaps between the impeller and the casing, which produces localized high pressure to generate the suspension force. Since the angles of acting surfaces are 45 degrees, the radial and axial suspension forces generated by the single injection channel are equal.

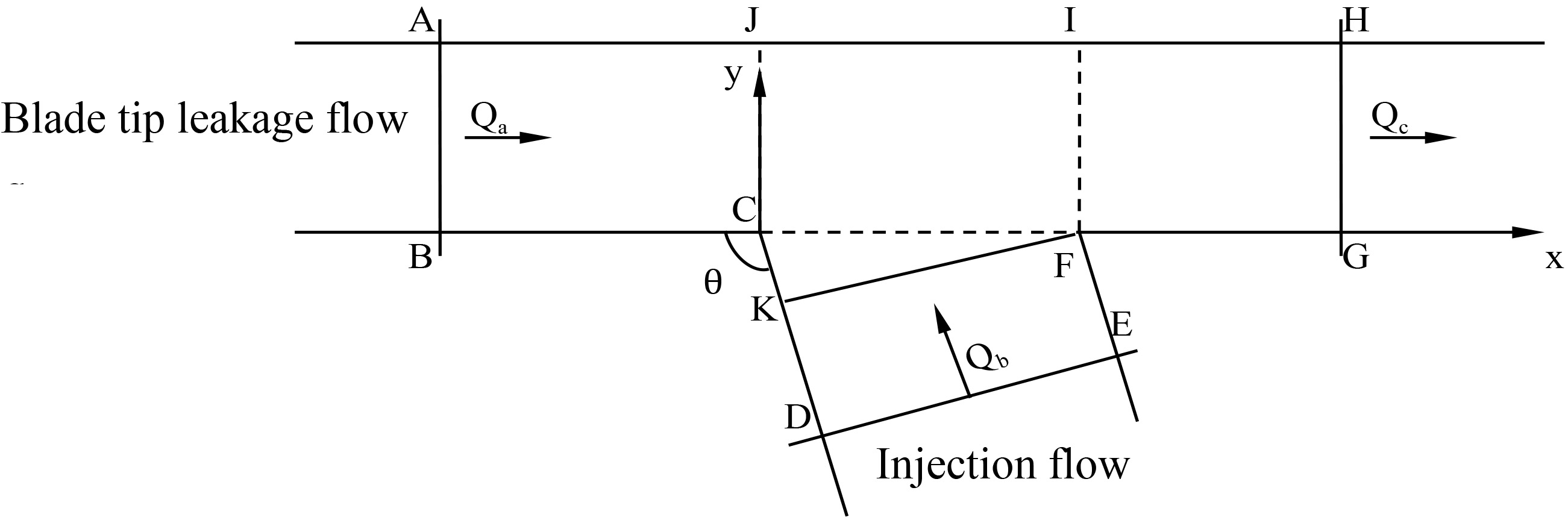
Figure 2.

Two-dimensional analysis of region around the outlet of injection channel.

2.2Computational fluid dynamics analysis

Figure 2 shows the 2D analysis of the region around the outlet of injection channel. The flow from the injection channel converges into the blade tip leakage flow. The momentum equation in the x direction for control volume ABCDEFGHA can be written as follows:

(1)

Vc⁢Qcg-Va⁢Qag-Vb⁢Qbg⁢cos⁡θ=Pa⁢Aaρ⁢g+Pb⁢Abρ⁢g⁢cos⁡θ-Pc⁢Acρ⁢g

where Q is the flow rate, P is the average pressure of section, V is the mean flow velocity of section, and θ is injection angle of channel. The subscript a, b, c represents section AB, DE, GH respectively.

According to the Eq. (1), Pc is inversely proportional to the injection angle θ (0∘⩽θ⩽ 180∘). The increase of the localized pressure Pc would generate high suspension force. Therefore, the optimization of injection angle is an effective way to increase the suspension force.

Numerical analysis with computational fluid dynamics (CFD) was employed to investigate the injection angle of the impeller. As the radial and axial suspension forces generated by the single injection channel were equal, the axial suspension force was chosen ashe evaluation parameter. The computational mesh was generated by the software package Hypermesh (Altair, Inc., USA), and the Fluent 15.0 (Ansys, Inc., USA) was applied to perform the numerical analysis. The motion of the impeller was incorporated using the multiple reference frame (MRF) approach. The rotation speed of impeller was set to 2000 rpm. No-slip boundary conditions were applied to the walls. The working fluid was assumed to be blood with a density of 1055 kg/m3 and a viscosity of 0.0035 Pa⋅s. The flow rate of inlet was set to 5 L/min with uniform velocity, and the pressure of outlet was set to 0 mmHg.

Considering the constraint of the impeller structure, the injection angle was increased from 30 to 150 degrees in increments of 10 degrees. Impellers with injection angles of 60∘, 90∘, and 120∘ are shown in Fig. 3. The axial bearing gap z was defined as 0 mm when the impeller was concentrically contacted with bottom casing. The total axial gap between the impeller and the casing was 0.6 mm. Therefore, when the bearing gap was 0.3 mm, the impeller was located at the center of the pump cavity. In order to analyze the suspension force acting on the impeller, the numerical analysis was performed at the bearing gaps of 0.15 mm and 0.3 mm, respectively. The axial forces acting on the impeller were numerically obtained at the different bearing gaps, and the difference between the two calculated values was the residual suspension force.

Figure 3.

Impellers with different injection angles. (a) 60 degrees. (b) 90 degrees. (c) 120 degrees.

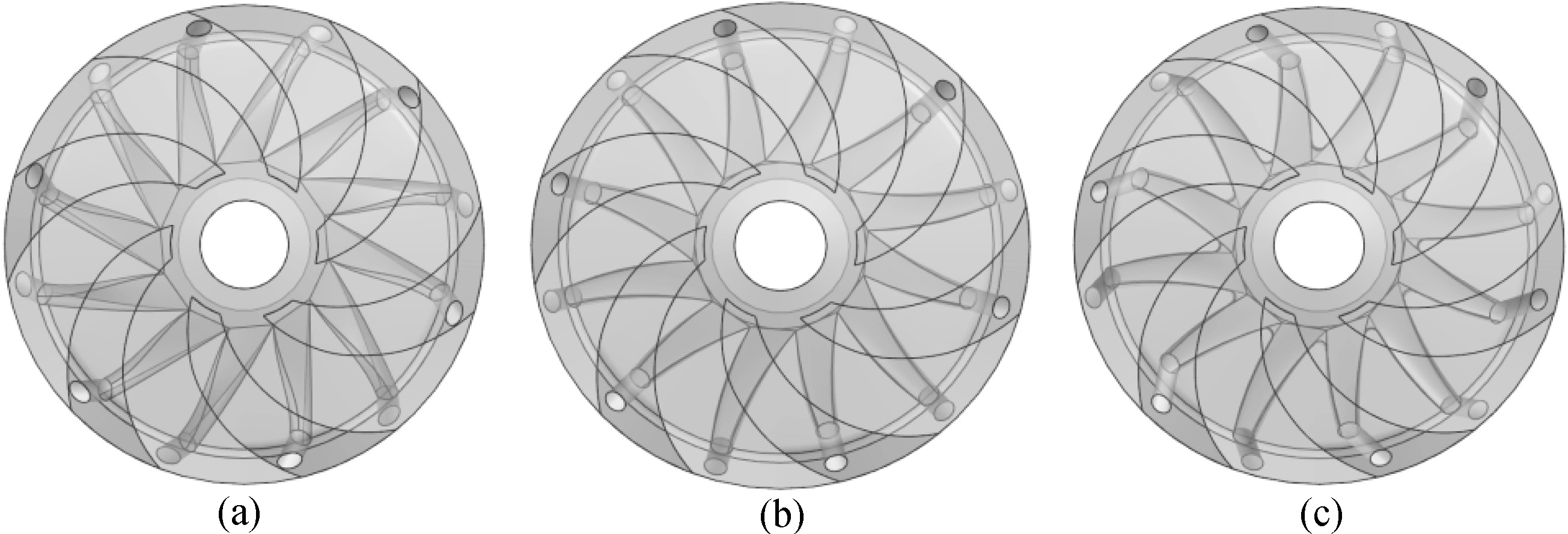
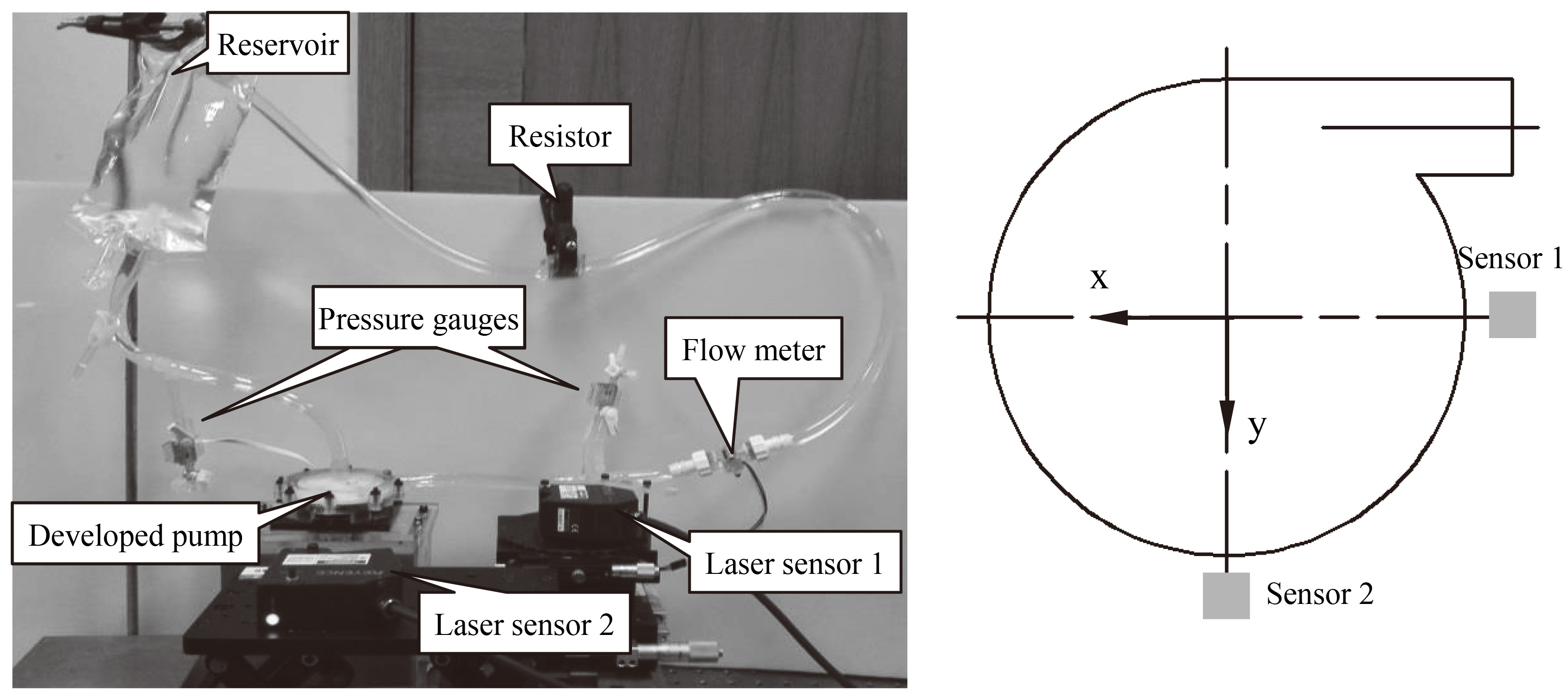
Figure 4.

Measurement system for measuring the impeller trajectory using two laser displacement sensors.

3.Results

Figure 5a shows the numerically obtained axial force versus injection angle when the bearing gaps were set to 0.15 mm and 0.3 mm. The axial force increased corresponding to the reduction of the axial bearing gap, which indicated that the injection flow was effective to produce the suspension force. Figure 5b shows the residual axial suspension force versus the injection angle. When the bearing gap changed from 0.15 mm to 0.3 mm, the residual axial suspension force had a maximum value at the injection angle of 60 degrees.

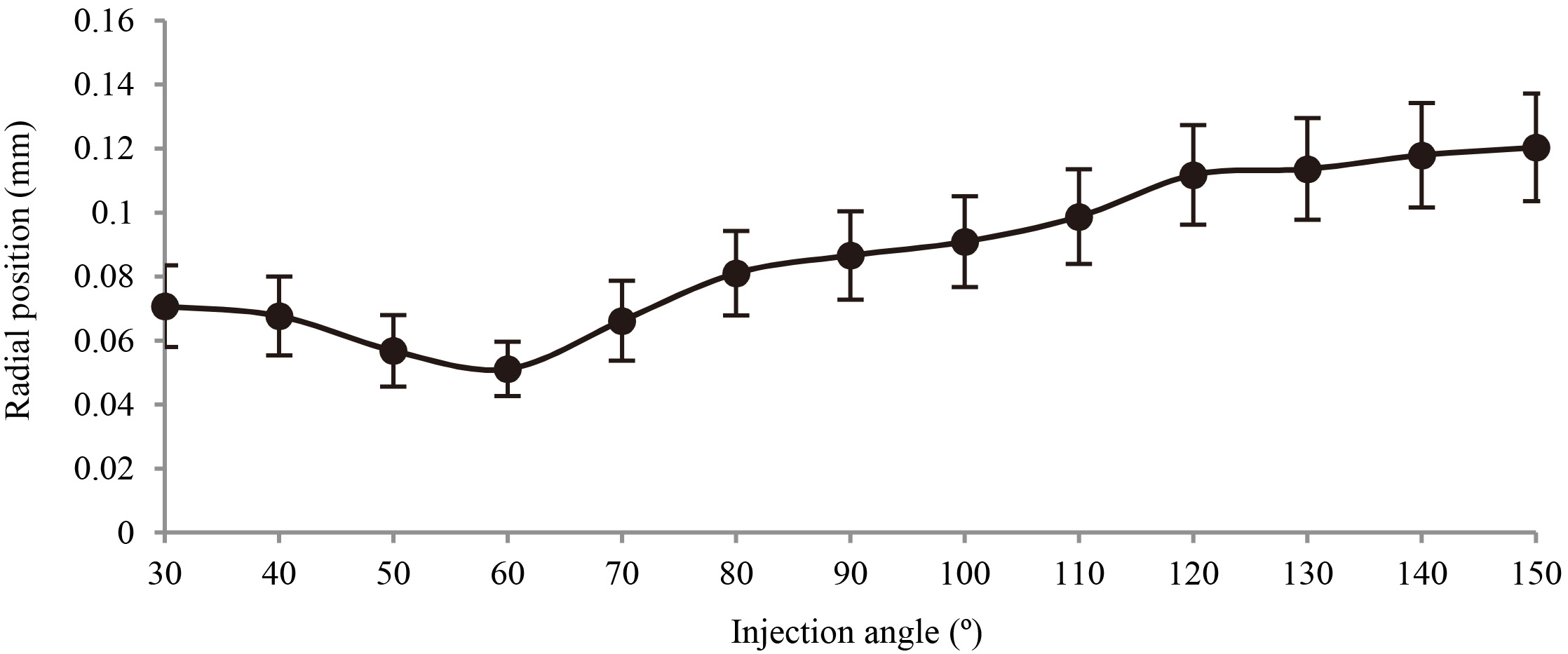
Figure 6 shows the mean impeller positions and radii of the orbit for the impellers with different injection angles. The solid circle indicates the mean impeller position, and the bar represents the radius of orbit. It was observed that the mean impeller position and the radius of orbit had a minimum value when the injection angle of impeller was 60 degrees. The measured orbital radius of the optimal model was 8.5 μm, and the mean impeller position was 51.1 μm.

Figure 5.

(a) Numerically obtained axial force acting on the impeller when the bearing gaps were set to 0.15 mm and 0.3 mm. (b) Residual axial suspension force versus the injection angle.

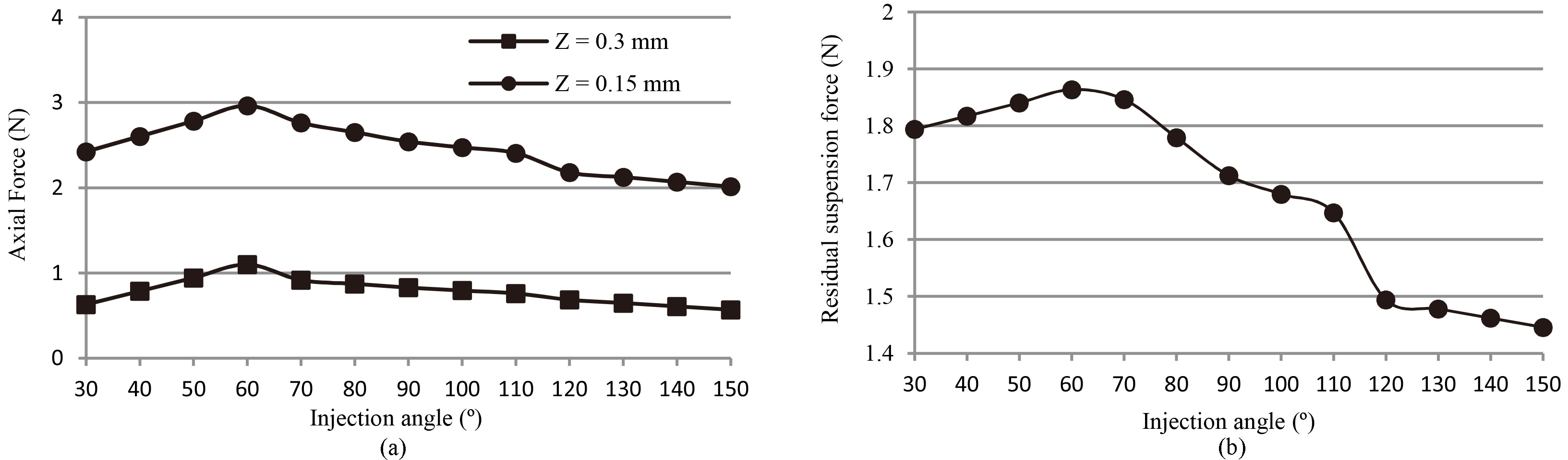
Figure 6.

Mean impeller position and radius of the orbit versus the injection angle.

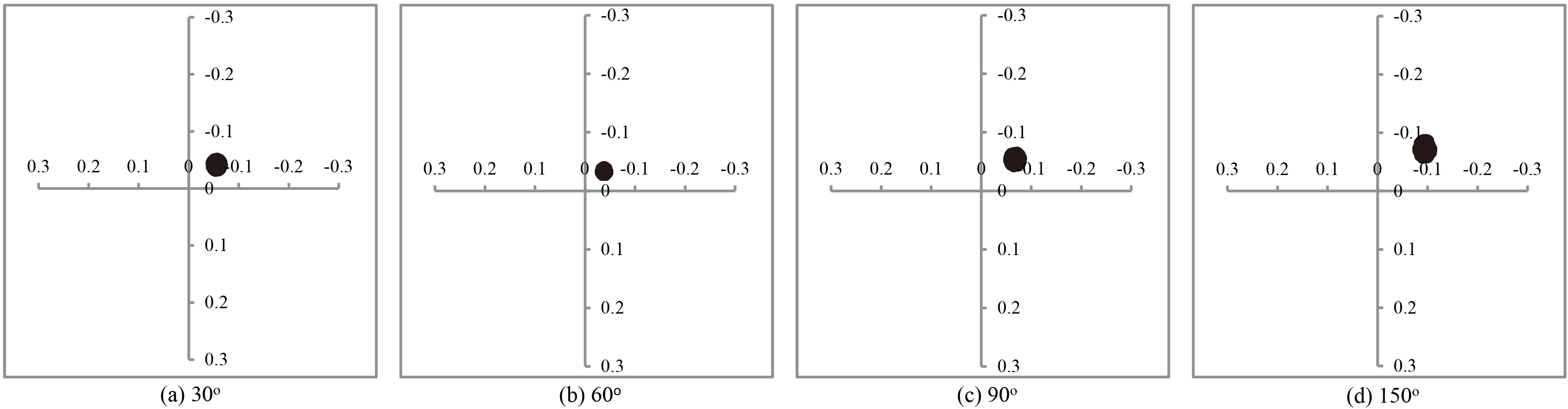
Four typical models were chosen to indicate the radial motion of impeller, as shown in Table 1 . The injection angles of the four impellers were 30∘, 60∘, 90∘, and 150∘, respectively. Figure 7 shows the examples of the radial trajectory of the impeller. The origin of the coordinate system corresponds to the center of the pump. It was found that the impeller had a steady radial motion for each model.

4.Discussion

From Eq. (1), the maximum suspension force was achieved when the injection angle was 30 degrees. Based on the results of numerical simulation, the maximum suspension force was obtained when the injection angle was 60 degrees. This inconsistency might be caused by the simplification of 2D analysis, which neglected the complicated flow pattern around the injection area in the practical situation. However, the 2D analysis was still an effective approach to provide foundation to optimize the injection angle of impeller.

After the optimization of the impeller, the maximum residual axial suspension force was about 1.86 N, an increase of about 60 percent comparing to previous research. The radial suspension force increased along with the increase of the axial suspension force. As the radial suspension force provides positive stiffness to suspend the impeller, the higher suspension force contributes to the improvement of radial stability of impeller. Although the radial stability of previous impeller was not evaluated quantitatively, the radial stability of optimal impeller was obviously superior to that of previous model. In addition, the most stable radial motion of impeller was experimentally obtained when the injection angle of impeller was 60 degrees, which was consistent with the result of numerical analysis. Therefore, the effectiveness of the numerical analysis was validated.

Figure 7 indicates the impeller moving toward the cutwater of the pump. The reason was that the velocity decreased as the fluid diffused from the cutwater into the outlet. Based on the Bernoulli equation, the reduction in pressure would occur when the fluid speed increases. Hence, low pressure around the cutwater produced a low pressure force. As a result, a net radial hydraulic force pointed towards the cutwater, which was a typical phenomenon for centrifugal pumps [17].

Figure 7.

Impeller trajectories for the model 1, 2, 3, and 4.

For a blood pump with a noncontact bearing, the radial stability of the impeller was a critical factor to affect the hemolysis [18]. When the radial motion of the impeller was in the stable mode, it was beneficial to reduce the shearing stress and the hemolysis. The hemolysis test of the prototype will be conducted in the future.

5.Conclusions

In this study, the injection angle of impeller was numerically investigated and experimentally evaluated to improve radial stability. According to the results of numerical analysis, the impeller with injection angle of 60 degrees generated the maximum radial suspension force. Through the results of radial motion measurement test, the impeller with injection angle of 60 degrees had the most stable radial motion, which verified the effectiveness of numerical analysis. In conclusion, the injection angle of impeller could be optimized to improve its radial stability.

Conflict of interest

None to report.