Design of a wearable cable-driven upper limb exoskeleton based on epicyclic gear trains structure

1.Introduction

Many countries, including Japan, Italy, and China are experiencing demographic shifts as their populations age [1]. Some basic activities of daily living (ADLs) are difficult for elderly people to complete independently due to declines in motor function. Researchers are developing wearable exoskeleton robots to help the aged and disabled with completing ADLs [2, 3, 4, 5, 6, 7, 8, 9]. Ideally, wearable exoskeleton should be ergonomical, light-weight, highly reliable and accurate, very stiff, and inexpensive [2].

Many researchers have been investigating and developing a variety of types of wearable exoskeletons. Sugar et al. [2] developed a wearable exoskeleton robot named RUPERT to assist with the rehabilitation of arm functions, after a loss of function. RUPERT is actuated by pneumatic muscles through a serial link mechanism. Martinez et al. [3] designed a five degree of freedoms (DOF) upper limb exoskeleton actuated by DC motors and pneumatic muscles; its actuators were placed on an external base to decrease the mass and inertia of the exoskeleton by transmitting power via cables. Although the pneumatic muscle can provide flexible driving torques, these wearable exoskeleton systems actuated by pneumatic muscles with air cylinder may be difficult for patients to carry. Serea et al. [4] developed a hybrid FES-Electric upper arm wearable exoskeleton. However, FES creates muscle fatigue problems that have not yet been solved [5]. Most of these exoskeletons have a serial structure, which is easy to control and has a large workspace. However, each DOF of the serial link mechanism is driven by a single link, which makes the serial mechanism less stiff when compared with the parallel mechanism. This results in the carrying capacity of serial mechanism being weaker than in the parallel mechanism.

The cable-driven mechanism allows the system to be quieter and have high accuracy and smooth transmissions which are necessary for wearable exoskeletons [6, 7, 8, 9]. Mao et al. [6, 7] developed a cable driven arm exoskeleton (CAREX) for upper arm rehabilitation and Shao et al. [8] designed a 3-DOF cable-driven upper arm exoskeleton. However, the cable-driven parallel mechanism with flexible links is hard to be controlled. Ball et al. [9], proposed a traditional serial structure 5-DOF rehabilitation robot with the driving energy transmitted by cables. It can be controlled easily, however, it still exhibits the shortcomings of serial mechanism.

To overcome these problems, a cable-driven upper limb wearable exoskeleton based on epicyclic gear trains is proposed in this paper. This new structure has 6 DOFs, a three epicyclic gear train, and sections that compose the exoskeleton system. The revolution motion and the spinning motion of the planet wheel forms a 2-DOF coupled motion produced by the driving wheel and the driving link. The upper arm, forearm, and palm of the user’s upper limb are driven by corresponding planet wheels, and each planet wheel is supported and driven by two parts, which is similar to the parallel mechanism. The traditional gear transmission structure is replaced with a cable transmission system. The principle of the cable transmission system is the same as the gear transmission structure. However, it does not transmit torque using the meshing force between gears, rather, it uses cables on wheel faces which results in a quiet process, higher accuracy, and smoother transmission. The main body of the exoskeleton is rigid which can be controlled more easily than the parallel mechanism with flexible links. Further, we design a pre-tensioner to ensure the reliability of cable-driven mechanisms.

2.Mechanical design

2.1DOF selection and Denavit-Hartenberg parameters

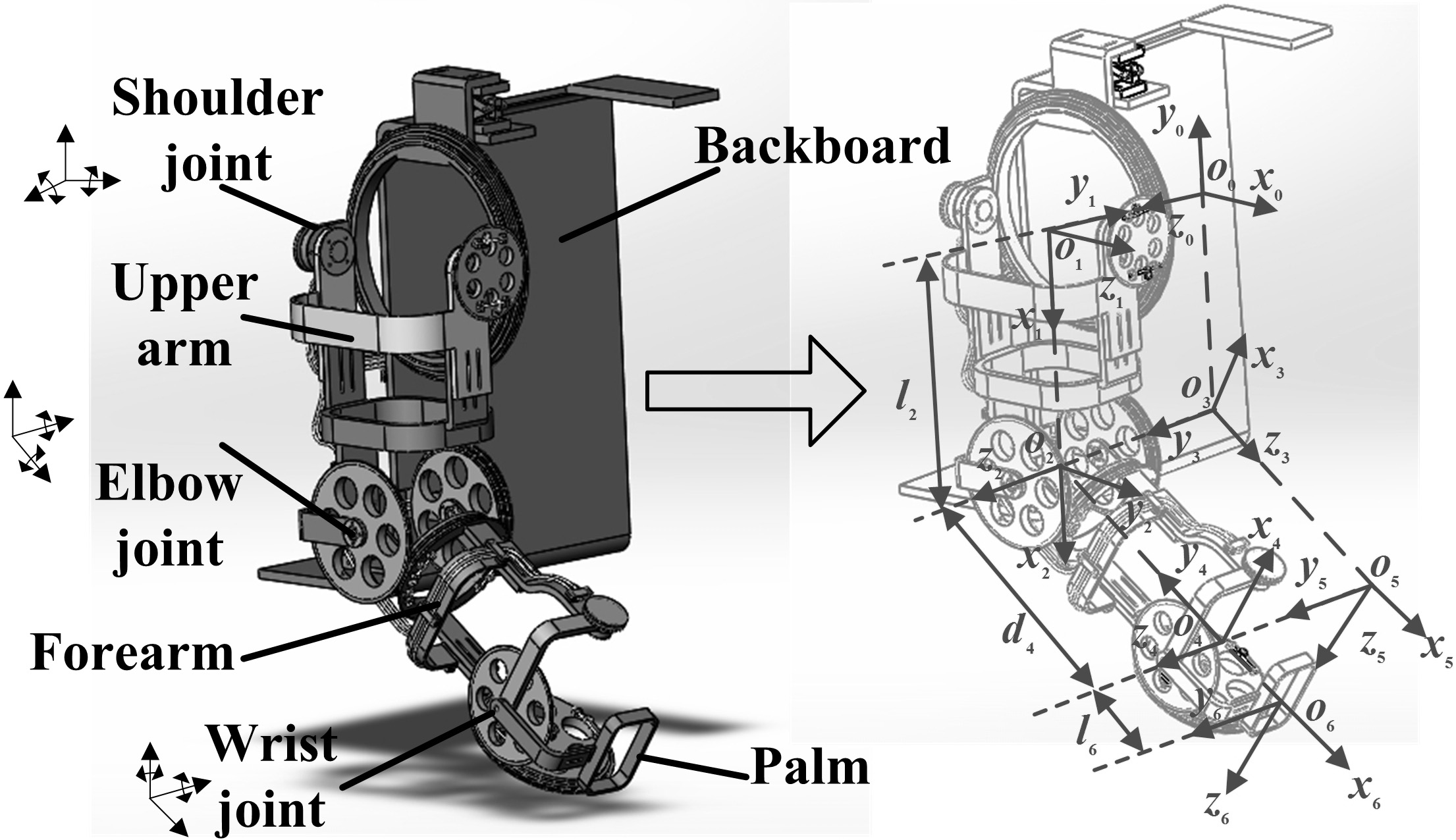
The shoulder internal/external rotation DOF is used less frequently than other DOFs [2]. The exosystem is composed of three epicyclic gear trains sections, ignoring the shoulder internal/external rotation DOF. As it has a large workspace, the exoskeleton could assist those with physical disabilities with most of the movements associated with ADLs as illustrated in Fig. 7 in section three. The model of the exoskeleton is shown in Fig. 1. All DC motors are placed on the backboard with an additional forces transmission system adapted from [3].

The Denavit-Hartenberg parameters of the exoskeleton listed in Table 1 can be obtained using the connecting rod coordinates established in Fig. 1. The range of the variable is based on Table 1. Here, l2 is the length of upper arm, d4 is the length of the forearm, and l6 is the distance between the wrist joint and the end point.

Table 1

The Denavit-Hartenberg parameters of the exoskeleton

Link i	Variable θi	αi	li	di	Range of variable θi
1	θ1	-90∘	0	0	-140∘	∼ 90∘
2	θ2	90∘	l2	0	-180∘	∼ 40∘
3	θ3	90∘	0	0	90∘	∼ 230∘
4	θ4	-90∘	0	d4	-90∘	∼ 90∘
5	θ5	90∘	0	0	-117∘	∼-63∘
6	θ6	0∘	l6	0	-73∘	∼ 70∘

Table 2

Comparison between CABexo and existing exoskeleton systems

Exoskeleton systems	DOF	Driving type	Configuration	Motor arrangement
CABexo	6	DC motor(cable)	Similar parallel	Backboard
ARMin [13]	6	DC motor	Series	Corresponding joint
RUPERT III [2]	5	Pneumatic muscle	Series	Corresponding joint
CAREX [9]	7	DC motor(cable)	Parallel	Backboard
IKO [3]	5	DC motor	Series	Backboard

Figure 1.

The 6-DOF upper limb exoskeleton model.

2.2The shoulder joint and the wrist joint parts of the exoskeleton

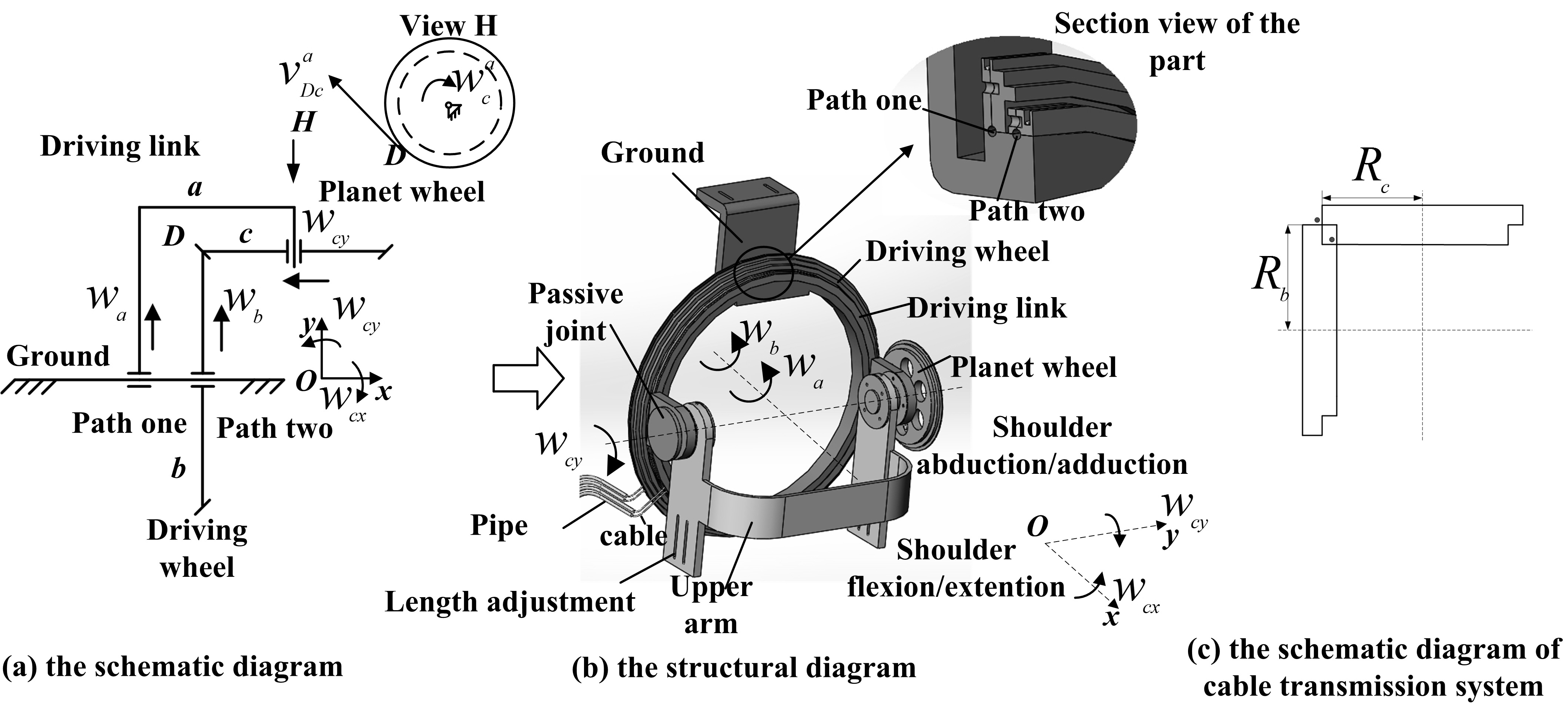
The shoulder joint part of the exoskeleton driving upper arm rotates with the shoulder joint and has two DOFs – the shoulder flexion/extension DOF and the shoulder abduction/adduction DOF. The schematic diagram of this part is shown in Fig. 2a and the structural diagram is illustrated in Fig. 2b. The radiuses of the driving wheel b and planet wheel c are Rb and Rc, respectively. The angular velocities of the driving link, driving wheel, and planet wheel are wa, wb and wc, respectively. The actual motion of the planet wheel is generated by the driving link and the driving wheel, which is composed of the revolution motion wc⁢x and the spinning motion wc⁢y. The angular velocity of the planet wheel relative to the driving link is represented by wca, which is equal to wc⁢y. It is clear that wc⁢x is equal to wa. This can be expressed in the following formula:

(1)

wc⁢x=wa,wc⁢y=wca

Figure 2.

The shoulder joint part of exoskeleton.

To obtain wca, we can virtually add a motion – wa which is in the opposite direction of the driving wheel of this epicyclic gear train. Then, the absolute linear velocity of point D on the planet wheel c represented by vD⁢ca should be equal to the absolute linear velocity of point D on the driving wheel b represented by vD⁢ba. This allows the angular velocity of planet wheel relative to the driving link to be easily obtained. Then, Eq. (1) can be re-expressed as Eq. (3).

(2)

vD⁢ca=vD⁢ba=Rb⁢(wb-wa),wca=vD⁢ca/Rc

(3)

wc⁢x=wa,wc⁢y=wca=Rb⁢(wb-wa)/Rc

If the direction wa or wb is in the opposite direction from that shown in Fig. 2a, the value of wa or wb in Eq. (3) is negative, and the direction of wc⁢y in view H will be clockwise if the value of wca in Eq. (3) is positive.

The traditional gear transmission structure is replaced with cable transmission system as shown in Fig. 2c. As the cable is a flexible one-way transmission body, each DOF of the cable-driven mechanism can be accomplished by two cables placed on a wheel with a phase difference of 180 degrees. The driving wheel and the planet wheel should be two-stage as shown in Fig. 2c.

As it is hard to process large rolling bearings, we adopt a similar structure as shown in the sectioned view of the part in Fig. 2b. Steel balls with the same diameter, are placed in path one and path two; the steel balls function as simplified rolling bearings. The driving wheel and the driving link are each divided into two parts making it convenient to place the steel balls.

The wrist joint part of the exoskeleton is similar to the shoulder part. It has two DOFs – the wrist flexion/extension DOF and the wrist radial deviation/ulnar deviation DOF. A detailed diagram of the wrist joint part of exoskeleton is shown in Fig. 3. The angular speeds of the revolution and rotation of the planet wheel can be obtained by Eq. (3).

Figure 3.

The wrist joint part of the exoskeleton.

2.3The elbow joint part of the exoskeleton

The elbow joint part of the exoskeleton has two DOFs: the elbow flexion/extension and the forearm supination/pronation. The schematic diagram of the elbow joint part of exoskeleton is shown in Fig. 4. The motion of the planet wheel driving the forearm of the user to rotate with the elbow joint is controlled by two driving wheels. The radiuses of the driving wheel a, b, and planet wheel c are Ra, Rb and Rc, respectively, and the angular velocities are wa, wb, and wc, respectively. The angular velocities of the planet wheel relative to the driving wheels a and b are represented by wca and wcb, respectively. According to the angular velocity composition theorem of intersecting axes, we can obtain the following relationships in Eq. (4). By projecting the vector equation Eq. (4) to the x axis and y axis, wc⁢x and wc⁢y can be obtained based on Figs 4 and 5. Below, the situation presented in Fig. 5a is used as an example:

(4)

wc→=wa→+wca→=wb→+wcb→

(5)

wc⁢x=wa-wca⁢cos⁡δ1=wb-wcb⁢cos⁡δ3,wc⁢y=0+wca⁢sin⁡δ1=0-wcb⁢sin⁡δ3

Figure 4.

The elbow joint part of the exoskeleton.

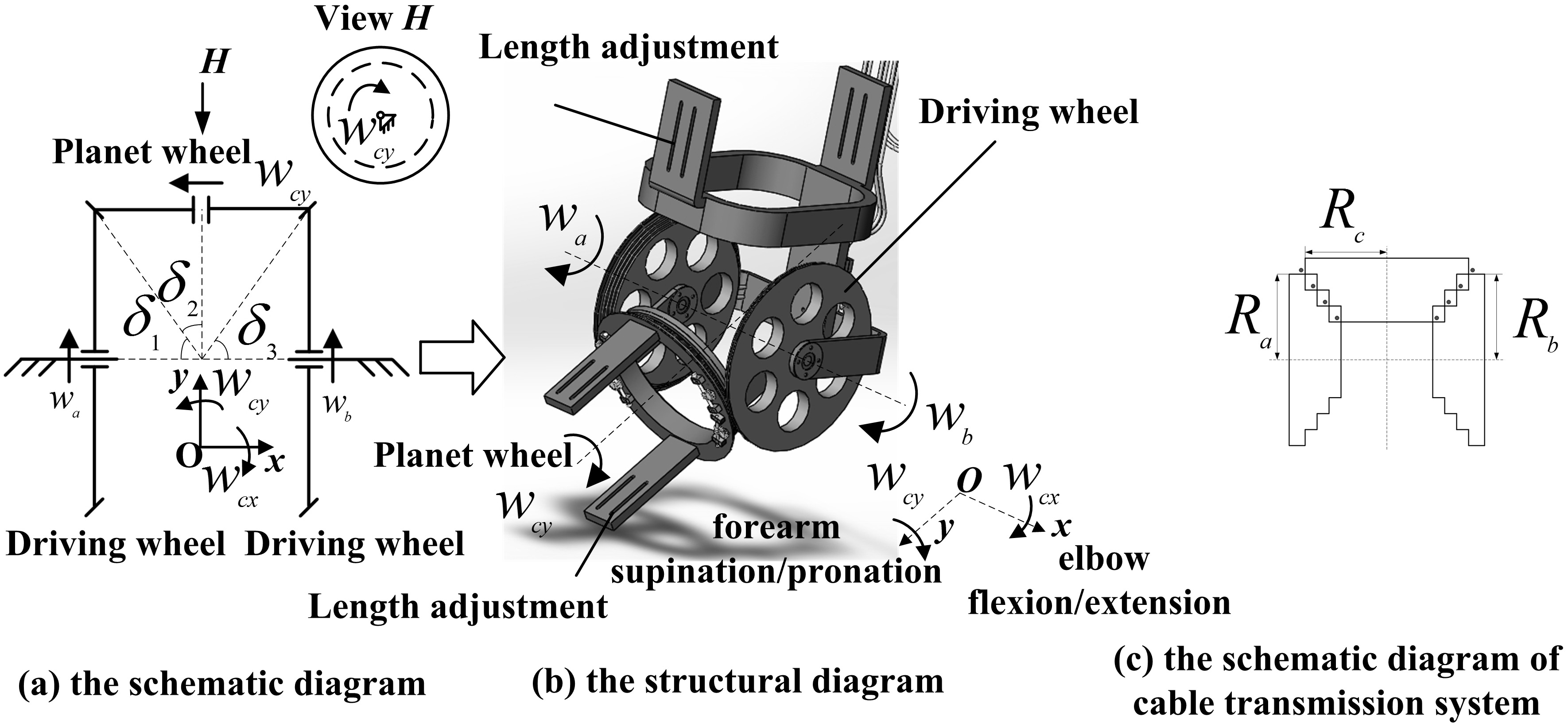
Figure 5.

The projection of the angular velocities.

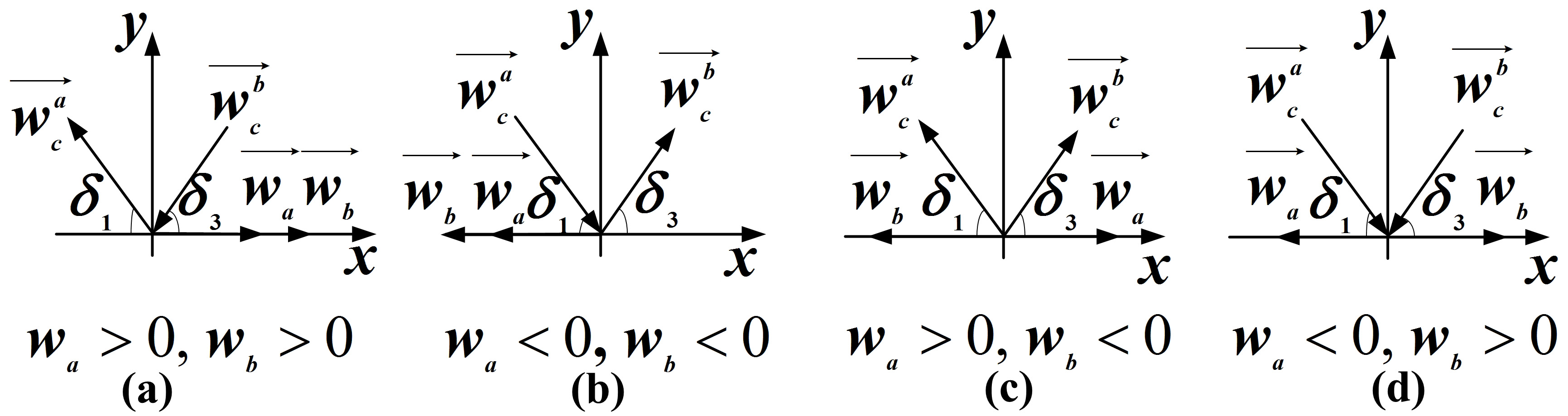
Figure 6.

The arrangement of pre-tensioner.

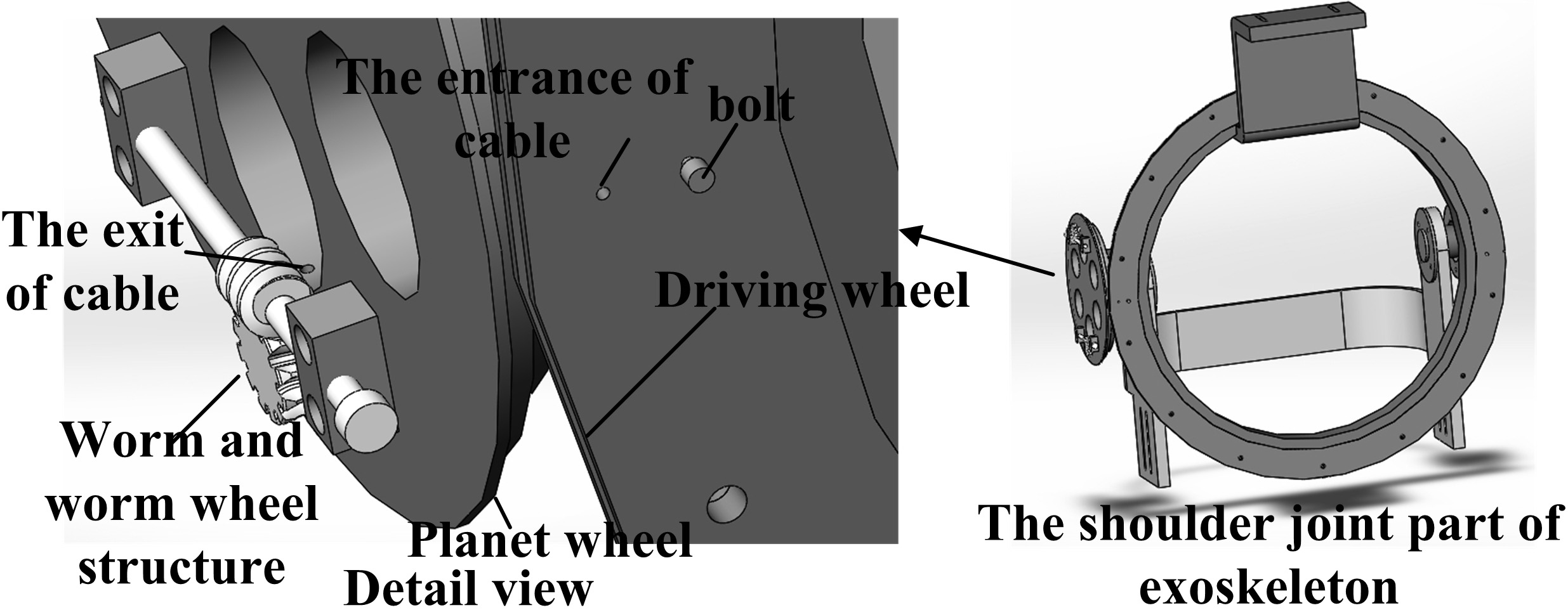
Figure 7.

The workspace of the exoskeleton.

According to Fig. 4a and c, the relationship between δ1, δ3 and Ra, Rb, Rc can be expressed as follows:

(6)

Ra=Rb,δ1=δ3,cot⁡δ1=cot⁡δ3=Rc/Ra

Then, Eq. (5) can be re-expressed as follows:

(7)

wc⁢x=(wa+wb)/2,wc⁢y=Ra⁢(wa-wb)/2⁢Rc

In the situations illustrated in Fig. 5b, c and d, wc⁢x and wc⁢y can also be obtained by Eq. (7). In Eq. (7), if the direction of wa or wb is opposite from the direction shown in Fig. 4a, the value of wa or wb is negative. The direction of wc⁢y in view H will be clockwise if the value of wc⁢y is positive and the direction of wc⁢x will be the same as wa, as shown in Fig. 4a, if wc⁢x is positive. The driving wheels and the planet wheel are in four-stages with incremental diameters as shown in Fig. 4c.

3.Forward kinematics and workspace

According to Fig. 1 and Table 1, the transformation matrixes can be obtained using the following equation:

Where s⁢θi and c⁢θi represent sine of θi and cosine of θi, respectively. l2 is the length of the upper arm, d4 is the length of forearm, and l6 is the distance between the wrist joint and the end point. The workspace of the exoskeleton illustrated in Fig. 7 can be obtained using Eq. (8), and the static workspace of the exoskeleton is reasonably large in order to meet the demands of assisting the aged and disabled to complete ADLs.

4.Analysis of the transmission characteristics of the cable transmission system

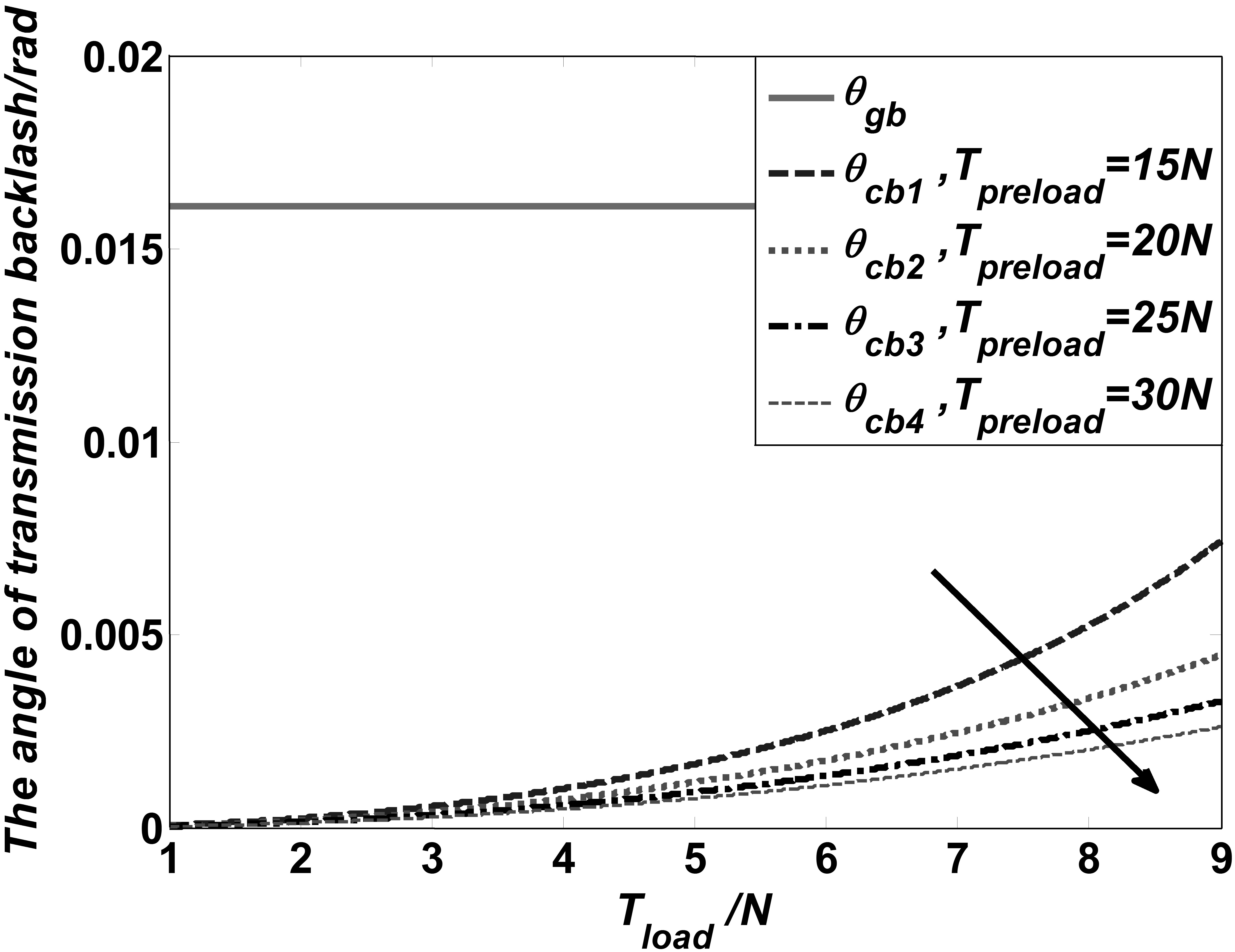
In this section, the transmission characteristics of the cable transmission system are compared with the traditional gear transmission structure. The angle of transmission backlash is a primary indicator reflecting transmission characteristics, which is well if the angle of transmission backlash is small enough [11, 12]. The angle of transmission backlash of the cable transmission system is obtained as follows:

Where θc⁢b and θg⁢b represent the angles of transmission backlash for the cable transmission system and the gear transmission system respectively. T𝑙𝑜𝑎𝑑 is the load force, T𝑝𝑟𝑒𝑙𝑜𝑎𝑑 is the preload force, r1 is the radius of the driving wheel, r2 is the radius of driven wheel, G is the tension rigidity, and μ represents the friction coefficient. Es⁢s⁢1 and Es⁢s⁢2 are the upper deviation of tooth thickness of the driving wheel and driven wheel. Ts⁢1 and Ts⁢2 are the tolerance of tooth thickness of the driving wheel and driven wheel. Es⁢Δ⁢1 and Es⁢Δ⁢2 are the compensation parts of the manufacturing error of the driving wheel and driven wheel. αn is the normal pressure angle.

If the wrist joint part is taken as an example, the value of some of the parameters are chosen as follows: T𝑙𝑜𝑎𝑑 is a variable, and other parameters can be obtained by referring to related tables in [13]. Then, the comparison of θc⁢b and θg⁢b is shown in Fig. 8. The results show that θc⁢b is much less than θg⁢b and θc⁢b decreases when the preload force increases, which means that the cable transmission system has better accuracy than the traditional gear transmission system. The cable transmission system transmits energy by static friction between the cable and wheel avoiding oscillation, which exists in the traditional gear transmission system on account of the gear meshing effect; therefore, the cable transmission system is quieter and has smoother transmission than the traditional gear transmission system.

Figure 8.

The angle of transmission backlash.

5.Discussion and conclusion

In this paper, a newly-designed cable-driven upper limb exoskeleton (CABexo) based on epicyclic gear trains is described. Comparisons between CABexo and some of the existing exoskeleton systems show that it is able to meet the movement needs of most disabled and elderly individuals. As CABexo is a cable-driven exoskeleton, the transmission system is smoother and more stable than ARMin, RUPERT III, and IKO. The revolution motion and the spinning motion of the planet wheel form a 2-DOF coupled motion in CABexo. The upper arm, forearm, and palm of the user’s upper limb are driven by corresponding planet wheels, and, in a parallel mechanism, each planet wheel is supported and driven by two parts. Although the CAREX exoskeleton system is a cable-driven system, it is harder to control than CABexo with a parallel mechanism. In CABexo, all DC motors are placed on the backboard with an additional force transmission system, which makes the weight supported by the user’s upper limb lighter than ARMin and RUPERT III. Additionally, a pre-tensioner based on the self-locking characteristics of the worm and worm wheel structure is considered in order to ensure the reliability of the cable-driven mechanisms in CABexo. Future work will optimize the transmission forces system and design a reasonable control system.

Conflict of interest

None to report.