A new generic method to improve machine learning applications in official statistics
Abstract
The use of machine learning algorithms at national statistical institutes has increased significantly over the past few years. Applications range from new imputation schemes to new statistical output based entirely on machine learning. The results are promising, but recent studies have shown that the use of machine learning in official statistics always introduces a bias, known as misclassification bias. Misclassification bias does not occur in traditional applications of machine learning and therefore it has received little attention in the academic literature. In earlier work, we have collected existing methods that are able to correct misclassification bias. We have compared their statistical properties, including bias, variance and mean squared error. In this paper, we present a new generic method to correct misclassification bias for time series and we derive its statistical properties. Moreover, we show numerically that it has a lower mean squared error than the existing alternatives in a wide variety of settings. We believe that our new method may improve machine learning applications in official statistics and we aspire that our work will stimulate further methodological research in this area.
1.Introduction
National statistical institutes (NSIs) currently apply many different types of machine learning algorithms. Classification algorithms are one of the most popular types of algorithms because publishing aggregate statistics of (sub)groups in a population is one of the main tasks of national statistical institutes. Classical examples of classification algorithms are logistic regression and linear discriminant analysis, but also new innovative algorithms have been introduced over the last decades, like additive models, decision trees and deep learning [1]. Classification algorithms are optimized to minimize the summed loss of individual units, such that each unit has a high probability to be classified correctly. However, classifying units individually can lead to biased results when generalizing these individual units to aggregate statistics, like a proportion of the population [2, 3]. The cause of the biased results are imbalanced errors.
Before we show how generalizing units to aggregate statistics can lead to bias, we first emphasize the difference between a classifier and a quantifier. A classifier is a model that labels each unit to a class and a quantifier is a model that counts the number of units labelled to a class. Quantifiers can use classifiers in their model by counting the number of labels that the classifier has assigned to each class. Classifiers and quantifiers are imperfect because classification algorithms can mislabel some units. Each unit has a classification probability of being labelled correctly by the classification algorithm. A well-performing classifier has high classification probabilities for each labelled unit. A well-performing quantifier is not particularly defined by the number of mislabeled units, but by how the number of mislabeled units are distributed among the classes. In almost all cases, the number of mislabeled units among the classes don’t cancel each other out and as a consequence, bias will occur. The bias that occurs from imbalanced classification errors is called misclassification bias.
Misclassification bias cannot simply be solved by improving the accuracy of the classification algorithm. Moreover, a more accurate classifier can increase misclassification bias. For example, classifier A with 10 false positives and 10 false negatives is a worse classifier than classifier B with 9 false positives and 5 false negatives. However, when aggregating the results of both classifiers to a quantification, classifier A turns out to have less misclassification bias than classifier B and is, therefore, a better quantifier. Classifier A has less misclassification bias than classifier B because the number of mislabeled units in classifier A are equally distributed among both classes, while the number of mislabeled units in classifier B are unequally distributed among the classes. Therefore, improving a classifier is not the solution to reduce misclassification bias [3, 2].
We illustrate misclassification bias more extensively using an image-labelling example. The example shows us why using a standard approach for aggregating classifications from machine learning classifiers leads to problems. Suppose that a local government wants to estimate the number of houses in a certain area with solar panels on their rooftops. There is no register whether a house has a solar panel installation or not. It is an expensive and time-consuming task to manually label each rooftop, so the government decides to use satellite images combined with a classification algorithm to quickly label each house whether it has solar panels or not. Our target population consists of 10,000 houses, whereof 1,000 houses with solar panels and 9,000 without solar panels. Thus, the true proportion of houses with solar panels is 10%. The target variable is the proportion of houses with solar panels installation. Assume that the classifier can predict the rooftop images fairly accurate: 98% of the houses with solar panels are classified correctly (sensitivity) and 92% of the houses without solar panels are classified correctly (specificity). The machine learning algorithm classifies then 98% of the houses with solar panels and 8% of the houses without solar panels as houses with solar panels. This aggregates to
Table 1
Confusion matrices of the target population and test set. Grey values are unknown in practice
| Estimate | |||
|---|---|---|---|
| True | Class 0 | Class 1 | Total |
| Class 0 |
|
|
|
| Class 1 |
|
|
|
| Total |
|
|
|
| Estimate | |||
|---|---|---|---|
| True | Class 0 | Class 1 | Total |
| Class 0 |
|
|
|
| Class 1 |
|
|
|
| Total |
|
|
|
(a) Target population
(b) Test set
In the literature, several corrections methods exist to reduce misclassification bias of the proportion of units labelled to the class of interest, i.e. the base rate. We compared statistical properties of the five most-used correction methods in a previous paper [4]. The correction methods contain information from the target population and a test set, see Table 1. The target population consists of
However, the result from that paper does not generalize to time series. In other words, the results could not be applied for populations where the base rate changes over time. The target populations that are interesting for national statistical institutes, where we produce statistics on a monthly, quarterly or annual basis, change from period to period. The solar panel case is a good quantification example for time series: households can place solar panels on their roofs or displace them during a certain period. Moreover, the proportion of houses with solar panels is an interesting statistic concerning the government’s aims of renewable energy. The drift that occurs when the target population changes over time, is called concept drift [5]. In this paper, we assume a special case of concept drift called prior probability shift. Prior probability shift assumes that the base rate of a target population changes over time, but that the classification probabilities of units conditioned on their true label remain constant over time [6].
The most effective, but most costly and time-consuming solution to deal with prior probability shift, is to construct a new test set for each period. A more cost-efficient solution is to construct a test set and use the same test from period to period. As a consequence, we then cannot assume that a test set is a simple random sample of the target population when the base rate changes over time. Therefore, new expressions for bias and variance are needed to evaluate the MSE of the five correction methods. These expressions were previously computed by [7]. They concluded that none of those estimators performs consistently well under prior probability shift.
The main contribution of this paper is a new generic method to correct for misclassification bias when dealing with prior probability shift. We will refer to the resulting estimator as the mixed estimator because it combines the strengths of two existing estimators. We will derive (approximate) closed-form expressions for the bias and variance of the mixed estimator. Moreover, we will numerically compare the mixed estimator’s MSE with the classical methods.
The remainder of the paper is organized as follows: in Section 2, we introduce the problem and assumptions and we recap the properties of the original correction methods. Section 3 introduces the mixed estimator. Moreover, we will compare the mixed estimator with the original correction methods. Section 4 contains a discussion and conclusion of this paper.
2.Model under prior probability shift
In this section, we introduce the quantifier under prior probability shift. We use the same mathematical approach as in [4] and therefore use the same parameters and assumptions. Before we dive into the mathematical expressions, we briefly discuss the terminology used in the later sections. The target population has
In this paper, we allow that the base rate can change over time. In other words, we allow for a nonzero prior probability shift. Therefore, we introduce the following notation. First, we need to distinguish a target population
Before we describe the differences between [4] and [7], we briefly introduce the correction methods. First, the baseline estimator (
Table 2
Overview of the estimators without prior probability shift from [4]
| Estimator | Equation | Bias | Variance |
|---|---|---|---|
| Baseline |
| No | Large |
| Classify-and-count |
| Large | Very low |
| Subtracted-bias |
| Medium | Low |
| Misclassification |
| Very low | Large |
| Calibration |
| No | Medium |
Table 3
Overview of the estimators under prior probability shift from [7]
| Estimator | Equation | Bias | Variance |
|---|---|---|---|
| Baseline |
| Large | Large |
| Classify-and-count |
| Large | Very low |
| Subtracted-bias |
| Medium | Low |
| Misclassification |
| Very low | Large |
| Calibration |
| Medium | Medium |
3.Mixed estimator
In this section, we introduce a new estimator: the mixed estimator. The mixed estimator is a combination between the misclassification estimator [9] and the calibration estimator [10]. In [4, 7], we found that the calibration estimator is unbiased under a fixed base rate, but becomes biased under prior probability shift. The misclassification estimator has a higher variance, but the MSE remains fairly stable under prior probability shift. These two properties can be combined: as an initial starting point, we take the calibration estimator
(1)
To the best of our knowledge, this is the first paper where the mixed estimator is introduced. Therefore, the closed-form expressions for bias and variance that we have derived are new as well.
.
The variance of the estimator
(2)
Similarly, the variance of
(3)
Moreover,
.
The mixed estimator
(4)
The variance of
(5)
Proof: See sec:appendix.
From Theorem 1, we see that the mixed estimator has a bias of
In the first simulation study, we consider a class-balanced dataset (
Figure 1.
Simulation study to observe the change in prediction error under concept drift using boxplots. The calibration, misclassification and mixed estimator are compared given an initial base rate
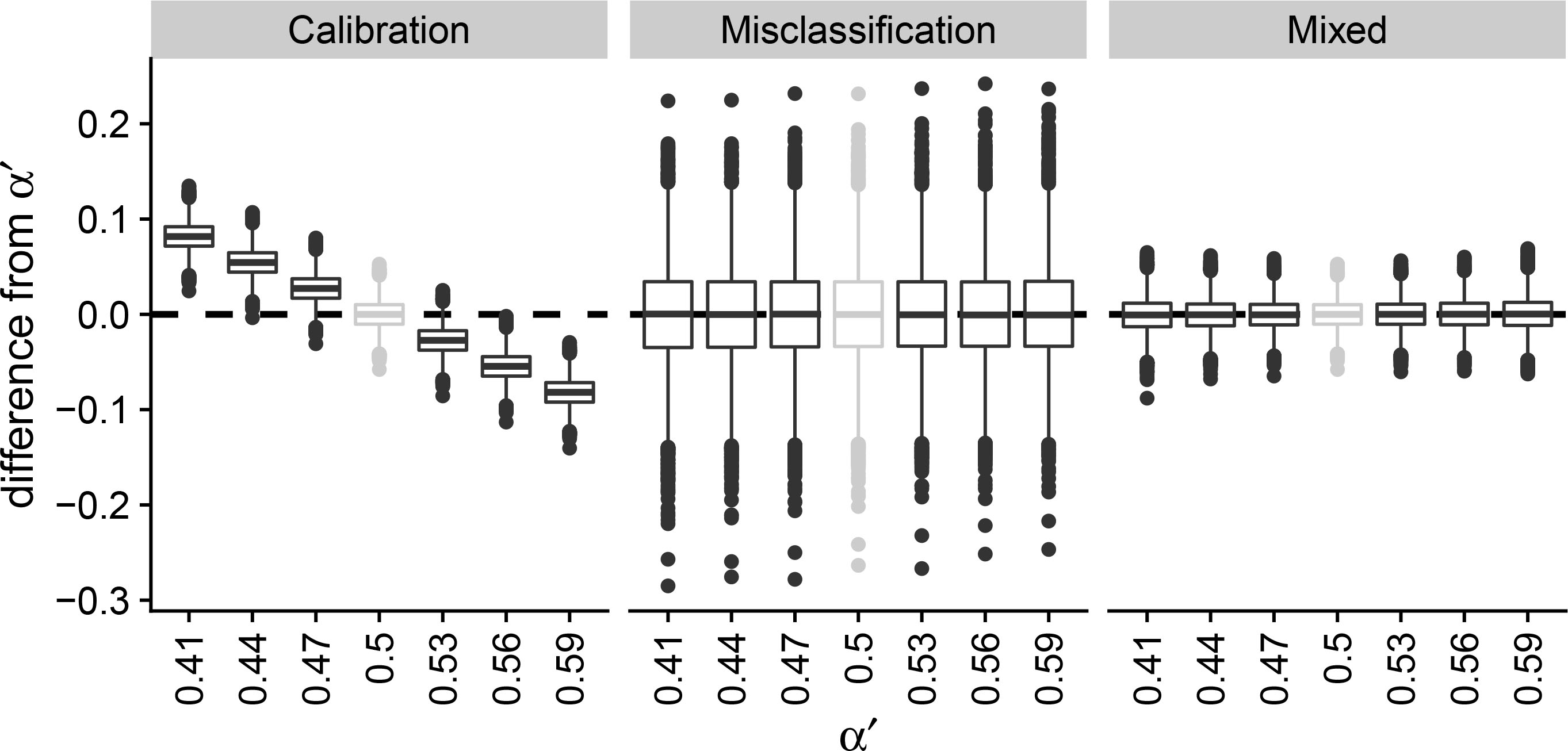
A situation where the mixed estimator does not work as well as expected, can be found in Fig. 2. We specify the following parameters:
Figure 2.
Simulation study to observe the change in prediction error under concept drift using boxplots. The calibration, misclassification and mixed estimator are compared given an initial base rate
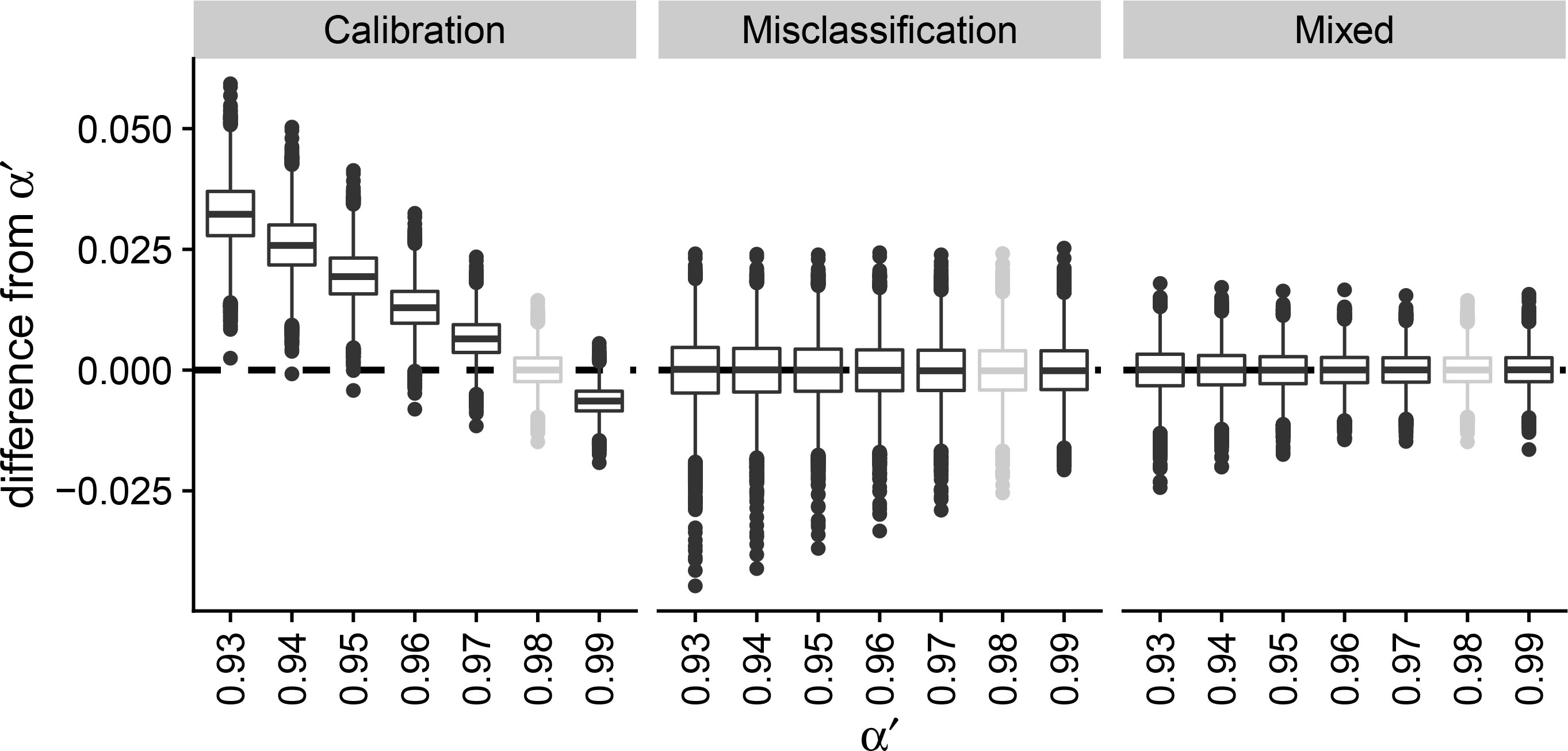
Figure 3.
Simulation study to observe the change in prediction error under concept drift using boxplots. The calibration, misclassification and mixed estimator are compared given an initial base rate
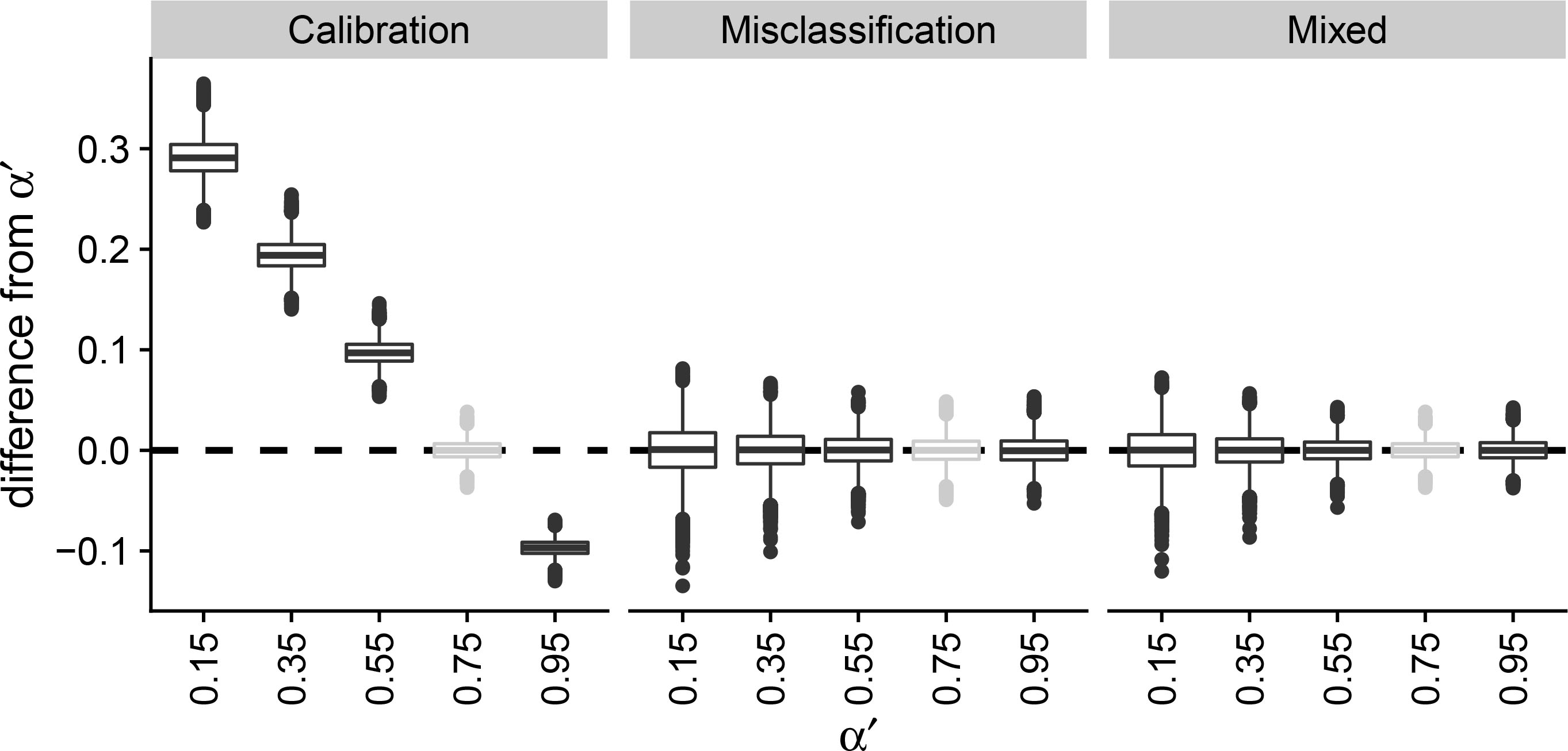
In the first two simulation studies, the misclassification estimator did not work properly, and we showed values of
4.Conclusion and discussion
We conclude that our mixed estimator outperforms the estimators currently available in the academic literature. The mixed estimator has less bias than the calibration estimator and less variance than the calibration estimator. The mixed estimator performs much better than the calibration estimator and the misclassification estimator when the variance of the misclassification estimator is large but consistent over time. Our results show that the mixed estimator outperforms both the calibration estimator and the misclassification estimator in any dataset and for any classification algorithm used.
Even though that the new mixed estimator performs better than the original correction methods, we still believe that the correction methods might be improved further. We could construct a new estimator by combining biased, but invariant correction methods. New research directions lay in combining the correction methods in such a way that both bias and variance of the new estimator will be consistently low.
The estimator could be extended for correction methods that can predict more than two classes. The downside is that the number of parameters increases quadratically and the quality measure should be adapted for multiple classes. A possible solution is to further elaborate the simulation studies, instead of computing closed-form mathematical expressions. A final extension that we recommend is allowing the classification probabilities to differ between the units within a group, see [8].
With this paper, we hope that we raised awareness that aggregating outcomes of machine learning algorithms can be very inaccurate, even if the algorithms have a high prediction accuracy. Furthermore, this paper
is an addition to the scientific literature on the theory of misclassification bias. Finally, we proposed a new generic method that can be used by NSIs to improve machine learning applications within official statistics.
References
[1] | Friedman JH, Hastie T, Tibshirani R, et al. The elements of statistical learning. vol. 1. Springer, New York; (2001) . |
[2] | Schwarz JE. The neglected problem of measurement error in categorical data. Sociological Methods & Research. (1985) . |
[3] | Scholtus S, van Delden A. On the accuracy of estimators based on a binary classifier. (2020) ; 202006. Discussion Paper, Statistics Netherlands, The Hague. |
[4] | Kloos K, Meertens QA, Scholtus S, Karch JD. Comparing correction methods to reduce misclassification bias. in: Artificial Intelligence and Machine Learning. Cham: Springer International Publishing; Baratchi M, Cao L, Kosters WA, Lijffijt J, van Rijn JN, Takes FW, eds, (2021) ; pp. 64-90. |
[5] | Webb GI, Hyde R, Cao H, Nguyen HL, Petitjean F. Characterizing concept drift. Data Mining and Knowledge Discovery. (2016) ; 30: (4): 964-994. |
[6] | Moreno-Torres JG, Raeder T, Alaiz-Rodríguez R, Chawla NV, Herrera F. A unifying view on dataset shift in classification. Pattern recognition. (2012) ; 45: (1): 521-530. |
[7] | Meertens QA, Diks CGH, Van Den Herik HJ, Takes FW. Understanding the output quality of official statistics that are based on machine learning algorithms; (2021) . |
[8] | van Delden A, Scholtus S, Burger J. Accuracy of mixed-source statistics as affected by classification errors. Journal of Official Statistics. (2016) ; 32: (3): 619-642. |
[9] | Buonaccorsi JP. Measurement error: Models, methods, and applications. Boca Raton, FL: Chapman & Hall/CRC; (2010) . |
[10] | Kuha J, Skinner CJ. Categorical data analysis and misclassification. in: Survey Measurement and Process Quality. Wiley; Lyberg LE, Biemer PP, Collins M, de Leeuw ED, Dippo C, Schwarz N, et al., eds, (1997) ; pp. 633-670. |
[11] | Knottnerus P. Sample survey theory: Some pythagorean perspectives. Springer Science & Business Media; (2003) . |
Appendices
Appendix
This appendix contains the proofs of the theorems presented in the paper entitled: A new generic method to improve machine learning applications in official statistics. Recall that we have assumed a population of size
It may be noted that the estimated probabilities
Preliminaries
Many of the proofs presented in this appendix rely on the following two mathematical results. First, we will use univariate and bivariate Taylor series to approximate the expectation of non-linear functions of random variables. That is, to estimate
(6)
The conditional variance decomposition follows from the tower property of conditional expectations [11]. Before we prove the theorems presented in the paper, we begin by proving Lemma 1.
Proof of Lemma 1 We approximate the variance of
The variance of
Finally, to evaluate
The second term is zero as before. The first term also vanishes because, conditional on the row totals
Note: in the remainder of this appendix, we will not add explicit subscripts to expectations and variances when their meaning is unambiguous.
Mixed estimator
In this section, we will prove the bias and the variance of the mixed estimator under concept drift. The mixed estimator is dependent on the calibration estimator at time 0, the misclassification estimator on time 0 and the misclassification estimator on time
Proof of Theorem 1 First, we will make a proof for the bias of the Mixed Estimator. The expression for the Mixed Estimator is:
(7)
The bias is defined as the difference between the expected value of the estimator minus the true value of the target variable:
(8)
Using Eq. (7), we can write out the expected value of the mixed estimator.
(9)
From [4], we already know that:
(10)
(11)
From [4], we used Taylor Series to approximate the expected value of
(12)
Now it only remains to calculate the expected values of the classify-and-count estimators.
(13)
(14)
(15)
Combining these expressions,
(16)
Combining Eqs (12) and (16) gives the expression that should be in the big expectation of Eq. (11).
(17)
Finalizing the proof given Eqs (8), (10) and (17).
(18)
Now it only remains to prove the variance of the mixed estimator. Recall that the mixed estimator can be written as
(19)
It clearly follows from Eq. (19) that the variance of this mixed estimator can be written as
(20)
From [4], we already know that the variance of the calibration estimator is equal to
(21)
The second term in Eq. (20) makes use of previous assumptions in this paper. We can say that
(22)
Assuming that
(23)
The expected value of the differences between the classify-and-count estimators is already computed in Eq. (16) and the variance term in Eq. (23) is already proven in [4]. This eases the derivation of the second term in Eq. (20).
(24)
Thus it remains to evaluate the covariance term in Eq. (20). By conditioning on the classify-and-count estimators
(25)
It can be proven that the second term of Eq. (25) is equal to zero. In Eq/ 10, we see that the expectation of the calibration estimator, given classify-and-count estimators, is equal to
(26)
We can derive an expression for the inner covariance, which is written as
(27)
The terms in Eq. (27) can be written in terms of the test set
(28)
We are able to evaluate both covariance terms with the same methods. We can condition on one of the row totals. Note that the other row total is also fixed, because we work with binary classifiers (
(29)
While we condition on the row totals, the other variables in the covariance functions are
with
(30)
(31)
we are able to compute first-order Taylor series approximations for these terms to obtain an approximation for
(32)
(33)
(34)
(35)
The approximation can be made with substituting
(36)
In order to use this approximation, we can use the following properties:
Substituting these elements gives
(37)
This expression simplifies to
(38)
Now that the inner covariance of Eq. (29) is computed, we can move on and calculate the inner expectations of Eq. (29). This can be done with a second-order Taylor series approximation.
(39)
(40)
(41)
(42)
Applying the Taylor rules for approximating an expected value and substituting
(44)
(45)
(47)
(48)
The next step is computing the outer expectation and the outer covariance of Eq. (29). The outer expectation can be approximated with a zero-order Taylor series.
(49)
Furthermore, it can be proven that the outer covariance of the two expectations is of
(50)
Let
(51)
(52)
If we substitute
(53)
(54)
It can be clearly seen that
(55)
Similarly,
and make a function dependent on
(56)
(57)
Accordingly, we can borrow the expectations from the previous covariance term. Therefore we end up with the following term:
(58)
This simplifies to:
(59)
The next step is computing the expected value of this expression.
(60)
The covariance between the expectations is again of a negligible low order, so the covariance term can be written as:
(61)
Now that we have obtained the two conditional covariance in Eqs (55) and (61), we can substitute these terms in Eq. (28).
(62)
Combining Eqs (26), (27) and (62), we can compute
(63)
Combining all elements gives the total variance of the mixed estimator.
(64)
This concludes the proof of the bias and variance of the mixed estimator. Note that all terms of



